Introduction

While many powerful imaging techniques are being used in neuroscience, extracellular recording remains the only choice that provides time resolution of activities in the brain at the single-neuron level. However, multiple single-unit extracellular recordings are useful only when the action potentials generated by different neurons can be classified by their particular waveforms, or spikes, from the digital signals detected by electronic instruments.

A well-chosen reduced feature set (RFS) will largely increase both the efficiency and accuracy of classifications. Suppose that each action potential, once detected, is sampled into a digital signal, or spike event. We collect N such events, each with λ samples, namely \( {\mathbf{v}}_{\text{n}} = \left( {v_{1}^{n} ,v_{2}^{n} , \ldots ,v_{\lambda }^{n} } \right) \) for n = 1, 2,…, N. The idea of an RFS is to choose ε positions (indices) 1 ≤ s 1 < s 2 < … < s ε ≤ λ such that ε is far less than λ and the (reduced feature) set,

$$ \left\{ {v_{S_1}^{n} ,v_{S_2}^{n} , \ldots ,v_{S_\varepsilon }^{n} \left| {{\text{n}} = 1,2, \ldots ,{\text{N}}} \right.} \right\}, $$

is good enough to classify the N events into K clusters. In a pioneering work on RFS, Dinning and Sanderson [1] selected features that independently maximize a distance between cluster means and minimize within-cluster variances. The features are far apart because of the requirement that \( \left| {si - sj} \right| \ge 4. \) They also made the assumption that the clusters have equal a priori probabilities; that is, each cluster has roughly N / K events. The K-means clustering algorithm [3] is applied to a feature set, and the number of clusters is indicated by an F-ratio criterion. They showed in two experiments with N around 50 and λ  = 34 that two and four clusters (K = 2, 4) were determined by three and four features (ε = 3, 4), respectively. Salganicoff et al. [6] presented an improved criterion that selects features according to their variance weighted by the distance from previously chosen positions. Their experiments were done with N around 100 and λ = 64, and three or more clusters were satisfactorily determined by six to eight features.

In a similar spirit with RFS, one may apply clustering algorithms on the first few components of the principal component analysis (PCA) of the events; see, for instance, the work of Eggermont et al. [2]. In order to make the clustering procedure more manageable, one of the main ideas is to reduce the dimension, and RFS and PCA are the most available means for this purpose. Recently, we have seen wavelet-based spike classifiers (WSCs) make their entrance into this field. For instance, Letelier and Weber [5] selected the few wavelet coefficients of the events that reveal clear signatures of spikes, and Hulata et al. [4] used wavelet packets for the same purpose.

The fundamental reason that WSCs work is that wavelet coefficients extract the signatures of the spikes. The wavelet coefficients are essentially the weighted differences of the averaged input data. But the averaging process would contrarily smooth out the signals. So WSCs actually reveal that the signatures are richer in differentiations rather than in the spikes themselves. This observation motivated us to use the finite differences of signals as the means to directly extract features from the events, that is, take the differentiation without prior smoothing. The result is the minimax reduced feature set (mRFS) method that we present in the next section.

Methods

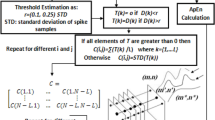
The mRFS method consists of two steps: (1) calculate the finite differences of the events to a pre-determined order, ρ-1, and (2) select RFS (two indices only) by minimum versus maximum two-dimensional plots (the mRFS plots). As only a small number of plots are required to select the RFS, they can be arranged on one screen panel to make effective observations.

To simplify the notation, we drop index n and denote an event by v = (v 1, v 2,…, v λ), of N such events. The finite difference of v of order k is denoted by D k v = (w 1, w 2,…, w λ) with

$$ w_{l} = \sum\limits_{j = 0}^{k} {\mathop {\left( { - 1} \right)}\nolimits^{j} } \mathop C\nolimits_{j}^{k} \mathop v\nolimits_{l - j} ,\quad l = 1,2, \ldots ,{{\uplambda}}, $$

where C k j is the combinatorial number \( k!/\left( {j!\left( {k - j} \right)!} \right). \) It is a convolution of event v and the finite difference coefficients \( \left( { - 1} \right)^{j} C_{j}^{k} . \) Event v is padded by constants when v l-j is out of range.

In Fig. 1, we show a plot of four events along with their differences of order 1, 2, and 3. Observe that the waveforms become increasingly separated as the order of difference grows. This is what we mean by “extracting the signatures” of the spikes.

Fig. 1
figure 1

Plots of four events (origin, k = 0) and their finite differences of order 1, 2, and 3 (k = 1, 2, and 3). Observe that the waveforms are separated further by the finite difference plots

Full size image

Then we prepare for the mRFS plots that allow an operator to select the features. Let p k be the index where most of the signals in D k v reach their minimum, and q k be the index where most of the signals in D k v reach their maximum. For each p k and q l, for 0 ≤ k, ℓ ≤ ρ−1, we make a (D k v) pk versus (D l v) ql plot. If we take finite differences up to order ρ−1, there are ρ 2 plots corresponding to each choice of k, ℓ = 0, 1,…, ρ−1 with N dots on each plot. A reasonable choice is ρ = 4, and there are 42 = 16 mRFS plots. In this case, one can easily arrange the plots on one screen and make a clear and confident decision based on the scatter patterns in the plots. An operator inspects the mRFS plots and chooses one with the most plausible number of clusters and whose clusters are the best separated. The (two) indices that comprise the “chosen” mRFS plot are the features we are looking for, and the spike templates are determined according to the clusters. See examples in the next section.

All computations in this article were performed by Matlab 6.5 running on an Intel PC.

Results

For a numerical simulation, we produce three types of test events by contaminating four typical artificial spikes with noise signals cut from real experiments (obtained from a published study by Tsai et al. [7]). The four artificial spikes are shown in the middle of Fig. 2. Let m be the magnitude of the minimal position of the smallest spike. In types 2SD, 3SD, and 4SD, we scale the noise such that the standard deviation is 1/2, 1/3, and 1/4 of m, respectively. To make a 10-s simulation signal, we add 1,600 artificial spikes (400 each) with random positions to each type of noise signal. Letting s be the standard deviation of the simulation signal, we run a spike detection algorithm that captures spikes when the “amplitude” is over 2 s. The detected spikes are aligned with their lowest positions. For instance, the algorithm has detected 1,320 spikes for the 3SD case, and their superimposed waveforms are shown on the right of Fig. 2. As we can see on the lower part of Fig. 2, some artificial spikes are not detected, and some noise signals are mistakenly included.

Fig. 2
figure 2

Upper: 1,600 superimposed noise signals cut from biological experiments (left). Four artificial spikes with typical waveforms (middle). The superimposed detected spikes in the 3SD case, aligned with their lowest positions (right). Lower: For each type of simulation signals, the total number of detected spikes, and a classification of what is really detected

Full size image

With ρ = 4, we present all 16 mRFS plots for each type of test event in Fig. 3. For instance, the plot title “2 vs. 0” means the plot of \( {(D_{2}{\mathbf{v}})_{p_{2}}}\) vs. \( {(D_{0}{\mathbf{v}})_{q_{0}}};\) that is, each event, v, is represented by one dot (x, y), where x is the entry of D 2 v at position p 2 and y is the entry of D 0 v = v at position q 0. It is clear that some scattering patterns stand out from the others with four clear clusters.

Fig. 3
figure 3

Sixteen mRFS plots (all of them) for each type of test event. Those with four clear clusters are marked by grey backgrounds

Full size image

Using the test events of the three types described in Fig. 2, we compare the performance of mRFS with RFS, WSC, and PCA. For the RFS method with two features, we make all ( 322 ) = 496 scatterplots for each pair of indices and choose those with four clusters by inspecting all of the plots. For the WSC method, we use the so-called Daub4 orthonormal wavelet (with eight coefficients) to perform the discrete wavelet transformation for each event. After the transformation, there are still 32 elements at five scales. We choose those with four clusters by inspecting all of the 496 scatterplots for each pair of transformed elements. Again, for the PCA method, we choose those with four clusters by inspecting all of the 496 scatterplots for each pair of principal components. In Table 1, we display the number of four-cluster plots out of the total number of scatterplots for each type of test event. Although the mRFS and other methods all failed to separate four-cluster plots under higher noise level (2SD), the mRFS shown the best efficiency among these methods under lower noise levels (3SD and 4SD).

Table 1 For each type of test event, and for each of the mRFS, WSC, RFS, and PCA methods, we list the total number of scatterplots (on the denominator) and the number of plots that show four clear clusters (on the numerator)
Full size table

Once the number of classes is determined and the two indices that made the “best” scatterplots are known, any clustering algorithm can be applied to the set of two indices for the actual classification. For instance, the Matlab function fcm() in the Fuzzy Logic Toolbox is a robust implementation of the Fuzzy C-Means clustering algorithm. For the test events, we applied fcm() to the two-index sets that produced four-cluster plots and estimated the accurate rates of each case. It can be seen on Table 1 that if only two features or components are allowed, the mRFS outperforms the other three methods under 3SD and 4SD noise conditions.

We also used real experimental data to show the practicality of this method. These spikes were recorded from the primary sensorimotor cortex of a rat (also obtained from the experimental data of Tsai et al. [7]). As shown in Fig. 4, which is similar to the numerical simulations, the best mRFS plot screened from 16 plots shows more distinct clusters than the other three best ones screened from 496 plots of the WSC, RFS, or PCA methods in each case. The test with real data indicates the merits of better sorting quality and less labor using the mRFS method.

Fig. 4
figure 4

A comparison of the performances of mRFS, WSC, RFS, and PCA methods on real neuronal spikes. The superimposed spikes consisted of 8,910 spikes; the width of each waveform is 1.6 ms, which covers the entire spike. The plot of mRFS was chosen from 16 plots, while the plots of the other three methods were chosen from 496 plots. Notice that the mRFS plots display more-distinct clusters in this case

Full size image

Discussion

Since an event consists of spike and noise, the finite difference applies to both parts of the event. If the process “magnifies” the spike, it should do the same thing to the noise. It seems only reasonable that the effects would cancel each other out. In general, this is true. In the particular situation of typical spike sorting, we are fortunate to see that the “signatures” of typical spikes are magnified more than the variances of noise. This is the essential way by which the mRFS method works. We explain this issue by the following mathematical model.

Let v = p + x where p is the spike and x is the noise modeled by a random variable with a mean of 0 and standard deviation of σ. By the linearity of finite differences, we have D k v = D k p + D k x. Here x = (x 1, x 2,…, x λ) is a noise, the component, x i , of which is a sample from a random variable, X i , the mean of which is 0 and standard deviation σ. By the definition of D k x and by the assumption that random variables X i and X j are independent (for i ≠ j), D k x consists of samples from a new random variable with a mean still 0 and a standard deviation of σ k σ. The constant, \( \sigma_{k} : = \sqrt {\sum {_{j} \left| {\left( { - 1} \right)} \right.}^{j} C_{j}^{k} } \left| {^{2} } \right. = \sqrt {\sum {_{j} \left( {C_{j}^{k} } \right)^{2} } ,} \) is considered the magnification factor for the random noise by the finite difference of order k.

As for D k p, there are no general descriptions for the spikes, and we can at best give a mathematical model for typical cases. For this purpose, we use p 0 = (…, 0, −1, 1, 0, 0,…) as a simple model that presents the essential pattern of spikes. Taking this model, it is easy to see that the nonzero elements of D k p 0 consist of ±C k+1 j , for instance D 2 p 0 = (…, 0, 0, −1, 3, −3, 1, 0, 0,…). It is natural to consider the constant,

$$ s_{k} : =\frac{{\max \left| {\mathop D\nolimits_{k} \mathop{\mathbf{p}}\nolimits_{0} } \right|}}{{\max \left| {\mathop {\mathbf {p}}\nolimits_{0} } \right|}} = \mathop C\nolimits_{{\left\lfloor {(k + 1)/2} \right\rfloor }}^{k + 1} , $$

as the magnification factor for the typical spike by the finite difference of order k.

Since the number of samples for an event is usually around 32, we do not need finite differences of arbitrarily high orders. In practice, we think that an order of k ≤ 6 will suffice. In this practical range of k, s k  > σ k ; that is, spikes are magnified more than the noise by the process of finite differences.

In this representation, we see that two features are enough for the classification. In case one needs more features that are not too close to the chosen ones, one can exclude the chosen indices together with their neighbors and run the mRFS procedure again to find the next pair of minimax features.

There were no more than four clusters sorted in the three types of simulated tests, suggesting that the mRFS method will not produce over-clustering results. However, the mRFS method cannot deal with the overlapping problem directly. The overlapped spikes will likely be detected by their long waveforms, and they will be observed as outliers in the mRFS scatterplots.