1 Introduction

1.1 Hollow cathode operation

Hollow cathodes are widely used electron emitters and have been the subject of extensive research for decades. Their durability and efficiency make hollow cathodes the preferred means to neutralize ion beams and provide electrons to generate a plasma discharge in electric space propulsion systems. Commonly used hollow cathodes use a cylindrical insert at the tip of a refractory metal tube that thermally emits electrons. A gas—typically an inert gas like xenon, argon, or krypton—is let into the tube, becomes ionized, and serves as the electrical conductor between the insert and the exterior of the cathode. At the downstream end of the tube, a small orifice serves as the outlet for the weakly ionized gas and chokes the gas flow to increase the internal cathode pressure to facilitate a gas discharge. The thermal electron emission of the insert can be described by the Richardson-Dushman law corrected for the Schottky effect [1]:

$$j_{{{\text{em}}}} = DT_{{\text{w}}}^{{2}} \exp \left( {\frac{{ - e{\Phi }_{{{\text{wf}}}} }}{{k_{{\text{B}}} T_{{\text{w}}} }}} \right)\exp \left( {\frac{e}{{k_{{\text{B}}} T_{{\text{w}}} }}\sqrt {\frac{{eE_{{\text{c}}} }}{{4\pi \in_{0} }}} } \right)$$
(1)

where \(j_{{{\text{em}}}}\) is the thermal emission current density, \({\Phi }_{{{\text{wf}}}}\) is the material work function in eV, \(T_{{\text{w}}}\) is the insert temperature, \(D\) is the material specific Richardson-Dushman constant adjusted for the temperature dependence of the work function, \(E_{{\text{c}}}\). is the surface electric field, \(\in_{0}\) is the vacuum permittivity, and \(k_{{\text{B}}}\) and \(e\) are the Boltzmann constant and elementary charge, respectively. For current densities necessary to extract currents on the order of a few amps assuming common insert dimensions, emitter temperatures well above 1000 K are generally necessary, assuming the most widely used emitter materials LaB6 and barium oxide (BaO). This constraint implies that for cathode start up, a heater assembly is generally required. Often a heating coil is wound around the tip of the cathode tube and additional heat shields reduce thermal radiation losses. During operation, a negative electron cloud forms at the surface of the emitter which is in contact with the bulk plasma of the insert region. This condition results in an insert sheath potential at the emitter surface, which accelerates the electrons into the bulk plasma, where they perform ionizing collisions with the neutral gas atoms, either by iact ionization or by stepwise excitation. The electrons are thermalized by frequent collisions and are thus commonly approximated by a Maxwellian velocity distribution [2]. At the same time, ions are accelerated onto the emitter walls by the sheath potential.

The plasma inside the orifice has distinctly different properties compared to the insert region plasma because the entire current that is extracted from the cathode needs to pass through the narrow orifice resulting in very high current densities. The plasma density thus needs to be sufficiently high to provide the necessary charge carriers to supply the discharge, necessitating a higher electron temperature compared to the insert plasma. The cathode plume region downstream of the orifice is characterized by a rapid decrease of the particle densities as the background pressure drops. The plume plasma serves as the bridge to an electric propulsion discharge or an external anode. The operating parameters, namely the current that is extracted and the mass flow rate (MFR) of the gas, and the cathode geometry have a significant impact on the cathode operation.

1.2 Heaterless C12A7:e- hollow cathodes

In recent years, research on heaterless hollow cathodes has gained considerable interest. Omitting the heater reduces power consumption and complexity, and allows for a more compact design of the cathode assembly. In this context, C12A7:e- is being researched at TUD as a potential candidate for heaterless hollow cathodes [3,4,5]. The molecular structure of the base material C12A7 is made up of unit cells where each unit cell is divided into 12 nanocages. The connections between neighboring cages allow for material transport within and between the unit cells. The cage frame has a net positive charge, and thus two O2− ions are randomly placed in two out of the 12 cages to electrically neutralize the unit cell [6]. It is possible to alter the material properties by replacing the O2− ions with different negatively charged ions like OH−, F−, Cl−, or H− [7]. In the electride form, the negative ions are replaced by electrons that can move freely within the material grid, but the electron distribution is still as such so that the unit cell is electrically neutral. Replacing the ions with electrons leads to electrically conductive properties similar to that of metals. Several publications have suggested a very low work function of C12A7:e-, but the exact value has been subject of debate. Toda et al. reported a work function of 0.6 eV, which is exceptionally low [8]. In a follow-up publication, the researchers published a work function of 2.1 eV [9] that was determined at higher temperatures compared to the first study. A third publication examined the work function using various different methods and showed a work function on the order of 2.4 eV [10], which is still low but would require operating temperatures similar to that of LaB6. Kim et al. [11] measured a work function of 0.6 eV at room temperature. Rand found the initial work function to be 0.76 eV but noticed an increase in work function with time to about 0.9 eV [12]. The span of different work functions of C12A7:e- published in the open literature is illustrated in Fig. 1.

Fig. 1
figure 1

Emission current densities for different emitter materials as a function of temperature

Full size image

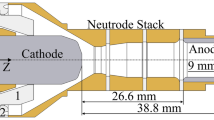
The range of work functions has strong implications on the operating temperatures. As evident in Fig. 1, a work function of 0.6 eV (assuming a Richardson-Dushman constant of 1,200,000 A/(m2K2)) allows emitting substantial currents at temperatures as low as 400–500 K. At 2.1 eV and 2.4 eV, the emitter temperature must be significantly higher, in excess of 1000 K for typical hollow cathode discharges. Temperatures of this magnitude can pose a problem to the material constraints and might limit the applicability to hollow cathodes because the melting temperature of C12A7:e- is approximately 1415 °C [6]. Rand argues that the surface work function can differ significantly from the bulk material. While slight surface defects might allow for an unimpeded electron extraction even at low temperatures, the effect could wear down in a simple field-emission test, as the electrons are quickly depleted, which would explain the increase in work function over time [13]. The bulk material, however, is likely to have a work function on the order of 2.4 eV. In a plasma environment, it is possible that the constant particle bombardment re-establishes the surface defects, yielding a constantly low effective work function and thus lowering the necessary operating temperature [14]. Different test series with C12A7:e- hollow cathodes at TUD showed successful heaterless ignition, while the temperature of the cathode backplate stayed on the order of 100 °C at a 2 A discharge, indicating a lower work function compared to commonly used materials. However, the emitters show signs of melting at the emitting surfaces after discharge tests, indicating high surface temperatures. The base of the insert, however, stays intact and does not show signs of overheating. Investigations at Fraunhofer IKTS showed a low thermal conductivity of 2.3 W/(mK) at 25 °C and 1.7 W/(mK) at 1000 °C [15], which could be one reason that the cathode backplate temperature stays low compared to common hollow cathodes. The high emitter surface temperatures nevertheless pose a problem to C12A7:e- hollow cathode operation. Cylindrical C12A7:e- inserts tend to melt at currents on the order of 2–3 A and clog the orifice and insert, preventing a discharge. As a countermeasure, a new disc-shaped insert geometry has been extensively tested, which proved to be much more thermally stable since thermal conduction from the disc to the cathode assembly is improved and excess heat can be more easily dissipated [5]. A schematic cross-section view of a hollow cathode using a disc emitter is shown in Fig. 2.

Fig. 2
figure 2

Cut-view of a C12A7:e- hollow cathode developed at TUD

Full size image

The plasma processes within this new kind of electron emitter are, however, unknown and the impact of the change in geometry has not yet been successfully quantified. Internal measurements of hollow cathodes prove to be very difficult due to the small dimensions, especially in the orifice region. Inserting plasma probes into the discharge volume is thus likely associated with high uncertainties.

1.3 Hollow cathode modeling background

In order to better understand the physics of hollow cathode plasma processes and provide design guidelines and optimization mechanisms, different modeling efforts have been carried out that substitute or supplement measurements. While 2D hollow cathode models provide the most insightful results and lead to a significantly increased understanding of hollow cathodes, their computational expensiveness and complexity limit their applicability. A plethora of volume-averaged (or 0D) models has been developed at different research institutes that provide sufficiently insightful results and can be used to identify trends and optimization mechanisms of hollow cathodes. For an extensive overview of a variety of 0D models, see Ref. [16]. There are, however, several critical issues with volume-averaged modeling approaches that are subjects of debate. In most models, the neutral flow is described by a Poiseuille flow [17, 18], an isentropic flow with sonic conditions in the orifice [19, 20], or an empirical expression [21]. While empirical expressions match experimental data very well, they cannot be universally applied to other cathode designs. Both the Poiseuille approach as well as the isentropic flow can be more generally applied to different cathode geometries, but they imply crude assumptions. As there are heat generation mechanisms inside the plasma, the isentropic flow, by and large, is invalid, but still delivers reasonably precise results. 2D models have shown that the flow of neutral gas can be well described by a Poiseuille flow at a large distance upstream of the orifice as compressibility can be neglected due to the low Mach number [22]. However, in the vicinity of the cathode plate, compressibility and viscous effects become more dominant and the Poiseuille solution loses accuracy. Similarly, the Poiseuille assumption at the orifice exit is questionable as the flow expands into a vacuum and transitions to a rarefied gas. Assuming a Poiseuille flow in both the cathode tube and the orifice region is thus questionable.

The correct treatment of the neutral gas and ion temperatures is also a subject of debate. While most models leave the heavy particle temperature as a free parameter, others equate it to the cathode wall temperature [19]. Often, thermal equilibrium between neutrals and ions is assumed. The insights provided by the 2D model analysis by Mikellides et al. [23] show that heavy particle temperatures are generally higher than the cathode walls as resonant charge exchange (CEX) collisions additionally heat up the neutral gas. In Domonkos’ analysis of the neutral flow [20], assuming a higher temperature on the order of 4000 K also yielded a better agreement with measurements. The 2D model by Ortega et al. [24] suggests that the assumption of a thermal equilibrium of ions and neutrals at a higher temperature than the cathode walls is warranted inside the cathode but loses validity in the cathode plume. On the other hand, the model approach by Sary et al. [25] shows that while neutral and ion temperatures in the cathode show similar temperature profiles, they are not in a thermal equilibrium.

A third subject of discussion is the effective emission length of the emitter. Electron emission does not occur homogeneously over the entire emitter surface but rather concentrates on a fraction of the entire emitter length, \({L}_{\mathrm{eff}}\). While some models ignore this reduced emission length [18], others try to correlate it to the internal pressure [19, 20], or to the energy exchange mean free path [21]. The effective electron emission length of the insert is difficult to implement in a 0D model, as it inherently depends on two-dimensional effects, as well as the mass flow rate and cathode dimensions. Up to now, 0D models must rely on strong assumptions or require empirical input.

Volume-averaged models have the advantage of being reasonably simple in terms of complexity, implementation, and computational expensiveness. This comes at the expense of crude assumptions and reduced accuracy. 0D model results must be taken with caution and should only be considered for preliminary analysis of cathodes. In the context of the presented work, the cathode model is a first attempt to obtain insights into the plasma processes inside hollow cathodes using C12A7:e- emitters and is solely used to crudely estimate the plasma parameters and serves as a preliminary design tool.

2 Hollow cathode model overview

The presented model is mainly based on the 0D hollow cathode models by Albertoni et al. [19, 26] and Gurciullo et al. [18]. The conservation equations are similar to the approach by Gurciullo et al., but the model incorporates specific aspects of the model by Albertoni et al., among others a lumped-node thermal model to estimate the cathode temperature, the choked-flow approach in the orifice, and the empirical treatment of the effective emission length. In the critical review of volume-averaged models by Wordingham et al. [16], useful improvements are suggested that have also been considered in the model. A version for cylindrical cathode inserts using xenon has been developed in order to compare the model output to literature data, as well as a version for disc-shaped emitters that are used for the TUD C12A7:e- cathodes assuming krypton, as most experiments were carried out using krypton. This publication will be mainly limited to the disc model. Throughout this publication, the electron temperature will be given in electronvolt, while heavy particle temperatures and cathode wall temperatures are all in kelvin.

The cathode geometry is divided into two computational domains, the emitter region and the orifice region. In both domains, a separate analytical plasma sub-model is used to calculate the volume-averaged plasma parameters, namely the electron temperature \({T}_{\mathrm{e}}\), the plasma density \({n}_{\mathrm{e}}\), and the neutral particle density \({n}_{\mathrm{n}}\). The two computational domains are coupled by the currents crossing a double-sheath at the boundary of the emitter and orifice region, where a planar sheath has been assumed. The assumption of a double-sheath at the orifice entrance has been used in various models [18,19,20, 27], but is disputed as 2D models do not suggest the existence of such sheaths. Most models that include a double-sheath at the orifice entrance cite the findings by Crawford et al. [28], where a double-sheath was experimentally observed at a constriction in a mercury discharge. However, operating conditions were distinctly different from hollow cathodes as the mercury discharge was operated at lower currents and lower pressures than hollow cathodes. 2D model results [29] rather suggest that the neutral gas flow drags the ions in the downstream direction near the orifice entrance at the centerline, which contradicts the existence of a double-sheath that accelerates ions from the orifice to the emitter region. Considering the overall low accuracy of 0D models, a double-layer was nevertheless assumed to simplify the boundary conditions. The ion current to the insert is therefore likely exaggerated.

The computational domains and the plasma output parameters of a cylindrical emitter hollow cathode are schematically shown in Fig. 3 as well as the respective current distributions. The model requires very little experimental input and is self-consistent. The main model inputs are the cathode geometry, operational parameters, and material properties. One drawback of the above-mentioned models is the treatment of the heavy particle temperature. Both models assume equilibrium of the neutrals and ions with the respective wall temperature. As stated above, the particle temperatures are likely significantly higher than the boundary wall temperatures. In the presented model, thermal equilibrium between the neutral and ion temperatures is assumed, but the temperature is left as a free parameter to investigate the influence and to adjust the model output to experimental data. The heavy particle temperature is denoted as \({T}_{\mathrm{n}}\).

Fig. 3
figure 3

Geometry and plasma parameters (top) and current distribution (bottom) of the cylindrical insert hollow cathode model

Full size image

The results of the plasma models in the emitter and orifice regions are used to calculate power inputs for the thermal model, which has largely been adapted from Albertoni et al. In the following, the modeling approach for the cylindrical configuration is shown. After that, the necessary adaptations for the disc configurations are presented.

2.1 Orifice model

A system of four equations is solved to obtain the electron temperature \({T}_{\mathrm{e},\mathrm{or}}\), the plasma density \({n}_{\mathrm{e},\mathrm{or}}\), the neutral gas density \({n}_{\mathrm{n},\mathrm{or}}\), and the ion current from the orifice to the emitter region \({I}_{\mathrm{i},\mathrm{or}-\mathrm{ins}}\). The system of equations is comprised of a current balance, an ion conservation equation, a bulk plasma power balance, and a pressure equation. The current distribution considered for the current balance for cylindrical inserts is illustrated in Fig. 3. The orifice current balance can then be written as:

$$-{I}_{\mathrm{i},\mathrm{or}}^{\mathrm{lat}}+{I}_{\mathrm{e},\mathrm{or}}^{\mathrm{lat}}+{I}_{\mathrm{e},\mathrm{ext}}-{I}_{\mathrm{i},\mathrm{ext}}-{I}_{\mathrm{i},\mathrm{or}-\mathrm{ins}}-{I}_{\mathrm{e},\mathrm{ins}-\mathrm{or}}=0$$
(2)

\({I}_{\mathrm{e},\mathrm{or}}^{\mathrm{lat}}\) is given by:

$$I_{{\text{e,or}}}^{{{\text{lat}}}} = en_{{\text{e,or}}} \sqrt {\frac{{eT_{{\text{e,or}}} }}{{2\pi m_{{\text{e}}} }}} \exp \left( { - \frac{{\phi_{{\text{s,or}}} }}{{T_{{\text{e,or}}} }}} \right)A_{{\text{or,lat}}}$$
(3)

\(\phi_{{\text{s,or}}}\) is the orifice wall sheath potential. In this model iteration, \(\phi_{{\text{s,or}}}\) is left as a free parameter in the cylindrical configuration. \(I_{{\text{i,or}}}^{{{\text{lat}}}}\) is the ion current to the orifice walls, which is given by the Bohm current:

$$I_{{\text{i,or}}}^{{{\text{lat}}}} = 0.606en_{{\text{e,or}}} \sqrt {\frac{{eT_{{\text{e,or}}} }}{{m_{{\text{n}}} }}} A_{{\text{or,lat}}}$$
(4)

\(I_{{\text{i,ext}}}\) is modeled as the thermal efflux of ions, assuming a Maxwellian velocity distribution:

$$I_{{\text{i,ext}}} = en_{{\text{e,or}}} \sqrt {\frac{{k_{{\text{B}}} T_{{\text{n,or}}} }}{{2\pi m_{{\text{n}}} }}} A_{{{\text{or}}}}$$
(5)

The electron current leaving the cathode \(I_{{\text{e,ext}}}\) can be derived from the discharge current \(I_{{\text{d}}}\) and the extracted ion current \(I_{{\text{i,ext}}}\):

$$I_{{\text{e,ext}}} = I_{{\text{d}}} + I_{{\text{i,ext}}}$$
(6)

Gurciullo et al., determine the ion current from the orifice to the insert \(I_{{\text{i,or - ins}}}\) and the incoming electron current from the insert \(I_{{\text{e,ins - or}}}\) using current conservation equations. In contrast, the Langmuir relation for planar double-sheath potentials was used in the presented model [30]:

$$I_{{\text{i,or - ins}}} = \sqrt {\frac{{m_{{\text{e}}} }}{{m_{{\text{n}}} }}} I_{{\text{e,ins - or}}}$$
(7)

Equation (7) eases the coupling of the sub-models compared to the model by Gurciullo et al. Combining Eq. (2) through Eq. (7), the orifice current continuity can be rewritten as:

$$- I_{{\text{i,or}}}^{{{\text{lat}}}} + I_{{\text{e,or}}}^{{{\text{lat}}}} + I_{{\text{d}}} - \left( {1 + \sqrt {\frac{{m_{{\text{e}}} }}{{m_{{\text{n}}} }}} } \right)I_{{\text{e,ins - or}}} = 0$$
(8)

Equation (8) provides the current flow across the double-sheath between the two domains, which is necessary for the emitter model.

The orifice ion current conservation balances the ion production rate due to electron impact ionization to the ion loss to the walls \(I_{{\text{i,or}}}^{{{\text{lat}}}}\), the upstream ion current \(I_{{\text{i,or - ins}}}\), and the ion current in the downstream direction \(I_{{\text{i,ext}}}\):

$$0 = eV_{{{\text{or}}}} n_{{\text{n,or}}} n_{{\text{e,or}}} \sigma_{{\text{i}}} v_{{\text{e}}} - I_{{\text{i,or}}}^{{{\text{lat}}}} - I_{{\text{i,or - ins}}} - I_{{\text{i,ext}}}$$
(9)

with \(V_{{{\text{or}}}}\) being the orifice volume and \(\sigma_{{\text{i}}} v_{{\text{e}}}\) the ionization reaction rate coefficient, which is the impact ionization cross-section averaged over a Maxwellian electron velocity distribution. A commonly used fit for \(\sigma_{{\text{i}}} v_{{\text{e}}}\) using xenon is given by Goebel [31].

$$\sigma_{{\text{i}}} v_{{\text{e}}} = 10^{ - 20} \left[ {\left( {3.97 + 0.643T_{{\text{e,or}}} - 0.0368T_{{\text{e,or}}}^{{2}} } \right)\exp \left( { - \frac{12.127}{{T_{{\text{e,or}}} }}} \right)} \right]\sqrt {\frac{{8eT_{{\text{e,or}}} }}{{\pi m_{{\text{e}}} }}}$$
(10)

The third equation of the orifice model is a power balance, similar to the approach by Goebel et al. [31]:

$$R_{{{\Omega },{\text{or}}}} I_{{\text{d}}}^{{2}} + {\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}T_{{\text{e,ins}}} I_{{\text{e,ins - or}}} + I_{{\text{e,ins - or}}} U_{{{\text{ds}}}} = eV_{{{\text{or}}}} n_{{\text{n,or}}} n_{{\text{e,or}}} \sigma_{{\text{i}}} v_{{\text{e}}} \in_{{\text{i}}} + I_{{\text{e,ext}}} {\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}T_{{\text{e,or}}} + I_{{\text{e,or}}}^{{{\text{lat}}}} \left( {2T_{{\text{e,or}}} + \phi_{{\text{s,or}}} } \right)$$
(11)

The orifice plasma is heated by Joule heating, a convection contribution of electrons that enter from the insert region, and a contribution from the insert electrons gaining energy from the double-sheath potential. The power gain is balanced by several power loss mechanisms. Following the reasoning by Albertoni et al. [19] referring to the spectroscopic measurements in hollow cathodes by Malik et al. [32], radiation and excitation losses are neglected as the plasma is considered optically thick. The first power loss term is the ionization process, with \(\in _{i}\) being the first ionization potential of the gas (12.13 eV for xenon [33]). Electrons leave the cathode in the downstream direction by convection extracting power of \(I_{{\text{e,ext}}} 5/2T_{{\text{e,or}}}\). The electrons hitting the orifice wall extract a power of \(\left( {2T_{{\text{e,or}}} + \phi_{{\text{s,or}}} } \right)\) from the plasma [31].

\(R_{{{\Omega },{\text{or}}}}\) in the Joule heating term of Eq. (11) accounts for the plasma resistance that is given by:

$$R_{{{\Omega },{\text{or}}}} = \eta \frac{{L_{{{\text{or}}}} }}{{A_{{{\text{or}}}} }}$$
(12)

with \(L_{{{\text{or}}}}\) as orifice length, \(A_{{{\text{or}}}}\) as orifice cross-section, and \(\eta\) as plasma resistivity, which is a function of the electron-ion and electron-neutral collision frequencies, given by:

$$\eta = \frac{{m_{{\text{e}}} \left( {\nu_{{{\text{ei}}}} + \nu_{{{\text{en}}}} } \right)}}{{e^{2} n_{{\text{e,or}}} }}$$
(13)

\(\nu_{{{\text{ei}}}}\) is the electron–ion collision frequency, given by:

$$\nu_{{{\text{ei}}}} = 2.9 \times 10^{ - 12} \frac{{n_{{\text{e,or}}} \ln {\Lambda }}}{{T_{{\text{e,or}}}^{{{\raise0.7ex\hbox{${3}$} \!\mathord{\left/ {\vphantom {{3} {2}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2}$}}}} }}$$
(14)

with \(\ln {\Lambda }\) being the Coulomb logarithm:

$$\ln {\Lambda } = 23 - \frac{1}{2}\ln \left( {\frac{{10^{ - 6} n_{{\text{e,or}}} }}{{T_{{\text{e,or}}}^{{3}} }}} \right)$$
(15)

The electron-neutral collision frequency \(\nu_{{{\text{en}}}}\) is expressed as:

$$\nu_{{{\text{en}}}} = \sigma_{{{\text{en}}}} n_{{\text{n,or}}} \sqrt {\frac{{8eT_{{\text{e,or}}} }}{{\pi m_{{\text{e}}} }}}$$
(16)

where \(\sigma_{{{\text{en}}}}\) is the electron-neutral collision cross-section. As suggested by Wordingham et al., \(\sigma_{{{\text{en}}}}\) is interpolated from Hayashi et al. [34] retrieved from the LXCAT database [35]. Equation (12) through Eq. (16) are provided in Ref. [31]. The double-sheath potential \(U_{{{\text{ds}}}}\) in Eq. (11) follows the derivations of Capacci et al. [27] applied to a planar sheath at the orifice entrance:

$$U_{{{\text{ds}}}} = \left( {\frac{{9I_{{\text{d}}} T_{{\text{e,or}}} }}{{7.5\pi R_{{{\text{or}}}}^{{2}} n_{{\text{e,or}}} e}}\sqrt {\frac{{m_{{\text{e}}} }}{2e}} } \right)^{\frac{3}{2}}$$
(17)

The last equation of the orifice model is a pressure balance that is solved for the neutral gas density \(n_{{\text{n,or}}}\). It is assumed, that the gas flow in the cathode can be described by continuum mechanics and that the flow is chocked resulting in sonic conditions in the orifice, as suggested by 2D model results by Mikellides et al. [29]. The validity of the continuum approach can be assessed using the Knudsen number Kn, which is the ratio of the mean free path and a characteristic length. Using the mean free path for CEX collisions of ions and neutrals, it has been shown that in the cathode interior Kn << 1, indicating a continuum flow regime. In the orifice, however, Kn has been shown to vary widely as shown by Taunay et al. for a variety of different hollow cathodes [36], with Kn ranging between 0.1 and > 1 in the orifice, showing a continuum or transitional regime. The assumption of a continuum flow throughout the cathode is thus not entirely valid. A transitional model would be more appropriate but exceeds the scope of the presented study. The neutral gas density \({n}_{n,or}\) is calculated by equating the sonic pressure in the orifice to the pressure that can be derived from the kinetic gas law, as suggested by Albertoni et al., using the orifice ionization degree \({\alpha }_{\mathrm{or}}\):

$$\alpha_{{{\text{or}}}} = \frac{{n_{{\text{e,or}}} }}{{n_{{\text{e,or}}} + n_{{\text{n,or}}} }}$$
(18)

The pressure equation can then be written as:

$$\left( {n_{{\text{e,or}}} + n_{{\text{n,or}}} } \right)k_{{\text{B}}} T_{{\text{n,or}}} \left( {1 + \alpha_{{{\text{or}}}} \frac{e}{{k_{{\text{B}}} }}\frac{{T_{{\text{e,or}}} }}{{T_{{\text{n,or}}} }}} \right) = \frac{{\dot{m}}}{{A_{{{\text{or}}}} }}\sqrt {\frac{{R_{{\text{s}}} T_{{\text{n,or}}} }}{\gamma }\left( {1 + \alpha_{{{\text{or}}}} \frac{e}{{k_{{\text{B}}} }}\frac{{T_{{\text{e,or}}} }}{{T_{{\text{n,or}}} }}} \right)}$$
(19)

In Eq. (19), \(R_{{\text{s}}}\) is the specific gas constant and \(\gamma\) is the isentropic exponent.

2.2 Insert model

2.2.1 Cylindrical emitter model

The insert model is comprised of a current conservation equation, a bulk plasma power balance, an ion conservation equation, and a pressure equation. The current conservation is expressed in accordance with Fig. 3:

$$- I_{{\text{i,ins}}}^{{{\text{up}}}} - I_{{\text{e,ins}}}^{{{\text{em}}}} - I_{{\text{i,ins}}}^{{{\text{lat}}}} + I_{{\text{e,ins}}}^{{{\text{lat}}}} - I_{{\text{i,ins}}}^{{{\text{plate}}}} + I_{{\text{e,ins}}}^{{{\text{plate}}}} + I_{{\text{e,ins - or}}} + I_{{\text{i,or - ins}}} = 0$$
(20)

\(I_{i,ins}^{up}\) is the ion current lost to the upstream cathode region, given by the Maxwellian velocity distribution:

$$I_{{\text{i,ins}}}^{{{\text{up}}}} = en_{{\text{e,ins}}} \sqrt {\frac{{k_{{\text{B}}} T_{{\text{i,ins}}} }}{{2\pi m_{{\text{n}}} }}} A_{{{\text{ins}}}}$$
(21)

with \(A_{{{\text{ins}}}} = \pi R_{{{\text{ins}}}}^{{2}}\). \(I_{{\text{e,ins}}}^{{{\text{em}}}}\) is the thermionic electron current emitted from the insert with an effective emission length \(L_{{{\text{eff}}}}\). The thermionic current is given by the Schottky-corrected Richardson-Dushman equation:

$$I_{{\text{e,ins}}}^{{{\text{em}}}} = DT_{{\text{w,ins}}}^{{2}} \exp \left( { - \frac{{e\phi_{{{\text{eff}}}} }}{{k_{{\text{B}}} T_{{\text{w,ins}}} }}} \right)2\pi R_{{{\text{ins}}}} L_{{{\text{eff}}}}$$
(22)

where \(\phi_{{{\text{eff}}}}\) is the effective insert work function [37]:

$$\phi_{{{\text{eff}}}} = \phi_{{{\text{wf}}}} - \sqrt {\frac{{eE_{{\text{c}}} }}{{4\pi \in_{0} }}}$$
(23)
$$E_{{\text{c}}} = \sqrt {\frac{{n_{{\text{e,ins}}} eT_{{\text{e,ins}}} }}{{ \in_{0} }}} \left( {2\sqrt {1 + 2\frac{{\phi_{{\text{s,ins}}} }}{{T_{{\text{e,in}}} }}} - 4} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}$$
(24)

\(\phi_{{\text{s,ins}}}\) is the insert sheath potential. \(I_{{\text{i,ins}}}^{{{\text{lat}}}}\) is the ion current hitting the emitter surface. The ions fall through a sheath potential and the current is thus given by the Bohm criterion:

$$I_{{\text{i,ins}}}^{{{\text{lat}}}} { = }0.606en_{{\text{e,ins}}} \sqrt {\frac{{eT_{{\text{e,ins}}} }}{{m_{{{\text{xe}}}} }}} 2\pi R_{{{\text{ins}}}} L_{{{\text{eff}}}}$$
(25)

\(I_{{\text{e,ins}}}^{{{\text{lat}}}}\) is the current of electrons in the tail of the Maxwellian distribution that have enough energy to overcome the repelling sheath potential to hit the emitter surface, given by:

$$I_{{\text{e,ins}}}^{{{\text{lat}}}} = en_{{\text{e,ins}}} \sqrt {\frac{{eT_{{\text{e,ins}}} }}{{2\pi m_{{\text{e}}} }}} \exp \left( { - \frac{{\phi_{{\text{s,ins}}} }}{{T_{{\text{e,ins}}} }}} \right)2\pi R_{{{\text{ins}}}} L_{{{\text{eff}}}}$$
(26)

The electron and ion currents to the orifice plate surfaces are analogously calculated to the currents to the insert. In contrast to Gurciullo et al., the electron current from the insert to the orifice \(I_{{\text{e,ins - or}}}\) can be derived from the orifice model by the double-sheath relation in Eq. (7). The emitter current conservation can now be rewritten in terms of the discharge current:

$$- I_{{\text{i,ins}}}^{{{\text{up}}}} - I_{{\text{e,ins}}}^{{{\text{em}}}} - I_{{\text{i,ins}}}^{{{\text{lat}}}} + I_{{\text{e,ins}}}^{{{\text{lat}}}} - I_{{\text{i,ins}}}^{{{\text{plate}}}} + I_{{\text{e,ins}}}^{{{\text{plate}}}} + \left( {1 + \sqrt {\frac{{m_{{\text{e}}} }}{{m_{{\text{n}}} }}} } \right)I_{{\text{e,ins - or}}} = 0$$
(27)

which can be simplified to:

$$- I_{{\text{i,ins}}}^{{{\text{up}}}} - I_{{\text{e,ins}}}^{{{\text{em}}}} - I_{{\text{i,ins}}}^{{{\text{lat}}}} + I_{{\text{e,ins}}}^{{{\text{lat}}}} - I_{{\text{i,ins}}}^{{{\text{plate}}}} + I_{{\text{e,ins}}}^{{{\text{plate}}}} + I_{{\text{d}}} - I_{{\text{i,or}}}^{{{\text{lat}}}} = 0$$
(28)

Equation (28) can be solved for the emitter sheath potential \(\phi_{{\text{s,ins}}}\), as several terms are functions of \(\phi_{s,ins}\). Analogous to the orifice model, the ion conservation is given by:

$$0 = eV_{{{\text{in}}}} n_{{\text{n,ins}}} n_{{\text{e,ins}}} \sigma_{{\text{i}}} v_{{\text{e}}} + I_{{\text{i,or - ins}}} - I_{{\text{i,ins}}}^{{{\text{lat}}}} - I_{{\text{i,ins}}}^{{{\text{plate}}}} - I_{{\text{i,ins}}}^{{{\text{up}}}}$$
(29)

The insert power balance is written as:

$$\begin{gathered} R_{{{\Omega },{\text{in}}}} \left( {I_{{\text{i,or - ins}}} + I_{{\text{e,ins - or}}} } \right)^{2} + I_{{\text{e,ins}}}^{{{\text{em}}}} \left( {2\frac{{k_{{\text{B}}} }}{e}T_{{\text{w,ins}}} + \phi_{{\text{s,ins}}} } \right) \hfill \\ \;\; = \left( {I_{{\text{i,ins}}}^{{{\text{up}}}} + I_{{\text{i,ins}}}^{{{\text{lat}}}} + I_{{\text{i,ins}}}^{{{\text{plate}}}} } \right) \in_{{\text{i}}} + \left( {I_{{\text{e,ins}}}^{{{\text{lat}}}} + I_{{\text{e,ins}}}^{{{\text{plate}}}} } \right)\left( {2T_{{\text{e,ins}}} + \phi_{{\text{s,ins}}} } \right) + I_{{\text{e,ins - or}}} \frac{5}{2}T_{e,ins} \hfill \\ \end{gathered}$$
(30)

The insert plasma resistance \(R_{{{{\Omega ,{\rm in}}}}}\) is given by Domonkos [20] (note that the original reference is missing the factor \(\pi\) in the denominator):

$$R_{{{\Omega },{\text{in}}}} = \eta \frac{{R_{{{\text{ins}}}} }}{{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}\pi R_{{{\text{ins}}}} L_{{{\text{eff}}}} }}$$
(31)

The last equation is a pressure equation that equates the pressure at the upstream boundary of the orifice to the kinetic gas pressure in the emitter region. The equation is based on the neutral flow derivations by Domonkos [20]. The pressure drop across the orifice length is then approximated by a Poiseuille flow with a correction for the orifice entrance pressure drop:

$$\left( {n_{{\text{e,ins}}} + n_{{\text{n,ins}}} } \right)k_{{\text{B}}} T_{{\text{n,ins}}} \left( {1 + \alpha_{{{\text{ins}}}} \frac{e}{{k_{{\text{B}}} }}\frac{{T_{{\text{e,ins}}} }}{{T_{{\text{n,ins}}} }}} \right) = \sqrt {\dot{m}\frac{16\mu }{{\pi R_{{{\text{ins}}}}^{{4}} }}R_{{\text{s}}} T_{{\text{n,or}}} L_{{{\text{or}}}} + p_{{\text{s}}}^{{2}} } + \frac{1}{2}\frac{{p_{{\text{s}}} }}{{R_{{\text{s}}} T_{{\text{n,or}}} }}\overline{u}^{2} \left( {1 + K_{{\text{l}}} } \right)$$
(32)

\(\alpha_{{{\text{ins}}}}\) is the insert region ionization degree, \(K_{{\text{l}}}\) is a loss constant that accounts for the restriction at the orifice entrance, approximated with 0.5, as suggested by Albertoni et al., \(p_{{\text{s}}}\) is the sonic pressure and \(\overline{u}\) is the average gas velocity, derived by Domonkos [20]:

$$\overline{u} = \frac{{\left( {2R_{{{\text{or}}}} } \right)^{2} }}{32\mu }\left( {\frac{{p_{{{\text{or}}}} }}{{L_{{{\text{or}}}} }}} \right)$$
(33)

In the approach by Albertoni et al., the dynamic viscosity \(\mu\) is calculated using the hard-sphere approximation. As Wordingham et al., point out, the hard-sphere viscosity does not match experimental data very well. A better approach is the dynamic viscosity calculated using the Chapman-Enskog approach with the Lennard-Jones 12-6 potential, that delivers significantly better results [16]. The dynamic viscosity is then calculated by:

$$\mu = \frac{5}{16}\frac{{\sqrt {\pi k_{{\text{B}}} T_{{\text{n,ins}}} m_{{\text{n}}} } }}{{\pi \sigma^{2} {\Omega }^{{\left( {2,2} \right)}} }}$$
(34)

where \(\sigma\) and \({\Omega }^{{\left( {2,2} \right)}}\) are temperature dependent material properties and are provided in Ref. [38]. It must be noted that the assumptions of a choked flow and a Poiseuille flow in the orifice are inconsistent with one another, but nevertheless have been used in the presented model for simplicity, given the overall low accuracy of 0D models. The neutral density in the emitter therefore likely has high uncertainties. The commonly used Poiseuille flow approach for the emitter region presented by Goebel et al. [31] to determine the emitter neutral density was not used in the model, as it cannot be applied to cathodes with disc emitters.

As stated in Sect. 1.3, no consensus has been reached to date on how to treat the effective emission length \(L_{{{\text{eff}}}}\) of the insert correctly. Wordingham et al. [39] present an analytical approach to approximate \(L_{{{\text{eff}}}}\) that was used for the cylindrical configuration:

$$L_{{{\text{eff}}}} = R_{{{\text{ins}}}} \left( {0.75832 + \frac{0.18239}{{\left( {2R_{{{\text{ins}}}} p} \right)^{1.22956} }}} \right)$$
(35)

where \(p\) is the insert region pressure. In Eq. (35), the pressure-diameter product is in Torr-cm. For the presented model, an empirical approach to determining the internal cathode pressure derived by Taunay et al. [40] was used to approximate the pressure conditions in the insert region. This scaling relationship considers the effects of the discharge current, cathode geometry, and mass flow rate on the pressure and is thus deemed appropriate to estimate \(L_{{{\text{eff}}}}\). The pressure obtained with the scaling relation by Taunay et al., and the plasma model output for the pressure showed a maximum deviation of approximately 10% for the considered range of operating points, resulting in uncertainties for the effective emission length of less than 0.1 mm. Given the overall low accuracy of volume-averaged models, the uncertainty was deemed acceptable. Future model iterations will be improved by using an additional convergence loop for the emission length.

2.2.2 Disc emitter model

Using a disc-shaped emitter material necessitates certain changes in the cathode geometry. As shown in Fig. 2, the orifice plate is omitted and a keeper electrode is placed directly opposite of the insert, which is used to ignite the cathode. Analogous to cylindrical cathodes, the keeper has a small orifice that is in principle equivalent to the orifice in cylindrical cathodes. The orifice model is therefore mainly unaltered in the disc configuration. However, the keeper is left floating during operation. The \(I_{{\text{e,or}}}^{{{\text{lat}}}}\) and \(I_{{\text{i,or}}}^{{{\text{lat}}}}\) to the orifice walls must therefore be equal and are calculated using the ion Bohm current.

Using disc-shaped emitters also requires changes to the insert model. The plasma output parameters of a disc emitter hollow cathode and the respective currents in the hollow cathode are shown schematically in Fig. 4. The conservation equations derived for the cylindrical configuration are deemed applicable to the changes in geometry as they consider particle and power losses at specific surfaces or the bulk plasma. In contrast to cylindrical cathodes, the effective emission length must be treated differently. Empirically derived relations for cylindrical cathodes (Taunay et al., for the pressure, Wordingham et al., for the effective emission length) are likely not applicable.

Fig. 4
figure 4

Plasma parameters in a hollow cathode (top) and current distribution (bottom) using a disc-shaped emitter

Full size image

Experiments at TUD have shown, that the entire surface of the C12A7:e- emitters shows visible alterations after tests that indicate plasma contact across the entire surface during operation. It is therefore assumed that the entire disc surface contributes to electron emission, with an effective emission radius \(R_{{{\text{eff}}}}\) that is equal to the disc radius, which is 5 mm. The plasma resistance needs to be adapted as well, because the cylindrical configuration assumes mainly radial conduction paths and the altered geometry in the disc configuration result in predominantly axial conduction paths. \(R_{{{\Omega },{\text{in}}}}\) in Eq. (31) is adjusted as follows:

$$R_{{{\Omega },{\text{in}}}} = \eta \frac{{l_{{\text{em,k}}} }}{{\pi R_{{{\text{eff}}}}^{{2}} }}$$
(36)

where \(l_{{\text{em,k}}}\) is the distance between the emitter and the keeper plate. Analogous to the orifice model, the electron and ion currents to the keeper plate, \(I_{{\text{e,ins}}}^{{\text{k}}}\) and \(I_{{\text{i,ins}}}^{{\text{k}}}\), must be equal as the keeper is left floating.

As most hollow cathode tests at TUD were performed using krypton instead of xenon, several model parameters must be adjusted. The ionization reaction rate coefficient (see Eq. (10) for xenon) is replaced by tabulated values for the ionization cross-section [41] that are integrated over a Maxwellian distribution of electrons and then interpolated in the model. Analogously, the electron-neutral collision cross section \(\sigma_{{{\text{en}}}}\) is replaced with tabulated data for krypton [42]. Similar to the cylindrical configuration, the assumption of an optically thick plasma in the disc configuration using krypton is deemed valid. The optical depth \(\tau\) for a Doppler-broadened line can be approximated by [43] (in cgs-units):

$$\tau = 5.4 \times 10^{ - 9} f_{{{\text{mn}}}} \lambda \left( {\frac{\mu }{T}} \right)^{\frac{1}{2}} n_{{\text{n}}} L$$
(37)

where \(f_{{{\text{mn}}}}\) is the oscillator strength, \(\lambda\) is the radiation wavelength, \(\mu\) is the atomic mass divided by the atomic mass unit, \(T\) is the temperature of the absorber (in eV), and \(L\) is a characteristic length of the plasma. For an assumed gas temperature of 0.1 eV, a particle density on the order of 1 × 1020 1/m3, a characteristic dimension equal to the orifice diameter of 0.4 mm, and an oscillator strength as low as 0.1, the optical depth is notably larger than 1 for the entire UV spectrum. It is therefore likely that the emitted radiation is largely reabsorbed by the plasma.

2.3 Thermal model

The thermal model is largely adapted from the approach by Albertoni et al., in which the cathode assembly is divided into lumped nodes that are assumed to have a uniform temperature. Neighboring nodes are thermally connected by thermal conduction. In contrast to Albertoni et al., node boundaries facing the environment radiate to a 300 K background temperature. For a detailed description of the thermal approach, the reader is referred to Ref. [19].

The orifice and insert models are used to determine power inputs into the thermal nodes representing the insert and the orifice walls. The insert wall experiences a power input from the ions bombarding the insert wall, \(P_{{\text{i,wall}}}\), and from the electrons overcoming the boundary sheath, \(P_{{\text{e,wall}}}\), and is cooled by the electron emission current, \(P_{{\text{e,em}}}\). The insert power contributions are expressed by:

$$P_{{\text{i,wall}}} = 0.606en_{{\text{e,ins}}} \sqrt {\frac{{eT_{{\text{e,ins}}} }}{{m_{{\text{n}}} }}} \left( {\frac{{T_{{\text{e,ins}}} }}{2} + \phi_{{\text{s,ins}}} + \in_{{\text{i}}} - \phi_{{{\text{wf}}}} } \right)A_{{{\text{eff}}}}$$
(38)
$$P_{{\text{e,wall}}} = \frac{1}{4}en_{{\text{e,ins}}} {\text{exp}}\left( { - \frac{{\phi_{{\text{s,ins}}} }}{{T_{{\text{e,ins}}} }}} \right)\sqrt {\frac{{8eT_{{\text{e,ins}}} }}{{\pi m_{{\text{e}}} }}} \left( {\phi_{{{\text{wf}}}} + 2T_{{\text{e,ins}}} } \right)A_{{{\text{eff}}}}$$
(39)
$$P_{{\text{e,em}}} = j_{{{\text{em}}}} \left( {\phi_{{{\text{eff}}}} + 2\frac{{k_{{\text{B}}} T_{{\text{w,ins}}} }}{e}} \right)A_{{{\text{eff}}}}$$
(40)

While Albertoni additionally considers heat transfer by convection and evaporation of the insert material, both aspects have not yet been implemented in the current model. Due to the small evaporation rates of the emitter, it is unlikely that the evaporation significantly contributes to the cooling of the emitter. Similarly, the low mass flow rates only result in little cooling of the nodes in contact with the gas that is deemed negligible. The orifice plate surface in the cylindrical configuration and the keeper plate in the disc configuration experience an additional power input, \(P_{{\text{k,ins}}}\):

$$P_{{\text{k,ins}}} = I_{{\text{e,ins}}}^{{\text{k}}} 2T_{{\text{e,ins}}} + I_{{\text{i,ins}}}^{{\text{k}}} \left( {\frac{{T_{{\text{e,ins}}} }}{2} + \phi_{{\text{s,k}}} - \phi_{{\text{wf,k}}} } \right)$$
(41)

with \(\phi_{{\text{wf,k}}}\) being the keeper work function and \(\phi_{{\text{s,k}}}\) being the keeper floating potential.

Albertoni et al., assume that the entire Joule heating occurring in the orifice region is transferred to the orifice walls. In contrast, it is assumed that the orifice node experiences a power input \(P_{{{\text{or}}}}\) from electron and ion wall bombardment as well as the ionization power in the presented model:

$$P_{{{\text{or}}}} = I_{{\text{i,or}}}^{{{\text{lat}}}} \left( {\frac{{T_{{\text{e,or}}} }}{2} + \phi_{{\text{s,or}}} + \in_{{\text{i}}} - \phi_{{\text{wf,or}}} } \right) + I_{{\text{e,or}}}^{{{\text{lat}}}} \left( {2T_{{\text{e,or}}} } \right)$$
(42)

with \(\phi_{{\text{wf,or}}}\) being the orifice wall work function.

2.4 Solution process

The solution process of the model is illustrated in Fig. 5 for the disc configuration. The model takes the geometry, the operating conditions, and an initial guess for the insert wall temperature (750 K for the disc configuration) and the insert electron temperature (1.4 eV) as inputs. The free parameters differ depending on the configuration and are summarized in Table 1.

Fig. 5
figure 5

Flow chart of the model solution process for the disc configuration

Full size image
Table 1 Free parameters of the model configurations
Full size table

The solution process consists of two convergence loops, one for the insert electron temperature and one for the insert wall temperature. The first loop starts by solving the orifice model. The output parameters are then used as the input for the insert model that provides a value for the insert electron temperature, which is compared to the initial guess. The value for the insert electron temperature for the next iteration step is determined by a simple bisection algorithm. This process is repeated until the difference between the input and output values falls below the limit of 1e−3. The orifice and insert model outputs are then used in the thermal model, where the cathode temperature profile and the insert wall temperature are determined. The value is then compared to the initial guess and adjusted accordingly for the next iteration step. If both the insert electron temperature and the insert wall temperature reach convergence, the solution process is finished. The model uses the Python SciPy fsolve routine that uses the MINPACK hybrid method [44] to find roots of a system of equations. The fsolve function requires an additional initial guess for the output parameters to restrict the computational domain. The solution process for one operating point takes approximately one to five minutes with an i7-7700 2.8 GHz CPU. An additional graphical user interface (GUI) was implemented to build and change the cathode geometry, assign materials, set operating conditions and initial guesses, and specify radiating boundaries. The division of the geometry into nodes was performed by comparing the thermal model output with a thermal simulation using the Ansys simulation software.

Here, the insert and orifice surface temperatures were compared using the same material and radiation properties, and specified power inputs. The node division was accepted if both the emitter and orifice temperatures deviated less than 5% from the Ansys simulation. This process highlighted the necessity of finely dividing components with high thermal gradients like the emitter and the orifice plate into small nodes.

In post-processing, additional operating parameters are determined that are useful for comparison to experimental data and evaluate heating mechanisms. The calculation of these parameters follows the derivations by Gurciullo et al. The discharge power \({P}_{\mathrm{d}}\) can be expressed as:

$$P_{{\text{d}}} = P_{{\text{s}}} + P_{{\text{R,ins}}} + P_{{{\text{ds}}}} + P_{{\text{R,or}}}$$
(43)

In Eq. (43), the plasma discharge is treated as a series circuit of resistors corresponding to each component of the plasma. The discharge power contribution of the orifice plate is neglected. \(P_{{\text{s}}}\) is the power that is needed to accelerate thermionic electron into the bulk plasma, given by:

$$P_{{\text{s}}} = I_{{\text{e,ins}}}^{{{\text{em}}}} \phi_{{\text{s,ins}}}$$
(44)

\(P_{{\text{R,ins}}}\) and \(P_{{\text{R,or}}}\) account for the resistive Joule heating in the insert and orifice regions:

$$P_{{\text{R,ins}}} { = }R_{{{\Omega },{\text{in}}}} \left( {I_{{\text{i,or - ins}}} + I_{{\text{e,ins - or}}} } \right)^{2}$$
(45)
$$P_{{\text{R,or}}} = R_{{{{\Omega ,{\text or}}}}} I_{{\text{d}}}^{{2}}$$
(46)

\(P_{{{\text{ds}}}}\) is the power spent in the double-sheath region between the insert and orifice regions:

$$P_{{{\text{ds}}}} = \left( {I_{{\text{i,or - ins}}} + I_{{\text{e,ins - or}}} } \right)U_{{{\text{ds}}}}$$
(47)

The discharge voltage \(U_{{\text{d}}}\) can then be derived from the discharge power and current:

$$U_{{\text{d}}} = \frac{{P_{{\text{d}}} }}{{I_{{\text{d}}} }}$$
(48)

3 Results and discussion

3.1 Cylindrical geometry results

The LaB6 hollow cathode that was used by Albertoni et al. [19] and Pedrini et al. [26] also served as a benchmark cathode for the presented model. The cathode body is made of tantalum with an outer tube diameter of 7.5 mm, a wall thickness of 0.3 mm, and a total length of 20 mm. The orifice diameter and length are 0.4 mm and 0.36 mm, respectively. The insert has an inner diameter of 1.5 mm and is assumed to have a total length of 10 mm. Xenon was considered as the supporting gas. The cathode uses an additional heatshield concentric to the cathode tube that reflects heat back to the cathode.

As the model does not include a cathode plume model, a direct comparison of the modeled discharge voltage to experimental data with an external anode is not valid. Pedrini et al. [26] nevertheless provide sufficient model results that were used for comparison. Figure 6 shows a comparison of the thermal model outputs of both models for an operating point of 3 A and 0.3 mg/s. A heavy particle temperature of 2000 K and an orifice sheath potential of 15 V were selected for the model runs. Note that an additional division of both the emitter domain and the orifice plate was used in the presented model to account for thermal gradients within the emitter material.

Fig. 6
figure 6

Comparison of the thermal outputs of the model presented by Pedrini et al. [26] (top) with this model (bottom)

Full size image

The presented model results in higher cathode temperatures compared to the presented data by Pedrini et al. The higher background temperature results in less radiative cooling but, as stated, evaporation of the insert and convection have not been implemented which slightly cool the insert and the orifice plate. Treating the insert and the orifice as single domains has the drawback that thermal gradients within the material lead to lower average temperatures. Moreover, a pronounced difference between the models can be seen in the effective emission length. The approach presented in Ref. [26] results in notably higher emission lengths compared to the presented model. For a given current density, the emitter temperature must therefore be higher. However, the overall differences are limited to less than 5% for the emitting insert domain and the orifice region.

In Figs. 7 and 8, the plasma densities and electron temperatures of the two models are compared as an example for \(T_{{\text{n}}}\) = 2000 K and \(\phi_{{\text{s,or}}}\) = 15 V. Both models show an increase of the plasma density with the discharge current and higher plasma densities in the orifice compared to the emitter.

Fig. 7
figure 7

Comparison of the plasma density of the model with data presented by Pedrini et al. [26] for a mass flow rate of 0.3 mg/s

Full size image
Fig. 8
figure 8

Comparison of the electron temperature of the model with data presented by Pedrini et al. [26] for a discharge current of 3 A

Full size image

The presented model provides notably higher plasma densities in both domains than the data provided by Pedrini et al. Both models show a trend of increasing electron temperature as the mass flow rate is reduced, with a steeper increase in the orifice region. The electron temperatures of the presented model are slightly higher in both domains. The differences between the models can be attributed to the changes in sheath voltage calculation, as well as differences in the power balances and the thermal model.

Further comparison of the model to literature data is shown in Table 2, where the model results for the NSTAR neutralizer hollow cathode at a mass flow rate of 0.36 mg/s and a current of 3.26 A using a \(T_{{\text{n}}}\) = 3000 K and \(\phi_{{\text{s,or}}}\)=15 V are shown alongside 2D model results [29] and the model by Albertoni et al. The presented model overestimates the electron temperature compared to the 2D results and is similar to Albertoni et al. The 2D model shows a strong gradient of both the neutral gas density and the plasma density. The neutral gas density provided by the presented model lies between the 2D values for the orifice inlet and outlet. The plasma density is notably lower compared to the maximum value of the 2D model and similar to the orifice outlet value.

Table 2 Comparison of different model results for the NSTAR neutralizer cathode
Full size table

3.2 C12A7:e- Cathode results

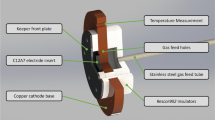
The C12A7:e- hollow cathode that was used as the basis for the disc emitter model was developed at TUD and is schematically shown in Fig. 9. The cathode consists of a stainless steel cathode assembly, a molybdenum keeper plate, and an electrical insulation made of the alumina silicate based machinable ceramic Rescor 902. The orifice has a diameter of 0.4 mm and a length of 0.5 mm. A preliminary test was carried out to measure the temperature during a 2 A discharge at a mass flow rate of 0.5 mg/s krypton. The positions of the thermocouples during the test are indicated in Fig. 9. The thermocouples located at the keeper tip and the backplate showed an equilibrium temperature of 605 K and 455 K, respectively.

Fig. 9
figure 9

Benchmark C12A7:e- hollow cathode

Full size image

As an elaborate verification of the model is to date not possible, the thermal measurement was used as a starting point to find a range of free parameters that fit the thermal measurement with an accuracy of ± 10%. The backplate temperature of 455 K was used as a constant heat sink temperature in most model runs, but the influence of the heat sink temperature was investigated as well.

For the disc configuration, a lower heavy particle temperature range compared to cylindrical inserts was assumed in the range of roughly 2-4 times the emitter wall temperature. Only a narrow range of work functions between 1.0 eV and 1.2 eV resulted in converging solutions for the given backplate temperature. While thermionic emission experiments suggest higher work functions (see Fig. 1), it is likely that electron emission in a hollow cathode plasma environment is facilitated. As Phillips et al. speculate [13], the electron emission at very low temperatures might be caused by material surface defects that are replenished by the particle bombardment in the plasma discharge. The following data are mainly intended to present trends in the plasma parameters, determine the influences of free parameters, and derive design optimizations.

3.2.1 Influence of the work function

As stated, the model provides converging solutions for different work functions in the range of 1.0–1.2 eV for the given heat sink temperature. Figure 10 shows the emitter and orifice wall temperatures for different work functions and an operating point of 2 A and 0.5 mg/s. Increasing \({\Phi }_{{{\text{wf}}}}\) from 1.0 to 1.2 eV leads to an emitter temperature increase of approximately 120 K as a higher work function necessitates a higher emitter temperature for the same current density.

Fig. 10
figure 10

Emitter and orifice wall temperatures for different work functions (\(T_{{\text{n}}}\)=2000 K)

Full size image

Both \(U_{{\text{d}}}\) and \(\phi_{{\text{s,ins}}}\), shown in Fig. 11, are also notably increased for a higher \({\Phi }_{{{\text{wf}}}}\), because of the higher heating power that is required to raise the emitter temperature and emit the necessary electrons. A higher sheath potential therefore leads to increased ion bombardment and emitter surface heating.

Fig. 11
figure 11

Discharge voltage and sheath potential for different work functions (\(T_{{\text{n}}}\)=2000 K)

Full size image

The plasma densities and electron temperatures in the emitter and orifice regions are shown in Figs. 12 and 13. The orifice plasma density is relatively unaffected by changes in the work function, but the emitter plasma density rises from 2.6 × 1020 m−3 to 3.5 × 1020 m−3. Both the emitter and the orifice electron temperatures are largely unaffected by the work function.

Fig. 12
figure 12

Emitter and orifice plasma densities for different work functions (\(T_{{\text{n}}}\)=2000 K)

Full size image
Fig. 13
figure 13

Emitter and orifice electron temperatures for different work functions (\(T_{{\text{n}}}\)=2000 K)

Full size image

More precise measurements of the work function of C12A7:e- in a hollow cathode discharge are necessary to minimize the uncertainty in the model results but the model data in the context of the thermal measurements indicate a work function well below 2 eV, which is highly beneficial for the use in hollow cathodes. To date, crude assumptions have to be made for lack of better knowledge. The work function was fixed at 1.1 eV for the remaining investigations.

3.2.2 Influence of the heavy particle temperature

The influence of the second free parameter \(T_{n}\) on the power distribution, the plasma density, and the electron temperature is shown in Figs. 14, 15 and 16 for an operating point of 2 A and 0.5 mg/s krypton.

Fig. 14
figure 14

Power distribution for different heavy particle temperatures (\(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 15
figure 15

Plasma density for different heavy particle temperatures (\(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 16
figure 16

Electron temperature for different heavy particle temperatures (\(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

Figure 14 shows the discharge power and the four power components introduced in Eq. (43) through (46). The model shows a slight increase in power at \(T_{{\text{n}}}\) = 1000 K due to a higher sheath power. The differences of the remaining power contributions are < 1 W. The orifice plasma density in Fig. 15 slightly drops with increasing \(T_{{\text{n}}}\) from 6.5 × 1020 m−3 at 1000 K to 4.5 × 1020 m−3 at 3000 K, whereas the emitter plasma density is relatively unaffected An increase of the orifice electron temperature from 2.63 to 2.89 eV with increasing \(T_{{\text{n}}}\) can be seen in Fig. 16. The emitter electron temperature stays approximately constant. The impact of the heavy particle gas temperature can be mainly attributed to the dependence of the gas viscosity and the internal cathode pressure on the temperature.

3.2.3 General model trends

In the following, general model trends are presented in more detail. The model runs were performed with a heavy particle temperature of 2000 K and a work function of 1.1 eV.

In Figs. 17 and 18, the emitter and orifice wall temperatures are plotted as functions of the discharge current and mass flow rate. The emitter temperature stays in the range of 720–800 K for currents up to 3 A, which highlights the advantages of a low work-function material. The emitter temperature increases with both discharge current and mass flow rate. The temperature increase with discharge current has also been observed in the models of Domonkos and Albertoni et al., and could be seen in measurements by several researchers [45,46,47]. As the current demand is increased, the insert wall temperature needs to be raised to ensure sufficient thermionic electron emission. The increase of the emitter temperature with mass flow rate has also been seen in the model by Albertoni et al., and has been experimentally observed by Polk et al. [47]. However, this trend contradicts temperature measurements by Goebel (Fig. 6–42 in Ref. [31]), where a higher mass flow rate is slightly cooling the insert, and Siegfried et al. [21], where a higher internal pressure results in a slight decrease in emitter surface temperature. It is possible that the cathode sheath voltage in those instances increases as the pressure is decreased, which would promote ion heating at lower pressures. The orifice temperature rises with both mass flow rate and discharge current. Both trends have been experimentally observed [47]. The orifice wall temperature lies in the range of 640–780 K. The rise in orifice wall temperature with discharge current can be explained by the power distribution, which is shown in Fig. 19 for a mass flow rate of 0.5 mg/s.

Fig. 17
figure 17

Emitter wall temperature for different MFRs and discharge currents (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 18
figure 18

Orifice wall temperature for different MFRs and discharge currents (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 19
figure 19

Power distribution for different discharge currents (\(T_{n}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

While it is obvious that the discharge power rises with discharge current, the individual power contributions change slightly. The insert sheath power is dominant throughout the investigated current range, but the contribution of the resistive orifice heating increases from 15.4% at 1 A to 24.1% at 3 A. The same trends in power distribution can be seen in the models by Albertoni et al., and Gurciullo et al., although the individual proportions differ slightly. It is also noteworthy that a significant proportion of the power in the disc cathode goes into the keeper plate, which leads to additional heating of the orifice node. The losses to the keeper are significantly higher compared to the losses to the orifice plate in the cylindrical configuration because a larger area of the keeper is exposed to the internal plasma. Reducing the radial dimensions of the cathode could thus lead to a reduction in power demand.

The electron temperatures in both domains are plotted in Figs. 20 and 21. The insert electron temperature is nearly constant with discharge current but decreases with mass flow rate. A higher mass flow rate leads to a higher neutral density and thus more frequent ionizing collisions. The excess ionization must be contained by lowering the electron temperature [20]. The same trend can be seen in the orifice. In the orifice, the electron temperature is significantly higher compared to the insert region. As described in Sect. 1.1, the current densities in the orifice are the highest in the hollow cathode. High degrees of ionization are thus necessary to supply the discharge, necessitating increased electron temperatures. In comparison to xenon discharges, the use of krypton results in an increased electron temperature, which can be attributed to the higher ionization potential of krypton. The electron temperature must thus increase to promote sufficient ionization.

Fig. 20
figure 20

Emitter electron temperature for different MFRs and discharge currents (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 21
figure 21

Orifice electron temperature for different MFRs and discharge currents (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

The emitter and orifice plasma densities are shown in Figs. 22 and 23, respectively. In both domains, the plasma density increases with mass flow rate and discharge current. As stated above, a higher mass flow rate increases the neutral particle density and results in more frequent ionizing collisions, increasing the plasma density. The trends are similar in the emitter and orifice regions, but the orifice plasma density is higher and shows a steeper gradient.

Fig. 22
figure 22

Emitter plasma density for different MFRs and discharge currents (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 23
figure 23

Orifice plasma density for different MFRs and discharge currents (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

3.2.4 Influence of the Orifice geometry

The influence of the orifice dimensions is examined

next. The plasma densities and electron temperatures are plotted as functions of the orifice diameter in Figs. 24 and 25. The electron temperature rises with increasing orifice diameter in both domains, while the plasma density especially in the orifice drops sharply. This trend was also observed in Ref. [20] and can be attributed to the drop in neutral gas density, illustrated in Fig. 26. The drop in neutral density leads to less ionizing collisions and the plasma density drops. This must be counteracted by increasing the electron temperature to enhance ionization. In Fig. 27, the power distribution is plotted as a function of the orifice diameter. The discharge power increases as the orifice diameter is decreased and the resistive heating in the orifice increases notably, which was also seen in the models by Albertoni et al. and Gurciullo et al. Experiments at TUD also showed a large increase in discharge power with reduced orifice diameter.

Fig. 24
figure 24

Plasma density as function of orifice diameter (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 25
figure 25

Electron temperature as function of orifice diameter (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 26
figure 26

Neutral density as function of orifice diameter (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 27
figure 27

Power distribution as function of orifice diameter (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

In Figs. 28 and 29, the influence on the plasma density and the electron temperature of the orifice length is shown. The electron temperature is relatively unaffected by the orifice length, but the orifice plasma density notably increases with orifice length. Both the Ohmic heating and the ionization process shown in Eq. (10) increase with the orifice length and therefore contribute to a higher plasma density. In Fig. 30, the power distribution is plotted for different orifice lengths. The overall discharge power slightly increases with orifice length. In particular, the contribution of orifice Joule heating notably increases with increasing orifice length due to a higher plasma resistance, consistent with Albertoni et al. [19] and Domonkos [20].

Fig. 28
figure 28

Plasma density as function of orifice length (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 29
figure 29

Electron temperature as function of orifice length (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 30
figure 30

Power distribution as function of orifice length (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

3.2.5 Influence of the heat sink temperature

A constant heat sink temperature of the cathode backplate \(T_{{{\text{bp}}}}\) of 455 K was assumed for the investigations presented above. Due to the compact design of the cathode and short thermal conduction paths, it is likely that the temperature of the heat sink node has a large impact on the emitter temperature and therefore electron emission. The plasma densities and wall temperatures as functions of \(T_{{{\text{bp}}}}\) are shown in Figs. 31 and 32, respectively. The orifice plasma density is relatively unaffected by \(T_{{{\text{bp}}}}\) and the emitter plasma density slightly decreases with \(T_{{{\text{bp}}}}\). The orifice node temperature increases from 710 K at \(T_{{{\text{bp}}}}\)=455 K to roughly 790 K at \(T_{{{\text{bp}}}}\)=650 K. The emitter wall temperature is slightly less affected. A \(T_{{{\text{bp}}}}\) increase of 200 K results in an increase of emitter temperature of roughly 40 K. As thermionic emission with low work function materials is very sensitive to changes in material temperature, the backplate temperature is an important parameter that needs to be measured more carefully for different operating points in order for the model to reproduce experimental data more accurately.

Fig. 31
figure 31

Plasma density as function of backplate temperature (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image
Fig. 32
figure 32

Wall temperatures as function of backplate temperate (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

3.2.6 Discharge voltage results

Lastly, the discharge voltage obtained by the model is shown in Fig. 33.

Fig. 33
figure 33

Model current–voltage characteristic (\(T_{{\text{n}}}\)=2000 K, \(\phi_{{{\text{wf}}}}\)=1.1 eV)

Full size image

The voltage obtained with the disc model ranges between 12 and 18 V. The discharge voltage decreases with increasing discharge current and increasing mass flow rate, which is commonly observed in hollow cathodes and indicates the transition to plume mode. Experimentally obtained discharge voltages using hollow cathodes with disc emitters and an external anode at TUD show an inverse trend of discharge current and voltage. The measured voltages are also notably higher on the order of 40–60 V for a current range of 1–3 A. Although a plume model has not been implemented, it is likely that the model underestimates the voltage of the cathodes.

4 Conclusion

A volume-averaged hollow cathode model was developed based on published 0D modeling approaches [18, 19] with incorporated improvements suggested by Wordingham et al. [16]. The model was adapted to classical cylindrical LaB6 hollow cathodes as well as novel disc emitter cathodes using C12A7:e-. For disc emitters, the overall trends of the plasma properties are largely in accordance with experimentally verified hollow cathodes. The output of the thermal model can be adjusted to fit thermal measurements well using the free parameters. The insights gained by the disc model to date are nevertheless limited for the following reasons:

  • Model validation is rudimentary and currently limited to comparing the thermal model output to thermal measurements. Thermal measurement was only conducted for a single operating point. As the heat sink temperature has a notable effect on the electron emission properties, more thorough thermal measurements over a broad range of operating points are necessary to test if the cathode backplate temperature notably varies.

  • Comparing the model discharge voltage to experimental data requires an additional plume model.

  • The thermionic emission properties of C12A7:e- in a hollow cathode plasma environment are unknown and can only be crudely estimated. It is thus likely that the implemented emission properties are not accurate. The thermal emission using low work function materials is highly sensitive to changes, which introduces a large uncertainty. However, the measured temperature distribution does indicate a work function well below 2 eV.

  • Assuming a double-sheath between the emitter and orifice regions has been used in many different models but lacks experimental evidence. While the assumption of a double sheath is computationally convenient, it will likely be removed in future model iterations.

The results obtained with the disc model are thus still preliminary and need to be taken with caution. However, the results are useful to obtain first approximations of the plasma parameters within the cathode, the thermionic emission properties of C12A7:e- in hollow cathodes, and to identify optimization potential. The disc model showed that power losses to keeper surfaces are significant. Reducing the radial dimensions of the cathode might therefore reduce the overall power consumption. However, a smaller emission area would require higher emitter temperatures and result in a reduction of radiating surface area, which might be problematic for the thermal constraints of C12A7:e-.

Future work will aim at obtaining sufficient experimental data with different emitter geometries that can be used to adapt and improve the model. While the temperature distribution and the discharge voltage are parameters that can easily be measured and compared to model outputs, they do not replace direct measurements of the plasma parameters.