Introduction

A consistent and self-sufficient simulation of the operation of a non-transferred arc plasma torch has been a challenging task for decades. The numerical simulation is complicated and time-consuming, but it is practically the only way to investigate the processes inside commercial plasma torches that are generally not equipped with observation windows or slits. The electric arc models which consider different temperatures for electrons and heavy species, also called two-temperature models, were shown to predict more accurately the arc current density and plasma temperature (Ref 1) as well as the electric arc voltage and arc behavior inside the torch (Ref 2, 3). The thermal non-equilibrium assumption can be essential in the prediction of the shape of the arc and anode arc attachment in a plasma torch because of a more complex geometry than that of transferred arcs with planar anodes (Ref 3). Adopting the local thermodynamic equilibrium (LTE) assumption in a plasma spray torch model can result in an overestimation of (i) the arc voltage in a wide range of arc current (Ref 3, 4) because of a higher resistance of the bulk of the arc column and (ii) plasma temperature even in the arc core (Ref 5, 6). An important aspect is the cold boundary layer. This layer develops at the anode wall and is too resistant to electric current when LTE is assumed. It is worthy to note that the LTE assumption can result in an underestimation of the arc voltage for a low current in the transferred arc models (Ref 7).

Another important issue in a self-sufficient torch model is the treatment of the cathode-plasma interface and non-equilibrium layer adjacent to the cathode surface, also called cathode sheath (Ref 8). As noted in Ref 5, the LTE assumption should be avoided in the model of the energy exchange in the near-cathode non-equilibrium layer, and two-temperature models should be favored. The non-equilibrium in the cathode layer is different from that observed in the arc fringes and usually requires a specific treatment. Some detailed reviews of the plasma-cathode interaction and its modeling are given in Ref 9,10,11.

Following the description given in Ref 10, 12, 13, the boundary layer adjacent to the cathode consists of

  1. 1.

    The space-charge sheath. This layer is adjacent to the cathode surface and mainly consists of positive ions attracted by the negative charge of the cathode surface. The violation of quasi-neutrality is localized in this layer, which facilitates the thermionic emission and accelerates the electrons to the velocity necessary for further ionization in the presheath. The space-charge sheath is characterized by a Debye radius of about 0.02 μm. The ions in the sheath are mostly forward-going and hence have a non-Maxwellian distribution.

  2. 2.

    The Knudsen layer. The thickness of this layer is on the order of the smallest mean free path; it has still a relatively low number of collisions, but can be considered as electrically neutral. The Knudsen layer enables the acceleration of ions up to a critical value required for the formation of the space-charge sheath (Ref 14). This critical velocity is called the “Bohm velocity.”

  3. 3.

    The presheath, also called ionization layer. In this layer, ionization prevails over recombination, and the chemical equilibrium is violated. The electrons emitted by the cathode are accelerated by the space-charge sheath and Knudsen layer; they bring their kinetic energy to the ionization layer where new ions are produced and accelerated towards the cathode surface. This layer is characterized by a recombination length of roughly 10-100 μm (Ref 15) and has a nearly Maxwellian ion distribution. The ion current at the boundary with the Knudsen layer is significant, while it is negligible at the boundary with the two-temperature plasma. The presheath can be simulated implicitly in a fully non-equilibrium plasma model that considers departure from chemical equilibrium (Ref 16, 17).

  4. 4.

    The thermal non-equilibrium layer or two-temperature plasma. In this layer, the temperatures of the heavy particles and electrons are different. It is characterized by the length of electron energy relaxation, which is on the order of magnitude of 100 μm. This layer can be simulated in a two-temperature plasma model. In some cases, it might be incorporated into the ionization layer (Ref 11).

A more accurate model of the coupling between the cathode and plasma taking into account the non-equilibrium effects was shown to improve the accuracy of electric arc model predictions (Ref 16, 18, 19). Plasma sheath models are used in various applications, e.g., simulations of transferred electric arcs (Ref 17, 20,21,22,23), conventional plasma torches with tapered cathodes (Ref 19, 24, 25) and RF plasma reactors (Ref 26). The model presented in Ref 19 combined a 3D non-equilibrium plasma model of a conventional plasma torch with a simplified cathode sheath model and effective local electrical conductivity. Meanwhile, the models presented in Ref 24, 25 considered a more sophisticated cathode sheath model calculating the balance of heat and electric current, non-uniform in Ref 24 and uniform in Ref 25. However, the plasma considered in Ref 24, 25 was 2D axisymmetric and steady, which does not make it possible to investigate transient and asymmetric phenomena. The effect of the cathode dopant diffusion on the cathode arc attachment was studied in Ref 27, 28.

The configuration of the cathode sheath model depends on the conditions and type of the discharge, type and geometry of the electrode, and required accuracy of the model. A review of the plasma sheath models, their evolution and the different approaches based on different assumptions is given in Ref 13. The choice of the cathode-plasma coupling approach depends on the goals and priorities. To the best of the authors’ knowledge, no published studies of 3D transient two-temperature plasma torch models combined with a cathode sheath model take into account the thermal and electric current balance at the cathode-plasma interface yet. This study was intended to tackle this problem in the context of a commercial DC plasma torch with a cascaded anode, the SinplexPro plasma torch from Oerlikon Metco.

Previously published studies of the simulation of the operation of this torch with an assumed constant cathode sheath voltage drop (Ref 3, 29) showed a significant mismatch in the thermal balance in the plasma torch. Normally, the equality between the input power (the arc current multiplied by the sum of arc and sheath voltages) and the dissipation terms (electrode heating in the arc attachments + radiation inside the torch + enthalpy flow through the nozzle exit) must be fulfilled. However, the constant voltage drop of 10 V assumed in Ref 3 for an arc current of 500 A resulted in a total input power of 37,100 W and dissipated power of 35,524 W. This mismatch of 4% seemed to result from the poor accuracy of the heat balance in the cathode arc attachment. Hence, the present study was also an attempt to correct the discrepancy in the thermal balance.

Model Description

The assumptions of the two-temperature plasma model used to model the SinplexPro torch are detailed in Ref 3, 29. The two-temperature approach for arc modeling was selected because of more plausible predictions of the cathode arc attachment, but also and mainly because of its higher accuracy in the prediction of the arc parameters and anode arc attachment. However, it should be noted that an LTE arc model combined with a cathode sheath model is often sufficient for a transferred arc simulation (Ref 11), e.g., in welding and high-intensity discharge lamps (HID).

The governing equations for the two-temperature model are shown in Table 1. Each governing equation includes a transient term, advection, diffusion and source terms for each solved variable. In each governing equation, the sum of the transient term, advection and diffusion is equal to the sum of the source terms. The solved variables include the fluid velocity \(\overrightarrow{u}\), the fluid pressure \(p\), the electron enthalpy \({h}_{e}\), the heavy species enthalpy \({h}_{h}\), the electric potential \(\varphi \), and the magnetic vector potential \(\overrightarrow{A}\). The properties needed to solve these equations are the density \(\rho \); the electron, heavy species and reactive components of the thermal conductivity \({\lambda }_{e}\), \({\lambda }_{h}\), \({\lambda }_{r}\); the continuum radiation \({\delta }_{e}{Q}_{r}\) attributed to the electrons as loss of enthalpy; the absorbed and non-absorbed line radiation \(\left(1-{\delta }_{e}\right){Q}_{r}\) attributed to the heavy species (Ref 30); the electron and heavy species components of the specific heat \({C}_{p}^{e}\), \({C}_{p}^{h}\); the coefficient of energy exchange in elastic collisions between electrons and heavy species \({K}_{\mathrm{exch}}\); the electrical conductivity \(\upsigma \). In addition, in Table 1, \(\left({\overrightarrow{\Gamma }}_{\mathrm{expl}}+{{\overline{\overline \Gamma }} }_{\mathrm{impl}}\overrightarrow{u}\right)\) is the momentum source term used to set to zero the momentum inside the electrodes (Ref 35), \(\overline{\overline{\tau }}\) is the viscous stress tensor, \(\overrightarrow{J}=-\upsigma \overrightarrow{\nabla }\left(\varphi \right)\) is the electric current density current derived from the electric potential according to Ohm’s law, \(\overrightarrow{B}=\nabla \times \overrightarrow{A}\) is the magnetic field derived from the magnetic vector potential, \(\overrightarrow{J}\wedge \overrightarrow{B}\) is the Lorentz force, \({Q}_{J}=\frac{1}{\upsigma }\overrightarrow{J}\cdot \overrightarrow{J}\) is the Joule power, \(\mathrm{k}\) is the Boltzmann constant, \(e\) is the electron charge, \({\mu }_{0}\) is the vacuum permeability. The electron and heavy species temperatures \({T}_{e}\) and \({T}_{h}\) are derived from \({h}_{e}\) and \({h}_{h}\) using the technique described in Ref 29.

Table 1 System of governing equations
Full size table

The exact values of the specific heat components depend on the enthalpy formulation, specifically whether the ionization energy is associated with electrons or heavy species. In this study, the plasma ionization energy is associated with electrons, hence \({C}_{p}^{e}\) includes the ionization component. The use of \({C}_{p}^{e}\) and \({C}_{p}^{h}\) in the denominators of the thermal diffusivities for electron and heavy species depends on the exact formulation of the two-temperature heat flux and is a separate topic. In this study, for the sake of consistency with (Ref 3, 29), the formulation of heat flux \(\frac{{\lambda }_{i}}{{C}_{p}^{i}}\overrightarrow{\nabla }{h}_{i}\) for the species \(i\) is retained. For the same reason, the reactive thermal conductivity is assigned to the heavy species, although Rat in Ref 31 suggests that the reactive thermal conductivity in plasmas formed from monatomic gases should instead be rather assigned to the electrons. The preliminary tests showed that the configuration with the reactive thermal conductivity assigned to the electrons works well when the cathode sheath is included in the model in the context of the SinplexPro plasma torch.

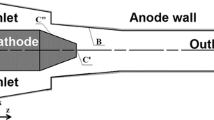
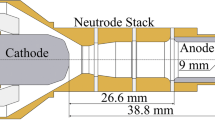
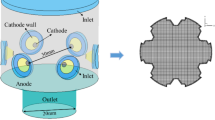
The geometry of the plasma torch is shown in Fig. 1. The model includes the tungsten parts of the cathode and anode shown in dark gray in Fig. 1, the cavity inside the torch, and outlet chamber. The copper neutrodes, copper parts of the electrodes, ceramic insulators between the neutrodes, ceramic insulator of the cathode (marked as 1 in Fig. 1), and gas injector ring (marked as 2 in Fig. 1) are not included into the computational domain. The gas injector ring was mimicked by the gas inlet boundary condition with an injection through 24 small jets with a 25° swirling angle. The computational domain and boundary conditions are presented in Fig. 2. A difference from the model presented in Ref 3, 29 was the inclusion of the whole tungsten part of the cathode which is around 25.5 mm long, in order to make the calculated thermal balance and temperature gradient inside the cathode body more realistic. Another difference was an axial temperature profile \({T}_{\mathrm{an}}\left(z\right)\) used as thermal boundary condition on the external surface of the anode tungsten liner. The temperature profile \({T}_{\mathrm{an}}\left(z\right)=\) − 2.2e8·z3 + 5.5e6·z2 − 6.2e4·z + 660, where z = 0 mm at the upstream edge of the anode and z = 0.0122 m at the nozzle exit, was obtained from the model of the torch cooling circuit developed by the torch manufacturer.

Fig. 1
figure 1

Internal geometry of the plasma torch SinplexPro™. The tungsten parts of electrodes are colored in dark gray and the copper neutrodes and copper parts of electrodes in orange. 1 is a ceramic electrode insulator. 2 is a gas injector ring

Full size image
Fig. 2
figure 2

Computational domain and boundary conditions used in this study

Full size image

The two-temperature model predicts an axisymmetric steady electric arc, even though the model itself was three-dimensional and unsteady. This prediction was confirmed by (i) the experimental observation of a brand-new anode operated for 5 min with 500 A and 60 NLPM of argon and (ii) the measurement of the arc voltage directly on the torch after filtering out the ripple of the power supply (Ref 3). Even if the predicted electric arc is axisymmetric, the model remains 3D in order to (i) capture the potential non-axisymmetric behavior of electric arc if it occurs, e.g., at low currents (Ref 29) (ii) be able to study non-axisymmetric plasma torch configurations in the future.

The predictions of the plasma torch model without the calculation of the cathode sheath parameters (Ref 3, 29) were used as initialization data for the model with the cathode sheath. Then, the results with and without the cathode sheath were compared to study the effect of the cathode sheath model on the simulation of the torch operation. The comparison was done for two sets of operating conditions for which the experimental measurements were readily available:

  1. 1.

    Regular mode: 500 A and 60 NLPM of pure argon

  2. 2.

    High-power mode: 675 A and 85 NLPM of pure argon

The theory of the cathode sheath model for bidirectional coupling of the cathode with the two-temperature plasma was adopted from the model of Cayla (Ref 21). Following the classification given by Javidi et al. (Ref 13), this study employs the partial LTE approach, since it combines the two-temperature plasma model in chemical equilibrium with the sheath model which considers the current density conservation, energy balance at the sheath/presheath interface and electron back diffusion. This approach is similar to the “approach with 2T description of arc bulk plasma” described by Benilov (Ref 11). The technique proposed by Cayla et al. (Ref 21) considered the total current density on the cathode surface as an input parameter and the cathode sheath voltage drop as an output value, which is more convenient for a bidirectional coupling. The cathode-plasma coupling implemented in the present SinplexPro torch model was bidirectional, because the further development of the model is intended to deal with non-axisymmetric gas flow configurations, which were found to have non-axisymmetric cathode arc attachment during preliminary tests. Thus, the developed 1D cathode-plasma coupling was rather the first step in the modeling of the cathode arc interaction in the SinplexPro plasma torch. In addition, the cathode in the SinplexPro plasma torch is significantly different from the tapered cathodes usually studied in the context of cathode-plasma coupling. Thus, there is no ground to neglect the effect of the plasma and cathode on the cathode sheath. In the current context, the approach of Cayla et al. (Ref 21) was optimal in terms of complexity and accuracy; it can be easily employed for the present application. This approach can be implemented as a relatively simple script in the programming language Python with only open-source tools as it does not require any external sources of large amounts of data or models. In addition, the use of such Python script with a polynomial approximation allows an easy transition to a non-axisymmetric cathode sheath with two dimensions (radial and azimuthal) if needed. However, in this study, only an axisymmetric cathode sheath was considered.

Model Assumptions

The model of the plasma torch was three-dimensional and unsteady. The time step used for the solution of the model equations was 10−7 s. All the conservation equations of the model in plasma and electrodes were solved with the finite volume method in the open-source CFD (computational fluid dynamics) software Code_Saturne (Ref 32). The specific assumptions for some certain parts of the model are given below.

Solid cathode and anode:

  1. 1.

    The cathode and anode were made of tungsten doped with lanthanum oxide.

  2. 2.

    The electrode material was assumed to be homogeneous. The cathode thermal and electrical conductivity, enthalpy and specific heat were that of pure tungsten. They were all functions of the temperature and taken from Ref 33. The tungsten properties used in this study covered the temperature range of the solid and liquid states with an enthalpy increment during the melting of the material (latent heat of fusion).

  3. 3.

    Only the tungsten parts of the electrodes were included.

  4. 4.

    The electrode surface was assumed perfectly smooth, without cracks or erosion.

  5. 5.

    The mass loss due to cathode material evaporation was considered negligible. Even if some cathode material evaporates, it is assumed that the vapor atoms are ionized in plasma and driven back to the cathode surface by the electric field. The assumption of negligible cathode mass loss was confirmed by tests with the SinplexPro plasma torch by the torch manufacturer. However, in the context of conventional plasma torches with tapered cathode, e.g., Oerlikon Metco F4MB-XL, the mass loss in cathode is notable over time as shown in Ref 34.

  6. 6.

    The computed momentum of the cells corresponding to the electrodes in the computational domain was set to zero according to the technique proposed by Patankar (Ref 35). This technique is necessary in Code-Saturne that solves the fluid equations both in fluid and solids parts.

  7. 7.

    The thermal equations for electrons and heavy species were identical in the solid electrodes.

  8. 8.

    The equations for the electric and magnetic vector potentials were solved in the same way as in plasma.

  9. 9.

    The anode sheath voltage drop was assumed to be 0 V due to the diffuse anode arc attachment (Ref 36, 37) as it was done in Ref 3 for the two-temperature torch model.

Cathode sheath model:

  1. 1.

    The thicknesses of the cathode sheath and presheath were not calculated.

  2. 2.

    The Knudsen layer was omitted as it was done in Ref 21. Instead, the cathode sheath was coupled with the presheath.

  3. 3.

    The cathode surface temperature \({T}_{\mathrm{cath}}\) was assumed to be the same as the heavy species temperature at the sheath/presheath interface. According to the experience of the plasma torch SinplexPro operation under the conditions of this study, the cathode surface temperature was not expected to be above the tungsten melting point.

  4. 4.

    The electron temperature \({T}_{e}\) was assumed to be constant in the sheath and presheath. This temperature was an unknown parameter; it was calculated by solving the equations of the cathode sheath model and, then, used as the thermal boundary condition for the two-temperature plasma model.

  5. 5.

    Due to the temperature of the plasma adjacent to the cathode surface predicted by the two-temperature plasma model, the ion charge \(Z\) near the cathode tip was assumed to be no more than 1. Benilov et al. (Ref 12) confirmed that an ion charge above 1 can be neglected for the cathode sheath parameters predicted in this study.

  6. 6.

    The space-charge sheath was assumed to be collision-free as its thickness is less than the mean free path in atmospheric pressure plasma.

  7. 7.

    The currents of the charged particles were constant across the sheath. A major fraction of the electric current in the sheath was expected to be due to the thermionic emission.

  8. 8.

    The cathode sheath was assumed to be steady due to the limited arc dynamics and almost steady voltage for the considered plasma torch and operation modes (Ref 3).

  9. 9.

    The effect of the cathode material vapor was neglected, because the cathode material loss during the initial stage of SinplexPro operation is negligible. The mass loss of the cathode measured by the torch manufacturer is less than 0.0001 g/h.

  10. 10.

    The electron number density and enthalpy at the sheath/presheath interface were determined using a two-temperature chemical composition approach as it was done in Ref 21, 38. The two-temperature chemical composition is a simplification in case of the ionization layer, but it was assumed to be the optimal solution when no computation of the plasma composition under chemical non-equilibrium according to the balance of each species at each region of the cathode tip is performed.

  11. 11.

    The voltage drop over the ionization layer was considered negligible compared to the computed space-charge sheath voltage drop according to the estimation given in Ref 12.

  12. 12.

    The thermionic emission electric current was assumed to follow the Richardson-Dushman law with the Schottky correction because the cathode used in the simulated plasma torch was made of tungsten and operated at high temperature (Ref 28).

  13. 13.

    The work function used to calculate the thermionic emission current density was equal to 2.72 eV which corresponds to tungsten doped with lanthanum oxide (Ref 39, 40). The same work function was assumed on the whole cathode surface since the cathode material was assumed to be homogeneous. This assumption might be unsatisfactory in the context of conventional plasma torches with tapered cathode, and the consideration of two physical states on the cathode surface might be necessary (Ref 24, 27, 28).

  14. 14.

    The effect of the plasma radiation and black-body radiation of the cathode itself on the cathode surface temperature was taken into account as an additional heat source term in the interface cells of the cathode. The black-body radiation of the cathode was taken into account to know its value for future studies, even though for the considered plasma torch, it was negligible both locally and globally.

  15. 15.

    The secondary emission was neglected due to the high electric current density (above 106 A/m2) and high thermionic emission on the hot surface of the refractory cathode (Ref 21, 28).

Two-temperature plasma model:

  1. 1.

    The plasma beyond the cathode sheath was in ionization equilibrium.

  2. 2.

    The two-temperature plasma composition beyond the cathode sheath was defined by the Saha equation with the formulation given in Ref 41. The plasma consisted of electrons, Ar, Ar+, Ar2+, Ar3+ and Ar4+.

  3. 3.

    The plasma flow was laminar, which is valid inside the torch (Ref 42).

  4. 4.

    The plasma flow was assumed to be weakly compressible and subsonic. However, the assumption of subsonic flow might be violated at the nozzle exit for some high-power operation modes. This makes it necessary to pay extra attention to the predicted Mach number and avoid using plasma jet parameters for which the Mach number approaches unity. That is why the present model should be rather considered mainly as a model of the processes inside the torch, rather than a model of the plasma jet outside the torch. Nevertheless, even when the Mach number at the torch nozzle exit predicted by the torch model approaches unity, the model still can be used to calculate arc parameters that can be used as input data for other non-MHD compressible plasma models.

Cathode-Plasma Coupling

The cathode-plasma interface in the torch model is a surface which separates the solid electrode from the fluid that is either the hot plasma at the arc attachment or the cold gas in the periphery. Due to the complicated physics of the arc-cathode interface and significant difference in the temperature dependency of enthalpy and transport properties of tungsten and argon, this interface cannot be resolved by a standard MHD model of electric arc and requires a special treatment. For that, a virtual thin wall between the cathode and plasma was built and treated as a boundary condition for both the cathode and plasma subdomains. The boundary condition type and value for all the solved variables (electron and heavy species enthalpies, electric and magnetic vector potentials) depend on the configuration of the cathode-plasma coupling. Two configurations were considered in this study: case without cathode sheath and case with cathode sheath.

Case without cathode sheath. In this case, the electric potential and electric current were assumed to be continuous on the cathode surface, and a constant cathode sheath voltage drop of 10 V was assumed for the calculation of the heat flux due to electric current on the cathode surface. The assumed constant cathode sheath voltage drop was later included into the torch voltage predicted by the model without cathode sheath. The heavy species enthalpy was coupled with the cathode tungsten enthalpy according to the continuity of the heavy species temperature and heat flux due to heat diffusion. The electron heat flux on the cathode surface was assumed to be zero. This case mostly repeats the simulation presented in Ref 29.

Case with cathode sheath. A radial profile of the cathode sheath voltage drop \({U}_{s}\) calculated in the cathode sheath model was introduced in the coupling of the electric potential at the cathode-plasma interface. At this interface, the electric potential was not continuous in the MHD model and underwent a corresponding increment. The continuity of electric current, heavy species temperature and heat flux due to heat diffusion was still preserved on the cathode surface. The value of the electron temperature on the cathode surface was calculated in the cathode sheath model and imposed as a boundary condition for the two-temperature plasma, which was an important improvement in the torch operation model. The computed distribution of the Schottky reduction in the work function was used during the calculation of the heat flux brought by the electric current on the cathode surface. The equations of the cathode sheath model used in this study were adopted from Cayla (Ref 21); they are presented below.

In both cases with and without cathode sheath model, the thickness of the layer of thermal non-equilibrium adjacent the cathode tip was about 200 μm which is consistent with the estimations found in the literature (Ref 11).

In both cases, the magnetic vector potential on the cathode surface was calculated according to the Biot–Savart law as described in Ref 43.

Equations of the cathode sheath model (Ref 21) are presented below:

  1. 1.

    Conservation of electric current at the cathode surface and sheath:

    $${j}_{\mathrm{cath}}=e\left(Z{\varphi }_{i}+{\varphi }_{\mathrm{em}}-{\varphi }_{\mathrm{bs}}\right)$$
    (1)
  2. 2.

    Conservation of energy at the sheath/presheath interface:

    $$ \begin{gathered} \varphi_{{{\text{em}}}} \left( {{\text{eU}}_{s} + 2{\text{kT}}_{{{\text{cath}}}} + {\text{kT}}_{e} \left( {{\text{ln}}\frac{{n_{e\infty } }}{{n_{{{\text{es}}}} }} - 3.2} \right)} \right) = \hfill \\ = \varphi_{{{\text{bs}}}} \left( {{\text{eU}}_{s} + {\text{kT}}_{e} \left( {{\text{ln}}\frac{{n_{e\infty } }}{{n_{{{\text{es}}}} }} - 1.2} \right)} \right) + \varphi_{i} \left( {E_{i} + {\text{ZkT}}_{e} \left( {3.2 - 0.5{\text{ln}}\frac{{n_{e\infty } }}{{n_{{{\text{es}}}} }}} \right)} \right) \hfill \\ \end{gathered} $$
    (2)

where \({\varphi }_{i}\) is the ion flux, \({\varphi }_{\mathrm{em}}\) is the flux of thermionic emission, \({\varphi }_{\mathrm{bs}}\) is the flux of back-diffused electrons, \({U}_{s}\) is the cathode sheath voltage drop, \({E}_{i}\) is the first ionization potential of argon equal to 15.76 eV, \({n}_{\mathrm{es}}\) is electron number density at the sheath/presheath interface, respectively, and \({n}_{e\infty }\) is the electron density in the two-temperature plasma beyond the presheath. Only the first ionization potential was taken into account, because the first ion was assumed to be dominant in the cathode vicinity. The secondary emission was not included into the equations because it was considered negligible in this cathode sheath model.

All the cathode sheath parameters were computed and used in the torch model as a function of the radius, i.e., as would be done in a 1D formulation.

The electric current due to the thermionic emission on the cathode surface is given by the following formula (Ref 44):

$${j}_{\mathrm{em}}=e{\varphi }_{\mathrm{em}}={\mathrm{AT}}_{\mathrm{cath}}^{2}\mathrm{exp}\left(-\frac{W-\Delta W}{{\mathrm{kT}}_{\mathrm{cath}}}\right)$$
(3)

where \(W\) is the work function of tungsten doped with lanthanum oxide equal to 2.72 eV, A is the Richardson constant equal to 8·104 A m−2 K−2 (Ref 39, \(\mathrm{k}\) is the Boltzmann constant, \({T}_{\mathrm{cath}}\) is the cathode surface temperature, and \(\Delta W\) is the Schottky reduction in the work function.

The Schottky reduction in the work function is given by the following formula (Ref 45):

$$\Delta W=\sqrt{\frac{{e}^{3}{E}_{c}}{4\uppi {\varepsilon }_{0}}}$$
(4)

where \({E}_{c}\) is the electric field at the electrode surface given by Eq 5 drawn from Ref 12:

$${E}_{c}={\left\{\frac{2{n}_{\mathrm{is}}}{{\varepsilon }_{0}}\left[{m}_{i}\left(\frac{{v}_{+}^{3}-{v}_{-}^{3}}{6{u}_{i}}-{v}_{\mathrm{is}}^{2}-\frac{{u}_{i}^{2}}{3}\right)-{\mathrm{ZkT}}_{\mathrm{e}}\left(1-\mathrm{exp}\left(\frac{{\mathrm{eU}}_{\mathrm{s}}}{{\mathrm{kT}}_{\mathrm{e}}}\right)\right)\right]\right\}}^\frac{1}{2}$$
(5)

Where \({n}_{is}\) is the ion number density at the sheath/presheath interface, \({T}_{e}\) is the electron temperature at the sheath/presheath interface, \({v}_{\pm }=\sqrt{{\left({v}_{\mathrm{is}}\pm {u}_{i}\right)}^{2}+\frac{2{\mathrm{ZeU}}_{\mathrm{s}}}{{m}_{i}}}\) are the ion velocities at the cathode surface after acceleration, \({u}_{i}=\sqrt{\frac{{\mathrm{kT}}_{\mathrm{cath}}}{{m}_{i}}}\) is the ion thermal velocity in the sheath, \({v}_{\mathrm{is}}=\sqrt{\frac{k\left({T}_{\mathrm{cath}}+{\mathrm{ZT}}_{\mathrm{e}}\right)}{{m}_{i}}}\) is the Bohm velocity, \({m}_{i}\) is the ion mass, and \({\varepsilon }_{0}\) is the vacuum permittivity.

The Bohm velocity is the minimum ion velocity defined in the Bohm’s criterion. This criterion requires that for the formation of the space-charge sheath, the ions enter the space-charge sheath with at least the velocity of the ion acoustic waves, also called Bohm velocity (Ref 14).

Since the ion Ar1+ prevailed (\(Z=1\)) due to the predicted electron temperature near the cathode, the number densities \({n}_{\mathrm{is}}\) and \({n}_{\mathrm{es}}\) at the sheath/presheath interface were equal.

The flux of the back-diffused electrons, that have a sufficient thermal energy to get to the cathode against the sheath voltage drop, is defined by the following formula according to Ref 12.

$${\varphi }_{\mathrm{bs}}=\frac{{n}_{\mathrm{es}}}{4}\sqrt{\frac{8{\mathrm{kT}}_{\mathrm{e}}}{\uppi {m}_{e}}}\mathrm{ exp}\left(-\frac{{\mathrm{eU}}_{\mathrm{s}}}{{\mathrm{kT}}_{\mathrm{e}}}\right)$$
(6)

where \(\sqrt{\frac{8{\mathrm{kT}}_{\mathrm{e}}}{\uppi {m}_{e}}}\) is the mean thermal speed of the electrons (Ref 46).

The flux of plasma ions to the cathode surface is equal to the ion number density at the sheath/presheath interface times the Bohm velocity (Ref 12).

$${\varphi }_{i}={n}_{\mathrm{is}}{v}_{\mathrm{is}}={n}_{\mathrm{is}}\sqrt{\frac{k\left({T}_{\mathrm{cath}}+{\mathrm{ZT}}_{\mathrm{e}}\right)}{{m}_{i}}}$$
(7)

Substituting the expressions 3-7 in Eq 1 and 2 yields a set of two equations with the unknown parameters \({U}_{s}\) and \({T}_{e}\). The unknown Schottky correction \(\Delta W\) is a function of the computed sheath parameters. Since the cathode sheath was assumed to be axisymmetric, the cathode sheath parameters were expressed as radial profiles \({U}_{s}(R)\), \({T}_{e}\left(R\right)\),\(\Delta W(R)\) on the cathode surface where \(R\) is a distance from the torch axis. Only the radial coordinate was considered, even for the conical part of the cathode tip, since it was sufficient to cover the essential part of the cathode tip. In addition, the cathode shape was considered in the MHD torch model and did not need to be considered again in the sheath model. The limit for the radial profiles of the cathode sheath parameters was \(R=4\) mm. Beyond 4 mm, the current density was negligible and the electron temperature was too low. Therefore, this distant periphery of the cathode tip was considered irrelevant for the electric coupling of the cathode and plasma. The input parameters taken from the MHD torch model in Code_Saturne for this sheath model were

  1. 1.

    The cathode surface temperature \({T}_{\mathrm{cath}}(R)\);

  2. 2.

    The electron temperature in the two-temperature plasma close to the cathode surface \({T}_{e\infty }(R)\) used to calculate the electron number density in the two-temperature plasma \({n}_{e\infty }(R)\);

  3. 3.

    The calculated total electric current density \({j}_{\mathrm{cath}}(R)\) on the cathode surface.

The solved sheath parameters \({U}_{s}(R)\), \(\Delta W(R)\), \({T}_{e}(R)\) and other parameters dependent on \({T}_{e}\), e.g., \({n}_{e}(R)\), \({h}_{e}(R)\) were imposed on the cathode surface and used as the boundary conditions at the cathode-plasma interface. The computed voltage drop \({U}_{s}(R)\) was used for the coupling of the electric potential in Code_Saturne. The computed electron enthalpy on the cathode surface \({h}_{e}(R)\) was used as a boundary condition for the electron enthalpy conservation equation in the two-temperature plasma model. The heat flux to the cathode was computed according to Eq 8 adopted from Ref 12 and complemented by the heat flux due to radiation and thermal diffusion.

$${q}_{\mathrm{cath}}={\varphi }_{i}\left(2k\left({T}_{h}-{T}_{\mathrm{cath}}\right)+{\mathrm{kZT}}_{\mathrm{e}}/2+{\mathrm{ZeU}}_{\mathrm{s}}+{E}_{i}-Z\left(W-\Delta W\right)\right)+{\varphi }_{bs}\left(2k{T}_{e}+\left(W-\Delta W\right)\right)-{\varphi }_{\mathrm{em}}\left(2k{T}_{\mathrm{cath}}+\left(W-\Delta W\right)\right)+{Q}_{\mathrm{pr}}^{\mathrm{abs}}-{Q}_{\mathrm{bbr}}^{\mathrm{em}}+{Q}_{\mathrm{diff}}$$
(8)

where \({T}_{h}\) is the heavy species temperature in the two-temperature plasma near the cathode tip, \({Q}_{\mathrm{pr}}^{\mathrm{abs}}\) is the plasma radiation absorbed by the cathode surface, \({Q}_{\mathrm{bbr}}^{\mathrm{em}}\) is the black-body radiation emitted by the hot cathode surface calculated as in (Ref 27), \({Q}_{\mathrm{diff}}\) is the heat diffusion to the cathode body from the heavy species adjacent to the cathode tip computed by Eq 9 based on the linear approximation of temperature inside the interface cells of cathode and plasma and the assumption of continuity of the heavy species temperature and heat flux at the cathode-plasma interface (Ref 4).

$${Q}_{\mathrm{diff}}=\frac{2{\lambda }_{\mathrm{elec}}{\lambda }_{\mathrm{hr}}^{\mathrm{pl}}}{{\lambda }_{\mathrm{elec}}{l}_{\mathrm{pl}}+{\lambda }_{\mathrm{hr}}^{\mathrm{pl}}{l}_{\mathrm{elec}}}\left({T}_{h}-{T}_{\mathrm{elec}}\right)$$
(9)

where \({\lambda }_{\mathrm{hr}}^{\mathrm{pl}}\) and \({T}_{h}\) are the heavy species thermal conductivity and temperature at the center of the plasma interface cell, respectively, \({\lambda }_{\mathrm{elec}}\) and \({T}_{\mathrm{elec}}\) are the thermal conductivity and temperature of the cathode solid at the center of the interface cell, respectively, and \({l}_{\mathrm{pl}}\) and \({l}_{\mathrm{elec}}\) are the plasma and electrode interface cell sizes perpendicular to the interface surface, respectively. The heavy species thermal conductivity included the reactive part. The thicknesses of the sheath and presheath were neglected when calculating the heat flux due to the heat diffusion to the cathode.

\({Q}_{\mathrm{diff}}\) was treated in the MHD torch model as a boundary condition on the cathode tip surface for the enthalpy equation in the cathode body, while the other terms in the right-hand side of Eq 8 are treated as the enthalpy source terms in the interface cathode cells. This differentiation was done in order to optimize the development of the model, but it did not change the overall heat transfer to the cathode at each interface face.

After all the sheath parameters were computed and imposed in the two-temperature MHD torch model in Code_Saturne, the model was started again until the convergence of the plasma and cathode properties was reached. Then, the new plasma and cathode properties were introduced into the cathode sheath model. The cathode sheath parameters were recomputed and imposed again in the two-temperature torch model in Code_Saturne. Thus, an iteration process (external iterations) was implemented between the cathode sheath model and two-temperature torch model in Code_Saturne, during which the radial profiles of the sheath voltage drop and electron temperature on cathode surface converged to asymptotic profiles.

The energy conservation at the sheath/cathode interface was ensured through the heat flux \({q}_{\mathrm{cath}}(R)\) to the cathode body. Thus, the cathode surface temperature was an output of the two-temperature MHD torch model, and the energy balance at the sheath/cathode interface was controlled implicitly during the external iterations between the MHD torch model and cathode sheath model. In this respect, this study is different from that of Cayla (Ref 21), where the energy balance at the sheath/cathode interface was provided by an additional equation in the cathode sheath model.

The initial estimate of \({T}_{e}\) for the 0th iteration of the cathode sheath model was the value predicted in the vicinity of the cathode by the two-temperature torch model without the cathode sheath. The initial estimate of \({U}_{s}\) was 4 V and was selected manually during the cathode sheath model development. The internal iterations of the cathode sheath model started from \(R=0\) mm and ended at \(R=4\) mm. The required number of external iterations between the two-temperature torch model and cathode sheath model varied from 7 to 15 depending on the initial estimate of the cathode sheath parameters. The sequence of the cathode sheath model iterations is shown in Fig. 3.

Fig. 3
figure 3

Flowchart of iterations between the two-temperature torch model and the cathode sheath model

Full size image

The solution of Eq 1 and 2 is done by a Python script using the scipy.optimize.fsolve. For the solution, a continuous function \({n}_{e}\left(\frac{{T}_{e}}{{T}_{h}},{T}_{e}\right)\) was created using scipy.interpolate.interp2d based on the lookup tables of the argon plasma properties. Once calculated, the radial profiles of the properties on the cathode surface were approximated by polynomials up to the power of 8 using scipy.optimize.curve_fit and fed into the two-temperature torch model in Code_Saturne. Recalculation of the cathode sheath parameters and generation of the corresponding polynomials for the entire cathode surface took 2-5 min depending on the complexity of the polynomials even in the single thread mode with an Intel® Xeon® Gold 6152 processor.

Results

The radial profiles of the cathode sheath voltage drop, electron temperature on the cathode surface, Schottky reduction in the work function, current density composition computed on the cathode surface converge during the external iterations. The converged parameters of the cathode sheath are shown in Fig. 4, 5, and 6. The cathode sheath voltage drop has its minimum value at the center of the cathode tip in both simulated operation modes. The minimum of the sheath voltage drop coincided with the maxima of the electron temperature and all the current density components as can be seen in Fig. 7. The sheath voltage drop at the cathode tip center was almost twice lower than its value in the cathode tip periphery, which emphasizes the importance of taking into account the radial evolution of the sheath voltage drop and not just an average value. A similar pattern can be seen in the Schottky correction. In addition, the maximum of the Schottky reduction in the work function was comparable with the work function itself. Therefore, the Schottky correction should not be replaced by some approximate constant value. The calculated electron temperature value on the cathode surface was imposed as the boundary condition for the two-temperature plasma instead of the zero flux boundary condition used for electron temperature in the MHD torch model without cathode sheath. This electron temperature boundary condition on the flat part of the cathode tip ranged approximately from 9300 to 9800 K which is significantly lower than the electron temperature of around 12000 K in the vicinity of the cathode tip predicted by the model without cathode sheath. The introduction of the calculated boundary condition resulted in a decrease in the electron temperature near the cathode tip down to around 11000 K. Combined with the radial profile of the cathode sheath voltage drop, they made the cathode arc attachment more constricted, as we will discuss below.

Fig. 4
figure 4

Asymptotic radial profile of cathode sheath voltage drop. Regular mode (500 A and 60 NLPM of argon) and high-power mode (675 A and 85 NLPM of argon)

Full size image
Fig. 5
figure 5

Asymptotic radial profile of the Schottky reduction in the work function of cathode surface. Regular mode (500 A and 60 NLPM of argon) and high-power mode (675 A and 85 NLPM of argon)

Full size image
Fig. 6
figure 6

Asymptotic radial profile of the electron temperature on cathode surface. Regular mode (500 A and 60 NLPM of argon) and high-power mode (675 A and 85 NLPM of argon)

Full size image
Fig. 7
figure 7

Asymptotic radial profiles of electric current density components on the cathode surface. Regular mode (500 A and 60 NLPM of argon) and high-power mode (675 A and 85 NLPM of argon)

Full size image

During each external iteration between the cathode sheath model and two-temperature torch model in Code_Saturne, the current density composition was recomputed. The resulting radial profiles of electric current density due to the thermionic emission, plasma ions, and back-diffused plasma electrons are shown in Fig. 7. At the same time, the superposition of the current density components calculated in the cathode sheath model must be equal to the current density calculated in the MHD model in Code_Saturne combined with the cathode sheath model shown in Fig. 8 according to Eq 1. This correspondence can be considered as another criterion of convergence. In general, the deviations were in the range ± 2%. The current density radial profiles from the model without the cathode sheath are also shown in Fig. 8 to demonstrate the difference between the two simulated configurations of the plasma-cathode coupling.

Fig. 8
figure 8

Radial profiles of electric current density on the cathode surface calculated in the two-temperature MHD model with and without cathode sheath model. Regular mode (500 A and 60 NLPM of argon) and high-power mode (675 A and 85 NLPM of argon)

Full size image

When the final radial profiles of the sheath voltage drop (Fig. 4) and electron temperature on the cathode surface (Fig. 6) were introduced into the two-temperature torch model, the cathode arc attachment became more constricted with a significantly higher electric current density at the cathode tip as seen in Fig. 9.

Fig. 9
figure 9

Electric current density streamlines at the cathode tip calculated in the two-temperature MHD model without (left) and with (right) cathode sheath model. Regular mode (500 A and 60 NLPM of argon)

Full size image

The stronger cathode arc attachment constriction with the cathode sheath model resulted in a higher self-induced magnetic field, Joule power and, therefore, higher plasma temperature near the cathode tip as seen in Fig. 10 and 11. The maximum plasma temperature increased by about 2000 K. It should be noted that the plasma temperature at the nozzle exit is very close in both cases with and without cathode sheath model.

Fig. 10
figure 10

Self-induced magnetic field calculated in the two-temperature MHD model without (top) and with (bottom) cathode sheath model. Regular mode (500 A and 60 NLPM of argon)

Full size image
Fig. 11
figure 11

Electron temperature calculated in the two-temperature MHD model without (top) and with (bottom) cathode sheath model. Regular mode (500 A and 60 NLPM of argon). The electron temperature in the cathode and anode is identical to the heavy species temperature

Full size image

The higher Joule power and plasma temperature with the cathode sheath model resulted in a higher heat flux due to the plasma radiation on the neutrode surface as seen in Fig. 12.

Fig. 12
figure 12

Heat flux due to the plasma radiation on the neutrode and anode surface calculated in the two-temperature MHD model without (top) and with (bottom) cathode sheath model. Regular mode (500 A and 60 NLPM of argon)

Full size image

The two-temperature torch model with the cathode sheath predicted a twofold increase in the total heat flux to the cathode at the center of the cathode tip (R < 0.7 mm) and a threefold decrease in the periphery of the cathode (2 mm < R < 4 mm) in both regular and high-power modes as it can be seen in Fig. 13. The change in the total heat flux in the periphery has a much higher impact compared to the total heat flux at the cathode tip center due to the larger surface area of the periphery. The threefold decrease in the total heat flux in the periphery led to a cathode surface temperature generally lower with the cathode sheath model. After the radial profiles of the cathode sheath were introduced, the cathode surface temperature decreased by about 500 K in the periphery in both the regular and high-power modes and by 150 K and 100 K at the cathode tip center in the regular and high-power modes, respectively. as can be seen in Fig. 13. The decrease in the temperature at the cathode tip center was less significant due to the much higher total heat flux with the cathode sheath at the cathode tip center. As a result, a much more significant peak at the center can be seen in the radial profiles of the temperature and total heat flux on the cathode surface with the cathode sheath. The radial profiles of the temperature and total heat flux on the cathode surface without the cathode sheath are flatter and exhibit a plateau over the whole flat part of the cathode tip (R < 1.6 mm). However, the maximum cathode temperature was below 3695 K, the melting point of tungsten, in all the model configurations as shown in Fig. 13. This agrees with the observations of a brand-new cathode tested for 5 min, which can be seen in the bottom of Fig. 13. In addition, the cathode tested for 60 min exhibited some superficial melting at the center of the cathode tip due to the probable local superficial depletion of the dopant (Fig. 13, middle), which matches better with the more pronounced central maxima in the cathode surface temperature and total heat flux distributions from the model with cathode sheath. However, dopant depletion was not considered in the model and its effect could not be modeled directly.

Fig. 13
figure 13

Radial profiles of the surface temperature and total heat flux on the cathode tip calculated in the two-temperature MHD model with and without the cathode sheath model. Comparison with cathodes tested for 5 and 60 min in the regular mode (500 A and 60 NLPM of argon). The spatial scale of the photographs is the same as that in the radial profiles shown above. Courtesy of Oerlikon Metco

Full size image

Both tested cathodes exhibited a jagged edge between the flat and conic parts of the cathode tip. This jagged edge matches with the peak in the heat flux shown in Fig. 13 predicted in both cases with and without cathode sheath model. As was noted in Ref 3, this jagged edge appears to be the result of tungsten recrystallization which was not accounted for in the model. The cathode surface temperature predicted in both cases is sufficient for recrystallization to occur. However, the cathode surface temperature predicted in the case with cathode sheath model did not exhibit any peak in the cathode surface temperature at the edge of the flat cathode tip.

The torch voltage predicted by the two-temperature MHD model with and without the cathode sheath and experimentally measured directly on the torch is given in Table 2. The torch voltage under the considered operation modes was steady. The way the voltage was measured specifically on the torch is described in Ref 3. As seen in Table 2, the cathode sheath model reduced the error in the predicted voltage from 7% in the regular mode and 6% in the high-power mode down to 1% in both modes. The error in the voltage predicted by the model without cathode sheath could be also conditioned by the assumed constant value of cathode sheath voltage drop.

Table 2 Torch voltage and cooling loss in the torch measured experimentally and predicted in the two-temperature MHD torch model with and without cathode sheath model
Full size table

Another important indicator of the torch operation was the cooling loss in the torch. It is essential to differentiate the cooling loss in the torch from the cooling loss in the whole plasma spray system which is usually indicated by the monitoring unit of the system (called JAMbox in Oerlikon system). In order to obtain the cooling loss in the torch, the cooling loss in the cables/hoses must be subtracted from the cooling loss in the whole system. The cooling loss in the cables/hoses equals the product of the current intensity and voltage drop on the cables/hoses. The latter equals the difference between the voltage measured in the monitoring unit and voltage measured directly on the torch. The values of the experimental cooling loss in the torch, determined based on the calculated cooling loss in the cables, together with the cooling loss predicted by the two-temperature MHD model with and without the cathode sheath, are given in Table 2. As it can be seen from these values, the cathode sheath model reduced the error in the predicted cooling loss in the torch from 2% in the regular mode and 6% in the high-power mode down to 1% in both modes. The way the cooling loss in the torch was calculated in the model without the cathode sheath is detailed in Ref 3. In the torch model with the cathode sheath, the heat transfer to the cathode was calculated according to Eq 8, while for the anode, the calculation method was the same as in Ref 3.

Thus, the incorporation of the cathode sheath into the two-temperature MHD model improved the accuracy of the predicted arc voltage and eliminated the assumed constant sheath voltage drop taken from the literature.

After the cathode sheath was incorporated into the two-temperature MHD model, the total input power of 35,000 W became much closer to the dissipated power of 34,933 W in the regular operation mode (500 A and 60 NLPM of argon). Hence, the thermal balance in the torch improved and the mismatch decreased down to 0.2%.

Conclusion

The previously developed two-temperature MHD model of the electric arc plasma torch, which has already shown higher accuracy in predicting the anode arc attachment compared to the LTE model, was complemented by a non-equilibrium cathode layer model, also called cathode sheath model. This model took into account the space-charge layer and ionization layer adjacent to the cathode surface that cannot be simulated by a two-temperature electric arc model.

Improved coupling at the cathode-plasma interface with the implementation of a cathode sheath model in a two-temperature model of the electric arc resulted in predictions of the torch voltage and cooling loss in the torch closer to the experimental values. The prediction error decreased from 7% in the regular mode and 6% in the high-power mode down to 1% in both modes for the torch voltage and from 2% in the regular mode and 6% in the high-power mode down to 1% in both modes for the cooling loss. The cathode sheath model changed not only the predicted operation indicators, but also the cathode arc attachment in general and the maximum electric current density and plasma temperature in particular. The cathode arc attachment with the cathode sheath model became more constricted; the maximum current density on the cathode surface and maximum plasma temperature near the cathode tip increased.

The cathode surface temperature predicted by the torch model with the cathode sheath was lower than that predicted by the model without the sheath over the whole surface of the cathode. The cathode temperature distribution from the two-temperature MHD model with the cathode sheath matched the experimental observations of a cathode tested for 60 min better than the distribution predicted by the two-temperature MHD model without the cathode sheath. However, the predicted maximum cathode temperature in both modes of operation was below the melting point of tungsten, probably because the cathode dopant depletion was neglected in the model.

The error in the thermal balance in the torch model decreased from 4% down to 0.2% in the regular operation mode after the cathode sheath model was introduced in the cathode-plasma coupling.

The obtained results show that the cathode sheath model is important when the phenomena inside the torch are studied, for example, during the development or improvement process of a plasma torch. However, the plasma temperature at the nozzle exit is not sensitive to the consideration of the cathode sheath.

Further developments of this torch model include (i) model validation with other gas flow rates and power output levels, (ii) application of the model to gas mixtures, e.g., argon and hydrogen, (iii) testing the model on other geometry configurations and other plasma torches, (iv) consideration of the presheath thickness in the cathode sheath model as was done by Gonzalez et al. (Ref 22) to improve the calculation of thermal balance at the cathode-plasma interface, v) consideration of cathode dopant diffusion (Ref 27, 28) and (vi) more detailed model of the anode non-equilibrium layer (Ref 47, 48).

Ultimately, the model should become a design tool for the development of new plasma torches and provide plasma flow parameters to other models for developing plasma spray applications.