Abstract
The Valles Marineris Explorer Cooperative Swarm navigation, Mission and Control research project aims to explore the Valles Marineris canyon system on Mars with, among others, multibody rotary-wing unmanned aerial vehicles (UAVs) comprising of a hexrotor system and a helium-filled balloon being attached to it by means of a rope. In this paper, we develop a high-fidelity closed-loop control system in MATLAB® and Simulink™ to present the application of an adequate flight controller guaranteeing (1) asymptotic tracking position control of the multibody flight system, (2) suppression of the balloon’s swinging motion in forward flight case, and (3) stabilization of the rope angle around its equilibrium for steady-state conditions. Applying feedback linearization for the outer loop and analytical backstepping for the inner loop of a nonlinear cascaded control design model of the hexrotor system, we propose an extension of the baseline flight controller by two artificial augmentation approaches to cope with the balloon dynamics. Basically, by utilizing oscillation damping feedbacks of the uncertain plant which are applied as additional commands to either the inner or the outer loop’s reference model. Simulation results are presented for an eight-shaped flight maneuver at the bottom of Valles Marineris proving that the augmentation units increase the flight controller capabilities to suppress modeling errors artificially—without changing the baseline control laws. The augmentation units actively damp the balloon motion in the forward flight case for non-steady-state conditions to counteract the rope oscillations and finally stabilize the rope angle around its equilibrium, so that the Mars vehicle is able to reach a steady-state in position when its extraterrestrial mission profile is successfully completed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Deeper questions that arise in countless scientific reports [1, 2] or [3] deal with the origin and evolution of life: How did life begin and where did it originate if not on Earth? These are questions that perplexed scientists for a long time and, eventually on account of that, triggered a wide search for extinct organisms on other planets in our solar system. The most promising terrestrial planet to solve this gap in understandings of humanity is Mars.
Valles Marineris Explorer Cooperative Swarm navigation, Mission and Control, in short called VaMEx-CoSMiC or VaMEx, is a German research project which was started in 2012 to focus on the exploration of the red planet or rather the Valles Marineris. Until today, the Valles Marineris is stated to be the largest canyon system in our solar system providing geological peak values of ~3000 km length, ~600 km width, and ~11 km depth in total. It is located in the southern hemisphere of the planet parallel to its equatorial axis and expands roughly from 0° to 20° S and from 50° to 90° W excluding the Tharsis region in the West. Due to the deep cliffs and fractured rock layers, geologists are hoping to reveal new insights into the history of Mars and find evidence for microbial life or even petrified microorganism being hidden into the Martian crust. The key purpose of VaMEx is therefore to develop, compare, and evaluate technologies for an unmanned autonomous robotic swarm mission exploring the Valles Marineris. Within the project, the Institute of Flight System Dynamics (FSD, TU Munich) is, inter alia, responsible for the design of rotary-wing platforms being used as swarm participants and their embedment into a high-fidelity simulation environment. This incorporates a model-based plant design of the flying platform and the derivation of a suitable flight controller both forming the closed-loop control system [4,5,6].
Regarding the thin atmosphere on Mars, the development of a fully operational multicopter concept is quite a difficult task. Since all propellers’ require high-density values to produce sufficient thrust, only the deepest points are investigated for an extraterrestrial mission profile leading to a geographic location of 14.035° S and 58.5° W at the bottom of Valles Marineris with an average height \({h}_{\mathrm{avg}}\) of −4907 m below the Martian geoid. At the FSD, conceptual studies for this given design point were conducted by [7] to determine a first suitable solution for a Martian rotary-wing unmanned aerial vehicle (UAV) being depicted in Fig. 1. A MATLAB®-based scalable, parametric design tool [8] was invented afterwards to reevaluate different vehicle configurations. As an ultimate version, a 6-rotor UAV with a balloon being attached to it by means of a flexible rope was chosen as most appropriate solution. The balloon provides additional buoyancy for the vehicle leading to an enhancement of the actuators’ battery lifetime and thus to a total flight time improvement.
VaMEx project emblem [6]
1.1 Literature overview
In the literature, several conceptual studies besides VaMEx exist to determine the optimal design of a flying platform on Mars as in [9]. In addition to rotary-wing UAV concepts, the Martian Autonomous Rotary-Wing Vehicle (MARV) [10], the Mars Helicopter Scout [11], or a meso-scaled 4-rotors UAV concept called Mesicopter [12] were published among many other concepts.
Flight control approaches for those Martian UAVs as well as their dynamic modeling into a simulation environment are rare to find in literature—not to mention multibody rotary-wing concepts like the proposed Mars vehicle of Sect. 1. Only limited data have been published [11, 12] which does not vary widely from terrestrial procedures. Based on these findings, we conclude that terrestrial methods for modeling UAV dynamics, incorporated control strategies, and their simulative setup, e.g., within MATLAB® and Simulink™, can likewise be used to build a virtual flight control system for Martian rotorcraft. As state-of-the-art simulation framework, the FSD Simulation Environment (FSDSE), which incorporates a high-fidelity six degree of freedom rigid-body model, is studied and used to develop a Martian simulation environment which meets the requirements of the VaMEx-CoSMiC project. Successful applications of the FSDSE are, e.g., given in [13, 14] and a comprehensive model description is given in [15]. A summary of commonly used approaches to design, model, and control terrestrial hybrid UAVs was conducted by [16]. Our main distinctions within the stated methods are reflected by three key issues:
First, we address the embedment of a realistic atmospheric model which is built on high-resolution atmospheric measurement data being smoothed and prepared by a meteorological database of Mars to best fit 14.035° S and 58.5° W, the vehicle’s geographic take-off location at Valles Marineris. Due to the low Reynolds numbers, propellers are not able to rotate as fast as on Earth which was also the most challenging factor presented in [10].
Second, we propose a procedure to develop a nine degrees of freedom multibody UAV model which relies on the classical Newtonian formulations in which a six degrees of freedom rigid-body model for the multirotor system and a three degrees of freedom point-mass model for the balloon are afflicted with one kinematic constraint each. The suspension line, or rather rope, is enforced with one kinematic constraint at each coupling point being obtained by a massless spring-damper oscillator model. This model significantly aids in the design of multibody dynamics which are, in general, derived with analytical mechanics leading to complex first- or second-order differential equations. For instance, the governing motions for comparable dynamic models as, e.g., a multibody Parafoil-UAV are obtained using either Lagrange’s equations, shown in [17], or the Hamiltonian procedure, published in [18]. In [19], Lagrange’s equations are likewise used to obtain the dynamic model system formulations of a multibody quadrotor UAV with cable-suspended payload.
Third, and main contribution of this paper, we present a flight controller which is capable to handle multibody flight dynamics guaranteeing
-
(i)
Asymptotic tracking position control of the multirotor system, while damping the suspension line oscillations simultaneously.
-
(ii)
Suppression of the balloon’s swinging motion in forward flight case.
-
(iii)
Stabilization of rope angle around its equilibrium for steady-state conditions.
Among a greater diversity of nonlinear flight controllers, Backstepping [20] and Nonlinear Dynamic Inversion (NDI) [21] are two of the most widely used control design methodologies for agile multirotor systems. Examples of successful applications are, e.g., given in [14, 22,23,24,25,26]. Essentially, Backstepping is a model-based approach to obtain, based on control-Lyapunov functions [20], asymptotical closed-loop stability of a feedback control system which provides a so-called strict feedback form [20], whereas NDI is a state transformation which ensures, without any approximations, linear input–output dynamics of a nonlinear system. It is therefore often called Feedback Linearization [21]. A comparison between NDI and analytical backstepping was conducted by [27] showing that both methods ensure the same satisfying controller performance for agile multirotor systems. Thus, in this paper, we propose a nonlinear flight controller which is a cascaded version of a backstepping-based attitude controller nestling inside a superior position controller, which is based on NDI, to meet objective (i).
The idea of both backstepping and NDI methodologies is, in general, to make a dynamic system or rather its state trajectory follow a desired reference trajectory by determining an appropriate control law. In case of uncertain dynamic systems, however, modeling errors are inevitable within the control design model which leads to a mismatch between the state and reference trajectory. A common approach to cope with modeling errors is to augment the baseline flight controller architecture for addressing secondary controller capabilities as stated in (ii) and (iii).
The first, and perhaps most intuitive, approach is to augment the baseline flight controller by input shapers [28] which are, e.g., used in multibody quadrotor UAVs with suspended load [29] or in helicopter slung load systems [30] to damp the swinging motion. Input shaping is a powerful feedforward technique where the natural frequency and damping ratios are estimated from the linearized well-known plant dynamics to determine an oscillation damping command being applied to the reference model. Since the actual reference model remains open-loop, robustness of this technique is often achieved by adding a delayed feedback of the uncertain plant to the closed-loop control system which is related to the theory of delayed feedback control [31]. This feedback is then added to the feedforward reference trajectory which results in an active vibration-damping and also delayed reference signal. Similar to the input shaping technique, control design parameters have to be determined from a linearized state-space model, where the actual time-delay needs to be modeled. Examples of successful applications are, e.g., given in [32] for container cranes or in [31, 33, 34] for helicopter slung load systems to actively damp the swing motion. In [24], a comparison between the usage of input shaping, delayed feedback control, and a combination of both techniques showed that the input shaping is indeed advantageous in suppressing unintended swing motions for a multibody hexrotor UAV with cable-suspended load, but also, that a delayed feedback controller pose a powerful standalone augmentation approach to address the controller capabilities (ii) and (iii).
In this paper, we summarize the nonlinear dynamic effects of the plant, being represented by oscillating motion of the suspension line, as uncertainties and suppress them by augmenting either the inner loop or outer loop’s reference model with oscillation damping feedbacks which are applied as additional commands to solve objective (ii) and (iii). Although this method is in the spirit of delayed feedback controllers [31], the augmentation signals are not subjected to time-delays. Additionally, we directly augment the input signals of the reference model which generates a closed-loop including both the uncertain plant and the reference model. The proposed artificial augmentation units are therefore assigned to the classical theory of closed-loop reference models [35, 36] which have their origin in the framework of adaptive control [37, 38]. In literature, augmentation approaches for multibody UAVs which explicitly use the theory of closed-loop reference models to satisfy the controller’s capabilities (ii) and (iii) could not have been identified.
1.2 Outline
The remainder of this paper is organized as follows: The plant design of the multibody Mars vehicle is presented in Sect. 2. Section 3 reviews the nonlinear control design model and derives the baseline flight controller. Two oscillation damping feedback augmentation approaches are presented in Sect. 4, both extending the baseline flight controller separately. Simulation results are stated in Sect. 5 to validate the control design including the artificial augmentation units. Section 6 summarizes the stated findings and provides a short conclusion.
2 Plant design
The Mars vehicle is modularly implemented into MATLAB® and the Simulink™ toolbox as multibody UAV forming the plant of the closed-loop control system. It consists of two nonlinear UAV models, a six degrees of freedom (6DoF) rigid-body model for the multicopter and a 3DoF point-mass model for the balloon. Both models are additionally afflicted with kinematic constraints to not only generate a linked connection, but also to support a modular design process. The general structure is depicted in Fig. 2. The high-fidelity simulation model consists of four main submodels, the environment submodel, the equations of motion (EoM), the multibody system formalism, and the airframe submodel. Its baseline architecture is inspired by the FSDSE [15].
Using the state-space model representation, the multirotor system is input affine in
the system’s commanded input vector, containing the square of the actuators’ commanded rotational speeds \({\omega }_{c,i}\in {\mathbb{R}}\). Its system dynamics can be described by
as well as the autonomous balloon system dynamics are described by
To uniquely describe the current situation of both dynamic systems for an arbitrary point in time, the multicopter state vector \({\varvec{x}}\in {\mathbb{R}}^{12}\) includes the position \({{\varvec{r}}}^{R}\in {\mathbb{R}}^{3}\), the kinematic velocity \({{\varvec{v}}}^{R}\in {\mathbb{R}}^{3}\), the angular rates \({{\varvec{\omega}}}^{IB}\in {\mathbb{R}}^{3}\), and the Euler Angles \({\varvec{\eta}}\in {\mathbb{R}}^{3}\) as attitude representation. The balloon state vector \({{\varvec{x}}}_{Bal}\in {\mathbb{R}}^{6}\) only includes the position \({{\varvec{r}}}^{Q}\in {\mathbb{R}}^{3}\) and the kinematic velocity \({{\varvec{v}}}^{Q}\in {\mathbb{R}}^{3}\). Summarizing both state vectors to \({{\varvec{x}}}_{P}={\left[\begin{array}{cc}{\varvec{x}}& {{\varvec{x}}}_{Bal}\end{array}\right]}^{T}\), the total plant state vector, it is possible to write the plant system dynamics to
so that the system output equation is given by
To determine the current plant state vector \({{\varvec{x}}}_{P}\)(t + ∆t) only by means of the last known plant state vector \({{\varvec{x}}}_{P}\)(t), Simulink™ provides a broad range of higher order ordinary differential equation (Ode) solvers like Ode4 which is based on the fourth-order Runge–Kutta method [39]. In contrast to first-order Ode solvers, where Euler's integration [39] serves as a base, the Ode4 solver determines an averaging value for the plant state vector's derivative \({\dot{{\varvec{x}}}}_{P}\)(t) at exactly four weighted sampling points. This not only ensures a higher accuracy to solve, respectively, propagate the UAVs' nonlinear state equations numerically, but also upholds the fact that \({\dot{{\varvec{x}}}}_{P}\)(t) is usually not constant during a time increment of ∆t. To build a time-history simulation [39], Ode4 is used as numerical integration method with a fixed sampling time ∆t of 0.001 s to step the plant state vector forward.
2.1 Environment submodel
To ensure that the multibody UAV can be simulated under realistic environmental conditions of planet Mars, a Martian Standard Atmosphere (MSA) is implemented inside the environment submodel which is related to the multicopter reference point R.
This atmospheric model is built on high-resolution atmospheric measurement data being smoothed and prepared by the Martian climate database (MCD) V5.2 [40]. For altitude definitions, a Martian reference ellipsoid with a geocentric radius \({r}_{M}\) of 3394.6 km is established which is based on the concept of the World Geodetic System 84 [41]. The obtained ellipsoid best fits the geographic location of 14.035° S and 58.5° W at the Valles Marineris, while its semi-major axis \(a\) equals 3396.2 km and the square of its first eccentricity \({e}^{2}\) equals 0.0117. This reference surface also defines the normal gravity potential \({g}_{0}:=3.717 \,\mathrm{m}/{\mathrm{s}}^{2}\) being required for the 1D quadratic gravitation model [42, 43].
In addition to seasonal and diurnal changes, the MSA is related to a Martian solar longitude of \(359^\circ\) and a local true solar time of \(12:00\) in Mars year 24. Regarding the vertical extension of the Valles Marineris, the crucial part of the MSA forms the Martian troposphere which can be considered as real polytropic up to a height of ~\(6.4 \,\mathrm{km}\) above the ground. Meteorological studies yield that the decrease of atmospheric temperature with altitude can be represented by two major dry adiabatic lapse rates [44] (DALRs) [40].
-
\({\Gamma }_{l}=2.99\frac{\mathrm{K}}{\mathrm{km}}\) for {\({H}_{G}\in {\mathbb{R}}\)|-\(5000 \,\mathrm{m}\)<\({H}_{G}\)≤\(1183\mathrm{ m}\)}
-
\({\Gamma }_{\mathrm{up}}=0.74\frac{\mathrm{K}}{\mathrm{km}}\) for {\({H}_{G}\in {\mathbb{R}}\)|-\(1183 \,\mathrm{m}\)<\({H}_{G}\)≤\(6405 \,\mathrm{m}\)}
very precisely, so that the Martian troposphere is divided into two layers, the lower Martian troposphere (index l) and the upper Martian troposphere (index up). Due to both constant DALRs, the barometric formula [42]
can be solved analytically which, in terms of the ideal gas law [44], leads to all formulas for atmospheric changes relative to the geopotential height [42]
where \({h}^{R}\) is the geodetic height of the multirotor system above the reference ellipsoid. A summary is listed in Tables 1 and 2 where \(T,\ p\), and \(\rho\) denoting the atmospheric temperature, pressure, and density as well as \(\mu\) represents the dynamic viscosity on Mars.
A proof, that the atmospheric model maps the MSA V5.2 measurement data with high accuracy is shown in Fig. 3. The only rough distinctions can be identified at ground level of Valles Marineris, due to the temperature ground effect as a result of cosmic radiation on Mars, and for heights beyond the upper Martian troposphere. These model uncertainties of the MSA are excluded within the flight envelope of the Mars vehicle, since simulation results are only evaluated from an average height \({h}_{\mathrm{avg}}\) of −4907 m below the Martian geoid. Therefore, they can be neglected for further investigations.
2.2 Equations of motion
For describing the state equations of the multirotor system, we use a body-fixed (B) frame and a North-East-Down (I) frame as reference frames being depicted in Fig. 4. The multicopter reference point R denotes the origin of the B-frame and is assumed to be congruent with its center of gravity G. This yields decoupled differential equations for the translation and rotation dynamics. The I-frame is located on the surface of Valles Marineris and has a non-relocatable placement at the multirotor system’s point of departure. Its \(x\)–\(y\)-plane is parallel to the local surface whereby the \({x}_{I}\)-axes points to the Martian north pole. By assuming that planet Mars is non-rotating and flat, without any elliptical shape, the I-frame is considered as inertial and can be used to apply Newton’s second law of motion [39]. The state propagation equations for position, translation, rotation, and attitude can thus be formulated by
whereby \({\varvec{I}}\in {\mathbb{R}}^{3x3}\) is the identity matrix and \({\varvec{H}}\left({\varvec{\eta}}\right)\in {\mathbb{R}}^{3x3}\) is given by
In Eq. (8), \(m=2.317 \,\mathrm{kg}\) denotes the total mass of the multirotor system including \(0.2 \,\mathrm{kg}\) of payload, \({{\varvec{F}}}^{R}\in {\mathbb{R}}^{3}\) and \({{\varvec{M}}}^{R}\in {\mathbb{R}}^{3}\) the total amount of all external forces and moments related to R, and \({{\varvec{J}}}^{R}\) represents the multicopter’s mass moment of inertia tensor which is approximately given by \(\mathrm{diag}\left(\begin{array}{ccc}0.131 \,\mathrm{kg}{\,\mathrm{m}}^{2}& 0.131 \,\mathrm{kg}{\,\mathrm{m}}^{2}& 0.261 \,\mathrm{ kg }{\,\mathrm{m}}^{2}\end{array}\right)\in {\mathbb{R}}^{3x3}\). To describe the attitude of the multirotor system, \({\varvec{\eta}}={\left[\begin{array}{ccc}{\Phi}& {\Theta}& {\Psi}\end{array}\right]}^{T}\in {\mathbb{R}}^{3}\) is defined as vector of Euler angles, where \(\Psi \in \left[-\pi; \,\pi \right]\) denotes the azimuth angle, \(\Theta \in \left[-\pi; \,\pi \right]\) represents the pitch angle, and \(\Phi \in \left[-\pi; \,\pi \right]\) symbolizes the roll angle. Together, they constitute the rotation matrix \({{\varvec{R}}}_{IB}={{\varvec{R}}}_{z}\left(-\Psi \right){{\varvec{R}}}_{y}\left(-\Theta \right){{\varvec{R}}}_{x}\left(-\Phi \right)\in {\mathrm{SO}}^{3}\) which maps a vector from the B-frame into the I-frame. To avoid the inherent singularity of Eq. (9) for \(\Theta =\pm \,\uppi /2\), the simulation model can be switched—based on the configuration values (see Fig. 2)—to quaternions [15] being used as 4-dimensional representation to describe the orientation of the multirotor system. In addition to the environment submodel of Sect. 2.1, the multicopter’s differential equation for its geodetic height is given by
where \({\dot{h}}^{R}\) denotes the time derivative of the geodetic height with respect to the I-frame being required for altitude definitions above the reference ellipsoid.
To describe the sate propagation equations of the balloon point-mass model, we choose Q as reference point and use a second body-fixed coordinate frame, the BBal-frame, to formulate its dynamics. The state propagation equations for position and translation are thus given by
where \({m}_{Bal}=0.06 \,\mathrm{kg}\) denotes the balloon mass and \({{\varvec{F}}}^{Q}\in {\mathbb{R}}^{3}\) the total amount of all external forces related to Q. In relation to Sect. 2.1, the balloon’s differential equation to propagate its geodetic height \({h}^{Q}\) can be formulated to
where \({\dot{h}}^{Q}\) denotes the time derivative of \({h}^{Q}\) with respect to the I-frame being required for altitude definitions above the reference ellipsoid.
2.3 Multibody system formalism
Complex first- or second-order differential equations do usually occur while working with multibody dynamics. These equations do not only require a lot of computing power, it is also much more difficult to maintain an analytical formulation using, e.g., the theory of virtual work [45] or the Lagrange equations [45], respectively, solving them. In this paper, we use the classical Newtonian formulations to impose kinematic constraints on both dynamic systems \(\dot{{\varvec{x}}}\) and \({\dot{{\varvec{x}}}}_{Bal}\) as massless spring-damper oscillator (SDO) model to approximate a realistic rope connection. This SDO model triggers \({{\varvec{F}}}_{rp}^{R}\in {\mathbb{R}}^{3}\) and \({{\varvec{F}}}_{rp}^{Q}\in {\mathbb{R}}^{3}\), the rope reaction forces, and adds them—as part of the airframe submodel—to the total amount of applied forces \({{\varvec{F}}}^{R}\) and \({{\varvec{F}}}^{Q}\) acting on both dynamic systems. For describing the kinematics of the SDO model, the multicopter rope (R*) frame as well as the balloon rope (R*Bal) frame are introduced as reference frames. Both R*- and R*Bal-frame are moving freely with the UAVs’ reference point while serving the following properties (see Fig. 4):
-
The \({x}_{{R}^{*}}/{x}_{{R}_{Bal}^{*}}\)-axis is always pointing in the rope’s direction of action.
-
The \({y}_{{R}^{*}}/{y}_{{R}_{Bal}^{*}}\)-axis is always aligned with the \({x}_{B}{y}_{B}/{x}_{{B}_{Bal}}{y}_{{B}_{Bal}}\)-plane.
-
The \({y}_{{R}^{*}}/{y}_{{R}_{Bal}^{*}}\)-axis and the \({z}_{{R}^{*}}/{z}_{{R}_{Bal}^{*}}\)-axis forming a right-hand coordinate system.
To describe the orientation of the resulting rope force relative to the B- and BBal-frame, \({\chi }_{{R}^{*}}\) and \({\gamma }_{{R}^{*}}\), respectively, \({\chi }_{{R}_{Bal}^{*}}\) and \({\gamma }_{{R}_{Bal}^{*}}\), are defined as rope angles. Together, they constitute the rotation matrix \({{\varvec{R}}}_{{R}^{*}B}={{\varvec{R}}}_{y}\left({+\gamma }_{{R}^{*}}\right){{\varvec{R}}}_{z}\left({\chi }_{{R}^{*}}\right)\in {\mathrm{SO}}^{3}\), respectively, \({{\varvec{R}}}_{{R}_{Bal}^{*}{B}_{Bal}}={{\varvec{R}}}_{y}\left({-\gamma }_{{R}_{Bal}^{*}}\right){{\varvec{R}}}_{z}\left({\chi }_{{R}_{Bal}^{*}}\right)\in {\mathrm{SO}}^{3}\), which are given through the geometric vector chains
and
whereby \({\varvec{I}}\in {\mathbb{R}}^{3x3}\) is the identity matrix. The multicopter rope angles can thus be calculated to
as well as the balloon rope angles to
2.3.1 Design of spring force
To design the spring force for the SDO model, it is assumed that a spring produces a restoring force proportional to its deflection \(\tilde{l }\). In case of the multicopter, \(\tilde{l }\) can be calculated through \(\Vert {\left({{\varvec{r}}}^{RQ}\right)}_{B}\Vert\) as well as \(\tilde{l }\) is determined by \(\Vert {\left({{\varvec{r}}}^{QR}\right)}_{Bal}\Vert\) for the balloon UAV. Using Eqs. (13) and (14), this leads to a spring force of [45]
for the multirotor system and likewise
for the balloon, where \({l}_{0}=5 \,\mathrm{m}\) implies the virtual spring’s norm length. Since the rope should act in a naturally flexible manner, the spring design may not be too stiff. The virtual spring stiffness \({k}_{\mathrm{sp}}\) is therefore chosen to equal \(0.5 \,\mathrm{kg}/{\mathrm{s}}^{2}\) which will, in the end, confer a smooth oscillating behavior to the SDO model. Regarding Eqs. (17) and (18), \(\varepsilon\), or rahter, \({\varepsilon }_{Bal}\) are both logical operators ensuring that only positive spring forces are transmitted by the rope. Otherwise, pushing forces would act on both UAVs for \(\tilde{l }\) being smaller than \({l}_{0}\) which is not desired. Thus
can be defined for the multicopter as well as
for the balloon UAV.
2.3.2 Design of damper force
To design the damping force for the SDO model, it is assumed that a damper always produces a force acting in opposite direction of its movement [45]. The damping force depends therefore on the UAVs’ change of position over time in rope direction which are given by
for the multirotor system and
for the balloon. Otherwise, kinematic velocity elements of multicopter or balloon in non-rope direction would wrongly lead to a damping force which is not desired. Based on the R*- and R*Bal-frame properties and coordinate definitions, the damping force of the SDO model can be formulated to
for the multicopter and likewise
for the balloon, where \(\varepsilon\), or rather, \({\varepsilon }_{Bal}\) are already predefined by Eqs. (19) and (20) ensuring that damping forces only occur, while the rope is oscillating due to a positive spring force. Furthermore, \({d}_{\mathrm{dp}}\) implies the virtual damping constant which is chosen to equal \(0.75 \,\mathrm{kg}/\mathrm{s}\). This choice of parameter is synergetic with the spring design of Sect. 2.3.1, so that a smooth oscillating behavior is damped in a short time period.
2.3.3 Rope force of SDO model
To design the rope force for the SDO model we simply use Eqs. (17) and (23), or rather, (18) and (24) and add them as part of a vector summation. In addition to the multicopter, it directly follows:
for its rope force being notated in the B-frame, as well as
for the balloon’s rope force being notated in the BBal-frame.
2.4 Airframe submodel
The airframe is the most extensive submodel in the plant. Its outputs are strongly interrelated to the EoM submodel of Sect. 2.2, since the state equations of multicopter and balloon can only be propagated with the total sum of all external forces and moments acting on the UAVs. The airframe’s task is to provide and prepare them. As the Martian density is most crucial to produce buoyancy for the balloon UAV, or rather, has a linear dependency to the thrust equation of the propellers, the airframe submodel is mainly depending on the MSA being embedded in the environment submodel (see Sect. 2.1).
In case of the multirotor system, all external forces and moments are given by
and
being subdivided into their physical types of origin which are propulsion (P), aerodynamics (A), gravity (g), ground contact (C), and rope (rp). To formulate the multicopter’s gravity force, we use the 1D quadratic gravitation model [42]
Since R is assumed to be congruent with the multicopter’s center of gravity, the gravitational force as well as the rope force, given by Eq. (25), induce no moments in Eq. (28) and therefore only contribute to the balance of forces in Eq. (27). To design a simplified behavior for the multirotor system’s ground contact, four contact points \({{\varvec{r}}}^{{C}_{i}}\in {\mathbb{R}}^{3}\), each of them given by the vector summation of \({{\varvec{r}}}^{R}\) and \({{\varvec{r}}}^{{RC}_{i}}\), are defined as landing gear exerting the total contact force
as well as the total contact moment
on the vehicle if, and only if, the vehicle is in direct contact with the valley surface of Valles Marineris. The particular contact force of each contact point \({{\varvec{F}}}^{{C}_{i}}\in {\mathbb{R}}^{3}\) is composed of frictional forces [45] in the \({x}_{B}\)-\({y}_{B}\) plane and an impact force in \({z}_{B}\)-direction both counteracting the vehicle’s movement. Since we assume that the landing gear carries the vehicle mass equally, i.e., each landing gear leg carries one quarter of the vehicle’s gravitational force, given by Eq. (29), the contact force of each contact point can be formulated as [45]
where \({\mu }_{fr}\) represents the frictional coefficient which equals 100. Applying Euler’s classical treatment of vector analysis [39], the kinematic velocity of each contact point is given by
The propulsive forces and moments are produced by six propellers. Each of them provides two blades, a calculated density of \(240 \,\mathrm{kg}/{\mathrm{m}}^{3}\), a blade radius \({r}_{bl}\) of \(0.2055 \,\mathrm{m}\), and a mass inertia \({J}_{zz}=8.9\cdot{10}^{-4} \,\mathrm{kg}/{\mathrm{m}}^{2}\) around its rotational axis [8]. To avoid an inherent minus sign within the propulsion unit modeling, six propeller-fixed (Pi) frames are introduced, where the \({z}_{{P}_{i}}\)-axis is perpendicular to the \({x}_{B}\)–\({y}_{B}\) plane and points in direction of positive thrust. The corresponding rotation matrix from the body-fixed B-frame into the particular Pi-frame is therefore simply given by \({{\varvec{R}}}_{{P}_{i}B}={{\varvec{R}}}_{x}\left(\pi \right)\in {\mathrm{SO}}^{3}\) and, while using the Pi-frame as notation frame, the rotational speeds vector of each propeller can be written as \({{\varvec{\omega}}}^{{P}_{i}{Rot}}={\left[\begin{array}{ccc}0& 0& {{\varepsilon }_{act,i}\cdot\omega}_{i}\end{array}\right]}^{T}\in {\mathbb{R}}^{3}\) depending on \({\varepsilon }_{act,i}\), the actuators’ predefined direction of rotation with respect to the \({z}_{{P}_{i}}\)-axis. For rotor one, three, and five, \({\varepsilon }_{act,i}\) equals \(1\), whereas for rotor two, four and six, \({\varepsilon }_{act,i}\) equals \(-1\). Assuming that the position of each propeller \({{\varvec{r}}}^{{T}_{i}}\in {\mathbb{R}}^{3}\) is given by the vector summation of \({{\varvec{r}}}^{R}\) and \({{\varvec{r}}}^{{RT}_{i}}\), the total propulsive force in Eq. (27) can be formulated to
as well as the corresponding total propulsive moment in Eq. (28) can be determined by
In Eqs. (34) and (35), the thrust-generating force is the aerodynamic force of the propeller which is indicated by an index A. We derive this force from the Blade Element Momentum Theory [46] while assuming the propeller can be approximated by a circular disc providing an elliptical circulation distribution and therefore a constant induced velocity distribution in radial direction. Based on [46], the aerodynamic force of each propeller can be written to
where the thrust coefficient \({C}_{T}\) equals \(0.074\) [8]. In Eq. (35), the propulsive moment of each propeller \({{\varvec{M}}}_{T}^{{T}_{i}}\) is composed of a gyroscopic moment \({{\varvec{M}}}_{Gyro}^{{T}_{i}}\) as well as an aerodynamic moment \({{\varvec{M}}}_{A}^{{T}_{i}}\), which corresponds to Eq. (36) and can thus be formulated to
Here, \({C}_{n}\) denotes the torque coefficient and is given by \(0.0164\) [8]. Based on Euler’s classical treatment of vector analysis [39], the gyroscopic moment can be written to
where \({{\varvec{J}}}^{{T}_{i}}=\mathrm{diag}\left(\begin{array}{ccc}0& 0& {J}_{zz}\end{array}\right)\in {\mathbb{R}}^{3x3}\) is the propeller’s mass moment of inertia tensor and \({\dot{{\varvec{\omega}}}}^{{P}_{i}{Rot}}\) the propeller’s angular acceleration which is related to the actuator model.
A common approach to reproduce the actuator’s dynamic behavior is to filter the propeller’s angular rate by a PT1 element instead of modeling the actual electric drive. This PT1 filter, based on [47], is given as
where \({t}_{PT1}\) is the filter’s time constant which equals \(0.05 \,\mathrm{s}\) and \({{\varvec{\omega}}}_{c}^{{P}_{i}{Rot}}\in {\mathbb{R}}^{3}\) is the actuator’s commanded rotational speed vector being related to the vector elements of the system’s commanded input \({{\varvec{u}}}_{c}\), given by Eq. (1), through
where \({\omega }_{c,i}^{2}\in {{\varvec{u}}}_{c}\).
As the multirotor system has no lift-generating surfaces, except the thrust-producing propellers, the aerodynamic force in Eq. (27) is solely approximated by the body drag. Based on the static MSA of Sect. 2.1, the aerodynamic velocity of the multicopter is equal to its kinematic velocity. Since the aerodynamic reference point is assumed to be congruent with the multirotor system’s center of gravity, or rather R, the aerodynamic force is, based on [46], written to
where the dimensionless drag coefficients \({C}_{Dx}\) and \({C}_{Dy}\) are assumed to equal \(-0.06\), respectively \({C}_{Dz}\) to equal \(-0.13\). In Eq. (41), the reference area \({S}_{r}\) is given by \(1 {\,\mathrm{m}}^{2}\). Similar to the rope and gravitational force, the aerodynamic force induces no moments in Eq. (28).
For the balloon UAV the total sum of all external forces simplifies, in contrast to the multirotor system, to
where the rope force is provided through Eq. (26). Since the balloon has no thrust-producing propulsion unit, the aerodynamic force \({{\varvec{F}}}_{A}^{Q}\in {\mathbb{R}}^{3}\) is the solely force acting on the UAV. In Eq. (42), one part of this force is generated by the balloon’s buoyancy and the other part by its body drag. For the sake of simplicity, we assume that the balloon can be approximated by a spherical shape and that unheated helium (\({R}_{\mathrm{He}}=2077 \,\mathrm{J}/\mathrm{kg K})\) is used as carrier gas which is less dense than the surrounding atmosphere in the Valles Marineris. Since the modeling of the balloon includes an envelope which generates a gravitational force due to its mass, the balloon’s net buoyant force can be formulated to
Here, \({\rho }_{\mathrm{evl}}=0.003128 \,\mathrm{ kg}/{\mathrm{m}}^{2}\) is the envelope’s areal density which corresponds to a polyethylene hull with an estimated film thickness of \(0.0034 \,\mathrm{ mm}\) [48], and \({S}_{Bal}\) is the balloon surface which is calculated to \(15.09 \,{\mathrm{m}}^{2}\) based on its spherical shape approximation. As per [48], the balloon’s buoyant force can be written as
where \({V}_{Bal}\) denotes the total volume of the balloon being predefined by \(5.51 \,{\mathrm{m}}^{3}\). Based on the static MSA of Sect. 2.1, the aerodynamic velocity of the balloon is equal to its kinematic velocity. Thus, the body drag force in Eq. (42) is, based on [46], calculated to
where the dimensionless drag coefficient \({C}_{D}\) equals \(-0.2\) and the reference area \({S}_{r,Bal}\) is predefined by \(3.77 \,{\mathrm{m}}^{2}\).
3 Control design
The goal of this section is to obtain a simplified mathematical description of the plant, so that the derived model can be used as a basis for the flight control design of the proposed Mars vehicle. In comparison to the high-fidelity simulation model in Sect. 2, this procedure only takes aspects and properties of physical significance into account. Thus, it is assumed that both multirotor system and balloon UAV can be decoupled in terms of flight characteristics so that the balloon dynamics and the SDO model are neglectable within the controller model.
To solve objective (i), the flight controller is designed using a nonlinear cascaded control design model (CDM) which is inspired by [26] and [49].
For describing the main dynamic aspects of the multirotor system, another body-fixed (b) frame is introduced which provides similar properties as the B-frame of Sect. 2.2 and is illustrated in Fig. 5. Referring to Eqs. (36) and (37), it is assumed that all force and moments of the propulsion unit are directly correlated to the propellers’ aerodynamic forces and moments. Let \({k}_{T}=4.1\cdot{10}^{-6} \,{\mathrm{Ns}}^{2}/{\mathrm{rad}}^{2}\) and \({k}_{M}=1.85\cdot{10}^{-7} \,{\mathrm{Nms}}^{2}/{\mathrm{rad}}^{2}\) denote constant coefficients of each rotor, and then, the aerodynamic forces and moments are proportional to the square of the rotors’ commanded rotational speed \({\omega }_{c,i}\) and can both be calculated, for the i-th rotor, as
Note that, since only main physical effects are considered, gyroscopic moments are neglected within the CDM. Equations (46) and (47) illustrate that all aerodynamic forces and moments are explicitly related to the commanded input vector of the plant, given by Eq. (1), which contains the square of the actuators’ commanded rotational speeds. Since the CDM’s output vector \({{\varvec{v}}}_{d}\in {\mathbb{R}}^{4}\) contains the desired virtual control effort and this effort is represented through the spatial distribution of all desired moments \({{\varvec{M}}}_{d}^{R}\) and through the total desired force \({T}_{d}^{R}\), both acting on the multirotor system’s reference point R, \({{\varvec{v}}}_{d}\) is directly correlated to the plant’s commanded input vector by
Note that the mapping between the desired virtual control and the set of the actuators’ squared commanded rotational speeds is described by the control matrix \({\varvec{B}}\in {\mathbb{R}}^{4\times 6}\). Based on Eqs. (46) and (47), this matrix is composed of \({{\varvec{B}}}_{M}\in {\mathbb{R}}^{3\times 6}\), which describes the linear mapping for the multicopter’s total propulsive moment \({\left({{\varvec{M}}}^{R}\right)}_{b}:={{\varvec{B}}}_{M}{{\varvec{u}}}_{c}\) being defined as
as well as \({{\varvec{B}}}_{T}\in {\mathbb{R}}^{1\times 6}\), which is describing the mapping for the multicopter’s total propulsive thrust \({T}^{R}:={{\varvec{B}}}_{T}{{\varvec{u}}}_{c}\) being defined as
In Eq. (49), \(l\) denotes the multicopter arm length which is predefined by \(0.4315 \,\mathrm{ m}\). By assuming a unique mapping similar to quadcopter configurations where \({{\varvec{v}}}_{d}\) and the number of actuators have the same dimension (\({{\varvec{B}}}^{-1}\) is quadratic and does exist), the commanded input vector of the plant can be calculated by introducing the Moore–Penrose pseudoinverse \({{\varvec{B}}}^{+}\in {\mathbb{R}}^{6\times 4}\), so that [50]
To ensure that the desired virtual control is mapped into the physically attainable set of the actuators’ squared commanded rotational speeds, Eq. (51) is further used to introduce the actuators’ rate constraints by saturating the vector elements of \({{\varvec{u}}}_{c}\) to \({\omega }_{c,i,min}^{2}=0 \,{\mathrm{rad}}^{2}/{\mathrm{s}}^{2}\) as well as \({\omega }_{c,i,max}^{2}={\left(6000\cdot\pi /30\right)}^{2} \,{\mathrm{rad}}^{2}/{\mathrm{s}}^{2}\).
Euler’s first and second law [45] serves as a basis for the controller model to derive the translational and rotational dynamics of the multirotor system which are both related to the I-frame used as an inertial reference frame. The translational dynamics can thus be written to
where \(m=2.317 \,\mathrm{ kg}\) denotes the multirotor system mass, \(m{{\varvec{g}}}^{R}\in {\mathbb{R}}^{3}\) its gravitational force including \({g}_{0}\), \({{\varvec{t}}}^{R}\in {\mathbb{R}}^{3}\) its total propulsive force, and \({\left({\dot{{\varvec{v}}}}^{R}\right)}^{II}\) its absolute acceleration which is the time derivative of the multicopter’s kinematic velocity with respect to the I-frame. Applying Euler’s classical treatment of vector analysis [39] as well as using the b-frame as notation frame, the rotational dynamics can be written to
where \({{\varvec{J}}}^{R}\in {\mathbb{R}}^{3\times 3}\) represents the multirotor system’s mass moment of inertia tensor, which is constantly chosen as \(\mathrm{diag}\left(\begin{array}{ccc}0.131 \,\mathrm{kg}{\mathrm{ m}}^{2}& 0.131 \,\mathrm{kg }{\mathrm{m}}^{2}& 0.261 \,\mathrm{kg }{\,\mathrm{m}}^{2}\end{array}\right)\). To obtain an attitude representation, Euler angles are introduced—similar to the plant design—where \(\Psi \in \left[-\pi; \,\pi \right]\) represents the azimuth angle, \(\Theta \in \left[-\pi; \,\pi \right]\) symbolizes the pitch angle, and \(\Phi \in \left[-\pi; \,\pi \right]\) is the roll angle. Together, they constitute the rotation matrix \({{\varvec{R}}}_{Ib}={{\varvec{R}}}_{z}\left(-\Psi \right){{\varvec{R}}}_{y}\left(-\Theta \right){{\varvec{R}}}_{x}\left(-\Phi \right)\in {\mathrm{SO}}^{3}\) which maps a vector from the \(b\)-frame into the \(I\)-frame. The first two CDM states are defined by the multicopter’s kinematic velocity \({{\varvec{v}}}^{R}\) as well as \({{\varvec{\omega}}}^{Ib}\) which is the vector of kinematic angular body rates. Their time-depending dynamic behavior is given by Eqs. (52) and (53). To control the position of the multirotor system, \({{\varvec{r}}}^{R}\in {\mathbb{R}}^{3}\) is defined as the CDM’s position state whereby its kinematic relation to the multicopter velocity is provided through \({\left({\dot{{\varvec{r}}}}^{R}\right)}^{I}{=\left({{\varvec{v}}}^{R}\right)}^{I}\). Instead of choosing \({\varvec{\eta}}\in {\mathbb{R}}^{3}\), the vector of Euler angles, as the CDM’s attitude state, we chose the multicopter’s total propulsive force \({{\varvec{t}}}^{R}\in {\mathbb{R}}^{3}\) as attitude state which can be calculated, while using the b-frame as notation frame, to
This thrust vector is composed of the total propulsive thrust \({T}^{R}\), given by Eq. (50), and \({{\varvec{z}}}_{b}={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{T}\), which defines the unit vector of the body \({z}_{b}\)-axis. To obtain the time derivative of Eq. (54), we use the I-frame as reference frame while applying Euler’s classical treatment of vector analysis [39] which yields
For a more compact notation of Eq. (55), the thrust vector dynamics can be reformulated into a matrix–vector form of notation [49] which includes \({\varvec{T}}\in {\mathbb{R}}^{3\times 3}\), the thrust-magnitude matrix, as well as \({{\varvec{T}}}_{\omega }\in {\mathbb{R}}^{3\times 3}\), the reduced thrust-magnitude matrix:
Note that this approach is based on a reduced attitude parametrization [51] where the multicopter’s yaw rate is excluded from the thrust vector dynamics in Eq. (55) or (56). Hence, a rotation around the \({z}_{b}\)-axis is not correlated to a change of the CDM’s attitude state based on Eq. (55) or (56), so that the multirotor system’s yaw control can be designed independently.
3.1 Baseline controller
Based on the CDM of Sect. 3, a flight controller for the Mars vehicle can be derived which is primarily inspired by [26] and [49]. The flight controller is a cascaded version of a backstepping-based attitude controller nestling inside a superior position controller which is based on Feedback Linearization [52]. Both nonlinear controllers are denoted as baseline controller, since they serve as a base for the artificial augmentation strategies presented in Sect. 4. Figure 6 summarizes the overall controller architecture.
Based on its cascaded structure, the flight controller is divided into an inner attitude loop being enclosed by an outer position loop. Since the dynamics of the inner loop are much faster than the dynamics of the outer loop, we conclude that both loops can be designed independently being justified by the theory of time-scale separation [53]. Inside the position loop, \({{\varvec{r}}}^{R}\) and \({{\varvec{v}}}^{R}\) are both controlled by stabilizing second-order error dynamics. Inside the attitude loop, \({{\varvec{t}}}^{R}\) is controlled using a two-step backstepping control law as well as \({\omega }_{z}^{Ib}\) is controlled using a one-step backstepping control law. The position as well as the yaw rate controller are fed by \({{\varvec{r}}}_{c}^{R}\) and \({\omega }_{z,c}^{Ib}\), the pilot’s position and yaw rate command, whereas the attitude controller is fed by a commanded thrust vector \({{\varvec{t}}}_{c}^{R}\) as feedforward. Since the overall controller testbed is treated as a model-in-the-loop (MIL) simulation, the controller states are initialized through the plant state vector \({{\varvec{x}}}_{P}\). Feasible reference trajectories, indicated by the subscript r, are not only provided by linear first- and second-order reference models (PT1 and PT2 filters), but also by a second-order nonlinear reference model [49], to define the controllers’ tracking objectives.
3.1.1 Baseline position controller
To derive the feedback law for the baseline position controller, position error dynamics are stabilized by the outer loop’s pseudo-control \({{\varvec{t}}}_{c}^{R}\) around its zero equilibrium. The control objective has been reached when \({{\varvec{r}}}^{R}\) tracks a desired reference trajectory \({{\varvec{r}}}_{r}^{R}\in {\mathbb{R}}^{3}\), so that the position tracking error \({{\varvec{e}}}_{p}\in {\mathbb{R}}^{3}\) and its time derivatives converge to zero:
We choose the I-frame as notation frame and insert Eq. (52) into (59) yielding
where \({\left({{\varvec{z}}}_{I}\right)}_{I}={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{T}\) denotes the \({z}_{I}\)-axis of the I-frame being notated in the I-frame. Next, we assume that a total commanded thrust \({{\varvec{t}}}_{c}^{R}\) does establish
which denotes a desired behavior of \({\ddot{{\varvec{e}}}}_{p}\). All matrices \({{\varvec{K}}}_{v}\), \({{\varvec{K}}}_{x}\), \({{\varvec{K}}}_{i}\) are Hurwitz and of the set \({\mathbb{R}}^{3\times 3}\). If the total thrust \({{\varvec{t}}}^{R}\) is selected according to the pseudo-control law
the desired position error dynamics in Eq. (61) and the real position error dynamics in Eq. (60) become equal so that the CDM’s position state \({{\varvec{r}}}^{R}\) and the translation state \({{\varvec{v}}}^{R}\) approach their reference trajectories exponentially fast.
3.1.2 Baseline attitude controller
The control objective of the baseline attitude controller is achieved when \({{\varvec{t}}}^{R}\) tracks a desired reference trajectory \({{\varvec{t}}}_{r}^{R}\in {\mathbb{R}}^{3}\), so that the attitude tracking error \({{\varvec{e}}}_{t}\in {\mathbb{R}}^{3}\) and its time derivative converge to zero:
We choose the I-frame as notation frame and insert Eq. (56) into (64) by using the rotation matrix \({{\varvec{R}}}_{Ib}\):
Here, \((\boldsymbol{*})\) defines the vector of pseudo-control variables for the thrust vector tracking (TVT). To derive the control law of this first backstepping step, a positive definite Lyapunov function (LF) candidate \({V}_{1}\) [53] is chosen in quadratic form as
whereby the time derivative of \({V}_{1}\in {\mathbb{R}}\) is calculated to
To obtain an exponential decay behavior of \({\dot{{\varvec{e}}}}_{t}\), Eq. (67) must ensure negative semi-definiteness. Therefore, let \({\dot{{\varvec{e}}}}_{t,d}=-{{\varvec{K}}}_{t}{{\varvec{e}}}_{t}\) denote a desired decay behavior of the real TVT error dynamics. Then, using Eq. (67) once more a desired time derivative of \({V}_{1}\) can likewise be written to
where \({{\varvec{K}}}_{t}\in {\mathbb{R}}^{3\times 3}\) is a Hurwitz matrix acting as feedback gain of \({{\varvec{e}}}_{t}\). We assume that \({\dot{V}}_{1,d}\) can be generated by a desired pseudo-control input \({{\varvec{u}}}_{1}={\left[\begin{array}{ccc}{u}_{1x}& {u}_{1y}& {u}_{1z}\end{array}\right]}^{T}\in {\mathbb{R}}^{3}\), so that for \((\boldsymbol{*})={{\varvec{u}}}_{1}\), the desired time derivative \({\dot{V}}_{1,d}\) and the time derivative of the actual LF \({\dot{V}}_{1}\) become equal. A comparison of Eqs. (67) and (68), while using the I-frame as notation frame, yields the pseudo-control law for the TVT
after inserting Eq. (65) into Eq. (67). Note that, since the thrust-magnitude matrix is quadratic and provides full column and row rank, its inverse \({{\varvec{T}}}^{-1}\in {\mathbb{R}}^{3\times 3}\) can be calculated to
In Eq. (70), a problem of singularity arises for the inverse thrust-magnitude matrix if the total propulsive thrust \({T}^{R}\) is equal to zero. To avoid that \({{\varvec{T}}}^{-1}\) becomes singular we saturate \({T}^{R}\) to a minimum permissible propulsive thrust of \(0.1 \,\mathrm{N}\). Concerning the general backstepping methodology [53], the error cross-coupling term lacks in Eq. (69) which illustrates the main distinction in deriving the baseline controllers’ pseudo-control laws compared to [26]. The attitude loop is stabilized independent of \({{\varvec{e}}}_{p}\) being justified by the theory of time-scale separation [53]. The baseline position controller shall lose some of its performance, since the inner loop and therefore also the plant’s commanded input vector \({{\varvec{u}}}_{c}\) receive less information of the outer loop.
Proceeding with the general backstepping methodology, the comparison between the desired pseudo-control law for the TVT, given by (69), and the current vector of pseudo-control variables \((\boldsymbol{*})\) (see Eq. (65)) leads to sub-targets of the primary control objective. Since both angular body rates \({\omega }_{x}^{Ib}\) and \({\omega }_{y}^{Ib}\) are related to the rotational dynamics, given by Eq. (53), they cannot be manipulated directly in a manner that \({{\varvec{\omega}}}_{xy}^{Ib}={\left[\begin{array}{cc}{\omega }_{x}^{Ib}& {\omega }_{y}^{Ib}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\) matches the desired pseudo-control \({{\varvec{u}}}_{1xy}={\left[\begin{array}{cc}{u}_{1x}& {u}_{1y}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\) at any time. Hence, to ensure angular rates tracking (ART), the ART error \({{\varvec{e}}}_{\omega xy}={\left[\begin{array}{cc}{e}_{\omega x}& {e}_{\omega y}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\) and its time derivative with respect to the b-frame must converge to zero:
To satisfy TVT and ART at the same time, the ART error must be included within the TVT error dynamics, so that Eq. (71) is reformulated to \({{\varvec{\omega}}}_{xy}^{Ib}={{\varvec{u}}}_{1xy}-{{\varvec{e}}}_{\omega xy}\) and inserted into Eq. (65) which yields
Since the actual pseudo-control variable \({\dot{T}}^{R}\) becomes an input for the inner loop while propagating it to a first-order integrator chain (see Fig. 6), and additionally, since we assume that every demanded, or rather desired, input for the inner loop can be generated in such a short period of time that it is always available, \({\dot{T}}^{R}\) matches its desired pseudo-control \({u}_{1z}\) at any time, so that no additional subordinated control error arises. For the sake of clarity, we rewrite Eq. (73) to
To derive the control law of this second backstepping step, the valid LF candidate \({V}_{1}\), given by Eq. (66), is extended to
whereby the time derivative of \({V}_{2}\in {\mathbb{R}}\) can be determined to
We use the I-frame to notate the TVT error and its dynamics as well as the b-frame to notate the ART error and its dynamics. After inserting Eq. (67) into Eq. (76), it follows:
By inserting the pseudo-control law for the TVT, given by Eq. (69), into Eq. (74), and additionally, using Eq. (72) for the ART error dynamics, Eq. (77) can be rewritten to
In addition to the general backstepping methodology [53], the error cross-coupling term in Eq. (78) must be retransformed, so that the ART error is explicitly included in the vector space \({\mathbb{R}}^{2}\). For this purpose, a weighted matrix \({\varvec{W}}\in {\mathbb{R}}^{3\times 2}\) is introduced which satisfies that \({\left(\begin{array}{ccc}{e}_{\omega x}& {e}_{\omega y}& 0\end{array}\right)}_{b}^{T}\) can be replaced by \({\varvec{W}}{\left({{\varvec{e}}}_{\omega xy}\right)}_{b}\). Since \({V}_{2}\), respectively its time derivative, is a scalar quantity, we transpose the error cross-coupling term \({\left({{\varvec{e}}}_{t}\right)}_{I}^{T}{{\varvec{R}}}_{Ib}{\varvec{T}}{\varvec{W}}{\left({{\varvec{e}}}_{\omega xy}\right)}_{b}\) and rewrite Eq. (78) to
Note that Eq. (79) includes the angular body accelerations \({\dot{\omega }}_{x}^{Ib}\) and \({\dot{\omega }}_{y}^{Ib}\) which are directly affected by the rotational dynamics, given by Eq. (53). Thus, \({\dot{{\varvec{\omega}}}}_{xy}^{Ib}\) defines the vector of pseudo-control variables for the ART. To render Eq. (79) negative semi-definite, which proofs stability of both tracking errors \({{\varvec{e}}}_{t}\) and \({{\varvec{e}}}_{\omega xy}\) around their zero equilibria \(\varvec{0}\in {\mathbb{R}}^{3}\) and \(\varvec{0}\in {\mathbb{R}}^{2}\), let \({\dot{{\varvec{e}}}}_{\omega xy,d}=-{{\varvec{K}}}_{\omega xy}{{\varvec{e}}}_{\omega xy}\) denote a desired decay behavior of the real ART error dynamics. Then, using Eq. (77) once more, a desired time derivative of \({V}_{2}\) can likewise be written to
where \({{\varvec{K}}}_{\omega xy}\in {\mathbb{R}}^{2\times 2}\) is a Hurwitz matrix acting as feedback gain of \({{\varvec{e}}}_{\omega xy}\). We assume that \({\dot{V}}_{2,d}\) can be generated by a desired pseudo-control input \({{\varvec{u}}}_{2xy}={\left[\begin{array}{cc}{u}_{2x}& {u}_{2y}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\), so that for \({\dot{{\varvec{\omega}}}}_{xy}^{Ib}={{\varvec{u}}}_{2xy}\), the desired time derivative \({\dot{V}}_{2,d}\) and the time derivative of the actual LF \({\dot{V}}_{2}\) become equal which yields the pseudo-control law for the ART:
Note that the pseudo-control law for the ART includes \({\dot{u}}_{1x}\) and \({\dot{u}}_{1y}\), the time derivatives of the TVT’s desired pseudo-controls. To obtain the dynamics of \({{\varvec{u}}}_{1xy}\) with respect to the b-frame, we use Eq. (69) and apply Euler’s classical treatment of vector analysis [39] which yields
In Eq. (82), the time derivative of the inverse thrust-magnitude matrix with respect to the b-frame can be calculated to [26]
and the time derivative of the rotation matrix \({{\varvec{R}}}_{bI}\) with respect to the b-frame is given by the following kinematics [26]:
being related to the Strapdown equation [39]. To finally constitute the pseudo-control law for the overall ART in the vector space \({\mathbb{R}}^{3}\) we use Eq. (81) and, additionally, assume that \({u}_{2z}\in {\mathbb{R}}\), which represents the pseudo-control law of the one-step backstepping yaw rate controller, is already given from Sect. 3.1.3 leading to
Since all vector elements of \({{\varvec{u}}}_{2}\in {\mathbb{R}}^{3}\) can be interpreted as a desired angular body acceleration around the \({x}_{b}\)-,\({y}_{b}\)-, and \({z}_{b}\)-axis of the CDM, the relation between the desired moments \({{\varvec{M}}}_{d}^{R}\) and \({{\varvec{u}}}_{2}\) is given by inserting Eq. (85) into the CDM’s rotational dynamics (see Eq. (53)):
Since the CDM’s output vector \({{\varvec{v}}}_{d}\), given by Eq. (48), also represents, conversely, the input to stabilize the inner loop of the CDM, Eq. (86) emphasizes that the angular body accelerations match their purposed desired values, being comprised in \({{\varvec{u}}}_{2}\), if \({{\varvec{v}}}_{d}\) is mapped into the attainable set of the actuators’ squared commanded rotational speeds, established through Eq. (51). This mapping also involves the total desired force \({T}_{d}^{R}\), or rather \({T}^{R}\), which can be determined by propagating the desired pseudo-control \({u}_{1z}\) to a first-order integrator chain:
With regard to Eq. (70), the initial condition of Eq. (87) is predefined by \({T}^{R}\left({t}_{0}\right)=0.1 \,\mathrm{N}\). The final result for the baseline flight controller’s desired virtual control vector can then be summarized to
3.1.3 Yaw rate controller
Using the thrust vector \({{\varvec{t}}}^{R}\) as reduced attitude state allows an independent yaw control design for the CDM, since the angular body rate \({\omega }_{z}^{Ib}\in {\mathbb{R}}\) is entirely decoupled from the attitude kinematics, given through Eqs. (55) and (56). The control objective of the yaw rate controller is achieved when \({\omega }_{z}^{Ib}\) tracks a desired reference trajectory \({\omega }_{z,r}^{Ib}\in {\mathbb{R}},\) so that the yaw motion tracking error \({e}_{\omega z}\in {\mathbb{R}}\) and its time derivative converge to zero:
To derive the control law for the yaw rate tacking, we choose again a positive definite LF candidate \({V}_{3}\) [53] in quadratic form as
whereby the time derivative of \({V}_{3}\in {\mathbb{R}}\) is calculated to
To enforce an exponential decay behavior of \({\dot{e}}_{\omega z}\), Eq. (92) must ensure negative definiteness. Therefore, let \({\dot{e}}_{\omega z,d}=-{k}_{\omega }\cdot{e}_{\omega z}\) denote a desired decay behavior of the real yaw rate error dynamics. Then, we use Eq. (92) once more and write a desired time derivative of \({V}_{3}\) as
where the feedback gain \({k}_{\omega z}\in {\mathbb{R}}\) is positive definite and constant. We assume that \({\dot{V}}_{3,d}\) is generated by a desired pseudo-control input \({u}_{3}\in {\mathbb{R}}\) such that for \({\dot{\omega }}_{z}^{Ib}={u}_{3}\), Eqs. (92) and (93) become equal which yields the pseudo-control law for the yaw rate tracking
after inserting Eq. (90) into Eq. (92). We conclude from Eq. (94) that yaw rate tracking is guaranteed under the assumption that the angular body acceleration is adjusted in a manner that \({\dot{\omega }}_{z}^{Ib}\) equals \({u}_{3}\) at any time, so that \({\dot{e}}_{\omega z}\) declines to zero exponentially fast. For the sake of consistency, we write \({u}_{2z}={u}_{3}\).
3.1.4 Reference models
Within this section, reference models are presented which are used to generate feasible trajectories for the baseline controllers that shall ultimately be tracked by the states of the plant. Feasible means that the reference trajectories shall be sufficient smooth, so that they can physically be achieved by the Mars vehicle. Otherwise, the baseline controllers’ tracking objectives would be doomed to fail in the long term [54].
Usually, linear reference models are used to obtain the \(r\)-trajectories since they provide the simplest approach to plan a desired trajectory by only using a n-dimensional filter. To obtain the desired trajectory for the yaw rate controller, the pilot’s yaw rate command \({\omega }_{z,c}^{Ib}\) is filtered by a PT1 element. This PT1 filter represents a linear first-order reference model and, based on [47], is given by
whereby the time constant \({t}_{\omega z}\) is constantly chosen as \(1.25 \,\mathrm{s}\). This emphasizes that the attainable vector space for a desired moment around the body \({z}_{b}\)-axis is reduced to a minimum (while the yaw rate controller is active) being beneficial with regard to the low-density conditions in Valles Marineris (see Sect. 2.1). In case of the baseline position controller, the linear second-order reference model [47]
is used, where \({t}_{p}=0.2 \,\mathrm{s}\), \(\zeta =1\) and \({k}_{s}=1\) define the second-order system parameter. In addition to the baseline attitude controller, the task is to generate smooth \(r\)-trajectories out of the commanded thrust vector \({{\varvec{t}}}_{c}^{R}\). In this case, it is reasonable not to use a PT2 filter as in Eq. (96). The reason for this is based on Eq. (54), since it is not guaranteed that \(\Vert {{\varvec{z}}}_{b}\Vert =1\) at every time instant. Hence, in terms of the thrust vector saturation subsystem (see Fig. 6), \({{\varvec{t}}}_{c}^{R}\) is separated into \({T}_{c}\), which indicates the commanded thrust magnitude, but also into the unit vector \({{\varvec{z}}}_{b,c}\), which indicates the pointing direction of the commanded thrust vector:
Note that, since the baseline position controller is based on the theory of Feedback Linearization [52], the total commanded thrust vector always tries to cancel out the system’s inherent dynamics being, inter alia, induced by the gravitational acceleration, so that \(1/\Vert {{\varvec{t}}}_{c}^{R}\Vert\) in Eq. (98) stays bounded at every time instant. To generate smooth r-trajectories out of Eqs. (97) and (98), the kinematics of the reference thrust vector \({{\varvec{t}}}_{r}^{R}\) must be derived in the first place. According to the classical treatment of direct vector differentiation [39], it follows:
To determine the thrust-magnitude reference trajectory \({T}_{r}^{R}\) and its time derivatives, a PT2 filter can be used, similar to Eq. (96), leading to [47]
whereby \({t}_{T}=0.05 \,\mathrm{s}\), \(\zeta =1\) and \({k}_{s}=1\) define the second-order system parameter. To obtain the directional reference trajectory \({{\varvec{z}}}_{b,r}\), we introduce a nonlinear reference model [49]
which provides the rotational dynamics of tracking the physical unit vector \({{\varvec{z}}}_{b,c}\) by the S-frame’s virtual unit vector \({{\varvec{z}}}_{S}={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{T}\). The parameters \({\omega }_{0,S}=1.75 \,\frac{1}{\mathrm{s}}\), \({\zeta }_{S}=1\), and \({k}_{s}=1\) are used to adjust how fast the virtual unit vector exponentially tracks \({{\varvec{z}}}_{b,c}\) by influencing the cross product on the right-hand side of Eq. (103) at every time instant. The tracking velocity is then indirectly conferred on \({{\varvec{\omega}}}^{IS}\) which indicates the S-frame’s angular velocity vector relative to the I-frame. Since \({{\varvec{\omega}}}^{IS}\) is related to the Strapdown equation [39] by the following kinematics:
Equation (104) serves \({{\varvec{R}}}_{IS}\). This rotation matrix not only implies the mapping from a vector being notated in the S-frame to a vector being notated in the I-frame, it can also be used to extract the required directional reference trajectory notated in the I-frame due to
Equation (105) only holds by setting up the exact same initial conditions \({{\varvec{\omega}}}^{IS}\left({t}_{0}\right)={{\varvec{\omega}}}^{Ib}\left({t}_{0}\right)\) such as \({{\varvec{R}}}_{IS}\left({t}_{0}\right)={{\varvec{R}}}_{Ib}\left({t}_{0}\right)\) within the virtual model. Thus, S-frame and b-frame are concurrent for \({t}_{0}\) which, upon reversion, means that the b-frame or rather its \({{\varvec{z}}}_{b}\)-axis tracks \({{\varvec{z}}}_{b,c}\). Euler’s treatment of vector differentiation [39] is finally used to obtain the \({{\varvec{z}}}_{b,r}\)-kinematics being required for Eqs. (99) to (101):
with
3.1.5 Stability analysis of closed-loop system
To provide a valid baseline flight controller, closed-loop stability of the CDM must be guaranteed which is shown in this section. To track the reference position \({{\varvec{r}}}_{r}^{R}\) as well as the reference velocity \({{\varvec{v}}}_{r}^{R}\), both given by Eq. (96), we define the total error of the CDM’s position loop \({{\varvec{e}}}_{pos}\in {\mathbb{R}}^{6}\) using Eqs. (57) and (58) to
As we are aiming to stabilize the dynamics of Eq. (109) around its zero equilibrium, we use the I-frame as notation and reference frame while applying Euler’s classical treatment of vector analysis [39] which yields
where \({\ddot{{\varvec{e}}}}_{p}\) is given by Eq. (60). To obtain a matrix–vector notation, the position loop error dynamics from Eq. (110) are reformulated into
where the matrices \({\varvec{M}}\in {\mathbb{R}}^{6x6}\), \({\varvec{A}}\in {\mathbb{R}}^{6x6}\), and \({\varvec{B}}\in {\mathbb{R}}^{6x3}\) are given by
including \({\varvec{I}}\in {\mathbb{R}}^{3\times 3}\) as identity matrix and \(\varvec{0}\in {\mathbb{R}}^{3\times 3}\) as zero matrix. Since it is assumed that every demanded input for the position loop is, based on the theory of time-scale separation [53], always available and disposable, \({{\varvec{t}}}^{R}\) equals \({{\varvec{t}}}_{c}^{R}\) at any time, so that we can insert Eq. (62) into Eq. (111) yielding
For the desired position error dynamics \({\ddot{{\varvec{e}}}}_{p,d}\), given by Eq. (61), we only consider the feedback matrices \({{\varvec{K}}}_{x}\) and \({{\varvec{K}}}_{v}\) in the closed-loop system. By multiplying Eq. (113) with \({{\varvec{M}}}^{-1}\), it follows:
with
denoting the error matrix of the position loop. All inherent nonlinearities of the CDM’s outer loop are canceled out by the pseudo-control law (62) which yields a linear state-space representation for \({\dot{{\varvec{e}}}}_{pos}\). To achieve asymptotic stability, meaning that the linear error dynamics (114) show an exponential decay behavior, so that \({{\varvec{e}}}_{pos}\) converges at its zero equilibrium \({\varvec{0}}\in {\mathbb{R}}^{6}\), \({\varvec{E}}\) must be a stability matrix, and thus, Eq. (115) is only allowed to exhibit poles in the left-half complex plane. To examine \({\varvec{E}}\), we use the so-called Lyapunov equation [53] which manifests that a positive definite LF \({V}_{pos}\in {\mathbb{R}}\) must be found satisfying \({V}_{pos}\left({{\varvec{e}}}_{pos}\right)>0\) and \({V}_{pos}\left({\varvec{0}}\right)=0\) for all \({{\varvec{e}}}_{pos}\ne {\varvec{0}}\). We obtain a valid LF candidate in quadratic form as
whereby the time derivative of \({V}_{pos}\) is calculated to
Equations (116) and (117) both include the matrix \({\varvec{P}}\in {\mathbb{R}}^{6\times 6}\) which we can chose arbitrarily. The only primary constraint is that \({\varvec{P}}\) must be positive definite as well as symmetric, so that \({\varvec{P}}={{\varvec{P}}}^{T}\) is always satisfied [53]. After inserting the linear error dynamics, given by Eq. (114), into Eq. (117), we find
so that the matrix \({\varvec{Q}}\in {\mathbb{R}}^{6\times 6}\) is given by the Lyapunov equation [53]:
While choosing, e.g., \({\varvec{P}}\) as identity matrix \({\varvec{I}}\in {\mathbb{R}}^{6\times 6}\), we conclude from Eq. (119) that \({\varvec{Q}}\) becomes positive definite and therefore that \({\varvec{E}}\) is Hurwitz [53]. Thus, Eq. (114) is a stable linear system while choosing the feedback gain matrices \({{\varvec{K}}}_{x}\) and \({{\varvec{K}}}_{v}\) positive definite which guarantees position and velocity tracking at any given time. Since the dynamics of the CDM’s inner loop are considerable faster than the dynamics of the outer loop, we conclude that the closed-loop system is stable under the pseudo-control inputs \({{\varvec{u}}}_{1}\) and \({{\varvec{u}}}_{2}\), given by Eqs. (69) and (85), provided that the feedback gain matrices \({{\varvec{K}}}_{t}\), \({{\varvec{K}}}_{\omega xy}\), and \({k}_{\omega z}\) are positive definite and constant. Note that the desired pseudo-control law for the TVT always exists, since we saturate \({T}^{R}\) to a minimum permissible propulsive thrust of \(0.1 \,\mathrm{N}\) to avoid that the inverse thrust-magnitude matrix \({{\varvec{T}}}^{-1}\), given through Eq. (70), becomes singular [53].
4 Artificial augmentation units
In this section, artificial augmentation units are developed to extend the baseline flight controller’s architecture, shown in Fig. 6, to increase its capabilities in suppressing modeling errors artificially. This procedure is advantageous to achieve objective (ii) and (iii), since the units work independent from the baseline controller. Thus, the control laws derived in Sect. 3.1 are still valid.
Due to the uncontrollability of the balloon UAV, unintended rope oscillations are causing steady-state errors [47] in the multirotor system’s position. Additionally, when the rope touches the rotor plane, or rather the propeller tips, the flight mission is endangered and may fail. The idea is therefore to damp the balloon motion artificially within the horizontal plane by generating a closed-loop reference model (CRM) [35] either for the inner or the outer loop of the CDM. Based on the developed methodology, we call our first approach the thrust vector augmentation (TVA), whereas our second approach is called the position command augmentation (PCA).
The general idea of both TVA and PCA is to embed a feedback of the uncertain plant into the reference model so that a closed-loop results. If this feedback is defined as an error, it tries to pull the reference model towards the plant so that both meet “half-way” and the error is, at least, reduced [35]. We use the balloon’s relative position to the multicopter \({{\varvec{r}}}_{xy}^{RQ}={\left[\begin{array}{cc}{x}^{RQ}& {y}^{RQ}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\), given by Eq. (13), and the balloon’s relative velocity \({{\varvec{v}}}_{xy}^{RQ}={\left[\begin{array}{cc}{u}^{RQ}& {v}^{RQ}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\), given by the vector subtraction of \({{\varvec{v}}}_{xy}^{R}={\left[\begin{array}{cc}{u}^{R}& {v}^{R}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\) from \({{\varvec{v}}}_{xy}^{Q}={\left[\begin{array}{cc}{u}^{Q}& {v}^{Q}\end{array}\right]}^{T}\in {\mathbb{R}}^{2}\), as error signals and embed them into the baseline controllers’ open-loop reference models (ORM). These error signals are then scaled by the Hurwitz matrices \({{\varvec{D}}}_{Bal}\) and \({{\varvec{K}}}_{Bal}\), the so-called Luenberger gains [35], which are both of the set \({\mathbb{R}}^{2\times 2}\).
4.1 Thrust vector augmentation
We implement the TVA approach by augmenting the commanded thrust vector \({{\varvec{t}}}_{c}^{R}\) which represents the pseudo-control input of the CDM’s outer loop. The augmented thrust vector is then defined as
whereby \({{\varvec{t}}}_{c}^{R}\) is given by Eq. (62) and the weighted matrix \({\varvec{W}}\in {\mathbb{R}}^{3\times 2}\) is given through Eq. (79). Due to the TVA, Eq. (98) is redefined, so that the unit vector \({{\varvec{z}}}_{b,c}\) indicates the pointing direction of \(\tilde{{\varvec{t}}}_{c}^{R}\) without violating that \(\Vert {{\varvec{z}}}_{b,c}\Vert =1\) at every time instant. Hence, while the Mars vehicle operates on a mission, a balance between a desired attitude command and a reduction of the balloon error signals is obtained. Since the error signals are only defined within the horizontal plane and, by scaling \({{\varvec{K}}}_{Bal}\) and \({{\varvec{D}}}_{Bal}\) to a lower level, the inner loop’s control objective remains and, finally, concludes in the stabilization of the rope angle \({\gamma }_{{R}^{*}}\) around \(90^\circ\) for steady-state conditions (see Fig. 4). The main advantage of the TVA is based on its robustness against external disturbances. While the TVA is activated, the baseline control target—to stabilize the tracking error \({{\varvec{e}}}_{p}\) around its equilibrium \({\varvec{0}}\in {\mathbb{R}}^{3}\)—cannot be bypassed. Only a significant growth of \({{\varvec{e}}}_{p}\) is obtained for non-steady-state conditions since a mismatch between the desired pseudo-control input \({{\varvec{t}}}_{c}^{R}\) and the actual augmented pseudo-control input \(\tilde{{\varvec{t}}}_{c}^{R}\) of the CDM’s outer loop is produced on purpose to stabilize the relative position of the balloon in the forward flight case.
4.2 Position command augmentation
To realize the PCA approach and generate a CRM inside the position loop, we augment the initial position command \({{\varvec{r}}}_{c}^{R}\), so that the new pilot command is defined as
whereby the weighted matrix \({\varvec{W}}\in {\mathbb{R}}^{3\times 2}\) is given through Eq. (79). In case of the PCA, the position tracking error in Eq. (57) is redefined to \(\tilde{{\varvec{e}}}_{p}=\tilde{{\varvec{r}}}_{r}^{R}-{{\varvec{r}}}^{R}\), since the r-trajectories of the second-order reference model, given by Eq. (96), are fed by the augmented position command \(\tilde{{\varvec{r}}}_{c}^{R}\) as feedforward. Hence, while the Mars vehicle operates on a mission, a balance between a desired position command and a reduction of the balloon error signals is obtained. Since the error signals are only defined within the horizontal plane and, by scaling \({{\varvec{K}}}_{Bal}\) and \({{\varvec{D}}}_{Bal}\) to a lower level, the outer loop’s control objective remains and, finally, concludes in the stabilization of the rope angle \({\gamma }_{{R}^{*}}\) around \(90^\circ\) for steady-state conditions (see Fig. 4). Although a disproportionate growth of \(\tilde{{\varvec{e}}}_{p}\) is prevented, by pulling the reference model towards the plant, the overall controller target, to reach a steady-state in the vehicle’s position, so that \({{\varvec{e}}}_{p}\) converges to zero, is only satisfied in the absence of stationary external disturbances. In case of, e.g., static wind, the error feedback \(\Vert {{\varvec{r}}}_{xy}^{RQ}\Vert\) is always positive and low-frequent. Thus, reference model and plant do constantly meet “half-way”, so that the overall control target is misled by the deviation between \(\tilde{{\varvec{r}}}_{r}^{R}\) and \({{\varvec{r}}}_{r}^{R}\). To overcome this problem, the linear error term \({{\varvec{K}}}_{Bal}{{\varvec{r}}}_{xy}^{RQ}\) is passed through a washout filter [39] satisfying that the outer loop’s control objective remains even under steady wind by only using the transient rate of the feedback. We embed the washout filter as second-order system and only use the first derivative for Eq. (121) which will solely produce non-zero augmentation signals when the linear error term is high-frequent and not steady. Figure 7 shows the schematic structure of the PCA approach including the washout filter where \({\omega }_{0}=0.6 \,\frac{1}{\mathrm{s}}\), \(\zeta =1\) and \({k}_{s}=1\) define its system parameters.
5 Simulation results
This section summarizes the simulation results of testing the CDM of Sect. 3 on the high-fidelity plant design model of Sect. 2. Since the overall simulation testbed is treated as MIL, the controller states are initialized through the plant state vector \({{\varvec{x}}}_{P}\) so that, inter alia, the CDM’s b-frame and the plant’s B-frame are congruent from scratch.
To demonstrate the controller performance, the closed-loop system response for the Mars vehicle’s position state \({{\varvec{r}}}^{R}\) is evaluated on a digital-8-flight-maneuver at the bottom of Valles Marineris. The flight path is obtained by a reference trajectory being in shape of a long curved “8” representing a suitable extraterrestrial mission profile to, e.g., scan the Martian surface from above and detect prominent spots where swarm participants should perform scientific experiments.
The mission has a total flight time of \(180 \,\mathrm{s}\). The actual maneuver starts eastwards and is performed within \(120 \,\mathrm{s}\). This provides a time slot of \(60 \,\mathrm{s}\) to not only reach a steady-state in the vehicle position, but also to eliminate steady-state errors [47]. The take-off location is initialized according to the environment submodel of Sect. 2.1 with a geodetic altitude of -\(4906 \,\mathrm{m}\) blow the Martian geoid. Since \({\gamma }_{{R}^{*}}\) describes the radial distance between the rope and the \({x}_{B}\)–\({y}_{B}\) plane of the multirotor system, \({\gamma }_{{R}^{*},ne}=20^\circ\) is defined as never exceed rope angle for a quantitative mission assessment. To make the handling more intuitive and, to provide proper smooth trajectories, the pilot’s position command arises from an integrated joystick-velocity command \({{\varvec{v}}}_{cmd}^{R}\). For the sake of comparability, \({{\varvec{v}}}_{cmd}^{R}\) is constantly given by \({\left[\begin{array}{ccc}\pm3& \pm3& \pm1\end{array}\right]}^{T}\), so that the pilot’s position command is determined as follows:
Equation (122) also ensures that, for every time instant, the multirotor system does not accelerate upwards faster than the balloon. For the baseline controllers, the feedback gain matrices \({{\varvec{K}}}_{v}=\mathrm{diag}\left(\begin{array}{ccc}2& 2& 1\end{array}\right)\), \({{\varvec{K}}}_{x}=\mathrm{diag}\left(\begin{array}{ccc}0.5& 0.5& 0.5\end{array}\right)\), \({{\varvec{K}}}_{i}=\mathrm{diag}\left(\begin{array}{ccc}0.1& 0.05& 0.05\end{array}\right)\), \({{\varvec{K}}}_{t}=\mathrm{diag}\left(\begin{array}{ccc}4& 4& 4\end{array}\right)\), as well as \({{\varvec{K}}}_{\omega xy}=\mathrm{diag}\left(\begin{array}{cc}20& 20\end{array}\right)\) and \({k}_{\omega z}=8\) are chosen constant and Hurwitz. With regard to the artificial augmentation units, \({{\varvec{K}}}_{Bal}=\mathrm{diag}\left(\begin{array}{cc}1.2& 0.8\end{array}\right)\) and \({{\varvec{D}}}_{Bal}=\mathrm{diag}\left(\begin{array}{cc}0.15& 0.3\end{array}\right)\) are constantly chosen for the PCA approach as well as \({{\varvec{K}}}_{Bal}=\mathrm{diag}\left(\begin{array}{cc}0.5& 1\end{array}\right)\) and \({{\varvec{D}}}_{Bal}=\mathrm{diag}\left(\begin{array}{cc}0.5& 0.75\end{array}\right)\) for the TVA approach.
Figure 8 shows the simulation results for three different flight controller configurations. On top, the Mars vehicle’s position tracking behavior for the baseline flight controller is depicted, whereas in the middle and on the bottom, the position tracking for the flight controller with activated PCA and TVA is shown. The balloon’s position \({{\varvec{r}}}^{Q}\) is depicted in green with a starting position of \({\left[\begin{array}{ccc}0& 0& -20\end{array}\right]}^{T}\) with respect to the I-frame. The true position of the Mars vehicle \({{\varvec{r}}}^{R}\) (blue) tracks the reference position \({{\varvec{r}}}_{r}^{R}\) (red) even under influence of the balloon UAV and rope dynamics very accurately which implies a satisfying robustness for all three controller configurations. In terms of the TVA, the oscillating offset between \({{\varvec{r}}}^{R}\) and \({{\varvec{r}}}^{Q}\) is reduced, so that an additional offset between \({{\varvec{r}}}^{R}\) and \({{\varvec{r}}}_{r}^{R}\) is caused on purpose, due to the mismatch between \({{\varvec{t}}}_{c}^{R}\) and \(\tilde{{\varvec{t}}}_{c}^{R}\), to reduce the rope oscillations. A significant reduction of this additional offset is achieved in terms of the PCA by smoothly shifting the aimed position tracking objective from the ORM to the CRM for non-steady-state conditions. Due to the fact that, while the PCA is activated, the augmented reference position \(\tilde{{\varvec{r}}}_{r}^{R}\) does distinguish from the nominal reference position \({{\varvec{r}}}_{r}^{R}\), the Mars vehicle’s position tracking for the flight controller with activated PCA shows the nominal trajectory for the reference position \({{\varvec{r}}}_{r}^{R}\), being depicted as black dashed line, and additionally, shows the actual augmented trajectory for the reference position \(\tilde{{\varvec{r}}}_{r}^{R}\), which is tracked, in red. For the sake of clarity, the position tracking for the flight controller with activated TVA also shows the nominal trajectory for the reference position \({{\varvec{r}}}_{r}^{R}\) (black dashed line), which is equal to the actual trajectory for the reference position (depicted in red) to emphasize the fact that the ORM of the CDM’s outer loop remains for the flight controller configuration with activated TVA.
Figure 9 depicts the vector elements of the position tracking error \({e}_{x,p}\), \({e}_{y,p}\), and \({e}_{z,p}\) (\({\tilde{e }}_{x,p}\), \({\tilde{e }}_{y,p}\) and \({\tilde{e }}_{z,p}\) for the PCA) in \({x}_{I}\)-, \({y}_{I}\)-, and \({z}_{I}\)-direction of the I-frame over time. In case of the TVA, the position errors are mainly capped between \(\mp 0.5 \,\mathrm{m}\) for \({e}_{x,p}\) and even \(\mp 2 \,\mathrm{m}\) for \({e}_{y,p}\), whereas for the baseline controller and for the baseline controller with PCA \({e}_{x,p}\) and \({e}_{y,p}\), respectively, \({\tilde{e }}_{x,p}\) and \({\tilde{e }}_{y,p}\), are settled below \(\mp 0.2 \,\mathrm{m}\) and \(\mp 0.6 \,\mathrm{m}\). Due to the artificial augmentation units, the Mars vehicle is able to not only reach a steady-state in position, but also to eliminate all steady-state errors, so that \(\Vert {{\varvec{e}}}_{p}\Vert\), or rather \(\Vert\tilde{{\varvec{e}}}_{p}\Vert\), converge to zero at the end of the simulation period. The baseline controller itself is not able to eliminate the steady-state errors which is caused by the modeling errors inside the CDM (neglection of balloon and rope dynamics).
For the sake of completeness, Fig. 10 illustrates the attitude tracking (TVT) in \({x}_{I}\)-, \({y}_{I}\)-, and \({z}_{I}\)-direction over time for the baseline controller during the digital-8-maneuver. The thrust vector elements \({t}_{x}^{R}\), \({t}_{y}^{R}\), and \({t}_{z}^{R}\) track the reference thrust vector elements \({t}_{x,r}^{R}\), \({t}_{y,r}^{R}\), and \({t}_{z,r}^{R}\) very accurately which implies a good controller performance similar to the position tracking simulation results presented before. This is expected since \({t}_{x,c}^{R}\), \({t}_{y,c}^{R}\), and \({t}_{z,c}^{R}\), the vector elements of the desired pseudo-control input for the CDM’s outer loop, are only used as virtual control to stabilize the position loop exponentially. The initial control objective to track the ORM remains without stabilizing the balloon dynamics in the forward flight case. Rope oscillations do clearly occur at the end of the simulation period which are propagated by the outer loop’s position and velocity error feedbacks to the inner loop of the CDM.
In Fig. 11, the attitude tracking (TVT) in \({x}_{I}\)-, \({y}_{I}\)-, and \({z}_{I}\)-direction over time for the baseline controller with PCA is presented during the digital-8-maneuver. The controller performance of tracking the reference thrust vector elements \({t}_{x,r}^{R}\), \({t}_{y,r}^{R}\), and \({t}_{z,r}^{R}\) by the vehicle’s estimated thrust vector elements \({t}_{x}^{R}\), \({t}_{y}^{R}\), and \({t}_{z}^{R}\) are comparably good as the simulation results of the TVT for solely using the baseline controller, without PCA, as shown in Fig. 10. The only difference can be recognized in the end of the simulation period. Here, all disturbing rope oscillations, illustrated by a swirling of \({t}_{x}^{R}\), \({t}_{y}^{R}\), and \({t}_{z}^{R}\), since the rope pulls the rotor plane back and forth, are canceled out entirely being established through \({t}_{x,c}^{R}\), \({t}_{y,c}^{R}\), and \({t}_{z,c}^{R}\). Based on the outer loop’s CRM, the desired pseudo-control \({{\varvec{t}}}_{c}^{R}\) propagates the augmented trajectories \(\tilde{{\varvec{r}}}_{r}^{R}\) and \(\tilde{{\varvec{v}}}_{r}^{R}\) for the position and velocity reference to the nonlinear reference model of the CDM’s inner loop which concludes in a “PCA-dominated” trajectory design for the reference thrust vector \({{\varvec{t}}}_{r}^{R}\).
In Fig. 12, the attitude tracking (TVT) in \({x}_{I}\)-, \({y}_{I}\)-, and \({z}_{I}\)-direction of the I-frame over time for the baseline controller with TVA is presented during the digital-8-maneuver. The elements of the estimated thrust vector \({t}_{x}^{R}\), \({t}_{y}^{R}\), and \({t}_{z}^{R}\) are tracking the reference thrust vector elements \({t}_{x,r}^{R}\), \({t}_{y,r}^{R}\), and \({t}_{z,r}^{R}\) with high accuracy which implies a good controller performance. Similar to the simulation results of the TVT while using the baseline controller with PCA, shown in Fig. 11, the rope oscillations do completely vanish in the end of the flight maneuver. However, for the TVT, the augmented thrust vector command \(\tilde{{\varvec{t}}}_{c}^{R}\) does distinguish from the nominal thrust vector command \({{\varvec{t}}}_{c}^{R}\). That is why, the attitude tracking in Fig. 12 shows the nominal trajectories for the thrust vector command \({t}_{x,c}^{R}\), \({t}_{y,c}^{R}\), and \({t}_{z,c}^{R}\), and, additionally, shows the actual augmented trajectories for the thrust vector command \({\tilde{t }}_{x,c}^{R}\), \({\tilde{t }}_{y,c}^{R}\), and \({\tilde{t }}_{z,c}^{R}\) to emphasize that the TVT objective is smoothly shifted from the ORM to the CRM for non-steady-state conditions. The elements \({\tilde{t }}_{x,c}^{R}\) and \({\tilde{t }}_{y,c}^{R}\) do, besides their initial task to control \({{\varvec{r}}}_{xy}^{R}\) and \({{\varvec{v}}}_{xy}^{R}\) by stabilizing second-order position error dynamics, also stabilize the balloon dynamics around their zero equilibria, so that the rope oscillations are canceled out entirely at the end of the simulation period. In addition to that, the TVT in \({z}_{I}\)-direction of the I-frame over time shows that \({\tilde{t }}_{z,c}^{R}\) and \({t}_{z,c}^{R}\) are equal, since the augmentation unit solely damps the balloon motion artificially within the horizontal plane. The latter two statements lead to the fact that the position error \({e}_{x,p}\) as well as \({e}_{y,p}\) in \({x}_{I}\)- and \({y}_{I}\)-direction of the I-frame must increase on average which can be confirmed by Fig. 9.
To provide a quantitative mission assessment, Fig. 13 shows the simulation results for the rope angle variation over time during the digital-8-maneuver for all three controller configurations. For the baseline controller, the rope angle \({\gamma }_{{R}^{*}}\) is capped between \(90^\circ\) and \(30^\circ\). For the baseline controller with PCA, \({\gamma }_{{R}^{*}}\) is capped between \(90^\circ\) and \(40^\circ\) which is further reduced to a range between \(90^\circ\) and \(50^\circ\) in terms of the baseline controller with TVA. The flight mission can be stated as successful and practicable for all of the three controller configurations since \({\gamma }_{{R}^{*},ne}\) is not undershot. In terms of a smallest possible rope angle range, the baseline controller with TVA shows the best performance, or rather, is most successful in damping the balloon motion artificially within the horizontal plane. Nevertheless, the rope oscillations can not only be reduced significantly, but also canceled out entirely at the end of the flight maneuver when the baseline controller is extended artificially by either the PCA or the TVA approach. At this time, the balloon is perfectly arranged above the multirotor system which cannot be achieved by solely using the baseline controller without the artificial augmentation units.
6 Summary, conclusion, and outlook
In this paper, we presented a nonlinear flight controller for a multibody Mars vehicle guaranteeing asymptotic tracking position control with active oscillation damping. Relating thereto, as main contribution, we have studied two artificial augmentation approaches for the baseline controller:
-
Thrust vector augmentation (TVA),
-
Position command augmentation (PCA),
which both increase the controller capabilities to suppress modeling errors artificially without changing the baseline control laws. Basically, by utilizing oscillation damping feedbacks of the uncertain plant which are applied as additional commands to either the inner or the outer loop of the controller’s reference model. We pose that both TVA and PCA approach are advantageous to cope with plant uncertainties and that they can be added to an existing controller architecture (linear/nonlinear).
By utilizing the classical Newtonian formulations, a nine degrees of freedom multibody UAV model was derived including a six degrees of freedom rigid-body model for a hexrotor system and a three degrees of freedom point-mass model for a balloon UAV to setup a first stage high-fidelity simulation model. Kinematic constraints were imposed on both UAV models as massless spring-damper oscillator model to approximate a realistic rope connection. To simulate the extraterrestrial flight mission under realistic conditions, an atmospheric model was built on high-resolution measurement data being smoothed and prepared by a meteorological database of Mars to best fit 14.035° S and 58.5° W, the vehicle’s geographic take-off location at Valles Marineris. A nonlinear control design model of the hexrotor system was created and considered as baseline controller providing a cascaded structure. Feedback linearization was applied for the outer loop and analytical backstepping for the inner loop to derive all feedback laws. To cope with uncertain dynamic effects of the plant, being represented by oscillating motion of the suspension line, two artificial augmentation units were developed (TVA and PCA approach) both extending the baseline flight controller’s architecture separately.
Simulation results were presented for an eight-shaped flight maneuver at the bottom of Valles Marineris proving that both augmentation units actively damp the balloon motion in the forward flight case for non-steady-state conditions to counteract the rope oscillations and finally stabilize the rope angle around its equilibrium while keeping the system within its limits. The Mars vehicle was only able to reach a steady state in position including either the TVA or PCA approach in the closed-loop control system underlining their importance for the extraterrestrial mission simulation. However, further analysis of both proposed approaches is still required, since stability or rather semi–global stability (concerning closed-loop reference models for uncertain plants whose states are accessible) was not in the focus of this paper.
Future work should therefore hone the artificial augmentation units in a second stage high-fidelity simulation model including sensor models and state estimators for both hexrotor system and balloon UAV. Additionally, proper trajectory planning should be examined to ensure that (a) smoother rope angle trajectories are provided by adding additional feedforward terms to the baseline controller’s architecture and (b) the closed-loop control system stays within predefined safety bounds. To investigate the performance of the controller when subjected to exogenous disturbances, different wind scenarios shall be applied to the controlled plant to reproduce mission-critical environmental conditions such as dust storms on Mars, and especially, in the Valles Marineris.
Abbreviations
- ART:
-
Angular rates tracking
- CDM:
-
Control design model
- CRM:
-
Closed-loop reference model
- DLR:
-
German Aerospace Center
- DoF:
-
Degrees of Freedom
- DALR:
-
Dry adiabatic lapse rate
- EoM:
-
Equations of motion
- FSD:
-
Institute of Flight Systems Dynamics
- FSDSE:
-
FSD Simulation Environment
- LF:
-
Lyapunov function
- MARV:
-
Martian autonomous rotary-wing vehicle
- MCD:
-
Mars Climate Database
- MIL:
-
Model-in-the-loop
- MSA:
-
Martian Standard Atmosphere
- MSE:
-
Martian Simulation Environment
- NDI:
-
Nonlinear Dynamic Inversion
- Ode:
-
Ordinary differential equation
- PCA:
-
Position command augmentation
- PT1:
-
First-order proportional transfer function
- SDO:
-
Spring-damper-oscillator
- TVA:
-
Thrust vector augmentation
- TVT:
-
Thrust vector tracking
- UAV:
-
Unmanned aerial vehicle
- VaMEx:
-
Valles Marineris Explorer
- \({\varvec{B}}\) :
-
Input matrix
- \({C}_{D}\) :
-
Aerodynamic drag coefficient
- \({C}_{T}\) :
-
Propulsive thrust coefficient
- \({C}_{n}\) :
-
Propulsive torque coefficient
- \({\varvec{D}}\) :
-
Feedback gain matrix
- \({d}_{\mathrm{dp}}\) :
-
Damping constant of virtual damper
- \({\varvec{E}}\) :
-
Error matrix
- \({\varvec{e}}\) :
-
Tracking error vector
- \(e\) :
-
Tracking error
- \({\varvec{F}}\) :
-
Force vector
- \(F\) :
-
Absolute force
- \({\varvec{f}}\) :
-
Nonlinear function
- \({g}_{0}\) :
-
Normal gravity potential of Mars
- \({\varvec{g}}\) :
-
Gravitational force vector
- \({\varvec{g}}\) :
-
Nonlinear function
- \({\varvec{H}}\) :
-
Orientation matrix of Euler Angles
- \({H}_{G}\) :
-
Geopotential height
- \({H}_{G,1}\) :
-
Transition height of Martian troposphere
- \({h}_{\mathrm{avg}}\) :
-
Average ground height of Valles Marineris
- \(h\) :
-
Geodetic height above reference ellipsoid
- \({\varvec{I}}\) :
-
Identity matrix
- \({\varvec{J}}\) :
-
Mass moment of inertia tensor
- \({J}_{zz}\) :
-
Mass inertia around rotational axis
- \({\varvec{K}}\) :
-
Feedback gain matrix
- \(k\) :
-
Feedback or steady-state gain
- \({k}_{\mathrm{sp}}\) :
-
Stiffness of virtual spring
- \({k}_{T},{k}_{M}\) :
-
Motor constants
- \(l\) :
-
Length
- \(\tilde{l}\) :
-
Spring deflection
- \({l}_{0}\) :
-
Norm length of virtual spring
- \({\varvec{M}}\) :
-
Vector of external moments
- \(M\) :
-
Aerodynamic moment of rotor
- \(m\) :
-
Mass
- \({\varvec{P}}\) :
-
Positive definite symmetric matrix
- \(p\) :
-
Atmospheric pressure
- \({\varvec{Q}}\) :
-
Positive definite symmetric matrix
- \({\varvec{R}}\) :
-
Rotation matrix
- \({R}_{\mathrm{He}}\) :
-
Gas constant of Helium
- \({R}_{\mathrm{Mars}}\) :
-
Gas constant of planet Mars
- \({\varvec{r}}\) :
-
Position vector
- \({{\varvec{r}}}_{c}\) :
-
Pilot position vector command
- \(\tilde{{\varvec{r}}}_{c}\) :
-
Augmented position command vector
- \({{\varvec{r}}}_{r}\) :
-
Filtered position command vector
- \({r}_{bl}\) :
-
Radius of propeller blade
- \(S\) :
-
Reference area
- \(T\) :
-
Atmospheric temperature
- \(T\) :
-
Total thrust force
- \({\varvec{T}}\) :
-
Thrust-magnitude matrix
- \({{\varvec{T}}}_{\omega }\) :
-
Reduced thrust-magnitude matrix
- \(t\) :
-
Time (time constant)
- \({\varvec{t}}\) :
-
Thrust vector
- \({{\varvec{t}}}_{c}\) :
-
Thrust vector command (pseudo-control)
- \({{\varvec{t}}}_{r}\) :
-
Filtered thrust vector command
- \(\tilde{{\varvec{t}}}\) :
-
Augmented thrust vector
- \({\varvec{u}}\) :
-
Input vector
- \({{\varvec{u}}}_{1/2}\) :
-
Pseudo control input vector of TVT/ART
- \({{\varvec{u}}}_{c}\) :
-
Input vector command
- \(u\) :
-
Pseudo control input
- \(u\) :
-
Kinematic velocity in direction of \(x\)-axis
- \(V\) :
-
Lyapunov control function
- \(V\) :
-
Total velocity
- \(V\) :
-
Total volume
- \({\varvec{v}}\) :
-
Kinematic velocity vector
- \({{\varvec{v}}}_{cmd}\) :
-
Mapped velocity vector of remote control
- \({\varvec{x}}\) :
-
State vector of multicopter
- \({{\varvec{x}}}_{Bal}\) :
-
State vector of balloon
- \({{\varvec{x}}}_{P}\) :
-
Plant state vector
- \(x\) :
-
Position in direction of \(x\)-axis
- \({\varvec{y}}\) :
-
Output vector
- \(y\) :
-
Position in direction of \(y\)-axis
- \({{\varvec{z}}}_{B/b/I/S}\) :
-
Z-Axis of B/b/I/S-frame
- \(z\) :
-
Position in direction of \(z\)-axis
- \(\alpha\) :
-
Defined angle to y-axis
- \(\Gamma\) :
-
Lapse rate
- \(\gamma\) :
-
Defined angle to z-axis
- \(\epsilon\) :
-
Logical operator
- \(\zeta\) :
-
Relative damping coefficient
- \(\Theta\) :
-
Pitch angle
- \(\eta\) :
-
Polytropic exponent
- \({\varvec{\eta}}\) :
-
Vector of Euler Angles
- \(\mu\) :
-
Dynamic viscosity
- \({\mu }_{fr}\) :
-
Frictional coefficient
- \({{\varvec{\nu}}}_{d}\) :
-
Desired control effort vector
- \(\Phi\) :
-
Roll angle
- \(\rho\) :
-
Atmospheric density
- \({\rho }_{\mathrm{evl}}\) :
-
Areal density of balloon envelope
- \(\sigma\) :
-
Gradient of dynamic viscosity decrease
- \({\varvec{\tau}}\) :
-
Pseudo control input vector
- \(\chi\) :
-
Defined angle to y-axis
- \(\Psi\) :
-
Azimuth angle
- \(\omega\) :
-
Angular velocity or rotational speed
- \({\omega }_{0}\) :
-
Eigenfrequency
- \({\omega }_{z,c}^{Ib}\) :
-
Pilot yaw rate command
- \({\omega }_{z,r}^{Ib}\) :
-
Filtered yaw rate command
- \({\varvec{\omega}}\) :
-
Vector of angular velocities
- \({\varvec{\Omega}}\) :
-
Skew-symmetric matrix of angular velocities
- \(\Vert \cdot\Vert\) :
-
Euclidean norm of a vector
- \(\times\) :
-
Cross product of two vectors
- \(\circ\) :
-
Dot product of two vectors
- \({\left(\cdot\right)}^{-1}\) :
-
Inverse of a matrix
- \({\left(\cdot\right)}^{+}\) :
-
Moore–Penrose inverse of a matrix
- \({\left(\cdot\right)}^{T}\) :
-
Transpose of a matrix
- \(\left(\cdot\right)\) :
-
Creation of a diagonal matrix
- \(d\left(\cdot\right)\) :
-
Total differential
-
 :
: -
(1) Point of reference
(2) Actual point
(3) Type of physical quantity
(4) Reference coord. system of first derivative
(5) Reference coord. system of second derivative
(6) Notation frame
References
McKay, D.S., Gibson, E.K., Jr., Thomas-Keprta, K.L., Vali, H., Romanek, C.S., Clemett, S.J., Chillier, X.D., Maechling, C.R., Zare, R.N.: Search for past life on Mars: possible relic biogenic activity in Martian meteorite ALH84001. Science 273(5277), 924–930 (1996)
Klein, H.P.: On the search for extant life on Mars. Icarus 120(2), 431–436 (1996)
Horneck, G.: The microbial world and the case for Mars. Planet. Space Sci. 48(11), 1053–1063 (2000)
National Aeronautics and Space Administration: Mars Trek. https://trek.nasa.gov/mars/. Accessed on: 07 Aug 2019
Sand, S., Zhang, S., Mühlegg, M., Falconí, G.P., Zhu, C., Krüger, T., Nowak, S.: Swarm exploration and navigation on Mars. In: 2013 International Conference on Localization and GNSS (ICL-GNSS), pp. 1–6. Turin, Italy (2013). https://doi.org/10.1109/ICL-GNSS.2013.6577272
Bestmann, U., Gäbel, M., Krüger, T., Nowak, S., Staudinger, E., Wiedemann, T., Zhang, S., Krenmayr, M., Henkel, P., Lee, Y.-H.: VaMEx CoSMiC: Abschlussbericht, TU Braunschweig (2018). https://doi.org/10.2314/KXP:1669080331
Teplitski, M.: Design of an autonomous Martian Multirotor flying vehicle: Master thesis. Technical University Munich (TUM) (2014)
Reiss, P.: Design of a UAV Concept for the Mars Valles Marineris exploration: Master thesis. Technical University Munich (TUM) (2016)
Young, L.A., Aiken, E., Lee, P., Briggs, G.: Mars rotorcraft: possibilities, limitations, and implications for human/robotic exploration. In: 2005 IEEE Aerospace Conference, pp. 300–318. Big Sky, Montana, USA (2005). https://doi.org/10.1109/AERO.2005.1559324
Datta, A., Roget, B., Griffiths, D., Pugliese, G., Sitaraman, J., Bao, J., Liu, L., Gamard, O.: Design of a Martian autonomous rotary-wing vehicle. J. Aircr. 40(3), 461–472 (2003)
Grip, H.F., Scharf, D.P., Malpica, C., Johnson, W., Mandić, M., Singh, G., Young, L.: Guidance and control for a Mars helicopter. In: 2018 AIAA Guidance, Navigation, and Control Conference, pp. 1–22. Kissimmee, Florida, USA (2018). https://doi.org/10.2514/6.2018-1849
Kroo, I., Prinz, F., Shantz, M., Kunz, P., Fay, G., Cheng, S., Fabian, T., Partridge, C.: The Mesicopter: a miniature rotorcraft concept. Phase II Interim Report, Stanford University (2000)
Wang, J., Raffler, T., Holzapfel, F.: Nonlinear position control approaches for quadcopters using a novel state representation. In: AIAA Guidance, Navigation, and Control Conference, pp. 1–18. Minneapolis, Minnesota, USA (2012). https://doi.org/10.2514/6.2012-4913
Raffler, T., Wang, J., Holzapfel, F.: Path generation and control for unmanned multirotor vehicles using nonlinear dynamic inversion and pseudo control hedging. IFAC Proceedings Volumes. 46(19), 194–199 (2013)
Wang, J.: Novel control approaches to quadrotors inspired by dynamic inversion and backstepping. PhD thesis, Technical University Munich (TUM) (2015)
Saeed, A.S., Younes, A. B., Islam, S., Dias, J., Seneviratne, L., Cai, G.: A review on the platform design, dynamic modeling and control of hybrid UAVs. In: 2015 International Conference on Unmanned Aircraft Systems (ICUAS), pp. 806–815. Denver, Colorado, USA (2015). https://doi.org/10.1109/ICUAS.2015.7152365
Wise, K.A.: Dynamics of a UAV with parafoil under powered flight. In: AIAA Guidance, Navigation, and Control Conference and Exhibit, pp. 1–23. Keystone, Colorado, USA (2006). https://doi.org/10.2514/6.2006-6795
Redelinghuys, C.: A flight simulation algorithm for a parafoil suspending an air vehicle. J. Guid. Control. Dyn. 30(3), 791–803 (2007)
Guerrero, M.E., Mercado, D.A., Lozano, R., García, C.D.: IDA-PBC methodology for a quadrotor UAV transporting a cable-suspended payload. In: 2015 International Conference on Unmanned Aircraft Systems (ICUAS), pp. 470–476. Denver, Colorado, USA (2015). https://doi.org/10.1109/ICUAS.2015.7152325
Krstić, M., Kanellakopoulos, I., Kokotović, P.: Nonlinear and adaptive control design. Wiley, New York (1995)
Slotine, J.-J.E., Li, W.: Applied nonlinear control. Prentice Hall, Englewood Cliffs (1991)
Voos, H.: Nonlinear control of a quadrotor micro-UAV using feedback-linearization. In: 2009 IEEE International Conference on Mechatronics, pp. 1–6. Málaga, Spain (2009). https://doi.org/10.1109/ICMECH.2009.4957154
Wang, J., Bierling, T., Hoecht, L., Holzapfel, F., Klose, S., Knoll, A.: Novel dynamic inversion architecture design for quadrocopter control. In: Advances in aerospace guidance, Navigation and Control, pp. 261–272. Springer (2011)
Klausen, K., Fossen, T.I., Johansen, T.A.: Nonlinear control with swing damping of a multirotor UAV with suspended load. J. Intell. Robot. Syst. 88, 379–394 (2017)
Pollini, L., Metrangolo, A.: Simulation and robust backstepping control of a quadrotor aircraft. In: AIAA Modeling and Simulation Technologies Conference and Exhibit, pp. 1–18. Honolulu, Hawaii, USA (2008). https://doi.org/10.2514/6.2008-6363
Falconí, G.P., Holzapfel, F.: Position tracking of a multicopter using a geometric backstepping control law. In: Proceedings of the EuroGNC 2013, 2nd CEAS Specialist Conference on Guidance, Navigation & Control, pp. 1527–1545. Delft, The Netherlands (2013)
Wang, J., Holzapfel, F., Peter, F.: Comparison of nonlinear dynamic inversion and backstepping controls with application to a quadrotor. In: Proceedings of the EuroGNC 2013, 2nd CEAS Specialist Conference on Guidance, Navigation & Control, pp. 1245–1263. Delft, The Netherlands (2013)
Singh, T., Singhose, W.: Input shaping/time-delay control of maneuvering flexible structures. In: Proceedings of the 2002 American Control Conference (IEEE Cat. No.CH37301), pp. 1717–1731. Anchorage, Alaska, USA (2002). https://doi.org/10.1109/ACC.2002.1023813
Homolka, P., Hromčík, M., Vyhlídal, T.: Input shaping solutions for drones with suspended load: first results. In: 2017 21st International Conference on Process Control (PC), pp. 30–35. Strbske Pleso, Slovakia (2017). https://doi.org/10.1109/PC.2017.7976184
Bisgaard, M., la Cour-Harbo, A., Bendtsen, J.D.: Input shaping for helicopter slung load swing reduction. In: AIAA Guidance, Navigation and Control Conference and Exhibit, pp. 1–12. Honolulu, Hawaii, USA (2008). https://doi.org/10.2514/6.2008-6964
Bisgaard, M., la Cour-Harbo, A., Bendtsen, J.D.: Swing damping for helicopter slung load systems using delayed feedback. In: AIAA Guidance, Navigation, and Control Conference, pp. 1–11. Chicago, Illinois, USA (2009). https://doi.org/10.2514/6.2009-5795
Masoud, Z.N., Nayfeh, A.H.: Sway reduction on container cranes using delayed feedback controller. J. Nonlinear Dyn. 34, 347–358 (2003)
El-Ferik, S., Syed, A.H., Omar, H.M., Deriche, M.A.: Anti-swing nonlinear path tracking controller for helicopter slung load system. IFAC Proceedings Volumes. 46(30), 134–141 (2013)
Omar, H.M.: Anti-swing controller based on time-delay helicopter feedback for helicopter slung load system near hover. J. Aerosp. Technol. Manag. 4(3), 297–305 (2012)
Gibson, T.E., Annaswamy, A.M., Lavretsky, E.: Closed-loop reference models for output–feedback adaptive systems. In: 2013 European Control Conference (ECC), pp. 365–370. Zurich, Switzerland (2013). https://doi.org/10.23919/ECC.2013.6669803
Gibson, T.E., Annaswamy, A.M., Lavretsky, E.: On adaptive control with closed-loop reference models: transients, oscillations, and peaking. IEEE Access 1, 703–717 (2013)
Aström, K.J., Wittenmark, B.: Adaptive control. Addison-Wesley, Reading (1989)
Ioannou, P.A., Sun, J.: Robust adaptive control. Prentice-Hall, Upper Saddle River (1996)
Stevens, B.L., Lewis, F.L.: Aircraft control and simulation. Wiley, New York (1992)
Millour, E., Forget, F., Spiga, A., Navarro, T., Madeleine, J.-B., Montabone, L., Pottier, A., Lefèvre, F., Montmessin, F., Chaufray, J.-Y., López-Valverde, M.A., González-Galindo, F., Lewis, S.R., Read, P.L., Huot, J.-P., Desjean, M.-C.: The Mars climate database (MCD version 5.2). In: European Planetary Science Congress 2015, EPSC 2015-438, Nantes, France (2015)
Hooijberg, M.: Time and reference systems. Geometrical Geodesy, 2nd edn., pp. 1–26. Springer, Berlin (2008)
Berberan-Santos, M.N., Bodunov, E.N., Pogliani, L.: On the barometric formula inside the Earth. J. Math. Chem. 47(3), 990–1004 (2010)
Smith, D.E., et al.: Mars Orbiter Laser Altimeter: experiment summary after the first year of global mapping of Mars. J. Geophys. Res. 106(E10), 23689–23722 (2001)
Fairbridge, W.R., Oliver, J.E.: Lapse rate. In: Oliver, J.E. (ed.) Encyclopedia of world climatology, pp. 448–450. Springer, Dordrecht (1987)
Meriam, J.L., Kraige, L.G., Bolton, J.N.: Engineering mechanics: dynamics, 8th edn. Wiley, New York (2015)
van der Wall, B.G.: Grundlagen der Hubschrauber-Aerodynamik. Springer, Berlin (2015)
Lunze, J.: Regelungstechnik 1. Springer, Berlin (2010)
Yajima, N., Imamura, T., Izutsu, N., Abe, T.: Scientific ballooning. Springer, Berlin (2009)
Falconí, G., Angelov, J., Holzapfel, F.: Adaptive Fault–Tolerant Position Control of a Hexacopter Subject to an Unknown Motor Failure. Proc. Int. J. Appl. Math. Comput. Sci. 28(2), 309–321 (2018)
Johansen, T.A., Fossen, T.I.: Control allocation—a survey. Automatica 49(5), 1087–1103 (2013)
Chaturvedi, N., Sanyal, A., McClamroch, N.: Rigid-body attitude control. IEEE Control. Syst. 31(3), 30–51 (2011)
Holzapfel, F.: Nichtlineare adaptive Regelung eines unbemannten Fluggerätes. PhD thesis, Technical University Munich (TUM) (2004)
Khalil, H.K.: Nonlinear systems, 3rd edn. Prentice Hall, Upper Saddle River (2002)
Narendra, K.S., Annaswamy, A.M.: Stable adaptive systems. Prentice Hall, Englewood Cliffs (1989)
Falconí, G.P., Holzapfel, F.: Position tracking of a hexacopter using a geometric backstepping control law - experimental results. In: 2014 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), pp. 20–25. Yogyakarta, Indonesia (2014). https://doi.org/10.1109/ICARES.2014.7024375
Acknowledgements
The results shown in this paper have been mostly developed from July 2017 until Dec. 2018 during the mid-term and master thesis of the first author at the Institute of Flight System Dynamics, Technical University Munich. The idea to only use the transient rate of the relative position error signal for the closed-loop reference model within the control design model’s outer loop has been developed from the first author during his research at the Institute of Air Transportation Systems, Technical University Hamburg, where he continued his study in control theory.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bodmer, D., Krenmayr, M. & Holzapfel, F. Asymptotic tracking position control with active oscillation damping of a multibody Mars vehicle using two artificial augmentation approaches. CEAS Space J 14, 125–149 (2022). https://doi.org/10.1007/s12567-021-00364-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12567-021-00364-6




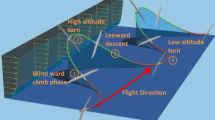













 :
: