Skip to main content

Advertisement

SpringerLink
Log in

A controllability perspective of dynamic soaring

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

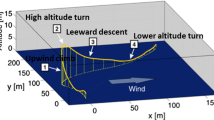
Dynamic soaring is an exquisite flying technique to acquire energy from the atmospheric wind shear. In this study, a geometric nonlinear controllability analysis of an unmanned aerial vehicle (UAV) under dynamic soaring conditions is performed. To achieve such an objective, the state-of-the-art mathematical tools of nonlinear controllability are summarized and presented to an aeronautical engineering audience. The dynamic soaring optimal control problem is then formulated and solved numerically. The controllability of the UAV along the optimal soaring trajectory is analyzed. More importantly, the geometric nonlinear controllability characteristics of generic flight dynamics are analyzed in the presence and absence of wind shear to provide a controllability explanation for the role of wind shear in the physics of dynamic soaring flight. It is found that the wind shear is instrumental in ensuring controllability as it allows the UAV attitude controls (pitch and roll) to play the role of thrust in controlling the flight path angle. The presented analysis represents a controllability-based mathematical proof for the energetics of flight physics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Abbreviations

AR:

Aspect ratio of the wing

b :

Wing span

C :

Controllability matrix

\(C_{\mathrm{L}}\) :

Lift coefficient

\(C_{\mathrm{D}}\) :

Drag coefficient

\(C_{\mathrm{D}_{0}}\) :

Zero lift drag coefficient

e :

Oswald efficiency factor

\(f({\varvec{x}})\) :

Drift vector

g :

Acceleration due to gravity

\(g_j({\varvec{x}})\) :

Control input vector field

K :

Aerodynamic coefficient

LARC:

Lie algebraic rank condition

m :

Mass of the vehicle

\(R_\Sigma ({\varvec{x}}_0, T)\) :

Reachable set from \(x_0\) in exactly time T

S :

Wing planform area

V :

True air speed

\(V_\mathrm{w}\) :

Wind velocity

x :

Position vector along east direction

y :

Position vector along north direction

z :

Altitude

\(\alpha \) :

Angle of attack

\(\gamma \) :

Flight path angle

\(\Delta \) :

Accessibility distribution

\(\theta \) :

Pitch angle

\(\rho \) :

Density of the air

\(\phi \) :

Bank angle

\(\Phi (t,\tau )\) :

State transition matrix

\(\psi \) :

Azimuth measured clockwise from the y-axis

References

  1. Wilson, J.: Sweeping flight and soaring by albatrosses. Nature 257(5524), 307–308 (1975)

    Article  Google Scholar 

  2. Denny, M.: Dynamic soaring: aerodynamics for albatrosses. Eur. J. Phys. 30(1), 75 (2008)

    Article  Google Scholar 

  3. Sachs, G., Traugott, J., Nesterova, A., Bonadonna, F.: Experimental verification of dynamic soaring in albatrosses. J. Exp. Biol. 216(22), 4222–4232 (2013)

    Article  Google Scholar 

  4. Pennycuick, C.: The flight of petrels and albatrosses (Procellariiformes), observed in South Georgia and its vicinity. Philos. Trans. R. Soc. Lond. B: Biol. Sci. 300(1098), 75–106 (1982)

    Article  Google Scholar 

  5. Zhao, Y.J., Qi, Y.C.: Minimum fuel powered dynamic soaring of unmanned aerial vehicles utilizing wind gradients. Optim. Control Appl. Methods 25(5), 211–233 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhao, Y.J.: Optimal patterns of glider dynamic soaring. Optim. Control Appl. Methods 25(2), 67–89 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  7. Wharington, J.M.: Heuristic control of dynamic soaring. In: Control Conference, 2004. 5th Asian, vol. 2, pp. 714–722. IEEE (2004)

  8. Richardson, P.L.: Upwind dynamic soaring of albatrosses and UAVs. Prog. Oceanogr. 130, 146–156 (2015)

    Article  Google Scholar 

  9. Akhtar, N.L.: Control system development for autonomous soaring (2010). https://dspace.lib.cranfield.ac.uk/handle/1826/6899

  10. Sukumar, P.P., Selig, M.S.: Dynamic soaring of sailplanes over open fields. J. Aircr. 50(5), 1420–1430 (2013)

    Article  Google Scholar 

  11. Lawrance, N., Acevedo, J., Chung, J., Nguyen, J., Wilson, D., Sukkarieh, S.: Long endurance autonomous flight for unmanned aerial vehicles. AerospaceLab 8, 1 (2014)

    Google Scholar 

  12. Sachs, G.: Minimum shear wind strength required for dynamic soaring of albatrosses. Ibis 147(1), 1–10 (2005)

    Article  Google Scholar 

  13. Pennycuick, C.J.: Gust soaring as a basis for the flight of petrels and albatrosses (Procellariiformes). Avian Sci. 2(1), 1–12 (2002)

    Google Scholar 

  14. Cone Jr., C.D., et al.: A mathematical analysis of the dynamic soaring flight of the albatross with ecological interpretations (1964). https://doi.org/10.21220/V5P88C

  15. Wood, C.: The flight of albatrosses (a computer simulation). Ibis 115(2), 244–256 (1973)

    Article  Google Scholar 

  16. Boslough, M.B.: Autonomous dynamic soaring platform for distributed mobile sensor arrays. Sandia National Laboratories, Sandia National Laboratories, Technical Report SAND2002-1896 (2002)

  17. Sachs, G., Grüter, B.: Dynamic soaring-kinetic energy and inertial speed. AIAA Atmospheric Flight Mechanics Conference, No. 2017-1862 (2017)

  18. Akhtar, N., Whidborne, J.F., Cooke, A.K.: Wind shear energy extraction using dynamic soaring techniques. American Institute of Aeronautics and Astronautics, AIAA, No. 2009-734 (2009)

  19. Akhtar, N., Whidborne, J., Cooke, A.: Real-time optimal techniques for unmanned air vehicles fuel saving. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 226(10), 1315–1328 (2012)

    Article  Google Scholar 

  20. Gao, X.-Z., Hou, Z.-X., Guo, Z., Fan, R.-F., Chen, X.-Q.: Analysis and design of guidance-strategy for dynamic soaring with UAVs. Control Eng. Pract. 32, 218–226 (2014)

    Article  Google Scholar 

  21. Ariff, O., Go, T.: Waypoint navigation of small-scale UAV incorporating dynamic soaring. J. Navig. 64(1), 29–44 (2011)

    Article  Google Scholar 

  22. Deittert, M., Richards, A., Toomer, C., Pipe, A.: Dynamic soaring flight in turbulence. In: AIAA Guidance, Navigation and Control Conference, Chicago, IL, vol. 2009-6012 (2009)

  23. Liu, Y., Longo, S., Kerrigan, E.C.: Nonlinear predictive control of autonomous soaring UAVs using 3DOF models. In: Control Conference (ECC), 2013 European, pp. 1365–1370. IEEE (2013)

  24. Lawrance, N.R., Sukkarieh, S.: A guidance and control strategy for dynamic soaring with a gliding UAV. In: IEEE International Conference on Robotics and Automation, 2009. ICRA’09, pp. 3632–3637. IEEE (2009)

  25. Baillieul, J., Lehman, B.: Open-loop control using oscillatory inputs. In: CRC Control Handbook, pp. 967–980 (1996)

  26. Marsden, J., O’Reilly, O., Wicklin, F., Zombros, B.: Symmetry, stability, geometric phases, and mechanical integrators. Nonlinear Sci. Today 1(1), 4–11 (1991)

    MathSciNet  MATH  Google Scholar 

  27. Marsden, J.E.: Geometric foundations of motion and control. In: Motion, Control, and Geometry: Proceedings of a Symposium, Board on Mathematical Science, National Research Council Education, National Academies Press, Washington, DC (1997)

  28. Murray, R.M., Sastry, S.S.: Nonholonomic motion planning: steering using sinusoids. IEEE Trans. Autom. Control 38(5), 700–716 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  29. Liu, W.: Averaging theorems for highly oscillatory differential equations and iterated Lie brackets. SIAM J. Control Optim. 35(6), 1989–2020 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  30. Liu, W.: An approximation algorithm for nonholonomic systems. SIAM J. Control Optim. 35(4), 1328–1365 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  31. Patterson, M.A., Rao, A.V.: GPOPS-II: a MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. (TOMS) 41(1), 1 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  32. Kalman, R.E., Ho, Y.C.K.N.: Controllability of linear dynamical systems. Contrib. Differ. Equ. 1, 189–213 (1963)

    MathSciNet  Google Scholar 

  33. Nijmeijer, H., Van der Schaft, A.: Nonlinear Dynamical Control Systems. Springer, Berlin (1990)

    Book  MATH  Google Scholar 

  34. Hassan, A.M., Taha, H.E.: Geometric control formulation and nonlinear controllability of airplane flight dynamics. Nonlinear Dyn. 88(4), 2651–2669 (2017)

    Article  MathSciNet  Google Scholar 

  35. Bullo, F., Lewis, A.D.: Geometric Control of Mechanical Systems: Modeling, Analysis, and Design for Simple Mechanical Control Systems, vol. 49. Springer, New York (2004)

    MATH  Google Scholar 

  36. Bianchini, R.M., Stefani, G.: Graded approximations and controllability along a trajectory. SIAM J. Control Optim. 28(4), 903–924 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  37. Brunovsky, P.: Local controllability of odd systems. Math. Control Theory 1, 39–45 (1974)

    Google Scholar 

  38. Crouch, P.E., Byrnes, C.I.: Local accessibility, local reachability, and representations of compact groups. Theory Comput. Syst. 19(1), 43–65 (1986)

    MathSciNet  MATH  Google Scholar 

  39. Hermes, H.: On local controllability. SIAM J. Control Optim. 20(2), 211–220 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  40. Jurdjevic, V., Kupka, I.: Polynomial control systems. Math. Ann. 272(3), 361–368 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  41. Sussmann, H.J.: A general theorem on local controllability. SIAM J. Control Optim. 25(1), 158–194 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  42. Sussmann, H.J., Jurdjevic, V.: Controllability of nonlinear systems. J. Differ. Equ. 12(1), 95–116 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  43. Stefani, G.: Local controllability of non-linear systems: an example. Syst. Control Lett. 6(2), 123–125 (1985)

    Article  MATH  Google Scholar 

  44. Eisa, S., Mir, I., Taha, H.: Controllability along trajectory: analysis of dynamic soaring (2018) (under review)

  45. Mir, I., Maqsood, A., Eisa, S.A., Taha, H., Akhtar, S.: Optimal morphing-augmented dynamic soaring maneuvers for unmanned air vehicle capable of span and sweep morphologies. Aerosp. Sci. Technol. 79, 17–36 (2018)

    Article  Google Scholar 

  46. Gordon, R.J.: Optimal dynamic soaring for full size sailplanes. Technical Report, Air Force Institute of Technology Wright-Patterson (AFB) OH, Department of Aeronautics and Astronautics (2006)

  47. Liu, D.-N., Hou, Z.-X., Guo, Z., Yang, X.-X., Gao, X.-Z.: Bio-inspired energy-harvesting mechanisms and patterns of dynamic soaring. Bioinspir. Biomim. 12(1), 016014 (2017)

    Article  Google Scholar 

  48. Guo, G., Qiao, J., Han, C.: Controllability of periodic systems: continuous and discrete. IEE Proc. Control Theory Appl. 151(4), 488–490 (2004)

    Article  Google Scholar 

  49. Munthe-Kaas, H., Owren, B.: Computations in a free Lie algebra. Philos. Trans. R. Soc. Lond. A: Math. Phys. Eng. Sci. 357(1754), 957–981 (1999)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Research Center for Modeling and Simulation, National University of Sciences and Technology, H-12 Campus, Islamabad, Pakistan

    Imran Mir & Adnan Maqsood

  2. Mechanical and Aerospace Engineering Department, University of California, Irvine, USA

    Haitham Taha & Sameh A. Eisa

Authors
  1. Imran Mir
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haitham Taha
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sameh A. Eisa
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Adnan Maqsood
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Haitham Taha.

Ethics declarations

Conflict of interest

The authors of this paper have no conflict of interest to declare.

Appendix A: Lie brackets

Appendix A: Lie brackets

In this appendix, we show some of the Lie brackets that completes the LARC (specified by Eq. (30)) between the vector fields \({\varvec{f}}\) and \({\varvec{g}}_p\) and \({\varvec{g}}_q\) under linear wind shear conditions.

$$\begin{aligned}&{[}{\varvec{g}}_p,{\varvec{g}}_q{]}= \begin{bmatrix} 0\\ 0\\ \frac{\cos \phi }{\cos \theta }\\ 0\\ 0\\ 0\\ \cos \phi \tan \theta \\ -\sin \phi \\ \end{bmatrix}, \;\;\\&{[}{\varvec{f}},{\varvec{g}}_p{]}= \begin{bmatrix} 0\\ \frac{C_{\mathrm{L}_{a}} \rho S V \sin \phi (\alpha _{0L} + \gamma - \theta )}{2m}\\ \frac{C_{\mathrm{L}_{a}} \rho S V \cos \phi (\alpha _{0L} + \gamma -\theta )}{2m\cos \gamma }\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{bmatrix}, \;\;\\&{[}{\varvec{g}}_p,[{\varvec{f}},{\varvec{g}}_p]{]}= \begin{bmatrix} 0\\ -\frac{C_{\mathrm{L}_a} \rho S V \cos \phi (\alpha _{0L} + \gamma - \theta )}{2m}\\ -\frac{(C_{\mathrm{L}_a} \rho S V \sin \phi (\alpha _{0L} + \gamma - \theta )}{2m\cos \gamma }\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{bmatrix},\\ \end{aligned}$$
$$\begin{aligned}&{[}{\varvec{f}},{\varvec{g}}_q{]} \begin{bmatrix} \frac{\beta V \cos \gamma \cos \psi \sin \gamma \sin \phi }{\cos \theta }- \frac{C_{\mathrm{L}_{a}}^2 K \rho S V^2 \cos \phi (2 \alpha _{0L} + 2 \gamma - 2\theta )}{2m}\\ -\frac{\beta \cos \psi \sin ^2\gamma \sin \phi }{\cos \theta }- \frac{C_{\mathrm{L}_{a}}\rho S V \cos ^2\phi }{2m} -\frac{C_{\mathrm{L}_{a}} \rho S V \sin ^2\phi \tan \theta (\alpha _{0L} + \gamma - \theta )}{2m} \\ \frac{C_{\mathrm{L}_{a}}\rho S V \cos \phi \sin \phi \tan \theta (\alpha _{0L} + \gamma - \theta )}{2 m \cos \gamma }-\frac{C_{\mathrm{L}_{a}}\rho S V \cos \phi \sin \phi }{2 m\cos \gamma }- \frac{\beta \sin \gamma \sin \phi \sin \psi }{\cos \gamma \cos \theta }\\ \frac{V \cos \gamma \cos \psi \sin \phi }{\cos \theta }\\ \frac{V \cos \gamma \sin \phi \sin \psi }{\cos \theta }\\ 0\\ 0\\ 0 \end{bmatrix}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mir, I., Taha, H., Eisa, S.A. et al. A controllability perspective of dynamic soaring. Nonlinear Dyn 94, 2347–2362 (2018). https://doi.org/10.1007/s11071-018-4493-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4493-6

Keywords

Search

Navigation