Promotion Time Cure Model with Local Polynomial Estimation

Abstract

In modeling survival data with a cure fraction, flexible modeling of covariate effects on the probability of cure has important medical implications, which aids investigators in identifying better treatments to cure. This paper studies a semiparametric form of the Yakovlev promotion time cure model that allows for nonlinear effects of a continuous covariate. We adopt the local polynomial approach and use the local likelihood criterion to derive nonlinear estimates of covariate effects on cure rates, assuming that the baseline distribution function follows a parametric form. This approach ensures that the model is identifiable and we adopt a flexible method to estimate the cure rate locally, the important part in cure models, and a convenient way to estimate the baseline function globally. An algorithm is proposed to implement estimation at both the local and global scales. Asymptotic properties of local polynomial estimates, the nonparametric part, are investigated in the presence of both censored and cured data, and the parametric part is shown to be root-n consistent. The proposed methods are illustrated by simulated and real data with discussions on the practical applications of the proposed method, including the selections of the bandwidths in the local polynomial approach and the parametric baseline distribution family. Extension of the proposed method to multiple covariates is also discussed.

Appendix

I. Derivation of the log likelihood function (4)

$$\begin{aligned} \ell&= \log \left( \prod ^{n}_{i=1}\lbrace [f_{T}(Y_{i};\theta (X_{i}),\gamma )]^{\Delta _{i}}[S_{T}(Y_{i};\theta (X_{i}),\gamma )]^{1-\Delta _{i}}\rbrace ^{I(Y_{i}< \infty )}\lbrace S_{T}(\infty ; \theta (X_{i}),\gamma )\rbrace ^{I(Y_{i} = \infty )} \right) \nonumber \\&= \sum ^{n}_{i=1} \left( I(Y_{i}< \infty )\left\{ \Delta _{i}[\log (\theta (X_{i})) + \log f(Y_{i}; \gamma ) - \theta (X_{i}) F(Y_{i}; \gamma )] - (1 - \Delta _{i})\theta (X_{i}) F(Y_{i}; \gamma ) \right\} \right. \nonumber \\&\left. -I(Y_{i} = \infty )[\theta (X_{i}) F(Y_{i}; \gamma )] \right) \nonumber \\&= \sum ^{n}_{i=1} \left( I(Y_{i} < \infty )\left\{ \Delta _{i}[\log (\theta (X_{i})) + \log f(Y_{i}; \gamma )] - \theta (X_{i}) F(Y_{i}; \gamma )\right\} - I(Y_{i} = \infty )[\theta (X_{i}) F(Y_{i}; \gamma )] \right) \nonumber \\&= \sum ^{n}_{i=1} \left\{ \Delta _{i}[\log (\theta (X_{i})) + \log f(Y_{i}; \gamma )] - \theta (X_{i}) F(Y_{i}; \gamma ) \right\} \end{aligned}$$

(14)

II. Proofs of the Lemmas and Theorems in Section 2

The conditions used in the Lemmas and Theorems are given first, followed by the details of their proofs.

Conditions (A)

• (A1) The kernel function $K(\cdot ) \ge 0$ is a bounded density with compact support.

• (A2) The function $m(\cdot )$ has a continuous $(p+1)$-th derivative around grid point x.

• (A3) The second derivative of the baseline function $F(\cdot )$ exists.

• (A4) The density of X, $f_X(x) >0$, is continuous on a compact support.

• (A5) For estimating the k-th derivative of $m(\cdot )$, $k=0, \dots , p$, $h \rightarrow 0$ and $nh^{2k+1} \rightarrow \infty$, as $n \rightarrow \infty$.

• (A6) The true value of $\gamma$, $\gamma _0$, in the baseline function $F(\cdot )$ is an interior point of its parameter space.

• (A7) There exists an $\eta > 0$ such that $E\{|\Delta - \theta (x)F(Y;\gamma _{0})|^{2+\eta }\}$ is finite and continuous at point $X=x$ for $0<\eta <1$.

• (A8) The functions $E\{\Delta |X\}$, $E\{F(Y; \gamma _{0})|X\}, E\{F^{'}(Y; \gamma _{0})|X\}$, $E\{F^{''}(Y; \gamma _{0})|X\}, E\{\xi (Y; \gamma _{0})|X\}$, $E\{\xi ^{'}(Y; \gamma _{0})|X\},$ and $E\{\xi ^{''}(Y;\gamma _{0})|X\}$ are continuous at point $X=x$, where $\xi (Y; \gamma ) = \log f(Y; \gamma )$.

• (A9) There exists a function M(y) with $EM(Y) < \infty$ such that

  $$\begin{aligned} \left| \frac{\partial ^{3}}{\partial \beta _{j}\partial \beta _{k}\partial \beta _{l}} \xi (y; \gamma ) \right| < M(y). \end{aligned}$$

Proof of Lemma 1

The log likelihood function (4) is the data version of the population log likelihood function

$$\begin{aligned} \ell _1= \Delta (\log \theta (X)+\log f(Y; \gamma )) - \theta (X)F(Y;\gamma ). \end{aligned}$$

With $\gamma =\gamma _0$, at point x, taking the derivative of $\ell _1$ with respect to $\theta (\cdot )$ and then taking the conditional expectation,

$$\begin{aligned} E\left( \frac{\partial \ell _1 }{\partial \theta (x)}|X = x \right) = E\left( \Delta ( 1/ \theta (x)) - F(Y; \gamma _{0})|X = x \right) , \end{aligned}$$

which is 0 at the true value of $\theta (x)$. Thus Lemma 1 is obtained. $\square$

Proof of Theorem 1

For simplicity, the subscript of $\beta _x$ is neglected in this proof. Recall that $\beta ^{0}$ is the true value of $\beta$. Given $\gamma = \gamma _{0}$, let $\alpha = H(\beta - \beta ^{0})$ with the true value of $\alpha =0$, where H is defined in Theorem 1. Then $\tilde{\text{ x }}_i^{T}\beta = \tilde{\text{ x }}_i^{T}\beta ^{0}+U_i^{T}\alpha$, where $U_{i} = H^{-1}\tilde{\text{ x }}_{i}$. The local likelihood (6) is rewritten as

$$\begin{aligned} \ell _{x} = \frac{1}{n} \sum ^{n}_{i=1}\{\Delta _{i}(\tilde{\text{ x }}^{T}_{i}\beta ^{0}+U^{T}_{i}\alpha ) + \Delta _{i} \log f(Y_{i}; \gamma _0) - \exp (\tilde{\text{ x }}^{T}_{i}\beta ^{0}+U^{T}_{i}\alpha )F(Y_{i}; \gamma _0)\}K_{h}(X_{i}-x). \end{aligned}$$

(15)

Taking the derivative of (15) with respect to $\alpha$ yields

$$\begin{aligned} \frac{1}{n} \sum ^{n}_{i=1}\{\Delta _{i} - \exp (\mathbf{\tilde{x}}^{T}_{i}\beta ^{0}+U^{T}_{i}\alpha )F(Y_{i};\gamma _{0})\}U_{i}K_{h}(X_{i}-x). \end{aligned}$$

(16)

Then it is equivalent to show that there exists a maximizer $\hat{\alpha }$ to the likelihood equation (16) such that $\hat{\alpha } {\mathop {\rightarrow }\limits ^{p}} 0$.

Let $B(0,\epsilon )$ be an open ball which centered at 0 with radius $\epsilon > 0$. Denote by $\alpha _j$ the j-th element of $\alpha$. By a Taylor expansion around the true $\alpha =0$, $\ell _{x}(\alpha ) = \ell _{x}(0) + \ell ^{'}_{x}(0)^{T}\alpha + \frac{1}{2}\alpha ^{T}\ell ^{''}_{x}(0)\alpha + R_{n}(\alpha ^{\star }),$ where $R_{n}(\alpha ) = \frac{1}{3!}\sum _{j,k,l} \alpha _{j} \alpha _{k} \alpha _{l} \frac{\partial ^{3}}{\partial \alpha _{j}\partial \alpha _{k}\partial \alpha _{l}}\ell _{x}(\alpha )$ and $\alpha ^{*}$ is between $\alpha$ and 0. For the term $\ell ^{'}_{x}(0)^{T}\alpha$,

$$\begin{aligned} \ell ^{'}_{x}(0)&= \frac{1}{n} \sum ^{n}_{i=1}\{\Delta _{i} - \exp (X^{T}_{i}\beta ^{0})F(Y_{i};\gamma _{0})\}U_{i}K_{h}(X_{i}-x) \\&{\mathop {\rightarrow }\limits ^{p}} f_{X}(x) E\{\Delta - \theta (x)F(Y;\gamma _{0})|X=x\}\int {\textbf {u}} K(u)du, \end{aligned}$$

where $\text{ u }$ is defined in Theorem 2. Based on Lemma 1, $\ell ^{'}_{x}(0)=0$. Thus for any $\epsilon > 0$, with probability tending to 1,

$$\begin{aligned} | \ell ^{'}_{x}(0)^{T} \alpha | \le \epsilon \ \ \text{ for } \alpha \in B(0,\epsilon ). \end{aligned}$$

For $\alpha ^{T}\ell ^{''}_{x}(0) \alpha$, taking the second derivative of (15) with respect to $\alpha$ yields $\ell _x^{''}$,

$$\begin{aligned} \ell ^{''}_{x}= & {} \frac{1}{n} \sum ^{n}_{i=1}\{-\exp (\mathbf{\tilde{x}}^{T}_{i}\beta ^{0}+U^{T}_{i}\alpha )F(Y_{i};\gamma _{0})\}U_{i}U^{T}_{i}K_{h}(X_{i}-x). \end{aligned}$$

Plugging in $\alpha =0$, the expectation of $\ell _x^{''}(0)$ is

$$\begin{aligned}{} & {} -E\{\exp (\mathbf{\tilde{x}}^{T}\beta ^{0})F(Y;\gamma _{0})UU^{T}K_{h}(X-x)\} \nonumber \\= & {} -\int \int \exp (m(X))F(Y;\gamma _{0})UU^{T}K_{h}(X-x)f_{Y|X}(Y|X) f_X(X)dXdY (1+ o_P(1)) \nonumber \\= & {} -\int \int \exp (m(x+hu))F(Y;\gamma _{0}){\textbf {uu}}^{\textbf {T}}K(u)f_{Y|X}(Y|X = x)f_X(x+hu)dudY (1+ o_P(1)) \nonumber \\= & {} -f_X(x)\int E(\theta (x)F(Y;\gamma _{0})|X=x) {\textbf {uu}}^{\textbf {T}}K(u)du (1+ o_P(1)) \nonumber \\= & {} -f_X(x) E(\Delta |X=x) \int {\textbf {uu}}^{\textbf {T}}K(u)du (1+ o_P(1))= -f_X(x)S_{1}(x) (1+ o_P(1)), \end{aligned}$$

(17)

where $S_{1}(x)$ is defined in Theorem 2. Thus for any $\epsilon > 0$,

$$\begin{aligned} \alpha ^{T}\ell ^{''}_{x}(0) \alpha < -f_X(x) \eta _{1} \epsilon ^{2} \text{ with } \text{ probability } \text{ tending } \text{ to } \text{1 }, \end{aligned}$$

where $\eta _{1}$ is the minimum eigenvalue of $S_{1}(x)$ (Horn et al. [39]).

Under condition (A9), $|R_{n}(\alpha )| \le C\epsilon ^{3}\frac{1}{n}\sum ^{n}_{i=1}M(Y_{i})=C\epsilon ^{3}\{E(M(Y))+o_{p}(1)\}$ for some constant $C > 0$. As a result, when $\epsilon$ is small enough, for any $\alpha \in B(0,\epsilon )$,

$$\begin{aligned} \ell _{x}(\alpha ) - \ell _{x}(0) \le 0 \text{ with } \text{ probability } \text{ tending } \text{ to } \text{1 }, \end{aligned}$$

which implies

$$\begin{aligned} \sup _{\alpha \in B(0, \epsilon )} \ell _{x}(\alpha ) - \ell _{x}(0) \le 0 \text{ with } \text{ probability } \text{ tending } \text{ to } \text{1 }. \end{aligned}$$

Thus $\ell _x(\alpha )$ has a local maximum in $B(0, \epsilon )$ so that the likelihood equation has a maximizer $\hat{\alpha }(\epsilon )$ and $||\hat{\alpha }|| \le \epsilon$ with probability tending to 1. This completes the proof of Theorem 1. $\square$

Proof of Theorem 2

We prove part (a) first. Following the proof of Theorem 1, from (15) with $\gamma =\gamma _0$, since $0 = \ell _x^{'}(\hat{\alpha }) \approx \ell _x^{'}(0) + \ell _x^{''}(0)\hat{\alpha },$

$$\begin{aligned} \hat{\alpha } \approx - \{\ell _x^{''}(0) (1+ o_P(1))\}^{-1} \ell _x^{'}(0). \end{aligned}$$

(18)

We next derive the asymptotic expressions of $\ell _x^{'}(0)$ and $Var\{\ell _x^{'}(0)\}$.

Taking the expectation of (16) and using Lemma 1,

$$\begin{aligned}{} & {} E\{ (\Delta - \exp (\mathbf{\tilde{x}}^{T}\beta ^{0})F(Y;\gamma _{0})) UK_{h}(X-x)\} \nonumber \\{} & {} = E_{X}\{E_{Y|X}\{\Delta - \exp (\mathbf{\tilde{x}}^{T}\beta ^{0} )F(Y;\gamma _{0}) \} U K_{h}(X-x)\} \nonumber \\{} & {} = E_{X}\{E_{Y|X}\{F(Y;\gamma _{0}) \exp (m(X)) - \exp (\mathbf{\tilde{x}}^{T}\beta ^{0} ) F(Y;\gamma _{0}) \} U K_{h}(X-x)\} \nonumber \\{} & {} = E_{X}\{E_{Y|X}\{ F(Y;\gamma _{0})[ \exp (m(X)) - \exp (\mathbf{\tilde{\text{ x }}}^{T}\beta ^{0})] \} U K_{h}(X-x) \}. \end{aligned}$$

(19)

By a Taylor expansion,

$$\begin{aligned} \exp (m(X)) - \exp (\mathbf{\tilde{\text{ x }}}^{T}\beta ^{0})= \theta (x)\frac{m^{(p+1)}(x)}{(p+1)!}(X-x)^{p+1} (1 + o_{p}(1)), \end{aligned}$$

and by a change of variables $X-x = hu$, (19) is

$$\begin{aligned}{} & {} \int \int \theta (x)\frac{m^{(p+1)}(x)}{(p+1)!}(hu)^{p+1}F(Y;\gamma _{0}){\textbf {u}} K(u)f_{Y|X}(Y|X = x)f_X(x+hu)du dY (1 + o_{p}(1)) \\{} & {} = f_X(x)\theta (x)\frac{m^{(p+1)}(x)}{(p+1)!}h^{p+1}\int \int F(Y;\gamma _{0})f_{Y|X}(Y|X = x)dY u^{p+1}{} {\textbf {u}} K(u)du (1 + o_{p}(1)) \\{} & {} = f_X(x)\theta (x)\frac{m^{(p+1)}(x)}{(p+1)!}h^{p+1} E\{F(Y;\gamma _{0})|X = x\} \int {\textbf {u}}u^{p+1}K(u)du (1 + o_{p}(1)). \end{aligned}$$

Applying Lemma 1 again, the last expression is

$$\begin{aligned} f_X(x)\frac{m^{(p+1)}(x)}{(p+1)!}h^{p+1} E\{\Delta |X = x\} \int {\textbf {u}}u^{p+1}K(u)du (1+ o_P(1)). \end{aligned}$$

(20)

By (17), (18), and (20), $b_n(x)$ is obtained.

For $Var\{\ell _x^{'}(0)\}$, it can be decomposed into two parts, the quadratic term, and the cross-product terms minus the squared of $E\{\ell _x^{'}(0)\}$. For the quadratic term,

$$\begin{aligned}{} & {} \frac{1}{n^{2}} E \left\{ \sum ^{n}_{i=1}K^{2}_{h}(X_{i}-x) ([\Delta _{i} - \exp (\mathbf{\tilde{x}}^{T}_{i}\beta ^{0})F(Y_{i};\gamma _{0})]U_{i} )([\Delta _{i} - \exp (\mathbf{\tilde{x}}^{T}_{i}\beta ^{0})F(Y_{i};\gamma _{0})]U_{i})^{T} \right\} \\= & {} \frac{1}{n}E\left\{ K^{2}_{h}(X-x) ([\Delta - \exp (\mathbf{\tilde{x}}^{T} \beta ^{0})F(Y; \gamma _{0})]U)([\Delta - \exp (\mathbf{\tilde{x}}^{T} \beta ^{0})F(Y; \gamma _{0})]U )^{T} \right\} \\= & {} \frac{1}{nh}f_X(x)\int K^{2}(u) ([\Delta - \theta (x)F(Y_{i};\gamma _{0})])^{2}{} {\textbf {u}}{} {\textbf {u}} )^{T}du (1+o_p(1)) \\= & {} \frac{1}{nh}f_X(x)S_{2}(x; \gamma _{0}) (1+o_p(1)), \end{aligned}$$

where $S_{2}(x; \gamma _{0})$ is defined in Theorem 2. Based on (20), the cross-product terms minus the squared of $E\{\ell _x^{'}(\beta ^0)\}$ is of order $n^{-1}h^{2(p+1)} (1+o_p(1))$. Hence

$$\begin{aligned} Var\{\ell _x^{'}(0)\} = (nh)^{-1} f_X(x)S_{2}(x; \gamma _{0}) (1+o_p(1)). \end{aligned}$$

(21)

Based on (17), (18), and (21), $Var(H \hat{\beta })$ in Theorem 2 is obtained.

To prove asymptotic normality, by the Cramer-Wold device, for any non-zero constant vector $b \in R^{p+1}$, we will show that

$$\begin{aligned} \sqrt{nh}\{b^{T} H (\hat{\beta }-\beta ) - b^{T} b_n(x)\} \rightarrow N (0, f_X(x)^{-1}b^T S^{-1}_{1}(x) S_{2}(x;\gamma _{0}) S^{-1}_{1}(x)b). \end{aligned}$$

Consider $\sqrt{nh}\{b^{T} \ell ^{'}_x(0)- b^{T}E(\ell ^{'}_x(0))\}$ at first. We verify the Lyapounov condition as follows. For $0< \eta <1$ and by condition (A7),

$$\begin{aligned}{} & {} \sum ^{n}_{i=1} E\{ |\sqrt{nh}n^{-1}b^{T} ([\Delta _{i} - \exp (\tilde{\text{ x }}^{T}_{i}\beta ^{0})F(Y_{i};\gamma _{0})]U_{i}K_{h}(X_{i}-x) \\{} & {} -E ([\Delta _{i} - \exp (\tilde{\text{ x }}^{T}_{i}\beta ^{0})F(Y_{i};\gamma _{0})]U_{i}K_{h}(X_{i}-x)) ) |^{2+\eta }\}\\\le & {} 2(n^{-1}h)^{1+\frac{\eta }{2}}n b^{T}E\{| [\Delta - \exp (\tilde{\text{ x }}^{T} \beta ^{0})F(Y; \gamma _{0})]U K_{h}(X -x)|^{2+\eta }\}\\\le & {} 2( (nh)^{\frac{-\eta }{2}}h^{1+\eta } b^{T}E\{| [\Delta - \exp (\tilde{\text{ x }}^{T} \beta ^{0})F(Y;\gamma _{0})]U K_{h}(X-x)|^{2+\eta }\} = O((nh)^{\frac{-\eta }{2}} ) \rightarrow 0. \end{aligned}$$

Then the asymptotic normality of $\sqrt{nh}\{b^{T} \ell ^{'}_{x}(0)- b^{T} E( \ell ^{'}_{x}(0))\}$ is shown; that is,

$$\begin{aligned} \sqrt{nh}\{ \ell ^{'}_{x}(0)- E( \ell ^{'}_{x}(0))\} \rightarrow N(0, f_X(x) S_{2}(x;\gamma _{0})). \end{aligned}$$

(22)

Finally, by (17), (18), and (22),

$$\begin{aligned} \sqrt{nh}\{H(\hat{\beta }-\beta ) - b_n(x)\}&= \sqrt{nh}\{\hat{\alpha } - b_{n}(x)\} \\&= \{-f_X(x)S_{1}(x) (1+ o_P(1))\}^{-1}\{ \ell ^{'}_{x}(0)- E( \ell ^{'}_{x}(0))\} + o_{p}(\sqrt{nh}h^{p+1}) \\&\rightarrow N(0, f_X(x)^{-1} S_{1}(x)^{-1} S_{2}(x;\gamma _{0})S_{1}(x)^{-1}). \end{aligned}$$

This completes the proof of Theorem 2(a).

To show Theorem 2(b), note that the results in (a) depend on $\gamma _0$ only through $S_2(x; \gamma _0)$. From the definition of $S_2(x; \gamma _0)$, it is clear that if $\hat{\gamma }$ is $\sqrt{n}$-consistent, then $F(Y; \hat{\gamma })$ is $\sqrt{n}$-consistent and the results in (21) and (22) continue to hold. $\square$

Proof of Theorem 3

(a) Given that $\theta (\cdot )$ is known, the poof is similar to proofs for standard maximum likelihood estimators. First,

$$\begin{aligned} 0 = \ell ^{*'}(\hat{\gamma }) \approx \ell ^{*'}(\gamma _{0}) + \ell ^{*''}(\gamma _{0})(\hat{\gamma }-\gamma _{0}). \end{aligned}$$

(23)

Then $\sqrt{n} (\hat{\gamma }-\gamma _{0}) \approx -\sqrt{n}(\ell ^{*''}(\gamma _{0}))^{-1} \ell ^{*'}(\gamma _{0}).$ From (7), the first derivative of $\ell ^{*}$ with respect to $\gamma$ is

$$\begin{aligned} n^{-1}\sum ^{n}_{i=1}I(Y_{i} < \infty )\left\{ \Delta _{i}[\xi ^{'}(Y_{i};\gamma )-\theta (X_{i})F^{'}(Y_{i};\gamma )] - (1-\Delta _{i})\left[ \frac{\theta (X_{i})F^{'}(Y_{i};\gamma )}{1 - \exp (-\theta (X_i)\bar{F}(Y_{i};\gamma ))}\right] \right\} , \end{aligned}$$

(24)

where $\xi (Y; \gamma )$ is defined in condition (A8), $\bar{F}(\cdot )= 1-F(\cdot )$, and $F^{'}(\cdot )$ and $\xi ^{'}(\cdot )$ are the first derivatives of F and $\xi$ respectively with respect to $\gamma$. Since $E\{ \ell ^{*'}(\gamma _{0}) \}=0$, the bias of $\hat{\gamma }$ is 0. We know that $\ell ^{*''}(\gamma _{0}) = {n}^{-1}\sum ^{n}_{i=1}\ell ^{*''}_i(\gamma _{0}) \rightarrow _{p} E\{ \ell ^{*''}_i(\gamma _{0})\}\equiv T_1(\gamma _0)$. The expression of $T_1(\gamma )$ is obtained by deriving $\frac{\partial ^{2}\ell ^{*}}{\partial \gamma ^{2} }$ from (24) and then taking expectation,

$$\begin{aligned} T_1(\gamma )= & {} E \left\{ I(Y < \infty )\left\{ \Delta [ \xi ^{''}(Y; \gamma ) - \theta (X)F^{''}(Y;\gamma )] +(1- \Delta ) \frac{\theta (X)}{1 - \exp (-\theta (X)\bar{F}(Y; \gamma ))} \right. \right. \nonumber \\{} & {} \hspace{0.5cm} \times \left. \left. \left[ F^{''}(Y; \gamma )+ \frac{F^{'^2}(Y; \gamma ) \exp (-\theta (X) \bar{F}(Y;\gamma ))}{1 - \exp (-\theta (X)\bar{F}(Y; \gamma ))} \right] \right\} \right\} . \end{aligned}$$

(25)

For $Var(\hat{\gamma }-\gamma _{0})$, based on (23), it is approximately $T_{1}(\gamma _{0})^{-1} E\{(\ell ^{*'}(\gamma _0))^2 \} T_{1}(\gamma _{0})^{-1}.$ For $E\{(\ell ^{*'}(\gamma _{0}))^2\}$, it is dominated by $n^{-2}\sum ^{n}_{i=1}E\{ (\ell _i^{*'}(\gamma _{0}))^2\} \equiv n^{-1} T_{2}(\gamma _0),$ where

$$\begin{aligned} T_{2}(\gamma )= E \left\{ I(Y < \infty )\left\{ \Delta [\xi ^{'}(Y ; \gamma )-\theta (X)F^{'}(Y; \gamma )] - (1-\Delta )\left[ \frac{\theta (X)F^{'}(Y ; \gamma )}{1 - \exp (-\theta (X)\bar{F}(Y;\gamma ))}\right] \right\} ^2 \right\} . \end{aligned}$$

(26)

Moreover $\sqrt{n}\ell ^{*'}(\gamma _{0})$ converges in distribution to $N(0, T_2(\gamma _0))$. By Slutsky’s theorem, Theorem 3(a) is proved.

(b) When $\theta (\cdot )$ is estimated at the rate in Theorem 2, the difference between the expected values of (24) with true $\theta (x)$ and $\hat{\theta }(x)$ for x evaluated at a data point $X_{i}$ is of rate $h^{(p+1)}$. The conditions $nh^{2p+2} \rightarrow 0$ and $nh \rightarrow \infty$ ensure that the asymptotic normality in (a) continues to hold. $\square$

III. Additional simulation results

This example is the same as Example 1 with $n=200$ except that the censoring time $C \sim U(0, 0.4)$, to increase the censoring rate. Then the censoring and cure rates are 26.8$\%$ and 13.5$\%$, respectively, which means $13.3\%$ observations are censored but not cured. We want to examine whether the performance seen in Example 1 is affected after increasing the censoring rate. We first try the bandwidth $h=$0.2, 0.4, and 0.6 in step 2 of the proposed algorithm. When $h=0.2$, the average $\hat{\gamma }$ (sd) in step 2 is 7.293 (1.049), which is not as good as in Example 1. For $h= 0.4$ and 0.6, the average $\hat{\gamma }$’s are 7.56 and 7.60 respectively, which shows a sizable difference from the true value 7. Hence we choose a smaller $h=0.2$ in step 2 and the corresponding $\widehat{se}$ and the average coverage probability are 1.398 and 96$\%$ respectively. Then $h=0.4$ and 0.6 are used in step 5 for estimating $m(\cdot )$ and the average MSE (sd) are 0.062 (0.043) and 0.041 (0.032) respectively when $\gamma$ is estimated. It is seen that $\hat{m}$ has larger MSEs generally as compared to those in Example 1, and in step 5, using $h=0.6$ has a smaller average MSE than that of $h=0.4$. The estimated functions and their cure rates (not shown) were examined. Overall, the estimated curves exhibit more variability than those of Example 1. From this example, it is seen that increasing the censoring rate affects the choice of h and estimation of both $m(\cdot )$ and $\gamma$.

IV. Computation Time Discussion

The computation time of the proposed method is discussed in this section. We have recorded the time of (1) data generation, (2) parameter tuning using the CV method (Section 3.2 of the main paper), and (3) the estimation by using Algorithm 1. The results are summarized in Table 6 below. It shows that the computation time are in a reasonable range. The time for parameter tuning is around 9 times of the estimation time since we consider 9 candidate bandwidths. The parameter tuning process may be time-consuming but note that it can be further reduced by incorporating parallel algorithm to compute the CV scores for each bandwidth candidates and to compute the estimates of $m(X_{i})$’s in step 2 of Algorithm 1.

Table 6 Summary of Computation Time for Simulation Example 1 (average (sd) in seconds)

V. Additional Data Analysis Results

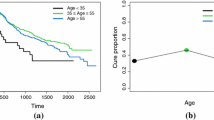
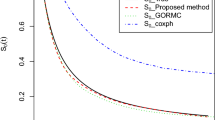
Although we have implemented an AIC based approach to select the baseline distribution family, it will be an interesting exploration to visualize the estimating curves using a different baseline distribution and to see if the resulting curves look different. The Weibull distribution family has been implemented in the Kidney transplant data analysis and the resulting curves with those from the exponential distribution (Fig. 3) are presented in Fig. 5. We observe that the results are only affected slightly and it does not affect our interpretations for this dataset.

Fig. 5

Comparison of the Estimated Curves Using Two Baseline Distributions. a the estimated cure rates with exponential baseline (blue solid line) as in Fig. 3a, and with Weibull baseline (red long dashed line); b the corresponding $\hat{m}(\cdot )$. The point symbols are the same as in the caption of Fig. 3