Statistical Methods for Selective Biomarker Testing

Abstract

Biomarkers are critically important tools in modern clinical diagnosis, prognosis, and classification/prediction. However, there are fiscal and analytical barriers to biomarker research. Selective Genotyping is an approach to increasing study power and efficiency where individuals with the most extreme phenotype (response) are chosen for genotyping (exposure) in order to maximize the information in the sample. In this article, we describe an analogous procedure in the biomarker testing landscape where both response and biomarker (exposure) are continuous. We propose an intuitive reverse-regression least squares estimator for the parameters relating biomarker value to response. An expression for robust standard error and corresponding confidence interval are derived. A simulation study is used to demonstrate that this method is unbiased and efficient relative to estimates from random sampling when the joint normal distribution assumption is met, and to compare the estimator to an alternative under a related sampling design. We illustrate application of proposed methods on data from a chronic pain clinical trial.

1 Background

A biological marker, or biomarker, is an objective measurement which indicates a biologic process or response [1]. This umbrella definition captures a range of measurements that may be representative of a disease course, from simple indicators like blood pressure to complex laboratory tests [2]. In this paper, we focus specifically on physical markers which are detectable via serum assays. In the past 20 years, the explosive use of biomarkers in medical research has coined the “biomarker revolution” [3]. Clinically relevant biomarkers can provide information on both disease mechanisms and subsequent outcomes [4]. In practice, a biomarker can serve as both a risk indicator and a surrogate for disease status. As such, the biomarker is a critically important tool in modern clinical diagnosis, prognosis, and classification/prediction.

Despite the clinical utility and popularity of biomarkers and continual advancements in collection technology, there remain fiscal and analytical barriers to biomarker research. The cost of conducting biomarker assays for a sufficiently powered study is a major limitation. For example, a luminex assay with 39 sample slots and the capacity to detect up to 20 biomarkers can cost between $300 and $600 before fees for consultation, lab materials, and labor [5]. This means that collecting biomarker samples for each person in a study of 800 participants could cost more than $12,600 when serum samples for each individual are collected at a single time point. Resource limitations have thus inspired the development of cost-effective experimental designs and corresponding statistical methodology [3, 6].

In genetics literature, one such approach concentrates sampling to the most informative observation units [7]. Selective genotyping [8] traditionally entails sampling individuals for genotyping based on extreme phenotypic values where genotype (exposure) is discrete (presence/absence; aa/Aa/AA) and phenotype (response) is continuous, most often assuming an ANOVA-style model [9]. From a statistical perspective, this is distinct from, but perhaps inspired by, the information perspective [10] for which the optimal design in regression analysis (i.e. sample) is the one that minimizes the variance of coefficient estimates [11].

Under selective genotyping, the response no longer follows a normal distribution and missing data in the middle of the phenotypic distribution must be accounted for [12]. Appropriate maximum likelihood methods have been developed for inference under such designs for QTL studies [7, 9], which have been shown to increase statistical power relative to random sampling using a fraction of the original sample [7, 13, 14]. However, the developed methods are highly specific to the field of genetics, modeling the exposure as discrete and accounting for elements such as backcross in models. Additionally, in genotyping studies it is advantageous to take a multistage approach wherein promising genetic markers are identified early out of a pool of candidates to meet study constraints [15, 16].

In this paper we study a selective biomarker-testing scheme, where similar to selective genotyping, individuals with extreme response values are selected for biomarker-testing. In contrast to typing the discrete genotypes in the selective genotyping, here the individuals’ continuous biomarker is measured. Selective genotyping and our selective biomarker-testing are both special cases of Outcome-Dependent Sampling (ODS) [10]. ODS (also known as response-dependent sampling) is a form of biased sampling, which has been studied in the context of likelihood-based estimation [17]. Zhou et al. [18] formally defined an ODS design for a linearly related continuous exposure and outcome where all response values are observed and covariate values are observed, as (1) a simple random sample (SRS) from the full available cohort and (2) additional SRS’s from regions of the response that are of particular interest. They proposed a semiparametric empirical likelihood estimation method for this ODS design which was shown to increase efficiency relative to simple random sampling [18]. Weaver and Zhou [19] extended this design to incorporate all available information from the full sample including those with unknown exposure values taking an estimated likelihood approach. Zhou’s original estimator has been expanded to accommodate different functional forms [20], auxiliary covariate information [21,22,23], multi-stage designs [23,24,25], mixed effects models [25], and more recently survival [26] and longitudinal endpoints [6, 27, 28].

Here we propose statistical analysis methods to analyze selective biomarker-testing data utilizing regression estimations available from standard statistical software. Notice that our selective biomarker-testing scheme can be considered as Extreme Outcome-Dependent Sampling (EODS) since we only sample individuals with extreme response values without the SRS from the full cohort (thus no biomarker-testing is conducted for any individual in the mid range of response values). The benefit, relative to the cost, of the incorporation of the primary SRS in traditional ODS designs is unknown. Selective genotyping literature suggests that there is no information to be gained by genotyping individuals outside the tails of the response variable distribution [7]. Also, while the ODS estimators in above literature are efficient, unbiased, and flexible under their statistical assumptions, the complexity of the semiparametric likelihood-based approach is a key barrier to their widespread use in practice. The least squares approach to estimation in regression analysis is standard, and therefore most accessible to researchers conducting biomarker-testing studies. However, least squares has been shown to be most susceptible to the bias induced by extreme sampling based designs [11]. To solve this issue, we propose a reverse-regression least squares estimation method for EODS designs with jointly normal distributed biomarker and response.

The organization of this article is as follows: In Sect. 2 we describe a general methodology for biomarker studies, including effect estimation, power/sample size considerations, and model checking methods as well as the BISP2 clinical trial dataset which motivated this research. In Sect. 3 we present numerical results of our estimator. We first study the finite sample properties of our estimator via simulation, then apply our estimator to the BISP2 Biomarker Study. We conclude with a discussion of strengths and limitations in Sect. 4 and a brief conclusion in Sect. 5.

2 Methods

In a clinical study, we are interested in the relationship between a response variable Y and a biomarker variable X. If both variables are measured on all subjects enrolled in the trial, we have a full data set consisting of $(X_1,Y_1)$,..., $(X_{n_F}, Y_{n_F})$. Here $n_F$ denotes the size of the full data set. For the EODS biomarker analysis, we observe the response variable for the full data set, $Y_1$,..., $Y_{n_F}$, but only observe the biomarker variable X on a subset corresponding to extreme values of Y. Say, we select $\gamma$ proportion of the full data set and measure the biomarker X on the selected subset of size $n_S = [\gamma n_F]$, where [d] denotes the closest integer to d. Without loss of generality, we can denote the first $n_S$ subjects as the selected ones. That is, in the selective biomarker analysis, we observe $(X_1,Y_1)$,..., $(X_{n_S}, Y_{n_S})$ and $Y_{n_S+1},..., Y_{n_F}$, while $Y_1$,..., $Y_{n_S}$ corresponds to the top $\gamma /2$ proportion and the bottom $\gamma /2$ proportion of $Y_1$,..., $Y_{n_F}$.

The aim of the statistical regression analysis is to study the dependence of response variable Y on the biomarker X:

$$\begin{aligned} E(Y|X) = \alpha _Y + \beta _Y X, \end{aligned}$$

(1)

where E(Y|X) denotes the conditional expectation of Y given X. When X and Y jointly follow a bivariate normal distribution, the full data set satisfies the standard regression model assumption:

$$\begin{aligned} Y_i = \alpha _Y + \beta _Y X_i + \varepsilon _{Y,i}, \qquad \varepsilon _{Y,i} \sim N(0, \sigma _{\varepsilon _Y}^2), \end{aligned}$$

(2)

for $i=1,..., n_F$.

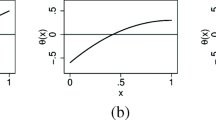
However, for the EODS biomarker analysis, naively conducting linear regression analysis directly on the subset $(X_1,Y_1)$,..., $(X_{n_S}, Y_{n_S})$ does not work. The reason is that, the regression model assumption (2) does not hold on the selectively sampled subset because the response follows a truncated distribution due to the selection of extreme values for Y as shown by the red part of the curves in Fig. 1a. The ordinary least squares (OLS) fit on the selectively sampled subset will lead to highly biased slope estimation as shown by the dotted red line. Therefore, specific analysis methods are needed for the selective biomarker analysis. In this paper, we propose a parametric analysis method which utilizes standard regression formulas on reverse-regression: regressing X on Y for the selectively sampled subset. The main insight for the proposal is that, when X and Y jointly follow a bivariate normal distribution, the standard regression model assumption holds for the reverse-regression on both full data set and the selectively sampled subset:

$$\begin{aligned} X_i = \alpha _X + \beta _X Y_i + \varepsilon _{X,i}, \qquad \varepsilon _{X,i} \sim N(0, \sigma _{\varepsilon _X}^2). \end{aligned}$$

(3)

To see why the reverse-regression model (3) holds also on selectively sampled subset, we notice that, for jointly normally distributed X and Y, the distribution of X conditional on any $Y=y$ value is normal with

$$\begin{aligned} E(X|Y=y) = \alpha _X + \beta _X y, \qquad Var(X|Y=y) = \sigma _{\varepsilon _X}^2, \end{aligned}$$

where $\sigma _{\varepsilon _X}$ is a constant not affected by the y values. The relationship between the reverse-regression parameters $(\alpha _X,\beta _X,\sigma _{\varepsilon _X})$ and the bivariate normal distribution parameters $(\mu _X,\mu _Y,\sigma _X,\sigma _Y, \rho )$ can be found in derivations in Appendix A. Therefore, for any sampling scheme that only uses the value of random variable Y, conditional on selected ($Y_1=y_1$,..., $Y_{n_S}=y_{n_S}$), the corresponding $X_i$ follows the normal distribution satisfying equation (3). That is, the reverse-regression model (3) holds for any selective sampling scheme based only on response values, of which the EODS is a special case. Figure 1b illustrates this phenomenon for bivariate normal distribution: conditional on selected Y values, X is still normally distributed with common variance and a linearly changing mean.

Fig. 1

Illustration of challenge posed to linear regression under extreme sampling

Armed with this insight, we can conduct the reverse-regression $E(X|Y) = \alpha _X + \beta _X Y$ using standard statistical software on the selectively sampled subset. Then we convert the reverse-regression fit results into regression inferences, with a little help of the additional response variable observations $Y_{n_S+1},..., Y_{n_F}$. In Appendix A, we provide detailed mathematical derivation of formulas converting the reverse-regression coefficients to regression coefficients. We describe the application of these conversion formulas for analyzing the EODS biomarker data in the rest of this section.

2.1 Hypothesis Test

One main focus of the biomarker analysis is to test whether a biomarker X affects the response variable Y. Statistically, this is usually done by the linear regression hypothesis testing

$$\begin{aligned} H_0: \beta _Y = 0 \qquad \text{ versus } \qquad H_A: \beta _Y \ne 0. \end{aligned}$$

(4)

Mathematically, the null hypothesis $H_0: \beta _Y = 0$ is equivalent to the reverse-regression null hypothesis $H_0: \beta _X = 0$. Thus we can simply carry out the reverse-regression hypothesis test on the selectively sampled subset for

$$\begin{aligned} H_0: \beta _X = 0 \qquad \text{ versus } \qquad H_A: \beta _X \ne 0. \end{aligned}$$

(5)

The p-value for the test of (5) is also valid for testing (4).

2.2 Effect Estimation

The effect of the biomarker X on response variable Y is measured by the slope $\beta _Y$ in the regression function. Naively fitting the regression equation (1) on the selectively sampled subset would result in an overestimation of the biomarker effect. As illustrated in Fig. 1a, the conditional (truncated) distribution of Y changes with the given X values, leading to OLS estimate (shown as the dotted red line) with much bigger slope magnitude than the true $\beta _Y$ value when $\beta _Y > 0$. For consistent estimation of $\beta _Y$, we use instead the parameter estimates ${\hat{\beta }}_X$ and ${\hat{\sigma }}^2_{\varepsilon _X}$ from fitting the reverse-regression (3) on the selectively sampled subset. These estimates can be obtained from conducting the reverse-regression using any standard software. Furthermore, from the full response variable observations of $Y_1$,..., $Y_{n_F}$, we have the sample mean ${\tilde{\mu }}_Y = \frac{1}{n_F} \sum _{i=1}^{n_F}Y_i$ and the sample variance ${\tilde{\sigma }}^2_Y= \frac{1}{n_F-1} \sum _{i=1}^{n_F} (Y_i - {\tilde{\mu }}_Y )^2$.

Using equation (18) in the Appendix, we have a point estimator for $\beta _Y$ as

$$\begin{aligned} {\hat{\beta }}_Y = \frac{1}{\frac{{\hat{\sigma }}^2_{\varepsilon _X}}{{\tilde{\sigma }}^2_Y} + {\hat{\beta }}^2_X } {\hat{\beta }}_X. \end{aligned}$$

(6)

Then the standard error for ${\hat{\beta }}_Y$ can be calculated as in equation (23),

$$\begin{aligned} s.e.\{{\hat{\beta }}_Y\} = \sqrt{\frac{\left( \frac{{\hat{\sigma }}^2_{\varepsilon _X}}{{\tilde{\sigma }}^2_Y}-{\hat{\beta }}^2_X\right) ^2 (s.e.\{{\hat{\beta }}_X\})^2 + \left( \frac{2 {\hat{\beta }}^2_X {\hat{\sigma }}^4_{\varepsilon _X}}{{\tilde{\sigma }}^4_Y}\right) \left( \frac{1}{n_s-2} + \frac{1}{n_F-1}\right) }{\left( \frac{{\hat{\sigma }}^2_{\varepsilon _X}}{{\tilde{\sigma }}^2_Y} + {\hat{\beta }}^2_X \right) ^4}}, \end{aligned}$$

whose detailed derivation is provided in the Appendix. Therefore, the $(1-\alpha )$ confidence interval for $\beta _X$ can be calculated as

$$\begin{aligned} {\hat{\beta }}_Y \pm z_{\alpha /2} s.e.\{{\hat{\beta }}_Y\}. \end{aligned}$$

Here $z_{\alpha /2}$ is the $\alpha /2$-upper quantile for the standard normal distribution.

2.3 Power/Sample Size Calculation

As derived in the Appendix, equation (27) gives the power formula of the hypothesis test in section :

$$\begin{aligned} power = P(W > FQ_{\alpha , df_1, df_2}), \end{aligned}$$

(7)

where W denotes a random variable following a non-central F-distribution with degrees of freedoms of $df_1 = 1$ and $df_2 = \gamma n_F-2$ and noncentral parameter $n_F f^2 2 \int _{z_{\gamma /2}}^{\infty } x^2 \phi (x) dx$, and $FQ_{\alpha , df_1, df_2}$ denotes the $\alpha$-upper quantile of a central F-distribution with degrees of freedoms of $df_1$ and $df_2$. Here $z_{\alpha }$ denotes the $\alpha$-upper quantile of a standard normal distribution N(0, 1) whose density is denoted as $\phi (x)$. And f is the Cohen’s effect size defined as

$$\begin{aligned} f^2 = \frac{R^2}{1-R^2} = \frac{\rho ^2}{1-\rho ^2}, \end{aligned}$$

(8)

where $R^2$ is the proportion of variation in the data explained by the regression equation.

Based on this, we can choose the proportion $\gamma$. We illustrate the sample size calculation with a simple example here. Assume that we have a full data set of sample size $n_F=200$, and we wish to detect a Cohen’s effect size $f=0.3$ with $90\%$ power at the significance level $\alpha =0.05$. When we select $10\%$ individuals in EODS for biomarker-testing (i.e., $n_S=200*0.1=20$, selecting 10 persons with largest Y values and 10 persons with smallest Y values), (7) gives $power=0.9150$. When we select $9\%$ individuals in EODS for biomarker-testing (i.e., selecting 9 persons with largest Y values and 9 persons with smallest Y values), (7) gives $power=0.8985$. Thus 20 individuals will be biomarker-tested to achieve the design goal of $90\%$ power.

In contrast, the standard t-test in simple linear regression for testing (4) has $power=0.8983$ when $n=118$ and $power=0.9007$ when $n=119$ as given by equation (24). Thus a clinical trial without the EODS will require 119 individuals with both X and Y measurements, needing an almost sixfold increase in cost of biomarker-testing for X than the EODS method.

2.4 Model Checking

Our methodology is based on the assumption that X and Y are jointly normally distributed. Mathematically, that is equivalent to the following two assumptions holding simultaneously: (A) the response variable Y is normally distributed and (B) conditional on Y, the biomarker variable X is normally distributed. We now consider how to check these two assumptions on observed data.

Assumption (A) can be checked with standard methods such as the normal probability plot on the fully observed $Y_1$,..., $Y_{n_F}$. For assumption (B), we do not observe X for the whole range of Y. But we can still check whether (B) holds for the selected Y values by applying standard model checking methods on the reverse-regression, e.g., the normal probability plot of the reverse-regression residuals.

2.5 Motivating Data Study Design

Biopsychosocial Influence on Shoulder Pain Phase I (BISP) was a single-center, pre-clinical “proof of concept” study of 190 adults to identify genetic and psychological characteristics related to chronic musculoskeletal pain [29]. Musculoskeletal pain is the general pain affecting the muscles, ligaments, tendons, or bones with chronic indicating that the pain is long-lasting or consistently recurring. In general, musculoskeletal pain is a large contributor to the $635 billion yearly healthcare cost of chronic pain in the United States [29]. Though this makes chronic pain a high priority research area, there are limited accepted treatment models due to the complexity of disease etiology. Treatment components must be personalized on the basis of genetic, psychological, environmental, and social risk factors, which all contribute to the individual variation in how people experience chronic pain.

Specifically, BISP targeted chronic musculoskeletal pain affecting the shoulder region by comparing predictors of pain level among healthy individuals pre- and post-induced shoulder pain. The target population was healthy adults. Participants were followed over the course of five days. Baseline covariates and DNA samples were collected on the first day of the study, before inducing shoulder pain. An exercise-based protocol was then used to create controlled shoulder pain through inflammation and muscular fatigue [29]. Four follow-up visits were conducted every 24 h post-injury induction. Shoulder impairment, genetic testing, and other covariates related to pain level defined a priori based on clinical expertise were measured at baseline and each follow-up visit. BISP identified multiple prognostic factors which were associated with increased shoulder pain, including promising genes which showed evidence of predicting shoulder impairment.

BISP Phase II (BISP2) was a single-center, randomized follow-up trial to BISP which aimed to test whether interventions personalized on the basis of genetic and psychological characteristics are effective for induced shoulder pain (ClinicalTrials.gov Identifier: NCT02620579) [30]. The two-factor factorial design randomized 261 individuals to either propranolol or placebo and psychological education or general education. Propranolol is a drug chosen to target Catechol-O-methyl-transferace (COMT), which metabolizes adrenal hormones and is associated with pain sensitivity. The psychological education was designed to target pain rumination, which is magnification of pain by focusing on the pain with a pessimistic attitude. Pre-randomization, shoulder injury was induced using the same protocol.

BISP2 participants provided daily report on pain intensity and disability over the 5-day onsite observation period. Pain level was measured using the Brief Pain Inventory (BPI) [31], which is an 11-point scale ranging from 0 (no pain) to 10 (worst pain intensity imaginable). Participants rated the intensity of current pain and pain intensity at its worst, best, and average over the past 24 h. Clinically relevant covariates and saliva samples for genetic testing were again taken at each follow up visit.

The BISP2 investigators targeted 14 genetic markers associated with pain in the study’s exploratory biomarker analysis. These biomarkers were chosen a priori based on clinical knowledge of propensity to release pro-inflammatory cytokines. All genetic samples were saliva-based. The primary question of interest for the exploratory analysis was: which biomarkers are associated with recorded level of shoulder pain at 48-hours post-randomization? As the response, pain, is measured via the BPI to represent a continuum pain, linear regression with pain level as the response is a typical analysis approach. However, the investigators were limited by the budget and time constraints of the BISP2 clinical trial. It was infeasible to biomarker-test every individual in the study. Therefore, the investigators began by biomarker-testing 31 individuals in the high and low tails of worst pain experienced at 48-hours post shoulder pain induction.

3 Results

3.1 Simulation Studies

In this section, we use simulations to check the finite sample performance of our proposed Outcome-Dependent Extreme biomarker-testing (ODEB) estimator. All simulations were conducted using R Statistical Software Version 3.6.0 [32].

3.1.1 Simulation Comparison with Ordinary Least Squares

We compare our ODEB estimation with the ordinary least squares (OLS) estimation in various parameter settings here. Data were simulated according to the probability model described in Equation (2). Specifically, $Y_i$ is generated such that

$$\begin{aligned} Y_i = 5 + \beta _Y X_i + \varepsilon _{Y,i}, \qquad {X \sim N(20,5)}{}, \qquad \varepsilon _{Y,i} \sim N(0, 5). \end{aligned}$$

(9)

Individual data sets consisting of $(X_1,Y_1)$,..., $(X_{n_F}, Y_{n_F})$ were randomly generated for each of $B=20,000$ Monte Carlo simulations. We studied combinations of the following sets of parameter values: $n \in \{100, 200, 400, 800\}$, $\beta _{Y} \in \{0,0.2,0.26,0.4,0.8,1\}$, $\gamma \in \{0.1,0.2,0.4\}$. For each iteration, both the extreme-outcome-dependent sampling and random sampling were conducted. $\beta _Y$ was then estimated for each sampling method using both OLS ($\hat{\beta }_{Y,OLS}$) and ODEB ($\hat{\beta }_{Y,ODEB}$) estimation.

To illustrates the impact of the proportion of selected extreme subsample, Fig. 2 plots the ODEB estimation for various proportion selected from a fixed dataset where $n=800$ and $\beta _Y=0.4$. As the proportion sampled increases, $\hat{\beta }_{Y,ODEB}$ trends closer to the true parameter value, and the 95% confidence interval contains $\beta _Y$ for all proportions sampled.

Fig. 2

ODEB point and interval estimation for $\hat{\beta }_Y$ under various proportions of the total study extreme sampled when $n=800$ and $\beta _Y=0.4$

Theoretically, both OLS and our ODEB provide valid inferences under random sampling, but only ODEB estimation is consistent under extreme sampling. The simulation results confirmed this.

Figure 3 displays the bias of $\hat{\beta }_Y$ when an extreme sample of 10% is taken from each tail of the response distribution (thus resulting in a total of 20% extreme sampling). When there is truly no effect of the biomarker X, both OLS and ODEB estimation are unbiased regardless of whether the sample is extreme or random. When there is a biomarker effect present, $\hat{\beta }_{Y,ODEB}$ under extreme or random sampling and $\hat{\beta }_{Y,OLS}$ under random sampling remain mostly unbiased, with only a small appreciable bias when $n=100$ which dissipates as the sample size reaches $n=400$. However, $\hat{\beta }_{Y,OLS}$ under extreme sampling is severely biased in the positive direction. The bias initially increases, then tapers, with the size of $\beta _Y$. For saving space, we omit the detailed numbers for simulations from other sampling proportions (10% and 40%) but summarize their bias patterns. The bias of $\hat{\beta }_{Y,OLS}$ under extreme sampling is exacerbated when $\gamma =0.1$ (i.e., 5% per tail), with estimation bias exceeding twice the magnitude of $\beta _Y$. The bias of $\hat{\beta }_{Y,OLS}$ decreases slightly when $\gamma = 0.4$, with more moderate observations included, but the overall bias magnitude is still unacceptably large.

Fig. 3

Bias of $\hat{\beta }_Y$ under 20% of the total study sampled for various $\beta _Y$’s

The root mean square error (RMSE) displays similar trends, as shown in Fig. 4. Under extreme sampling, $\hat{\beta }_{Y,ODEB}$ has the smallest RMSE of the four considered combinations across both study sample sizes and true $\beta _Y$’s. This reflects the efficient use of information by $\hat{\beta }_{Y,ODEB}$. In contrast, $\hat{\beta }_{Y,OLS}$ has the largest RMSE across study sample sizes and $\beta _Y$’s when applied to an extreme sample. Of note, under random sampling, $\hat{\beta }_{Y,OLS}$ and $\hat{\beta }_{Y,ODEB}$ perform similarly in terms of RMSE, but $\hat{\beta }_{Y,ODEB}$ still beats $\hat{\beta }_{Y,OLS}$ as $\beta _Y$ becomes bigger.

Fig. 4

Root mean square error (RMSE) of $\hat{\beta }_Y$ under 20% of the total study sampled for various $\beta _Y$’s

In addition, $\hat{\beta }_{Y,ODEB}$ provides a practical increase in power to detect biomarker effect when combined with extreme sampling. First, for ODEB test under all sampling methods, the type I error rate for the test of the null hypothesis $H_0: \beta _Y = 0$ is controlled at the nominal level of 5% as illustrated in the upper-left panel of Fig. 5. When $\beta _Y \ne 0$, random sampling generally has less power to detect a biomarker effect than extreme sampling, with the dashed lines (random sampling) falling below the solid lines (extreme sampling) in each panel. This highlights the utility of focusing on those observations with extreme response values. Taking $\beta _Y = 0.2$ as an illustrative example of this notion, the stars placed on the upper-right panel emphasize the increase in power afforded by successively more extreme samples. For the three starred cases, each sample contains 80 biomarker-tested observations but a more extreme sample from a larger population has the advantage in terms of power to detect the effect. A 96.2% power is achieved by the 10% extreme sample from 800 observations. In contrast, 20% and 40% extreme samples respectively from 400 and 200 observations results in 88.9% and 73.8% power only.

Fig. 5

Power to detect a nonzero effect of biomarker level on pain for various $\beta _Y$’s

Figure 6 studies the performance of the 95% confidence interval for $\beta _Y$ for OLS and ODEB. Only the OLS-based confidence interval under extreme sampling does not achieve correct nominal 95% coverage. Its poor coverage displayed is worsened both with larger total study sample size and larger size of $\beta _Y$. This is particularly severe when $\beta _Y=1$, with coverage probabilities of effectively 0% for $n=200,400, \text { and } 800$. The OLS-based confidence interval under extreme sampling also displays the longest confidence interval length (Fig. 7). ODEB estimation affords the most precise confidence interval compared to OLS, particularly when applied to an extreme sample.

Fig. 6

95% $\beta _Y$ confidence interval coverage under 20% of the total study sampled for various $\beta _Y$’s

Fig. 7

95% $\beta _Y$ confidence interval length under 20% of the total study sampled for various $\beta _Y$’s

The conclusions of comparison between OLS and our ODEB estimation under example sampling are also summarized in Fig. 8 by fixing $\beta _Y$ and examining the resulting RMSE, bias, average confidence interval coverage, and average confidence interval length for various sampling proportions. RMSE, bias, and confidence interval length are all higher for OLS estimation. Also, only ODEB-based confidence intervals maintain nominal coverage.

Fig. 8

Operating characteristics of ODEB and OLS estimation for $\beta _Y=0.2$ under extreme sampling

3.1.2 Simulations with Non-normal Residuals and Non-normal Inputs

To explore the degree to which the ODEB estimation method is affected by violations to the assumption of joint normality, the simulation above was repeated for $\varepsilon _{Y,i}$ following a scaled t distribution (scale $\sqrt{5}$) with $DF \in \{10, 20\}$ and a shifted log-Normal distribution with a mode of zero and variance of 5.

Fig. 9

Power of $\hat{\beta }_{Y,ODEB}$ under skewed (log-normal) or heavy-tailed (t) residual distributions and an extreme sample of 20% (Normal residual distribution also plotted for reference)

From the upper-left panel (the case of no biomarker effect with $\beta _Y=0$) of Fig. 9, the hypothesis test to detect the effect always has the correct level of $\alpha =0.05$ even if the normality assumption is violated. This is expected because, whatever the residual distribution is, there is no effect in the reverse-regression when the regression effect $\beta _Y=0$. The power of the test improves when the residuals are skewed (shifted log-normal) and deteriorates when the residual distribution becomes more heavily tailed (smaller degrees of freedom for t-distribution). In all simulated settings, the power of detection exceeds $80\%$ (shown as the horizontal dotted red line) when the full sample size is $n_F=800$ (with $n_S=160$ selected for biomarker-testing).

Fig. 10

Bias of $\hat{\beta }_{Y,ODEB}$ under skewed (log-normal) or heavy-tailed (t) residual distributions and an extreme sample of 20% (Normal residual distribution also plotted for reference)

Fig. 11

Coverage of 95% confidence interval for $\beta _Y$ under skewed (log-normal) or heavy-tailed (t) residual distributions and an extreme sample of 20% (Normal residual distribution also plotted for reference)

The bias of $\hat{\beta }_{Y,ODEB}$ is affected by the residual distributions as seen in Fig. 10. Correspondingly, the coverage probability of the $95\%$ confidence interval is no longer valid for non-normal residuals in Fig. 11. The coverage deteriorates when the effect sizes increases, when the sample size increases, and when the tails of residual distribution become heavier.

We also conduct similar simulations to check the effect of non-normal inputs X. Instead of non-normal residuals, we repeat the simulation above for covariate X following a scaled t distribution (scale $\sqrt{5}$, mean of 20) with $DF \in \{10, 20\}$. The effect patterns are the same as those observed above when the residual distribution is heavy-tailed. That is, ODEB estimation with an extreme sampling scheme still provides good power to detect an effect, but the estimation and confidence interval coverage deteriorate as $\beta _Y$ increases.

Overall, when the normality assumption is violated, the effect detection test is still valid and powerful but the effect estimation is no longer reliable.

3.1.3 Comparison with MSELE Estimator

Additionally, we compared the ODEB estimator to the MSELE estimator [18]. Notice that the MSELE estimator cannot be applied directly for data from extreme outcome-dependent sampling. It requires an additional simple random sample (SRS) so that some of the individuals with medial Y values are biomarker-tested also. Thus the comparison is conducted on extreme outcome-dependent sampling data plus some SRS data, mostly as a sanity check for the new ODED estimator against a well-established estimator in a setting close to extreme outcome-dependent sampling. We generate data following the ODS experimental design outlined by Zhou et al [18].

Again, for each of $B=20,000$ iterations, individual data sets consisting of $(X_1,Y_1)$,..., $(X_{n_F}, Y_{n_F})$ were randomly generated. This data was eligible for extreme outcome-dependent sampling. An additional SRS of size $n_{SRS}=80$ was generated. For each combination of parameter values described above, an extreme sample of size $\gamma n_F$ was selected. Both $\hat{\beta }_{Y,ODEB}$ and $\hat{\beta }_{Y,MSELE}$ were calculated on the merged sample consisting of the extreme sample and the additional SRS for a total sample size of $n = \gamma n_F + n_{SRS}$. The ODS package [33] in R was used to calculate $\hat{\beta }_{Y,MSELE}$ and its corresponding standard error.

Fig. 12

Root mean square error (RMSE) of $\hat{\beta }_{Y,MSELE}$ compared to $\hat{\beta }_{Y,ODEB}$ under 40% of the total study sampled for various $\beta _Y$’s

Figure 12 compares the RMSE of $\hat{\beta }_{Y,MSELE}$ and $\hat{\beta }_{Y,ODEB}$. The $\hat{\beta }_{Y,MSELE}$ is obtained from an iterative numerical optimization algorithm, and it does depend on the starting values which poses a challenge in convergence. We also plotted proportion of convergence of $\hat{\beta }_{Y,MSELE}$ out of $B=20,000$ simulation runs on the figure. The convergence rate of $\hat{\beta }_{Y,MSELE}$ is around $50\%$ or lower when the effect size is small. As the effect size increases, the divergence issue alleviates but is still significant even when $\beta _Y=1$. The RMSE of $\hat{\beta }_{Y,MSELE}$ from the convergent runs are plotted, and are much higher than RMSE of $\hat{\beta }_{Y,ODEB}$.

Fig. 13

Median absolute error (MAE) of $\hat{\beta }_{Y,MSELE}$ compared to $\hat{\beta }_{Y,ODEB}$ under 40% of the total study sampled for various $\beta _Y$’s

The RMSE is heavily affected by outliers. Sometimes, $\hat{\beta }_{Y,MSELE}$ converges to a value that is far from the true value, indicating failure of the iterative algorithm to find the true root. These wrong convergent cases inflate the RMSE of $\hat{\beta }_{Y,MSELE}$ a lot. To be fairer for $\hat{\beta }_{Y,MSELE}$, Fig. 13 presents the median absolute error (MAE) comparison instead. The MAE of $\hat{\beta }_{Y,MSELE}$ is now closer to, but still clearly exceeds, the MAE of $\hat{\beta }_{Y,ODEB}$. This accuracy improvement by $\hat{\beta }_{Y,ODEB}$ is expected here as it utilizes the correct parametric assumption which $\hat{\beta }_{Y,MSELE}$ does not make. As $\beta$ grows larger, this gap in performance between $\hat{\beta }_{Y,MSELE}$ and $\hat{\beta }_{Y,ODEB}$ shrinks.

These results confirm that, in a setting close to extreme outcome-dependent sampling, the proposed ODEB estimator provides correct answer. When the parametric assumptions hold, the ODEB estimator has smaller estimation error than MSELE as expected. For extreme outcome-dependent sampling, MSELE cannot be used, and ODEB should work well.

3.2 Data Analysis/Application to BISP2 Trial

The dependent variable of interest in the BISP2 Trial, pain intensity, is measured via the BPI to represent an underlying pain continuum for all participants. A pilot sample of 31 participants in the high and low tails of worst pain experienced at 48-hours post shoulder pain induction was selected for initial biomarker-testing. As the BPI is a discrete index represented on a continuous scale, there were ties for the highest and lowest pain scores. To determine which of the equal scores were included in the pilot sample, those who responded vs. did not respond to the treatment were selected in a balanced manner. Based on promising results from the initial pilot sample, a follow-up sample of 57 participants was selected in the same manner. All biomarkers were logarithm (base 10, for interpretability) transformed based on prior knowledge of the typical biomarker distribution. We model the relationship between pain and log-transformed biomarker linearly as:

$$\begin{aligned} y_{Pain} = \alpha + \beta log(x_{Biomarker}) + \epsilon \end{aligned}$$

Two pain-related outcomes of interest were explored using the above methodology: worst pain experienced at 48-hours post shoulder pain induction and change in worst pain from 48- to 96-hours post induction. Additionally, a self-reported disability score (Quick-DASH) at 48-hours post induction and change in Quick-DASH score from 48- to 96-hours post induction was investigated as outcomes to assess endpoint specificity. The results of modeling the association between pain-related outcomes and log-transformed biomarkers are discussed below. The distribution of worst pain at 48-hours in each stage of sampling is given in Fig. 14. For each pain-related outcome, reverse-regression based estimates of the effect of each log-transformed biomarker on pain ($\beta$) are reported with standard errors, 95% confidence intervals, and p-values. The the reverse-regression model assumption was assessed using diagnostic plots of residuals.

Fig. 14

Worst pain experienced at 48-hours shoulder pain induction for each sampling stage, combined stages, and the full BISP2 study population

The results of the analysis of the combined stages 1 and 2 data for worst pain and change in pain are shown in Tables 1 and 2. Table 1 shows evidence of association between CCL2 and worst pain at 48 h, with an effect estimate of 1.92 (95% CI: 0.24, 3.61). This indicates that for a tenfold increase in CCL2, we expect the worst pain at 48 h to increase by 1.92 points on the BPI scale. For change in pain, there is evidence of association from CRP (${\hat{\beta }} = 0.71$ (95% CI 0.05, 1.37)). We also see potential from IL10 and IL6, however the evidence in this sample is insufficient to conclude such. In additional analyses for self-reported disability outcomes (whose full result tables are omitted for succinctness), CRP shows evidence of association with Quick-DASH score. For a tenfold increase in CRP, we expect an increase of 3.92 points in the Quick-DASH score.

Table 1 Summaries from univariable reverse-regression based extreme sampling estimation and inference: worst pain at 48 h regressed on log-scale biomarkers

Table 2 Summaries from univariable reverse-regression based extreme sampling estimation and inference: change in worst pain from 48 h to 96 h regressed on log-scale biomarkers

Fig. 15

Model checking: normal QQ plot example for the change in pain outcome and the reverse-regression of $Y_{Pain\,Change}$ on $log(X_{CRP})$

Figure 15 provides the model checking diagnostic plots for the change in pain outcome and the residuals of the reverse-regression of log-transformed CRP on change in pain. Our joint normality assumption appears to be reasonable for this example.

4 Discussion

We proposed a new least squares approach to analysis for data generated by extreme outcome-dependent sampling based on the joint normality assumption. Prior methods developed for outcome-dependent sampling data are analyzed through likelihood-based methods [18] with an additional SRS to provide some observations in the middle range of response values. The ODS sampling schemes described in such works are the closest to EODS in the statistical literature. However, due to the presence of the supplemental SRS across the entire range of the response in the traditional ODS designs, the prior analysis approaches proposed are not applicable to data generated from an EODS design. Despite the differences in analysis needs, it is helpful in defining the future development of this novel method to contrast ODEB with the existing MSELE methodology.

The MSELE estimator is a semi-parametric empirical likelihood-based analysis method. The main advantage of this likelihood approach is that no parametric distributional assumption is needed, as the supplemental SRS provides knowledge of the range of the response outside of the typically extreme regions of interest. In contrast, through the joint normality assumption, our method provides two significant practical advantages. First, our method allows concentration of all sampling to the more informative individuals with the most extreme response values, resulting in great cost reduction for the expensive biomarker-testing. Taking on a parametric model allows us to assume the shape of the relationship in the medial region of the response range where no data were collected.

However, a primary limitation of this estimation is that in practice the joint normality assumption cannot be taken for granted. As in many model-based analyses, thorough knowledge of the relationship between the response and biomarkers to be studied is recommended to plan whether a reasonable transformation can be applied before the sampling design is enacted. Additionally, the diagnostic plots for model checking described in Sect. 2 must be thoroughly inspected to ensure validity of estimation. When the normality assumption is violated, the confidence interval coverage deteriorates only for very heavy-tailed residuals, but the hypothesis testing for effect detection always remains valid.

The second practical advantage is that our method is simple and can be conducted with existing standard statistical software. As seen in the simulation, often the likelihood method diverges or it converges to wrong parameter values, thus its data analysis often requires much care from an expert statistician. On the other hand, our method only requires applications of simple formulas on standard least-square estimates from the reverse-regression, and can be handled by any practitioner with a minimum statistical training. Furthermore, the model checking techniques used for the joint normality assumption are standard, with familiarity among any who have had fundamental training in linear regression.

This approach to analysis of EODS data is promising, but future development of the estimation method is key. In particular, extension to multiple regression analysis, which accounts for the correlation between biomarkers, is needed. In principle, derivation of formulas assuming joint normal distribution of a response variable and multiple biomarker variables may follow the same approach, but is non-trivial and hence the topic of future study. If the biomarkers and response variable Y jointly follow the multivariate normal distribution, then each biomarker and Y follows the bivariate normal distribution, thus the proposed inference methods are valid to apply separately on each biomarker even when multiple biomarkers are correlated amongst themselves. However, the test statistics of (5) for multiple biomarkers are correlated, thus an appropriate multiple testing adjustment (beyond the conservative Bonferroni correction or the step-down testing procedure) for variable selection needs to be carefully developed in the future. Additionally, exploration of whether the joint normality assumption can be relaxed is another future step.

5 Conclusion

We proposed an intuitive least squares-based estimator appropriate for EODS biomarker-testing studies with response and biomarker following a bivariate normal distribution, and showed via simulation that the estimation method is efficient and unbiased when compared to OLS estimation. To our knowledge, this is the first approach proposed for EODS which was not specifically developed for the genetics literature, where the variable X is discrete.

Our new ODEB estimator is easy to understand and implement, and so may be a bridge between practitioners who may benefit from ODS designs but do not have the background to immediately understand the likelihood-based methods by serving as an accessible introduction to ODS analysis. In the future, multivariate extension to our ODEB estimator will be particularly suited for exploratory biomarker studies due to its cost savings and ease of usage.

Appendices

Appendix A Mathematical Derivation of Formulas Relating Parameters of Regression and Reverse-regression

We assume that (X, Y) follows the bivariate normal distribution

$$\begin{aligned} N\left( \left( \begin{array}{c} \mu _X \\ \mu _Y \end{array} \right) , \left( \begin{array}{cc} \sigma ^2_X &{} \rho \sigma _X \sigma _Y \\ \rho \sigma _X \sigma _Y &{} \sigma _Y^2 \end{array} \right) \right) . \end{aligned}$$

Under this assumption, we consider how to get regression parameters $\alpha _Y$, $\beta _Y$ and $\sigma _{\varepsilon _Y}$ from the reverse-regression parameters $\alpha _X$, $\beta _X$ and $\sigma _{\varepsilon _X}$.

Conditional on X, we have the regression equation

$$\begin{aligned} Y = \alpha _Y + \beta _Y X + \varepsilon _Y, \end{aligned}$$

(10)

where $\varepsilon _Y \sim N(0, \sigma ^2_{\varepsilon _Y})$ with $\sigma ^2_{\varepsilon _Y}= (1 - \rho ^2) \sigma ^2_Y$. Similarly, conditional on Y, we have the reverse-regression equation

$$\begin{aligned} X = \alpha _X + \beta _X Y + \varepsilon _X, \end{aligned}$$

(11)

where $\varepsilon _X \sim N(0, \sigma ^2_{\varepsilon _X})$ with $\sigma ^2_{\varepsilon _X}= (1 - \rho ^2) \sigma ^2_X$.

Firstly we derive how the regression parameters of equation (11) relate to the bivariate normal distribution parameters. To do this, we consider the standardized versions of X and Y as $X^*=\frac{X- \mu _X}{\sigma _X}$ and $Y^*=\frac{Y- \mu _Y}{\sigma _Y}$. Then clearly, $(X^*,Y^*)$ follows the bivariate normal distribution

$$\begin{aligned} N\left( \left( \begin{array}{c} 0 \\ 0 \end{array} \right) , \left( \begin{array}{cc} 1 &{} \rho \\ \rho &{} 1 \end{array} \right) \right) . \end{aligned}$$

Hence we have

$$\begin{aligned} X^* = 0 + \rho Y^* + \sqrt{1-\rho ^2} Z, \end{aligned}$$

(12)

where $Z \sim N(0,1)$ is independent of Y. Plug $X^*=\frac{X- \mu _X}{\sigma _X}$ and $Y^*=\frac{Y- \mu _Y}{\sigma _Y}$ into equation (12) and compare with equation (11), we can express the reverse-regression parameters in terms of the bivariate normal distribution parameters as

$$\begin{aligned} \begin{array}{cl} \alpha _X &{} =\mu _X - \beta _X \mu _Y \qquad = \mu _X - \rho \frac{\sigma _X}{\sigma _Y} \mu _Y,\\ \beta _X &{} = \rho \frac{\sigma _X}{\sigma _Y}, \\ \sigma ^2_{\varepsilon _X} &{} = (1 - \rho ^2) \sigma ^2_X. \end{array} \end{aligned}$$

(13)

Secondly, by symmetry, similar derivations give the regression parameters’ formulas in terms of the bivariate normal distribution parameters as

$$\begin{aligned} \begin{array}{cl} \alpha _Y &{} =\mu _Y - \beta _Y \mu _X \qquad = \mu _Y - \rho \frac{\sigma _Y}{\sigma _X} \mu _X,\\ \beta _Y &{} = \rho \frac{\sigma _Y}{\sigma _X}, \\ \sigma ^2_{\varepsilon _Y} &{} = (1 - \rho ^2) \sigma ^2_Y. \end{array} \end{aligned}$$

(14)

We now find formulas to express regression parameters $\alpha _Y$, $\beta _Y$ and $\sigma _{\varepsilon _Y}$ in terms of $\alpha _X$, $\beta _X$, $\sigma _{\varepsilon _X}$, $\mu _Y$ and $\sigma _Y$.

We start from the parameter of most interest $\beta _Y$. Combine the middle equations in (13) and (14), we get

$$\begin{aligned} \beta _Y = \rho \frac{\sigma _Y}{\sigma _X} = \left( \rho \frac{\sigma _X}{\sigma _Y}\right) \frac{\sigma ^2_Y}{\sigma ^2_X}= \beta _X \frac{\sigma ^2_Y}{\sigma ^2_X}. \end{aligned}$$

(15)

Now, to get the desired expression of $\beta _Y$, we only need to express $\sigma ^2_X$ in terms of $\alpha _X$, $\beta _X$, $\sigma _{\varepsilon _X}$, $\mu _Y$ and $\sigma _Y$.

From the middle equation in (13),

$$\begin{aligned} \beta _X = \rho \frac{\sigma _X}{\sigma _Y} \qquad \Rightarrow \qquad \beta _X {\sigma _Y} = \rho {\sigma _X}. \end{aligned}$$

(16)

Square both sides of equation (16) and divides the last equation in (13), we get

$$\begin{aligned} \frac{\beta ^2_X {\sigma ^2_Y}}{\sigma ^2_{\varepsilon _X}} = \frac{\rho ^2}{1-\rho ^2}. \end{aligned}$$

Therefore, we solve $\rho ^2$ in this expression to get

$$\begin{aligned} \rho ^2 = \frac{1}{1+\frac{\sigma ^2_{\varepsilon _X}}{\beta ^2_X {\sigma ^2_Y}}}, \qquad \text{ and } \qquad 1-\rho ^2 = 1- \frac{1}{1+\frac{\sigma ^2_{\varepsilon _X}}{\beta ^2_X {\sigma ^2_Y}}}= \frac{\frac{\sigma ^2_{\varepsilon _X}}{\beta ^2_X {\sigma ^2_Y}}}{1+\frac{\sigma ^2_{\varepsilon _X}}{\beta ^2_X {\sigma ^2_Y}}} = \frac{1}{1+\frac{\beta ^2_X {\sigma ^2_Y}}{\sigma ^2_{\varepsilon _X}}}. \end{aligned}$$

(17)

Plug this back into the last equation in (13) to solve for $\sigma ^2_X$, we get

$$\begin{aligned} \sigma ^2_X \qquad = \frac{\sigma ^2_{\varepsilon _X}}{1-\rho ^2} \qquad = \sigma ^2_{\varepsilon _X}\left[ 1+\frac{\beta ^2_X {\sigma ^2_Y}}{\sigma ^2_{\varepsilon _X}}\right] \qquad = \sigma ^2_{\varepsilon _X} + \beta ^2_X {\sigma ^2_Y}. \end{aligned}$$

Put this into equation (15), we have the desired expression for $\beta _Y$ as

$$\begin{aligned} \beta _Y \qquad = \beta _X \frac{\sigma ^2_Y}{\sigma ^2_{\varepsilon _X} + \beta ^2_X {\sigma ^2_Y}} \qquad = \frac{1}{\frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X } \beta _X \qquad = \frac{\beta _X{\sigma ^2_Y}}{{\sigma ^2_{\varepsilon _X}} + \beta ^2_X {\sigma ^2_Y} }. \end{aligned}$$

(18)

Next, we express $\alpha _Y$ in terms of $\alpha _X$, $\beta _X$, $\sigma _{\varepsilon _X}$, $\mu _Y$ and $\sigma _Y$. From the first equation in (13), $\mu _X = \alpha _X + \beta _X \mu _Y$. Plug this and (18) both into the first equation of (14), we get

$$\begin{aligned} \alpha _Y \qquad =\mu _Y - \beta _Y \mu _X \qquad =\mu _Y - \left( \frac{\beta _X{\sigma ^2_Y}}{{\sigma ^2_{\varepsilon _X}} + \beta ^2_X {\sigma ^2_Y} }\right) (\alpha _X + \beta _X \mu _Y) \qquad = \frac{\sigma ^2_{\varepsilon _X}\mu _Y - \alpha _X \beta _X{\sigma ^2_Y}}{{\sigma ^2_{\varepsilon _X}} + \beta ^2_X {\sigma ^2_Y} }. \end{aligned}$$

(19)

Finally, for the expression of $\sigma ^2_{\varepsilon _Y}$, we plug (17) into the last equation of (14) to get

$$\begin{aligned} \sigma ^2_{\varepsilon _Y} \qquad =\frac{1}{1+\frac{\beta ^2_X {\sigma ^2_Y}}{\sigma ^2_{\varepsilon _X}}} \sigma ^2_Y \qquad = \frac{\sigma ^2_Y \sigma ^2_{\varepsilon _X}}{\sigma ^2_{\varepsilon _X}+\beta ^2_X {\sigma ^2_Y} }. \end{aligned}$$

(20)

Equations (18), (19) and (20) give the relationship between the theoretical parameters, where the quantities $\beta _Y$, $\alpha _Y$ and $\sigma ^2_{\varepsilon _Y}$ on the left-hand side are the desired parameters for regression analysis but cannot be directly estimated from data (their OLS estimates are inconsistent). Since the quantities on the right-hand side can be consistently estimated directly on the extremely sampled data through reverse-regression, as explained in the main text, plugging-in those estimators to equations (18), (19) and (20) result in consistent estimators ${\hat{\beta }}_Y$, ${\hat{\alpha }}_Y$ and ${\hat{\sigma }}^2_{\varepsilon _Y}$ for the desired parameters.

Furthermore, we can use the Delta Method [34, p. 61] to derive the standard errors of estimators for the plug-in estimators since the standard errors for the right-hand side quantities estimators are available directly from the reverse-regression. Particularly, for ${\hat{\beta }}_Y$, we first find the following partial derivatives from the equation (18):

$$\begin{aligned} \begin{array}{cll} \frac{\partial }{\partial \beta _X}\beta _Y &{} = \frac{1}{\frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X } + \beta _X \frac{-1}{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X \right) ^2} (2 \beta _X) &{} = \frac{\frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y}-\beta ^2_X}{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X \right) ^2}, \\ \frac{\partial }{\partial (\sigma ^2_{\varepsilon _X})}\beta _Y &{} = \frac{-\beta _X}{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X \right) ^2} \frac{1}{\sigma ^2_Y} &{}= \frac{\frac{-\beta _X}{\sigma ^2_Y}}{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X \right) ^2}, \\ \frac{\partial }{\partial (\sigma ^2_Y)}\beta _Y &{} = \frac{-\beta _X}{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X \right) ^2} \frac{-\sigma ^2_{\varepsilon _X}}{(\sigma ^2_Y)^2} &{}=\frac{\frac{\beta _X \sigma ^2_{\varepsilon _X}}{\sigma ^4_Y}}{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X \right) ^2}. \end{array} \end{aligned}$$

(21)

Since ${\hat{\beta }}_X$, ${\hat{\sigma }}^2_{\varepsilon _X}$ and ${\tilde{\sigma }}^2_Y$ are uncorrelated with each other, using the Delta Method, ${\hat{\beta }}_X$ is asymptotically normally distributed whose variance estimation is

$$\begin{aligned} \begin{array}{cl} (s.e.\{{\hat{\beta }}_Y\})^2 &{}= \left( \frac{\partial }{\partial \beta _X}\beta _Y\right) ^2 (s.e.\{{\hat{\beta }}_X\})^2 + \left( \frac{\partial }{\partial (\sigma ^2_{\varepsilon _X})}\beta _Y \right) ^2(s.e.\{{\hat{\sigma }}^2_{\varepsilon _X}\})^2+ \left( \frac{\partial }{\partial (\sigma ^2_Y)}\beta _Y\right) ^2(s.e.\{{\tilde{\sigma }}^2_Y\})^2 \\ &{} =\frac{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y}-\beta ^2_X\right) ^2 (s.e.\{{\hat{\beta }}_X\})^2 + \left( \frac{\beta ^2_X}{\sigma ^4_Y}\right) (s.e.\{{\hat{\sigma }}^2_{\varepsilon _X}\})^2+ \left( \frac{\beta ^2_X \sigma ^4_{\varepsilon _X}}{\sigma ^8_Y}\right) (s.e.\{{\tilde{\sigma }}^2_Y\})^2 }{\left( \frac{\sigma ^2_{\varepsilon _X}}{\sigma ^2_Y} + \beta ^2_X \right) ^4}. \end{array} \end{aligned}$$

(22)

For the quantities in the formula (22), $s.e.\{{\hat{\beta }}_X\}$ can be gotten from outputs of standard linear regression fit packages, and

$$\begin{aligned} (s.e.\{{\tilde{\sigma }}^2_Y\})^2 = \frac{2 \sigma ^4_Y}{n_F-1}, \qquad (s.e.\{{\hat{\sigma }}^2_{\varepsilon _X}\})^2 = \frac{2 \sigma ^4_{\varepsilon _X}}{n_s-2}, \end{aligned}$$

from the variance formula of the Chi-square distribution.

Plug-in the point estimators for each quantity into equation (22), we estimate the standard error for ${\hat{\beta }}_Y$ as

$$\begin{aligned} s.e.\{{\hat{\beta }}_Y\} = \sqrt{\frac{\left( \frac{{\hat{\sigma }}^2_{\varepsilon _X}}{{\tilde{\sigma }}^2_Y}-{\hat{\beta }}^2_X\right) ^2 (s.e.\{{\hat{\beta }}_X\})^2 + \left( \frac{2 {\hat{\beta }}^2_X {\hat{\sigma }}^4_{\varepsilon _X}}{{\tilde{\sigma }}^4_Y}\right) \left( \frac{1}{n_s-2} + \frac{1}{n_F-1}\right) }{\left( \frac{{\hat{\sigma }}^2_{\varepsilon _X}}{{\tilde{\sigma }}^2_Y} + {\hat{\beta }}^2_X \right) ^4}}. \end{aligned}$$

(23)

Appendix B Mathematical derivation of power formulas

For the standard simple linear regression on a data set of size n, the power of an $\alpha$ level t-test (testing the zero slope null hypothesis) is given

$$\begin{aligned} power = P( NF_{ncp=n f^2, df_1=1, df_2=n-2} > FQ_{\alpha , df_1=1, df_2=n-2}), \end{aligned}$$

(24)

where $NF_{ncp=n f^2, df_1=1, df_2=n-2}$ denotes a random variable following a non-central F-distribution with noncentral parameter $n f^2$, degrees of freedoms of 1 and $n-2$, and $FQ_{\alpha , df_1=1, df_2=n-2}$ denotes the $\alpha$ upper quantile of a central F-distribution with degrees of freedoms of 1 and $n-2$. Here f is the Cohen’s effect size defined as

$$\begin{aligned} f^2 = \frac{R^2}{1-R^2} = \frac{\rho ^2}{1-\rho ^2}, \end{aligned}$$

(25)

where $R^2$ is the proportion of variation in the data explained by the regression equation.

We are doing the reverse-regression hypothesis test for

$$\begin{aligned} H_0: \beta _X = 0 \qquad \text{ versus } \qquad H_A: \beta _X \ne 0. \end{aligned}$$

If we have observations of both X and Y on the full data set, then the power is given by formula (26) with $n=n_F$. Now we derive the power formula when the test is conducted on the selectively sampled subset. Besides the changes in sample size from $n_F$ to $n_S$, the effect size also changes from the full data set to the selectively sampled subset. The $R^2$ in (25) would be larger in the subset due to selectively sampling the extreme values. To derive the change in effect size, we reexpress (25) as

$$\begin{aligned} f^2 = \frac{R^2}{1-R^2} = \frac{1}{\frac{1}{R^2}-1} = \frac{1}{\frac{1}{\rho ^2}-1} = \frac{\beta ^2_X {\sigma ^2_Y}}{\sigma ^2_{\varepsilon _X}}, \end{aligned}$$

where the last equality comes from equation (17). Notice that both quantities $\beta ^2_X$ and $\sigma ^2_{\varepsilon _X}$ remain invariant on the full data set and the subset since the reverse-regression model (11) holds on both data sets. $\sigma ^2_Y$ differs in the two data sets. Since only the extreme $\gamma$ proportion of Y is selected, the variance of selected $Y_S$ is bigger on the selectively sampled subset than the variance of Y on the full data set. To calculate $\sigma ^2_{Y_S}$, we note that the selected $Y_S$ do not follow the $N(\mu _Y, \sigma ^2_Y)$ distribution anymore. Rather it follows the normal distribution truncated at the upper and lower $(\gamma /2)$-tails. Let $z_{\gamma /2}$ denotes the upper $(\gamma /2)$-quantile of the standard normal distribution N(0, 1). Let $\phi (x)=\frac{1}{\sqrt{2\pi }}e^{x^2/2}$ denotes the density function of the standard normal distribution N(0, 1). Then the variance of selected $Y_S$ is

$$\begin{aligned} \sigma ^2_{Y_S} = \sigma ^2_{Y_F} 2 \int _{z_{\gamma /2}}^{\infty } x^2 \frac{1}{\gamma } \phi (x) dx. \end{aligned}$$

(26)

Therefore, compared to the effect size on the full data set, the effect size $f^2$ on the subset increases by a factor of $2 \int _{z_{\gamma /2}}^{\infty } x^2 \frac{1}{\gamma } \phi (x) dx$. Since the sample size $n_S$ of the subset is $\gamma$ proportion of the full data set size $n_F$ so that $n_S/\gamma =n_F$, the power of t-test on the subset becomes

$$\begin{aligned} \begin{array}{cl} power &{} = P( NF_{ncp=n_S f^2 2 \int _{z_{\gamma /2}}^{\infty } x^2 \frac{1}{\gamma } \phi (x) dx, df_1=1, df_2=n_S-2}> FQ_{\alpha , df_1=1, df_2=n_S-2}) \\ &{} = P( NF_{ncp=n_F f^2 2 \int _{z_{\gamma /2}}^{\infty } x^2 \phi (x) dx, df_1=1, df_2=\gamma n_F-2} > FQ_{\alpha , df_1=1, df_2=\gamma n_F-2}). \end{array} \end{aligned}$$

(27)