Abstract
neurolib is a computational framework for whole-brain modeling written in Python. It provides a set of neural mass models that represent the average activity of a brain region on a mesoscopic scale. In a whole-brain network model, brain regions are connected with each other based on biologically informed structural connectivity, i.e., the connectome of the brain. neurolib can load structural and functional datasets, set up a whole-brain model, manage its parameters, simulate it, and organize its outputs for later analysis. The activity of each brain region can be converted into a simulated BOLD signal in order to calibrate the model against empirical data from functional magnetic resonance imaging (fMRI). Extensive model analysis is made possible using a parameter exploration module, which allows one to characterize a model’s behavior as a function of changing parameters. An optimization module is provided for fitting models to multimodal empirical data using evolutionary algorithms. neurolib is designed to be extendable and allows for easy implementation of custom neural mass models, offering a versatile platform for computational neuroscientists for prototyping models, managing large numerical experiments, studying the structure–function relationship of brain networks, and for performing in-silico optimization of whole-brain models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Mathematical modeling and computer simulations are fundamental for understanding complex natural systems. This is especially true in the field of computational neuroscience where models are used to represent neural systems at many different scales. At the macroscopic scale, we can study whole-brain networks that model a brain that consists of brain regions which are coupled via long-range axonal connections. A number of technological and theoretical advancements have transformed whole-brain modeling from an experimental proof-of-concept into a widely used method that is now part of a computational neuroscientist’s toolkit, the first of which is the widespread availability of computational resources.
An integral contribution to this development can be attributed to the success of mathematical neural mass models that represent the population activity of a neural network, often by using mean-field theory [1, 2] which employs methods from statistical physics [3]. While microscopic simulations of neural systems often rely on large spiking neural network simulations where the membrane voltage of every neuron is simulated and kept track of, neural mass models typically consist of a system of differential equations that govern the macroscopic variables of a large system, such as the population firing rate. Therefore, these models are considered useful for representing the average activity of a large neural population, e.g., a brain area. Biophysically realistic population models are often derived from networks of excitatory (E) and inhibitory (I) spiking neurons by assuming the number of neurons to be very large, their connectivity sparse and random, and the post-synaptic currents to be small [4]. At the other end of the spectrum of neural mass models, simple phenomenological oscillator models [5,6,7,8] are also used to represent the activity of a single brain area, sacrificing biophysical realism for computational and analytical simplicity.
In the past, whole-brain models have been employed in a wide range of problems, including demonstrating the ability of whole-brain models to reproduce BOLD correlations from functional magnetic resonance imaging (fMRI) during resting-state [9, 10] and sleep [11], explaining features of EEG [12] and MEG [5, 6] recordings, studying the role of signal transmission delays between brain areas [13, 14], the differential effects of neuromodulators [7, 15], modeling electrical stimulation of the brain in-silico [16,17,18,19], or explaining the propagation of brain waves [20] such as in slow-wave sleep [21]. Previous work often focused on finding the parameters of optimal working points of a whole-brain model, given a functional dataset [22].
However, although it is clear that whole-brain modeling has become a widely-used paradigm in computational neuroscience, many researchers rely on a custom code base for their simulation pipeline. This can result in slow performance, avoidable work due to repetitive implementations, the use of lengthy boilerplate code, and, more generally, a state in which the reproduction of scientific results is made harder. In order to address these points, we present neurolib, a computational framework and a Python library, which helps users to set up whole-brain simulations. With neurolib, parameter explorations of models can be conducted in large-scale parallel simulations. neurolib also offers an optimization module for fitting models to experimental data, such as from fMRI or EEG, using evolutionary algorithms. Custom neural mass models can be implemented easily into the existing code base. The main goal of neurolib is to provide a fast and reliable framework for numerical experiments that encourages customization, depending on the individual needs of the researcher. neurolib is available as free open-source software released under the MIT license.
Results
Whole-Brain Modeling
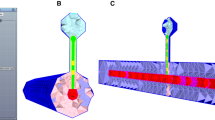
Construction of a whole-brain model. Structural connectivity from DTI tractography is combined with a neural mass model that represents a single brain area in each of the \(N = 80\) brain regions. The depicted neural mass model consists of an excitatory (red) and an inhibitory (blue) subpopulation. The default output of each region, e.g., the excitatory firing rate, is converted to a BOLD signal using the hemodynamic Balloon–Windkessel model. For model optimization, the models’ output is compared to empirical data, such as an EEG power spectrum or to fMRI functional connectivity (FC) and its temporal dynamics (FCD)
A whole-brain model is a network model which consists of coupled brain regions (see Fig. 1). Each brain region is represented by a neural mass model which is connected to other brain regions according to the underlying network structure of the brain, also known as the connectome [23]. The structural connectivity of the brain is typically obtained by diffusion tensor imaging (DTI) which is used to infer the long-range axonal white matter tracts in the brain, a method known as fiber tractography. When combined with a parcellation scheme that divides the brain into N different brain regions, also known as an atlas, the brain can be represented as a brain network with the N brain regions being its nodes and the white matter tracts being its edges. Figure 1 shows structural connectivity matrices that represent the number of fibers and the average fiber length between any two regions. In a simulation, each brain area produces activity, for example a population firing rate, and a BOLD signal. To assess the validity of a model, the simulated output can then be compared to empirical brain recordings.
Framework Architecture
In the following, we will describe the design principles of neurolib and provide a brief summary of the structure of the Python package (see Fig. 2). Later, the individual parts of the framework will be discussed in more detail. At the core of neurolib is the Model base class from which all models inherit their functionality. The base class initializes and runs models, manages parameters, and handles simulation outputs. To reduce memory the footprint of long simulations, chunkwise integration can be performed using the autochunk feature, which will be described later. The outputs of a model can be converted into a BOLD signal using a hemodynamic model which allows for a comparison of the simulated outputs to empirical fMRI data. The Dataset class handles structural and functional datasets. A set of post-processing functions and a Signal class is provided for computing functional connectivity (FC) matrices, applying temporal filters to model outputs, computing power spectra, and more. The simulation pipeline interacts with two additional modules that provide parameter exploration capabilities using the BoxSearch class, and enable model optimization using the Evolution class. Both modules utilize the ParameterSpace class which provides the appropriate parameters ranges for exploration and optimization.
Installation and Dependencies
The easiest way to install neurolib is through the Python Package Index PyPI using the command pip install neurolib. This will make the package available for import. For reading and editing the source code of neurolib (which is advised for more advanced users), we recommend cloning the GitHub repository directly. Detailed instructions for this are provided on neurolib’s GitHub page https://github.com/neurolib-dev/neurolib. In this paper, we present a set of examples with code and describe use cases for whole-brain modeling. However, for a more extensive list of examples, the reader is advised to explore the Jupyter Notebooks provided in the examples directory on neurolib’s GitHub page.
The main Python dependencies of neurolib’s high-level functions include pypet [24], a Python parameter exploration toolbox which provides parallelization and data storage capabilities, and DEAP [25], which is used for optimization with evolutionary algorithms. Data arrays are provided using the packages numpy [26], pandas [27], and xarray [28] and signal processing is handled by the scipy [29] package. The numerical integration is accelerated using numba [30], a just-in-time compiler for Python. All dependencies will be automatically installed when installing neurolib using pip. All presented results and the code in this paper is based on neurolib’s release version 0.6.
Neural Mass Models
Several neural mass models for simulating the activity of a brain area are implemented in neurolib (see Table 1). Some neural mass models, for example the ALN model [31, 32] or the Wilson–Cowan model [33, 34], consist of multiple neural populations, namely an excitatory (E) and an inhibitory (I) one, which are referred to as subpopulations in order to distinguish them from an entire brain area, which we refer to as a node. Every brain area is a node coupled to other nodes in the whole-brain network. It should be noted that some phenomenological models like the Hopf model [35] only have a single variable that represents neural activity, and therefore, the distinction between E and I subpopulations does not apply.
Phenomenological and Biophysical Models
Biophysically grounded neural mass models that are derived from an underlying network of spiking neurons produce an output that is a firing rate, akin to the mean spiking rate of a neural network. An example of such a model is the ALN model, which is based on a network of spiking adaptive exponential (AdEx) integrate-and-fire neurons [36]. Phenomenological models usually represent a simplified dynamical landscape of a neural network and produce outputs that are abstract and do not have physical units. An example is the Hopf model, where the system dynamics can be used to describe the transition from steady-state firing to neural oscillations [6]. The Wilson–Cowan model can be mentioned as a middle ground between simple and realistic. It describes the activity of excitatory and inhibitory neurons while relying on simplifications such as representing the fraction of active neurons, rather than the actual firing rate of the population, and uses an analytical firing rate transfer function.
Model Equations
The core module of neurolib consists of the Model class that manages the whole-brain model and its parameters. Every model is implemented as a separate class that inherits from the Model class and represents the entire brain network. Typically, a model is implemented as a system of ordinary differential equations which can be generally expressed as
Here, the vector \(\mathbf {x}_i = (x_{i1}, ..., x_{id})\) describes the d-dimensional state of the i-th brain region which follows the local node dynamics \(\mathbf {f}\), with \(i \in [0, N-1]\) and N being the number of brain regions. This vector contains all state variables of the system, including, for example, firing rates and synaptic currents. The second term describes the coupling between the i-th and j-th brain regions, given by a coupling scheme \(\mathbf {g}\). This coupling term typically depends on the \(N \times N\) adjacency matrix \(\mathbf {G}\) (with elements \(G_{ij}\)), the current state vector of the i-th brain area, and the time-delayed state vector of the j-th brain area, which itself depends on the \(N \times N\) inter-areal signal delay matrix \(\mathbf {D}\) (with elements \(D_{ij}\)). The matrices \(\mathbf {G}\) and \(\mathbf {D}\) are defined by the empirical structural connectivity datasets. The third term \(\mu _i(t)\) represents a noise input to every node which is simulated as a stochastic process for each brain area (or subpopulation) individually.
The main difference between the implemented neural mass models is the local node dynamics \(\mathbf {f}\). Some models, such as the Hopf model, additionally support either an additive coupling scheme \(\mathbf {g}\), where the coupling term only depends on the activity of the afferent node \(\mathbf {x}_j\), or a diffusive coupling scheme, where the coupling term depends on the difference between the activity of the afferent and efferent nodes, i.e., \(\mathbf {x}_i - \mathbf {x}_j\). Other coupling schemes, such as nonlinear coupling, can be also implemented by the user.
Noise Input
Every subpopulation \(\alpha\), with for example \(\alpha \in \{E, I\}\), of each brain area i (index omitted) receives an independent noise input \(\mu _{\alpha }(t)\), which, for the models in Table 1, comes from an Ornstein–Uhlenbeck process [42],
where \(\mu _{\alpha }^{\text {ext}}\) represents the mean of the process and can be thought of as a constant external input, \(\tau _{ou}\) is the time scale, and \(\xi (t)\) is a white noise process sampled from a normal distribution with zero mean and unit variance. The noise strength parameter \(\sigma _{\text {ou}}\) determines the standard deviation of the process, and, therefore, the amplitude of fluctuations around the mean.
Bifurcation Diagrams
Figure 3 shows the bifurcation diagrams (or state spaces) of a single node of a selection of models in order of increasing complexity. The diagrams serve as a demonstration of the parameter exploration module of neurolib, which we will describe in more detail in a later section. Understanding the state space of a single node allows one to interpret its behavior in the coupled case. Starting from the Hopf model (Fig. 3a), we can see how the transition to the oscillatory state is caused by an eponymous supercritical Hopf bifurcation controlled by the parameter a. Figures 3b and c show the time series of the activity variable (including noise) in the steady-state, i.e., a fixed point, for \(a < 0\), and an oscillatory state, i.e., a limit cycle, for \(a > 0\), respectively. The Wilson–Cowan model (Fig. 3d) has two Hopf bifurcations, where the low-activity down-state is separated from the high-activity up-state by a limit cycle region in which the activity alternates between the E and I subpopulations. The time series of the activity variable in Fig. 3e shows the system in the down-state with short excursions into the limit cycle due to the noise in the system, whereas in Fig. 3f, the system is placed inside the limit cycle and reaches the up- and the down-state occasionally. The bifurcation diagram of the ALN model in Fig. 3g has a more complex structure and its validity has been verified using large spiking network simulations before [32]. Here, we can see that the down-state and the up-state are separated by a limit cycle as well. Therefore, the bifurcation structure of the Wilson—Cowan model can be thought of as a simplified version of a slice through the limit cycle of this two-dimensional diagram in the horizontal plane. In Fig. 3h, the ALN model is placed in the down-state close to the limit cycle and the time series of the excitatory firing rate \(r_e\) shows brief excursions into the oscillatory state. Without the adaptation mechanism that is derived from the underlying AdEx neuron, we can also observe a bistable regime in the bifurcation diagram Fig. 3g, where both up- and down-state coexist. An example time series is shown in Fig. 3i, where the activity shows noise-induced transitions between the up- and down-states. When the adaptation mechanism of the underlying AdEx model is enabled (not shown), the bistable region transforms into a new, slowly oscillating limit cycle [32, 43].
Overview of neural mass models. (a) Bifurcation diagram of the Hopf model. For \(a<0\), solutions converge to a fixed point (FP). For \(a>0\), solutions converge to a limit cycle (LC). (b) Example time series of x of the Hopf model in the FP with \(a=-0.25\), noise strength \(\sigma _{\text {ou}} = 0.001\), and noise time scale \(\tau _{\text {ou}} = 20.0\)ms. (c) Time series at the bifurcation point \(a=0\) with the same noise properties as in (b). (d) Wilson–Cowan model with the activity of the excitatory population (E) plotted against the external input Eext. The system has two fixed-points with low (down) and high (up) activity and a limit cycle in between. (e) Time series of E with Eext\(=0.5\), \(\sigma _{\text {ou}} = 0.01\), and \(\tau _{\text {ou}} = 100.0\)ms. (f) Eext\(=1.9\). (g) Two-dimensional bifurcation diagram of the ALN model depending on the input currents to the excitatory (E) and inhibitory (I) subpopulation. The color denotes the maximum firing rate \(r_\text {E}\) of the E population. Regions of low-activity down-states (down) and high-activity up-states (up) are indicated. Dashed green contours indicate bistable (bi) regions where both states coexist. Solid white contour indicates oscillatory states within the fast E-I limit cycle (LCEI). (h) Time series of \(r_\text {E}\) with mean input currents \(\mu _{E}^{\text {ext}} = 0.5\) mV/ms and \(\mu _{I}^{\text {ext}} = 0.5\) mV/ms and noise parameters like in (e). (i) \(\mu _{E}^{\text {ext}} = 2.0\) mV/ms and \(\mu _{I}^{\text {ext}} = 2.5\) mV/ms and \(\sigma _{\text {ou}} = 0.3\). Each point in the bifurcation diagrams was simulated without noise for 5 seconds and the activity of the last second was used to determine the depicted state. All remaining parameters are kept at their default values
Numerical Integration
The models are integrated using the Euler–Maruyama integration scheme [44]. The numerical integration is written explicitly in Python and then accelerated using the just-in-time compiler numba [30], providing a performance similar to running native C code. Compared to pure Python code, this offers a speedup in simulation time on the order of \(10^4\). For computational efficiency, each neural mass model is implemented as a coupled network such that the single-node case is a special case of a network with \(N=1\) nodes. Likewise, the noise process in Eq. 2 is also implemented within every model’s integration and then added to the appropriate state variables of the system, i.e., the membrane currents of E and I in the case of the ALN model.
Example: Single Node Simulation
In the example in Listing 1, we load a single isolated (E-I) node of the ALNModel and initialize it. Every model has a set of default parameters (defined in each model’s parameter definition file defaultParams.py) which we can be changed by setting entries of the params dictionary attribute. To demonstrate this, we set the external noise strength which is simulated as an Ornstein–Uhlenbeck process with a standard deviation \(\sigma _{\text {ou}} = 0.1\) (Eq. 2) and then run the model. The results from this simulation can be accessed via the model object’s attributes t which contains the simulation time steps, and output which contains the firing rate of the excitatory population. All other state variables of a model can be accessed via the dictionary attribute outputs. An example time series of the excitatory firing rate is shown in Figure 3h.

Empirical Datasets
Loading Datasets from Disk
For simulating whole-brain models where multiple neural mass models are coupled in a network, neurolib provides an interface for loading structural and functional datasets from disk using the Dataset class (Listing 2). Datasets are stored as MATLAB .mat matrices in the data directory. An instance of the Dataset class makes subject-wise as well as group-averaged matrices available to the user as numpy [26] arrays. Structural matrices can be normalized using one of the available methods. An example of how to load a dataset is shown in Listing 2.
Structural connectivity data are stored as \(N \times N\) matrices, and functional time series are \(N \times t\) matrices, N being the number of brain regions and t the number of time steps. Example datasets are included in neurolib and custom datasets can be added by placing them in the dataset directory. Throughout this paper, we use preprocessed data from the ConnectomeDB of the Human Connectome Project (HCP) [45] with \(N = 80\) cortical brain regions defined by the AAL2 atlas [46].
Structural DTI Data
For a given parcellation of the brain into N brain regions, the \(N \times N\) adjacency matrix Cmat, i.e., the structural connectivity matrix, determines the coupling strengths between brain areas. The fiber length matrix Dmat determines the signal transmission delays, i.e., the time it takes for a signal to travel from one brain region to another. Example structural matrices are shown in Fig. 1.
In the following, we outline the preprocessing steps necessary to extract fiber count and fiber length matrices from T1- and diffusion-weighted images (DTI) using FSL [47]. The resulting structural matrices are included in neurolib. Any other processing pipeline that results in a matrix of connection strengths and signal transmission delays between brain regions, such as with the fiber tractography software DSIStudio [48], is equally applicable. The following should serve as a rough guideline only.
First, the non-brain tissue was removed form the T1-weighted anatomical images and a brain mask was generated using the brain extraction toolbox (BET) in FSL. The same extraction was then applied to the DTI, followed by head motion and eddy current distortion correction. Then, a probabilistic diffusion model was fitted to the DTI using the BEDPOSTX toolbox in FSL. Each subject’s b0 image was linearly registered to the corresponding T1-weighted image, and the high-resolution volume mask from the AAL2 atlas was transformed from MNI space to subject space. Probabilistic tractography was performed with 5000 random seeds per voxel using FSL’s probabilistic tractography algorithm PROBTRACKX [49]. The resulting \(N \times N\) adjacency matrix with \(N=80\) cortical brain regions, as defined by the AAL2 atlas, contains the total fiber counts from each region to any other region as the elements. The fiber length matrix of the same shape was obtained during the same procedure, containing the average fiber length of all fibers connecting any two regions in units of mm. This procedure was done for every subject individually.
Connectivity Matrix Normalization
The elements of the structural connectivity matrix Cmat typically contain the number of reconstructed fibers from DTI tractography. Since the number of fibers depends on the method and the parameters of the (probabilistic or deterministic) tractography, they need to be normalized using one of the three implemented methods in the Dataset class which can be automatically applied upon initialization by the use of the appropriate argument, i.e., Dataset(name, normalizeCmats=method), where name refers to the name of the data set used, and method to one of the following methods.
The first method max is applied by default and simply divides the entries of Cmat by the largest entry, such that the largest entry becomes 1. The second method waytotal divides the entries of each column of Cmat by the number of fiber tracts generated from the respective brain region during probabilistic tractography in FSL, which is contained in the waytotal.txt file. The third method nvoxel divides the entries of each column of Cmat by the size, i.e., the number of voxels, of the corresponding brain area. The last two methods yield asymmetric connectivity matrices, while with the first one they remain symmetric. Normalization is applied on the subject-wise matrices (accessible via the attributes Cmats and Dmats). Finally, group-averaged matrices are computed for the dataset and made available as the attributes Cmat and Dmat.
Functional MRI Data
Subject-wise fMRI time series are in a \((N \times t)\)-dimensional format, where N is the number of brain regions and t the length of the time series. Each region-wise time series represents the BOLD activity averaged across all voxels of that region, which can be also obtained from software like FSL. Functional connectivity (FC) matrices capture the spatial correlation structure of the BOLD time series across the entire time of the recording. Subject-wise FC matrices are accessible via the attribute FCs and are generated by computing the Pearson correlation of the time series between all regions, yielding a \(N \times N\) matrix for each subject. Example FC matrices from resting-state fMRI (rs-fMRI) recordings are shown in Fig. 1.
To capture the temporal fluctuations of time-dependent FC(t), which are lost when computing correlations across the entire recording time series, functional connectivity dynamics matrices (FCDs) are computed as the element-wise Pearson correlation of time-dependent FC(t) matrices in a moving window across the BOLD time series [50] of a chosen window length of, for example, 1 min. This yields a \(t_{FCD} \times t_{FCD}\) FCD matrix for each subject, with \(t_{FCD}\) being the number of steps the window was moved.
The rs-fMRI data included in neurolib were processed using the FSL FEAT toolbox [51]. First, head motion was corrected using the McFLIRT algorithm. Functional images were linearly registered to each subject’s anatomical image using FLIRT. A brain mask was created using BET. MELODICA ICA was conducted and artefacts (motion, non-neural physiological artefacts, scanner artefacts) were removed using the ICA FIX FSL toolbox [52, 53]. Finally, the AAL2 mask volumes were transformed from MNI space to each subject’s functional space and the average BOLD time series for each brain region was extracted using the fslmeants command in Fslutils.
Example: Whole-Brain Simulation
In a whole-brain model, the main activity variables of each neural mass are coupled with each other. If the neural mass model has E and I subpopulations, the coupling is usually implemented between the activity variables of the E subpopulations, resulting in a whole-brain model with global excitation and local inhibition. The adjacency matrix Cmat determines the relative coupling strengths between all brain areas. The elements of the delay matrix Dmat contain the average fiber lengths between any two brain regions.
In all of the following brain network examples, we use the empirical dataset from the HCP loaded using the Dataset class (Listing 2). As discussed above, this dataset contains structural matrices Cmat and Dmat for \(N=80\) cortical nodes from the AAL2 atlas, as well as averaged BOLD time series of 10 minute length for all N brain regions.
Given the structural matrices, we initialize a brain network model by passing the group-averaged matrices Cmat and Dmat to the model’s constructor. We set a long-enough simulation time of 10 minutes in order to match the length of the empirical BOLD data. Finally, we choose to simulate a BOLD signal by using the appropriate argument in the run method.

Whole-Brain Model Parameters
If left unchanged, all parameters of a model are kept at their default values, which are defined in each model’s parameter definition file (i.e., defaultParams.py). Each model has their specific set of local parameters. Examples for the ALNModel are the noise strength sigma_ou (see Listing 2), the synaptic time constants tau_se and tau_si, internal delays between E and I nodes de and di, and more (see Table 2).
However, all implemented models also share a common set of global parameters that apply on the network level and affect the coupling between nodes. These are the global coupling strength Ke_gl and the signal transmission speed signalV. To determine the absolute coupling strength between any two nodes, the relative coupling strengths contained in the adjacency matrix Cmat are multiplied by Ke_gl. The entries of the fiber length matrix Dmat are divided by signalV to determine the time delay in units of ms for signal transmission between brain regions.
BOLD Model
Every brain area has a predefined default output variable which is typically one of its state variables. The default output variable of the ALN model, for example, is the firing rate of the excitatory subpopulation of every brain area. The default output can be used to simulate a BOLD signal using the implemented Balloon–Windkessel model [54,55,56]. The BOLD signal is governed by a set of differential equations that model the hemodynamic response of a brain area to neural activity. After integration, the BOLD signal is then subsampled at 0.5hz to match the sampling rate of fMRI recordings. The BOLD signal is integrated alongside the neural mass model and stored in the model’s outputs. To enable the simulation of the BOLD signal, the user simply passes the argument bold = True to the run method (see Listing 2).
Example: Custom Model Implementation
In the following, we present how a custom model can be implemented in neurolib. Every model consists of two parts. The first part is the class that implements the model and that inherits most of its functionality from the Model base class. The second part is the timeIntegration() function that governs the numerical integration over space and time. In this example, we implement a simple linear model with the following equation
This class of models is popular due to its analytical tractability and can be used to apply linear control theory to brain networks [19, 57]. As before, this equation represents N nodes that are coupled in a network. \(x_i\) are the elements of an N-dimensional state vector \(\mathbf {x}\), \(\tau\) is the decay time constant, \(G_{ij}\) are elements of the adjacency matrix \(\mathbf {G}\), and K is the global coupling strength. We implement this model as the class LinearModel in Listing 3.

In the definition of the model class, we specified necessary information, such as the names of the state variables state_vars, the default output of the model default_output, and the variable names init_vars, holding the initial conditions at \(t=0\). The timeIntegration() function has two parts: One, in which the variables for the simulation are prepared, and another, where the actual time integration takes place, i.e., njit_int(). The latter has a decorator @numba.njit which ensures that the integration will be accelerated with the just-in-time compiler numba. The equations of the model are then integrated using the Euler–Maruyama integration scheme. This simple model can be run like the other models before, supports features like chunkwise integration (see below), and can produce a BOLD signal.
Chunkwise Integration for Memory-Intensive Experiments
Some of the important applications of whole-brain modeling require very long simulation times in order to extract meaningful data from the model and to compare it to empirical recordings. Examples are computing BOLD correlations, such as FC and FCD matrices, from time series with a very low sampling rate of around 0.5 Hz, or the computation of power spectra over a long time period, or measuring event statistics based on, for example, transitions between up- and down-states [21]. This poses a major resource problem, since the neural dynamics is usually simulated with an integration time step on the order of 0.1 ms or less, producing large amounts of data that an ordinary computer is not able to handle efficiently in its memory (RAM).
To overcome this issue, we designed a chunkwise integration scheme called autochunk which can be enabled by running a model using the command model.run(chunkwise=True). It supports all models that follow the implementation guidelines. In this scheme, all dynamical equations are integrated for a short duration \(T_\text {chunk}\) (e.g., 10 seconds) as defined by the number of time steps of a chunk, chunksize. The chunk duration \(T_\text {chunk}\) largely determines the amount of necessary RAM for a simulation and is typically a lot smaller than the total duration of the simulation \(T_\text {total}\). This means that the entire simulation will be integrated in \(\lceil [ \rceil \big ]{T_\text {total}/T_\text {chunk}}\) chunks.
After the i-th chunk is integrated, only the last state vector of the system, \(\mathbf {x}_i(T_\text {chunk})\), is temporarily kept in memory, which in the case of a delayed system is a \(n \times (d_\text {max} + 1)\) matrix, with n being the number of state variables, and \(d_\text {max}\) being the number of time steps according to the maximum delay of the system. In the next step, all memory is cleared, and \(\mathbf {x}_i(T_\text {chunk})\) is used as an initial state vector \(\mathbf {x}_{i+1}(0)\) for the next chunk. If BOLD simulation is enabled, it will be integrated in parallel to the main integration and kept in memory, while the system’s past state variables, such as the firing rates, will be forgotten. After a long simulation is finished, the output attribute of the model will contain the long BOLD time series (e.g., 5 minutes) with a low sampling rate and the firing rates of the last simulated chunk (e.g., 10 seconds) with a high sampling rate.
Parameter Exploration
One of the main features of neurolib is its ability to perform parameter explorations in a unified way across models. Parameter explorations are useful for determining the behavior of a dynamical system when certain parameters are changed. The exploration module of neurolib relies on pypet [24] which manages the parallelization and the data storage of all simulations. The user can define the range of parameters that should be explored in a grid using the ParameterSpace class and pass it, together with the model, as an argument to the BoxSearch class (Listing 4). All simulated output will be automatically stored in an HDF5 file for later analysis.
Example: State Space Exploration of a Single Node
A useful example for parameter exploration is a state space exploration of a neural mass model in the case of an isolated single node. For example, by measuring the minimum and maximum activity of a model given a parameter configuration, we can draw bifurcation diagrams that depict changes in the model’s dynamical state, i.e., transitions from constant activity to an oscillatory state. Figure 3 shows the bifurcation diagrams of the Hopf model, the Wilson–Cowan model, and the ALN model. Given these diagrams, we can choose the parameters of the system in order to produce a desired dynamical state. The time series in Fig. 3 show how the models behave at different points in the bifurcation diagrams. Listing 4 shows how to set up a parameter exploration of the ALNModel for changing input currents to the E and I subpopulations.

Here, we use the numpy [26] function np.linspace to define the parameters in a linear space between 0 and 3 in 31 steps. The ParameterSpace class then computes the Cartesian product of the parameters to produce a configuration for all parameter combinations. When the exploration is done, the results can be loaded from disk using search.loadResults(), which organizes all simulations and their outputs as a pandas DataFrame [27] available as the attribute dfResults.
The result of this exploration is shown in Fig. 3g as a two-dimensional state space diagram of a single node. A contour around states with a finite amplitude of the excitatory firing rate indicates bifurcations from states with constant firing rates to oscillatory states. Drawing bifurcation diagrams in terms of the external input parameters, as in Fig. 3d and g, is particularly useful because it allows an interpretation of how the dynamics of an individual node in a brain network would change depending on the inputs from other brain areas. When the system is in the down-state, for example, enough excitatory external input from other brain areas would be able to push it over the bifurcation line into the oscillatory state.
It should be noted that, when the exploration of local model parameters is used in the case of a whole-brain model, in the default implementation, all parameters are homogeneous across nodes, meaning that, in the example above, we change the external input currents to all brain regions at once. However, adjusting a model to work with heterogeneous parameters is easy and simply requires the use of vector-valued parameters instead of scalar ones. The numerical integration needs then to be adapted to use the elements of the parameter vector for each node accordingly.
Example: Frequency-Dependent Effects of Brain Stimulation
In this example, we demonstrate how neurolib can be used to simulate the effects of stationary or time-dependent stimulation on brain activity, an ongoing research topic in the field of whole-brain modeling [58, 59]. neurolib offers a convenient way of constructing stimuli using the Stimulus class, which includes a variety of different types of stimuli such as sinusoidal inputs, step inputs, noisy inputs, and others. Stimuli can be concatenated and added to another using the operators & and + to help the user design a wide range of different stimulus time series. In Listing 5, we show how to create a simple sinusoidal stimulus and set the appropriate input parameter, i.e., ext_exc_current for the ALNModel, to couple the stimulus to the model.

We can use the Stimulus class in combination with the exploration module to stimulate the brain network with sinusoidal stimuli of variable frequencies. In the ALNModel, an equivalent electric field stimulus can be incorporated as externally induced mean membrane currents of the neural excitatory population [32]. We chose the zero-to-peak amplitude of the sinusoidal stimulus as 0.025 mV/ms, which is equivalent to an extracellular electric field strength of around 1 V/m [60]. If the stimulus is a one-dimensional vector, by default, it is delivered to all brain areas simultaneously. If it is N-dimensional (N being the number of brain regions), each brain region receives an independent input. The whole-brain model is parameterized to be in the bistable regime in the bifurcation diagram in Fig. 3g and was previously fitted to resting-state fMRI and sleep EEG data to yield the same power spectrum as observed in deep sleep, with a peak in the slow oscillation regime at around 0.25 Hz. The fitting procedure is outlined in the Model optimization section below with the resulting parameters provided in Table 2. Similar to Listing 4, we use the BoxSearch class to run the whole-brain model with different stimulus frequencies ranging from 0 Hz to 2 Hz in 21 linear steps. We run each configuration for 5 minutes and repeat each run 10 times with independent noise realizations to obtain statistically meaningful results.
In Fig. 4a, we show how the stimulus frequency affects the statistics of the whole-brain oscillations. First, we determine for each brain area in every time step, whether it is in a down-state by simply thresholding the firing rate for values below 5 Hz, which is always lower than the up-state activity (see Fig. 3g). We can then measure the number of local and global oscillations for each stimulus frequency. We define a local oscillation as one in which between 25%-75% of all brain areas simultaneously participated in a down-state. Global oscillations are defined as a participation of at least 75% of brain areas in the down-state. We classify each oscillation as either local or global and count their occurrence for each stimulus condition. In Fig. 4a, we can observe a clear peak around 0.5 Hz, where the number of local oscillations is in a minimum and the number of global oscillations is at a maximum. Interestingly, observing the frequency spectrum in Fig. 4b, we see that the peak of the frequency spectrum of the system without stimulation is at around 0.25 Hz. This peak is clearly amplified with a stimulus frequency of 0.5 Hz, which is in line with the approximately 15 oscillations per minute observed in Fig. 4a. Figure 4b shows the firing rate of the system averaged across all brain regions with and without stimulation. With stimulation, oscillations have a larger amplitude and reach an brain-averaged firing rate of nearly 0 Hz more often, indicating many global oscillations into the down-state, i.e, a participation of nearly 100% is reached in multiple oscillation cycles.
Effect of whole-brain stimulation on oscillations. (a) Number of local (red) and global (green) down-state waves across the whole brain as a function of stimulation frequency. Each measurement was repeated 10 times with independent noise realizations. The shaded regions indicate the standard deviation around the mean and the lines indicate the mean values across 10 runs. The dashed horizontal lines indicate the average number of oscillations without stimulation. (b) Node-averaged power spectra obtained with getMeanPowerSpectrum without stimulation (black) and with stimulation (colored). (c) Time series of the averaged firing rate across the brain without stimulation (top panel) and with 0.5 Hz stimulation (bottom panel)
Model Optimization
Model optimization, in general, refers to a search for model parameters that maximize (or minimize) an objective function that depends on the output of a model, leading to a progression towards a predefined target or goal. In the case of whole-brain models, the goal is often to reproduce patterns from (i.e., fit the model to) empirical brain recordings. Optimizations can also be carried out for a single node. An example of this is finding local node parameters that produce an oscillation of a certain frequency, in which case the objective to minimize is the difference between the oscillation frequency of the model’s activity and a predefined target frequency, which could be based on, for example, empirical EEG or MEG recordings.
Whole-brain models are often fitted to empirical resting-state BOLD functional connectivity (FC) data from fMRI measurements [10]. The goodness of fit to the empirical data is determined by computing the element-wise Pearson correlation coefficient between the simulated FC matrix and the empirical FC matrix. If the optimization is successful, the model produces similar spatial BOLD correlations as was measured in the empirical data. The FC Pearson correlation ranges from 0 to 1, where 1 means maximum similarity between simulated and empirical data.
To ensure that a model also produces temporal correlation patterns similar to fMRI recordings, the functional connectivity dynamics (FCD) matrix can also be fitted to empirical data [61]. The FCD matrix measures the similarity of the temporal correlations between time-dependent FC matrices in a sliding window. The similarity between simulated and empirical matrices is usually determined by the Kolmogorov–Smirnoff (KS) distance [62] between the distributions of the entries of both matrices. The KS distance ranges from 0 to 1, where 0 means maximum similarity.
In a whole-brain model, the relevant parameters that affect these correlations are typically the distance to a bifurcation line that separates the steady-state from an oscillatory state (see Figs. 3a, d, and g), the global coupling strength K that determines how strongly all brain regions are coupled with each other, and other parameters, such as the signal transmission speed or the strength of the external noise.
Example: Fitting a Whole-Brain Model to fMRI Data
Before we demonstrate the optimization features of neurolib in the following sections, we want to approach the task of finding optimal model parameters using a parameter exploration approach first. In this example, we present a common scenario in which the simulated BOLD functional connectivity of a whole-brain model is compared to an empirical data set, e.g., resting-state fMRI recordings from the HCP dataset. Using the parameter exploration module, we investigate how the quality of the fit changes as a function of model parameters, and thus can identify optimal operating points for our model.
One of the most important parameters of a whole-brain model is the global coupling strength Ke_gl, which scales the relative coupling strength between brain regions given by the adjacency matrix Cmat. The coupling strength Ke_gl affects the global dynamics and can amplify correlations of the BOLD activity between brain regions. Therefore, this parameter is often used to characterize changes in whole-brain dynamics of brain networks [61, 63].
Note that the default behavior of BoxSearch is to simulate the model and store its outputs to the file system. Alternatively, as shown in Listing 6, the user can pass the argument evalFunction which calls a separate function for every parameter combination instead. This enables the user to perform pre- and postprocessing steps for each run, such as computing the fit to the data set. In this example, we determine of the fit by computing the FC matrix correlation of the simulated output to the empirical fMRI dataset for each subject separately and then average across all subjects. Similarly, we also determine the KS distance for the entire fMRI data set.
The exploration produces similar results as reported in previous studies: We observe a broad peak of high FC correlations depending on the coupling strength Ke_gl [61, 63] that moves with changing noise strength sigma_ou (Fig. 5a). When overlaying the FCD fit with the FC fit in Fig. 5b, we can also see that the region of overall good fits becomes narrower with sharp drops of the KS distance at around Ke_gl \(= 250\) while the FC correlation remains fairly high at values above 0.5, which is also similar to previous reports [64, 65].
Model fit to resting-state fMRI data. (a) Correlation between simulated and empirical functional connectivity (FC, higher is better) as a function of the global coupling strength Ke_gl is shown for three levels of noise strength sigma_ou. The correlation was averaged across all subjects. (b) The FC correlation and the functional connectivity dynamics distance (FCD, lower is better) for all 7 subjects from the HCP dataset are plotted individually. All other parameters are as in Listing 6

Evolutionary Algorithms
neurolib supports model optimization through evolutionary algorithms built using the evolutionary algorithm framework DEAP [25]. Evolutionary algorithms are stochastic optimization methods that are inspired by the mechanisms of biological evolution and natural selection. Multi-objective optimization methods, such as the NSGA-II algorithm [66], are crucial in a setting in which a model is fit to multiple independent targets. These could be features from fMRI recordings, such as FC and FCD matrices, or from other data modalities such as EEG. In a multi-objective setting, not one single solution but a set of solutions can be considered optimal, called the Pareto front, which refers to the set of solutions that cannot be improved in any one of the objectives without diminishing its performance in another one. These solutions are also called non-dominated.
In the evolutionary framework, a single simulation run is called an individual. Its particular set of parameters are called its genes and are represented as a vector with one element for each free parameter that should be optimized. A set of individuals is called a population. For every evolutionary round, also called a generation, the fitness of every new individual is evaluated by simulating the individual and computing the similarity of its output to the empirical data. With the example fitness calculation shown in Listing 6, this would result in a two-dimensional fitness vector with each element of the vector representing the FC and FCD fits, respectively.
Evolutionary optimization (a) Schematic of the evolutionary algorithm. The optimization consists of two phases, the initialization phase (red) in which the parameter space is uniformly sampled, and the main evolutionary loop (blue). \(N_\text {init}\) is the size of the initial population, \(N_\text {pop}\) is the size of the population during the evolution. (b) Improvement of the fitness over all generations of a whole-brain evolutionary optimization with the color indicating the score per individual (top panel) and averaged across the population (bottom panel) with the minimum and maximum range in the shaded area. The fitness score is a weighted sum of all individual fitness values, i.e., higher values are better. (c) Optimization results for the input currents to the E and I subpopulations depicted in the bifurcation diagram of the ALN model. Green dots indicate optimal parameters for fits to fMRI data only (progression shown in a), red dots show fits to fMRI+EEG simultaneously. In the fMRI+EEG case, the adaptation strength b and timescale \(\tau _A\) were allowed to vary. In the fMRI-only case, \(b=0\) was kept constant. (d) Best fit results of the fMRI+EEG case. Simulated (top panel) and empirical (bottom panel) BOLD FC matrices, (e) FCD matrices, and (f) the average power spectrum of the simulated firing rate and empirical EEG data during sleep stage N3. The spectra of the individual subjects is shown in color, the average spectrum is shown in black
A schematic of a general evolutionary algorithm is shown in Fig. 6a. The optimization can be separated into an initialization phase and the main evolutionary loop. In the initialization phase, all individuals are uniformly sampled from the parameter space and are evaluated for their fitness. The optimization then enters the second phase in which the population is reduced to a subset of size \(N_\text {pop}\) from which parents are selected to generate offspring for the next generation. These offspring are mutated, added to the total population, and the procedure is repeated until a stopping condition is reached, such as a maximum number of generations.
As an alternative to the NSGA-II algorithm, which is particularly useful for multi-objective optimization settings, an adaptive evolutionary algorithm [67] is also implemented. In the adaptive algorithm, the mutation step size, which is analogous to a learning rate, is also learned during the evolution by treating it as an additional gene during the optimization. This algorithm has been successfully used to optimize whole-brain models with up to 8 free parameters; however, it is not guaranteed to produce satisfactory results in a multi-objective optimization setting. All steps in the evolutionary algorithm can be modified by implementing custom operators or by using the ones available in DEAP.
Example: Brain Network Model Optimization
In the following, we show how an evolutionary optimization is set up in neurolib using the NSGA-II algorithm. We use the brain network model from Listing 2 and fit the BOLD output of the model to the empirical BOLD data to capture its spatiotemporal properties, as described above. In Listing 7, we specify the parameters to optimize and their respective boundaries, and define a weight vector that determines whether each fitness value is to be maximized (+1) or minimized (-1). In our case, we want to maximize the first measure, which is the FC correlation, and minimize the second, which is the FCD distance. The size of the initial population \(N_\text {init}\), the ongoing population \(N_\text {pop}\) size, and the number of generations \(N_\text {gen}\) largely determine the time for the optimization to complete.

We visualize the increasing score of the population in Fig. 6b, defined as the weighted sum of all objectives, as the evolution progresses. As expected, we find all good fits (with FC correlation > 0.35 and FCD distance < 0.5) close to the bifurcation line between the down-state and the limit cycle, shown in Fig. 6c. Note that while we have optimized 4 parameters simultaneously, only the input current parameters to E and I are shown, which correspond to the axis of the bifurcation diagram in Fig. 3g. In another example, we also included EEG power spectra in our optimization procedure to produce a model with an appropriate spectral density. Here, we used EEG data from sleep recordings during the sleep stage N3 [21], or slow-wave sleep, in which sleep slow oscillations are prevalent. In order to assess the fit to the power spectrum, we computed the mean of the power spectra of the excitatory firing rate of all nodes during the last 60 seconds of the simulation using the function getMeanPowerSpectrum() which uses the implementation of Welch’s method [68] scipy.signal.welch in SciPy [29] with a rolling Hanning window of length 10s. The same method was applied to the channel-wise EEG data to first compute subject-wise average power spectra, and then average all subject-wise spectra to a single empirical power spectrum. To assess the similarity of the simulated and the empirical data, we computed the Pearson correlation between both power spectra in a range between 0 and 20 Hz.
In order for the model to produce slow oscillations that fit the data, we included the spike-frequency adaptation strength parameter b and the adaptation time scale \(\tau _A\) in our optimization, culminating in a total of six free parameters. In a single node, adaptation-induced oscillations can have a frequency between roughly 0.5 and 5 Hz [32]. Figure 6 c shows the location of all good fits in the bifurcation diagram (FC and FCD thresholds as above, EEG power spectrum correlation > 0.7). All fits are close to where the bistable regime is in the case without adaptation, where the activity of an E-I system can slowly oscillate between up- and down-states if the adaptation mechanism is strong enough [32, 43, 69].
Figures 6 d-f show the simulated and empirical FC and FCD matrices, as well as the power spectra of a randomly chosen fit of the fMRI+EEG optimization from Fig. 6c. The parameters of this fit are given in Table 2. The empirical FC and FCD matrices are shown for one subject only. The correlation between simulated and empirical FC matrices was 0.55 averaged across all subjects with the best subject reaching 0.70. The KS distance of the distribution of FCD matrix entries averaged across all subjects was 0.28 with the best subject reaching 0.07. The correlation coefficient between the power spectra of the simulated firing rate EEG was 0.86.
Heterogeneous Brain Modeling with MultiModel
Here, we present a recent addition to neurolib’s core simulation capabilities called MultiModel, which achieves heterogeneous brain modeling in which more than one type of neural mass model, each with their own set of differential equations, can be simulated in a network. The dynamics of individual nodes are coupled by an activity variable, which typically represents the average population firing rate.
Models in MultiModel are implemented and simulated in an hierarchical fashion with three different levels: The first level is a neural mass, representing a single homogeneous neural population which is defined by a set of differential equations. An example of this is the excitatory subpopulation of the ALNModel. The second level is a node, defined as a collection of neural masses. The subpopulations of a node are coupled via a local connectivity matrix. An example of this is a single node of the ALNModel with excitatory and inhibitory subpopulations. Finally, in the third level, a collection of nodes is represented as a network, in which nodes are connected according to a global connectivity matrix. In the case of a brain network, these are the fiber count and fiber length matrices from DTI. The dynamical equations within all levels in the hierarchy can be implemented by the user, and, more importantly, once defined, can be reused and “plugged together” with other models. MultiModel integrates the equations of each neural mass on the lowest level, and handles the synchronization and coupling of all relevant variables according to the predefined local and global coupling schemes on all higher levels.
Example: Thalamocortical Motif Fit to Sleep EEG Power Spectrum
In this example, we use MultiModel to construct a thalamocortical network model that consists of two separate neural mass models, with one ThalamicMassModel representing a thalamic node with excitatory (TCR) and inhibitory (TRN) subpopulations [41], and another ALNModel representing a cortical node with connectivity between nodes as shown in Fig. 7a. An abbreviated implementation of this model is shown in Listing 8.

Our goal is to find model parameters that produce a similar cortical power spectrum as the one observed in EEG during sleep stage N3. In the power spectra shown Fig. 6f, we can see that, while the EEG power spectrum has a peak in the \(\sigma\)-band between 10-14 Hz, the whole-brain model does not. This is due to the fact that the cortical model alone, when parameterized in the bistable regime and adaptation is enabled, is only capable of generating slow oscillations between up- and down-states with a major peak in the power spectrum in the slow oscillation range between 0.2-1.5 Hz. Indeed, the peak in the \(\sigma\) band can only be reproduced by a thalamic model that can generate spindle oscillations in the respective frequency bands [41]. In this example, we use MultiModel to combine both models such that the power spectrum of the cortical node more closely resembles the EEG power spectrum during N3 sleep.
The free parameters of the ThalamicMassModel are the conductances of the K-leak current g_LK and the rectifying current g_h. The parameters of the ALNModel subject to optimization are the mean input currents input_mu to the E and I subpopulations, and the strength and the time scale of the adaptation currents b and tauA. Furthermore, we also optimize the coupling strength between the ALNModel and the ThalamicMassModel in both directions. This makes a total of 8 free parameters.
We use the power spectrum analysis Python package FOOOF [71] to compute the fitness of the model. We first subtract a fitted 1/f baseline from the power spectrum of the simulated firing rate and from the EEG power spectrum. We then compute the Pearson correlation between both remainders of the power spectra to measure the similarity between the two. Subtracting the 1/f baseline ensures that the correlation between the simulated and the empirical power remains sensitive to the secondary peak in the spindle frequency range in addition to the stronger peak in the slow oscillation range. We then also use FOOOF to compute the power of the two main peaks in the simulated power spectrum. This results in a three-dimensional fitness vector containing the correlation with the empirical spectrum, the power of the slow oscillation peak, and the power of the spindle oscillation peak. We set up an optimization that maximizes all of these measures, similar as in Listing 7. We run the evolution for 50 generations with an initial population size of 960 and an ongoing population size of 640. A detailed description of the fitting procedure, the fitness calculation, and the definition of the entire model would exceed the scope of this article and are thus provided in the examples directory of neurolib’s GitHub repository.
The resulting optimized parameters for the input currents to E and I of the ALNModel, as well as the conductances of the ThalamicMassModel can be seen in 7b. The input currents for the ALNModel again cluster in the bistable regime in which slow oscillations are generated in the presence of adaptation (similar to Fig. 6c). The conductances of the ThalamicMassModel also cluster in a range in which the model generates spindle oscillations with a typical waning and waxing dynamics, in agreement with the regime previously reported [41]. The time series of the best fitting model in Fig. 7c shows that indeed the cortical ALNModel shows slow transitions between a down- and an up-state, whereas the ThalamicMassModel produces waxing and waning spindles. The parameters of this model are given in Table 3. The spindle oscillations generated in the thalamic node modulate the cortical firing rate in the sigma band, which is visible as a corresponding peak in the cortical power spectrum in Fig 7d (bottom panel).
Optimization of the power spectrum of a thalamocortical motif. (a) Schematic of the thalamocortical motif with excitatory (red) and inhibitory (blue) populations of the cortical module (top) and the thalamic module (bottom). Arrows indicate connections between neural masses, with black (gray) arrows denoting excitatory (inhibitory) connections. (b) Parameter spaces of the cortical module (left panel) with respect to the mean input currents to the excitatory and inhibitory subpopulations and the thalamic module (right) with respect to the conductances of the K-leak current \(g_{\text {LK}}\) and rectifying current \(g_\text {h}\) of the TCR population. The blue contours indicate regions with slow oscillations (left) and spindle oscillations (right) present. Green dots show all results of the optimization that produced a Pearson correlation above 0.7 between the 1/f-subtracted power spectra of the EEG and the simulated cortical excitatory firing rate. (c) Time series of the firing rates of the excitatory subpopulations of the cortical (left panel) and the thalamic (right) modules of the best fitting model. Parameters are given in Table 3. (d) Power spectrum of the EEG data in sleep stage N3 (top panel) and the firing rates (bottom) of the excitatory subpopulation of the cortical module shown in (c) with peaks in the slow oscillation (0.2-1.5 Hz) and the spindle oscillation (10-14 Hz) regimes. The blue dashed line shows the 1/f fit. The Pearson correlation between the 1/f-subtracted remainders is 0.87
Summary and Discussion
In this paper, we introduced neurolib, a Python library for simulating whole-brain networks using coupled neural mass models. We demonstrated how to simulate a single neural mass model, how neurolib handles empirical data from fMRI and DTI measurements, and how to simulate a whole-brain network. A set of neural mass models that are part of the library were presented, as well as how to implement a custom neural mass model.
We demonstrated how to conduct parameter explorations with neurolib which can be used to characterize the dynamical landscape of a model. Lastly, we presented how the multi-objective evolutionary optimization algorithm in neurolib can be used to fit a whole-brain model to functional empirical data from fMRI and EEG as well as how to construct a hybrid thalamocortical model.
Existing Software
Numerous software frameworks have been developed in the past to facilitate the simulation of neural systems. Many of these projects focus on microscopic neuron models. Examples include NEST [72], Brian [73], NetPyNE [74], and NEURON [75] which are particularly useful for simulating large networks of spiking neurons, with a focus on point neurons in the case of NEST and Brian, or morphologically extended neurons in the case of NetPyNE and NEURON. In many cases, the accuracy of neural mass models can be validated using these software frameworks by simulating large networks of neurons from which neural mass models are often derived [32]. Other existing frameworks are specifically designed for simulating mesoscopic systems, such as NENGO [76], which focuses on applications in cognitive science, or the Brain Modeling Toolkit [77] which focuses on simulating multiscale neural population circuits. The mentioned frameworks can be used to simulate systems with a few populations but are rarely used (and not specifically designed and optimized) for macroscopic whole-brain modeling, partly due to the computational costs and the resulting difficulty for calibrating model parameters.
For macroscopic whole-brain modeling, a well-established alternative to neurolib is The Virtual Brain (TVB) [78, 79] which is an easy-to-use platform for running brain network simulations. TVB can load structural connectivity data, has a long list of implemented models for simulating brain regions, and allows users to set up monitors to record activity. TVB can also simulate BOLD signals and various other forward models, such as simulated electroencephalography (EEG), magnetoencephalography (MEG) and local field potentials (LFP). Many of the features of TVB can be accessed and configured using a graphical user interface (GUI); however, more complex use cases, such as fitting a model to empirical data, or further analyzing model outputs, need to be managed outside of the graphical environment.
In contrast, neurolib does not have a GUI and encourages users with programming experience to modify the code of the framework itself to suit their individual use case, to implement their own models, and to use their own datasets to run large numerical experiments. neurolib also offers parameter exploration and model optimization capabilities. The simple and efficient architecture of neurolib allows for fast prototyping of custom models.
Performance and Parallelization
To accelerate the numerical integration of models and thus enhance the single-core performance of simulations, models that are implemented in Python use the just-in-time compiler numba. Although TVB also uses accelerated numba code, only the calculation of the derivatives of the models are accelerated but not the integration itself. In neurolib, the entire numerical integration, including the loops across all nodes of the brain network, are accelerated, resulting in a simulation speed that is 8-24x faster compared to TVB (see Fig. 8) when comparing single-threaded simulations.
In order to speed up parameter explorations and optimizations on a multi-core architecture, neurolib utilizes the parallelization capabilities of pypet [24] which can run multiple simulations on a single CPU simultaneously. To deploy simulations on distributed systems, such as large computing clusters, pypet can run jobs on multiple machines using the Python module SCOOP [80]. A lightweight alternative to this is is the mopet [81] Python package, which can run parameter explorations on multiple machines simultaneously using the distributed computing framework Ray [82].
Performance comparison. Wall time (real time) plotted against the simulated time in neurolib (orange) and The Virtual Brain (TVB) (blue) for different models. The dashed gray line indicates the identity line at which simulated time is equal to wall time. At each data point, a whole-brain model with 76 brain regions was simulated. Before each measurement, the simulation was run once to avoid additional waiting times due to precompilation of the code. Performance was measured on a MacBook Pro 2019 with a 2.8 GHz Quad-Core Intel Core i7 CPU
Future Development
Current work on neurolib focuses on improving the performance of the MultiModel framework and adding more specialized models for different brain areas with the ultimate goal of heterogeneous whole-brain modeling, such as combining a cortical model with models of thalamic or hippocampal neural populations. This will enable us to model different brain rhythms generated in specialized neural circuits and study their whole-brain interactions.
Another goal of the development efforts is to support more sophisticated forward models like the ones used in TVB. This includes making use of lead-field matrices to simulate an EEG/MEG signal that is more spatially accurate in sensor space, making comparisons to real recordings more faithful than by simply analyzing neural activity in source space.
Conclusion
The primary development philosophy of neurolib is to build a framework that is lightweight and easily extensible. Future work will also include the implementation and support for more neural mass models. Since neurolib is open source software, we welcome contributions from the computational neuroscience community. Lastly, our main focus in developing neurolib is the computational efficiency with which simulations, explorations, and optimizations can be executed. We believe that this not only has the potential to save valuable time, but allows researchers to pursue ideas and conduct numerical experiments that would otherwise be only achievable with access to a large computing infrastructure.
Data Availability
All of our code including examples and documentation can be accessed on our public GitHub repository which can be found at https://github.com/neurolib-dev/neurolib. The documentation including more examples of how to use neurolib can be found at https://neurolib-dev.github.io/.
References
Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex. 1997;7(3):237–52. http://www.ncbi.nlm.nih.gov/pubmed/9143444.
van Vreeswijk C, Sompolinsky H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science (New York, N.Y.). 1996;274:1724–1726.
Haken H. Cooperative phenomena in systems far from thermal equilibrium and in nonphysical systems. Rev Mod Phys. 1975;47(1):67–121.
Renart A, Brunel N, Wang XJ. Mean field theory of irregularly spiking neuronal populations and working memory in recurrent cortical networks. 2004. http://www.cns.nyu.edu/wanglab/publications/pdf/renart2003b.pdf
Cabral J, Luckhoo H, Woolrich M, Joensson M, Mohseni H, Baker A, Kringelbach ML, Deco G. Exploring mechanisms of spontaneous functional connectivity in MEG: How delayed network interactions lead to structured amplitude envelopes of band-pass filtered oscillations. NeuroImage. 2014;90:423–35. https://doi.org/10.1016/j.neuroimage.2013.11.047.
Deco G, Cabral J, Woolrich MW, Stevner AB, van Hartevelt TJ, Kringelbach ML. Single or multiple frequency generators in on-going brain activity: A mechanistic whole-brain model of empirical MEG data. NeuroImage. 2017;152:538–50. https://doi.org/10.1016/j.neuroimage.2017.03.023.
Demirtas M, Burt JB, Helmer M, Ji JL, Adkinson BD, Glasser MF, Van Essen DC, Sotiropoulos SN, Anticevic A, Murray JD. Hierarchical Heterogeneity across Human Cortex Shapes Large-Scale Neural Dynamics. Neuron. 2019;101(6):1181-1194.e13.
Schmidt R, LaFleur KJR, de Reus MA, van den Berg LH, van den Heuvel MP. Kuramoto model simulation of neural hubs and dynamic synchrony in the human cerebral connectome. BMC Neurol. 2015;16(1):54. http://bmcneurosci.biomedcentral.com/articles/10.1186/s12868-015-0193-z.
Hansen EC, Battaglia D, Spiegler A, Deco G, Jirsa VK. Functional connectivity dynamics: Modeling the switching behavior of the resting state. NeuroImage. 2015;105:525–35. http://dx.doi.org/10.1016/j.neuroimage.2014.11.001.
Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P. Predicting human resting-state functional connectivity from structural connectivity. Proceedings of the National Academy of Sciences of the United States of America. 2009;106(6):2035–40. http://www.pnas.org/content/106/6/2035.short.
Jobst BM, Hindriks R, Laufs H, Tagliazucchi E, Hahn G, Ponce-Alvarez A, Stevner ABA, Kringelbach ML, Deco G. Increased stability and breakdown of brain effective connectivity during slow-wave sleep: mechanistic insights from whole-brain computational modelling. Sci Rep. 2017;7(1):4634. http://www.nature.com/articles/s41598-017-04522-x.
Endo H, Hiroe N, Yamashita O. Evaluation of resting spatio-temporal dynamics of a neural mass model using resting fMRI connectivity and EEG microstates. Front Comput Neurosci. 2020;13:1–11.
Cabral J, Hugues E, Sporns O, Deco G. Role of local network oscillations in resting-state functional connectivity. NeuroImage. 2011;57(1):130–9. http://www.ncbi.nlm.nih.gov/pubmed/21511044.
Deco G, Jirsa V, McIntosh AR, Sporns O, Kotter R. Key role of coupling, delay, and noise in resting brain fluctuations. Proc Natl Acad Sci. 2009;106(25):10302–7. https://www.pnas.org/content/106/25/10302.short
Kringelbach ML, Cruzat J, Cabral J, Knudsen GM, Carhart-Harris R, Whybrow PC, Logothetis NK, Deco G. Dynamic coupling of whole-brain neuronal and neurotransmitter systems. Proc Natl Acad Sci U S A. 2020;117(17):9566–76.
Chouzouris T, Roth N, Cakan C, Obermayer K. Applications of nonlinear control to a whole-brain network of FitzHugh-Nagumo oscillators. arXiv preprint. 2021. http://arxiv.org/abs/2102.08524.2102.08524.
Gollo LL, Roberts JA, Cocchi L. Mapping how local perturbations influence systems-level brain dynamics. NeuroImage. 2017;160:97–112. http://dx.doi.org/10.1016/j.neuroimage.2017.01.057.1609.00491.
Griffiths JD, McIntosh AR, Lefebvre J. A Connectome-Based, Corticothalamic Model of State- and Stimulation-Dependent Modulation of Rhythmic Neural Activity and Connectivity. Front Comput Neurosci. 2020;14:113. https://www.frontiersin.org/articles/10.3389/fncom.2020.575143/full.
Muldoon SF, Pasqualetti F, Gu S, Cieslak M, Grafton ST, Vettel JM, Bassett DS. Stimulation-Based Control of Dynamic Brain Networks. PLoS Comput Biol. 2016;12:9.
Roberts JA, Gollo LL, Abeysuriya RG, Roberts G, Mitchell PB, Woolrich MW, Breakspear M. Metastable brain waves. Nat Commun. 2019;10(1):1–17. https://doi.org/10.1038/s41467-019-08999-0.
Cakan C, Dimulescu C, Khakimova L, Obst D, Flöel A, Obermayer K. A deep sleep model of the human brain: How slow waves emerge due to adaptation and are guided by the connectome. arXiv. 2020. http://arxiv.org/abs/2011.14731.2011.14731.
Breakspear M. Dynamic models of large-scale brain activity. Nat Neurosci. 2017;20(3):340–52. http://www.nature.com/doifinder/10.1038/nn.4497.
Sporns O, Tononi G, Kötter R. The human connectome: A structural description of the human brain. PLoS Comput Biol. 2005;1(4):0245–51.
Meyer R, Obermayer K. Pypet: A python toolkit for data management of parameter explorations. Frontiers in Neuroinformatics. 2016;10:1–15.
Fortin FA, De Rainville FM, Gardner MA, Parizeau M, Gagńe C. DEAP: Evolutionary algorithms made easy. J Mach Learn Res. 2012;13:2171–5.
Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ. Array programming with NumPy. Nature. 2020;585(7825):357–62.
McKinney W. Pandas: a foundational Python library for data analysis and statistics. Python for High Performance and Scientific Computing. 2011;14(9):1–9.
Hoyer S, Hamman J. xarray: ND labeled arrays and datasets in Python. J Open Res Softw. 2017;5:1.
Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods. 2020;17(3):261–272.
Lam SK, Pitrou A, Seibert S. Numba: A LLVM-based python JIT compiler. Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC - LLVM ’15. 2015;1–6. http://dl.acm.org/citation.cfm?doid=2833157.2833162.
Augustin M, Ladenbauer J, Baumann F, Obermayer K. Low-dimensional spike rate models derived from networks of adaptive integrate-and-fire neurons: comparison and implementation. PLoS Comput Biol. 2017;13.
Cakan C, Obermayer K. Biophysically grounded mean-field models of neural populations under electrical stimulation. PLoS Comput Biol. 2020;16(4). http://dx.doi.org/10.1371/journal.pcbi.1007822.1906.00676.
Landau LD. On the problem of turbulence. In Dokl Akad Nauk USSR. 1944;44:311.
Stuart JT. On the non-linear mechanics of wave disturbances in stable and unstable parallel flows Part 1. The basic behaviour in plane Poiseuille flow. J Fluid Mech. 1960;9(3):353–370.
Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12(1):1–24. http://www.cell.com/article/S0006349572860685/fulltext.
Brette R, Gerstner W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J Neurophysiol. 2005;94(5):3637–42. http://www.ncbi.nlm.nih.gov/pubmed/16014787.
Wong KF. A Recurrent Network Mechanism of Time Integration in Perceptual Decisions. J Neurosci. 2006;26(4):1314–28. http://www.jneurosci.org/cgi/doi/10.1523/JNEUROSCI.3733-05.2006.
FitzHugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophys J. 1961;1(6):445–66.
Nagumo J, Arimoto S, Yoshizawa S. An active pulse transmission line simulating nerve axon*. Proc IRE. 1962;50(10):2061–70.
Kuramoto Y. Chemical oscillations, waves and turbulence. arXiv:1011.1669v3. https://www.springer.com/gp/book/9783642696916
Schellenberger Costa M, Weigenand A, Ngo HVV, Marshall L, Born J, Martinetz T, Claussen JC. A Thalamocortical Neural Mass Model of the EEG during NREM Sleep and Its Response to Auditory Stimulation. PLoS Comput Biol. 2016;12(9):1–20.
Uhlenbeck GE, Ornstein LS. On the theory of the Brownian motion. Phys Rev. 1930;36(5):823.
Tartaglia EM, Brunel N. Bistability and up/down state alternations in inhibition-dominated randomly connected networks of LIF neurons. Sci Rep. 2017;7(1):1–14. http://dx.doi.org/10.1038/s41598-017-12033-y.
Kloeden PE, Pearson RA. The numerical solution of stochastic differential equations. The Journal of the Australian Mathematical Society. Series B. Applied Mathematics. 1977;20(1): 8–12.
Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Wu-Minn HCP Consortium. The WU-Minn human connectome project: an overview. Neuroimage. 2013;80:62–79.
Rolls ET, Joliot M, Tzourio-Mazoyer N. Implementation of a new parcellation of the orbitofrontal cortex in the automated anatomical labeling atlas. NeuroImage. 2015;122:1–5.
Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. Fsl. Neuroimage. 2012;62(2):782–90.
Yeh FC, Verstynen TD, Wang Y, Fernández-Miranda JC, Tseng WYI. Deterministic diffusion fiber tracking improved by quantitative anisotropy. PloS One. 2013;8(11).
Behrens TEJ, Berg HJ, Jbabdi S, Rushworth MFS, Woolrich MW. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? NeuroImage. 2007;34(1):144–55.
Preti MG, Bolton TAW, Van De Ville D. The dynamic functional connectome: State-of-the-art and perspectives. NeuroImage. 2017.
Woolrich MW, Ripley BD, Brady M, Smith SM. Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage. 2001;14(6):1370–86.
Griffanti L, Salimi-Khorshidi G, Beckmann CF, Auerbach EJ, Douaud G, Sexton CE, Zsoldos E, Ebmeier KP, Filippini N, Mackay CE, Moeller S, Xu J, Yacoub E, Baselli G, Ugurbil K, Miller KL, Smith SM. ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. NeuroImage. 2014;95:232–47.
Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM. Automatic denoising of functional MRI data: Combining independent component analysis and hierarchical fusion of classifiers. NeuroImage. 2014;90:449–68.
Deco G, Ponce-Alvarez A, Mantini D, Romani GL, Hagmann P, Corbetta M. Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. The Journal of neuroscience: The Official Journal of the Society for Neuroscience. 2013;33:27.
Friston K, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19(4):1273–302. http://www.sciencedirect.com/science/article/pii/S1053811903002027.
Friston KJ, Mechelli A, Turner R, Price CJ. Nonlinear responses in fMRI: The balloon model, Volterra kernels, and other hemodynamics. NeuroImage. 2000;12(4):466–77.
Gu S, Pasqualetti F, Cieslak M, Telesford QK, Yu AB, Kahn AE, Medaglia JD, Vettel JM, Miller MB, Grafton ST, Bassett DS. Controllability of structural brain networks. Nat Commun. 2015;6:8414. http://www.nature.com/doifinder/10.1038/ncomms9414.
Kunze T, Hunold A, Haueisen J, Jirsa V, Spiegler A. Transcranial direct current stimulation changes resting state functional connectivity: A large-scale brain network modeling study. NeuroImage. 2016.
Ponce-Alvarez A, He BJ, Hagmann P, Deco G. Task-driven activity Reduces the cortical activity space of the brain: experiment and whole-brain modeling. PLoS Comput Biol. 2015;11(8):e1004445. http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1004445.
Aspart F, Ladenbauer J, Obermayer K. Extending integrate-and-fire model neurons to account for the effects of weak electric fields and Input Filtering Mediated by the Dendrite. PLoS Comput Biol. 2016;12(11):1–29.
Hansen ECA, Battaglia D, Spiegler A, Deco G, Jirsa VK. Functional connectivity dynamics: Modeling the switching behavior of the resting state. Neuroimage. 2015;105:525–35.
Hodges JL. The significance probability of the Smirnov two-sample test. Arkiv för Matematik. 1958;3(5):469–86.
Deco G, Jirsa VK. Ongoing cortical activity at rest: Criticality, multistability, and ghost attractors. J Neurosci. 2012;32(10):3366–75.
Deco G, Kringelbach ML. Metastability and Coherence: Extending the Communication through Coherence Hypothesis Using A Whole-Brain Computational Perspective. Trends Neurosci. 2016;39(3):125–35. http://www.sciencedirect.com/science/article/pii/S0166223616000023.
Triebkorn P, Zimmermann J, Stefanovski L, Roy D, Solodkin A, Jirsa V, Breakspear M, Mcintosh AR, Ritter P. Identifying optimal working points of individual virtual brains: a large-scale brain network modelling study short title : optimal working points of individual virtual brain. BioRxiv. 2020.
Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–97.
Eiben AE, Smith JE. Introduction to evolutionary computing, vol. 53. Springer. 2003.
Welch P. The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoust. 1967;15(2):70–3.
Nghiem TAE, Tort-Colet N, Górski T, Ferrari U, Moghimyfiroozabad S, Goldman JS, Teleńczuk B, Capone C, Bal T, di Volo M, Destexhe A. Cholinergic switch between two types of slow waves in cerebral cortex. Cereb Cortex. 2020;1–16.
Brunel N. What Determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J Neurophysiol. 2003;90(1):415–430. http://jn.physiology.org/cgi/doi/10.1152/jn.01095.2002. arXiv:1011.1669v3.
Donoghue T, Haller M, Peterson EJ, Varma P, Sebastian P, Gao R, Noto T, Lara AH, Wallis JD, Knight RT. Parameterizing neural power spectra into periodic and aperiodic components. Nat Neurosci. 2020;23(12):1655–65.
Gewaltig M-O, Diesmann M. NEST (NEural Simulation Tool). Scholarpedia. 2007;2(4):1430.
Stimberg M, Goodman DFM, Benichoux V, Brette R. Equation-oriented specification of neural models for simulations. Front Neuroinform. 2014;8:6.
Dura-Bernal S, Suter BA, Gleeson P, Cantarelli M, Quintana A, Rodriguez F, Kedziora DJ, Chadderdon GL, Kerr CC, Neymotin SA. NetPyNE, a tool for data-driven multiscale modeling of brain circuits. Elife. 2019;8:e44494.
Carnevale, NT, Hines ML. The NEURON book. Cambridge University Press. 2006.
Bekolay T, Bergstra J, Hunsberger E, DeWolf T, Stewart TC, Rasmussen D, Choo X, Voelker A, Eliasmith C. Nengo: a Python tool for building large-scale functional brain models. Front Neuroinform. 2014;7:48.
Dai K, Gratiy SL, Billeh YN, Xu R, Cai B, Cain N, Rimehaug AE, Stasik AJ, Einevoll GT, Mihalas S. Brain Modeling ToolKit: An open source software suite for multiscale modeling of brain circuits. PLoS Comput Biol. 2020;16(11).
Ritter P, Schirner M, Mcintosh AR, Jirsa VK. The Virtual Brain Integrates Computational Modeling and Multimodal Neuroimaging. Brain Connect. 2013;3(2):121–45.
Sanzleon P, Knock SA, Woodman MM, Domide L, Mersmann J, Mcintosh AR, Jirsa V. The virtual brain: A simulator of primate brain network dynamics. Front Neuroinform. 2013;7.
Hold-Geoffroy Y, Gagnon O, Parizeau M. Once you SCOOP, no need to fork. In Proceedings of the 2014 Annual Conference on Extreme Science and Engineering Discovery Environment. 2014;1–8.
Cakan C, Rebscher L. Mopet: The mildly ominous parameter exploration toolkit. 2021. https://zenodo.org/record/4541667.
Moritz P, Nishihara R, Wang S, Tumanov A, Liaw R, Liang E, Elibol M, Yang Z, Paul, W, Jordan MI. Ray: A distributed framework for emerging AI applications. In 13th Symposium on Operating Systems Design and Implementation (OSDI 18). 2018;561–577.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project number 327654276 - SFB 1315 and by the Operational Programme Research, Development and Education, Ministry of Education, Youth and Sport of the Czech Republic (co-funded by the EU) - project no. CZ.02.2.69/0.0/0.0/19_074/0016209
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
Caglar Cakan, Nikola Jajcay, and Klaus Obermayer declare that they have no conflict of interest.
Ethical Approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cakan, C., Jajcay, N. & Obermayer, K. neurolib: A Simulation Framework for Whole-Brain Neural Mass Modeling. Cogn Comput 15, 1132–1152 (2023). https://doi.org/10.1007/s12559-021-09931-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12559-021-09931-9