Accuracy of small area mortality prediction methods: evidence from Poland

Abstract

We investigate the forecasting accuracy of several simple methods for predicting mortality in small regional areas in Poland. We focus on methods that scale country-level forecasts appropriately and, therefore, can be used by official statistical agencies to improve population projections. We examine data from 379 sub-NUTS-3 districts in Poland for the period 2006–2019, divided into three subperiods. The first period is treated as the training sample and the latter two the testing subperiods. The mortality surface method delivers the most accurate forecasts of the mortality profiles whereas using the district-level standardized mortality rates (SMR) calculated for several broad age groups to scale the country-level mortality forecasts gives the best life expectancy at birth predictions. The latter approach is far better than using the NUTS-2-based standardized mortality rate (SMR), as practiced by the Polish statistical agency. For single age-groups predictions, the SMR-based methods deliver relatively accurate forecasts for young cohorts, but their forecasting accuracy deteriorates significantly with age.

Introduction

Aging societies and the importance of accurate mortality forecasts in the effective design of national pensions and healthcare systems seem to drive the interest in mortality forecasting. As a result, many methods of forecasting mortality rates for different populations or for several, suitably large, sub-populations have been developed in the recent decades.

The mortality forecasting methods for large, single populations are dominated by the seminal Lee-Carter model (Lee and Carter, 1992) and its numerous extensions, summarized by Booth and Tickle (2008), Janssen (2018) or Basellini et al. (2023). Coherent, that is ensuring non-divergence of mortality trajectories for several subpopulations, multi-population forecasting is the natural extension of this baseline model and to that end, Li and Lee (2005), Cairns et al. (2011), and Hyndman et al. (2013) have developed popular algorithms.

From a national policy perspective, mortality forecasting for relatively small, regional areas, inhabited by several dozen or tens of thousands of people, is seen as less important. Thus, significantly less attention has been paid to developing and testing appropriate methods for this. Nonetheless, such research is critical for regional demographic projections based on cohort component methods. These projections, most often prepared by national statistical agencies, are crucial for the development and evaluation of regional policies, such as healthcare and urban planning. Although migration is the key component shaping the future state and structure of populations at the local level, the aging process is increasing the importance of accurate mortality forecasts in regional demographic projections. The catalyst for improvement in such projections is the growing availability of relevant demographic databases at the local administrative level.

The methods for small-area mortality forecasting usually differ from those developed for a few large subpopulations that are calculated in data-rich environments. Regional demographic datasets are often characterized by short time-series and noisy mortality age profiles caused by the small number of deaths, particularly among younger age groups (Wilson, 2018). Moreover, generally, regional mortality forecasts are calculated as part of larger population projections prepared by statistical agencies. Because of resource constraints, these institutions may not be able to apply sophisticated approaches, which can be computationally intensive with extensive data manipulations and adjustments, especially in other stages of the projection, such as forecasting migration, which also requires a lot of work.

The usual approaches for the aforementioned requirements are primarily relational, as classified by Wilson (2018), linking regional mortality forecasts with national forecasts through simple relationships. These are simple national mortality age schedules scaled by a plain rate ratio (RR) or a standardized mortality rate (SMR) between a region and the entire country or regional death rates declining by the same proportion as forecasted national death rates (Smith et al., 2013). A refined version of the rate ratio (RR) approach is the TOPALS (Tool for Projecting Age-specific rates using Linear Splines) method which involves smoothing rate ratio age profiles using linear splines (de Beer, 2012). Gonzaga and Schmertmann (2016) developed a TOPALS-based method to estimate small area age-specific mortality rates for small areas with incomplete death registrations in Brazil. Dyrting (2020) extended this method using a penalized-splines approach, where the smoothness of the fit is controlled with a single parameter.

A separate and more complex approach is the relational model proposed by Brass (1971) and its extensions (Ewbank et al., 1983; Murray et al., 2003). These are regression models, where the explanatory variable is the logit of the surviving population count taken from regional life tables, while the explanatory variable is its national-level counterpart. The estimated relation is subsequently used to forecast regional mortality assuming that the relationship remains constant.

An alternative method of forecasting are relational models using the so-called mortality surface. Regional mortality is projected in terms of life expectancy at birth, and then death rates which correspond to the assumed life expectancy are selected from the mortality surface (Wilson, 2014, 2015, 2018).

An important topic in mortality forecasting with relational methods in small scale population areas is the issue of input data quality as usually death data time series are very short, there are data gaps, especially in cohorts for first years of life, the data lacks consistency and can be very noisy. Simpson and Snowling (2011) evaluated three methods for preparing input data for small area cohort-component forecasts where input data were not available. The difficulties in generating life table statistics for small areas that would be robust to the common data quality problems are shown by Scherbov and Ediev (2011). Anson (2018) proposed several suggestions on how to deal with this problem. Congdon (2009) produced county-level life expectancy estimates based on a structured random effects model with a regression extension.

In addition to the relational models described above, the literature also provides many other methods for forecasting demographic processes for small areas. An in-depth review of methods for Small Area population forecasts is presented by Wilson et al. (2022). The large part of the recent literature has focused on developing Bayesian methods for estimation and forecasting of mortality for small areas multi-populations. This idea first appeared in the work of Congdon (2009) and was subsequently extended for Bayesian multilevel models (Alexander et al., 2017; Jonker et al., 2012; Wakefield et al., 2019).

The toolbox of small area population forecasting methods and techniques is still modest relative to that for national and large subnational regional forecasting (Wilson et al., 2022). However, this field of research has been experiencing significant development recently.

The simplest approaches are widely used in various statistical offices. For example, mortality rate scaling is employed for regional projections by Eurostat (European Commission, 2021) and in the UK (Office for National Statistics, 2021). Scotland (National Records of Scotland, 2016) and Poland apply SMR scaling (Statistics Poland, 2014), although in Poland, the SMRs are calculated at the nomenclature of territorial units for statistics NUTS-2 level, whereas mortality forecasts are calculated for the sub-NUTS-3 areas. One of the two approaches is used in France as well (Insee, 2017). Italy seems to be the exception here, as its statistical office employs a more involved approach in which separate Lee Carter models are built for each region (Istat, 2018).

The aim of this study is to investigate the forecasting performance of several relational models for predicting small regional areas mortality in Poland. We look for models that generate more accurate forecasts than those currently in use, and at the same time are simple enough to be widely applied by statistical offices.

We use data from 379 Polish districts, which can be classified as sub-NUTS-3 regions with typical populations ranging from 55,000 to 110,000 inhabitants. Our dataset covers the period 2006–2019, divided into three subperiods. The first is the training period used for calculating projections for the next five and nine years, and the latter two are the testing subsamples utilized to assess forecast accuracy. Our forecasting experiment covers only relatively simple prediction methods, which can be applied by official statistical agencies. The above criterion for selecting research models means that we consider a narrow group of models. We limit ourselves only to numerically simple relational models whose implementation costs are acceptable in practice from the point of view of statistical offices. Therefore, this article does not include, for example, studies using multi-population Bayesian modeling and multipopulation modifications of the Lee-Carter model.

Most methods analyzed here rely on scaling country-level forecasts either by the SMR or by simple mortality RRs. Among the methods considered in this study, we also examine an extension to a simple scaling approach aimed at dealing with the data scarcity problem. Our method uses data from neighborhood districts to complement datasets with a low number of observations. To the best of our knowledge, this is a novel modification that has not yet been tried. We also consider slightly more sophisticated approaches, including the mortality surface method and the Brass relational model. Therefore, our study can be seen as a test of the relative performance of the methods used by official agencies in Poland against other available alternatives.

Our approach is similar to the forecasting experiment conducted by Wilson (2018), who examined the performance of similar forecasting methods using 88 administrative regions in Australia. However, our study differs in the following important aspects. First, the population of Polish districts is about one order of magnitude smaller than the populations of the regions considered by Wilson (2018), which range between 100 and 500 thousand inhabitants. Thus, the problem of data scarcity in these Polish districts is considerably more pronounced. Moreover, Australia is a developed country, whereas Poland is a developing country, which translates into considerable differences in mortality profiles. For example, life expectancy at birth in Poland in the recent decade is about five years less than that in Australia. Other differences include a neighborhood-complementing modification and a more detailed investigation of forecast accuracy for life expectancy. Thus, the conclusions of both studies may not coincide.

The results of our study show that with regard to mortality profiles and life expectancy at birth, the most accurate predictions are generated by the mortality surface, the rate ratios methods and the SMR scaling for broad age groups. In addition, the simple SMR scaling at the district level outperforms the equally simple SMR scaling at the NUTS-2 regional level, currently used by Statistics Poland—which suggests room for improvement in official forecasting accuracy in Poland. The solid performance of the mortality surface and the RR-based methods primarily results from their accurate mortality forecasts of the oldest cohorts. Finally, the neighborhood-complemented versions of the SMR- and RR-based methods perform slightly better than their baseline counterparts, but the differences are rather small. This suggests that data scarcity does not pose a very serious problem in our study.

The remainder of this paper is organized as follows. The next section describes our dataset, forecasting methods, and forecast accuracy measures. In Sect. 3, we present and discuss our results. Section 4 discusses the results and concludes the study.

Data and methods

Data

We collect data on 379 districts in Poland. In the NUTS hierarchy, these are classified between the NUTS-3 subregions and municipalities that are the lowest local administrative levels. Of the areas, 65 are municipal districts formed by the biggest cities, while the remaining 314 cover smaller towns and the surrounding counties.

Our main dataset covers the period 2006–2019. The initial year is determined by the availability of detailed data on deaths among the older age groups in the districts. We choose to exclude the COVID pandemic period; therefore, the dataset ends at 2019. We excluded the pandemic year 2020 because we didn’t want to mix “normal” and pandemic years. Having one pandemic year in the testing period is likely to deteriorate forecast accuracy for the older cohort, but would be insufficient to assess reliably forecasting performance during the pandemic that lasted about three years. Undoubtedly, it is interesting to extend the study to the pandemic period but we leave it for our further investigation.

For many districts, annual data on the number of age-specific deaths contain too few cases to aggregate data into typical five-year intervals. As a result, we consider three subperiods: 2006–2010, 2011–2015, and 2016–2019. We use the first subperiod to calculate the forecasts, while we use the latter two for our testing subperiods. Data on population and deaths for the districts are from Statistics Poland. To calculate the forecasts, we also use Polish and German data on population and deaths from the Human Mortality Database.

The population distribution for each district is presented in Table 1.The number of inhabitants ranges from 211 to 1707 thousand, with the median population equal to 76.2 thousand. Although the upper bound is rather high, there is only one district with a population exceeding 1 million and five over 500 thousand inhabitants. It should be noted that because we consider mortality rates separately for each sex, the total size of the population at risk in the districts is about half of the values reported in the table.

Table 1 The quantiles of population distribution in the districts in the first subperiod.

The estimated life expectancies at birth for the districts are shown in Fig. 1. These are characterized by substantial heterogeneity. For men, life expectancy varies from 67.2 to 74.9 years with a standard deviation of 1.4 years. Life expectancy is somewhat longer for women, ranging from 76.9 to 82.7 years with a standard deviation of 0.9 years. Of note, the smallest municipal districts are characterized usually by longer life expectancy than their surrounding districts.

Fig. 1

Source: Author’s calculation. Data source: Statistics Poland

Life expectancy at birth for men (left) and women (right) in the first subperiod for the districts.

Forecasting methods

We forecast age-sex-specific central rates of mortality for the standard abridged age groups: 0, 1–4, 5–9, 10–14, …, 75–79, 80–84, and 85 + . These age intervals are the same for both men and women. The central mortality rate is defined as the ratio of the average number of deaths to the average population at risk in the subperiod. Given district i and sex s, it is calculated as follows:

$${}_{n(x)}{m}_{x}(i,s,t)=\frac{{\overline{D} }_{x,x+n\left(x\right)}(i,s,t)}{{\overline{P} }_{x,x+n\left(x\right)}(i,s,t)},$$

(1)

where ${\overline{D} }_{x,x+n\left(x\right)}(i,s,t)$ and ${\overline{P} }_{x,x+n\left(x\right)}(i,s,t)$ represent, respectively, the average number of deaths and the average population at age x to $x+n\left(x\right),$ for given subperiod $t\in \left\{0, 1, 2\right\};$ and $n(x)$ is the age interval width.

Most methods we examine rely on country-level mortality forecasts. To calculate them, generally, we follow the approach taken by Statistics Poland and employ a variant of the mortality surface method, with the West German population serving as the benchmark.¹ In particular, independently for each sex, we look for the year when life expectancy at birth in Germany is the closest to its Polish counterpart in 2008, the center of the first subperiod. Then, we take the percentage change in the sex-specific mortality rates in Germany after five and nine years (since our last subperiod lasts just four years) and assume that the same changes occur in 2013 and 2017 in Poland. These country-wide mortality forecasts are denoted as ${m}_{x}^{f}\left(POL,s,t\right)$.

We consider 10 simple methods for mortality forecasting for the districts. With just two exceptions, all of these are also considered by Wilson (2018).

• 1. Country-level mortality (POL). In this simple approach, the forecasts for the districts are equal to the corresponding forecasts for all of Poland:

  $${}_{n(x)}{m}_{x}^{f}(i,s,t)\equiv {m}_{x}^{f}\left(i,s,t\right)={m}_{x}^{f}\left(POL,s,t\right),$$

  (2)

  where the index $f$ denotes a forecast.

• 2. Standardized mortality rates at the regional level (SMR-REG). This is the method currently used by Statistics Poland. The forecasts for the districts equal the corresponding forecasts for the NUTS 2 regions in which the districts are located. The regional forecasts equal the national mortality scaled by the standardized mortality rates calculated for a region in the first subperiod:

  $${m}_{x}^{f}\left(i,s,t\right)=SMR\left(REG\left(i\right),s\right)\cdot {m}_{x}^{f}\left(POL,s,t\right),$$

  (3)

  where the standardized mortality rate for a particular area r is calculated as follows.

  $$SMR\left(r,s\right)=\frac{\sum_{x}{m}_{x}\left(r,s,0\right)\cdot {\overline{P} }_{x,x+n\left(x\right)}(r,s,0)}{\sum_{x}{m}_{x}\left(POL,s,0\right)\cdot {\overline{P} }_{x,x+n\left(x\right)}(r,s,0)}$$

  (4)

  In other words, SMR for an area is the ratio of the total death in this area to the theoretical number of deaths if mortality in the area were equal to the country-level mortality.

• 3. Standardized mortality rates at the district level (SMR).

  This approach is similar to the previous one, but the standardized mortality rates are calculated at the district level:

  $${m}_{x}^{f}\left(i,s,t\right)=SMR\left(i,s\right)\cdot {m}_{x}^{f}\left(POL,s,t\right)$$

  (5)

• 4. Standardized mortality rates with broad age groups at the district level (SMR-BAG). The standardized mortality rates for a district are calculated separately for three broad age groups: 0-64, 65-74, and 75+:

  $${m}_{x}^{f}\left(i,s,t\right)=SM{R}_{a\left(x\right)}\left(i,s\right)\cdot {m}_{x}^{f}\left(POL,s,t\right),$$

  (6)

  where $a(x)$ denotes the broad age group for people of age x.

• 5. Neighborhood-complemented standardized mortality rates at the district level (SMR-NC).

  This is a novel approach designed to be an intermediate approach between using SMR calculated for wide NUTS-2 regions and SMR for particular districts. The latter can suffer from deaths scarcity problem whereas the former disregards idiosyncratic characteristics of individual districts. We suggest using data from neighborhood districts to calculate SMR for districts with small populations and low expected number of deaths to solve the data scarcity problems and keeping the district-specific characteristics. In particular, let ${P}^{*}$ denote the threshold population level under which it is necessary to complement the data with information from neighboring regions. The mortality rates are calculated using the standard formulas (4) and (1):

  $$SM{R}_{NC\left(i,s\right)}=\frac{\sum_{x}{m}_{x}^{nc}\left(i,s,0\right)\cdot {\overline{P} }_{x,x+n\left(x\right)}^{nc}\left(i,s,0\right)}{\sum_{x}{m}_{x}\left(POL,s,0\right)\cdot {\overline{P} }_{x,x+n\left(x\right)}^{nc}\left(i,s,0\right)},$$

  (4')
  $${m}_{x}^{nc}\left(i,s,0\right)=\frac{{\overline{D} }_{x,x+n\left(x\right)}^{nc}\left(i,s,0\right)}{{\overline{P} }_{x,x+n\left(x\right)}^{nc}\left(i,s,0\right)},$$

  (1')

  but their components ${\overline{D} }_{x,x+n\left(x\right)}^{nc}$ and ${\overline{P} }_{x,x+n\left(x\right)}^{nc}$ are complemented with data from neighborhood districts:

  $${\overline{D} }_{x,x+n\left(x\right)}^{nc}\left(i,s,0\right)={\overline{D} }_{x,x+n\left(x\right)}\left(i,s,0\right)+\theta \left(i,s\right){\sum }_{r\in nc(i)}{\overline{D} }_{x,x+n\left(x\right)}\left(r,s,0\right);$$

  (7)
  $${\overline{P} }_{x,x+n\left(x\right)}^{nc}\left(i,s,0\right)={\overline{P} }_{x,x+n\left(x\right)}\left(i,s,0\right)+\theta (i,s){\sum }_{r\in nc(i)}{\overline{P} }_{x,x+n\left(x\right)}\left(r,s,0\right)$$

  (8)

  where the weight $0<\theta \left(i,s\right)<1$ is defined as follows:

  $$\theta (i,s)=\left\{\begin{array}{ll}0& \mathrm{if }{\sum }_{x}{\overline{P} }_{x,x+n\left(x\right)}\left(i,s,0\right)\ge {P}^{*}\\ \frac{\left({P}^{*}-{\sum }_{x}{\overline{P} }_{x,x+n\left(x\right)}\left(i,s,0\right)\right)}{{P}^{*}}& {\text{otherwise}}.\end{array}\right.$$

  (9)

  The weight $\theta$ governs the impact of data from the neighborhood districts. It grows as the population of a district i is lower as compared with the threshold ${P}^{*}$. We performed several preliminary experiments with the different definitions of neighborhood districts (by a geographical distance or common borders) and the threshold populations. In this study, we show the results that delivered the most accurate life expectancy at birth predictions: the neighborhood regions are those that share a common border and the threshold population is set at 27,500, implying that approximately 25% of the districts requires complementation.

• 6. Rate ratio scaling (RR).

  In this method, sex-age-specific death rate ratios are calculated for each region and country-level forecasts are scaled by the ratios:

  $${m}_{x}^{f}\left(i,s,t\right)=R{R}_{x}\left(i,s\right)\cdot {m}_{x}^{f}\left(POL,s,t\right),$$

  (10)

  where,

  $$R{R}_{x}\left(i,s\right)=\frac{{m}_{x}\left(i,s,0\right)}{{m}_{x}\left(POL,s,0\right)}$$

  (11)

• 7. Rate ratio scaling for broad age groups (RR-BAG).

  This approach is similar to the previous one, but the rate ratios are calculated separately for the BAGs:

  $${m}_{x}^{f}\left(i,s,t\right)=R{R}_{a(x)}\left(i,s\right)\cdot {m}_{x}^{f}\left(POL,s,t\right)$$

  (12)

• 8. Neighborhood-complemented rate ratio scaling (RR-NC).

  Prior to calculating the rate ratios, data for regions with small populations are complemented with data from neighborhood districts, exactly in the same way as for the SMR-NC method:

  $${m}_{x}^{f}\left(i,s,t\right)=R{R\_NC}_{x}\left(i,s\right)\cdot {m}_{x}^{f}\left(POL,s,0\right)$$

  (13)

  where the neighborhood-complemented rate ratios $R{R\_NC}_{x}\left(i,s\right)$ are calculated as follows:

  $$R{R\_NC}_{x}\left(i,s\right)=\frac{{m}_{x}^{nc}\left(i,s,0\right)}{{m}_{x}\left(POL,s,0\right)}$$

  (14)

  and ${m}_{x}^{nc}\left(i,s,0\right)$ is defined by (1’). It should be stressed that the problem of data scarcity is considerably more severe in the case of rate ratios than for the standardized mortality rates, because the former are calculated separately for each age intervals, whereas the latter average over all the intervals. As a result, neighborhood complementation is likely to affect the results of the RR-based predictions more than for the SMR method.

• 9. Mortality surface (MS).

  In this approach, the district forecasts are calculated in the same way as the country-level forecasts for Poland. In particular, we look for the year in which the life expectancy in West Germany is the closest to the one observed in a district in the first subperiod and analyze the changes in mortality profiles that took place in Germany after five and nine years. We assume that the same changes will occur in the analyzed district.

• 10. Brass relational model (BR).

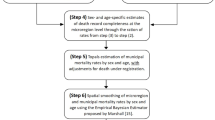
  We estimate the linear regression models between the logit-transformed surviving populations for districts in the first subperiod and their counterparts for the whole country. Subsequently, the models are used to predict the surviving populations for districts in the next two subperiods, given the country-level forecasts. The procedure consists of the following steps:

  • Step I From the central rates of mortality, we calculate the probabilities of dying ${{}_{n(x)}q}_{x}(r,s)$:

    $${{}_{n\left(x\right)}q}_{x}\left(r,s,t\right)=\left\{\begin{array}{cc}\frac{n\left(x\right)\cdot {{}_{n\left(x\right)}m}_{x}\left(r,s,t\right)}{1+\left(n\left(x\right)-{a}_{x}(s)\right){\cdot {}_{n\left(x\right)}m}_{x}\left(r,s,t\right)}& {\text{if}} x<85\\ 1& {\text{otherwise}}\end{array}\right.$$

    (15)

    where ${a}_{x}(s)$ denotes the mean life length in the last age interval of people dying in that interval. We assume that ${a}_{x}(s)$ are time- and district-invariant and are equal to the values taken from the country-level abridged life tables for Poland in 2008 as reported by Human Mortality Database. Having ${q}_{x}\left(r,s,t\right)$, we subsequently calculate the surviving populations ${l}_{x}\left(r,s,t\right)=\left(1-{q}_{x}\left(r,s,t\right)\right){l}_{x-n\left(x\right)}(r,s,t)$ where the radix is set at ${l}_{0}\left(r,s,t\right)=\mathrm{100,000}$.

  • Step II We estimate the parameters of the linear regression model of the form: ${Y}_{x}=\alpha +\beta {Z}_{x}$, where ${Y}_{x}=\frac{1}{2}{\text{ln}}\left(\frac{1-{l}_{x}\left(i,s,0\right)}{{l}_{x}\left(i,s,0\right)}\right)$ and ${Z}_{x}=\frac{1}{2}{\text{ln}}\left(\frac{1-{l}_{x}\left(POL,s,0\right)}{{l}_{x}\left(POL,s,0\right)}\right)$.

  • Step III Using the estimated coefficients as well as the country-wide forecasts of the surviving populations ${l}_{x}^{f}\left(POL,s,t\right),\mathrm{ we}$ calculate the forecasts for a region ${l}_{x}^{f}\left(i,s,t\right)$.

  • Step IV From the forecasted surviving populations ${l}_{x}^{f}\left(i,s,t\right),$ we calculate the implied central rates of mortality ${m}_{x}^{f}\left(i,s,t\right)$. As it is impossible to derive the implied mortality for the last age group 85+ , we assume ${m}_{85}^{f}\left(i,s,t\right)={m}_{85}\left(i,s,0\right)$.

Assessing forecast quality

Our forecast accuracy assessment covers three different measures. First, we analyze the accuracy of the mortality profile forecasts using the simple mean absolute error. By mortality profile, we mean the set of mortality rates for all 19 age intervals. MAE is calculated as follows:

$$MAE\left(i,s,t\right)=\frac{100}{19}{\sum }_{x}\left|{m}_{x}^{f}\left(i,s,t\right)-{m}_{x}\left(i,s,t\right)\right|.$$

(16)

Subsequently, we aggregate the measure over the districts, sex, and subperiods by calculating the appropriate means of the individual MAEs.

The simple MAE measure does not account for the fact that the true mortality rates ${m}_{x}\left(i,s,t\right)$ are not observed. Instead, we use the estimates based on the available data. Reliability of these estimates can vary considerably and we use weights to differentiate the impact of different mortality rates on the final value of the measure according to their reliability. Chiang (1979, p. 48) shows that the variance of the mortality rate ${s}^{2}\left({m}_{x}\right)$ is given by:

$${s}^{2}\left({m}_{x}\right)=\frac{{m}_{x}\cdot \left(1-{q}_{x}\right)}{{P}_{x}}\approx \frac{{m}_{x}}{{P}_{x}},$$

(17)

In practice, it is difficult to calculate reasonable weights based on the whole formula for the variance because (1) in small samples, the estimates of ${m}_{x}$ are not very reliable (for some methods, it happens that ${m}_{x}^{f}=0$ and the estimated variance of the mortality rate.

${s}^{2}\left({m}_{x}^{f}\right)=0$); (2) weighting by ${m}_{x}$ would hugely overweight groups with small ${m}_{x}$ (for example, 1–14 cohort gets about 50% of the weight) transforming MAE into MAPE, which is not a reasonable measure for assessing accuracy of the mortality profiles (see Wilson, 2018, p. 11). As a result, we use only the denominator of the variance formula (17) for weighting the forecast errors which gives us a simple, yet reliability-sensitive population-weighted MAE formula:

$$WMAE\left(i,s,t\right)=100\cdot \frac{{\sum }_{x}{\overline{P} }_{x,x+n\left(x\right)}\left(i,s,0\right)\cdot \left|{m}_{x}^{f}\left(i,s,t\right)-{m}_{x}\left(i,s,t\right)\right|}{{\sum }_{x}{\overline{P} }_{x,x+n\left(x\right)}\left(i,s,0\right)}.$$

(18)

For further aggregation of the measure across the districts, sex, and time periods, we also employ the populations from the baseline periods. The WMAE measure generally puts the higher weights to younger cohorts.

A reasonable alternative approach for weighting mortality rates is to consider life expectancy at birth. Therefore, we also compare the life expectancies at birth implied by the forecasts with their observed counterparts. To calculate ${e}_{0}$, we use the same linear model for life tables as described in the Brass forecasting method. In particular, we employ formula (15) for ${q}_{x}$ and assume the same mean life length in the last age intervals. For life expectancy, we analyze the mean errors and mean absolute errors. MAE for life expectancy can be thought as the more sophisticated version of the absolute total error measure considered by Wilson (2018).

Results

We begin by analyzing the accuracy of the mortality profile forecasts. Table 2 contains the mean MAE for the mortality profiles and the MAE for life expectancy at birth. It reports the values for the full verification sample of 379 districts, two subperiods, and two sexes, as well as for several subsamples. To improve readability, we use the color scale, where red represents high errors and green indicates more accurate forecasts.

Table 2 Mean absolute errors for the mortality profiles.

For the pure mortality profiles in the full sample, the first method (POL) has the highest errors where the district forecasts coincide with their country-level counterparts ($MAE=0.238)$. However, the SMR-based methods are only marginally better. In contrast, the most accurate forecasts are delivered by the mortality surface (MS) approach ($MAE=0.202$). The RR, RR-NC, and SMR-BAG methods also perform relatively well. Almost the same results in terms of the method ranking are obtained when using the population-weighted MAE measure.

Also looking at the implied life expectancy, generally, the picture is similar, too, although now SMR-BAG is the most accurate method. For the POL method, the MAE is equal to 0.898 years, whereas in the current Statistics Poland approach (SMR-REG), the error drops by almost 0.16 years. However, switching to the district-level SMR reduces the error further by 0.23 years and using the SMR-BAG method decreases the error by 0.31 years compared with the SMR-REG method.

Figure 2 shows the spatial distribution of the gains from switching from the SMR-REG to the SMR method and the most accurate SMR-BAG approach. There is some noticeable gain in most districts. Even the plain SMR method delivers, on average, more accurate forecasts in more than two-thirds of the districts. In the SMR-BAG method, that fraction reaches almost 75%. The effects of these two methods are even greater in the case of municipal districts, reaching 89 and 94%, respectively.

Fig. 2

Source: Author’s calculation. Data source: Statistics Poland, Human Mortality Database

Spatial distribution of the decrease in MAE for life expectancy forecasts by switching from SMR-REG to SMR-BAG (left) and SMR (right).

In general, the results for the whole sample, displayed in the top section of Table 2, are robust to changes in the scope of the sample. However, stratifying the sample reveals some interesting differences. For example, the SMR-BAG method performs very well in the shorter 5-year horizon, whereas MS dominates the longer one. Also, the BR approach generates relatively accurate forecasts in the longer horizon. The last two parts of the table show that the poor forecasting performance of the POL and SMR-REG methods are driven primarily by large errors in the municipal districts, which are about two times higher than those of the other methods. Finally, it is also worth noting that the neighborhood-complemented methods deliver only slightly more accurate forecasts than their baseline counterparts. The highest accuracy gains can be observed in the case of life expectancy forecasts.

We also investigate, to what extent the forecast errors are affected by the calibration errors of the model. For that purpose, we calculate the forecasts for 2006–2010 period using the observed mortalities in Poland in this period. The results are reported in Table 3. Excluding RR-based methods for which the calibration error by construction is small or 0, the calibration errors are large relative to MAE for both horizons (taken from Table 2 in the manuscript) and amount between 59 and 95%. The error is correlated with the forecast accuracy measures (Spearman correlation coefficient for the two series is equal to 0.69) but the differences in MAE 2011–16 are much smaller than the differences in the calibration errors.

Table 3 Calibration errors for the analysed methods.

Table 4 shows the bias in the life expectancy forecasts. Interestingly, in the full testing sample and the two separate testing subperiods, the first two methods are characterized by the lowest absolute bias, while the remaining methods, on average, underestimate life expectancy by 0.12–0.24 years. However, these results are highly unstable across sex and district types. By construction, the bias of the forecasts for individual districts are primarily driven by the accuracy of the gender-specific country-level predictions. Therefore, if the forecast for Poland is negatively biased, the forecasts for individual districts will also be negatively biased, on average.

Table 4 Bias (ME) of the life expectancy forecasts.

Forecast accuracy for each single age group is summarized in Table 5. Here, the forecasting accuracy of the methods differs significantly from the mortality profile case. Generally, the most accurate forecasts are generated by the SMR, SMR-BAG, and SMR-NC methods. The performance of the MS method, which is the best among the mortality profile forecasts, is poor, particularly for young age groups. This is also the case for the RR and RR-NC methods. The accuracy of the POL and SMR-REG methods varies considerably by age group. They are more accurate in forecasting life expectancy than most other methods for young age groups, but their relative forecasting accuracy deteriorates with age. This is especially true for the POL method.

Table 5 MAE of the mortality rate forecasts for the different age groups. Source: Author’s calculation.

It should be stressed that the apparent contradiction in results between Tables 2 and 5 and results from the fact that the mortality rates for the oldest cohorts are much higher than for the remaining groups. Therefore, the MAE values are dominated by forecast errors for these groups. As a result, a method that performs well for most of age intervals but fails for the oldest groups exhibits a poor overall performance in terms of MAE.

In Table 6 and Fig. 3, we show the spatial distribution of the forecast errors. For brevity, the errors in Table 6 are aggregated into 16 NUTS-2 regions. The accuracy ranking for the regions is summarized in the last column, which shows the median error for the methods.

Table 6 MAE of the mortality rate forecasts for the different regions. Source: Author’s calculation.

Fig. 3

Source: Author’s calculation. Data source: Statistics Poland, Human Mortality Database

Spatial distribution of the MAE measure.

The most accurate forecasts of mortality rates are observed in eastern and south-eastern Poland, when the life expectancy is generally higher. On the other side the largest errors are observed in northern Poland and Opolskie region in southern Poland. It should also be noted that the most accurate approaches, namely SMR-BAG and MS generally perform well in all regions.

Discussion and conclusion

Generally, the results presented in the previous section are well in line with those obtained by Wilson (2018). In particular, we find that the mortality surface method outperforms slightly the other approaches like the SMR-BAG, RR, and Brass models in terms of MAE but the differences between the best methods are rather small. Similarly, the SMR-BAG method delivers the most accurate forecasts of life expectancy with the RR and MS approaches sharing the second place and the Brass model following them. Exactly the same rating is given by Wilson (2018) for the values of his absolute total error measure. It should also be noted that the values of errors obtained for Poland is very close to those calculated for Australia. For example, the overall MAE for our best mortality surface method equal to 0.202 corresponds to the total absolute error equal to 0.038 which matches exactly the number reported by Wilson (2018). Nevertheless, our study offers several other, novel insights.

First, as far as forecasting mortality profiles, the SMR-REG approach currently used by Statistics Poland is far from optimal. There are other simple approaches that deliver considerably more accurate forecasts, such as the RR, RR-NC, and MS methods. While the latter two can be more involved than the SMR-REG method, the pure RR requires RR calculations for each district and age group and then scaling country-level forecasts by these numbers. Thus, the calculations are as simple as those for the SMR-REG approach and can be performed readily on a spreadsheet. It should also be noted that for implied life expectancy, the district-level SMR method outperforms the SMR-REG approach considerably. These findings are robust to changes in the periods covered by the test sample and sex.

Second, this study analyzes a novel method that uses data from neighborhood districts to generate more accurate estimates of SMRs and RRs. While this modification increases forecast accuracy, the improvement is small. This seems to imply that aggregating district mortality data across age and time is sufficient for reliable estimation of mortality rates. We suppose that the modification could be more successful in more data-scarce environments.

Third, the ranking of the methods changes significantly when analyzing the forecasts by single age groups. In general, the relative performance of the various methods is very much age-dependent. Specifically, the SMR-REG method performs well for young cohorts, and the alternatives offer only a slight or no improvement. Thus, this method seems a reasonable choice for infant mortality forecasting. However, the alternatives that use standardized mortality rates, such as the SMR, SMR-BAG, or SMR-NC methods, still outperform the SMR-REG method for most age groups. Notably, the methods that are the most accurate for forecasting mortality profiles (RR, RR-NC, MS) are definitely more accurate than the alternatives for the oldest cohort, which dominates our accuracy measures.

Given the heterogeneity of the forecasting performance for the different age intervals it would be interesting to consider a joint forecasting method that blends a SMR-based approach for most of the intervals with the MS, BR, or RR approach for the oldest cohorts. However, we leave this possibility for future research.

The reliability of our conclusions is limited by several issues. The most important is our short dataset that consists of just three subperiods, with one as the training subsample and the remaining two as the testing periods. In Poland, longer comparable series at the district level are not available. As a result, we are not able to assess forecasting accuracy for horizons longer than 10 years. However, the lack of a longer time series is, to some extent, compensated for by the number of districts used for our forecasts, which considerably improves the reliability of the forecast accuracy assessment. It should be also remembered that past forecasting performance may not hold in the future, as stressed by Booth and Tickle (2008).

In addition, we do not examine several more involved methods for small-area mortality predictions. Currently, advanced software or data requirements make it difficult for statistical agencies to apply these methods in practice and the potential gains in accuracy from switching to these remain unknown. This issue also remains open to future investigation. The Author hopes that due to the simplicity of calculations, the models used in this study have a chance to be implemented in practice by the Statistics Poland.