1 Introduction and Literature Review

Due to its high structural resolution, the AFM [1] was not only a prime instrument to obtain qualitative information down to the atomic-scale, but it is now also a widely used and traceable tool in nanometrology [2]. In particular the semiconductor industry’s need to determine the roughness of sidewalls led to a still ongoing development of different approaches to measure near vertical, vertical or even undercut surface features [3]. Boot-shaped cantilever tips [4] measure critical dimensions (CD) like feature width, edge profile or line edge roughness. To improve the anisotropic stiffness of conventional CD-AFMs, a cantilever with flexure hinge structures has been shown [5]. While sidewalls are well resolved by CD-AFMs, the shape of the tip leads to a poor resolution of flat parts of a feature. Furthermore, tip characterization and the subsequent correction of the dilation caused by the finite tip size is quite laboriously, because measurements are conducted at the whole circumference of the tip [6].

A different approach to measure vertical or near vertical surface features is to introduce an inclination between the measuring object and the cantilever. This might be done by tilting the sample [7, 8], or by tilting the cantilever [9,10,11] in one direction. Also the measurement of a micro sphere with a setup including an AFM and a rotational axis has been shown [12]. In [13] an AFM based on two rotational axes [14] to adjust the probe direction to cover a complete hemisphere has been demonstrated. Conventional AFMs are usually constructed in a very compact manner and with materials with a small thermal expansion coefficient, but the two aforementioned axes greatly enlarge the metrology frame by materials with a comparatively high expansion coefficient. The AFM is therefore operated within a thermostating housing with a long-term temperature stability of 17 mK [15]. Within this housing, the thermal sensitivity has been determined to be 1.3 nm/mK and the long-term measurement precision of the sensor system with 6.7 nm was also mainly attributable to this thermal sensitivity [16]. Nevertheless, a further source of inaccuracy might be the sensor holder that is the connection between the rotational axes and the cantilever. In the previous design, the sensor holder introduced one adhesive bond, a soldered connection and a geometrically undefined clamping into the metrology circle. It has therefore been redesigned to a clamped sensor holder, which will be presented, evaluated and compared to the previous glued sensor holder within this paper.

Another way to reduce the effects of thermal variations during a measurement is the improvement of the measuring speed. Approaches that have been shown are the combinations of slow large-range positioning systems with motion ranges of several millimetres with fast one-dimensional piezoelectric positioning stages with a motion range of several micrometres [17, 18]. A further reduction of the weight that needs to be moved at high frequencies is achieved by moving the cantilever itself, instead of moving the measuring object [19]. In the redesigned sensor holder, the piezoelectric actuator that is necessary to operate the cantilever in intermitted contact-mode is therefore further on used as actuator of a high-speed closed-loop control that keeps the cantilever within its characteristic curve. As piezoelectric actuators suffer from hysteresis and creepage [20], provisions have been made to measure the extension of the piezoelectric actuator by a fibre optic distance sensor. This high-speed AFM and its limitations will be presented in Sect. 4. In Sect. 3 the metrological characteristics of the redesigned sensor holder are shown and compared with the characteristics obtained with the previous sensor holder. The following section starts with the introduction of the setup, namely the mechanical design of the complete AFM, of both sensor holders and of the signal processing.

2 Setup

The flexibility to adjust the probe direction of the AFM was achieved by the utilization of a commercial SCL-Sensortech Piezo-Resistive Sensing (PRS) cantilever with a length of \(110\, \upmu {\text{m}}\), a width of \(48\, \upmu {\text{m}}\) and a silicon tip with a nominal radius of <15 nm. Self-sensing methods, like the piezoresistive deflection measurement [21], are very compact but still offer a similar high signal-to-noise ratio compared to the commonly used optical beam deflection method [22]. In order to reduce contact forces and therefore to minimize elastic or plastic deformations of the sample and the tip, the cantilever was operated in intermitted contact-mode [23]. As tip wear occurs mainly at the beginning of a cantilever’s usage [24], several pre-scans have been conducted. All measurements have been conducted within a thermostating housing and the set temperature was 20 \(^\circ\)C.

Fig. 1
figure 1

Simplified schematic of the setup: 1 first axis; 2 second axis; 3 sensor holder; 4 invar spacer; 5 y-interferometer; 6 Zerodur frame; 7 corner mirror; 8 z-interferometer; 9 piezoelectric actuator; 10 piezoresistive cantilever; 11 measuring object; 12 spacer

Full size image
Fig. 2
figure 2

Schematic of the previous (left) and the redesigned (right) sensor holder: 1 fibre optic distance sensor; 2 piezoelectic actuator; 3 grub screw; 4 glass plate; 5 nut; 6 headless ball pressure screw; 7 flexure hinge; 8 fixed clamping jaw; 9 socket; 10 piezoresistive cantilever

Full size image

2.1 Mechanical design of the AFM

The whole setup, shown schematically in Fig. 1, consists of the first axis (1), an Aerotech ANT95R-180 with a positioning range of 180\(^\circ\) and the second axis (2), a SmarAct SR-2812 with a positioning range of 360\(^\circ\) mounted under an angle of 45\(^\circ\) to the first axis by an angle piece. A sensor holder (3) connects the second axis with the socket of a piezoresistive cantilever (10). The piezoelectric actuator (9), a PI Ceramic PICMA® PL055.31, stimulates the cantilever over the flexure hinge to operate the AFM in intermitted contact-mode. The whole setup is installed into a NMM-1 with a motion range of \(25 \times 25 \times 5\,\text {mm}^{3}\) and a resolution of less than 0.1 nm [25, 26]. The NMM-1 fulfils the Abbe comparator principle in all three coordinate axes by keeping the measuring system, consisting of three perpendicular interferometers (two of them are shown, namely 5 and 8) fed by stabilized helium-neon lasers, fixed and moving the measuring object (11). The measuring object is placed on a corner mirror (7) which defines the coordinate system of the NMM-1 and provides the three orthogonal measuring mirrors for the interferometers. The location of the tip of the cantilever at the intersection point of the three interferometers, the so-called Abbe point, would ensure the highest accuracy. Nevertheless, it limits the adjustment range of the probe direction to about half of a hemisphere, as the positioning range of the first axis is limited to about 90\(^\circ\) to avoid a collision with the corner mirror. In order to sustain the full positioning range, the sensor is located 5 mm above the Abbe point. Therefore, a spacer (12) is used for flat measuring objects and invar spacers (4) enlarge the Zerodur frame (6) of the NMM-1 to integrate the sensor system. However, the additional angle sensors and the angle control of the corner mirror about the x- and y-axis of the NMM-1 reduce the angular deviations during movement and thus any first-order deviations that arise.

2.2 Sensor holder

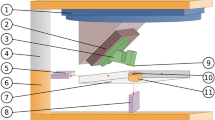
The previous sensor holder and the redesigned sensor holder are shown schematically in Fig. 2. While the socket (9) is glued to the sensor holder in the left design, the circuit board of the piezoresistive cantilever (10) is placed in the socket and clamped by the movable and fixed clamping jaw (8) sideways in the right design. The movable clamping jaw is tensioned by a grub screw (3). This whole anterior part is moved over the flexure hinge (7) by the piezoelectric actuator (2). The pre-strain on the piezoelectric actuator is adjusted by a headless ball pressure screw (6), which is locked by a nut (5). The planar distribution of pressure on the piezoelectric actuator is ensured by a glass plate (4). Therefore, in the redesign the adhesive bond between the sensor holder and the flexible circuit board, the soldered connection between the flexible circuit board and the socket as well as the geometrically undefined clamping of the circuit board of the piezoresistive cantilever in the socket are removed from the metrology circle.

To use the piezoelectric actuator for both, to oscillate the cantilever and as actuator of a high-speed closed loop control, its whole travel range of \(2.2\, \upmu {\text{m}}\) is needed. Therefore, for the redesigned sensor holder special attention has been paid to the dimensioning of the flexure hinge so that it is not overstrained nonetheless. According to the manufacturer’s specification [27], a pre-strain \(P_{\mathrm {pre}}\) of 15 MPa should be applied to the piezoelectric actuator to ensure an operation without any tensile stress, while the stiffness \(k\) of the spring generating the pre-strain should not exceed 10 % of the piezoelectric actuator’s stiffness \(k_{\mathrm {pd}}\), which is about 227 kN mm-1. Therefore a force \(F_{\mathrm {pre}}\) of 375 N should be applied to the piezoelectric actuator with the dimensions \(5 \times 5 \times 2\) mm3 and \(k\) should be below 22.7 kN mm-1. The hinge is modelled as bending beam as depicted in Fig. 3. The geometrical moment of inertia \(I\) of a rectangular section is given by [28, p. 85]

$$\begin{aligned} I= \frac{wh^3}{12} \, , \end{aligned}$$
(1)

with \(w\) being the width and \(h\) being the height of the particular section. In order to prevent sharp edges increasing the notch effect, the bar’s height is designed as semicircle with the radius \(b/2\) (cf. Fig. 3). Simplifying, the mean height \(\bar{h}\) over \(b\) given by

$$\begin{aligned} \bar{h} = h_{\mathrm {0}}+0.5b\cdot (1-0.25\pi ) \end{aligned}$$
(2)

is used to calculate \(I\). The deflection \(v\) of a bending beam is given by [28, p. 151]

Fig. 3
figure 3

Model of the flexure hinge as bending beam

Full size image
$$\begin{aligned} v= \frac{Mx^2}{2EI} \, , \end{aligned}$$
(3)

with \(M\) denoting the bending moment and \(E\) denoting the elastic modulus. Applying Hooke’s law,

$$\begin{aligned} k= \frac{2EIF}{Mx^2} \end{aligned}$$
(4)

or

$$\begin{aligned} k= \frac{2EI}{mb^2} \, , \end{aligned}$$
(5)

with \(M= Fm\) and \(x= b\). Substituting Eq. 1 in Eq. 5 yields

$$\begin{aligned} k= \frac{Ew\bar{h}^3}{6 mb^2} \, . \end{aligned}$$
(6)

After simulations with different materials, steel 1.4301 (\(E\) = 190 GPa [29, TB 10-4]) was chosen. With \(h_{\mathrm {0}}\) = 1.25 mm, \(w\) = 10.5 mm, \(b\) = 4.0 mm and the vertical lever (measured from the centre of the force introduction) \(m\) = 6.125 mm, \(k\) is 16.1 kN mm-1 and therefore well below the limit. Furthermore it is possible to apply 50 % of \(F_{\mathrm {pre}}\) without exceeding the material limits for sure. As only a minor portion of the travel range of the piezoelectric actuator is needed to stimulate the cantilever, 50 % of \(F_{\mathrm {pre}}\) might reasonably be regarded as sufficient to ensure an operation of the piezoelectric actuator without any tensile stress.

Since piezoelectric actuators suffer from creepage and hysteresis, provision is made to measure the extension of the piezoelectric actuator by a focused fibre optic distance sensor (1 in Fig. 2), a FDM-1 of the fionec GmbH. This is essential since the piezoelectric actuator is further on used as actuator of a high-speed closed-loop control, as will be described in Sect. 4. Nevertheless, the integration of this sensor proved to be very difficult. On the one hand the reflectivity of the target area was insufficient, on the other hand a stable conjunction of the fibre end and the sensor holder that also would bear a movement of the rotational axes was not feasible in practice. Therefore, the FDM-1 was not integrated for the studies presented within this paper. In Fig. 4 the sensor holder as it was integrated into the NMM-1 is depicted. Also shown is the second rotational axis.

Fig. 4
figure 4

Redesigned sensor holder integerated into the NMM-1

Full size image

2.3 Signal processing

During the experiments the probe sensor signal evaluation was conducted with a Zurich Instruments HF2LI lock-in amplifier. A sinus signal \(V_{\mathrm {Ref}}\) was impedance converted by a current feedback amplifier (LT1206 of Analog Devices) and has stimulated the piezoelectric actuator near the cantilever’s resonance frequency. The signal of the piezoresistive cantilever was amplified by a commercial pre-amplifier of SCL-Sensortech. The amplified signal \(V_{\mathrm {AFM}}\) was transduced to the lock-in amplifier, which calculated the phase-independent amplitude of the oscillation \(R_{\mathrm {AFM}}\). \(R_{\mathrm {AFM}}\) is the measuring signal passed to the analog-to-digital converter (ADC) of the NMM-1 with a band-limitation of 3 kHz to control the x-, y- and z-axis according to the sensor orientation and current probing direction specified in the measuring command. Therefore, measurements were conducted in amplitude controlled closed-loop intermitted contact-mode. The band-limitation of 3 kHz is reasonable since the sampling frequency of the probe signal ADCs of the NMM-1 is 6.25 kHz.

3 Investigations on the metrological characteristics

In order to compare the redesigned sensor holder with the previous sensor holder, the investigations described thereafter are similar to the ones that have already been conducted with the previous sensor holder in [16].

3.1 Short-term precision

Instead of using standards to calibrate the AFM, it is possible to use the stabilized lasers of the NMM-1. By repeating the calibration routine for several times, the short-term precision (repeatability) of the sensor was derived. The second axis was in its zero position and the probe direction was against the direction of the z-axis of the NMM-1. Therefore, the calibration was done against the traceable z-interferometer. For the calibration, the sample was moved towards the cantilever until full contact with an approach velocity of 100 nm/s. The amplitude of the oscillation of the cantilever \(R_{\mathrm {AFM}}\) and the distance value of the z-interferometer \(z_{\mathrm {NMM}}\) were recorded with a point distance of 0.1 nm. In Fig. 5 the result of a calibration is shown.

Fig. 5
figure 5

Result of a calibration. The characteristic curve \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\) is calcuated within the range indicated by the dashed horizontal lines. An offset has been added to \(z_{\mathrm {NMM}}\) for illustrative purposes

Full size image

Within the range indicated by the two dashed horizontal lines, the characteristic curve \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\), where \(d_{\mathrm {AFM}}\) is the deflection of the cantilever, is calculated as cubic polynomial. This range is therefore slightly less than the free oscillation amplitude of the cantilever. The calibration was conducted 50 times within a period of time of about two minutes. For each calibration the characteristic curve \(d_{\mathrm {AFM}}\) was calculated. In Fig. 6 the deviation \(\Delta z= d_{\mathrm {AFM}}(R_{\mathrm {AFM}})-z_{\mathrm {NMM}}\) is shown. \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\) was calculated by one of the characteristic curves. Depicted in red are the residues of this characteristic curve. Shown in green are the deviations to the other 49 calibrations. There are some systematic periodic deviations perceptible. Nevertheless, these might also be caused by \(z_{\mathrm {NMM}}\), as periodic nonlinearities of interferometers are a well known phenomena occurring mainly with a periodicity of half of the laser’s wavelength \(\lambda\) [25, p. 67 et seq.]. To investigate this hypothesis, the Fourier coefficients \(a_{\mathrm {1}}\) and \(b_{\mathrm {1}}\) for \(\lambda /2\) of \(\Delta z\) over \(d_{\mathrm {AFM}}\) are calculated for each characteristic curve. There is a strong correlation (correlation coefficient = 0.83) between the mean of \(\Delta z\) of each characteristic curve and the phase \(\varphi\) of its Fourier sequence, given by

$$\begin{aligned} \varphi = \mathrm {atan2}(b_{\mathrm {1}}/ a_{\mathrm {1}}) \, . \end{aligned}$$
(7)
Fig. 6
figure 6

Deviations of the deflection of the cantilever to the z-values of the NMM-1 for 50 calibrations. Residues are shown in red

Full size image

As the thermal sensitivity of the sensor system exceeds the thermal sensitivity of \(z_{\mathrm {NMM}}\) by far, the correlated movement of the periodic deviations and the mean of \(\Delta z\) indicates that these nonlinearities are caused by \(z_{\mathrm {NMM}}\) rather than by the AFM. Future research therefore will take the quantitative evaluation and correction of these periodic nonlinearities into account as well.

To determine the short-term precision (repeatability) of the sensor, every characteristic curve is applied to the measuring points of every calibration and \(\Delta z\) is calculated. In Fig. 7, \(\Delta z\) is shown as histogram with its standard deviation \(\sigma _{\mathrm {calibration}}\), which is 3.5 nm. The deviations are mainly caused by variations of the offset of the characteristic curves, as the standard deviation of these offsets is 2.4 nm.

After the calibration, the controller of the NMM-1 was enabled to keep \(d_{\mathrm {AFM}}\) in the middle of the characteristic curve and data were recorded for three times 90 s with the maximum sampling frequency of the NMM-1 (6.25 kHz). The results are shown in Fig. 8. The three standard deviations of \(z_{\mathrm {NMM}}\) are 2.2 nm (red), 0.9 nm (green) and 1.2 nm (blue). The combination of these values yields \(\sigma _{\mathrm {standstill}}\), which is 1.5 nm. Of course, this value is effected by thermal variations, too. Nevertheless, it is possible to deduce the noise level as standard deviation of \(d_{\mathrm {AFM}}\), as the controller compensates the mainly temperature-induced low-frequency variations. The three standard deviations of \(d_{\mathrm {AFM}}\), and therefore also \(\sigma _{\mathrm {noise}}\), are 0.2 nm.

Fig. 7
figure 7

\(\Delta z\) as histogram with its standard deviation \(\sigma _{\mathrm {calibration}}\), which is 3.5 nm

Full size image
Fig. 8
figure 8

Three standstill measurements in closed-loop mode over 90 s. Above, an offset has been added to \(-z_{\mathrm {NMM}}\) for illustrative purposes

Full size image

3.2 Long-term precision

To determine the long-term (intermediate) measurement precision of the sensor, standstill measurements were conducted for 15 s every 10 min. The measured z-value \(z_{\mathrm {M}}\) was calculated according to Eq. 8. For each measurement the offset was calculated as mean of \(z_{\mathrm {M}}\). Between the measurements the cantilever was withdrawn from the surface to avoid tip or sample damage. In Fig. 9 the mean of \(z_{\mathrm {M}}\) over 18 hours after stabilization is shown. Within this period of time the standard deviation of the offset, \(\sigma _{\mathrm {long\text{- }term}}\), is 6.5 nm.

$$\begin{aligned} z_{\mathrm {M}}= -z_{\mathrm {NMM}}+ d_{\mathrm {AFM}}\end{aligned}$$
(8)

3.3 Scans on a calibration grating

Closed-loop scans were conducted on a calibration grating (TGZ1 of NT-MDT) with a nominal step height of (21.4 ±1.5) nm. The measured values within the (negated) coordinate system of the NMM-1 were firstly calculated according to Eq. 8. Afterwards, the measured values were transformed into the workpiece coordinate system (WCS).

Because of the low-pass filtering associated with the calculation of \(d_{\mathrm {AFM}}\), as well as different ADCs used for the probe signal and for the interferometers of the NMM-1, a latency between the signals of the interferometers and the probe signal is inevitable. In order to avoid effects caused by this latency, the scan velocity was chosen to be only \(5\, \upmu {\text{m}}\)/s and the point distance was 1 nm. The scan length was \(90\, \upmu {\text{m}}\) and the step height was determined according to ISO 5436-1 [30]. The grating was placed within the xy-plane of the NMM-1. For the 30 scans on the same line at the measured object, the mean of the determined step heights is 20.54 nm, which agrees with the nominal value, and the associated standard deviation \(\sigma _{\mathrm {step~height}}\) is 55 pm. The high reproducibility of the scans is also shown in Fig. 10, where 30 scans of the complete scan length (above) and of an irregularity on one step (below) are depicted.

3.4 Comparison of both sensor holders

In Table 1 the results of the investigations of the metrological characteristics of the sensor system with both sensor holders are shown.

Table 1 Comparison of both sensor holders
Full size table

As can be seen, there are no significant differences between the values of both sensor holders.

Fig. 9
figure 9

Long-term precision over 18 hours

Full size image
Fig. 10
figure 10

30 scans on the same line at the measured object of the complete scan length (above) and of an irregularity on one step (below) on the calibration grating

Full size image

4 High-speed AFM

As only a minor portion of the positioning range of the piezoelectric actuator is needed to stimulate the cantilever near its resonance frequency, it is possible to implement a high-speed closed-loop control that keeps the cantilever within its characteristic curve. The closed-loop control adjusts the offset signal \(V_{\mathrm {Offset}}\), which is added to the reference signal \(V_{\mathrm {Ref}}\) and therefore utilizes the piezoelectric actuator as its actuator. The signal processing of this high-speed AFM is shown schematically in Fig. 11. Instead of using the current feedback amplifier, a PiezoDrive PD200 amplifies the signal to the piezoelectric actuator by a factor of 20, leading to a value of \(V_{\mathrm {Piezo}}\) of up to 100 V. Within the lock-in amplifier, \(R_{\mathrm {AFM}}\) is calculated with a band-limitation of 50 kHz and used for the high-speed closed-loop control. Nevertheless, to the ADC of the NMM-1 it is passed with a band-limitation of still 3 kHz. Also passed to the NMM-1 is \(V_{\mathrm {Offset}}\).

The parameters of the proportional-integral (PI)-controller have been determined empirically following the Ziegler and Nichols method [31]. The limits of \(V_{\mathrm {Offset}}\) have been set to 0.35 V and 4.64 V, leading to an offset of \(V_{\mathrm {Piezo}}\) between 7 V and 92.8 V. In Fig. 12 the results of the calibration of the piezoelectric actuator are shown. \(d_{\mathrm {AFM}}\) was kept at its setpoint by the high-speed closed-loop control by adjusting \(V_{\mathrm {Offset}}\) while the stage of the NMM-1 was moved forwards and backwards in z-direction for almost \(2\, \upmu {\text{m}}\). For the measuring points between \(V_{\mathrm {Offset,\,min}}\) and \(V_{\mathrm {Offset\,max}}\) the characteristic curve \(p_{\mathrm {piezo}}(V_{\mathrm {Offset}})\) was calculated as cubic polynomial. The range of the characteristic curve and therefore the applicable positioning range of the high-speed closed-loop control is \(1.54\, \upmu {\text{m}}\). Nevertheless, the accuracy of \(p_{\mathrm {piezo}}\) is deteriorated significantly by \(b_{\mathrm {Piezo}}\), which is the hysteresis of the piezoelectric actuator. It is determined to be 335 nm. The angular variation is about 0.01\(^\circ\) and therefore neglectable.

For the active mode of operation of the sensor, the piezoelectric actuator is controlled to the middle of its stroke by the additional slower control of the NMM-1. This results in only short-term and mostly smaller deviations being compensated by the piezoelectric actuator according to the measured surface [19]. The hysteresis is also reduced in accordance with the lower stroke.

Fig. 11
figure 11

Schematic of the signal processing with the high-speed closed-loop control implemented within the lock-in amplifier

Full size image

5 Summary, conclusion and outlook

In this article, a redesigned sensor holder for an AFM with an adjustable probe direction has been presented and evaluated. The short-term precision of repeated calibrations on the NMM-1 was determined to be 3.5 nm and repeated standstill measurements revealed a standard deviation of 1.5 nm. A major portion of the measurement error is attributable to the thermal sensitivity of the sensor system, especially the rotational kinematics. Therefore the long-term measurement precision was determined to be 6.5 nm within a thermostating housing with a long-term standard deviation of the temperature of about 4 mK [15]. For the determination of the step height of a calibration grating the mainly low-frequency temperature deviations are negligible. Therefore, the precision of determined step heights was only 55 pm. Although the redesigned sensor holder in comparison to the previous sensor holder removed one adhesive bond, a soldered connection and a geometrically undefined clamping from the metrology circle, these changes did, unexpectedly, not result in superior metrological characteristics. On the contrary, both sensor holders show very similar metrological characteristics. Measurement errors arising from these three connections would most probably be in the low-frequency range, where, for the presented system, thermally caused measurement errors are predominant. Therefore, the measurement errors arising from the three connections are insignificant for the sensor system presented.

Furthermore, a high-speed closed-loop control that keeps the cantilever within its characteristic curve has been shown. It utilizes the piezoelectric actuator that is necessary to operate the cantilever in intermitted contact-mode further on as actuator.

Fig. 12
figure 12

Calibration of the piezoelectric actuator. An offset has been added to \(z_{\mathrm {NMM}}\) for illustrative purposes

Full size image

While the combination of a low-amplitude, high-frequency signal for the stimulation and a high-amplitude signal with a lower frequency for the actuation proved to work applying a commercial voltage amplifier, the hysteresis of the piezoelectric actuator led to significant measurement errors. Nevertheless, the intended integration of a fibre optic distance sensor to measure the extension of the piezoelectric actuator was not feasible in practice, so far.

For some time past, self-sensing cantilevers with an integrated micro heater for the stimulation of the cantilever are known and also available commercially [32]. Their metrological characteristics have been investigated thoroughly and the actuator might be used for both, stimulation of the cantilever near its resonance frequency combined with the deflection of the cantilever at lower frequencies for high-speed applications [33]. The use of such a cantilever within the shown AFM promises an essential simplification of the sensor holder combined with an improvement of the metrological characteristics. For one thing the removal of the piezoelectric actuator is beneficial due to the known creepage of such actuators. On the other side it enables the construction of a sensor holder with a higher stiffness which might be less prone to oscillate due to environmental vibrations. As for the determined precisions in the low single-digit nm-range also the uncertainty of the interferometers becomes significant, their periodic nonlinearities will be taken into account and will be corrected in future works.