1 Introduction

Nearly four decades ago, Norio Taniguchi forecasted the future development of machining accuracy by extrapolating historical data and predicted that by the turn of the millennium, ultraprecision machining could achieve an accuracy of 1 nanometer, or one-millionth of a millimeter [1]. Now, the future has become the past, and Taniguchi’s forecasts have been proven to be correct [2,3,4]. In particular, the ultraprecise production of miniaturized, truly three-dimensional structures [5] or mesoscale components with microscale features [6] was made possible. These ultraprecise production processes are applied in many different areas, such as optics to produce free-form surfaces [7, 8], power engineering to fabricate miniaturized turbine impellers [9], medicine to manufacture penetrating microelectrodes [10], and the consumer industry to achieve decorative effects [11].

For dimensional metrology, this still-ongoing trend of miniaturization was and still is a challenge because simple downscaling of established procedures is impossible due to scaling effects, i.e., effects negligible in the mesoscale become crucial in the microscale and nanoscale [12]. Upcoming, highly accurate positioning systems, like the Nano Measuring Machine NMM-1 [13] and shortly thereafter the Ultra Precision Coordinate Measuring Machine [14], which both fulfil the Abbe comparator principle [15] or rather the deduced Bryan principle [16] enabled positioning within a three-dimensional volume over several millimeters in each axis with an uncertainty of several nanometers. Nevertheless, because of the lack of suitable sensors, there was, and partly still is, a metrological gap in performing nanometrological measurements on truly three-dimensional structures [17, 18].

The approaches used to fill the gap in three-dimensional nanometrology can be classified into two categories [19]: In a top-down approach, three-dimensional but not nanometrological sensor systems have been miniaturized and aligned to comply with the demands of nanometrology. A current review of such systems can be found in [20]. Conversely, in a bottom-up approach, highly accurate and nanometrological but, in principle, one-dimensional sensors mainly applied in surface metrology, such as the atomic force microscope (AFM) [21], have been tailored to be applicable for three-dimensional measurements.

The second approach can be further subdivided into approaches modifying the sensor and approaches modifying the positioning system. Moreover, as the semiconductor industry needs to determine critical dimensions, such as feature width, edge profile, or line edge roughness [22], several modified AFM cantilevers, e.g., with a boot-shaped tip [23], a further glued cantilever [24], a glued probing sphere [25], or particularly long cantilevers for the measurement of high aspect ratios [26, 27], have been developed. An alternative for the measurement of vertical or near-vertical surface features, or surfaces with a varying surface normal, is to apply a modified positioning system and introduce an inclination between the measuring object and the cantilever, which can be done by adjusting the sample [28,29,30,31] or tilting the cantilever [32,33,34,35,36] in one direction. A current review of the application of the AFM to measure critical dimensions can be found in [37].

More versatile, at the FAU Erlangen-Nürnberg [38] and, more recently, at the TU Ilmenau [39], a rotational kinematics has been integrated into a NMM-1 to adjust the probe direction of a sensor in two directions, thereby enabling the conduction of truly three-dimensional measurements with a one-dimensional sensor. Examples are the integration of a fixed scanning tunneling microscope [40], an oscillating tunneling microscope [41], a fiber-optic distance sensor [42] or an AFM [43]. With the AFM, some preliminary investigations on the achievable measurement precision have already been reported [44, 45]. The sensor system achieves a certain noise level and a short-term measurement precision in the low single-digit nanometer range. Furthermore, the standard deviation of the measured height of a calibration grating, both placed within and tilted to the horizontal plane with the probe direction adjusted accordingly, is in the double-digit picometer range, with a mean value that is consistent with the nominal step height. However, the empirically determined thermal sensitivity of the sensor system, which is mainly attributable to the rotational kinematics that greatly enlarges the metrology frame of the measuring system by materials with a comparatively high coefficient of thermal expansion, is 1.3 nm/mK. Thus, the achievable long-term measurement precision, which is particularly crucial when conducting complex and time-consuming measurements, is limited.

To reduce the thermal sensitivity of the system, the redesign of the rotational kinematics is mandatory. However, for the moment, some preliminary investigations on the application of a commercially available, self-sensing cantilever with an integrated micro heater for its stimulation will be presented. In previous investigations, a piezoelectric actuator has been applied to stimulate the cantilever. However, the removal of the piezoelectric actuator, which is enabled by the application of a cantilever with an integrated micro heater, enables an essential simplification of the sensor holder. Thus, in the future it might be possible to use materials with a low coefficient of thermal expansion, which nevertheless are often difficult to machine and therefore allow for only rather simple geometries. Furthermore, because of the creepage of piezoelectric actuators [46], their removal from the metrology frame might lead to improved metrological characteristics.

A possible application of the redesigned sensor system is the highly accurate and nondestructive measurement of the crack length of a compact tension specimen according to the ASTM E 647-08 standard. Such specimens are applied in the experimental determination of the fracture mechanical parameters of clinchable metal sheets [47].

This paper is organized as follows: In Sect. 2, the measuring system is introduced. In Sect. 3, the metrological characteristics of the measuring system equipped with a cantilever with integrated sensing and actuation are investigated and compared with the previous system, including a piezoelectric actuator. In Sect. 4, a detailed analysis of the error sources contributing to the short-term precision is presented. Finally, in Sect. 5, the results are summarized and discussed, and an outlook is given.

2 Setup

The flexibility to adjust the probe direction of the AFM was achieved by utilizing the commercial SCL-Sensortech Piezo-Resistive Sensing & Active (PRSA) cantilever with a length of 110 \(\upmu \)m, a width of 48 \(\upmu \)m, and a silicon tip with a nominal radius of < 15 nm. Self-sensing methods, such as the piezoresistive deflection measurement [48], are compact but still provide a high signal-to-noise ratio similar to the commonly used optical beam deflection [49]. To reduce the contact forces and minimize the elastic or plastic deformations of the sample and tip, the cantilever was operated in intermittent-contact mode [50]. The micro heater applied to the cantilever stimulates it without the need for an external actuator [51]. As tip wear mainly occurs at the beginning of the usage of a cantilever [52], several pre-scans have been conducted to ensure that the effect of tip wear is insignificant. All measurements have been conducted within a thermostating housing with a long-term temperature stability of 17 mK [53] and a set temperature of 20 \(^\circ \)C.

2.1 Mechanical Design

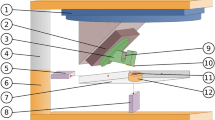
The entire setup, shown schematically in Fig. 1, consisted of the first axis (1), i.e., the Aerotech ANT95R-180 with a positioning range of 180\(^\circ \), and the second axis (2), i.e., the SmarAct SR-2812 with a positioning range of 360\(^\circ \) mounted under an angle of 45\(^\circ \) to the first axis by an angle piece.

Fig. 1
figure 1

Simplified schematic of the setup: 1 first axis; 2 second axis; 3 sensor holder; 4 invar spacer; 5 y-interferometer; 6 Zerodur frame; 7 corner mirror; 8 z-interferometer; 9 piezoresistive cantilever; 10 measuring object; 11 spacer. Figure modified from [44]

Full size image

A sensor holder (3) connected the second axis to the socket of a piezoresistive cantilever (9) with integrated actuation. The entire setup was installed in the NMM-1 [54, 55] with a range of motion of 25 mm \(\times \) 25 mm \(\times \) 5 mm. The NMM-1 fulfills the Abbe comparator principle in all three coordinate axes by keeping the measuring system (i.e., three perpendicular homodyne Michelson interferometers fed by stabilized helium-neon lasers with a resolution of less than 0.1 nm each; two of them are shown, namely, 5 and 8) fixed and moving the measuring object (10). The measuring object was placed on a corner mirror (7), which defines the coordinate system of the NMM-1 and provides the three orthogonal measuring mirrors for the interferometers. The location of the tip of the cantilever at the intersection point of the three interferometers, the so-called Abbe point, would ensure the highest accuracy. Nevertheless, it limits the adjustment range of the probe direction to approximately half of a hemisphere, as the positioning range of the first axis is limited to approximately 90\(^\circ \) to prevent collision with the corner mirror. To sustain the full positioning range, the sensor was located approximately 5 mm above the Abbe point. Therefore, a spacer (11) was used for the flat measuring object, and invar spacers (4) were used to enlarge the Zerodur frame (6) of the NMM-1 to integrate the sensor system. However, the additional angle sensors and the angle control of the corner mirror around the x- and y-axes of the NMM-1 reduced the angular deviations during movement and thus any first-order deviations that arise because of the vertical distance to the Abbe point. A detailed explanation of the sensor holder is given in [45]. Figure 2 shows the sensor holder integrated into the NMM-1.

Fig. 2
figure 2

Setup integrated into the NMM-1

Full size image

2.2 Signal Processing

During the experiments, probe sensor signal evaluation was conducted using the Zurich Instruments HF2LI lock-in amplifier. A sinus signal \(V_{\mathrm {Ref}}\) was subjected to impedance conversion by the Analog Devices LT1206 current feedback amplifier and used to stimulate the micro heater on the cantilever with slightly less than half of the resonance frequency of the cantilever. The dissipated power can be calculated as follows:

$$\begin{aligned} P= \frac{V_{\mathrm {Heater}}^2}{R} \, , \end{aligned}$$
(1)

where \(V_{\mathrm {Heater}}\) denotes the applied voltage and \(R\) denotes the ohmic resistance of the micro heater. \(P\) is proportional to the square of \(V_{\mathrm {Heater}}\). Therefore, the cantilever is stimulated near its resonance frequency [56]. The signal of the piezoresistive cantilever was amplified by the SCL-Sensortech commercial preamplifier. The amplified signal \(V_{\mathrm {AFM}}\) was transduced to the lock-in amplifier, which calculated the phase-independent amplitude of the oscillation at the second harmonic of the driving signal, \(R_{\mathrm {AFM}}\). \(R_{\mathrm {AFM}}\) is the measuring signal passed to the analog-to-digital converter (ADC) of the NMM-1 with a band limitation of 3 kHz to control the x-, y-, and z-axes according to the sensor orientation and current probing direction specified in the measuring command. Therefore, measurements were conducted in amplitude-controlled closed-loop intermittent-contact mode. The band limitation of 3 kHz is reasonable because the sampling frequency of the probe signal ADCs of the NMM-1 is 6.25 kHz. Figure 3 shows the schematic representation of the signal flow.

Fig. 3
figure 3

Schematic representation of the signal flow. Figure modified from [45]

Full size image

3 Investigations on the Metrological Characteristics

To compare the application of a cantilever with integrated stimulation to the previously applied stimulation by a piezoelectric actuator, the investigations described thereafter within this section are similar to those that have already been conducted with piezoelectric stimulation in [45]. In particular, systematic errors in the characteristic curves will be corrected only in the subsequent section.

3.1 Short-Term Precision

Instead of using standards, such as a type PPR or PGR material measure according to ISO 25178-70 [57], to calibrate the AFM, i.e., to obtain the characteristic curve \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\) that links the signal of the cantilever to its deflection \(d_{\mathrm {AFM}}\), the use of the interferometers with stabilized lasers of the NMM-1 [58] by moving the stage of the NMM-1 one-dimensionally through the measuring range of the cantilever and recording both \(d_{\mathrm {AFM}}\) and the position of the stage measured by the interferometers is possible. For the calibration, the second axis of the rotational kinematics (cf. Fig. 1) was in its zero position, and the probe direction was opposite the direction of the z-axis of the NMM-1. Therefore, the calibration was done against the traceable z-interferometer. The sample was moved toward the cantilever until full contact with an approach velocity of 100 nm/s. The amplitude of the oscillation of the cantilever \(R_{\mathrm {AFM}}\) and the distance value of the z-interferometer \(z_{\mathrm {NMM}}\) were recorded with a point distance of 0.1 nm. Afterward, the characteristic curve \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\) was fitted as cubic polynomial within the intermittent-contact range. Thus, the range of the characteristic curves was slightly less than the free oscillation amplitude of the cantilever.

By repeating the calibration routine several times, the short-term precision (repeatability) of the sensor was derived. The calibration was conducted 50 times within approximately 2 min, and for each calibration, a characteristic curve was derived. The deviations between repeated characteristic curves are a measure of the repeatability of the sensor along its entire measuring range.

Figure 4 shows the deviation

$$\begin{aligned} {\Delta} z= d_{\mathrm {AFM}}(R_{\mathrm {AFM}})- z_{\mathrm {NMM}}\,, \end{aligned}$$
(2)

where \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\) is calculated using the first characteristic curve. Depicted in red are the residues of the characteristic curve. Shown in green are the deviations to the 49 other calibrations. Some significant drifts of the characteristic curves and systematic periodic deviations are detected. These errors will be investigated in the subsequent section.

Fig. 4
figure 4

Deviations of the deflection of the cantilever to the z values of the NMM-1 for 50 calibrations. The residues of the first curve are shown in red

Full size image

To obtain a single value for the short-term precision (repeatability) of the sensor, every characteristic curve is applied to the measuring points of every calibration and \({\Delta} z\) is calculated according to Eq. (2). Figure 5 shows \({\Delta} z\) as a histogram, with its standard deviation \(\sigma _{\mathrm {calibration}}\), which is 3.1 nm.

Fig. 5
figure 5

\({\Delta} z\) as a histogram, with its standard deviation \(\sigma _{\mathrm {calibration}}\), which is 3.1 nm

Full size image

To investigate the noise level of the cantilever, standstill measurements were conducted by enabling the controller of the NMM-1 to keep \(d_{\mathrm {AFM}}\) in the middle of the characteristic curve, and data were recorded three times for 90 s with the maximum sampling frequency of the NMM-1 (6.25 kHz). The results are shown in Fig. 6. The three standard deviations of \(z_{\mathrm {NMM}}\) are 2.4 nm (red), 2.5 nm (green), and 2.7 nm (blue). The combination of these values yields \(\sigma _{\mathrm {standstill}}\), which is 2.5 nm. This value is affected by thermal variations. Nevertheless, deducing the noise level as the standard deviation of \(d_{\mathrm {AFM}}\) is possible as the controller compensates for the mainly temperature-induced low-frequency variations. The three standard deviations of \(d_{\mathrm {AFM}}\) and thus \(\sigma _{\mathrm {noise}}\) are 0.2 nm.

Fig. 6
figure 6

Three standstill measurements in closed-loop mode over 90 s. On the upper panel, an offset has been added to \(-z_{\mathrm {NMM}}\) for illustrative purposes

Full size image

3.2 Long-Term Precision

Thus far, the investigations presented have been on a timescale of several minutes only. Nevertheless, complex measurements might last several hours. Thus, the precision of the sensor needs to be investigated on a longer timescale as well. To determine the long-term (intermediate) measurement precision of the sensor, standstill measurements were conducted for 15 s every 10 min for several hours. The measured z value \(z_{\mathrm {M}}\) was calculated using the following equation:

$$\begin{aligned} z_{\mathrm {M}}= -z_{\mathrm {NMM}}+ d_{\mathrm {AFM}}\end{aligned}$$
(3)

For each 15 s-measurement, the offset was calculated as the mean of \(z_{\mathrm {M}}\). Between the measurements, the cantilever was withdrawn from the surface to prevent tip or sample damage. Figure 7 shows the mean of \(z_{\mathrm {M}}\) over 18 h after stabilization. Within this period, the standard deviation of the offset, \(\sigma _{\mathrm {long-term}}\), is 6.6 nm.

Fig. 7
figure 7

Long-term precision over 18 h

Full size image

3.3 Scans on a Calibration Grating

Closed-loop scans were conducted on a calibration grating (TGZ1 of NT-MDT), a type PPR material measure according to ISO 25178-70 [57] with a nominal step height of (21.4 ± 1.5) nm. First, the measured values within the (negated) coordinate system of the NMM-1 were calculated according to Eq. (3). Afterward, the measured values were transformed into the workpiece coordinate system (WCS).

Because of the low-pass filtering associated with the calculation of \(d_{\mathrm {AFM}}\), as well as different ADCs used for the probe signal and interferometers of the NMM-1, latency between the signals of the interferometers and the probe signal is inevitable [43]. To avoid the effects caused by this latency, the scan velocity was set to only 5 \(\upmu \)m/s, and the point distance was set to 1 nm. The scan length was 90 \(\upmu \)m, and the step height was determined according to ISO 5436-1 [59]. The grating was placed within the xy-plane of the NMM-1. For the 30 scans on the same line at the measuring object, the mean of the determined step heights is 20.92 nm, which is consistent with the nominal value, and the associated standard deviation \(\sigma _{\mathrm {step~height}}\) is 59 pm. The high reproducibility of the scans is shown in Fig. 8, where 30 scans of the complete scan length (upper panel) and an irregularity on one step (lower panel) are depicted.

Fig. 8
figure 8

Thirty scans on the same line on the measuring object of the complete scan length (upper panel) and an irregularity on one step (lower panel) on the calibration grating

Full size image

3.4 Comparison

Table 1 shows the results of the investigations on the metrological characteristics of the sensor system, both with actuation by a piezoelectric actuator and a cantilever with integrated micro heater. Apart from \(\sigma _{\mathrm {standstill}}\), the results are similar. However, thermal variations certainly influence all standard deviations, except for \(\sigma _{\mathrm {noise}}\) and \(\sigma _{\mathrm {step~height}}\). Because of the stochastic nature of thermal variations, ensuring that the results are equally influenced by these variations is impossible. To separate the effects of thermal variations from the determined short-term precision \(\sigma _{\mathrm {calibration}}\), the drift between the characteristic curves will be rectified in the subsequent section. However, for the sake of completeness, the obtained values for the offset-corrected \(\sigma _{\mathrm {calibration}}\), \(\sigma _{\mathrm {cal.,c}}\), which is 0.4 nm for the cantilever with integrated micro heater and 0.5 nm for the actuation with a piezoelectric actuator, are also included in Table 1. Therefore, because the characteristics unaffected by thermal variations (i.e., \(\sigma _{\mathrm {cal.,c}}\), \(\sigma _{\mathrm {noise}}\), and \(\sigma _{\mathrm {step~height}}\)) are nearly identical and the other characteristics are still similar, we can conclude that the metrological characteristics are not deteriorated by the application of a cantilever with integrated micro heater. Furthermore, as stated in the Introduction, the application of such a cantilever drastically simplifies the requirements for the sensor holder, thus enabling the application of materials with a low coefficient of thermal expansion, which are often difficult to machine.

Table 1 Comparison of both modes of actuation
Full size table

4 Error Sources

Figure 4 shows significant drifts between the calibrations and some systematic periodic deviations. As drifts between the calibrations are most likely attributable to low-frequency thermal variations, the effects of these drifts will be rectified in Sect. 4.1. The systematic periodic deviations may arise from nonlinearities of the interferometers of the NMM-1, which will be discussed in Sect. 4.2.

4.1 Drift

The offset of the characteristic curve \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\) is equal to its polynomial coefficient of the order zero. By subtracting this offset from the values of \(z_{\mathrm {NMM}}\) and recalculating the characteristic curve, we obtain the offset-corrected characteristic curve. After this correction, the offset-corrected \(\sigma _{\mathrm {calibration}}\), \(\sigma _{\mathrm {cal.,c}}\), can be calculated, as discussed in the previous section. In Fig. 9, \({\Delta} z\) of the offset-corrected calibrations is shown as a histogram, with its standard deviation \(\sigma _{\mathrm {cal.,c}}\), which is 0.4 nm.

Figure 10 shows \({\Delta} z\) of the offset-corrected calibrations, where \(d_{\mathrm {AFM}}(R_{\mathrm {AFM}})\) is calculated using the first characteristic curve, and the residues of this characteristic curve are depicted in red. The subsequent section discusses how far the remaining systematic deviations might arise from periodic nonlinearities of the z-interferometer of the NMM-1.

Fig. 9
figure 9

\({\Delta} z\) of the offset-corrected calibrations as a histogram, with the standard deviation \(\sigma _{\mathrm {cal.,c}}\), which is 0.4 nm

Full size image
Fig. 10
figure 10

Deviations of the deflection of the cantilever to the offset-corrected z values of the NMM-1 for 50 calibrations. The residues of the first curve are shown in red. The dashed line denotes a sine curve with a periodicity of \(\lambda /12\)

Full size image

4.2 Periodic Nonlinearities of the z-interferometer

To achieve directional sensitivity, as well as a resolution far below the laser’s wavelength \(\lambda \) with a homodyne interferometer, two signals with a phase shift of 90\(^\circ \) are evaluated, which is also known as phase quadrature measurement [60]. However, because of the mismatched amplitude or offset of the signals, as well as a phase shift different from 90\(^\circ \), significant nonlinearities of the evaluated length values may occur, mainly with a periodicity of \(\lambda /2\) (in the case of a \(\lambda /2\)-interferometer) [61, p. 67 et seq.]. Peter Heydemann proposed the correction of these nonlinearities by fitting an ellipse to the quadrature signals and rectifying them onto a circle [62]. This procedure, known as the Heydemann correction, will be applied to the repeated, offset-corrected calibrations (cf. Fig. 10).

To determine the parameters of the ellipse of the z-interferometer, the stage of the NMM-1 has been moved 30 times for 2 \(\upmu \)m in the z-direction with the cantilever being in free air just before the sample. \(z_{\mathrm {NMM}}\) and the unprocessed quadrature signals \(Q_{\mathrm {A}}\) and \(Q_{\mathrm {B}}\) were recorded with a point distance of 1 nm. The equation of the ellipse is given by

$$\begin{aligned} AQ_{\mathrm {A}}^2+BQ_{\mathrm {B}}^2+CQ_{\mathrm {A}}Q_{\mathrm {B}}+DQ_{\mathrm {A}}+EQ_{\mathrm {B}}= 1 \, , \end{aligned}$$
(4)

where \(A\), \(B\), \(C\), \(D\), and \(E\) denote the coefficients of the equation of the ellipse. These coefficients are determined by fitting Eq. (4) to the measured data. With these coefficients, the relevant parameters of the ellipse, which are the phase deviation \(\alpha \), radius ratio \(r\), offset of \(Q_{\mathrm {A}}\), \(O_{\mathrm {A}}\), and offset of \(Q_{\mathrm {B}}\), \(O_{\mathrm {B}}\), can be calculated using Eqs. (5)–(8).

$$\begin{aligned}&\alpha = \arcsin \left(\frac{C}{\sqrt{4AB}}\right) \end{aligned}$$
(5)
$$\begin{aligned}&r= \sqrt{\frac{B}{A}} \end{aligned}$$
(6)
$$\begin{aligned}&O_{\mathrm {A}}= \frac{2BD-CE}{C^2-4AB} \end{aligned}$$
(7)
$$\begin{aligned}&O_{\mathrm {B}}= \frac{2AE-CD}{C^2-4AB} \end{aligned}$$
(8)

In a final step, the corrected signals are obtained as follows [61, p. 69]:

$$\begin{aligned}&Q_{\mathrm {A,c}}= Q_{\mathrm {A}}- O_{\mathrm {A}}\end{aligned}$$
(9)
$$\begin{aligned}&Q_{\mathrm {B,c}}= \frac{Q_{\mathrm {A,c}}\cdot \sin (\alpha )+r(Q_{\mathrm {B}}-O_{\mathrm {B}})}{\cos (\alpha )} \end{aligned}$$
(10)

In Fig. 11, the uncorrected and corrected quadrature signals are shown in red and blue, respectively, and the corrected quadrature signals of the calibrations are shown in green. Notably, only approximately a quarter of the complete quadrature is covered when conducting the calibrations. From the quadrature signals, the length value is obtained by demodulation. The demodulated z value of the NMM-1 for the uncorrected quadrature signals is \(z_{\mathrm {NMM}}\), and the demodulated value for the corrected signal is \(z_{\mathrm {NMM,c}}\). In Fig. 12, the error between both values, i.e., \({\Delta} _{\mathrm {NMM}}\,= z_{\mathrm {NMM}}\,- z_{\mathrm {NMM,c}}\), is shown. The amplitude of this error is approximately 1.5 nm. The spatial Fourier analysis revealed the main error components of \(\lambda /2\) and \(\lambda /4\).

Fig. 11
figure 11

Uncorrected (red) and corrected (blue) quadrature signals of the z-interferometer of the NMM-1. Shown in green are the corrected quadrature signals of the calibrations

Full size image
Fig. 12
figure 12

Error between the uncorrected and corrected length values of the z-interferometer of the NMM-1 (upper panel) and the Fourier spectrum of this error (lower panel)

Full size image

Nevertheless, as depicted in Fig. 10, the error on the characteristic curves has a wavelength of approximately \(\lambda /12\), which is probably caused by reflections on the surface of the beam splitter cube in the measuring arm that leads to multibeam interference. Thus, it cannot be corrected by the Heydemann correction.

As the range of the characteristic curves is only approximately 80 nm, only approximately a quarter of the complete quadrature is covered when conducting the calibrations (cf. Fig. 11); thus, the error components of \(\lambda /2\) and \(\lambda /4\) might lead to systematic errors on the obtained characteristic curves, e.g., a mismatched inclination of the characteristic curve, but will not lead to errors between repeated calibrations conducted approximately at the same location of the quadrature. As a consequence, the Heydemann correction does not reduce \(\sigma _{\mathrm {cal.,c}}\) (which is still 0.4 nm), although it is in large part caused by the z-interferometer of the NMM-1.

5 Summary, Conclusion, and Outlook

In this article, the application of a cantilever with integrated sensing and actuation as part of an AFM with an adjustable probe direction has been shown and evaluated. Although the thermal sensitivity of the rotational axes limits the achievable long-term measurement precision to approximately 7 nm, when correcting these mainly thermally induced low-frequency errors, standard deviations in the picometer range are obtained. Systematic periodic errors are detected on the characteristic curve, with a standard deviation of approximately 0.4 nm. As these errors occur in large part with a spatial frequency of \(\lambda /12\), they are most likely caused by the interferometer. The comparison of the metrological characteristics of the sensor system equipped with the cantilever with an integrated micro heater for its stimulation and the sensor system equipped with a piezoelectric drive for its stimulation shows no significant differences between the two modes of actuation.

This study intended to verify the applicability of a cantilever with integrated sensing and actuation. This verification was successful; therefore, the redesign of the rotational kinematics will be based on the cantilever with integrated sensing and actuation. The removal of the piezoelectric actuator enables the simplification of the sensor holder and the application of materials with a low coefficient of thermal expansion. Furthermore, the effects of the creepage of piezoelectric actuators might have been erroneously attributed to thermal variations, so far. Thus, the removal of the piezoelectric actuator from the metrology frame might result in improved metrological characteristics, as well. Possible means to reduce the thermal sensitivity of the rotational kinematics are the application of smaller rotational axes or a different arrangement of the rotational axes. Placing the first axis above the Zerodur frame (cf. Fig. 1), reducing the length of the invar spacers, and connecting the first axis with the angle piece by materials with a low or even negative expansion coefficient, might result in compensating thermal expansions of the first axis and the remaining part of the sensor system.