1 Introduction

1.1 Research Background and Significance

On the whole, mechanical products comprise parts and components. Assembly of mechanical products refers to a process in which parts and components are matched and joined by complying with technical requirements, producing semi-finished or finished products. Assembly process is not a simple connection of qualified parts. It is consistent with technical requirements of all levels of component assembly and general assembly. Besides, it ensures the process of qualifying product quality through correction, adjustment, balance, matching and repeated tests. Accordingly, product assembly should be stressed.

The quality of parts is the basis of the quality of products. Unqualified parts cannot be assembled with qualified parts to satisfy technical requirements. Thus, in almost all current assembly operations, only qualified parts are taken for assembly, so considerable unqualified parts are treated as waste. Though its comprehensive manufacturing has been noticeably improved over the past few years, China still lags behind developed nations (e.g., the United States and Japan). As suggested by the National Bureau of Statistics in 2017, the average product quality in China was 57.1%, whereas the product qualification rate took up 93.8%. This indicates that considerable unqualified parts per year, wasting resources and costs remain. In actual production activities, some parts with unqualified assembly dimensions cannot be assembled with other qualified parts, whereas they may be assembled with other unqualified parts to comply with technical requirements.

Accordingly, the present study proposed an intelligent matching assembly system based on unqualified parts with tolerances out of range. The assembly meeting the technical requirements was completed, so the unqualified parts could be reused, which could greatly reduce production costs and improve assembly efficiency.

1.2 Research Status

To our best knowledge, the reuse of unqualified parts has been rarely studied. To explore intelligent matching assembly, this study was conducted upon assembly tolerances, achieving the effect of reusing unqualified parts. This method pertains to assembly optimization, and the existing research status on this point is described below.

In foreign nations, in the 1980s, Bourjault studied the optimization of assembly sequence planning and proposed the concept of assembly sequence priority relationship and the assembly relationship diagram model. Based on the mentioned relationship, he presented the assembly order [1]. next, Homem de Mello and Sanderson proposed a disassembly method to solve assembly sequences, improve assembly sequence planning efficiency, and express assembly sequences with AND/OR diagrams [2, 3]. Tonshoff summarized some typical knowledge (e.g., process flow, part matching type, and assembly connection). Based on the definition of knowledge priority, the effect of the mentioned factors on the assembly order can be distinguished to some extent [4]. The Fraunhofer Institute of Industrial Engineering (IAO) in Germany developed a VR-based assembly planning system that simulates assembly operations in a virtual environment, which allowed assembly and disassembly to be performed interactively, generated pre-assembly trends, and provided users with a comprehensive analysis of assembly time and costs to yield the optimal assembly sequence solution [5].

Since the late 1980s, the relevant research has also been conducted in China. Kang Youshu and Zhou Ji studied the trajectory planning problem in assembly design, and the method of collisional interference tests and constrained reasoning were employed to generate the assembly trajectory of components [6]. Gu Tingquan et al. studied the automatic generation and assessment of assembly sequences, and they developed an automatic assembly sequence generation algorithm based on cut sets [7]. With a directed constraint graph to express the constraint relationship between parts, Hu Xiaomei and Zhu Wenhua developed a directed constraint decomposition method based on association cancellation to yield an optimal assembly sequence [8]. Li Hailong and Dong Jinxiang designed a method to express the positional assembly relationship based on constraint representation. The constraint was solved after being transformed into an equation [9].

1.3 Organization and Innovation Points

The rest of the paper is organized as follows. In Sect. 2, the architecture of the intelligent matching system, key matching strategies and revenue estimation method are introduced. In Sect. 3, the algorithm applied in intelligent matching, the matching process to obtain the matching scheme, and the design of the optimal solution are presented. In Sect. 4, a simulation by Monte Carlo method is presented, followed by the matching scheme yielded by the system, and the results of the strength analysis and benefit assessment. Lastly, in Sect. 5, the conclusion and research value are drawn.

The innovations of the present study are as follows: (1) an intelligent matching system was added to the existing assembly process to reuse some unqualified parts, which reduced the production assembly cost; (2) the concept of mating bases was proposed, and the matching relationship was quantified between parts by the function expression of size data; (3) the matching program with genetic algorithm was designed to find the optimal matching scheme at a faster speed; (4) Monte Carlo method was used to simulate the actual part data and to verify the system effectiveness and practicability.

2 The Design of intelligent Matching Assembly System

2.1 Architectural Design of Intelligent Matching Assembly System

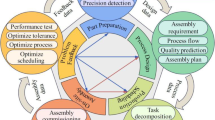
The first step in assembly activities of most factories refers to quality inspection of the parts to be assembled. The test determines whether geometrical and dimensional tolerances abide by design requirements, and whether the surface of parts is defective [10]. Parts passing the test will participate in the assembly activity, and the unqualified parts will be treated as waste. To change this phenomenon and reduce losses, this study designed an intelligent matching assembly system, and added it to the conventional system. The structure of the system designed is illustrated in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the intelligent matching assembly system

Full size image

The primary task of the system refers to labelling the parts having been judged to be unqualified by quality inspection, and to record all the dimensional data recorded into the database of unqualified parts. The matching object of the system is the part whose partial dimensional tolerance does not abide by design requirements. Thus, before running the matching program, data screening should be conducted to eliminate the part judged as a defective one due to surface defects or material problems.

To complete the assembly activity, the product structure to be assembled should be first analyzed to determine the positional relationship between product components (e.g., the feature attributes of components and the matching relationship between components) [11]. Accordingly, the matching strategy is to understand the connection relationship between the parts, the transmission relationship and the assembly technical requirements, extract the dimensional elements of the respective part to be assembled, and then establish the relationship between the dimension of the respective part according to the assembly relationship expressed as a function. lastly, according to the assembly relationship, the most suitable parts are matched with the ultra-difference parts to complete the assembly activities.

Intelligent matching is based on matching strategy, with the maximum utilization or the average assembly effect as the objective function, finding the most suitable assembly object for the respective part, and using the intelligent algorithm to find the optimal matching scheme.

The matching result may not be applied to the actual assembly activity because it may happen that the assembly task can be completed, but the assembled components or products do not meet the strength or technical requirements. Thus, it is necessary to calculate the dimensions of the final assembled product and strength properties such as tensile and compressive resistances by the dimensional data of the respective part. Lastly, through the calculation of costs and benefit, the feasibility and economy of the scheme are determined.

2.2 Design of Matching Strategy

The matching strategy is to express the connection relationship between the parts to be assembled by mathematical letters and symbols, and express the assembly technical requirements by the effective interval of the dimension matching. In fact, the respective part has multiple dimensions, whereas not all dimensions participate in the assembly and coordination. Accordingly, given the actual situation, the dimensions involved in the assembly should be extracted as the feature data of the part, and the other dimensions should be recorded as the remaining data. Next, by analyzing the transmission-connection relationship between the parts, the feature dimensions of the other parts required to be matched with a certain feature dimension are identified, and a plurality of mating bases form a dimensional relationship network. Lastly, according to the tolerance range of the qualified parts and the technical requirements of the matching, a reasonable sized matching range is determined as the constraint condition corresponding to the associated feature size, so the design of the matching strategy is completed.

Suppose that a product is assembled from n parts, and the ith part has \({m}_{i}\) feature dimensions, then the feature dimension variable set of the ith part is expressed as

$$X_{i} = \{ x_{i,1} ,x_{i,2} ,x_{i,3} \ldots x_{{i,m_{i} }} \}$$
(1)

Each mating base covers two or more feature sizes (e.g., the simplest hole and shaft fit) (regardless of the geometric tolerance), composed of the diameters of the shaft and hole. The product assembly yields a finite number of mating bases, each of which was given a reasonable fit interval by the limit of technical requirements and tolerance grade. The constraint is expressed as Eq. 2. Lastly all mating bases and their reasonable mating intervals takes up the matching strategy.

$$\emptyset_{1} \le f\left( {x_{i,j} ,x_{m,n} ...} \right) \le \emptyset_{2}$$
(2)

where \(x_{i,j}\) denotes the jth feature dimension of the ith part;\(\emptyset = \left[ {\emptyset_{1} ,\emptyset_{2} } \right]\) expresses the effective interval of the mating base (Fig. 2).

Fig. 2
figure 2

Schematic diagram of the allocation strategy

Full size image

2.3 Quality Inspection and Benefit Assessment

To ensure that the assembled product abides by the quality inspection requirements, the quality of each product yielded in each sub-solution of the final matching scheme should be tested. The test generally detected strength and shape sizes. The strength test results were determined by the feature dimension and remaining dimension of the respective part. The general method aimed to calculate the area of the contact surface between the parts. Moreover, the attribute data of the material could be exploited to yield the maximum force transmitted by the respective contact surface. The maximum bearing capacity of the product could be determined by dividing the minimum transmission force by a certain safety factor. Lastly, maximum bearing capacity was compared with the design requirements of the product to verify whether it is qualified. Next, the unqualified assembly sub-plan released the data of the part to the database of unqualified parts, waiting for the next matching assembly.

Each match produced a certain number of qualified sub-solutions, and the products assembled with matching scheme would also comply with the technical requirements, which explains the reason why there were more qualified products than the current assembly system. As impacted by the operation of the intelligent matching system, however, the management cost, inventory cost and parts transportation and assembly costs additionally increased. Thus, the final income is expressed as:

$$profit = N*p - C_{m} - C_{r} - C_{t}$$
(3)

where N denotes the number of qualified products yielded by the system; p represents the price of a single product; \(C_{m}\) expresses the management fee; \(C_{r}\) is the inventory fee; \(C_{t}\) denotes the part transportation and assembly cost. On the whole, the latter three expenses were related to the actual production situation of the respective factory, so the empirical value could be calculated only based on historical production data. If the last calculated benefit is positive, the assembly scheme will be practicable; otherwise, the matching scheme will be abandoned.

3 Algorithm Design of Intelligent Matching Program

3.1 Genetic Algorithm

Overall, there are many solutions to the part matching problem. However, if there exist assessment criteria for the solution, the optimal one should be selected. To find the optimal solution, a number of classic algorithms should be applied [12]. Numerous algorithms have been developed to solve this simple problem, i.e., finding the optimal solution (e.g., simulated annealing, particle swarm optimization, genetic algorithm and hill climbing algorithm). Each algorithm has its own advantages and disadvantages and scope of applications [13]. As impacted by the wide applicability and easy convergence of genetic algorithm, the present study adopted genetic algorithm to yield the optimal solution.

The idea of genetic algorithm was derived from Darwin's theory of evolution and Mendel's theory of genetics. Darwin considers that each species will progressively adapt to the environment in development. Several characteristics of each individual will be inherited by its offspring, whereas they are not equivalent to the parents’ characteristics. The mentioned novel features will be retained if they are adapted to the environment; otherwise, they will be eliminated. Genetic algorithm aims to represent a group of solutions as a group of chromosomes, introduce them in the environment of the problem following the principle of survival of the fittest, and select the chromosomes exhibiting higher fitness. Next, the mentioned chromosomes will be duplicated to form the parent chromosome, which will be crossed and mutated to produce a novel generation of chromosomes more adaptive to the environment. Accordingly, the continuous evolution from generation to generation will lastly converge to an individual that is most adaptive to the environment [14]. The schematic diagram of the overall genetic algorithm is presented in Fig. 3.

Fig. 3
figure 3

Program flow chart of genetic algorithm

Full size image

3.2 Program Design of Matching Scheme

Suppose that a product assembly requires n different parts, numbered 1, 2…n, that the number of the respective part required for a product is \(n_{1} ,n_{2} \ldots n_{n}\), and that the number of parts able to be called in the database of unqualified parts is \(N_{1} ,N_{2} \ldots N_{n}\). In theory, the maximum number of completed products for the respective type of part is \(Z_{i}\):

$$Z_{i} = N_{i} /n_{i} .$$
(4)

Next, the parts are sorted from small to large sizes by complying with the maximum number of products of each kind of parts. To prevent the parts late for match from having no resources for matching, priority is given to the parts in the front of the order. For instance, if the order is \(Z_{5} ,Z_{2} ,Z_{6} \ldots\), the matching method is as follows. With part 5 being the initial part, part 2 is selected based on the mating bases of parts 5 and 2, and then part 6 is selected under the mating base containing part 6. On that basis, the sub-matching scheme is obtained.

The key of the algorithm of this program refers to designing the selection function according to the situation of the mating base. With the above case as an example, part 2 with part 5 is selected as the initial part. First, find the mating bases between part 5 and part 2 and the reasonable matching range from the distribution strategy. It is assumed that there are two mating bases between them:

$$f_{1} \left( {X_{2,1} ,X_{5,3} } \right) = X_{2,1} - X_{5,3}$$
(5)
$$f_{2} \left( {X_{2,2} ,X_{5,1} } \right) = X_{2,1} + X_{5,3}$$
(6)

In Eq. 5, \(X_{2,1}\) expresses the first feature dimension of part 2, and \(X_{5,3}\) denotes the third feature dimension of part 5. The letters in Eq. 5 have the identical implication.

On the whole, the more the value of the mating base in the center of the qualified range, the more effectively the assembly will satisfy the design requirements. There may be two or more mating bases between the two parts, so a certain weight should be set by complying with the importance of the mating base in the actual assembly. On that basis, the selection function is designed as

$$F_{5,2} = \alpha \left| {f_{1} \left( {X_{2,1} ,X_{5,3} } \right) - \emptyset_{1}^{*} \left| { + \left( {1 - \alpha } \right)} \right|f_{2} \left( {X_{2,2} ,X_{5,1} } \right) - \emptyset_{2}^{*} } \right|$$
(7)

where \(\alpha\) denotes the weighting factor indicating the degree of importance; \(\emptyset_{i}^{*}\) represents the median of the qualified range of the mating base, and the qualified interval is determined by the tolerance range of the qualified parts of the two parts.

According to part 5, the method of selecting part 2 from the unqualified part database refers to traversing the data of all the parts 2 in the library, as well as selecting the part 2 with the minimal \(F_{5,2}\) value as the matching object. The function for selecting part 6 is the weighted sum of the selection function values of parts 5 and 2, as well as the selection function values of parts 6 and 2. The weighting factor is determined by the importance of the two matrices.

$$F_{{6,\left( {5,2} \right)}} = \beta F_{6,5} + \left( {1 - \beta } \right)F_{6,2}$$
(8)

where \(\beta\) denotes the weighting factor that represents the degree of importance.

This method is capable of matching the other parts most suitable for a certain part 5. This process is illustrated in Fig. 4. To ensure the rationality of the matching sub-scheme in depth, the qualification test is lastly performed. The test method aims to verify whether the calculated results of all the mating bases of the sub-scheme pertain to the corresponding qualified interval.

Fig. 4
figure 4

Single solution assembly process chart

Full size image

If the sub-matching scheme fails to pass the qualification test, the sub-assembly scheme is proved to be not consistent with the design requirements. Next, the initial part data will be skipped, and the data of other matching parts will be released.

3.3 Design of Optimal Solution Program

The program design presented in Sect. 3.2 allows the data of a set of initial parts to be matched to the other parts fitting the best, which addresses the matching problem of a sub-scheme in the matching scheme. In fact, a part may have considerable group data in the database. For instance, the initial part 5 of the above example may cover 100 sets of data in the database, i.e., there are 100 different parts 5 of the unqualified condition. By matching the other parts by complying with different priorities, different total matching schemes will be formed, so the system adopts genetic algorithm to select the optimal matching order, as an attempt to yield the optimal matching scheme.

First, a number is set for each set of initial part data read from the database of unqualified parts. Assume that there are 10 sets of data for the initial part in the database, the encoding of one chromosome may be written as:

$$\left[ {8,3,5,9,10,2,6,4,1,7,5} \right]$$
(9)

The result of the interpretation of the above chromosome is presented below. Priority for the data of the eighth set of initial parts to match other parts, followed by the 3rd group, in this order till the data of each group are matched to the other parts. As a result, a general matching scheme is formed.

The steps to determining the optimal solution based on the idea of genetic algorithm are elucidated below:

Step 1: N sets of effective solution codes are randomly generated to form the parent genome. On the whole, the value of N is an even number ranging from 10 to 20.

Step 2: Chromosome crossing is performed, the parent chromosome set is randomly divided into N/2 groups, gene exchange is conducted between two chromosomes of each group in the random segment, and then feasible treatment is performed to obtain N child chromosomes. Assume that 3–6 segments of genes of two chromosomes of a group are exchanged (Fig. 5).

Fig. 5
figure 5

Schematic diagram of gene crossing

Full size image

Step 3: Chromosomal variation is performed. To prevent the solution from converging to the local optimal solution, the child chromosome should be altered. The general mutation method aims to exchange the genetic code of the two random positions on the chromosome.

Step 4: Fitness is calculated. The respective chromosome can be interpreted as an assembly matching scheme. To assess the quality of the scheme, the fitness function should be designed. The fitness function developed with the maximum utilization rate as the goal is written as:

$$F = Z^{*} /Z$$
(10)

where \(Z^{*}\) is the number of effective sub-schemes in the scheme; \(Z\) expresses the maximum number of finished products of initial parts.

The fitness function developed to maximize the average assembly effect is defined as:

$$F = Z^{*} /\left( {\mathop \sum \limits_{m = 1}^{{m = Z^{*} }} \mathop \sum \limits_{n = 1}^{k} (\left| {f_{n}^{\left( m \right)} \left( {X_{i1,j1} ,X_{i2,j2} } \right) - \emptyset_{n}^{*} } \right| - \varphi } \right)$$
(11)

where k represents the total number of mating bases; \(\emptyset_{n}^{*}\) expresses the effective interval center value of the nth mating basis; \(\varphi\) denotes the maximum allowable deviation value, i.e., the distance value from the effective interval center to the boundary.

Step 5: The next set of parent chromosomes is selected by employing roulette method, so the probability, i.e., each chromosome is selected, is proportional to its fitness.

$$P_{i} = F_{i} /\mathop \sum \limits_{i = 1}^{n} F_{i} \quad i \in \left( {1,2N} \right)$$
(12)

where \(F_{i}\) denotes the fitness value of the i-th chromosome; \(P_{i}\) represents the probability that the i-th chromosome is selected:

$$q\left( i \right) = \mathop \sum \limits_{j = 1}^{i} P_{i} \quad i \in \left( {1,2N} \right)$$
(13)

where \(q\left( i \right)\) denotes the cumulative probability of the ith chromosome.

The selection method is presented below. A random number r is generated in the range of [0, 1]. If r < q(1), the first chromosome is selected; otherwise, the kth chromosome is selected to satisfy the condition of q(k − 1) < r < q(k). The mentioned selection method is repeated N times, and N chromosomes act as the parent of the next iteration.

Step 6: The operations are performed from step 2 to step 5 till the predetermined number of iterations is met. Subsequently, the chromosome with the largest fitness value is selected from the last set of parent chromosomes and then interpreted as the final solution.

The structure diagram of the entire intelligent matching assembly system is presented in Fig. 6. The system first solves the matching problem of a single assembly scheme (sub-scheme). The method aims to obtain the corresponding mating bases by analyzing the matching constraints between the parts, subsequently design the selection function as the basis for matching parts, and lastly match the respective part in turn to obtain a feasible assembly solution. Specific to the respective type of part with many ultra-difference parts, there are different assembly methods following different priority matching orders. Thus, the system adopts genetic algorithm to solve the problem. First, the objective function is selected given the demand of production, and then the fitness function is designed with the constraints of the matching basis. Lastly, the optimal matching order is iteratively calculated. Accordingly, the system is capable of using a single assembly matching scheme in sequence by complying with the optimal matching order to yield the global optimal assembly scheme.

Fig. 6
figure 6

Intelligent matching assembly system structure diagram

Full size image

4 Example Verification Based on Monte Carlo Simulation

4.1 Example Data Generation Based on Monte Carlo Simulation

In the present study, the effectiveness of the system was verified by the assembly of a bolt and a nut and the connected parts with two through holes. The assembly drawing is illustrated in Fig. 7. The bolt was made of M10 × 1.5 standard parts; the tensile strength of the material was 170 N/mm2; the nut adopted the standard part of M10 × 1.5; the tolerance band was 6H/6 g; the diameter of the through hole of the two connected parts was 11 mm; the tolerance grade reached JS11. Through the national standard query and calculation, qualified range of feature dimensions for the respective part are listed in Table 1.

Fig. 7
figure 7

Schematic diagram of the case assembly

Full size image
Table 1 Qualified range of feature dimensions for the respective part
Full size table

Practice proved that no matter how stable the conditions are maintained in the production process. Even if the operators, machines, raw materials, processing methods, processing environment and other conditions are identical, the characteristics of the respective batch of products produced will fluctuate. Such a type of fluctuation is unavoidable and exists in any process. Through considerable data analysis, the final product quality was found to be normally distributed under the effect of random fluctuation [15].

In the present study, Monte Carlo simulation method was adopted to simulate the distribution of tolerances in actual machining by computer technology to establish a database of non-conforming parts. Monte Carlo simulation refers to a method based on probability and mathematical statistics to approximate the random variables [16]. When the parameter in the problem acted as a random variable, the parameters were sampled by Monte Carlo method to simulate the actual situation and employed to address the problem. The key to Monte Carlo simulation was recognized as the establishment of random sequences. Subsequently, some properties of the sequence were established (e.g., probability distribution and mathematical expectation in relation to practical problems). Moreover, the objectivity of the sequence should be ensured, and lastly solved and outputted [17,18,19] (Fig. 8).

Fig. 8
figure 8

Data acquisition flow chart of Monte Carlo simulation

Full size image

This example assumes that all parameters receive the normal distribution. The qualified tolerance range of the part size was taken as the confidence interval, and the pass rate was confidence. Subsequently, the normal distribution parameters of the respective size was calculated (Table 2).

Table 2 Normal distribution parameter table for the respective part size
Full size table

The normal distribution random number x is defined as follows:

$$R = \sqrt { - 2\ln \left( {u_{1} } \right)} \cos \left( {2\pi u_{2} } \right)$$
(14)
$$x = \mu + \sigma R$$
(15)

where \(u_{1}\) and \(u_{2}\) denote random numbers uniformly distributed by (0, 1).

With the simulation method, the data of 1000 bolts, nuts, the connected member 1 and the connected member 2 were simulated. The data of each dimension complied with the normal distribution of the corresponding parameters. Next, the data of the unqualified parts were filtered out and imported into the database. In Fig. 9, the simulation result was more consistent with the actual situation, with the distribution of the pitch diam of bolts as an example. The final statistical results of the data are listed in Table 3.

Fig. 9
figure 9

Simulation data distribution diagram of the pitch diam of bolts

Full size image
Table 3 Details of the simulation data
Full size table

4.2 Intelligent Matching Scheme

The mating bases in this assembly operation and their effective ranges are listed in Table 4.

Table 4 Mating base and effective interval table in the case
Full size table

In this scenario, only one component was required for each component of a product. Accordingly, as revealed from the Monte Carlo simulation data, the maximum number of completions of the connected parts 1 was the least in this matching scheme. Thus, the connected parts 1 was an initial part, and the connected member 2, the nut, and the bolt were sequentially matched under the condition of the mating base. Given the content of the matching method in the third subsection, the specific method aimed to select the connected part 2 by complying with the mating base 4, subsequently select the nut given the mating base 6, and lastly select the bolt based on the mating bases 1, 2, 3, and 5. The weight coefficient was determined by the importance score.

The initial part of this case had 52 sets of data, so the chromosome coding length reached 52. Next, the maximum utilization and maximum assembly effect were respectively taken as the target functions. The genetic algorithm was adopted to yield the optimal matching scheme. As impacted by the limited space, Table 5 only lists the details of the first 10 sub-programs.

Table 5 Data detail table for partial matching sub-scheme
Full size table

The analysis data of the matching schemes of the two optimal solutions are listed in Table 6:

Table 6 Comparison of analysis data between two matching schemes
Full size table

According to the presented table, the intelligent matching system could complete the matching by complying with the size data of the unqualified parts and make it abide by the assembly requirements. Nearly 160 unqualified parts were reused to achieve matching assembly.

4.3 Strength Analysis and Benefit Assessment

The obtained matching scheme should pass the strength analysis before it could be applied to the actual assembly. For the threaded fastener of this example, the joint strength was reflected by calculating the effective stress sectional area. According to the national standard GB/T 16,823.1–1997, the effective stress cross-sectional area of the bolt is expressed as:

$$A_{1} = 0.7854\left( {{\text{d}} - 0.9382{\text{P}}} \right)^{2}$$
(16)

where d denotes the major diameter of the thread; P expresses the pitch.

The tensile strength of the bolt of this example was 170 N/mm2. The maximum carrying capacity of all sub-schemes of the matching scheme targeting the maximum utilization is illustrated in Fig. 10.

Fig. 10
figure 10

Maximum bearing capacity distribution of each sub-scheme

Full size image

According to Fig. 10, the products with the assembly of the unqualified parts had a maximum bearing capacity over 9000 N. If the safety factor reaches 1.5, this batch of products can be employed in working environments with a bearing capacity less than 6000 N.

In this scenario, if the intelligent matching system is not employed, and only qualified parts are used for the assembly, 924 products can be lastly completed, and the production pass rate takes up 92.4%. With the intelligent matching system, an additional 39 products can be added, and the production pass rate increases to 96.3%. According to the domestic market, the price of a set of M10 bolts and nuts was 3.5 yuan. Assuming the price of two connected parts is 10 yuan, the final assembled product costs at least 27 yuan. If the extra management inventory and other expenses are ignored, the final additional income generated by the matching scheme aiming at the maximum utilization ratio will be no less than 1053 yuan.

The case calculations in the present section proved that the intelligent matching assembly system can really improve the qualification rate of the product assembly, thereby improving production efficiency and corporate profits. Moreover, in the production activities of some high-value parts assembly, the intelligent matching assembly system will bring higher profits, thereby verifying the practical value of the system designed.

5 Conclusion

Through the analysis of the mating relationship between the parts in the assembly activity, the present study proposed the concept of the mating base, which underpinned the judgement of whether the parts can be matched. In addition, the present study designed an intelligent matching assembly system by adopting genetic algorithm to match the original unqualified parts one by one, which abided by the assembly constraints and product technical requirements, and greatly improved the product production qualification rate and reduced the product cost. The system is expected to be employed in the actual assembly work, providing new solutions to the assembly optimization problem at this stage, and adding a new design solution for the assembly production system.