Introduction

Spatial variability of soil physical and chemical properties within or among agricultural fields is inherent in nature due to geologic and pedologic soil forming factors, but some of the variability may be induced by tillage and other management practices. These factors interact with each other across spatial and temporal scales, and are further modified locally by erosion and deposition processes (Iqbal et al. 2005). Geostatistics have proved useful for assessing spatial variability of soil properties and have increasingly been utilized by soil scientists and agricultural engineers in recent years (Webster and Oliver 2001). Semivariograms and cross-semivariograms have been used to characterize and model spatial variance of data to assess how data points are related with separation distances while kriging uses modeled variance to estimate values between samples (Journel and Huijbregts 1978).

Despite the importance of soil texture and its relative ease of determination using conventional methods, soil maps are produced at large scales to adequately represent their spatial distribution. Quantitative information on soil surface texture would be extremely useful for modeling, planning, and managing the soils (Scull et al. 2005). Duffera et al. (2007) report some soil properties including particle size distribution (soil texture) shows horizontal spatial structure and captured by soil map units i.e. soil texture maps.

The objectives of this study were to determine the degree of spatial variability of some soil physical and chemical properties, variance structure, and model the sampling interval of Jadwal Al_Amir Project/Babylon/Iraq.

Materials and Methods

Description of the Study Area

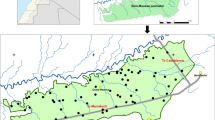
This study was conducted within Jadwal Al_Amir Project that was located in Hilla/Babylon province, 100 km (62 mi) south of Baghdad, rising 35 m above sea level. The study area was about 940 ha of the Project which was located between 44°26′50.661″ to 44°28′43.937″ of Eastern longitude and 32°20′52.074″ to 32°25′12.36″ Northern latitude (Fig. 1).

Fig. 1
figure 1

Map of the study area showing 150 soil sampling locations at Jadwal Al_Amir Project, Babylon, Iraq

Full size image

The total area of the Project is about 450,000 ha which is considered to have a desert climate. During the year, there is virtually no rainfall. This climate is considered to be BWh according to the Köppen–Geiger climate classification. Temperatures in the summer can reach as high as 50 °C, the average annual temperature is 23.1 °C, and winters are generally mild. The rainfall here averages 114 mm.Footnote 1

Soil Sampling and Laboratory Analysis

Soil samples were randomly taken from 150 locations in May 2016. The locations of sampling points were identified by global positioning system (GPS) showed in Fig. 1 and samples were taken at depths of 0–30 cm. Soil samples were oven dried to a constant weight, analyzed for particle size distribution, electrolytic conductivity (ECe), calcium carbonate minerals content (CaCO3), and organic matter content (O. M.). Soil texture was determined using the hydrometer method (Gee and Bauder 1986). The ECe values of samples were determined by EC meter with a glass electrode (Page et al. 1982). Calcium carbonate minerals content was determined using the method described by Loeppert and Suareze (1996). Organic matter content was determined using method described by Nelson and Sommers (1996).

The data were collected from the Ministry of Water Resources/National Center for Water Resources Management for characterization of the standard physical and chemical properties of the soils of the Project area.

Statistical Analysis and Interpolation

The data analyses were conducted in two stages: (a) distribution was analyzed by classical statistics (minimum, maximum, mean, median, skewness, kurtosis, standard deviation, and coefficient of variations); (b) geostatistical parameters were calculated for each variable as a result of corresponding semivariogram and cross-semivariogram analysis.

Skewness is the most common form of departure from normality. If a variable has positive skewness, the confidence limits on the variogram are wider than they would otherwise be and consequently, the variances are less reliable. A logarithmic transformation is considered where the coefficient of skewness is greater than 1 and a square-root transformation applied if it is between 0.5 and 1 (Bahri et al. 1993; Webster and Oliver 2001). Exploratory statistical analyses were performed by IBM® SPSS® Statistics v.23.0 Software.

Geostatistical analyses, including fitting semivariogram model and ordinary kriging procedure were carried out using ArcGIS (v.10.4.1 Software 2015) to assess the degree of spatial variability of each soil property used in this study. Semivariograms are a key tool in regionalized variables theory and are formed by three basic parameters: nugget, sill, and range which describe the spatial structure as: γ(h) = C0 + C.

Semivariogram is computed as half the average squared difference between the components of data pairs (Webster and Oliver 2007). The function is expressed as:

$$ \gamma (h) = \frac{1}{2N(h)}\sum\limits_{i = 1}^{N(h)} {[Z(x_{i} ) - Z(x_{i} + h)]^{2} } $$
(1)

where γ(h) is the semivariance for the distance interval class h, N(h) is the number of sample pairs separated by lag distance (separation distance between sample positions), Z(xi) is a measured variable at spatial location i, Z(xi + h) is a measured variable at spatial location i + h.

In this study, the Spherical, Gaussian, Circular, and Stable, models were selected. The spherical model defined in Eqs. 2 and 3 provided the best fit for the experimental semivariance of soil textural fractions, silt, and sqrtECe.

$$ \gamma (h) = C_{0} + C\left[ {\frac{3}{2}\left( {\frac{h}{a}} \right) - \frac{1}{2}\left( {\frac{h}{a}} \right)^{3} } \right]h \le a $$
(2)

and

$$ \gamma (h) = C_{0} + C \quad h > a $$
(3)

The Gaussian model is similar to the exponential model but assumes a gradual rise for the y-intercept (Journel and Huijbregts 1978).

$$ \gamma (h) = C_{0} + C\left[ {1 - \exp \left( { - \frac{{h^{2} }}{{a^{2} }}} \right)} \right]\quad h \ge 0 $$
(4)

The circular model defined in Eqs. 5, 6, and 7 provided the best fit for the experimental semivariance of CaCO3 minerals, and log O.M.

$$ \gamma (h) = C_{0} + C\left[ {1 - \frac{2}{\pi } \cos^{ - 1} \left( {\frac{h}{a}} \right) + \sqrt {1 - \frac{{h^{2} }}{{a^{2} }}} } \right]\quad 0 < h \le a $$
(5)
$$ \gamma (h) = C_{0} + C\quad h > a $$
(6)
$$ \gamma (0) = 0 $$
(7)

The stable model defined in Eq. 8 provided the best fit for the experimental semivariance of sand fraction.

$$ \gamma (h) = C_{0} + C\left[ {1 - \exp \left( { - \frac{{3h^{w} }}{{a^{w} }}} \right)} \right]\quad 0 < w \le 2 $$
(8)

Cross-semivariances were also calculated to examine a spatial relationship between two variables at the same location and then variables are said to be co-regionalized or interrelated (Heisel et al. 1999). The cross-dependency between two variables u and v has a cross-semivariogram expressed as:

$$ \hat{\gamma }_{uv} (h) = \frac{1}{2N\left( h \right)}\mathop \sum \limits_{i = 1}^{N\left( h \right)} \left[ {\left\{ {z_{u} \left( {x_{i} + h} \right) - z_{u} \left( {x_{i} } \right)} \right\}*\left\{ {z_{v} \left( {x_{i} + h} \right) - z_{v} \left( {x_{i} } \right)} \right\}} \right] $$
(9)

where \( \hat{\gamma }_{uv} (h) \) is cross-semivariance between u and v variables for the interval distance class, h is the lag distance, N(h) is the total number of pairs for lag interval h, \( z_{u} \left( {x_{i} } \right) \) and \( z_{u} \left( {x_{i} + h} \right) \) are the measured values of variable \( z_{u} \), \( z_{v} \left( {x_{i} } \right) \) and \( z_{v} \left( {x_{i} + h} \right) \) are the measured values of variable \( z_{v} \) at points \( x_{i} \) and \( x_{i} + h, \) respectively (Journel and Huijbregts 1978). Maps of ordinary co-kriged predictions from fitted cross-semivariograms were produced using GS+ software.

Results and Discussion

Descriptive Statistics

Descriptive statistics for soil properties selected in this study are given in Table 1. The CV values of measured and estimated soil properties ranged between 20.71% for CaCO3 minerals and 106.43% for sqrtECe. The variability of soil properties within the study area was classified as medium (15–75%) to high (> 75%) based on the CV values according to the groupings described by Dahiya et al. (1984). This indicates that sqrtECe exhibit high variability while the remaining soil properties quantified in this study exhibit medium variability (15–75%) within the study area. sqrtECe was higher in the study area which faced with a lot of salinity related problems.

Table 1 Descriptive statistics for selected soil physical and chemical properties (n = 150) for surface soil horizons (0–30 cm)
Full size table

Geostatistical Methods

Semivariogram Analysis

Anisotropic semivariograms did not show any differences in spatial dependency based on direction and therefore isotropic semivariograms were chosen. The geostatistical analysis indicated different spatial distribution models and spatial dependency levels for the soil properties. Spherical, Gaussian, Circular, and Stable, models were obtained as the best fit to the experimental results (Figs. 2 and 3). The R2 values in Table 2 show that models fit the experimental semivariogram data for all soil properties. The nugget effect, which represents random variation caused mainly by the undetectable experimental error and field variation within the minimum sampling space (Bo et al. 2003; Aşkın and Kızılkaya 2006; Ersahin and Brohi 2006) was higher in silt, clay fractions and O.M. content than in the other soil properties (Table 2).

Fig. 2
figure 2

Isotropic variograms and models for the physical soil properties: a sand fraction, b silt fraction, c clay fraction

Full size image
Fig. 3
figure 3

Isotropic variograms and models for the chemical soil properties: a sqrtECe, b CaCO3 minerals content, c log O.M. content

Full size image
Table 2 Semivariogram models and parameters for the soil properties
Full size table

Generally, strong spatial dependency of soil properties is related to structural intrinsic factors such as parent material and mineralogy, and weak spatial dependency is related to random extrinsic factors such as plowing, fertilization and other soil management practices (Zheng et al. 2009; Muhaimeed et al. 2013).

Cross-Semivariogram Analysis

The isotropic cross-semivariograms of clay fraction with sqrtECe, CaCO3 minerals, and log O.M. are shown in Figs. 4, 5 and 6. Cross-semivariograms were calculated to explore and determine spatial interrelations using co-regionalized models between clay fraction and other measured soil properties. Among different theoretical cross-semivariogram models tested, Gaussian model was best fitted to the experimental values of clay fraction with sqrtECe, CaCO3 minerals, and logO.M., respectively. The spatial interrelations coefficients of Cross-semivariogram model are presented in Table 3. The R2 and the RSS for theoretical cross-semivariogram model to fit the experimental values between clay fraction with sqrtECe, CaCO3 minerals, and log O.M., are given in Table 3. The R2 and RSS values in Table 3 show that Gaussian model fit the experimental cross-semivariance data exceptionally well in all cases used in this study.

Fig. 4
figure 4

Cross-semivariogram of Clay × sqrtECe

Full size image
Fig. 5
figure 5

Cross-semivariogram of Clay × CaCO3 Minerals

Full size image
Fig. 6
figure 6

Cross-semivariogram of Clay × log O.M.

Full size image
Table 3 Cross-semivariogram model and parameters for combination of soil properties
Full size table

Using the criteria suggested by Cambardella et al. (1994) to evaluate the spatial interrelation between two related soil properties, the cross-semivariograms exhibited a strong negative spatial interdependency between clay fraction with sqrtECe, log O.M. and a strong positive spatial interdependency for clay separates with CaCO3 minerals. Table 3 gives the structural correlation coefficients from Gaussian model of co-regionalization for clay fraction with sqrtECe, CaCO3 minerals, and log O.M. The cross-semivariograms were negative for clay fraction with sqrtECe, and log O.M. indicating that values of the two variables tend to vary in opposite directions, while the cross-semivariogram was positive for clay fraction with CaCO3 minerals indicating that values of the two variables tend to vary jointly or dependently (McBratney and Webster 1983).

Ordinary Kriged Maps

The spatial distribution of sand content follows the sediments carried by the Tigris and the Euphrates rivers. Besides some material of aeolian origin, blown out of the desert is accumulated and mixed with fluvial deposits (Figs. 7 and 8). The spatial distribution map of silt content indicated that higher values were located in the south-western corner of the study area due mainly to the effect of physiographic, geological, and pedological processes (Figs. 9 and 10). The spatial prediction map of clay content shows that higher values were located in the north-eastern corner and gradually decreased toward south-western corner of the study area (Figs. 11 and 12). This type of distribution may be due to the effect of pedogenic processes and to some extent to geomorphic processed (Muhaimeed et al. 2014). Figures 13 and 14 shows spatial distribution patterns of soil sqrtECe within the study area follows semiarid conditions, and topographical feature. These variations of soil sqrtECe may be related to the application of waters containing soluble salts, weathering of primary and secondary minerals in soils.

Fig. 7
figure 7

Ordinary kriged map for sand fraction at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 8
figure 8

Area_Percent of sand fraction at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 9
figure 9

Ordinary kriged map for silt fraction at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 10
figure 10

Area_Percent of silt fraction at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 11
figure 11

Ordinary kriged map for clay fraction at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 12
figure 12

Area_Percent of clay fraction at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 13
figure 13

Ordinary kriged map for sqrtECe at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 14
figure 14

Area_Percent of sqrtECe at Jadwal Al_Amir Project, Babylon, Iraq

Full size image

The spatial distribution map of CaCO3 minerals content shows that higher values were located in the north-eastern and south-western parts of the study area (Figs. 15 and 16). The spatial distribution map of soil log O.M. follows differences in tillage treatments and other management practices (Figs. 17 and 18).

Fig. 15
figure 15

Ordinary kriged map for CaCO3 minerals content at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 16
figure 16

Area_Percent of CaCO3 minerals content at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 17
figure 17

Ordinary kriged map for log O.M. content at Jadwal Al_Amir Project, Babylon, Iraq

Full size image
Fig. 18
figure 18

Area_Percent of log O.M. content at Jadwal Al_Amir Project, Babylon, Iraq

Full size image

Ordinary Cokriged Maps

Spatial prediction maps were produced by the ordinary cokriging procedure using the cross-semivariogram coefficients in Table 3 for selected soil properties. The spatial distribution of clay content was associated with the spatial distribution and variation of sqrtECe in the soil (Fig. 19). The spatial prediction map of clay content shows a similar scenario with high values of CaCO3 minerals (Fig. 20). Similarly, spatial distribution of clay content was also associated with the spatial distribution of log O.M. content in the soil (Fig. 21) reflecting the poor natural drainage under topographical conditions and high ground- water table.

Fig. 19
figure 19

Ordinary cokriged surface for Clay × sqrtECe

Full size image
Fig. 20
figure 20

Ordinary cokriged surface for Clay × CaCO3 Minerals

Full size image
Fig. 21
figure 21

Ordinary cokriged surface for Clay × log O.M.

Full size image
Perform Cross Validation Analysis

The cross validation analysis are presented in Figs. 22, 23 and 24. The standard error predictions of the linear regression equations for combination of primary and secondary variables: clay × sqrtECe, clay × CaCO3 minerals, and clay × log O.M. were 0.015, 0.027, and 0.363 respectively while the standard error prediction of the linear regression equation for clay was 1.190 using the ordinary kriging procedure (Fig. 25).

Fig. 22
figure 22

Cross-validation (CoKriging) of Clay × sqrtECe

Full size image
Fig. 23
figure 23

Cross-validation (CoKriging) of Clay × CaCO3 Minerals

Full size image
Fig. 24
figure 24

Cross-validation (CoKriging) of Clay × logO.M.

Full size image
Fig. 25
figure 25

Cross-validation (Kriging) of Clay

Full size image

Conclusions

The spatial variation of physical and chemical soil properties was assessed using geostatistical methods. Cross-semivariograms exhibited a strong spatial interdependency between clay content and soil sqrtECe, CaCO3 minerals content, log O.M. content indicating that co-kriging improved predictions for clay content with soil sqrtECe, CaCO3 minerals content, log O.M. content. Thus, co-kriging is considered to be an accurate and adequate procedure for spatial interpolation and evaluation of soil properties considered in this study.