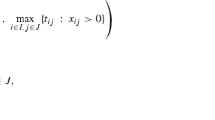1 Introduction

Multi-objective discrete optimization problems arise in a variety of areas of applications of operations research, for example in production scheduling and vehicle routeing, and they can be solved numerically by various techniques which can be exact or approximate; see for example Erhgott and Gandibleux (2000) and Halffmann et al. (2022) for general surveys on multi-objective discrete optimization. In particular, problems of this type can be approached by multi-objective extensions of exact solution methods for single-objective problems, such as branch-and-bound, but this approach is best suited for cases with only few objectives; see Parragh and Tricoire (2019) for an example of such a method for bi-objective problems.

Considering problems with relatively few objectives and moderate number of non-dominated solutions, a well established approach is to use weighted Tchebycheff methods, see for example Dächert et al. (2012), to find all such solutions. Recent research in this area focuses on increasing computational efficiency by employing hybrid methods, which include components such as \(\epsilon \)-constraint scalarisation and augmented weighted Tchebycheff objectives, see for example Dai and Charkhgard (2018), Leitner et al. (2016), and Fotedar et al. (2023).

Most common in practice are multi-objective metaheuristics, which are approximate approaches. For a recent survey on this topic, see Liu et al. (2020). The most popular metaheuristics for multi-objective optimization, in general and for discrete problems in particular, are those that are population-based, since they can very naturally be extended from the single-objective case to generate a diversity of solutions to multi-objective problems. For a recent survey on population-based metaheuristics for multi-objective optimization, see Giagkiozis et al. (2015).

Common to metaheuristics, both for single and multiple objectives, and a major drawback of these optimization techniques is that they do not provide any estimates of the quality of the solutions found, in relation to exact optima. It is therefore not possible to assess solution quality, without resorting to some additional procedure to find such estimates.

A very well established way to find estimates of the optimal value in single-objective optimization, and in particular for discrete problems, is to calculate bounds for the optimal objective value by means of Lagrangian relaxation (e.g. Wolsey 1998, Chapter 10). This bounding principle also naturally leads to an approximate solution paradigm that is different from metaheuristics; solution methods based on this principle are commonly referred to as Lagrangian heuristics. The Lagrangian relaxation and heuristic approach has proved to perform very well for a variety of applications, with the advantage of providing estimates of the quality of the solutions found.

For a minimization problem the Lagrangian relaxation gives lower bounds for the optimal objective value while the Lagrangian heuristic gives feasible solutions and upper bounds to the same value, and the lower bounds can then be used to judge the quality of the upper bounds. This is illustrated to the left in Fig. 1. In this work, we extend the Lagrangian bounding and heuristic approach to the case of bi-objective discrete optimization. An outcome of this approach is illustrated to the right in Fig. 1, for a bi-objective minimization problem. The Pareto frontier is enclosed by a set of mutually non-dominated objective outcomes and a piecewise linear outer approximation of, and bound for, the frontier.

Fig. 1
figure 1

To the left, single-objective bounding of the optimal value (\(z^*\)) by Lagrangian relaxation (LBD) and a heuristically found feasible solution (UBD). To the right, corresponding bounding for a bi-objective problem. Here, the circles represent the Pareto frontier, the convex piecewise linear curve is an outer bound for the Pareto frontier, and the plus signs represent mutually non-dominated objective outcomes

Full size image

Although the field of multi-objective discrete optimization is vast we have found only a few articles that are related to our work, which consists of two parts. First, we construct an outer approximation of the Pareto frontier by a Lagrangian dualisation of complicating side constraints, together with a weighted-sum scalarisation of the objective functions. The result of this relaxation is an intersection of a finite number of closed half-spaces, which contains the Pareto frontier. Second, we use a Lagrangian heuristic to construct non-dominated objective outcomes which are candidates for being Pareto optimal. The use of a Lagrangian heuristic to construct non-dominated objective outcomes, has to the best of our knowledge not been explored earlier.

Concerning the construction of the outer approximation of the Pareto frontier, an obvious alternative is to consider partial linear programming relaxations, as in Olivares-Benitez et al. (2012). It has also been suggested to use surrogate relaxation, for the specific case of multi-objective multi-knapsack problems (Cerqueus et al. 2015).

Lagrangian relaxation of multi-objective problems is quite extensively treated in Ehrgott (2006). However, the focus is on combining the multiple objective functions, expressed as auxiliary constraints, into a single objective function by means of Lagrangian relaxation, which in essence results in a weighted-sum scalarisation of the objective functions.

Most commonly in multi-objective optimization it is the compromise between the conflicting objectives and the reformulation into single-objective problems that are considered to be the challenges. The feasible set is then paid little attention. In contrast, we consider a bi-objective problem where the structure of the feasible set is challenging, because of the presence of complicating side constraints, while the bi-objective nature of the problem is not the primary difficulty.

We here develop a Lagrangian bounding and heuristic principle for bi-objective discrete optimization, since this is the most appropriate setting, although it can be directly extended to problems with more than two objectives. Further, we aim for bi-objective problems where the number of non-dominated solutions is assumed to be very large, which makes methods such as those presented in Dächert et al. (2012), Dai and Charkhgard (2018), Leitner et al. (2016), and Fotedar et al. (2023) less suitable.

The work most closely related to ours is by Erhgott and Gandibleux (2007). They give a very general framework for relaxing multi-objective problems, both in the objective functions and of the feasible set, which together with a weighted-sum scalarisation of the relaxed objective functions create outer approximations of the Pareto frontier. Although closely related, as far as we can see our bounding procedure does not follow directly from the general framework in Erhgott and Gandibleux (2007).

The outline of this paper is as follows. In Sect. 2.1 we derive a Lagrangian lower bounding principle for bi-objective discrete optimization problems. This principle provides an outer approximation of the Pareto frontier, and can therefore be used for assessing the quality of non-dominated solutions in relation to an unknown Pareto frontier. Another way of bounding the Pareto frontier is by using the linear programming relaxation; in Sect. 2.2 it is established that the Lagrangian bounding is always at least as strong as the linear programming bounding. In Sect. 2.3 we propose quantitative measures for assessing bound quality for a bi-objective problem. Section 2.4 gives a framework for Lagrangian heuristics for finding non-dominated, and hopefully also near Pareto optimal, solutions to a bi-objective problem. In order to illustrate the potential usefulness of the developed methodology, Sect. 3 gives an example application to a bi-objective facility location problem; the experimental results in this application are very encouraging. In Sect. 4 we draw conclusions and make some suggestions for continued research. The material presented in Sect. 3 is based on the bachelor thesis (Åkerholm 2022).

2 Derivation

Let the vectors \(c_1, c_2 \in {\mathbb {R}}^n\), the vector \(b \in {\mathbb {R}}^m\), and the matrix \(A \in {\mathbb {R}}^{m \times n}\). Further, let the set \(X \subset {\mathbb {R}}^n_+\) be non-empty and finite, and consider a bi-objective discrete optimization problem with complicating side constraints stated as

$$\begin{aligned} \min&~ \left( z_1, z_2 \right) = \left( c_1^{\textrm{T}}x, c_2^{\textrm{T}}x \right) \end{aligned}$$
(1a)
$$\begin{aligned} \text {s.t.}&~~ Ax \ge b, \end{aligned}$$
(1b)
$$\begin{aligned}&~~ x \in X, \end{aligned}$$
(1c)

which is assumed to have a feasible solution. The set X is typically described by constraints and integrality restrictions on variables, but its actual representation is of no interest. It is assumed that the primary difficulty of the problem lies in the side constraint (1b) rather than in its bi-objective nature. We further assume that it is inexpensive to minimize a linear objective over the set X, as compared to finding non-dominated solutions to problem (1). Let Z be the set of feasible objective outcomes, that is, \(Z = \left\{ \left( c_1^{\textrm{T}}x, c_2^{\textrm{T}}x \right) \vert \, x \in X ~ \text {and} ~ Ax \ge b \right\} \). The set Z is clearly finite, and for simplicity it is assumed that \(Z \subset {\mathbb {R}}^2_{++}\). Further, let \(Z^* \subseteq Z\) be the set of Pareto optimal outcomes (that is, the points in Z that are non-dominated).

2.1 Lagrangian bounding

Let the weight \(w \in [0,1]\) define a convex combination of the two objectives into a single objective, and let \(z^*: [0,1] \mapsto {\mathbb {R}}_{++}\) be the function of optimal values for the resulting scalarised reformulation of problem (1), that is,

$$\begin{aligned} z^*(w) = \min ~&\left[ wc_1 + (1-w)c_2\right] ^{\textrm{T}}x \end{aligned}$$
(2a)
$$\begin{aligned} \text {s.t.} ~&Ax \ge b, \end{aligned}$$
(2b)
$$\begin{aligned} ~&x \in X, \end{aligned}$$
(2c)

or, alternatively,

$$\begin{aligned} z^*(w) = \min _{(z_1,z_2) \in Z} \, wz_1+(1-w)z_2. \end{aligned}$$
(3)

Since the set Z is finite, the function \(z^*\) is piecewise linear and concave on [0, 1]. Problem (2) is always solved by some Pareto optimal solution, but due to the non-convexity of problem (1) there may be Pareto points that can not be found by solving problem (2) for any value of \(w \in [0,1]\); those that can actually be found are referred to as exposed (or supported) Pareto points.

Consider the set

$$\begin{aligned} Z_{\text {conv}}^+ = \text {conv}(Z) + {\mathbb {R}}^2_+, \end{aligned}$$

which is convex, polyhedral, and unbounded. Clearly, \(Z^* \subseteq Z \subset Z_{\text {conv}}^+\). Using that the defining equality (3) implies that \(wz_1+(1-w)z_2 \ge z^*(w)\) holds for all \((z_1,z_2) \in Z\), we obtain the alternative characterisation

$$\begin{aligned} Z_{\text {conv}}^+ = \bigcap _{w \in [0,1]} \left\{ \left( z_1, z_2 \right) \vert \, wz_1+(1-w)z_2 \ge z^*(w) \right\} . \end{aligned}$$

Only a finite number of values of \(w\in [0,1]\) are of interest in this intersection. This is because the function \(z^*\) is piecewise linear, and the values of interest are the breakpoints of \(z^*\). (It can easily be shown that if w is not a breakpoint of \(z^*\), then the constraint \(wz_1+(1-w)z_2 \ge z^*(w)\) is a convex combination of the corresponding constraints at the two breakpoints that are adjacent to w, and therefore such a value of w is of no interest.)

The relationship \(Z^* \subset Z_{\text {conv}}^+\) is the tightest possible convex inclusion of \(Z^*\) (in the minimization direction); it is however demanding to compute, since it requires a one-parametric analysis of problem (2), which is in itself, by assumption, computationally hard. We therefore replace \(z^*(w)\) with a computationally inexpensive lower bound to \(z^*(w)\) obtained by Lagrangian relaxation. This yields an outer approximation of the set \(Z_{\text {conv}}^+\).

Let \(u \in {\mathbb {R}}^m_+\) be a vector of Lagrangian multipliers for constraint (2b) and define \(h:[0,1] \times {\mathbb {R}}^m_+ \mapsto {\mathbb {R}}\) as

$$\begin{aligned} h(w,u)&= \min _{ x \in X} ~ \left[ wc_1 + (1-w)c_2\right] ^{\textrm{T}}x+ u^{\textrm{T}} \left( b-Ax \right) \nonumber \\&= u^{\textrm{T}}b + \min _{ x \in X} ~ \left[ wc_1 + (1-w)c_2 - A^\textrm{T}u \right] ^{\textrm{T}}x , \end{aligned}$$
(4)

that is, the optimal value in the relaxed problem. Since X is finite, the function \(h(w,\cdot )\) is the pointwise minimum of a finite number of affine functions, and it is therefore piecewise linear and concave on its domain. Weak Lagrangian duality yields that \( wz_1+(1-w)z_2 \ge z^*(w) \ge h(w,u)\) holds for all \((z_1,z_2) \in Z\). Hence,

$$\begin{aligned} Z^* \subset Z_{\text {conv}}^+ \subseteq \left\{ \left( z_1, z_2 \right) \vert \, wz_1+(1-w)z_2 \ge h(w,u) \right\} \end{aligned}$$

holds for any \(w \in [0,1]\) and any \(u \in {\mathbb {R}}^m_+\). Defining the set

$$\begin{aligned} Z_{\text {LD}} = \bigcap _{w \in [0,1]} \bigcap _{u \in {\mathbb {R}}^m_+} \left\{ \left( z_1, z_2 \right) \vert \, wz_1+(1-w)z_2 \ge h(w,u) \right\} , \end{aligned}$$

which is clearly convex, the following result is then immediate.

Proposition 1

\(Z^* \subset Z_{\textrm{LD}}\).

Hence, the set \(Z_{\text {LD}}\) provides a convex outer approximation of the set of Pareto optimal outcomes.

We next consider the function \(h^*: [0,1] \mapsto {\mathbb {R}}\) with

$$\begin{aligned} h^*(w) = \max _{u \in {\mathbb {R}}^m_+} ~ h(w,u), \end{aligned}$$
(5)

that is, the optimal value of the Lagrangian dual problem for the relaxation (4). From weak Lagrangian duality follows that \(h^*(w) \le z^*(w)\). For the given \(w \in [0,1]\) the duality gap is \(z^*(w)-h^*(w)\). (The maximum value in (5) is clearly always attained since \(h(w,\cdot )\) is piecewise linear, with a finite number of pieces, and h(w, u) is bounded from above by \(z^*(w)\).)

Proposition 2

The set \(Z_{\mathrm{{LD}}}\) is polyhedral.

Proof

If \((z_1,z_2) \in Z\) then \(wz_1+(1-w)z_2 \ge h(w,u)\) holds for any \(u \in {\mathbb {R}}^m_+\), and therefore

$$\begin{aligned} wz_1+(1-w)z_2 \ge \max _{u \in {\mathbb {R}}^m_+} ~ h(w,u) = h^*(w). \end{aligned}$$

holds. Hence,

$$\begin{aligned} Z_{\text {LD}} = \bigcap _{w \in [0,1]} \left\{ \left( z_1, z_2 \right) \vert \, wz_1+(1-w)z_2 \ge h^*(w) \right\} . \end{aligned}$$

Problem (4) is a Lagrangian relaxation of problem (2) and therefore

$$\begin{aligned} h^*(w) = \min&~ \left[ wc_1 + (1-w)c_2\right] ^{\textrm{T}}x \end{aligned}$$
(6a)
$$\begin{aligned} \text {s.t.}&~~ Ax \ge b, \end{aligned}$$
(6b)
$$\begin{aligned}&~~ x \in \text {conv}(X). \end{aligned}$$
(6c)

This is a linear program with a bounded feasible set. Further, it is a scalarised reformulation of the bi-objective linear program

$$\begin{aligned} \min&~ \left( z_1, z_2 \right) = \left( c_1^{\textrm{T}}x, c_2^{\textrm{T}}x \right) \end{aligned}$$
(7a)
$$\begin{aligned} \text {s.t.}&~~ Ax \ge b, \end{aligned}$$
(7b)
$$\begin{aligned}&~~ x \in \text {conv}(X). \end{aligned}$$
(7c)

Since the two objectives are linear, the image of the polyhedral convex feasible set onto the space of the two objectives is a polyhedral convex set. Hence, the set

$$\begin{aligned} Z_{\text {LD}}&= \bigcap _{w \in [0,1]} \left\{ \left( z_1, z_2 \right) \vert \, wz_1+(1-w)z_2 \ge h^*(w) \right\} \end{aligned}$$
(8a)
$$\begin{aligned}&= \left\{ \left( c_1^{\textrm{T}}x, c_2^{\textrm{T}}x \right) \vert \, x \in \text {conv}(X) ~\text {and} ~ Ax \ge b \right\} + {\mathbb {R}}^2_+ \end{aligned}$$
(8b)

is polyhedral. \(\square \)

Note that the characterisation (6) shows that the function \(h^*\) is finite, piecewise linear and concave on its domain. Further, because of the piecewise linearity of \(h^*\), only a finite number of values of \(w\in [0,1]\) are of interest in (8a).

The boundary of the polyhedral convex set \(Z_{\text {LD}}\) can be characterised as

$$\begin{aligned} \text {bd}(Z_{\text {LD}}) = \bigcup _{w \in [0,1]} \, \mathop {\mathrm {arg\,min}}\limits _{(z_1,z_2) \in Z_{\text {LD}}} wz_1+(1-w)z_2. \end{aligned}$$

Since \(Z^* \subset Z_{\text {LD}}\), every point in \(\text {bd}(Z_{\text {LD}})\) is non-dominated by every point in \(Z^*\). The boundary of \(Z_{\text {LD}}\) therefore forms a Lagrangian lower bounding frontier for the set of Pareto optimal outcomes of the given bi-objective discrete optimization problem. This bound is a bi-objective extension of the Lagrangian dual bounding principle that is commonly used for single-objective discrete problems with complicating side constraints.

It is of course also possible to construct an outer approximation of the set \(Z_{\text {LD}}\) and a resulting lower bounding frontier for the set of Pareto optimal outcomes by using any finite collections of weights \(w \in [0,1]\) and vectors \(u \in {\mathbb {R}}^m_+\) of Lagrangian multipliers, as stated below.

Proposition 3

Let \(\{ w_k \}_{k=0}^K \subset [0,1]\) and \(\{ u^l \}_{l=0}^L \subset {\mathbb {R}}^m_+\). Then

$$\begin{aligned} Z^* \subset Z_{\mathrm{{LD}}} \subseteq \bigcap _{k=0}^K \left\{ \left( z_1, z_2 \right) \vert \, w_kz_1+(1-w_k)z_2 \ge \max _{l=0,\ldots ,L} h(w_k,u^l) \right\} . \end{aligned}$$

One way of constructing such an outer approximation of the set \(Z^*\) is to first choose the collection \(\{ w_k \}_{k=0}^K \subset [0,1]\) and then for each \(w_k\), \(k=0,\ldots ,K\), use subgradient optimization to find a near-optimal solution to the Lagrangian dual problem

$$\begin{aligned} h^*(w_k) = \max _{u \in {\mathbb {R}}^m_+} ~ h(w_k,u). \end{aligned}$$

Letting \(u^k\) be the near-optimal solution found for the weight \(w_k\), the approximate outer approximation is

$$\begin{aligned} \bigcap _{k=0}^K \left\{ \left( z_1, z_2 \right) \vert \, w_kz_1+(1-w_k)z_2 \ge h(w_k,u^k) \right\} \supseteq Z_{\text {LD}} \supset Z^*. \end{aligned}$$
(9)

It is clearly, like \(Z_{\text {LD}}\), polyhedral and therefore the approximate lower bounding frontier constructed in this way is piecewise linear. To reduce the computational effort, the subgradient optimization on each of the Lagrangian dual problems can of course be restarted from the already found dual point that gives the maximal value of the current dual objective function \(h(w_k,u)\).

2.2 Comparison with linear programming bounding

If the set X is described by linear constraints and integrality restrictions on the variables, such as \(X = \left\{ x \in {\mathbb {Z}}^n_+ \, \vert \, Dx \ge e \right\} \), then a bounding of the Pareto frontier of problem (1) can alternatively be based on the linear programming relaxation of the scalarised problem, that is, on the function \(z_{\text {LP}}^*: [0,1] \mapsto {\mathbb {R}}\) with

$$\begin{aligned} z_{\text {LP}}^*(w) = \min&~ \left[ wc_1 + (1-w)c_2\right] ^{\textrm{T}}x \end{aligned}$$
(10a)
$$\begin{aligned} \text {s.t.}&~~ Ax \ge b, \end{aligned}$$
(10b)
$$\begin{aligned}&~~ Dx \ge e, \end{aligned}$$
(10c)
$$\begin{aligned}&~~ x \in {\mathbb {R}}^n_+ . \end{aligned}$$
(10d)

The function \(z_{\text {LP}}^*\) is piecewise linear and concave, and it can be calculated exactly by performing a standard one-parametric analysis of the linear program. Similarly to above, we define the polyhedral convex set

$$\begin{aligned} Z_{\text {LP}} = \bigcap _{w \in [0,1]} \left\{ \left( z_1, z_2 \right) \vert \, wz_1+(1-w)z_2 \ge z_{\text {LP}}^*(w) \right\} . \end{aligned}$$

Since \(z_{\text {LP}}^*(w) \le z^*(w)\) holds for all \(w \in [0,1]\), we have that \(Z^* \subset Z_{\text {LP}}\) and that \(\text {bd}(Z_{\text {LP}})\) provides a lower bounding for the Pareto frontier.

Using the characterisation of the function h given by problem (6) together with the relationship \(\text {conv}(X) \subseteq \left\{ x \in {\mathbb {R}}^n_+ \, \vert \, Dx \ge e \right\} \), we conclude that \(h^*(w) \ge z_{\text {LP}}^*(w)\) holds for all \(w \in [0,1]\), which implies that \(Z_{\text {LD}} \subseteq Z_{\text {LP}}\).

Suppose that the set \(\left\{ x \in {\mathbb {R}}_+ \, \vert \, Dx \ge e \right\} \) has the integrality property, that is, that all its extreme points are integer-valued. Then (e.g. Wolsey 1998, Section 10.2), \(\text {conv}(X) = \left\{ x \in {\mathbb {R}}_+ \, \vert \, Dx \ge e \right\} \), the Lagrangian relaxed problem (4) can be solved as a linear program, even though it is discrete, which implies that \(h^*(w) = z_{\text {LP}}^*(w)\) holds for all \(w \in [0,1]\) and that \(Z_{\text {LD}} = Z_{\text {LP}}^*\). Hence, the Lagrangian lower bounding frontier \(\text {bd}(Z_{\text {LD}})\) to the set of Pareto optimal outcomes does in this case have the same strength as the bounding frontier obtained from the linear programming relaxation of the scalarised single-objective reformulation of the original bi-objective discrete problem. (These results are analogous with those that hold in the single-objective case.)

If the set \(\left\{ x \in {\mathbb {R}}_+ \, \vert \, Dx \ge e \right\} \) does not have the integrality property, then the Lagrangian relaxed problem is a genuine integer program, which needs to be solved by using for example branch-and-bound. It can then be expected that \(h^*(w) > z_{\text {LP}}^*(w)\) typically holds and that \(Z_{\text {LD}} \subset Z_{\text {LP}}\). Hence, in this case it can be expected that the Lagrangian bounding frontier to the set of Pareto optimal outcomes is stronger than the linear programming bounding frontier.

Example 1

To illustrate the Lagrangian bounding of the Pareto frontier and compare it to the linear programming bounding, we use the following small numerical zero–one example.

$$\begin{aligned} \min&~ (z_1 = 8x_1+9x_2+x_3+9x_4+2x_5+7x_6+6x_7+8x_8+x_9+3x_{10}, \nonumber \\&~~\, z_2 = x_1+x_2+7x_3+3x_4+7x_5+4x_6+2x_7+x_8+6x_9+2x_{10}) \nonumber \\ \mathrm {s.t.}&~ 6x_1+5x_2+5x_3+4x_4+8x_5+6x_6+6x_7+x_8+7x_9+7x_{10} \ge 28, \end{aligned}$$
(11)
$$\begin{aligned}&~ 6x_1+3x_2+6x_3+8x_4+8x_5+8x_6+3x_7+9x_8+3x_9+2x_{10} \ge 26, \end{aligned}$$
(12)
$$\begin{aligned}&~ x \in \left\{ 0, 1 \right\} ^{10} \end{aligned}$$
(13)

The set X is here defined by (12) and (13). It contains 608 points, out of which 449 are feasible. These give 284 distinct objective outcomes, out of which 10 are on the Pareto frontier, and out of these 6 are exposed. Figure 2 shows, to the left, the points on the Pareto frontier (circles), the boundary of \(Z_{\text {conv}}^+ = \text {conv}(Z) + {\mathbb {R}}^2_+\) (solid), the Lagrangian lower bounding frontier \(\textrm{bd}(Z_{\mathrm{{LD}}})\) (dash-dotted), and the linear programming lower bounding frontier \(\textrm{bd}(Z_{\mathrm{{LP}}})\) (dashed). Lagrangian relaxation of (11) gives a knapsack problem, which does not have the integrality property, and the Lagrangian bounding frontier is therefore tighter than the linear programming bounding frontier. The asterisks indicate the breakpoints of the Lagrangian and linear programming frontiers. For the latter, a breakpoint corresponds to a certain optimal basis, while for the former it corresponds to a certain knapsack solution (point in X).

2.3 Evaluating bound quality

We here introduce a measure that can be used to assess the strength of a lower bound on the set of Pareto optimal outcomes. This measure is later used to compare the strength of the Lagrangian lower bounding versus the strength of the linear programming bounding.

Let \(\underline{z}: [0,1] \mapsto {\mathbb {R}}\) be a lower bounding function for \(z^*\), obtained from a relaxation of the original bi-objective problem, so that it by construction holds that \(\underline{z}(w) \le z^*(w)\) for all \(w \in [0,1]\). For a fixed value of w the duality gap associated with the relaxation is \(\Gamma (w) = z^*(w) - \underline{z}(w)\). The obvious examples of lower bounding functions are \(z_{\text {LP}}^*\) defined by the linear programming relaxation (10) and \(h^*\) defined by (4) and (5).

We suggest to generalise the concept of a duality gap associated with a given relaxation of a non-convex single-objective optimization problem to the case of two objectives by defining the bi-objective duality gap

$$\begin{aligned} \Gamma = \int _0^1 \Gamma (w) \, dw = \int _0^1 z^*(w) \, dw - \int _0^1 \underline{z}(w) \, dw. \end{aligned}$$
(14)

Based on this quantity, we next define a measure for the deviation between a set of mutually non-dominated objective outcomes and a lower bound to the Pareto frontier.

Suppose that the set of non-dominated objective outcomes is \({\bar{Z}} \subseteq Z\) and define the upper bounding function \(UBD: [0,1] \mapsto {\mathbb {R}}_{++}\) with

$$\begin{aligned} UBD(w) = \min _{(z_1,z_2) \in {\bar{Z}}} \, wz_1+(1-w)z_2. \end{aligned}$$

Clearly, UBD is a piecewise linear and concave function and \(z^*(w) \le UBD(w)\) always holds. Let LBD be a lower bounding function for the original bi-objective problem, so that \(LBD(w) \le z^*(w)\) always holds. It can be \(z_{\text {LP}}^*\) or \(h^*\), but it can also be lower bounds to these functions. Note however that LBD shall be a positive function. Then the relative deviation between the set of non-dominated objective outcomes and the lower bounding function is

$$\begin{aligned} {\bar{\Gamma }}_r = \frac{\int _0^1 UBD(w) \, dw - \int _0^1 LBD(w) \, dw}{\int _0^1 LBD(w) \, dw}. \end{aligned}$$
(15)

Since \(LBD(w) \le z^*(w) \le UBD(w)\), it holds that \({\bar{\Gamma }}_r \ge \Gamma / \int _0^1 z^*(w) \, dw \). Further, a small value of \({\bar{\Gamma }}_r\) shows that the lower bounding function is tight to \(z^*\) and that the set of mutually non-dominated objective outcomes is close to, or coincides with, the exposed points on the Pareto frontier. If \({\bar{Z}} = Z^*\), \(LBD = z^*_{\text {LP}}\), \(X = \left\{ x \in {\mathbb {Z}}^n_+ \, \vert \, Dx \ge e \right\} \), and \(\left\{ x \in {\mathbb {R}}_+ \, \vert \, Dx \ge e \right\} \) has the integrality property, then \({\bar{\Gamma }}_r = 0\). A large value of \({\bar{\Gamma }}_r\) can indicate that the relaxation or the procedure used for computing the lower bounding function are inadequate, or that the set \({\bar{Z}}\) lacks many points that are exposed Pareto optimal outcomes or that are close to such points.

Since the quantities \(\Gamma \) and \({\bar{\Gamma }}_r\) are based on the scalarised single-objective reformulation of the bi-objective problem, they can only capture problem characteristics related to the exposed points on the Pareto frontier, This weakness is however of minor importance in our context since we use \({\bar{\Gamma }}_r\) (or rather an approximation thereof) to compare two relaxations and their resulting lower bounding functions.

It may be practically impossible to calculate all the integrals in the expressions (14) and (15) exactly. It is however quite easy to find lower and upper bounds to the values of these integrals by making discretisations. One possible way of doing this is given in Appendix 1.

The appendix also discusses the special case when the lower bounding in (15) is based on the Lagrangian dual problem (5), but only uses approximate solutions to the dual problem for discrete values of w, together with the above-mentioned lower bound calculation. It is established that this approximation will result in an overestimate of the correct value of \({\bar{\Gamma }}_r\).

Example 2

(Continuation on Example 1) Figure 2 shows, to the right, the functions \(z^*\) (solid), \(h^*\) (dash-dotted), and \(z_{\mathrm{{LP}}}^*\) (dashed) for the numerical instance in Example 1. Here, \(\int _0^1 z^*(w) \, dw \approx 16.36\), \(\int _0^1\,h^*(w) \, dw \approx 15.74\), and \(\int _0^1 z_{\mathrm{{LP}}}^*(w) \, dw \approx 15.05\). The relative deviations (15) between \(UBD=z^*\) and the alternative lower bounding functions \(LBD=h^*\) and \(LBD=z_{\mathrm{{LP}}}^*\) are \(3.9\%\) and \(8.7\%\), respectively.

Fig. 2
figure 2

To the left, we show three frontiers. The circles are the points on the Pareto frontier, the solid curve is the boundary of \(Z_{\text {conv}}^+\), the dash-dotted curve shows the Lagrangian frontier \(\text {bd}(Z_{\text {LD}})\), and the dashed curve shows the linear programming frontier \(\text {bd}(Z_{\text {LP}})\). Asterisks show breakpoints. To the right, we show three functions of \(w\in [0,1]\). The solid, dash-dotted and dashed curves show \(z^*\), \(h^*\), and \(z_{\mathrm{{LP}}}^*\), respectively

Full size image

2.4 Bi-objective Lagrangian heuristics

If a computationally challenging single-objective optimization problem (minimization) is approached with a Lagrangian relaxation scheme in order to compute lower bounds to the optimal value, then it is common to augment the scheme with a procedure that tries to find feasible, and hopefully also near-optimal, solutions, and thereby upper bounds to the optimal value. Such a procedure is known as a Lagrangian heuristic. Both the number of possible applications of Lagrangian heuristics and the number of design options in such heuristics are large, which is reflected by the huge literature on the subject.

With reference to Larsson and Patriksson (2006), a Lagrangian heuristic works as follows: (i) it is initiated at a primal vector in the set defined by the non-relaxed constraints, (ii) it adjusts this vector by executing a finite number of operations, with the aim of reaching feasibility in the relaxed constraints, (iii) it utilises information from the Lagrangian dual problem, (iv) the sequence of vectors generated remains within the set defined by the non-relaxed constraints, and (v) the final vector is, if possible, primal feasible and hopefully also near-optimal in the primal problem. There is in general no guarantee that a feasible solution is found.

A common realisation of a Lagrangian heuristic is to initiate with a relaxed, and therefore infeasible, solution, often found in an iteration of a subgradient optimization scheme for the Lagrangian dual problem. The modifications made of this solution strive for feasibility in the relaxed constraints, without violating the non-relaxed constraints, and they are typically guided by an objective metric, which has the purpose of steering the modifications so that the objective value of an eventually found feasible solution becomes near-optimal. Common examples of objective metrics are the objective of the primal problem and the objective of the Lagrangian relaxed problem. How the relaxed solution is modified when striving for feasibility depends primarily on the structure of the problem at hand and the relaxation made (which is often a design question), which results in specific structures of the non-relaxed and the relaxed constraints that the modifications must be adapted to, but it is also a matter of design of the heuristic.

Lagrangian heuristics for single-objective problems are usually run many times, typically from relaxed solutions obtained for different dual solutions, both because a single run can fail to find a feasible solution but also in order to find a diversity of feasible solutions and resulting upper bounds, out of which the best one is hopefully near-optimal. In our bi-objective context, the Lagrangian heuristic should aim at finding near Pareto optimal solutions to the original problem (1). If the heuristic finds a candidate point that is dominated by already known near Pareto optimal solutions, then it can be discarded.

The modifications made by the heuristic can be guided by the scalarised objective (2a). The heuristic will then aim at finding an exposed Pareto optimal solution, but it can of course still end up with a non-exposed Pareto point. Another possibility is to let the heuristic be guided by the objective (4) of the Lagrangian relaxed scalarised problem. Still another possibility is to let the heuristic be guided by the bi-objective (1a) of the original problem. This may for example be made by using already known and mutually non-dominated solutions, and make the heuristic modifications of a new relaxed solution with the aim of finding a feasible solution that is non-dominated with respect to the known solutions. If the heuristic succeeds in finding a new non-dominated solution, then some of the previously known solutions may of course become dominated and therefore discarded.

The diversification aspect of a Lagrangian heuristic is even more important for a bi-objective problem, when a near Pareto frontier is sought for. A natural way of diversifying is to consider various values of w, and for each of them consider various dual solutions, obtained when optimizing the Lagrangian dual problem for each value of w, and for each dual solution initiate the heuristic at the relaxed solution. Worth noting is that if the objective metric used depends of both w and the dual solution, then these can be combined independently in the metric, in order to promote diversity. One can for example consider a particular dual solution and the corresponding relaxed solution, and run the heuristic repeatedly from the relaxed solution for various values of w.

In the application reported in next section we consider a number of values of w, and for each of these we consider a number of associated dual solutions. For each dual solution the heuristic is initiated at the relaxed solution obtained, and the modifications made on the solution with the aim of reaching feasibility are guided by the weighted objective (2a). This strategy work very well, and experiments with other options are left for future research.

3 An application to bi-objective facility location

We here describe an application of the developed methodology, with the purpose of illustrating its potential usefulness.

In recent years there has been an increasing interest in research about the trade-offs between cost and environmental impact, often CO2 emissions, within the fields of supply chain and transportation planning. Examples of this are the works Harris et al. (2011), Zhang et al. (2017) and Gholipour et al. (2021).

The work Harris et al. (2011) considers a bi-objective single-sourcing capacitated facility location problem, where the bi-objective aspect is due to the simultaneous minimization of the CO2 emissions and costs that arise when locating depots and transporting goods to customers. (Multi-objective facility location problems in general are surveyed in Farahani et al. (2010).) The solution approach in Harris et al. (2011) is hierarchical; it first employs an evolutionary multi-objective algorithm for locating depots to some of a number of possible sites and then uses a Lagrangian relaxation based heuristic for assigning the customers to the selected depots.

We here apply our Lagrangian lower bounding and heuristic principle to the bi-objective discrete optimization problem studied in Harris et al. (2011), and make experiments on the problem instances used in that work.

3.1 Problem formulation

The notations used in our formulation of the model are:

I       set of possible depot sites, indexed by i

J       set of customers, indexed by j

\(d_j\)       demand of customer j,

\(c_{ij}^1 \)       CO2 emission from satisfying demand \(d_j\) from depot i,

\(c_{ij}^2 \)       cost for satisfying demand \(d_j\) from depot i,

\(f_i^1\)       CO2 emission from running depot i,

\(f_i^2\)       fixed cost for locating depot i,

\(q_i\)       capacity of depot i,

\(n_i\)       number of customers that can be assigned to depot i.

The binary decision variables used are:

\(x_{ij}\)       equals 1 if customer j is assigned to depot i, and 0 otherwise,

\(y_i\)       equals 1 if a depot is located to site i, and 0 otherwise.

Letting the total CO2 emission and the total cost be denoted by \(z_1\) and \(z_2\), respectively, the bi-objective function to be optimized is

$$\begin{aligned} \min&~ \bigg (z_1=\sum _{i \in I}f_i^1y_i+\sum _{i \in I}\sum _{j \in J}c_{ij}^1x_{ij}, ~ z_2=\sum _{i \in I}f_i^2y_i+\sum _{i \in I}\sum _{j \in J}c_{ij}^2x_{ij}\bigg ) \end{aligned}$$
(16a)
$$\begin{aligned} \text {s.t.}&~~ \sum _{i \in I} x_{ij} = 1, \quad j \in J \end{aligned}$$
(16b)
$$\begin{aligned}&~~ x_{ij} \le y_i, \quad i \in I ,j \in J \end{aligned}$$
(16c)
$$\begin{aligned}&~~ \sum _{j \in J} d_j x_{ij} \le q_i, \quad i \in I \end{aligned}$$
(16d)
$$\begin{aligned}&~~ \sum _{j \in J} x_{ij} \le n_i, \quad i \in I \end{aligned}$$
(16e)
$$\begin{aligned}&~~ \sum _{i \in I} q_i y_i \ge \sum _{j \in J} d_j \end{aligned}$$
(16f)
$$\begin{aligned}&~~ \sum _{i \in I} n_i y_i \ge |J |\end{aligned}$$
(16g)
$$\begin{aligned}&~~ x_{ij} \in \{ 0,1 \}, \quad i \in I, ~j \in J \end{aligned}$$
(16h)
$$\begin{aligned}&~~ y_i \in \{ 0,1 \}, \quad i \in I. \end{aligned}$$
(16i)

Constraint (16b) ensures that each customer is assigned to exactly one depot (that is, single-sourcing), and constraint (16c) ensures that customers are only assigned to depots at the selected location sites. Further, constraint (16d) states that the total demand of the customers that are assigned to a depot may not violate its capacity, and (16e) states that the number of customers assigned to a depot may not be larger than possible. Constraints (16f) and (16g) guarantee that enough depots are selected with respect to their total capacity and the maximal total number of customers they can handle, respectively. Finally, (16h) and (16i), are definitional constraints.

Single-objective facility location problems have been extensively studied. This includes several works where such problems are approached by Lagrangian relaxations, see for example Barcelo and Casanovas (1984), Klincewicz and Luss (1986), Pirkul (1987), Cornuejols et al. (1991), Beasley (1993), Holmberg et al. (1999), and Cortinhal and Captivo (2003). It is also popular to construct Lagrangian heuristics for such problems, see for example Pirkul (1987), Beasley (1993), and Cortinhal and Captivo (2003).

Note that constraint (16f) is redundant, since it is implied by constraints (16b), (16c) and (16d). Similarly, constraint (16g) is redundant since it is implied by constraints (16b), (16c) and (16e). Constraints (16f) and (16g) are still included in the model because they are not redundant in the Lagrangian relaxed problem to be constructed in Sect. 3.2, which will result in a more restricted relaxed problem and therefore stronger lower bounds.

3.2 Lagrangian relaxation

We apply Lagrangian relaxation to the single-sourcing constraint (16b). For the standard single-objective facility location problem, the same type of relaxation was first used in Bitran et al. (1981), and for the case of single sourcing it was first used in Sridharan (1993).

First the weight \(w \in [0,1]\) is used to scalarise the objective (16a), giving the scalarised problem

$$\begin{aligned} z^*(w) = \min \sum _{i \in I}\left( wf_i^1+(1-w)f_i^2\right) y_i +\sum _{i \in I}\sum _{j \in J}\left( wc^1_{ij}+(1-w)c^2_{ij}\right) x_{ij} \end{aligned}$$
(17a)
$$\begin{aligned} \text {s.t.}&~ {\rm (16b)}-{\rm (16i)}. \end{aligned}$$
(17b)

Then constraint (16b) is Lagrangian relaxed with multipliers \(u_j\), \(j \in J\). Letting \(f_i(w)= wf_i^1+(1-w)f_i^2\), \(i \in I\), and \(c_{ij}(w,u)= wc^1_{ij}+(1-w)c^2_{ij}-u_j\), \(i \in I\), \(j \in J\), we obtain the relaxed problem

$$\begin{aligned} h(w,u) = \sum _{j \in J} u_j + \min&~\sum _{i \in I} \bigg [ f_i(w) y_i + \sum _{j \in J} c_{ij}(w,u) x_{ij} \bigg ] \end{aligned}$$
(18a)
$$\begin{aligned} \text {s.t.}&~{\rm (16c)}-{\rm (16i)}, \end{aligned}$$
(18b)

with \(h(w,u) \le z^*(w)\). We denote a solution to (18) by (x(w, u), y(w, u)).

For a fixed \(w \in [0,1]\), the Lagrangian dual problem is

$$\begin{aligned} h^*(w) = \max _{u \in {\mathbb {R}}^{|J |}} ~ h(w,u) \end{aligned}$$
(19)

and the duality gap is \(\Gamma (w) = z^*(w) - h^*(w) \ge 0\).

The relaxed problem can be solved in two stages. In the first stage we consider for each \(i \in I\) the cases \(y_i=0\) and \(y_i=1\). For each of these cases we solve with respect to \(x_{ij}\), \(j \in J\). If \(y_i=0\) holds, then the solution is trivial; due to constraint (16c), \(x_{ij}=0\) must hold for all \(j \in J\), which results in a zero contribution to the objective value. If \(y_i=1\) holds, then the contribution to the objective value is

$$\begin{aligned} v_i(w,u) = f_i(w) + \min&~ \sum _{j \in J} c_{ij}(w,u) x_{ij} \end{aligned}$$
(20a)
$$\begin{aligned} \text {s.t.}&~ \sum _{j \in J} d_j x_{ij} \le q_i, \end{aligned}$$
(20b)
$$\begin{aligned}&~ \sum _{j \in J} x_{ij} \le n_i, \end{aligned}$$
(20c)
$$\begin{aligned}&~ x_{ij} \in \{ 0,1 \}, \quad j \in J. \end{aligned}$$
(20d)

This problem is solved for every \(i \in I\). In the second stage the optimal values of \(y_i\), \(i \in I\), are found by using the results from the first stage. The second stage problem is

$$\begin{aligned} h(w,u) = \sum _{j \in J} u_j + \min&~\sum _{i \in I} v_i(w,u) y_i \end{aligned}$$
(21a)
$$\begin{aligned} \text {s.t.}&~ \sum _{i \in I} q_i y_i \ge \sum _{j \in J} d_j \end{aligned}$$
(21b)
$$\begin{aligned}&~ \sum _{i \in I} n_i y_i \ge |J |\end{aligned}$$
(21c)
$$\begin{aligned}&~ y_i \in \{ 0,1 \}, \quad i \in I, \end{aligned}$$
(21d)

which gives the solution y(w, u). If some \(y_i(w,u)=1\), \(i \in I\), then the values of \(x_{ij}(w,u)\), \(j \in J\), are given by a solution to problem (20), while otherwise \(x_{ij}(w,u) = 0\), \(j \in J\). The relaxed solution is used for calculating a subgradient of the dual objective function h(w, u) and also for initiating a heuristic which constructs feasible solutions to the original problem.

Note that both the \(\vert I \vert \) first stage problems and the single second stage problem are cardinality side constrained knapsack problems, which are in practice typically quite easily solved. Further, the second stage problem is typically much smaller, and hence the main computational burden lies in the first stage.

Furthermore, in the problem instances used for our experiments, all depots have the same capacity and can handle the same number of customers, that is, \(q_i=q\) and \(n_i=n\) for all \(i \in I\). Constraints (16f) and (16g) can then be combined into the single, and also stronger, constraint

$$\begin{aligned} \sum _{i \in I} y_i \ge \max \left( \lceil D/q \rceil , \, \lceil |J |/ n \rceil \right) , \end{aligned}$$
(22)

where \(D = \sum _{j \in J} d_j\). This simplification leads to a second stage problem that is trivial to solve.

3.3 Overview of numerical experiment

We have made an implementation of the Lagrangian bounding principle derived in Sect. 2.1 and the Lagrangian heuristic principle outlined in Sect. 2.4 for the bi-objective facility location problem. An overview of the implementation is shown in Fig. 3.

We use \(K = 101\) equidistant values of the weight \(w \in [0,1]\) to combine the two objectives. For each value of the weight the Lagrangian dual objective function (18) is maximized using subgradient optimization, each iteration of which includes the solution of the problems (20) and (21). The near-optimal dual solutions found are then used to construct a bound for the Pareto frontier according to equation (9).

A Lagrangian heuristic is run within each subgradient iteration, initiated at the relaxed solution found when solving problems (20), \(i \in I\), and (21). All feasible solutions found by the heuristic are recorded, and finally a near Pareto optimal frontier is constructed by sorting out the non-dominated solutions; this set is called ND.

For comparison purposes, we also construct the linear programming bound for the Pareto frontier. This is done by simply solving the linear programming relaxation of the scalarised problem (17) for the K values of the weight w. Further, the scalarised problem (17) is solved for each of the K values; this will generate a set of exposed Pareto points, denoted \(P_w\).

In order to assess the quality of the near Pareto optimal solutions found by the heuristic, we also calculate points on the actual Pareto frontier. First the problem is solved with only CO2 emission as objective and with only cost as objective; this will give the two endpoints of the Pareto frontier and the possible ranges for the two objectives. We then apply the \(\epsilon \)-constraint method to search for other Pareto optimal solutions, with cost as objective and a bounding constraint for CO2 emission. This bound is initially set to the lower end of the range for CO2 emission and then gradually increased up to the upper end of its range. Due to the nature of the problem, there is a huge number of Pareto optimal solutions, and the number actually found by the \(\epsilon \)-constraint method depends of the size of the increment with which the bound on CO2 emission is increased. We have used 501 equidistant bounds within the possible range for CO2 emission; the set of Pareto points found is denoted \(P_\epsilon \).

We made an implementation in Python 3.10.6Footnote 1 together with the solver Gurobi 9.5.1.Footnote 2 This implementation was run on an Apple M1 Max, 10-core CPU at 2.06–3.22 GHz, with 64GB RAM memory.

Ten problem instances (1–10) adopted from Harris et al. (2011) are used. (Table 3 in Appendix 2 gives references to the names used in Harris et al. (2011)) They all include 10 possible depots, while the number of customers are 2000, 4000, 6000, 8000 or 10000. For each number of customers, there are two instances, with capacity ratio 4.0 and 8.0, respectively. This ratio is the total capacity of the depots in relation to the total demand from the customers. The fixed costs for locating depots and the CO2 emissions from running them are created so that the fixed cost for locating a depot is 1.25 times its capacity and the ratio between the the fixed cost for a depot and its CO2 emission is 24.4. Hence, the fixed cost for a depot is significantly larger than its CO2 emission.

Fig. 3
figure 3

Overview of the implementation. Here SNDP is the set of non-dominated points

Full size image

3.4 Implementation of subgradient optimization

The scalarised problem (17) is considered for K equidistant weights, that is, \(w_k=k/K\), \(k=0,\ldots ,K\). We used \(K=101\). For each weight a straightforward subgradient optimization method, see e.g. Shor (1985) or Strömberg et al. (2020), is used to find a near-optimal solution to the Lagrangian dual problem (19).

We denote by s the subgradient iteration for a given weight \(w_k\). For a dual iterate \(u^s \in {\mathbb {R}}^{|J |}\), a relaxed solution \((x(w_k,u^s),y(w_k,u^s))\) is found by solving problems (20) and (21). A subgradient \(\gamma ^s \in {\mathbb {R}}^{|J |}\) of \(h(w_k,u)\) at \(u^s\) is given by

$$\begin{aligned} \gamma ^s_j = 1-\sum _{i \in I} x_{ij}(w_k,u^s), \quad j \in J. \end{aligned}$$

In the unlikely case that \(\gamma ^s = 0\), an optimal dual solution has been found and the method is terminated. Otherwise the next iterate is \(u^{s+1} = u^s + t_s \gamma ^s\), where \(t_s >0\) is a step length. We use the well known Polyak step length formula

$$\begin{aligned} t_s = \lambda \frac{UBD_k-h(w_k,u^s)}{\vert \vert \gamma ^s \vert \vert ^2}, \end{aligned}$$

where \(\lambda \in (0,2)\) and \(UBD_k \ge h^*(w_k)\). The upper bound \(UBD_k\) is the best objective value \(w_kz_1 + (1-w_k)z_2\) among all feasible solutions to the original problem (16) that have been found; these solutions are generated within the subgradient optimization by using the Lagrangian heuristic described in Sect. 3.5. The subgradient optimization method is terminated when \((UBD_k-LBD_k)/LBD_k \le \varepsilon \), where \(LBD_k\) is the best found lower bound to \(h^*(w_k)\) and \(\varepsilon = 10^{-4}\), or after 100 iterations. If termination occurs because of the former criterion, then a verified very near-optimal solution to the dual problem has been found. The parameter \(\lambda \) is initialised to the value 1.5 and halved whenever \(LBD_k\) has not improved for ten consecutive iterations since the most recent halving.

After termination for a given weight \(w_k\), the next value, \(w_{k+1}\), is considered. Since the two values of the weight differ only little, it is reasonable to assume that the corresponding optimal dual solutions are also rather similar. The subgradient optimization is therefore initialised at the best dual solution found for the previous value of the weight; this dual solution will often yield a good initial value of \(LBD_k\). For \(k=0\), all dual variables are initialised to 500. The upper bound \(UBD_k\) is initialised as the best objective value \(w_kz_1 + (1-w_k)z_2\) among all available feasible solutions to (16). (For \(k=0\), when no feasible solution is known, we initiate \(UBD_0\) to a large number.)

The numerical parameter values introduced above are based on some preliminary experiments which are not reported. The performance of the overall method is however insensitive to the values of the parameters.

3.5 Lagrangian heuristic

A Lagrangian relaxed solution \((x(w_k,u^s),y(w_k,u^s))\) is of course fulfilling the non-relaxed constraints (16c)–(16i), but it is unlikely that the relaxed single-sourcing constraint (16b) is fulfilled. (If (16b) actually becomes fulfilled, then, for the current value of w, the duality gap is zero, u solves (19), and (x(w, u), y(w, u)) solves the scalarised problem (17).) In case u is near-optimal, it is however likely that most of the constraints in (16b) are fulfilled.

Our heuristic is very similar to that in Cortinhal and Captivo (2003), see Phase I, but randomised to create diversity. The aim of the heuristic is to modify the relaxed solution so that the violated constraints in (16b) become fulfilled, without violating any already fulfilled constraint. In order to strive for a feasible solution that is near-optimal, the modifications made are guided by the weighted costs \(wc^1_{ij}+(1-w)c^2_{ij}\). The heuristic works in four steps, as outlined below. (It is here most convenient to use the terminology from the application.)

The first step is to find the customers that are not assigned to any depot and those that are assigned to multiple depots. (This information is readily available from the subgradient at the current dual iterate.) If more than \(30\%\) of the customers are unassigned, then the heuristic is not run. This is because if many customers are unassigned, then the heuristic will be time-consuming and the feasible solutions found will typically be inferior. The latter is due to the large degree of infeasibility and also that the heuristic is partly random, in order to promote diversity. The case that the heuristic is not run appears mainly in the early subgradient iterations, when the dual solution is far from being near-optimal.

The second step is to remove all but one of the depots from customers that are assigned to multiple depots. The depot that remains assigned is one with lowest weighted cost \(wc^1_{ij}+(1-w)c^2_{ij}\). (The fixed depot costs are not considered since removed depots are still available for other customers.) The removals made in this step will clearly keep or improve the feasibility in constraints  (16d) and (16e).

The third step is to try to assign all unassigned customers to the depots that are available (that is, with \(y_i(w,u)=1\)). These customers are considered in a random order; this is done to promote diversity among the solutions found in different runs of the heuristic. For each customer the available depots are examined according to increasing weighted cost \(wc^1_{ij}+(1-w)c^2_{ij}\), and the customer is assigned to the first depot where this is possible without violating constraint (16d) or (16e). If all unassigned customers can be assigned to the available depots, then the heuristic has found a feasible solution, and otherwise it has failed.

If the heuristic has been successful, then the last step is to remove any depot that is lacking assigned customers. Thereafter, the resulting feasible solution and its two objective values, \(z_1\) and \(z_2\), are returned.

3.6 Results

We give detailed results for one problem instance and aggregated results for all of them. Since the Lagrangian heuristic described in Sect. 3.5 is randomised, the results obtained will vary between different runs. The variation in the results between runs is however very small, and we therefore only give results for a single run.

Figure 4 displays detailed results for problem instance No. 1, which includes 2000 customers. The results for this instance are representative for all the instances. Notice that because of the huge difference in magnitude between the two objectives, the scales of the axes differ with a factor of ten. The red dots are Pareto optimal outcomes, the blue curve is the linear programming bound, the green curve is the Lagrangian bound, the blue dots are the objective values of the feasible solutions found by the heuristic, and the plus signs are the non-dominated feasible solutions found by the heuristic.

An important observation is that the Lagrangian bound is tight along the entire Pareto frontier, and that the linear programming bound is strong when emphasis is on minimizing CO2 emission but weak when emphasis is on minimising cost. The latter is due to the large costs for locating each of the (few) depots, which results in large cost savings when the linear programming relaxation allows for fractional depots. In contrast, the Lagrangian relaxation does not allow fractional depots, and therefore provides a stronger bound.

With emphasis on minimizing CO2 emission, more depots are located to reduce CO2 emission from transports, until the emissions from the depots exceed the reduction of emission from shorter transports. With more depots located, there is enough capacity to assign all customers to nearby depots. Therefore, a linear programming solution will become integral, or almost integral, and the corresponding bound will be close to the Pareto frontier.

We have noticed that when emphasis is on minimizing CO2 emission, the linear programming bounds are actually sometimes slightly stronger than the Lagrangian bounds, even though the latter is at least as strong as the former if Lagrangian dual problem (19) is solved exactly; the subgradient optimization used on (19) is however only approximate.

The heuristic is clearly able to produce a wide range of feasible solutions, and those that are mutually non-dominated are very close to the Pareto frontier. It can be noticed that the feasible solutions are roughly distributed on eight cost levels, which are related to the number of located depots. There are Pareto points on the three lowest levels, which contain solutions with three, four, and five located depots, respectively.

Fig. 4
figure 4

Frontiers and feasible objective points for problem instance No. 1. The red dots are Pareto optimal outcomes, the blue curve is the linear programming bound, the green curve is the Lagrangian bound, the blue dots are the objective values for the feasible solutions found by the heuristic, and the plus signs are the non-dominated feasible solutions found by the heuristic (colour figure online)

Full size image

We next give results for all the problem instances, in Tables 1 and 2 and in Figs. 5 and 7. Our Lagrangian bounding and heuristic principle for bi-objective discrete optimization aims at confining an unknown Pareto frontier. We therefore first study the strength of the bounding of the Pareto frontier achieved by the Lagrangian relaxation compared to that obtained by the linear programming relaxation. This is done by, for both relaxations, calculating approximate values of the relative deviations between the set of non-dominated objective outcomes found by the heuristic and the lower bounding function, according to expression (15) and using the approximation described in Appendix 1.

Figure 5 shows the results of these calculations. We can observe that the relative deviations of both the Lagrangian bound and the linear programming bound are consistent over all the problem instances. The Lagrangian relaxation used is very strong, in the sense that it provides tight lower bounds; this is because the solution of the Lagrangian relaxed problem amounts to first solving one knapsack problem for each depot and then an additional knapsack problem to select depots. The Lagrangian bounds are therefore consistently much stronger than the linear programming bounds, and the improvement is in the range of 96.3–97.2%.

Fig. 5
figure 5

For each problem instance, relative deviations between non-dominated objective outcomes and the Lagrangian and linear programming bounds, respectively

Full size image

Table 1 provides results for the Lagrangian heuristic. It shows, for each instance, the number of Pareto points found by the \(\epsilon \)-constraint method (\(\vert P_\epsilon \vert \)), and by using problem (17) for the K weights (\(\vert P_w\vert \)), respectively, the number of feasible solutions found by the heuristic, and how many out of these that are mutually non-dominated (\(\vert ND\vert \)). Further, we report how many points in ND that coincide with points in \(P_\epsilon \) and how many that are not dominated by such points. (As described in Sect. 3.3, the Pareto points are found by the \(\epsilon \)-constraint method with 501 increments in CO2 emission.) To assess the overall quality of the set ND versus the known Pareto points in \(P_\epsilon \), we apply the hypervolume (dominated-space) metric introduced in Zitzler and Thiele (1998). We report normalised metric values with respect to the ideal and anti-ideal points as suggested in Medaglia and Fang (2003). We also apply the coverage measure described in Mesquita-Cunha et al. (2022, eq. (1)), using Euclidean distance. The same analyses are made for the set \(P_w\).

Table 1 The number of Pareto points in the sets \(P_\epsilon \) and \(P_w\) (\(\vert P_\epsilon \vert \) and \(\vert P_w\vert \), respectively), the number of feasible solutions found by the heuristic (# Feas), the number out of these that are mutually non-dominated (\(\vert ND\vert \)), how many points in ND that coincide with any point in \(P_\epsilon \) (In \(P_\epsilon \)), and how many that are not dominated by points in \(P_\epsilon \) (Not \(P_\epsilon \))
Full size table

As can be seen, the number of Pareto points, feasible solutions, and non-dominated solutions vary a lot between the instances. This is due to the varying properties of the problem instances, but also to the varying number of subgradient iterations made (see Table 2). Further, some of the solutions found by the heuristic are Pareto optimal. For the vast majority of the heuristic solutions it is not known whether they are Pareto optimal, but the fact that they are not dominated by the large number of known Pareto optimal solutions indicates that they are at least near Pareto optimal.

We note that the hypervolume measure is consistently better for ND compared with \(P_w\), and that the coverage measure of ND is always at least as good as that of \(P_w\) and often much better. One reason for ND being superior is that the Lagrangian heuristic finds a diversity of non-dominated solutions, while set \(P_w\) only contains exposed Pareto points.

Figure 6 shows Pareto points and mutually non-dominated objective points found by the heuristic for instance No. 3. To the right is a magnification of a cluster of points in the figure to the left. Clearly, many mutually non-dominated objective points are found, they span the objective space within this cluster, and they are all near Pareto optimal.

Fig. 6
figure 6

Known Pareto points and mutually non-dominated objective points found by the heuristic for instance No. 3. A red dot shows a Pareto point and a plus sign shows a non-dominated objective point found by the heuristic. To the right is a magnification of the cluster indicated by the black box in the picture to the left (colour figure online)

Full size image

In Appendix 3 we give plots of the known Pareto points and the mutually non-dominated objective points found by the heuristic for all the instances. An illustration of actual locations of depots and of customer assignments in various feasible solutions for one instance is given in Appendix 1.

Table 2 gives some statistics for the subgradient optimization method, as described in Sect. 3.4. It gives the total number of iterations used for the 101 values of the weight w, the median number used over these values, and how many times the maximal number of iterations, which is 100, is reached. As can be seen, the subgradient optimization is commonly terminated because \((UBD_k-LBD_k)/LBD_k \le \epsilon \) holds, so that the maximal number of iterations is not needed. This indicates that the relative duality gap \((z^*(w) - h^*(w))/h^*(w)\) is, for most instances and values of the weight, very small, and that the reoptimization strategy used in the subgradient optimization works well. When the duality gap is large, the method will of course run the maximal number of iterations.

Table 2 Number of iterations used in the subgradient method
Full size table

Figure 7 gives the run times for finding the linear programming bound, the Lagrangian bound (including running the heuristic), the Pareto points in \(P_w\), and the Pareto points in \(P_\epsilon \). Worth noticing is that the computing times for the linear programming bounding is mostly less than that for the Lagrangian bounding, but that the time needed for the latter is never of a different magnitude, although the Lagrangian bounds are consistently much stronger and the Lagrangian scheme also provides a large number of feasible solutions. Also worth noticing is that the computation of the Pareto points in \(P_w\) and \(P_\epsilon \) are typically much more expensive, with the latter being far more expensive.

As can be seen in Fig. 7, the computing time for the Lagrangian bounding varies a lot. This is partly because it is affected by the number of depots and customers as well as the capacity ratio. The main reason is however that the computing time is dominated by the solution of the knapsack problems (20) in each iteration of the subgradient optimization, and as can be seen in Table 2, the number of such iterations varies considerably.

Notice also that the number of feasible solutions found, shown in Table 1, is strongly correlated to the number of subgradient iterations used, since the heuristic run in each of these iterations.

Fig. 7
figure 7

For each problem instance, run times in seconds for finding the linear programming bound, the Lagrangian bound (including running the heuristic), the Pareto points in \(P_w\), and the Pareto points in \(P_\epsilon \). Note that the scales on the y-axes are very different. The red line in the right figure corresponds to the upper limit on the y-axis in the left figure (colour figure online)

Full size image

The overall conclusion from our experiments is that the developed Lagrangian bounding and heuristic principle for bi-objective discrete optimization problems performs well on the studied application. The non-dominated solutions found are near Pareto optimal and diverse, and of high quality compared to the sets \(P_w\) and \(P_\epsilon \). The computation times for finding the Lagrangian bounding frontier are of the same magnitude as those for finding the linear programming bound, but the Lagrangian bounding is much stronger. Further, the computation times are much shorter compared to the times needed to find the sets \(P_w\) and \(P_\epsilon \).

We conclude this section with a few comments about our results in comparison to those given in Harris et al. (2011). Their heuristic first applies an evolutionary multi-objective optimization algorithm to find several good selections of depots and thereafter applies a Lagrangian relaxation based heuristic to each selection to assign customers. They find non-dominated solutions on the same cost levels as we do with our approach (and also with the \(\epsilon \)-constraint method), but in total they find only between 4 and 10 non-dominated solutions for every problem instance. This is little compared to our heuristic, which finds over 20 non-dominated solutions for each instance, as shown in Table 1.

As also shown in that table, the \(\epsilon \)-constraint method with 501 increments in CO2 emission often produced many Pareto optimal solutions. To further examine the number of Pareto optimal points for the problem instances used, we ran the \(\epsilon \)-constraint method with several thousand increments in CO2 emission on instance No. 1. This run took more than 15 h and gave 1688 Pareto points. Runs on other instances gave similar, and even higher, results. Hence, the instances studied seem to have thousands of Pareto optimal points. The large numbers of Pareto optimal solutions are mainly due to the many possible ways to assign customers for each selection of depots, since the number of reasonable locations of depots is quite limited.

Our heuristic finds more non-dominated solutions than that used in Harris et al. (2011); most likely this is because the problem (21) finds the same selection of depots in several subgradient iterations and the random component of the heuristic then allows it to find different assignments of customers for this selection. Even though our heuristic produces more non-dominated solutions than the heuristic used in Harris et al. (2011), the major advantage of our approach is that it also creates a bounding frontier for an unknown Pareto frontier, which enables an assessment of the quality of the non-dominated solutions found.

4 Conclusions and future work

We have derived a Lagrangian bounding and heuristic principle for the approximate solution of bi-objective discrete optimization problems for which it is computationally challenging to find the Pareto frontiers. Our work extends well established Lagrangian dual techniques for single-objective discrete optimization to the bi-objective case. The bounding part produces a convexified frontier that bounds the Pareto frontier, while the heuristic provides non-dominated objective outcomes, that is, candidates for Pareto optimal solutions; the bounding method and the heuristic will therefore together confine the Pareto frontier. A key feature of the Lagrangian bounding is that it has the potential to be stronger than the linear programming bounding of the Pareto frontier.

To demonstrate the applicability of the derived approach we considered a bi-objective facility location problem. The numerical results presented are very encouraging. First, the Lagrangian bounding frontier is tight to the Pareto frontier and it is much stronger than the linear programming bounding; this is due to the use of a strong, tailored Lagrangian relaxation for the application at hand. Second, the heuristic used succeeds to find a large number of feasible solutions, and the feasible solutions that are non-dominated are very close to the Pareto frontier. Further, the computation times are very favourable compared to using the \(\epsilon \)-constraint method or the weighted-sum scalarisation method.

Our results are promising for further applications of bi-objective discrete optimization. Further, the overall strategy of using Lagrangian relaxation and Lagrangian heuristics allows for many different realisations for a specific application, such as choice of relaxation, choice of solution method for the Lagrangian dual problem, and design of the Lagrangian heuristic.

Worth noticing is that the Lagrangian dual problem can often be solved with a cutting plane method, which in the primal space is equivalent to column generation (Dantzig–Wolfe decomposition). Suppose that the set X consists of N points, say \(x^j\), \(j=1,\ldots ,N\), and let \(\lambda _j\), \(j=1,\ldots ,N\), be convexity weights for these points. Then the characterisation (6) can be rewritten as

$$\begin{aligned} h^*(w) = \min&~ \sum _{j=1}^N \left[ wc_1^{\textrm{T}}x^j + (1-w)c_2^{\textrm{T}}x^j \right] \lambda _j \end{aligned}$$
(23a)
$$\begin{aligned} \text {s.t.}&~ \sum _{j=1}^N \left( A x^j \right) \lambda _j \ge b, \end{aligned}$$
(23b)
$$\begin{aligned}&~ \sum _{j=1}^N \lambda _j = 1, \end{aligned}$$
(23c)
$$\begin{aligned}&~ \lambda _j \ge 0, ~ j=1,\ldots ,N. \end{aligned}$$
(23d)

This is a linear optimization problem that can be solved by column generation. Letting \(y \in {\mathbb {R}}_ +^m\) and \(v \in {\mathbb {R}}\) be given values of the linear programming dual variables for constraints (23b) and (23c), respectively, the column generation problem is

$$\begin{aligned} \min _{x \in X} \left\{ \left[ wc_1 + (1-w)c_2 - A^{\textrm{T}} y \right] ^{\textrm{T}} x - v \right\} , \end{aligned}$$

that is, the minimization of a linear objective over X. If problem (23) is solved for all values \(w \in [0,1]\), then the bounding frontier \(\text {bd}(Z_{\text {LD}})\) will be found exactly. The theory concerning this column generation strategy for bi-objective discrete optimization has been outlined in Larsson and Quttineh (2023). Its practical application is a topic for further research.

Finally, an obvious topic for continued research is the extension of our approach to discrete optimization problems with more that two objectives, although this is, in principle, straightforward.