1 Introduction

Prior to the Covid-19 pandemic, the global economy was significantly boosted up by the aviation sector, with 87.7 million jobs supported and US$3.5 trillion generated (corresponding to 4.1% of the global gross domestic product in 2018) (Air Transport Action Group 2019). The direct and indirect impacts of the aviation industry have been recognised in business and trade development, infrastructure development and tourism, among others (Acar and Karabulak 2015). These developments, in turn, fuel the demand for air transportation, especially in the Asia-Pacific region (Heshmati and Kim 2016). A recent report from the IATA forecast revealed that the net profits of the Asia-Pacific’s aviation industry reached US$6.3 billion in 2016, second to North America. However, the report pointed out that airlines operating in the Asia-Pacific region performed differently, and thus an examination of the efficiency and performance of Asia-Pacific’s airlines is justified (IATA 2016).

Researchers in the transportation field have witnessed the rise of the frontier analysis approach in evaluating the performance and efficiency of homogeneous decision-making units (DMUs) such as airports (Assaf et al. 2014; Ngo and Tsui 2020), airlines (Adler et al. 2013; Heshmati and Kim 2016), ports (Tovar and Wall 2017), railways (Lan and Lin 2005; Azadeh et al. 2018) and buses (Viton 1997; Kang et al. 2019). The idea of frontier analysis can be traced back to the possible production frontier, in which DMUs are compared with a benchmark (i.e. the best practice frontier): a DMU is efficient if it operates on the frontier and inefficient otherwise. To estimate the best practice frontier, one can use a parametric approach [e.g. stochastic frontier analysis (SFA]) or a non-parametric approach [e.g. data envelopment analysis (DEA)]. These approaches have their own pros and cons (see, for example, Coelli et al. 2005); for example, DEA is often used in cases of small samples, whereas SFA often requires larger samples.

An important difference between these two approaches is that in the non-parametric model, if a DMU is away from the best practice frontier, the deviation is treated as inefficiency; in the parametric approach, the deviation or the error is broken down into inefficiency and pure error (e.g. measurement errors or luck). The argument for DEA is that if a DMU deviates from the frontier, for whatever reason, it is inefficient. However, statisticians (of SFA) tend to argue that if the reason is exogenous, such as a flood in agriculture, it should be distinguished from inefficiency. Specifically, in SFA, the frontier is first estimated via the ordinary least squares (OLS) model, and the residuals between the observed and estimated data are decomposed via the maximum likelihood estimation (MLE) approach (Aigner et al. 1977; Meeusen and van den Broeck 1977; Bogetoft and Otto 2011; Ngo et al. 2019). These econometric techniques allow one to make statistical inferences about SFA efficiency estimates, such as the confidence intervals. In contrast, the non-parametric approach has been characterised as deterministic (as opposed to the econometric approach) and thus it is deemed to be a non-statistical approach (Gong and Sickles 1992; Banker 1996).

To remedy the non-statistical deficiency of the non-parametric approach of performance analysis, several approaches have been introduced (see, for example, Grosskopf 1996; Olesen and Petersen 2016). The recent review of Olesen and Petersen (2016) summarised these approaches as three directions. The first direction is to extend DEA to be able to handle the estimated deviations as random deviations (Banker 1988,1996; Banker et al. 2015). The second direction is to extend DEA to be able to handle random errors in data based on the bootstrap technique (Simar and Wilson 1998; Lothgren and Tambour 1999). The last direction is to extend DEA to regard the estimated frontier as a random or stochastic frontier, also based on random variation in the data (Huang and Li 2001; Ruggiero 2004; Kao and Liu 2009; Azadeh et al. 2017). These three directions have their own limitations. The first does not include any estimation of the sampling distributions of the estimated efficiency scores, implying that no information can be extracted on the confidence intervals for each of the estimated DEA efficiency scores. The second contributes to the issue by resampling the data to get an approximation of these unknown sampling distributions and extract confidence intervals for the estimated DEA efficiency scores (Olesen and Petersen 2016); however, these pseudo-bootstrapped data and efficiency scores provide limited implications for managers to improve the performance of the DMUs being studied. The last one departs from the deterministic frontier basis of DEA; from the managerial perspective, it is also not very convincing to argue that the observed inputs and outputs data of the involved DMUs are not ‘real’ but random or stochastic (Olesen and Petersen 2016).

In this paper, we extend the first direction of random deviations introduced by Banker (1988, 1996) and Banker et al. (2015) to provide confidence intervals for DEA efficiency scores. Specifically, in contrast with the second and third directions above, we argue that the observed data is unique, so does the efficient frontier enveloped from those data. However, estimation errors can happen in DEA, like in any regression/estimation model, resulting in randomness in the DEA inefficiency scores. To simply put, DEA inefficiency measurement is affected at some extent by errors and noise, and thus we need to disentangle them from the ‘pure’ inefficiency component. This is similar to the situation of SFA, as discussed above, so one can use the MLE approach to solve this problem and also extract important information on the ‘pure’ inefficiency scores, the ‘pure’ efficiency scores and their confidence intervals. This information is useful for managerial implications and our approach therefore overcomes the limitation of the first direction pointed out by Olesen and Petersen (2016) as discussed above.

Empirically, this study employed a two-stage DEA model where the frontier as well as the DEA inefficiency (or deviations) were estimated during the first-stage estimation via the conventional DEA model. These inefficiencies were then decomposed into ‘pure’ inefficiency and noise via the MLE approach. In this sense, our approach is a combination of DEA and SFA and therefore is named as the data envelopment analysis and stochastic (DEAS) model. This novel DEAS approach is similar to traditional SFA, except the DEAS deviations are computed between the observed data points and the (piece-wise) DEA frontier instead of the estimated OLS frontier, as in SFA. The validity and robustness of the proposed DEAS model in this study is further verified by a Monte Carlo simulation, in which the results show that the ‘pure’ inefficiency component of the novel DEAS model has similar characteristics to those of the DEA model, and the ‘pure’ random errors component of DEAS follows a normal distribution. Therefore, this novel DEAS approach is a good alternative to conventional DEA and bootstrap DEA for measuring the performance and efficiency of DMUs. In our view, it can be a compliment or robustness-checking tool for bootstrap DEA.

For an empirical application, this study applied the DEAS model to examine the operational and financial efficiency levels of 14 major Asia-Pacific airlines. The International Air Transport Association (IATA) has acknowledged that the Asia-Pacific aviation market in 2016 was the second largest aviation industry in the world, with a net profit of US$6.3 billion, second only to North America’s. IATA (2016) also pointed out that Asia-Pacific airlines performed differently, and thus a thorough examination of the efficiency and performance of Asia-Pacific airlines via this novel DEAS model is justified.

The rest of the paper is constructed as follows. Section 2 reviews the methodologies of SFA and bootstrap DEA, and explains the proposed DEAS model. A Monte Carlo simulation for illustrative purposes is presented in Sect. 3. Section 4 applies the DEAS model to measure the operational performance of the sampled Asia-Pacific airlines and discusses the findings. Section 5 concludes the key findings and indicates directions for future research.

2 Confidence interval estimation in frontier analysis

As discussed previously, this section provides some information on SFA as well as bootstrap DEA, the most popular approach dealing with confidence interval estimation in DEA. We then discuss some limitations of bootstrap DEA in comparison to SFA and then introduce our DEAS model—note that relevant discussions on the so-called stochastic DEA (the first direction mentioned in Olesen and Petersen 2016) are also presented in this sub-section.

2.1 Using SFA to estimate the confidence intervals of efficiency scores

SFA was simultaneously introduced by Aigner et al. (1977) and Meeusen and van den Broeck (1977). The basic idea of SFA is that in the residuals \({\varepsilon }_{i}\) between the observed and OLS-estimated data, one can distinguish the inefficiency \({u}_{i}\) from the stochastic error \({v}_{i}\) so that:

$$y_{i} = \alpha + {\upbeta }x_{i} + \varepsilon_{i} = \alpha + {\upbeta }x_{i} + v_{i} - u_{i} ,$$
(1)

where \(y\) represents the output, \(x\) represents the set of inputs used to produce output \(y\), \(\beta\) is a vector of coefficients to be estimated by using OLS, \(i\) denotes the observation or DMU, \(v\) is the ‘pure’ random error and \(u\) gets a negative sign, since it represents inefficiency. Note that in Eq. (1), the SFA frontier and the ‘pure’ inefficiency component \(u\) are still deterministic; only the error component \(v\) is stochastic.

One basic assumption for the two components \({u}_{i}\) and \({v}_{i}\) is that they are independent and identically distributed across observations [although there is an argument that \({u}_{i}\) should not be identical (Olesen and Petersen 2016)], and thus \({u}_{i}\) has a constant mean of \({\mu }_{u}\) and a variance of \({\sigma }_{u}^{2}\), whereas \({v}_{i}\) has a constant mean of 0 and a variance of \({\sigma }_{v}^{2}\). The optimal values of the parameters \(\alpha\), \(\beta\), \({\sigma }_{u}\) and \({\sigma }_{v}\) (and any other parameters) that can maximise the log-likelihood function in Eq. (2) also specify the SFA frontier, allowing us to estimate the efficiency and related confidence intervals. Note that it is under the assumption that \({u}_{i}\) follows a half-normal distribution, whereas \({y}_{i}\) follows a normal distribution (for other assumptions, please see Kumbhakar et al. (2015), among others).

$$L_{i} = - \ln \left( \frac{1}{2} \right) - \frac{1}{2}\ln \left( {\sigma_{u}^{2} + \sigma_{v}^{2} } \right) + \ln \phi \left( {\frac{{\varepsilon_{i} }}{{\sqrt {\sigma_{u}^{2} + \sigma_{v}^{2} } }}} \right) + \ln {\Phi }\left( {\frac{{\mu_{*i} }}{{\sigma_{*} }}} \right)$$
(2)

where:

$$\mu_{*i} = \frac{{ - \sigma_{u}^{2} \varepsilon_{i} }}{{\sigma_{u}^{2} + \sigma_{v}^{2} }},$$
(3)
$$\sigma_{*}^{2} = \frac{{\sigma_{u}^{2} \sigma_{v}^{2} }}{{\sigma_{u}^{2} + \sigma_{v}^{2} }}.$$
(4)

Accordingly, the SFA efficiency scores can be estimated as in Eq. (5), following Jondrow et al. (1982):

$$SFA_{i} = E\left( {u_{i} |\varepsilon_{i} } \right) = \mu_{*i} + \sigma_{*} \left[ {\frac{{\phi \left( {\mu_{*i} /\sigma_{*} } \right)}}{{{\Phi }\left( {\mu_{*i} /\sigma_{*} } \right)}}} \right].$$
(5)

The confidence intervals of the efficiency scores in Eq. (5) are further estimated following Horrace and Schmidt (1996) and Hjalmarsson et al. (1996), as in Eq. (6):

$$\exp \left( { - \mu_{*i} - \sigma_{*} {\Phi }^{ - 1} \left\{ {\frac{\alpha }{2}{\Phi }\left( {\frac{{\mu_{*i} }}{{\sigma_{*} }}} \right)} \right\}} \right) \le SFA_{i} \le \exp \left( { - \mu_{*i} - \sigma_{*} {\Phi }^{ - 1} \left\{ {\left( {1 - \frac{\alpha }{2}} \right){\Phi }\left( {\frac{{\mu_{*i} }}{{\sigma_{*} }}} \right)} \right\}} \right)$$
(6)

2.2 Using bootstrap DEA to estimate the confidence intervals of efficiency scores

The bootstrap method is an intensive resampling method that can approximate the sampling distribution of the estimator and thus provides inferences in complex problems (Efron and Tibshirani 1994). Following this approach, Simar and Wilson (1998) and Lothgren and Tambour (1999) argued that by using bootstrap, one can resample the observed sample to be an approximation of the population. Simply put, the efficiency scores observed from DEA are only a sample of the population (of the efficiency scores) and therefore bootstrap DEA can provide better estimators of the efficiency scores as well as permitting valid inferences.

Conventional DEA examines a set of \(n\) firms (or DMUs), each using \(m\) inputs \({x}_{k}\) (\(k=1,\dots ,m\)) to produce \(s\) outputs \(y_{r}\) (\({\text{r}} = 1, \ldots ,{\text{s}}\)). In this sense, the efficiency score of \(DMU_{j}\) can be estimated as:

$$\begin{gathered} DEA_{j} = \max_{u,v} \frac{{\mathop \sum \nolimits_{r}^{s} u_{r} y_{rj} }}{{\mathop \sum \nolimits_{k}^{m} v_{k} x_{kj} }} \hfill \\ {\text{subject}}\,{\text{to}}:\, \frac{{\mathop \sum \nolimits_{r}^{s} u_{r} y_{rj} }}{{\mathop \sum \nolimits_{k}^{m} v_{k} x_{kj} }} \le 1,\quad j = 1,..,n; \hfill \\ u_{r} , v_{k} \ge 0, \,r = 1,..,s,\,k = 1,..,m, \hfill \\ \end{gathered}$$
(7)

where u and v are the two sets of multipliers or weights to be estimated for the outputs y and the inputs x of \(DMU_{j}\), respectively.

Equation (7) seeks for an optimal weights u and v so that \(DEA_{j}\) is maximised. Note that the first constraint of Eq. (7) requires those weights to be applicable to all DMUs in the sample so that the efficiency scores of all DMUs cannot exceed unity. In bootstrap DEA, Simar and Wilson (1998) proposed that both \(DEA_{j}\) and the first constraint can be computed by using pseudo- (or resampling) data. In contrast, Lothgren and Tambour (1999) argued that although the calculation of \(DEA_{j}\) can use pseudo-data, the first constraint should use the original data instead. Simar and Wilson (2000) have criticized that Lothgren and Tambour (1999)’s approach is incorrect; however, there are evidence that the latter one still has some empirical values (e.g. Tziogkidis 2012). Nevertheless, it is obvious that bootstrap DEA can estimate the confidence intervals for the DEA efficiency scores by using data resampling; however, the trade-off is that the bootstrapped DEA scores and their confidence intervals are estimated from the pseudo-efficiency scores (derived from pseudo-data) but not the original ones, and thus there is limited implications for managers to improve the performance of the firms involved (Olesen and Petersen 2016). It is therefore necessary to construct the confidence intervals based on the observed efficiency scores of the sampled DMUs so that after the ‘pure’ efficiency scores are estimated, the results can be used by managers.

2.3 Using DEAS to estimate the confidence intervals of efficiency scores

Following Banker (1988, 1996) and Banker et al. (2015), the proposed DEAS model in this study differs from other DEA extensions in that the frontier is not based on the assumption of random data so that our estimated ‘pure’ efficiency scores are linked to the observed data. As discussed earlier, it is not very convincing to argue that the observed data for a DMU are not the ‘true’ data, or that the frontier constructed from the observed data is not the ‘true’ frontier, and there are many stochastic data and frontiers lying around that can affect the ‘true’ efficiency scores. Therefore, we base our study on the unique DEA frontier enveloped from the unique dataset of the observed DMUs. This is indeed consistent with SFA, where the data, frontier and inefficiency are unique or deterministic, and only the noise is stochastic.

The stochastic DEA introduced by Banker (1988, 1996) and Banker et al. (2015) attempted to test for the sensitivity of DEA measurements under different settings, arguing that the deviation between a certain DMU and the frontier is a combination of the DEA inefficiency and a symmetric random error. In this sense, by introducing (and adjusting) the weight of the inefficiency component, one can estimate different efficiency scores for that DMU—this helps explain the sensitivity and stability of stochastic DEA. However, since stochastic DEA focuses more on the inefficiency term and its weight, no confidence intervals for the efficiency scores can be estimated. We therefore extend this direction to be able to provide the confidence intervals for DEA efficiency scores by exploring the statistics of both the inefficiency and the random errors, similar to the SFA approach.

In DEAS, we first estimate a unique DEA linear frontier by following the basic Charnes et al. (1978) or the Charnes–Cooper–Rhodes (CCR) DEA model using Eq. (7) under the assumption of constant returns to scale. Nguyen et al. (2018) have showed that the frontiers of CCR-DEA and OLS SFA are very similar whilst the difference between variable returns to scale DEA and OLS SFA is only a practical issue. What we argue next is that even though the frontier is unique as well as the deviations (i.e. the DEA inefficiency scores), those deviations could still be impacted by statistical noise or random errors—the same argument has been applied in SFA. In other words, if a DMU deviates from the frontier, it may not all be attributed to inefficiency, but deviations could also be caused by random errors, such as luck or bad weather. Following the SFA approach, we decompose those deviations into two components, the ‘pure’ inefficiency (which can be later transformed into ‘pure’ efficiency) and the ‘pure’ errors. It is therefore more convincing to understand the difference between DEA inefficiency and ‘pure’ inefficiency from a managerial perspective, since there is no stochastic data or frontier involved.

Following Stevenson (1980), Banker (1988), and Banker and Maindiratta (1992), it is convenient and common to assume that the ‘pure’ errors follow a normal distribution whereas the inefficiency scores follow a non-zero mean truncated-normal distribution. Since the efficiency scores are bounded by [0, 1], one can even imply a half-normal distribution for these efficiency scores. However, we choose the truncated-normal distribution because it is more general (Kumbhakar et al. 2015)—it is only a technical matter to extend our model to other distribution assumptions. It is also well known that the deviations themselves also follow a normal distribution because they are consistent with the residuals estimated from regression (Banker, 1988). Therefore, our aim is to estimate the two components of the DEA inefficiency scores so that these conditions are satisfied. The DEAS model can be formalized as follows.

Step 1 Compute the DEA efficiency scores (\(DEA\)) by using the CCR DEA model as in Eq. (7) above. The inefficiency scores (\(IEF\)) can be consequently computed as follows—the construction of efficiency scores in DEA differs from that of SFA explaining why Eqs. (8) and (16) are also different:

$$IEF_{j} = 1 - DEA_{j}, \quad j = 1,..,n$$
(8)

Step 2 Use MLE to estimate the ‘pure’ inefficiency (\(pIEF\)) component and the ‘pure’ error (\(pER\)) component from the observed \(IEF\) by maximising the log-likelihood function in Eq. (9) below, given the conditions in Eqs. (10)–(14). Note that steps 2, 3 and 4 exactly follow the SFA process given in Eqs. (1)–(6) above.

$$L_{j} = - \ln \left( \frac{1}{2} \right) - \frac{1}{2}\ln \left( {\sigma_{pIEF}^{2} + \sigma_{pER}^{2} } \right) + \ln \phi \left( {\frac{{IEF_{i} }}{{\sqrt {\sigma_{pIEF}^{2} + \sigma_{pER}^{2} } }}} \right) + \ln {\Phi }\left( {\frac{{\mu_{*j} }}{{\sigma_{*} }}} \right),$$
(9)

where:

$$IEF_{j} \sim i.i.d.N\left( {\mu_{IEF} ,\sigma_{IEF} } \right);$$
(10)
$$pIEF_{j} \sim i.i.d.N\left( {\mu_{pIEF} ,\sigma_{pIEF} } \right);$$
(11)
$$pER_{j} \sim i.i.d.N\left( {0,\sigma_{pER} } \right);$$
(12)
$$\mu_{*j} = \frac{{ - \sigma_{pIEF}^{2} IEF_{j} }}{{\sigma_{pIEF}^{2} + \sigma_{pER}^{2} }};$$
(13)
$$\sigma_{*} = \frac{{\sigma_{pIEF}^{2} \sigma_{pER}^{2} }}{{\sigma_{pIEF}^{2} + \sigma_{pER}^{2} }}.$$
(14)

Step 3 The approach of Jondrow et al. (1982) can be used to derive the predictor of \(pIEF\) as in Eq. (15). The values of the ‘pure’ efficiency scores (\(DEAS_{j}\)) can then be obtained via Eq. (16):

$$\widehat{{pIEF_{j} }} = \mu_{*j} + \sigma_{*} \left[ {\frac{{\phi \left( {\mu_{*j} /\sigma_{*} } \right)}}{{\Phi \left( {\mu_{*j} /\sigma_{*} } \right)}}} \right];$$
(15)
$$DEAS_{j} = exp\left( { - pIEF_{j} } \right).$$
(16)

Step 4 We can further construct the confidence intervals for \(DEAS_{j}\) at an \(\left( {1 - \alpha } \right)100\)% level of significance, following Horrace and Schmidt (1996) and Hjalmarsson et al. (1996):

$$L_{j} = \mu_{*j} + \sigma_{*} {\Phi }^{ - 1} \left\{ {\left( {1 - \alpha /2} \right){\Phi }\left( {\mu_{*j} /\sigma_{*} } \right)} \right\};$$
(17)
$$U_{j} = \mu_{*j} + \sigma_{*} {\Phi }^{ - 1} \left\{ {\alpha /2{\Phi }\left( {\mu_{*j} /\sigma_{*} } \right)} \right\};$$
(18)
$${\text{exp}}\left( { - U_{j} } \right) \le DEAS_{j} \le {\text{exp}}\left( { - L_{j} } \right).$$
(19)

3 Monte Carlo simulation

3.1 Data generation process

To illustrate the functions of the proposed approach, we used a simple Monte Carlo experiment, following Giraleas et al. (2012). In particular, we examine a set of DMUs, which can be in any industry or sector, operating under the same constant return to scale Cobb–Douglas production function:

$$Y_{i} = K_{i}^{0.5} L_{i}^{0.5} exp\left( {\varepsilon_{i} } \right),$$
(20)

where \(Y_{i}\) is the output of DMU \(i\), \(K_{i}\) is the capital input of DMU \(i\), \(L_{i}\) is the labour input of DMU \(i\) and \(\varepsilon_{i}\) is the random deviation following a normal distribution associated with DMU \(i\). Note that \(\varepsilon_{i}\) will be treated as inefficiency by DEA but is further decomposed by SFA and DEAS. It is also important to note that all DEA and SFA simulations apply similar models to Eq. (20), in which inefficiency is defined as \(\varepsilon_{i}\). In this sense, SFA and DEAS identify and estimate ‘pure’ inefficiency (and thus its counterpart ‘pure’ efficiency) based on \(\varepsilon_{i}\). In contrast, bootstrap DEA estimates the bias-corrected efficiency based on the original DEA efficiency scores \(DEA_{i}\) and thus has a weak relationship with \(\varepsilon_{i}\). Consequently, bootstrap DEA will be less accurate than SFA and DEAS, as shown in Table 1.

Table 1 Accuracy results of different efficiency measures
Full size table

The data for K and L are randomly generated following a uniform distribution of \(U\left[ {0, 1} \right]\), whereas \(\varepsilon_{i}\) is randomly generated following an uniform distribution of \(U\left( {0, 0.1} \right)\). The data of \(Y_{i}\) are then computed via Eq. (20) above, in which no DMU is fully (i.e. 100%) technically efficient because of the inclusion of \(\varepsilon_{i}\). Since most DEA studies have a limited number of DMUs, we focused more on the simulated data of 100 DMUs; however, another simulation dataset of 200 DMUs was also generated for testing the robustness of our DEAS model.

As discussed previously, one basic characteristic that distinguishes SFA from DEA is how they treat \(\varepsilon_{i}\). Since in DEAS, we are trying to do the same as in SFA, in contrast to DEA, we are also interested in how the pure inefficiency component (\(DEAS\)) behaves compared with that of SFA. Therefore, we compare and contrasted the deviations from the frontiers by the simulated DMUs, which are \(\varepsilon_{i}\) (for the true frontier), \(v_{i}\) (for the SFA frontier), \(IEF_{i}\) (for the DEA frontier) and \(pER_{i}\) (for the DEAS frontier). In particular, by looking at the distributions of those components (i.e. the probability density function (PDF) and the cumulative distribution function (CDF)), we can check if they are normally distributed with a zero mean, a basic characteristic of the residuals.

Several indicators are also calculated from these simulated datasets, including the true efficiency scores \(EF_{i} = exp\left( { - \varepsilon_{i} } \right)\), the SFA efficiency scores \(SFA_{i}\) (Eq. 5), the DEA efficiency scores \(DEA_{i}\) (Eq. 7) and the DEAS efficiency scores \(DEAS_{i}\) (Eq. 16), for each of the simulated DMUs. To compare and contrast with bootstrap DEA, two indicators using Simar and Wilson (1998) approach (\(SW98_{i}\)) and Lothgren and Tambour (1999) approach (\(LT99_{i}\)) are also estimated. The results from SFA, DEA, bootstrap DEA and DEAS will be compared with those of the true frontier [as in Eq. (20)] to gain a better insight into the accuracy of each method. In particular, we used the following accuracy indicators:

$$MAD = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {EF_{i} - sEF_{i} } \right|;$$
(21)
$$MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {EF_{i} - sEF_{i} } \right)^{2} ;$$
(22)
$$AC = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{EF_{i} }}{{sEF_{i} }},$$
(23)

where \(EF_{i}\) is the ‘true’ efficiency scores; \(sEF_{i}\) are \(SFA_{i}\), \(DEA_{i}\), \(SW98_{i}\), \(LT99_{i}\) and \(DEAS_{i}\), respectively; \(MAD\) measures the mean absolute deviation of each indicator \(sEF_{i}\) from \(EF_{i}\); \(MSE\) measures the mean square error of each indicator \(sEF_{i}\) from \(EF_{i}\); \(AC\) measures the accuracy level of each indicator \(sEF_{i}\) compared with \(EF_{i}\) and \(n\) is the number of DMUs. According to Eqs. (21, 23), the indicator \(sEF_{i}\) will be more accurate and will more closely estimate the ‘true’ \(EF_{i}\) when \(MAD\) and \(MSE\) are small and when \(AC\) is closer to unity. \(MAD\) and \(MSE\) were used by Giraleas et al. (2012) and \(AC\) was used by Cross and Färe (2015), among others.

3.2 Results

In general, the analysis found that DEAS outperforms SFA in terms of deviation decomposition. In particular, DEAS provides less skewed efficiency scores and more normally distributed random errors.

In Fig. 1, we first illustrated the PDF and CDF of the simulated deviations from the estimated frontiers of SFA, DEA and DEAS, represented by \(v_{i}\), \(IEF_{i}\) and \(pER_{i}\), respectively. The ‘true’ frontier is defined in Eq. (20) and thus the ‘true’ deviations are given as \(\varepsilon_{i}\). Although the distributions of \(IEF_{i}\) and \(pER_{i}\) are very similar to those of \(\varepsilon_{i}\) (Panels A, C and D in Fig. 1), one can see that \(v_{i}\) (Panel B in Fig. 1) is an exception: it is left-skewed with a significantly lower variance (and thus a shorter tail). One may argue that since our data generation process only created positive deviations \(\varepsilon_{i} \subset U\left( {0, 0.1} \right)\), whereas SFA will estimate \(v_{i} \subset N\left( {0, \sigma_{v}^{2} } \right)\), some skewness in \(v_{i}\) is acceptable. We are not neglecting this issue; however, even if we account for the normal distribution of the random errors, DEAS still can be considered to be better than SFA, as \(pER_{i}\) follows \(N\left( {0, \sigma_{v}^{2} } \right)\) more closely than \(v_{i}\) (see Panel D in Fig. 1). We therefore concluded that the ‘pure’ random error component \(pER_{i}\) estimated from DEAS is well-behaved and satisfies the requirements for decomposition.

Fig. 1
figure 1

Distribution functions of the random errors from examined methods. CDF: cumulative distribution function, PDF: probability density function, represents the (simulated) deviations from the ‘true’ frontier, indicates the deviations estimated by SFA, IEFi indicates the deviations estimated by DEA and indicates the deviations estimated by DEAS

Full size image

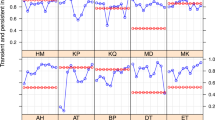
Regarding the confidence intervals of the stochastic efficiency scores, we compared results from SFA, bootstrap DEA (SW98 and LT99) and DEAS for the 95% level of confidence. Since those estimated efficiency scores are different, especially for bootstrap DEA due to the characteristic of randomness in resampling, we expected to see some differences in their lower bounds and upper bounds as well. As discussed by many studies, \(SFA_{i}\) and its confidence intervals are higher than those based on DEA (Hjalmarsson et al. 1996; Bauer et al. 1998) and thus it is not a surprise to see that those measures are closer to unity (Panel A in Fig. 2). Panels B, C and D in Fig. 2 visually show that the three DEA-based measures (namely \(SW98_{i}\), \(LT99_{i}\) and \(DEAS_{i}\)) have a similar pattern, suggesting that DEAS can be seen as an alternative to bootstrap DEA, which is more computation intensive, bringing DEA closer to SFA in terms of statistical characteristics.

Fig. 2.
figure 2

95% confidence intervals for the efficiency scores of the examined methods. Values on the vertical axis represent the efficiency scores; the horizontal axis represents the DMUs from 1 to 100. SW98 indicates efficiency scores estimated via Simar and Wilson (1998). LT99 indicates efficiency scores estimated via Lothgren and Tambour (1999). LB, lower bound; UB, upper bound

Full size image

Figure 2 also shows that SFA sometimes estimates a proportion of DMUs to be located far from their ‘true’ efficiency (i.e. large differences between \(EF_{i}\) and \(SFA_{i}\)), and that estimates from DEA and DEAS are located closer together (i.e. smaller differences between \(EF_{i}\) and both \(DEA_{i}\) and \(DEAS_{i}\)). We then used mean absolute deviation \(\left( {MAD} \right)\), mean square error (\(MSE)\) and accuracy level (\(AC)\) to further test for the accuracy of different efficiency measures. The simulation sample was increased to 200 DMUs to test for the robustness of DEAS – most DEA applications used DEA because of the small sample size issue and ended up with less than 200 DMUs. Table 1 presents the simulation results, where \(DEAS_{i}\) has the lowest \(MAD\) and \(MSE\) throughout all simulations. In addition, we also observed that SFA tends to underestimate the efficiency (AC > 1), whereas DEA and its derrivatives (i.e. \(SW98_{i}\), \(LT99_{i}\) and \(DEAS_{i}\)) tend to overestimate the ‘true’ efficiency score (AC < 1), which is caused by the characteristics of DEA and SFA, as discussed in Smith (1997) and Bauer et al. (1998). Table 1 also suggests that increasing the simulated sample size from 100 to 200 DMUs helps to improve the accuracy of all DEA-based models, though it is not significant for SFA (e.g. \(MAD\) increases, but \(MSE\) and \(AC\) decrease).

4 Measuring the operational performance of Asia-Pacific airlines via the DEAS model

The previous section suggested that the proposed DEAS approach is a good alternative efficiency measure that combines the strengths and addresses the weaknesses of the SFA and DEA models. This section applies the new DEAS approach to examine the operational and financial efficiency of 14 Asia-Pacific airlines.

4.1 Data and model specification

The global economy is significantly boosted up by the aviation sector, with 62.7 million jobs created and US$2.7 trillion generated [corresponding to 3.5% of the global gross domestic product (GDP)] in 2016 (Air Transport Action Group 2016). The direct and indirect impacts of the aviation industry have been recognised in business and trade development, infrastructure development and tourism, among others (Acar and Karabulak 2015). These developments, in turn, fuel the demand for air transportation, especially in the Asia-Pacific region (Heshmati and Kim 2016). A recent report from the IATA forecast revealed that the net profits of the Asia-Pacific’s aviation industry reached US$6.3 billion in 2016, second to North America. However, the report pointed out that airlines operating in the Asia-Pacific region performed differently, and thus an examination of the efficiency and performance of Asia-Pacific’s airlines is justified (IATA 2016).

In our DEAS model, three key airline indicators (available seat-kilometres (\(ASK\)), available tonne-kilometres (\(ATK\)) and operating expenses (\(EXPENSES\))) are used as inputs; another three key indicators (revenue passenger-kilometres (\(RPK\)), revenue tonne-kilometres (\(RTK\)) and operating revenues (\(REVENUES\))) are used as outputs. These variables are commonly used in prior DEA studies in air transportation (Barbot et al. 2008; Lee and Worthington 2014; Min and Joo 2016) which allow us to analyse the overall performance of the sampled Asia-Pacific airlines in both operational and financial aspects. Note that operational performance and financial performance are equally important to airlines in seeking for profit maximization.

We further extended the DEAS model by using a two-stage approach: after the ‘pure’ efficiency scores (\(DEAS_{i}\)) were estimated as the true efficiency scores of the sampled airlines (excluding errors and biases) during the first-stage efficiency analysis, they were then regressed on the identified explanatory variables to see whether the air transport-related external factors affected the efficiency of the sampled Asia-Pacific airlines during the study period. Equation (24) presents the model specification of the second-stage regression analysis with the explanatory variables selected following prior air transportation studies (e.g. Heshmati and Kim (2016) and are discussed below.

$$\begin{aligned} DEAS_{{it}} &= \beta _{0} \,+\, \beta _{1} FLAG\_CARRIER_{i} \\ \,&\quad+ \beta _{2} ALLIANCE_{{it}} \\ &\quad+ \beta _{3} LISTED_{{it}} \\ &\quad+ \beta _{4} {\text{ln}}ASSETS_{{it}} \\ &\quad+ \beta _{5} GFC_{t} \,+\, \beta _{6} MH\_ACCIDENTS_{t} \\ &\quad+ \beta _{7} {\text{ln}}GDP~per~capita_{{it}} \\ &\quad+ \beta _{8} lnTOURIST\_ARRIVALS_{{it}} \\ &\quad+ \beta _{9} {\text{ln}}TRADE\_VOLMES_{t} \\ &\quad+ \beta _{{10}} {\text{ln}}FUEL\_PRICES_{{it}} \,+\, {\epsilon}_{{it}} \\ \end{aligned}$$
(24)

where:

  • \(FLAG\_CARRIER_{i}\) is a dummy variable that equals 1 if airline \(i\) is a national flag carrier and 0 otherwise. This variable was previously used in Fethi et al. (2002), Barros and Peypoch (2009) and Chen et al. (2017), among others;

  • \(ALLIANCE_{it}\) is a dummy variable that equals 1 if airline \(i\) belongs to an airline alliance (Oneworld, SkyTeam or Star Alliance) at year t and 0 otherwise (Park and Cho 1997; Kleymann and Seristö, 2001; Min and Joo 2016);

  • \(LISTED_{it}\) is a dummy variable that equals 1 if airline \(i\) was listed in the stock market at year t and 0 otherwise (Mar and Young 2001; Lu et al. 2012);

  • \({\text{ln}}ASSETS_{it}\) is the logarithmic value of the total assets of airline \(i\) in year t. This variable is used to capture the size of an airline (Feng and Wang 2000; Backx et al. 2002);

  • \(GFC_{t}\) is a dummy variable that equals 1 for the year 2008 and 0 otherwise. This variable is used to capture the impact of the Global Financial Crisis (GFC) of 2008 on airline operations (Merkert and Morrell 2012; Tsui 2017);

  • \(MH\_ACCIDENTS_{t}\) is a dummy variable that equals 1 for the period of 2014–2015, 0 otherwise. This variable is used to capture the impact of the two Malaysia Airlines flight accidents (MH370 and MH17) in 2014 on international air transportation demand (Hunter and Lambert 2016; Yang et al. 2018);

  • \({\text{ln}}GDP per capita_{it}\) is the logarithmic value of the GDP per capita at year t of the country where airline \(i\) is based. This variable is used to capture the size of an economy as well as its air transportation demand (Khadaroo and Seetanah 2008; Gaggero and Bartolini 2012);

  • \({\text{ln}}TOURIST\_ARRIVALS_{it}\) is the logarithmic value of the number of international tourist arrivals at year t to the country where airline \(i\) is based on. This variable is used to capture tourist arrivals using air transport (Bieger and Wittmer 2006; Khadaroo and Seetanah 2008; Rehman Khan et al. 2017);

  • \({\text{ln}}TRADE\_VOLUMES_{it}\) is the logarithmic value of the total trade volumes (exports + imports) at year t of the country where airline \(i\) is based. This variable is used to capture the air cargo demand of the country (Yamaguchi 2008; Tsui and Fung 2016);

  • \({\text{ln}}FUEL\_PRICES_{t}\) is the logarithmic value of fuel prices at year t (Assaf 2011; Lim and Hong 2014);

  • \(\epsilon_{it}\) is random errors.

This study examines 14 major airlines operating in the Asia-Pacific region during the period of 2008–2015 (see Table 2). Data were collected from the statistical reports of the Association of Asia Pacific Airlines (AAPA 2016). Because of data limitations, and for the panel data regression in the second stage of analysis, we devised a multi-period sample covering the years 2008, 2010, 2012, 2014, and 2015. Table 2 presents the variables of interest used for the DEAS model in the first-stage efficiency analysis and the second-stage regression analysis in this study. The values of all variables are in million US dollars, except for \(TOURIST\_ARRIVALS\), which is in persons; \(FUEL\_PRICES\), which is in US dollars; and dummy variables, which are binary. The variation in the variables of interest across the sampled airlines suggests that independent results from single-dimensional analysis such as \(EXPENSES\) or \(REVENUES\) may contradict each other and therefore a multi-dimensional efficiency analysis of the Asia-Pacific airlines with different indicators is needed.

Table 2 Descriptive statistics and data source
Full size table

4.2 Efficiency of Asia-Pacific airlines

4.2.1 First-stage efficiency analysis (DEAS model)

In this stage, the DEAS model is independently applied to yearly data (e.g. 2008 or 2010) to obtain the ‘pure’ efficiency scores, \(DEAS_{i}\). In general, the sampled Asia-Pacific airlines performed relatively well during the period of 2008–2015, with high \(DEAS_{i}\) values between 0.943 and 0.997 (see Table 3).

Table 3 Pure efficiency scores of Asia-Pacific airlines estimated via DEAS
Full size table

Table 3 also indicates a decreasing trend in the average efficiency of the sampled airlines, where the average \(DEAS_{i}\) dropped from the level of 0.994 in 2008 to 0.973 in 2015. This finding is in line with Li et al. (2016), who found that the efficiency of the major Asian carriers (e.g. Air China, Korean Air, Singapore Airlines, Asiana and Malaysia Airlines) declined during the period of 2008–2012. The results in the last two columns of Table 3 further confirm the impact of the GFC of 2008 and the two Malaysia Airlines flight accidents in 2014, as presented later in this section.

However, a further examination of the airline efficiency levels in Fig. 3 provides a different perspective of Asia-Pacific airlines’ performance over the study period. At first, if one looks at the results from the DEA model (i.e. the dotted line for \(DEA_{i}\) in Fig. 3), it shows that the sampled Asia-Pacific airlines performed differently from each other: the high-performing group with the highest possible efficiency score of 1.000 or 100% efficiency includes EVA Air, Qantas and Vietnam Airline; the low-performance group includes Garuda Indonesia, Royal Brunei, All Nippon Airways and Thai Airways. If we look at the ‘pure’ efficiency derived from the DEAS model (i.e. the solid line for \(DEAS_{i}\) in Fig. 3), however, we still see that airlines performed differently but were less volatile (the average \(DEAS_{i}\) efficiency scores are between 0.976 and 0.985). Differences between the means of \(DEA_{i}\) and \(DEAS_{i}\) are statistically significant at 1% (t-test); however, the two approaches ranked the examined airlines similarly (Mann–Whitney test). As shown in this study, DEAS has less discriminatory power than DEA. It is not surprising, however, since DEAS is in the same line with SFA, and SFA is well known to have higher efficiency scores and lower standard deviation compared to DEA (Hjalmarsson et al. 1996; Bauer et al. 1998; Michaelides et al. 2009; Roberts 2014).

Fig. 3
figure 3

Average efficiency scores derived from DEA and DEAS models

Full size image

In particular, the findings of the \(DEAS_{i}\) scores of the efficient airlines (e.g. Singapore Airlines, China Airlines, Korean Air or Japan Airlines) are consistent with those in previous studies (Arjomandi and Seufert 2014; Chang et al. 2014), which suggests that these airlines are top performers in the Asia-Pacific region as well as globally (notice that the \(dEF_{i}\) scores rank them as second-tier performers, behind EVA Air, MH, Qantas and Vietnam Airline). In addition, Thai Airways is now considered as a good performer in the group, which is more reasonable and in line with the argument that Thai Airways should perform well thanks to its high managerial efficiency (Lee and Worthington 2014; Min and Joo 2016). The relatively low-performing group according to their \(DEAS_{i}\) scores still consists of Garuda Indonesia and Royal Brunei but also Philippine Airlines. It is noted that DEA also provides information on peer DMUs (i.e. efficient DMUs that can be the role models for inefficient ones) while SFA does not. Since DEAS stands between DEA and SFA, for the managerial implications and decision-making, airline managers still can utilise the peers’ information from the first stage DEA [i.e. Equation (7)] to compare their performance against other sampled airlines, although this is not reported here due to the scope of our research.

In terms of the confidence intervals for the \(DEAS_{i}\) scores, at the 95% level of significance, we can confidently argue that it was possible that some of the sampled Asia-Pacific airlines in this study did not perform well and were less efficient than other airlines in the group during the analysis period. For example, the efficiency of Royal Brunei went down to 0.810 in 2015 and the efficiency of Garuda Indonesia in 2014 also dropped to 0.752 (see Fig. 4). By comparing the ‘pure’ efficiency scores of Royal Brunei and Garuda Indonesia to those of other sampled airlines in the same year, we can see that if we exclude the random errors and statistical noise from the DEA efficiency scores, other factors potentially had significant impact on the sampled Asia-Pacific airlines’ operations and hindered their performance. Therefore, a second-step regression analysis is performed for examining the significant determinants of the efficiency and performance of the sampled Asia-Pacific airlines.

Fig. 4
figure 4

Confidence intervals of the DEAS efficiency scores of Asia-Pacific airlines. All the plots are presented in 95% confidence intervals

Full size image

4.2.2 Second-stage of regression analysis

The second-stage Tobit regression analysis was estimated following Eq. (24) in Sect. 4.1. The coefficients of the explanatory variables are shown in Table 4, where results from DEAS and bootstrap DEA are generally consistent but DEAS provides more insights (i.e. more significant variables). Those results therefore strengthen the value of DEAS in comparison to bootstrap DEA.

Table 4 Results of the second-stage Tobit regression of airlines’ ‘pure’ efficiency
Full size table

With regard to \(DEAS_{i}\), the significant variables affecting the sampled Asia-Pacific airlines’ performance during the study periods are the three macroeconomic variables (i.e. \(GFC\), \(MH\_ACCIDENTS\) and \({\text{ln}}FUEL\_PRICES\)). The remaining variables are statistically insignificant although the directions of the relationships (i.e. the signs of the coefficients) between the predictors and the pure efficiency scores are consistent with those in the literature (\({\text{ln}}GDP per capita\), \({\text{ln}}TRADE\_VOLUMESS\) and \({\text{ln}}TOURIST\_ARRIVALS\) are positively associated with \(DEAS_{i}\)). Note that Tobit regression using \(DEA_{i}\) as a dependent variable resulted in no significant predictor—this result was not reported here but is available upon request.

Regarding the significant explanatory factors that influenced the performance of the sampled Asia-Pacific airlines during the period of 2008–2015, both the GFC of 2008/09 and the two Malaysia Airlines flight accidents in 2014 had statistically significant and negative impacts on the airlines’ pure efficiency: these empirical findings confirm our expectation of the expected negative impacts of exogenous shocks, as shown in the last two columns of Table 3. These empirical results are also consistent with the findings of Heshmati and Kim (2016), who found that the Asian financial crisis of 1997/98, the 9/11 terrorist attacks, and the GFC 2008 had negative shocks to (cost) efficiency of 39 airlines in 33 different countries during the period of 1998–2012. For the managers, it indicates that Asia-Pacific airlines need to take steps to improve their efficiency by overcoming and mitigating the hindrances of any exogenous shocks, and by leveraging other inputs (such as careful strategic planning in airline connectivity and routes).

Interestingly, fuel prices were reported to have a significant and positive impact on airlines’ efficiency. This empirical finding is mainly because fuel prices dropped continuously during the study period (i.e. from US$2.964 per gallon in 2008 to a sharp decrease in 2010 and continued to US$1.522 per gallon in 2015). One might argue that lower fuel prices allowed the sampled Asia-Pacific airlines to save more on operating costs, as fuel prices are the largest operating cost for airlines (Ryerson et al. 2014; Zou et al. 2014) and thus they improved their financial performance. However, the revenues of the sampled airlines also decreased, cancelling out the effect of lower fuel prices. Specifically, as shown in Fig. 5, \({\text{ln}}FUEL\_PRICES\) and \({\text{ln}}EXPENSES\) for the sampled Asia-Pacific airlines were moving together with a similar pattern, and although the two variables decreased continuously during the 2012‒2015 period, \({\text{ln}}REVENUES\) of the sampled Asia-Pacific airlines also faced a sharp decline during the same period. Consequently, it is reasonable that the drop in fuel prices did not contribute much to the revenue as well as the financial and overall performance of the sampled Asia-Pacific airlines.

Fig. 5
figure 5

Relationship between fuel prices and the operating revenues and expenses of Asia-Pacific airlines (2008–2015)

Full size image

5 Conclusions

This study has proposed a novel DEAS approach to decompose the deviations of DMUs from the frontier derived via DEA with a SFA-like method. The key contribution of the novel DEAS approach in this study is its ability to estimate the confidence intervals for the calculated efficiency scores of DMUs. In addition, Monte Carlo simulations showed that the ‘pure’ efficiency scores (\(DEAS_{i}\)) decomposed from DEA (in)efficiency are accurate measures of the ‘true’ efficiency scores (\(EF_{i}\)), and thus the DEAS approach is believed to be a good alternative or compliment for conventional DEA and bootstrap DEA for analysing the efficiency levels of DMUs.

For the empirical application, this study applied the proposed model to measure the performance of key Asia-Pacific airlines during the period of 2008‒2015. We found that after accounting for the ‘pure’ random errors, the sampled Asia-Pacific airlines performed well during the study period but their ‘pure’ efficiency was declining. Although the key reasons for efficiency deterioration were mainly attributed to uncontrollable factors (i.e. the GFC 2008/09 and the two Malaysia Airlines flight accidents in 2014), there is still room for improvement.

Although the novel DEAS model used in this study is shown to be a robust and fruitful approach to measuring the performance and efficiency of DMUs (e.g. Asia-Pacific airlines) in the Monte Carlo simulation, this study examines neither the likely impacts of airline-related characteristics (e.g. national flag carrier status or alliance membership) nor the macroeconomic environment (e.g. GDP per capita or number of international tourist arrivals) on their performance and efficiency because of data limitations. For future research, it would be meaningful to extend the dataset to include more airlines (legacy and low-cost carriers) and longer (continuous) time periods to explore their likely impact on airline efficiency and performance. Furthermore, this novel DEAS model can be further extended; for example, for considering the variable return to scale assumption (Banker et al. 1984) or incorporating the explanatory variables directly into the DEAS model (Battese and Coelli 1995; Simar and Wilson 2007) for performance and efficiency measurement.