Risk minimisation using options and risky assets

Abstract

We consider mean-risk portfolio optimisation models, with risk measured by symmetric measures (variance) as well as downside or tail measures (lower partial moments, conditional value at risk). A framework for including index options in the universe of assets, in addition to stocks, is provided. The exercise of index options is settled in cash, making this implementable with a variety of strike prices and maturities. We use a dataset with stocks from FTSE 100 and index options on FTSE100. Numerical results show that, for low risk-low return and to medium risk-medium return portfolios, the addition of an index put further reduces the risk to a considerable extent, particularly in the case of mean-CVaR efficient portfolios, where the left tail of the portfolio return distribution is dramatically improved. For high risk-high return portfolios, the inclusion of an index call improves the right tail of the return distribution, creating thus the opportunity for considerably higher returns.

1 Introduction

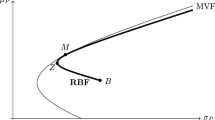
The portfolio selection problem is about how to divide an investor’s wealth amongst a set of available securities. One basic principle in finance is that, due to the lack of perfect information about the future asset returns, financial decisions are made in the face of trade-offs. Markowitz (1952) identified the trade-off faced by the investors as risk versus expected return and proposed variance as a measure of risk. He introduced the concepts of efficient portfolio and efficient frontier and proposed a computational method for finding efficient portfolios.

Following notations given in Roman and Mitra (2009), we consider an example of portfolio selection with one investment period. A rational investor is interested in investing their capital such that, at the end of the investment period, the return is maximised.

Consider a set of n assets, with asset $j\in \{ 1\ldots n \}$ having a return $R_{j}$ at the end of the investment period. Since the future price of the asset is unknown, $R_{j}$ is a random variable.

A portfolio is defined by the percentage of money invested in each asset j. Let $x_{j}$ be the percentage of capital invested in asset j and let $x=(x_{1},\ldots ,x_{n})$ denote the portfolio choice. This portfolio’s return is the random variable

$$\begin{aligned} R_{x}=x_{1}R_{1}+\cdots +x_{n}R_{n} \end{aligned}$$

with distribution function $F(r)=P(R_{x} \le r)$ that depends on the choice of $x=(x_{1},\ldots ,x_{n})$.

The weights $(x_{1},\ldots ,x_{n})$ belong to a set of decision vectors given in the simplest form as

$$\begin{aligned} X=\{(x_{1},\ldots ,x_{n})|\sum _{j=1}^{n}x_{j}=1,x_{j}\ge 0,\forall j\in \{1,\ldots ,n \}\} \end{aligned}$$

(1)

To interpret the portfolio selection problem, let us consider another portfolio return $R_y$ that is determined by the decision vector $y=(y_1,\ldots , y_n)\in X$: $R_y=y_1R_1+\cdots +y_nR_n.$ The problem of choosing between portfolios x and y becomes the problem of choosing between the two random variables $R_x$ and $R_y$. Thus, models for choosing amongst random variables are required. The first purpose of such a model is to define a preference relation among random variables and the second purpose is to identify the non-dominated random variables with respect to that preference relation.

One paradigm for choosing among random variables is mean-risk. Here, a random variable $R_{x}$ representing the return of a portfolio x is characterized using two statistics of its distribution: the expected value/mean (large value are desired) and a “risk” value (low values are desired). The preference relationship is defined based on these two statistics: one random variables is “preferred” to another if it has higher mean and lower risk. A non-dominated random variable under this relationship represents an “efficient” portfolio: one that has the lowest risk for a specified level of expected return. An efficient portfolio is found by solving an optimisation problem in which we minimise risk subject to a constraint on the expected return. Varying the level of expected return, we obtain different efficient portfolios.¹

Markowitz (1952) proposed variance as a measure of risk. Criticism of variance, mainly due to its symmetric nature that penalizes upside potential as well as downside deviations, led to proposal of other risk measures, most notably below target risk measures such as Lower Partial Moments (see Fishburn 1977; Bawa and Lindenberg 1977) and quantile based risk measures such as Value-at Risk (VaR) and Conditional VaR (see Rockafellar and Uryasev 2000; Tasche 2002 ). A review of financial risk measures can be found in Roman and Mitra (2009) and Albrecht (2004). Mean risk models with various risk measures have been implemented (see for example Roman and Mitra (2009) and references within); this has been mainly in the context when the universe of assets consists of stocks and bonds.

A closely related area of research concerns financial scenario generation: this is about simulating future values for asset prices or returns with the purpose of serving as parameters in optimisation models. Commonly used methods of financial scenario generation include sampling or bootstrapping (see Efron and Tibshirani 1994 ) from historical data, or methods based on econometric models (see Bollerslev 1986). More recently, general purpose scenario generators were proposed and used in financial optimisation models, such as the moment matching method (see Høyland et al. 2003) or Hidden Markov Models (see Messina and Toscani 2008; Erlwein et al. 2011). A review of desirable properties for scenario generators is given in Kaut and Wallace (2003).

Options are financial assets that give the right (not the obligation) to trade an asset at a specified price. They can be of great use as they put a limit on the losses that could be incurred. However, including options in portfolio optimisation is not an easy task due to several reasons.

Identifying the return distribution of an option is difficult if the option is traded before its maturity date. Options for each of the component stocks with the maturity equal to its investment period may not be available. Constructing a portfolio of stocks and adding options for each stock may seem one straightforward way to integrate options, however, even in the case when such options are available, it may be one very costly approach, leading to great decrease in portfolio return.

Research efforts towards portfolio optimisation in the presence of options include Alexander et al. (2006), Papahristodoulou and Dotzauer (2004), Horasanlı (2008), and Faias and Santa-Clara (2017). In Alexander et al. (2006), CVaR minimisation for portfolios of options only is considered. They demonstrated possible computation of optimal CVaR with low number of assets. In Ortobelli et al. (2013), portfolios of stocks and portfolios of options are constructed, employing several preference criteria of decision makers. Portfolios of options are created, based on maximisation of variability measures of the underlying stock returns. The results are very good; however, the authors underline that there are strong assumptions at the basis of the computational study, including the fact that options on individual stocks may not be available (computed Black–Scholes, instead of real option prices are used). In Faias and Santa-Clara (2017), an expected utility maximisation is used for a portfolio of options where the payoffs are simulated from distribution of the underlying asset. Since options put a limit on the maximum loss, options have been considered in the context of robust optimisation (see Zymler et al. 2011).

In this study, we propose to use index options, in addition to a set of stocks, in mean-risk scenario based optimisation models. Index options are settled in cash (an investor is not required to trade the underlying, i.e. the index) making it an implementable strategy with a variety of maturities and exercise prices and with transaction costs. The motivation and contribution of this work lies in finding answers to the following research questions:

• 1. Can improved (in terms of mean-risk trade-off) portfolios be obtained by adding index options? How does the addition of options change the return distribution?

• 2. Which risk measures are more sensitive to the introduction of index options?

• 3. What is the numerical framework to use when the universe of assets is composed of stocks and index options?

The computational results presented here add interesting insights that, to our knowledge, have not been reported in the literature.

The rest of the paper is organised as follows. Risk measures and the algebraic for-mulations of the corresponding mean-risk optimisation models is presented in Sect. 2. Section 3 describes the background for incorporating an index option in the portfolio op-timisation. Computational results are presented in Sect. 4. Conclusions are drawn in Sect. 5.

2 Risk measures

Adopting the terminology used in Albrecht (2004), there are two types of risk measures. Risk measures of the first kind measure the magnitude of deviations from a specific point. These risk measures can be further divided into symmetric risk measures and asymmetric risk measures; asymmetric risk measures quantify risk by taking into account only outcomes below a target, that could be either fixed or distribution specific. Variance is the best known symmetric risk measure. Lower partial moments (LPM) and central semi-deviations are among the important asymmetric risk measures (see Fishburn 1977; Bawa and Lindenberg 1977; Ogryczak and Ruszczyński 1999).

Risk measures of the second kind measure the overall significance of possible losses. These risk measures are concerned only with a certain number of worst outcomes (the left tail), of the return distribution. The commonly used risk measures in this category are Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR) (see Jorion 2001; Rockafellar and Uryasev 2000, 2002). This section gives a brief overview on the risk measures (variance, LPM, VaR and CVaR) that will be used in this work (see also Maasar et al. 2016.

• Variance

  Variance is a well-known indicator used in statistics for the spread around the mean of a random variable. The variance of a random variable $R_{x}$ is defined as its second central moment:

  $$\begin{aligned} \sigma ^2(R_{x})=E[(R_{x}-E(R_{x}))^2] \end{aligned}$$

  The variance of a portfolio return $R_{x}=x_{1}R_{1}+\cdots +x_{n}R_{n}$ is a quadratic function of $x=(x_{1},\ldots ,x_{n})$ (see Luenberger 1998; Markowitz 1952):

  $$\begin{aligned} \sigma ^2(R_{x})=\sum _{j=1}^{n}\sum _{k=1}^{n}x_{j}x_{k}\sigma _{jk} \end{aligned}$$

  (2)

  Where $\sigma _{jk}$ is the covariance between $R_{j}$ and $R_{k}$.

• Lower partial moments (LPM)

  LPM is a generic name for asymmetric measures that consider a fixed target below which an investor does not want the return to fall; it quantifies, loosely speaking, the average deviation below target.

  Let $\tau$ be a predefined target value for the portfolio return $R_{x}$, and let $\alpha \ge 0$.

  The LPM of order $\alpha$ around $\tau$ of the random variable $R_{x}$ with distribution function F is defined as [see Fishburn (1977)]:

  $$\begin{aligned} LPM_{\alpha }(\tau ,R_{x})=E\{[max(0,\tau -R_{x})]^\alpha \}=\int _{-\infty }^{\tau }(\tau -r)^\alpha dF(r) \end{aligned}$$

  While $\tau$ is a target fixed by decision maker, $\alpha$ is a parameter describing risk aversion. The larger the value of $\alpha$ , the more risk-averse the investor is (Fishburn (1977)).

  Commonly, LPMs of order 1 and 2 are used in practice. The LPM of order 1 is commonly referred to as “expected downside risk”, while the LPM of order 2 is referred to as “target semivariance” (see for example Albrecht (2004), Roman and Mitra (2009).) When the LPM of order 1 is constrained to not exceed a user specified threshold (rather than being used as an objective function to minimise), this constraint is referred to as an “integrated chance constraint”, introduced in the literature by Klein Haneveld (Klein Haneveld (1986), Klein Haneveld and van der Vlerk (2006).)

• Value-at-risk (VaR)

  One of the most popular quantile-based risk measures is the Value-at-Risk (VaR) (see Jorion 2001). The VaR at parameter $\alpha \in (0,1)$, or confidence level $(1-\alpha )$, is defined as the negative of the $\alpha -$percentile of the portfolio return distribution, or as the $(1-\alpha )$-percentile of the portfolio loss distribution, where $\alpha$ is typically chosen as 0.01 or 0.05. Thus, with probability of at least $(1-\alpha )$, the loss² will not exceed VaR.

  Although widely used in practice, VaR has been criticized for not being a coherent risk measure of risk (see Artzner et al. 1999) and not being convex with respect to $x_{1}\ldots x_{n}$; this makes it difficult to optimise (see Pflug 2000). This is also explained in Larsen et al. (2002), Pang and Leyffer (2004) and references therein.

• Conditional value-at-risk (CVaR)

  Conditional Value-at-Risk (see Rockafellar and Uryasev 2000, 2002) was proposed as an alternative quantile-based risk measure, to measure approximately the average loss beyond VaR. It has gained interest from practitioners and academics due to its desirable computational and theoretical properties. Informally speaking, CVaR at parameter $\alpha \in (0,1)$ (or at confidence level $(1-\alpha )$) is the average loss under the worst A% of scenarios, where $\alpha =$ A%. A more formal definition involves the concept of “$\alpha$-tail distribution”; this is the distribution obtained by rescaling the worst A% part of the portfolio return distribution . The CVaR at parameter $\alpha$ (confidence level $(1-\alpha )$)is the negative of the expected value of the alpha tail distribution. For more details, see Rockafellar and Uryasev (2000). Interesting relations between CVaR and the LPM of order 1 have been developed in Ogryczak and Ruszczyński (2002).

2.1 CVaR calculation and optimisation

It has been shown by Rockafellar and Uryasev (2002) that CVaR can be optimised using an auxiliary function $F:X\times {\mathbf {R}}\mapsto {\mathbf {R}}$:

$$\begin{aligned} F_{\alpha }(x,v)=\frac{1}{\alpha }E[\max (-R_{x}+v,0]-v \end{aligned}$$

In practice, a portfolio return $R_{x}$ is considered as a discrete random variable because the random returns are usually described by their realisations under various scenarios. This makes CVaR optimisation a linear program. Suppose that $R_{x}$ has m possible outcomes $r_{1x},\ldots ,r_{mx}$ with probabilities $p_{1},\ldots ,p_{m}$ with $r_{ix}=\sum _{j=1}^{n}x_{j}r_{ij},\forall i\in \{1\ldots m\}$, then:

$$\begin{aligned} F_{\alpha }(x,v)=\frac{1}{\alpha }\sum _{i=1}^{m}p_{i}[\max (v-r_{ix},0)]-v=\frac{1}{\alpha }\sum _{i=1}^{m}p_{i}\left[ \max \left( v-\sum _{j=1}^{n}x_{j}r_{ij},0\right) \right] -v \end{aligned}$$

The optimal CVaR is obtained by minimizing $F_\alpha$ over (x, v) (Rockafellar and Uryasev 2000, 2002); this result is used in the formulation of the mean-CVaR optimisation model

We present below the algebraic formulation of the three mean-risk models used in our computational analysis. We use the following notation:

The parameters are:

$$\begin{aligned} \begin{array}{ccl} m & = & \hbox {the number of (equally probable) scenarios};\\ n & = & \hbox {the number of assets};\\ r_{ij}&=& \hbox {the return of asset} j \hbox {under scenario } i;\, j=1\ldots n, i=1\ldots m;\\ \mu _{j} & = & \hbox {the expected rate of return of asset } j;\,j=1\ldots n;\\ \sigma _{kj }& = & \hbox {the covariance between returns of asset } k \hbox {and asset } j;\,k, j=1\ldots n; \\ d & = & \hbox {target expected rate of return for the portfolio}.\\ \end{array} \end{aligned}$$

The decision variables are:

$$\begin{aligned} \begin{array}{ccl} x_{j}& = & \hbox {the fraction of the portfolio value invested in asset } j, j=1\ldots n.\\ \end{array} \end{aligned}$$

2.2 The mean-variance model (MV)

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{x} {\displaystyle \sum _{j=1}^{n}\sum _{k=1}^{n}\sigma _{kj}x_{j}x_{k}} \\ \text {subject to:}\\ \displaystyle \sum _{j=1}^{n}\mu _{j}x_{j} \ge d \\ x\in X\\ \end{array} \end{aligned}$$

2.3 The mean-expected downside risk model (M-LPM0)

We consider the target $\tau =0$ (hence the negative rates of return are penalised under each scenario) and $\alpha = 1$, (thus, a risk measure sometimes referred to in the literature as the expected downside risk). In addition to the decision variables $x_{j}$, there are m decision variables, representing the magnitude of the downside deviations of the portfolio return from target, for every scenario $i\in \{1\ldots m\}$:

$$\begin{aligned}&\displaystyle y_{i}=\left\{ \begin{array}{rcl}-\displaystyle \sum _{j=1}^{n}r_{ij}x_{j},& & \hbox {if}\displaystyle \sum _{j=1}^{n}r_{ij}x_{j}\le 0;\\ 0,& & \hbox{otherwise}. \end{array} \right. \\&\begin{array}{ll} \displaystyle\min & {\displaystyle \frac{1}{m}\displaystyle \sum _{i=1}^{m}y_{i}} \\ \text {subject to:}&\\ &-\displaystyle \sum_{j=1}^{n}r_{ij}x_{j} \le y_{i} ;\quad \forall i \in \{1\ldots m\} \\&\quad \quad \qquad y_{i} \ge 0 ;\quad \forall i \in \{ 1\ldots m \} \\&\displaystyle \sum _{j=1}^{n}\mu _{j}x_{j} \ge d ; \\ & \quad \quad\qquad x\in X\\ \end{array} \end{aligned}$$

2.4 The mean-CVaR$_{\alpha }$ model (M-CVaR$_{\alpha }$)

For this model, in addition to the decision variables $x_{j}$, there are $m+1$ decision variables. The variable v represents the negative of an $\alpha$-quantile of the portfolio return distribution. If the $\alpha -$quantile is unique, the optimal value of v is the $\hbox {VaR}_\alpha$ of the return distribution of the solution portfolio. The other m decision variables represent the magnitude of downside deviations of the portfolio return from the $\alpha$-quantile, for every scenario $i\in \{1\ldots m\}$:

$$\begin{aligned}&\displaystyle y_{i}=\left\{ \begin{array}{rcl} -v-\displaystyle \sum _{j=1}^{n}r_{ij}x_{j},& & \hbox {if} \displaystyle \sum _{j=1}^{n}r_{ij}x_{j}\le -v;\\ 0,& & \hbox {otherwise}. \end{array} \right. \\&\begin{array}{ll} \displaystyle \min & {v+\displaystyle \frac{1}{\alpha m}\displaystyle \sum _{i=1}^{m} y_{i}}\\ \text {subject to:}\\ &\displaystyle \sum _{j=1}^{n}-r_{ij}x_{j}-v \le y_{i} ;\quad \forall i \in \{1\ldots m\} \\ &\quad \quad \qquad y_{i} \ge 0 ;\quad \forall i \in \{ 1\ldots m \} \\ &\displaystyle \sum _{j=1}^{n}\mu _{j}x_{j} \ge d ; \\ & \quad \quad \qquad x\in X\\ \end{array} \end{aligned}$$

3 Portfolio optimisation with options

3.1 Basics of option pricing

An option is a financial derivative described as a contract when the holder of the contract is given the right (but not the obligation) to exercise a deal: to buy or sell an underlying asset at a specified price, at or within a specified time.

A call option gives the holder the right to buy the underlying asset (stock, real estate etc.) under the specified conditions, while a put option gives the holder the right to sell the underlying asset. The price of underlying specified in the contract is known as the exercise price or strike price, while the date in the contract is known as the expiration date or maturity (see Hull and Basu 2016).

In this work, we consider only European options, meaning, they can only be exercised at maturity.

The payoff of an option depends on the price $S_{T}$ of the underlying asset at maturity T. If the strike price is K, the payoff functions for a put and a call are:

$$\begin{aligned} V_{put}(S_{T})=\max \{0,K-S_{T}\}, \end{aligned}$$

and

$$\begin{aligned} V_{call}(S_{T})=\max \{0,S_{T}-K\}, \end{aligned}$$

respectively.

The net profit is obtained by subtracting from the payoff the price paid for the option.

Determining the “correct” price of an option has been a widely researched subject and of practical importance. Options are great in reducing risk, if held long, as the maximum amount that can be lost is known in advance; however, they also reduce the profit because of their cost. If held short, options can be very risky, hence their price should be high enough to compensate for this. For European options, the Black–Scholes pricing formula (see for example Bodie et al. 2014) has been widely used, although often with adjustments and corrections (see Zvi et al. 2004).

In this study, option prices are obtained from Datastream (see Reuters 2010) for the at-the-money index options, that is, options whose strike price is equal to the current price of the underlying asset. Our dataset is explained further in Sect. 4.

3.2 Incorporating index options into portfolio optimisation

We consider a one period investment problem with decisions made at time t and evaluation made at time $(t+1)$. We consider an initial universe of assets consisting of the component stocks of the FTSE 100. To this, we add a call and a put option on the FTSE 100 index as two extra assets, with (real) prices at time t (obtained from Datastream.) We only consider assets being held in long positions (their weights in the portfolio being positive); we consider the ask (buy) price of the options.

We employ the historical “look-back” approach, that is, we use past (historical) rates of return for the component assets of FTSE100 as scenarios for the rates of return between t and $(t+1)$. These historical rates of return are computed using past prices monitored between periods of time equal to the investment period.

Similarly to Faias and Santa-Clara (2017), we employ a scenario based approach in order to simulate the returns of the options at the end of the investment period. In order to do this, we first simulate the price of the underlying FTSE100 at the end of the investment period $t+1$, knowing the current price at time t.

We use the historical returns of FTSE 100 (calculated in the same way as the historical returns of the component assets), as scenario returns for FTSE 100 between t and $t+1$. Using the current (known) price of FTSE100, denoted by $S_t$, we simulate prices for FTSE100 at time $(t+1)$ by multiplying $S_t$ with the scenario returns for FTSE100. We summarise the scenario generation as follows:

• 1. Using the historical prices for the underlying FTSE 100 (monitored over the same time periods as the stocks in the universe of assets) we compute the corresponding historical rates of return. For example, if the investment period is one month, t denoting the current time and $t+1$ next month, we compute past monthly rates of return and use them as scenarios for the rate of return between now and next month.

• 2. The rates of return from step 1 are used to generate scenarios for the next period’s underlying (FTSE100) value $S_{t+1}$, given its current (known) value $S_t$:

  $$\begin{aligned} S_{t+1}=S_{t}(1+r_{t+1}) \end{aligned}$$

  where $r_{t+1}$ is a scenario rate of return obtained at step 1.

• 3. Denoting by the $K_{c}$ the strike price of the call, and by the $K_{p}$ the strike price of the put, and using one period simulated underlying asset value $S_{t+1}$, we simulate option payoffs at their maturity $t+1$. Thus the payoffs for call and put are given respectively as:

  $$\begin{aligned} V_{t+1,C}=\max (S_{t+1}-K_{c},0), \end{aligned}$$

  and

  $$\begin{aligned} V_{t+1,P}=\max (K_{p}-S_{t+1},0). \end{aligned}$$

• 4. Using the simulated payoff above, the rates of return of the options are:

  $$\begin{aligned} r_{t+1,C}=\displaystyle \frac{V_{t+1,C}}{C_{t}}-1, \end{aligned}$$

  for index call options, and

  $$\begin{aligned} r_{t+1,P}=\displaystyle \frac{V_{t+1,P}}{P_{t}}-1 \end{aligned}$$

  for index put options, where $C_{t}$ and $P_{t}$ are the (real) prices of the call and put index option, respectively, at decision time t, as described in Sect. 3.1.

4 Computational results

4.1 Objectives, dataset and computational setup

The objectives of the computational work relate to the research questions stated at the end of Sect. 1. More precisely, the first objective (related to the first research question) is to investigate whether the inclusion of index options leads to a significant decrease in risk, and thus significantly better optimal portfolios in terms of mean-risk trade-off; we also investigate the correlation of the return distributions obtained (of efficient portfolios of stocks only and efficient portfolios composed of stocks and index options) with the return distribution of the index. The second objective is related to the second research question posed at the end of Sect. 1. More precisely, we investigate the composition of optimal portfolios in terms of: (a) the proportion of options in the optimal portfolios, and (b) whether the portfolios with options have similar stock composition compared to their ‘stock-only’ counterpart, for each of the risk measures employed. A third computational objective is to investigate the effect of the risk measure employed on the return distribution of the optimal portfolios.

For the first two objectives, we implement mean-variance and mean-CVaR model (at parameter 0.05) with a universe of assets composed of (a) stocks only; (b) the same stocks and two index options, a call and a put, with maturity equal to the investment period.

For the third objective, we implement the mean-variance, mean-expected downside risk and M-CVaR$_{0.05}$ models with a universe of stocks consisting of the component stocks of FTSE 100. We choose efficient portfolios with the same expected return and investigate the properties of their return distributions.

The data used for this analysis is drawn from the FTSE100. The investment period is one month. Monthly returns of the 87 stock components of the index from January 2005 until May 2014 are considered. The dataset for the in-sample analysis has 100 time periods, initially from Jan 2005 until May 2013; we employ a one month rolling window approach in which we consider 12 in-sample data sets by adding a next month of data and removing the oldest data point (thus, always having 100 time periods in the in-sample data set). For backtesting analysis, the portfolio is examined over the twelve months period of June 2013 until May 2014.

We consider at-the-money (that is, strike price equals to current price) call and put index options, with maturity one month. The prices are taken from Datastream codes ESXC.SERIESC (for calls) and ESXC.SERIESP (for puts) for our analysis in Sect. 4.3. All data are obtained from Datastream (see Reuters 2010) and models were implemented in AMPL (see Fourer et al. 1993) and solved using the CPLEX 12.5 (see ILOG 2012) optimisation solver.

The characteristics of efficient portfolios may vary depending on the target return, d. Based on our data set, the maximum level of asset expected return is 0.0349 and the minimum is at $-0.007323$. We chose three different level of d as $d_{1}=0.01$, $d_{2}=0.02$, and $d_{3}=0.03$. We solve the three mean-risk models considered above for every level of expected return $d_{1}$, $d_{2}$, and $d_{3}$.

4.2 In-sample analysis: stocks only

The return distributions of the efficient portfolios are discrete with 100 equally probable outcomes. We analyse these distributions using in sample parameters of standard deviation, skewness, minimum, maximum, and range. We compare sets of three distributions, each having the expected values of $d_{1}$, $d_{2}$, and $d_{3}$, respectively; thus, we look at portfolios in different regions of efficient frontier: low mean-low risk, medium mean-medium risk, high mean-high risk.

For a portfolio distribution, it is desirable to have smaller standard deviation and range, and to have larger median, skewness, minimum, and maximum.

In all three cases (refer Tables 1, 2, 3) the LPM0 efficient portfolios have the highest median, while obviously the M–V efficient portfolios have the lowest standard deviation. The other three statistics are consistently better for M-CVaR$_{0.05}$ efficient portfolios. This is somewhat expected for the minimum and skewness, as they are statistics describing the left tail (and mean-CVaR efficient portfolios should have a better left tail) but interestingly, also the maximum is the highest in the case of mean-CVaR. They are also the only return distributions that are positively skewed.

Table 1 Statistics for the mean-risk efficient distributions with expected value $d_{1}=0.01$

Table 2 Statistics for the mean-risk efficient distributions with expected value $d_{2}=0.02$

Table 3 Statistics for the mean-risk efficient distributions with expected value $d_{3}=0.03$

4.3 Introducing index options in the universe of assets

We add the two index options as described in Sect. 4.1, and test the performance on two mean-risk models, the M–V and the M-CVaR$_{0.05}$, for $d_{1}$, $d_{2}$, and $d_{3}$. (For brevity, we omit the mean-LPM0 model in which the introduction of index options has a similar effect to that obtained with the other two models, especially the mean-variance model.) We perform optimisation on 12 data sets, obtained as described in 4.1 by using a rolling window of one month.

Table 4 displays the optimal weights of the put and call index options, together with the number of assets in the optimal portfolios. We can observe the following.

Firstly, for low to medium expected rates of return (1% and 2%), the M–V efficient portfolios contain more assets than the M-CVaR$_{0.05}$ efficient portfolios.

Secondly, the index put is (and the call is not) in the composition of these portfolios (at 1% and 2% expected rate of return), for both M–V and M-CVaR efficient portfolios. The put is in a considerably higher proportion in M-CVaR efficient portfolios.

Finally, for high mean—high risk portfolios (mean at 3%), it is the index call that is in the composition of the optimal portfolios, and in considerably higher amount in the M-CVaR$_{0.05}$ efficient portfolios.

4.4 In-sample results for the case of stocks and index options

Table 4 The number of assets in the composition of mean-risk portfolios with weight of index options

The contribution of index call and put options into the expected rate of return of the M-CVaR efficient portfolio is provided in Table 5.

It is observed that the inclusion of the put option contributes negatively to the expected rate of return of the portfolio. This is the case because the put does work as an insurance for the portfolio, improving the left tail of the return distribution.

On the other hand, the inclusion of a call option (in the high risk- high return portfolios, with in-sample expected returns of 3%) contributes positively to the total expected return.

This is happening because call options are used to achieve higher returns. Further explanation about the effect of this contribution to the level of risk is illustrated in Table 7.

Table 5 Contribution of index call and put options to the expected rate of return of the In-sample M-CVaR efficient portfolios

These results are further explained by the correlation of the return distributions of the optimal portfolios with the return distribution of the index (see Table 6). While all efficient portfolios composed of stocks only are positively correlated to the index, by adding put options we obtain portfolios that are uncorrelated with the index or with a much lower correlation. This is particularly true in the case of M-CVaR$_{0.05}$ efficient portfolios with low in-sample expected return (1%) and to somewhat a lesser extent, in the case of medium expected return (2%). The M–V efficient portfolios at 1% and 2% expected return are still positively correlated to the index but to a lesser extent than their stocks only counterparts. For high risk-high return portfolios, it is index calls that are in the composition of the efficient portfolios. This makes the resulting portfolio to be even more correlated with the index, in both M–V and M-CVaR_0.05 models.

Table 6 Correlation coefficients of the return of FTSE 100 index with the return of efficient portfolios, composed of stocks only (“S”) and composed of stocks + index options (“OS”)

Table 7 Optimal CVaR for M-CVaR$_{0.05}$ efficient portfolio; with (OS) and without (S) options

Table 7 presents the optimal CVaR values in case of stocks only (S-portfolio) versus stocks + options (OS-portfolio). It is remarkable that risk is substantially decreased, especially at low in-sample expected returns. In the case of CVaR, risk is drastically reduced for each target returns of $d_{1}$ and $d_{2}$. This is because for these two target returns, the optimal portfolios includes a higher weight of put option as part of the portfolio. For high risk-high return portfolios ($d_{3}=3\%$) the decrease in risk obtained by adding index options is marginal. This is explained by the fact that index calls are mostly present in the composition of optimal portfolios (rather than puts) and these are used in order to achieve even higher return, rather than to reduce risk. A similar pattern, but to a lesser extent, is observed in case of M–V efficient portfolios (Table 8).

Table 8 Optimal standard deviations for M–V efficient portfolio; with (OS) and without (S) options

We investigate the composition of the efficient portfolios in the models considered. More precisely, we are interested to see whether by including an option we obtain a similar portfolio with the case of stocks only, scaled down to include the option weight. The difference of the composition of two portfolios $x=(x_1,\ldots ,x_n)$ and $y=(y_1,\ldots ,y_n)$ using the Euclidean distance for an n-dimensional space. This is indicated by $D_{x,y}=\sqrt{(x_1-y_1)^2+\ldots +(x_n-y_n)^2}$.

Table 9 Composition of efficient portfolios: stocks only (S) and stocks $+$ options (OS) in M-CVaR$_{0.05}$ and M–V models (for d = 2%)

We provide an example of the composition of efficient portfolios in the case of $d=2\%$ as shown in Table 9. We also display the Euclidean distance values at the bottom of every composition to show the overall difference between OS and S-portfolios for the two models. We can see that the difference in portfolio composition is more obvious and significantly higher for M-CVaR$_{0.05}$ portfolios. Thus, we conclude that the ‘addition’ of options into the universe of assets is more sensitive to M-CVaR$_{0.05}$ model because the nature of minimising CVaR as a left-tail risk.

Apart from the value of Euclidean distance, we can emphasize this ‘sensitivity’ by looking at the proportion of wealth invested in options for both M–V and M-CVaR$_{0.05}$ portfolios. It is clear that the proportion for index put options is lower for the M–V portfolios at 1.67% compared to 2.02% for portfolio under M-CVaR$_{0.05}$ implementation.

Based on portfolio compositions, we see that the stock only portfolios (S-portfolios) show substantial reshuffling after we include index options. This is more obvious for the case of M-CVaR$_{0.05}$ optimal portfolio, whereas for M–V optimal portfolio, the change from S-portfolios is somewhat close to scaling up (and down) of the proportion of investment in each stocks when options are included.The same reshuffling also happening for different optimisation runs, with higher Eucliden distance is found for M-CVaR$_{0.05}$ compared to M–V implementation.

5 Backtesting

We run backtesting on a monthly basis using as out of sample data the 12 months June 2013–May 2014. We use as in-sample data the 100 months preceding the “backtested period”. For example, we use data from Jan 2005 to May 2013 in optimisation and the optimal weights are used to compute an “actual” (realised) return on June 2013; the realised returns of the options are computed by using the (real) price of the options on May 2013 and the realised pay-off (computed using the price of the FTSE100 index on June 2013). We repeat this by removing the oldest data point and adding the next month of data. In general, this backtesting exercise is done to see how the 12 in-sample portfolios obtained in Sect. 4.3 would have perfomed in reality.

We compare the 12 realised returns of mean-CVaR efficient portfolios composed of stocks only (S-portfolios) and composed of stocks and index options (OS-portfolios).

Table 10 Returns for S-portfolios and OS-portfolios under M-CVaR$_{0.05}$ optimisation for each target returns d

We summarise the performance of S-portfolios and OS-portfolios by looking at mean, minimum, maximum and standard deviation of the realised returns. Table 10 shows the realised returns for the M-CVaR$_{0.05}$ model. The performance of portfolios is different based on the in-sample target portfolio expected return. Performance of OS-portfolios under target returns $d_{1}=1\%$ and $d_{2}=2\%$ shows better statistics in its standard deviation and its minimum. The mean of the realised returns is slightly lower in the case of OS-portfolios. However, if we take into account worst case realisations, OS-portfolios perform substantially better as they avoid extreme losses. This is explained by the fact that OS portfolios, at 1% and 2% in-sample expected return, have index put options in their composition, which make profit from the decrease in price of the index; thus they help in reducing the loss.

There is a different situation in the case of portfolios with in-sample expected return $d_{3}=3\%$. The OS-portfolios incur highest losses comparable to those of their stocks only counterparts. What remarkable is their “best case” realisations, similarly to a right tail. While the worst case realisations are somewhat similar for S and OS-portfolios, the best case realisations are much better in the case of OS-portfolios (as a consequence, there is more variability in the realised returns). The OS-portfolios, which include index call options, can generate much higher returns than their stocks only counterparts.

6 Conclusions and further work

We have presented a framework for introducing index options, in addition to stocks, in scenario based mean-risk models. Our numerical results indicate that index options can be used to substantially improve the risk-return trade-off, especially when risk is quantified by a tail measure such as CVaR; in this case, the proportion of index options in the portfolios is higher than in the case when risk is measured by variance. The way index options are selected and their effect on the portfolio return distribution depends on the (in-sample) expected portfolio return.

Portfolios in “low risk-low return” or “medium risk-medium return” areas of the efficient frontier have index put options in their composition. The addition of the put acts as a safety net, as it substantially reduces worst case scenario losses. The stocks-only portfolios have a return distribution that is positively correlated with the return distribution of the index; by introducing put options, we obtain portfolios very different in composition, whose return distributions are uncorrelated with index (in the case of mean-CVaR portfolios) or with low correlation with the index (in case of mean-variance portfolios). Hence, when the index falls in price—and when stocks only portfolios incur losses to some extent—put options help in curtailing this loss without reducing much the upside potential.

Portfolios in the “high risk-high return” area of the efficient frontier have index call options in their composition. In-sample, the risk (either measured by CVaR or by variance) is reduced in comparison to the risk of their stocks only counterparts, but only marginally; while, in contrast, the inclusion of put option in less aggressive portfolios can dramatically reduce the risk. The new portfolios have return distributions that are even more correlated with the index, as compared to the stocks only portfolios. In-sample summary of risk-return characteristics would indicate in a first instance that, with the addition of index call options, there is only a marginal improvement. However, a more detailed analysis of return distribution show that, while there might not be a substantial improvement in the left tail, there is a substantial improvement in the right tail: by considering the call options, in addition to stocks, much higher returns can be achieved, as compared to stocks only portfolios or the index itself. These observations are consistent with the backtesting results.

For further research, we consider the idea of generalizing this approach beyond the use of maturing options, using known deltas of options.