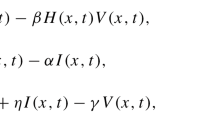1 Introduction

We are interested in qualitative properties of mathematical models of viral infections. Such models attract much attention during last years, especially after wide spread of viral diseases, including COVID-19, HIV, hepatitis B and C. Many viruses continue to be a major global public health issues.

World Health Organization (WHO) reports [41, p.3] “As of 20 April 2022, more than 504.4 million confirmed COVID-19 cases and over 6.2 million related deaths had been reported to WHO.” Moreover [41, p.2] “the long-term impact of infection on people’s health is not yet fully understood.” “A recent systematic review reported a prevalence of persistent symptoms in patients after mild COVID-19 infection ranged from 10% to 35% . Cognitive impairment, various neuropsychiatric symptoms, fatigue, headaches and other complaints are among the conditions reported four or more weeks after the initial infection. A detailed understanding of these long-lasting symptoms has not yet been achieved.”

According to WHO ’354 million people globally live with a hepatitis B or C infection’ (296 million with chronic hepatitis B and 58 million with chronic hepatitis C).Footnote 1 More data (2017) are collected in [40].

In such a situation, any step toward understanding the qualitative (particularly, long-time asymptotic) behaviour of viral infection models is important.

The classical models [21, 22] contain ordinary differential equations (without delay) for three variables: susceptible host cells T, infected host cells \(T^{*}\) and free virus particles V. The intracellular delay is an important property of the biological problem, so we start discussion with the delay problem (for a particular case of DeAngelis-Beddington functional response f see e.g. [9, 15])

$$\begin{aligned} \left\{ \begin{array}{l} \dot{T}(t) = \lambda - d T(t) - f(T(t),V(t)), \\ \dot{T}^{*}(t) = e^{-\omega h} f(T(t-h),V (t-h)) - \delta T^{*}(t), \\ \dot{V}(t) = N\delta T^{*}(t) - cV (t). \\ \end{array} \right. \end{aligned}$$
(1.1)

In (1.1), susceptible cells T are produced at a rate \(\lambda \), die at rate dT, and become infected at rate f(T, V). Properties and examples of incidence function f are discussed below. Infected cells \(T^{*}\) die at rate \(\delta T^{*}\), free virions V are produced by infected cells at rate \( N\delta T^{*}\) and are removed at rate cV(t). In (1.1) \(h>0\) denotes the delay between the time a virus particle contacts a target susceptible cell and the time the cell becomes actively infected (start to produce new virions). It is clear that the constancy of the discrete delay is an extra assumption which essentially simplifies the analysis, but has no biological background.

Since the precise value of the discrete delay h may be difficult to find, viral models with a distributed delay may provide another way to study the dynamics of a disease. For ODE cases and motivations see e.g. [12, 20, 37] and references therein. For motivations for a state-selective delay see Introduction in [23].

For discussion of different viral infection models we refer to [12,13,14,15, 19, 28, 29, 31, 36, 37]. PDE models which take into account spatial mobility of cells and virus, possibility of cell-to-cell transmission of the infection (see e.g. [3]) as well as natural time delay effects are discussed in many papers (see e.g. [18, 30, 38, 39] and references therein).

Let \(\Omega \subset {\mathbb {R}}^3\) be a connected bounded domain with a smooth boundary. Let \(T(t,x),T^{*}(t,x),V(t,x)\) represent the densities of uninfected cells, infected cells and free virions at position \(x\in \Omega \) at time t.

In this note we are interested in the following PDEs system with delay

$$\begin{aligned} \left\{ \begin{array}{l} \dot{T}(t,x) = r T(t,x) \left( 1- \frac{T(t,x)}{T_K}\right) - d T(t,x) - f(T(t,x),V(t,x)) + d^1 \Delta T(t,x), \\ \dot{T}^{*}(t,x) = e^{-\omega h} \int ^0_{-h} f(T(t+\theta ),x),V (t+\theta ),x)) \xi (\theta , x, u_t)\, d\theta - \delta T^{*}(t,x)\\ + d^2 \Delta T^{*}(t,x), \\ \dot{V}(t,x) = N\delta T^{*}(t,x) - cV (t,x) + d^3 \Delta V(t,x), \quad x\in \Omega . \\ \end{array} \right. \end{aligned}$$
(1.2)

Here the dot over a function denotes the partial derivative with respect to time i.e, \(\dot{T}(t,x) = \frac{\partial T(t,x)}{\partial t}\), all the constants \(d, \delta , N, c, r, N, \omega \) including \(d^i, i=1,2,3\) (diffusion coefficients) are positive. We consider a general functional response f(T, V) satisfying natural assumptions presented below. In earlier models (with constant or without delay) the study was started in case of bilinear \(f(T,V) =\text{ const }\cdot T V\) and then extended to more general classes of non-linearities. For more details and discussion see [18, 30].

As usual, for a delay system we denote \(u_t=u_t(\theta )\equiv u(t+\theta )\) for \(\theta \in [-h,0], h>0\). For general theory on delay equations see [8, 10, 16, 33, 42].

We need initial conditions for the delay problem (1.2):

$$\begin{aligned} u(\theta ,x) =\varphi (\theta ,x) \equiv (T(\theta ,x),T^{*}(\theta ,x),V(\theta ,x)), \quad \theta \in [-h,0] \end{aligned}$$
(1.3)

or shortly \(u_0=\varphi \).

In the papers cited above, the main goal was to study asymptotic stability of stationary solutions. In case of a globally asymptotically stable stationary solution, the long-time behaviour of the system looks very simple. We are interested in a more general case when the existence of a global attractor (for the corresponding dynamical system) may, in general, allow the co-existence of multiple stationary solutions, periodic orbits, invariant manifolds. In case when the existence of a global attractor is proved, the important question arises if the attractor is finite-dimensional (for general facts on attractors see e.g. [4, 34]). The existence of a finite-dimensional global attractor forms a theoretical basis for finite-dimensional approximations which reflect all the asymptotic behaviour of the original system.

Our main mathematical tool in studying of the asymptotic behaviour of solutions is the quasi-stability method developed by I.D.Chueshov (for more details and definitions see [6]). For applications of this metod to delay PDEs see [5] where a model with discrete state-dependent delay is studied. For connections between PDEs with a discrete state-dependent delay [25,26,27] and considered in the current paper PDEs with a distributed state-selective delay see [23, 24].

To the best of our knowledge, the existence of a finite-dimensional global attractor for a viral infection model has not been investigated before (except the simple case of a globally asymptotically stable stationary solution). It is important to mention that the problem under consideration is infinite-dimensional in both space coordinate (as PDE [4, 34]) and time coordinate (as delay problem [8, 10, 16]).

2 Main Results

We combine two lines of investigations, one is in a Hilbert space, while the other is in a Banach space.

2.1 Study in \(L^2(\Omega )\). Part 1

We start with the Hilbert space approach.

Define the following linear operator

$$\begin{aligned} -{\mathcal {A}} = diag \, \left( d^1 \Delta -\frac{d}{2}, d^2 \Delta -\frac{\delta }{2}, d^3 \Delta -\frac{c}{2} \right) \text{ in } H\equiv [L^2(\Omega )]^3 \end{aligned}$$
(2.1)

with domain \(D({\mathcal {A}})\equiv D(d^1 \Delta )\times D(d^2 \Delta ) \times D(d^3 \Delta )\). Here we set \(D(d^i \Delta )\equiv \{ v\in L^2(\Omega ) : \Delta v\in L^2(\Omega ), \frac{\partial v(x)}{\partial n} |_{\partial \Omega }=0\}\). We consider operator \( -\Delta \) in \(L^2(\Omega )\) with the Neumann boundary conditions. This type of conditions is more adequate to biological nature of the problem.

Operator \( {\mathcal {A}} \) is a positive self-adjoint operator in \([L^2(\Omega )]^3\). It is a positive self-adjoint operator with discrete spectrum i.e. there exists an othonormal basis \(\{ e_k \}^\infty _{k=1}\) of H, where \(e_k\) are eigenvectors of \( {\mathcal {A}} \) : \( {\mathcal {A}} e_k = \lambda _k e_k, 0 < \lambda _1 \le \lambda _2 \le ..., \lim _{k\rightarrow \infty } \lambda _k = + \infty \) (see e.g., [6, Definition 4.1.1] ). Hence we can define spaces \(H_\alpha \equiv D({\mathcal {A}}^\alpha )\), \(H_0=H\).

Let \(C_\alpha \equiv C([-h,0]; H_\alpha ) \subset C_0 = C \equiv C([-h,0]; H)\) for \(\alpha \in [0,1)\).

We write, the system (1.2) in the following abstract form

$$\begin{aligned} \frac{d}{dt} u(t) + {\mathcal {A}} u(t) = F(u_t), \qquad t>0. \end{aligned}$$
(2.2)

The non-linear mapping \(F: C\equiv C_0 \rightarrow H\) is defined by

$$\begin{aligned} F(\varphi )(x)=\left( \begin{array}{l} r\, \varphi ^1(0,x) \left( 1- \frac{\varphi ^1(0,x)}{T_K}\right) - \frac{d}{2} \varphi ^1(0,x) - f(\varphi ^1(0,x),\varphi ^3(0,x)) \\ B(\varphi ,x) - \frac{\delta }{2} \varphi ^2(0,x) \\ N\delta \varphi ^2(0,x) - \frac{c}{2} \varphi ^3 (0,x)\\ \end{array} \right) .\nonumber \\ \end{aligned}$$
(2.3)

Here \( \varphi = ( \varphi ^1,\varphi ^2,\varphi ^3)\in C\) and the nonlinear distributed delay term has the following form

$$\begin{aligned} B(\varphi ,x) \equiv e^{-\omega h} \int ^0_{-h} f(\varphi ^1(\theta ,x),\varphi ^3 (\theta ,x)) \xi (\theta , x, \varphi )\, d\theta , \quad x\in \Omega . \end{aligned}$$
(2.4)

We assume the following

(H1) Let \(f: {\mathbb {R}}^2 \rightarrow {\mathbb {R}} \) be continuous, \(\xi : C \rightarrow L^1(-h,0; L^\infty (\Omega ))\) be continuous and bounded, i.e.

$$\begin{aligned}{} & {} \int _{-h}^0 ||\xi (\theta ,\cdot ,\varphi ) - \xi (\theta ,\cdot ,\psi ) ||_{L^\infty (\Omega )} d\theta \rightarrow 0, \quad \text { as } ||\varphi - \psi ||_C \rightarrow 0, \\{} & {} \int _{-h}^0 ||\xi (\theta ,\cdot ,\varphi ) ||_{L^\infty (\Omega )} d\theta \le M_{\xi ,1}, \quad \forall \varphi \in C. \end{aligned}$$

Considering \(||B(\varphi ,\cdot ) - B(\psi ,\cdot ) ||_{L^2(\Omega )}\) one can check that assumptions (H1) imply continuity \(B: C \rightarrow L^2(\Omega )\). It implies continuity \(B: C_\alpha \rightarrow L^2(\Omega )\) for \(\alpha \in [0,1)\).

Hence, the form (2.3) and the above continuity of B give that F is a nonlinear continuous mapping from \(C_\alpha \) into H for all \(\alpha \in [0,1)\) and is bounded on bounded sets in \(C_\alpha \).

We use the standard

Definition 2.1

We call a function \(u\in C([-h,T];H_\alpha )\) a mild solution (\(H_\alpha \)-mild) of the problem (2.2), (1.3) if \(u_0=\varphi \) and

$$\begin{aligned} u(t)= e^{-t { A}}u(0) + \int ^t_0 e^{-(t-\tau ) { A}} F(u_\tau )\, d\tau , \quad t\in [0,T]. \end{aligned}$$
(2.5)

The local existence of a mild solution to (2.2), (1.3) is standard due to the continuity of F, its boundedness on bounded sets and Schauder’s fixed point theorem (see [35]).

Now we assume the nonlinear term B has the form (2.4) and

(H2) f is Lipschitz, \(\xi \) is Lipschitz and bounded in the following norms

$$\begin{aligned}{} & {} \int _{-h}^0 ||\xi (\theta ,\cdot ,\varphi ) - \xi (\theta ,\cdot ,\psi ) ||_{L^\infty (\Omega )} d\theta \le L_{\xi ,1} ||\varphi - \psi ||_C, \end{aligned}$$
(2.6)
$$\begin{aligned}{} & {} \int _{-h}^0 ||\xi (\theta ,\cdot ,\varphi ) ||_{L^\infty (\Omega )} d\theta \le M_{\xi ,1}, \quad \forall \varphi \in C. \end{aligned}$$
(2.7)

Theorem 2.2

Let f, \(\xi \) satisfy (H2). Then, for any initial \(\varphi \in C_\alpha \) with \(\alpha \in [0,1)\) there exist \(T=T_\varphi >0\) and an unique mild solution to (2.2), (1.3) on \([-h,T]\). The solution continuously depends on initial function \(\varphi \) i.e. for two mild solutions \(||u^i(t)||_{\alpha } \le R, i=1,2\) one has

$$\begin{aligned} ||u^1(t) - u^2(t)||_\alpha \le C_{{\widehat{T}},R} ||\varphi ^1 - \varphi ^2||_{C_\alpha }, \quad t\in [0, {\widehat{T}}],\quad {\widehat{T}}\equiv \min \{ T_{\varphi ^1}; T_{\varphi ^2}\}.\nonumber \\ \end{aligned}$$
(2.8)

Proof

To prove Theorem 2.2 we need only to show that \(F : C_\alpha \rightarrow H\) is locally Lipschitz. We start with the following

Lemma 2.3

Assume (H2) is satisfied. Then the nonlinear distributed delay term B (2.4) is locally Lipschitz continuous

$$\begin{aligned} || B(\varphi ,\cdot ) - B(\psi ,\cdot ) ||_{L^2(\Omega )} \le L_B(R) ||\varphi - \psi ||_C, \quad \forall ||\varphi ||_C, ||\psi ||_C \le R \end{aligned}$$
(2.9)

with \(L_B(R) = e^{-\omega h} L_f \left( 2 M_{\xi ,1} + L_{\xi ,1} \cdot R \right) \).

Proof of Lemma

Consider the difference

$$\begin{aligned}{} & {} B(\varphi ,x) - B(\psi ,x) \\{} & {} \quad =e^{-\omega h} \int ^0_{-h} \left( f(\varphi ^1(\theta ,x),\varphi ^3 (\theta ,x)) - f(\psi ^1(\theta ,x),\psi ^3 (\theta ,x)) \right) \xi (\theta , x, \varphi )\, d\theta \\{} & {} \qquad + e^{-\omega h} \int ^0_{-h} f(\psi ^1(\theta ,x),\psi ^3 (\theta ,x)) \left( \xi (\theta , x, \varphi ) - \xi (\theta , x, \psi ) \right) \, d\theta . \end{aligned}$$

We have \( || B(\varphi ,\cdot ) - B(\psi ,\cdot ) ||_{L^2(\Omega )} \)

$$\begin{aligned}{} & {} \le e^{-\omega h} \int ^0_{-h} ||(f(\varphi ^1(\theta ,\cdot ),\varphi ^3 (\theta ,\cdot )) - f(\psi ^1(\theta ,\cdot ),\psi ^3 (\theta ,\cdot ))) \xi (\theta , \cdot , \varphi )\, ||_{L^2(\Omega )}\, d\theta \\{} & {} \quad + e^{-\omega h} \int ^0_{-h} ||f(\psi ^1(\theta ,\cdot ),\psi ^3 (\theta ,\cdot )) \left( \xi (\theta , \cdot , \varphi ) - \xi (\theta , \cdot , \psi ) \right) ||_{L^2(\Omega )}\, d\theta \equiv I. \end{aligned}$$

To estimate the \(L^2(\Omega )\)-norm in the first term we consider (notice the square of the norm)

$$\begin{aligned}{} & {} \int _\Omega |f(\varphi ^1(\theta ,x),\varphi ^3 (\theta ,x)) - f(\psi ^1(\theta ,x),\psi ^3 (\theta ,x))|^2 |\xi (\theta , x, \varphi )|^2\, dx \\{} & {} \quad \le || |f(\varphi ^1(\theta ,\cdot ),\varphi ^3 (\theta ,\cdot )) - f(\psi ^1(\theta ,\cdot ),\psi ^3 (\theta ,\cdot ))|^2 ||_{L^1(\Omega )} || |\xi (\theta , \cdot , \varphi )|^2 ||_{L^\infty (\Omega )} \\{} & {} \quad \le 2 L_f^2 ||\varphi -\psi ||^2_{C} \cdot || \xi (\theta , \cdot , \varphi ) ||_{L^\infty (\Omega )}^2. \end{aligned}$$

Here we used properties \(\int _\Omega |a(x) b(x)|\, dx \le ||a||_{L^1(\Omega )} ||b||_{L^\infty (\Omega )} \), \(|| |b|^2||_{L^\infty (\Omega )} = ||b||_{L^\infty (\Omega )}^2 \) and the Lipschitz property of f. Similar properties for the second term give

$$\begin{aligned}{} & {} \int _\Omega |f(\psi ^1(\theta ,\cdot ),\psi ^3 (\theta ,\cdot )|^2 |\xi (\theta , \cdot , \varphi ) - \xi (\theta , \cdot , \psi )|^2 \, dx\\{} & {} \quad \le L_f^2 ||\psi ||_C^2 \cdot ||\xi (\theta , \cdot , \varphi ) - \xi (\theta , \cdot , \psi ) ||_{L^\infty (\Omega )}^2. \end{aligned}$$

These estimates and (H2) allow to continue

$$\begin{aligned} I \le e^{-\omega h} L_f \left( 2 M_{\xi ,1} + L_{\xi ,1} \cdot ||\psi ||_C \right) ||\varphi -\psi ||_{C} \le L_B(R) ||\varphi - \psi ||_C, \end{aligned}$$

\(\forall ||\varphi ||_C, ||\psi ||_C \le R\) with \(L_B(R) = e^{-\omega h} L_f \left( 2 M_{\xi ,1} + L_{\xi ,1} \cdot R\right) \). It completes the proof of lemma.

Next, we notice that for \(\alpha >0\) and \(v\in H_\alpha \) one has \(||v|| \le \lambda _1^{-\alpha } ||v||_\alpha \). Hence (2.9) implies similar Lipschitz property in smaller space

$$\begin{aligned} || B(\varphi ,\cdot ) - B(\psi ,\cdot ) ||_{L^2(\Omega )} \le L_{B,\alpha }(R) ||\varphi - \psi ||_{C_\alpha }, \quad \forall ||\varphi ||_{C_\alpha }, ||\psi ||_{C_\alpha } \le R\nonumber \\ \end{aligned}$$
(2.10)

with \(L_{B,\alpha }(R) = \lambda _1^{-\alpha } e^{-\omega h} L_f \left( 2 M_{\xi ,1} + L_{\xi ,1} \cdot R \right) \). Finally, (2.10) and (2.3) give the local Lipschitz property of F (since all the other terms are polynomials): for every \(R>0\) there exists \(L_{F,\alpha }(R)\) such that

$$\begin{aligned} || F(\varphi ) - F(\psi ) ||_{L^2(\Omega )} \le L_{F,\alpha }(R) ||\varphi - \psi ||_{C_\alpha }, \quad \forall ||\varphi ||_{C_\alpha }, ||\psi ||_{C_\alpha } \le R.\quad \end{aligned}$$
(2.11)

The rest of the proof is standard (see e.g. [35, 6, theorem 6.1.6]). We do not repeat it here. \(\square \)

2.2 Study in \(C({\overline{\Omega }})\)

We use the basic functional framework described in [17] and applied in [30].

Define the following linear operator \( -{\mathcal {A}}^0 \) \(= diag \, (d^1 \Delta -\frac{d}{2}, d^2 \Delta -\frac{\delta }{2}, d^3 \Delta -\frac{c}{2})\) in \(C({\overline{\Omega }}; {\mathbb {R}}^3)\) with \(D({\mathcal {A}}^0)\equiv D(d^1 \Delta )\times D(d^2 \Delta ) \times D(d^3 \Delta )\). Here, for \(d^i\ne 0\) we set \(D(d^i \Delta )\equiv \{ v\in C^2({\overline{\Omega }}) : \frac{\partial v(x)}{\partial n} |_{\partial \Omega }=0\}\) and \(D(d^j \Delta )\equiv C({\overline{\Omega }})\) for \(d^j= 0\). We omit the space coordinate x, for short, for unknown \(u(t)=(T(t),T^{*}(t),V(t))\in X\equiv [C({\overline{\Omega }})]^3\equiv C({\overline{\Omega }}; {\mathbb {R}}^3)\). It is well-known that the closure \(-{\mathcal {A}}\) \(=-{\mathcal {A}}_C\) (in X) of the operator \(-{\mathcal {A}}^0\) generates a \(C_0\)-semigroup \(e^{-{\mathcal {A}} t}\) on X which is analytic and nonexpansive [17, p.5]. We denote the space of continuous functions by \(C_X\equiv C([-h,0]; X)\) equipped with the sup-norm \(||\psi ||_{C_X}\equiv \max _{\theta \in [-h,0]} ||\psi (\theta )||_X\).

We can use the abstract form (2.2) and nonlinear map (2.3), changing linear operator (\({\mathcal {A}}={\mathcal {A}}_C\) instead of \( {\mathcal {A}}\), see (2.1)) and corresponding spaces.

Definition 2.4

We call a function \(u\in C([-h,T];X)\) a mild solution (\(C({\overline{\Omega }})\)-mild) of the problem (2.2), (1.3) if \(u_0=\varphi \) and (2.5) holds with \({\mathcal {A}}={\mathcal {A}}_C\) instead of \( {\mathcal {A}}\).

We notice that Definitions 2.1 and 2.4 give different notions of mild solutions (belong to different spaces and use different semigroups \(e^{-t{\mathcal {A}}}\) on \(H_\alpha \) and \(e^{-t {\mathcal {A}}_C}\) on X).

Now we assume the nonlinear term B has the form (2.4) and (c.f. (H2))

(H3) f is Lipschitz, \(\xi \ge 0\) is Lipschitz and bounded in the following norms

$$\begin{aligned}{} & {} \int _{-h}^0 ||\xi (\theta ,\cdot ,\varphi ) - \xi (\theta ,\cdot ,\psi ) ||_{C({\overline{\Omega }})} d\theta \le L_{\xi ,C} ||\varphi - \psi ||_{C_X}, \end{aligned}$$
(2.12)
$$\begin{aligned}{} & {} \int _{-h}^0 ||\xi (\theta ,\cdot ,\varphi ) ||_{C({\overline{\Omega }})} d\theta \le M_{\xi ,C}, \quad \forall \varphi \in C_X. \end{aligned}$$
(2.13)

We need further assumptions on Lipschitz function f :

$$\begin{aligned} \mathbf{(Hf_1+)} \quad \left\{ \begin{array}{l} f(T,0)=f(0,V)=0, \quad \text { and } f(T,V)>0 \text { for all } T>0,V>0; \\ f \text { is strictly increasing in both coordinates for all } T>0,V>0; \\ \text {there exists } \mu >0 \, \text { such that } |f(T,V)|\le \mu |T| \,\, \text {for all } T, V\in {\mathbb {R}}. \end{array} \right. \nonumber \\ \end{aligned}$$
(2.14)

Define the set

$$\begin{aligned}{} & {} \Omega ^{log} \equiv \left\{ \varphi = (\varphi ^1,\varphi ^2,\varphi ^3) \in C = C_X : \quad 0\le \varphi ^1(\theta )\le M^1\equiv \frac{r}{2d} T_K, \right. \nonumber \\{} & {} \quad \left. 0\le \varphi ^2(\theta )\le M^2\equiv e^{-\omega h} \frac{\mu r}{d \delta } T_K M_{\xi , C}, 0\le \varphi ^3(\theta )\le M^3\equiv 2 e^{-\omega h} \frac{N\mu r}{d c} T_K M_{\xi , C} \right\} \nonumber \\ \end{aligned}$$
(2.15)

where \(\theta \in [-h,0]\), \(\mu \) is defined in \((Hf_1+)\) and all the inequalities hold pointwise w.r.t. \(x\in {\overline{\Omega }}.\)

We have the following result

Theorem 2.5

Let non-linear Lipschitz function f satisfy \((Hf_1+)\) (see (2.14)), \(\xi \) satisfy (H3). Then \( \Omega ^{log}\) is invariant i.e. for any \(\varphi \in \Omega ^{log}\) the unique \(C({\overline{\Omega }})\)-mild solution to problem (2.2), (1.3) exists and satisfies \(u_t \in \Omega ^{log}\) for all \(t\ge 0\).

Proof

We start with the local Lipschitz property of \(B: C_X\rightarrow X \). Assumptions (H3) give

$$\begin{aligned} || B(\varphi ,\cdot ) - B(\psi ,\cdot ) ||_{C({\overline{\Omega }})} \le L_{B,C}(R) ||\varphi - \psi ||_{C_X}, \quad \forall ||\varphi ||_{C_X}, ||\psi ||_{C_X} \le R\nonumber \\ \end{aligned}$$
(2.16)

with \(L_{B,C}(R) = e^{-\omega h} L_f \left( M_{\xi ,C} + L_{\xi ,C} \cdot R \right) \).

One can check that \(F: C_X \rightarrow X\) is locally Lipschitz. The existence and uniqueness of a mild solution \(u\in C([-h,T];X)\) to the problem (2.2), (1.3) is standard. The proof of the invariance part follows the invariance result of [17] with the use of the Lipschitz property of nonlinearity F. The estimates (for the subtangential condition) are the same as for the constant delay case, see e.g. [18, Theorem 2.2].

Consider \(\rho \ge 0\) and \(\varphi \in \Omega ^{log}\).

\(\varphi (0,x) + \rho F(\varphi ,x) \) \(= \left( \begin{array}{l} \varphi ^1(0,x) + \rho r\, \varphi ^1(0,x) \left( 1- \frac{\varphi ^1(0,x)}{T_K}\right) - \rho \frac{d}{2} \varphi ^1(0,x)\\ \quad - \rho f(\varphi ^1(0,x),\varphi ^3(0,x)) \\ \varphi ^2(0,x) + \rho B(\varphi ,x) - \rho \frac{\delta }{2} \varphi ^2(0,x) \\ \varphi ^3(0,x) + \rho N\delta \varphi ^2(0,x) - \rho \frac{c}{2} \varphi ^3 (0,x)\\ \end{array} \right) \)

We use notation \(F=(F^1,F^2,F^3)^T\) and estimate separately each of three coordinates above.

(a) We notice that the logistic term (see the first equation in (1.2)) \( r T \left( 1- \frac{T}{T_K}\right) \) has its maximum at point \( T=T_K/2\), so \(r T \left( 1- \frac{T}{T_K}\right) \le \frac{1}{4} r T_K\) for all \(T\in {\mathbb {R}}\).

Hence, for small enough \(\rho \ge 0\) and \(\varphi ^1 (0,x)\in [0,M^1]\) (see (2.15)) we have

$$\begin{aligned} \varphi ^1 (0,x) + \rho F^1(\varphi ,x) \le \varphi ^1 (0,x) + \rho \left( \frac{1}{4} r T_K -\frac{d}{2} \varphi ^1 (0,x)\right) \le M^1. \end{aligned}$$

(b) For the second coordinate we use (see (2.13) and (2.14))

$$\begin{aligned}B(\varphi ,x) \le e^{-\omega h} \int ^0_{-h} \mu |\varphi ^1 (\theta ,x)| \xi (\theta ,x,\varphi ) d\theta \le e^{-\omega h} \mu \frac{r}{2d} T_K M_{\xi ,C}. \end{aligned}$$

This estimate gives for small enough \(\rho \ge 0\) and \(\varphi ^2 (0,x)\in [0,M^2]\) (see (2.15)):

$$\begin{aligned} \varphi ^2 (0,x) + \rho F^2(\varphi ,x) \le \varphi ^2 (0,x) + \rho e^{-\omega h} \mu \frac{r}{2d} T_K M_{\xi ,C} -\rho \frac{\delta }{2} \varphi ^2 (0,x) \le M^2. \end{aligned}$$

(c) For small enough \(\rho \ge 0\) and \(\varphi ^3 (0,x)\in [0,M^3]\) (see (2.15)) one has

$$\begin{aligned} \varphi ^3 (0,x) + \rho F^3(\varphi ,x) \le \varphi ^3 (0,x) + \rho N \delta M^2 - \rho \frac{c}{2} \varphi ^3 (0,x) \le N \delta M^2 \frac{2}{c} = M^3. \end{aligned}$$

Combining the estimates above, one can check that for small enough \(\rho \ge 0\) and \(\varphi \in \Omega ^{log}\)

$$\begin{aligned} \left( \begin{array}{l} 0\\ 0\\ 0 \end{array} \right) \le \varphi (0,x) + \rho F(\varphi ,x) \le \left( \begin{array}{l} M^1\\ M^2\\ M^3 \end{array} \right) \equiv M \end{aligned}$$

or shortly \(\varphi (0,x) + \rho F(\varphi ,x) \in [0,M]\subset {\mathbb {R}}^3 \) for all \(x\in \Omega \).

The above implies \(\lim _{\rho \rightarrow 0+} dist \{\varphi (0,\cdot ) + \rho F(\varphi ,\cdot ); [0,M]_X \} = 0, \quad \forall \varphi \in \Omega ^{log}\subset C_X. \)

It gives the subtangential condition and allows to apply the invariance result of [17, 32].

The proof of Theorem 2.5 is complete. \(\square \)

2.3 Study in \(L^2(\Omega )\). Part 2

In this section we continue our study of \(H_\alpha \)-mild solutions and use results of Theorem 2.5 obtained for \(C({\overline{\Omega }})\)-mild solutions. The key point here is the Sobolev imbedding theorem [1, p.85] which suggests values of \(\alpha \) for which the imbedding \(H_\alpha \rightarrow C({\overline{\Omega }})\) holds.

Let us remind the part we need of the Sobolev imbedding theorem [1, p.85].

Let \(\Omega \) be a domain in \({\mathbb {R}}^n\). Let \(j\ge 0, m \ge 1\) be integers and let \(1\le p< \infty \). Suppose \(\Omega \) satisfies the strong loc.Lipschitz condition. If \(mp>n>(m-1)p\), then \(W^{j+m,p}(\Omega ) \rightarrow C^{j,\lambda }({\overline{\Omega }})\) for \(0< \lambda \le m -\frac{n}{p}\).

In our case, \(n=3, p=2\). We have (see condition \(mp>n>(m-1)p\)) that \(m\in (\frac{3}{2}, \frac{5}{2})\). We are interested in \(m< 2\), so consider \(m\in (\frac{3}{2}, 2)\).

In case \(A = -\Delta \), the condition \(m\in (\frac{3}{2}, 2)\) corresponds to \(\alpha \in (\frac{3}{4}, 1)\).

We notice the importance of the restriction \(\alpha \in (\frac{3}{4}, 1)\) which guaranties \(u(t)\in X=[C({\overline{\Omega }})]^3\).

Combining this property with the uniqueness results for both \(H_\alpha \)-mild solutions and \(C({\overline{\Omega }})\)-mild solutions (both for the same initial function \(\varphi \)) one has the following key property: for any initial \(\varphi \in C_\alpha , \alpha \in (\frac{3}{4}, 1)\) the \(H_\alpha \)-mild solution is \(C({\overline{\Omega }})\)-mild solution.

Our goal is to construct a dynamical system in phase space \( \Omega ^{log}_\alpha \equiv C_\alpha \cap \Omega ^{log}, \alpha \in (\frac{3}{4}, 1). \) On this space we define evolution operator \(S_t \varphi = u_t, t\ge 0\), where u is the unique mild solution of problem (2.2), (1.3).

Now we need the following space

$$\begin{aligned} {Y}_\beta \equiv \{ v\in C_\alpha : |v|_{{ Y}_\beta }<\infty \}, \end{aligned}$$

where \(\beta \in (\alpha , 1)\) and

$$\begin{aligned} |v|_{{ Y}_\beta } \equiv \max _{\theta \in [-h,0]}||{\mathcal {A}}^\beta v(\theta ) ||+ \max _{\theta _1,\theta _2\in [-h,0],\theta _1\ne \theta _2} \frac{||{\mathcal {A}}^\alpha ( v(\theta _1)-v(\theta _2)) ||}{|\theta _1-\theta _2|^{\beta -\alpha }}. \end{aligned}$$
(2.17)

We remind the following result (formulated for an abstract equation of the form (2.2)).

Proposition 2.6

[6, p. 293] Let \({\mathcal {A}}\) be a linear positive self-adjoint operator with discrete spectrum on H. Let \(F:C_\alpha \rightarrow H\) be a locally Lipschitz mapping i.e. for every \(R>0\) (2.11) holds. Assume that the problem (2.2), (1.3) generates a dynamical system \((C_\alpha , S_t)\). Let D be a forward invariant bounded set in \(C_\alpha \).

Then

  1. (1)

    For every \(t>h\) the set \(S_t D\) is bounded in \({ Y}_\beta \) for arbitrary \(\beta \in (\alpha ,1)\). Moreover, for every \(\delta >0\) there exists \(R_\delta \) such that

    $$\begin{aligned} S_tD \subset B_\beta = \{ u \in { Y}_\beta : |u|_{{ Y}_\beta } \le R_\delta \} \quad \text {for all}\quad t\ge \delta +h. \end{aligned}$$
    (2.18)

    In particular, this means that the dynamical system \((C_\alpha , S_t)\) is conditionally compact and thus asymptotically smooth.

  2. (2)

    The mapping \(S_t\) is Lipschitz from D into \({ Y}_\beta \). Moreover, for every \(h<a<b<+\infty \) there exists a constant \(M_D(a,b)\) such that

    $$\begin{aligned} |S_t\varphi - S_t \psi |_{{ Y}_\beta } \le M_D(a,b) ||\varphi -\psi ||_{C_\alpha }, \quad \text {}\quad t\in [a,b], \varphi ,\psi \in D. \end{aligned}$$
    (2.19)

    In particular, this means that the dynamical system \((C_\alpha , S_t)\) is quasi-stable at any time \(t\in [a,b]\).

We remind (see, e.g., [4, 34])

Definition 2.7

A global attractor of the dynamical system \((C_\alpha ,S_t)\) is defined as a bounded closed set \({ U}\subset C_\alpha \) which is invariant (\(S_t { U}={ U}\) for all \(t>0\)) and uniformly attracts all bounded sets

$$\begin{aligned} \lim _{t\rightarrow +\infty } \sup \{\textrm{dist}_{C_\alpha }(S_ty,{ U}):\ y\in B\} = 0 \quad \text{ for } \text{ any } \text{ bounded } \text{ set } \text{ B } \text{ in } C_\alpha \text{. } \end{aligned}$$

Our main result is the following

Theorem 2.8

Let \(\alpha \in (\frac{3}{4}, 1)\), non-linear Lipschitz function f satisfy \((Hf_1+)\) (see (2.14)), \(\xi \) satisfy (H2), (H3). Then the pair \((S_t; \Omega ^{log}_\alpha ) \) constitutes a dynamical system constructed by problem (2.2), (1.3). This dynamical system possesses a finite-dimensional global attractor.

Proof

The well-posedness of the problem (2.2), (1.3) (the existence, uniqueness and continuous dependence on initial function \(\varphi \in C_\alpha \)) is given by Theorem 2.2.

First we remind an important estimate (and its derivation) which is a part of the property (2.18). For more details, see [6, p.294]. Let D be a forward invariant bounded set in \(C_\alpha \) (for this part \(\alpha \ge 0\)). Consider \(\beta \in (\alpha ,1)\) and a mild solution \(u(t)=S_t\varphi \), see (2.5). We use property \(||{\mathcal {A}}^\alpha e^{-t {\mathcal {A}}}|| \le \left( \frac{\alpha }{e t}\right) ^\alpha , t>0, \alpha \ge 0\) (with the rule \(0^0=1\)) to get

$$\begin{aligned} ||u(t)||_\beta \le \left( \frac{\beta -\alpha }{e(t-s)}\right) ^{\beta -\alpha } ||u(s)||_\alpha + \int ^t_s \left( \frac{\beta }{e(t-\tau )}\right) ^{\beta } ||F(u_\tau )||\, d\tau \end{aligned}$$

for all \(t>s\ge 0\). Since \(S_t\varphi \in D\) for all \(t\ge 0\) one has \(||u(t)||_\alpha \le C_D, \forall t\ge 0\). So

$$\begin{aligned} ||u(t)||_\beta \le \left( \frac{\beta -\alpha }{e(t-s)}\right) ^{\beta -\alpha } C_D + K_D(F) \left( \frac{\beta }{e}\right) ^{\beta } \frac{|t-s|^{1-\beta }}{1-\beta } \end{aligned}$$

for all \(t>s\ge 0\), where \(K_D(F) = \sup \{ ||F(v)|| : v\in D\}\). If we choose \(s=t - \delta \), then

$$\begin{aligned} S_t D \subset \{u\in C_\beta : ||u||_\beta \le R^*_\delta \}, \quad \text {for all} \quad t\ge \delta + h, \end{aligned}$$
(2.20)

where

$$\begin{aligned} R^*_\delta \equiv \left( \frac{\beta -\alpha }{e\delta }\right) ^{\beta -\alpha } C_D + K_D(F) \left( \frac{\beta }{e}\right) ^{\beta } \frac{\delta ^{1-\beta }}{1-\beta }. \end{aligned}$$

This estimate is a part of the property (2.18), see (2.17).

Since parameter \(\alpha \) is a smoothness parameter of the space \(C_\alpha \) and phase space \(\Omega ^{log}_\alpha \), we change notations in (2.20) to adopt it for the proof of the dissipativeness (the existence of a bounded absorbing set). More precisely, we consider a solution \(||u(t)||_\gamma \le C_D, \forall t\ge 0\). Here \(\gamma \ge 0\) instead of \(\alpha \). Now we estimate \(||u(t)||_\alpha , \alpha \in (\gamma ,1)\) instead of \( ||u(t)||_\beta \). The estimate, similar to (2.20) gives

$$\begin{aligned} S_t D \subset \{u\in C_\alpha : ||u||_\alpha \le {{\widehat{R}}}^*_\delta \}, \quad \text {for all} \quad t\ge \delta + h, \end{aligned}$$
(2.21)

where

$$\begin{aligned} {{\widehat{R}}}^*_\delta \equiv \left( \frac{\alpha -\gamma }{e\delta }\right) ^{\alpha -\gamma } C_D + K_D(F) \left( \frac{\alpha }{e}\right) ^{\alpha } \frac{\delta ^{1-\alpha }}{1-\alpha }. \end{aligned}$$

Notice that for any \(v\in [C({\overline{\Omega }})]^3 \subset [L^2(\Omega )]^3\) one has \(||v||_0=||v||_{[L^2(\Omega )]^3} \le ||v||_{[C({\overline{\Omega }})]^3}\cdot |\Omega |\) with \(|\Omega |\equiv \int _\Omega 1 dx\).

We apply the above property (2.21) for \(\gamma =0\) and \(D=\Omega ^{log}_\alpha \subset \Omega ^{log}\) (bounded in \(C_X\)). Hence for \(\gamma =0\) the property \(||u(t)||_0 \le C_D, \forall t\ge 0\) holds. As a result, (2.21) implies (a) mild solutions are global (defined for all \(t\ge -h\)) and (b) the dissipativeness of the dynamical system \((S_t; \Omega ^{log}_\alpha )\) for each \(\alpha \in (\frac{3}{4}, 1)\).

Now by Proposition 2.6 [6, p.293] our dynamical system \((S_t; \Omega ^{log}_\alpha )\) is quasi-stable.

We can apply [6, Theorem 6.1.12] to the dynamical system \((S_t; \Omega ^{log}_\alpha )\) to get the main result - the existence of a finite-dimensional global attractor.

It completes the proof of Theorem 2.8. \(\square \)

2.4 Examples of the Distributed Delay Term

Consider the nonlinear delay term B of the form (2.4). We present a simple example of function \(\xi : [-h,0]\times \Omega \times C \rightarrow {\mathbb {R}}\) (c.f. [23, 24])

$$\begin{aligned} \xi (\theta , x, \varphi ) = e^{-\sigma (-\eta (\varphi )-\theta )^2} g(x),\quad \sigma >0, \end{aligned}$$

where

  1. (i)

    \(\eta : C\rightarrow [0,h]\) is Lipschitz continuous and \(g \in L^\infty (\Omega )\) to satisfy (H2) and

  2. (ii)

    \(\eta : C_X\rightarrow [0,h]\) is Lipschitz continuous and \(g \in C({\overline{\Omega }})\) to satisfy (H3).

For motivations for such a state-selective delay see e.g. [23]. The profile function \(e^{-\sigma (c-\theta )^2}\) was chosen for simplicity to show that the delay term of the form \(\int ^0_{-h} e^{-\sigma (c-\theta )^2} \phi (\theta ) d\theta \) has the maximal historical impact in a neighbourhood of the time moment c (the maximum of function \(e^{-\sigma (c-\theta )^2}\) at point \(\theta =c\)). In our example this maximum point can be state-selective [23] (state-dependent) \(c=-\eta (\varphi )\in [-h,0]\).

We mention some well-known examples of non-linear functions f used for viral infection models. The first one is the DeAngelis-Bendington [2, 7] functional response \(f(T,V)=\frac{kTV}{1+k_1 T+k_2 V}\), with \(k,k_1\ge 0,k_2>0\). We also mention that the functional response includes as a special case (\(k_1=0\)) the saturated incidence rate \(f(T,V)=\frac{kTV}{1+k_2 V}\). Another example of the nonlinearity is the Crowley-Martin incidence rate \(f(T,V)=\frac{kTV}{(1+k_1 T)(1+k_2 V)}\), with \(k\ge 0,k_1,k_2>0\) and more general the Hattaf-Yousfi functional response of the form \(\frac{kTV}{k_0+k_1 T+k_2 V +k_3 TV}\) [11]. For more general class of functions f see, e.g. [11, 18, 29]. We notice that, in contrast to [11, 18], we do not assume here the differentiability of f.

We also mention that our assumptions on f are naturally less restrictive comparing to the ones in the mentioned above works where asymptotic stability of stationary solutions are discussed.

3 Conclusion

In this paper we study a virus dynamics model with reaction-diffusion, logistic growth terms and a general non-linear infection rate functional response. The model has a distributed delay, including the case of state-selective delay which is a distributed ‘analog’ to a discrete state-dependent delay.

Our main mathematical tool in studying of the asymptotic behaviour of solutions is the quasi-stability method developed by I.D.Chueshov [6]. We construct a dynamical system in a Hilbert space and prove the existence of a finite-dimensional global attractor. To prove the natural for a virus dynamics model dissipativness of the dynamical system we conduct a parallel study in a Banach space.