Bifurcation of Periodic Orbits of a Three-Dimensional Piecewise Smooth System

Abstract

We consider a three-dimensional piecewise smooth system having an invariant surface and a closed orbit of multiplicity k on the invariant surface. By using bifurcation techniques and analyzing the number of solutions of bifurcation equations, we study certain bifurcation phenomena near the multiple k closed orbit and obtain some conditions for the existence of periodic orbits bifurcated from it. Moreover, our partial analytical results are demonstrated by some examples.

Appendix

The proof of Lemma 1

Transformation (2.4) can be rewritten as

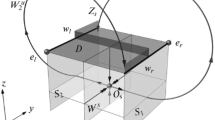
$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{x}=\varvec{u}(\theta )+\varvec{z}(\theta )h_1 \equiv \varvec{\varphi } (\theta , h_1),\\ y=h_2, \end{array}\right. } \end{aligned}$$

(5.1)

where $\varvec{z}(\theta )= (-v_2(\theta ),v_1(\theta ))^\top$, and

$$\begin{aligned} \ v_i(\theta )= {\left\{ \begin{array}{ll} v^+_i(\theta ), ~~~~0 \le \theta \le T_1, \\ v^-_i(\theta ), ~~~~T_1 < \theta \le T, \end{array}\right. } \ \ \ i=1,2. \end{aligned}$$

It is straightforward that (2.4) is continuous, one-to-one and periodic in $\theta$ if and only if the map $\varphi :(\theta ,h_1)\mapsto (x_1,x_2)$ is continuous, one-to-one and periodic in $\theta$. Firstly, the continuity and periodicity are obvious. Secondly, for one-to-one property, we introduce two sets

$$\begin{aligned} G_1= & {} \{\varvec{\varphi } (\theta , h_1)| \ 0\le \theta \le T_1, |h_1|<\varepsilon _0\},\\ G_2= & {} \{\varvec{\varphi } (\theta , h_1)|\ T_1< \theta \le T, |h_1|<\varepsilon _0\}, \end{aligned}$$

where $\varepsilon _0$ is a small positive constant. From (2.4), for $0\le \theta \le T_1$

$$\begin{aligned} \varvec{\varphi }(\theta ,h_1)= \begin{pmatrix} u_1^+(\theta ) \\ u_2^+(\theta ) \end{pmatrix} + \begin{pmatrix} -v_2^+(\theta ) \\ v_1^+(\theta ) \end{pmatrix} h_1\equiv \varvec{\varphi }^+(\theta ,h_1). \end{aligned}$$

It follows from the above equation that

$$\begin{aligned} \det \left. {\frac{\partial \varvec{\varphi }^+}{\partial (\theta ,h_1)}}\right| _{h_1=0}&=\left| \begin{array}{cc} (u^+_1)'(\theta ) &{} -v^+_2(\theta ) \\ (u^+_2)'(\theta ) &{} v^+_1(\theta ) \end{array}\right| \\&=(u_1^+)'(\theta )v_1^+(\theta )+(u_2^+)' (\theta )v_2^+(\theta )\\&=|\varvec{f}(\varvec{u}^+(\theta ))|>0. \end{aligned}$$

Thus $\varvec{\varphi }:\{(\theta ,h_1)| \ 0\le \theta \le T_1, |h_1|<\varepsilon _0\}\mapsto G_1$ is one-to-one. Similarly, $\varvec{\varphi }:\{(\theta ,h_1)| \ T_1<\theta \le T, |h_1|<\varepsilon _0\}\mapsto G_2$ is also one-to-one.

By condition (2.3), the function $\varvec{\varphi }(\theta ,h_1)$ is continuous at $\theta =0$, $T_1$, T, satisfying $\varvec{\varphi }(0,h_1)=\varvec{\varphi }(T,h_1)$, and the union $G_1\cup G_2$ forms a neighborhood of the periodic orbit L. Therefore,

$$\begin{aligned} \varvec{\varphi }:\{(\theta ,h_1)| \ 0\le \theta \le T, |h_1|<\varepsilon _0\}\mapsto G_1\cup G_2 \end{aligned}$$

is an one-one transformation. This completes the proof of Lemma 1. $\square$

The proof of Lemma 2

For $0\le \theta \le T_1$ or $T_1<\theta \le T$, applying Theorem 1.4 of chapter two of reference [8] or the Theorem 1.2. of chapter VI in Ref. [10], the transformation of (2.4) transforms system (2.1) into a system with $\theta , h$ as follows

$$\begin{aligned} \dot{\theta }&=1+\tilde{f}_1(\theta ,\varvec{h})+\varvec{H}(\theta ,\varvec{h}) \begin{pmatrix} \varvec{P}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h},\varepsilon ) \\ Q(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h},\varepsilon ) \end{pmatrix}\varepsilon ,\end{aligned}$$

(5.2)

$$\begin{aligned} \dot{\varvec{h}}&=\varvec{A}(\theta )\varvec{h}+\varvec{f}_2(\theta ,\varvec{h})+\varvec{B}(\theta ,\varvec{h}) \begin{pmatrix} P(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h},\varepsilon ) \\ Q(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h},\varepsilon ) \end{pmatrix}\varepsilon , \end{aligned}$$

(5.3)

where

$$\begin{aligned} \varvec{U}(\theta )&=\left( \begin{array}{c} \varvec{u}(\theta ) \\ 0 \end{array}\right) , ~~~~~~~\varvec{V}(\theta )=\left( \begin{array}{c} \varvec{v}(\theta ) \\ 0 \end{array}\right) , ~~~~~~~\tilde{\varvec{x}}=\left( \begin{array}{c} \varvec{x} \\ y \end{array}\right) ,\nonumber \\ \varvec{H}(\theta ,\varvec{h})&=[|\varvec{U}'(\theta )|+\varvec{V}^\top (\theta ) \varvec{Z}^\prime (\theta ) \varvec{h}]^{-1}\varvec{V}^\top (\theta ),\nonumber \\ \varvec{A}(\theta )&={\varvec{Z}^\top (\theta )}[{-\varvec{Z}^\prime (\theta )} +{\tilde{\varvec{f}}_{\tilde{\varvec{x}}}} (\varvec{U}(\theta ))\varvec{Z}(\theta )],\nonumber \\ \tilde{f}_1(\theta ,\varvec{h})&= \varvec{H}(\theta ,\varvec{h})[\tilde{\varvec{f}}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})-\tilde{\varvec{f}}(\varvec{U}(\theta )) -\varvec{Z}^\prime (\theta ) \varvec{h}],\nonumber \\ \varvec{B}(\theta ,\varvec{h})&={\varvec{Z}^\top (\theta )}[I-\varvec{Z}^\prime (\theta )\varvec{h} \varvec{H}(\theta ,\varvec{h})],\nonumber \\ \varvec{f}_2(\theta ,\varvec{h})&= {-\varvec{Z}^\top (\theta )}{\varvec{Z}^\prime (\theta )}\varvec{h}\tilde{f}_1(\theta ,\varvec{h})\nonumber \\&\quad +{\varvec{Z}^\top (\theta )}[\tilde{\varvec{f}}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) -\tilde{\varvec{f}}(\varvec{U}(\theta ))-{\tilde{\varvec{f}}_ {\tilde{\varvec{x}}}}(\varvec{U}(\theta ))\varvec{Z}(\theta )\varvec{h}],\nonumber \\ \tilde{\varvec{f}}(\tilde{\varvec{x}})&= \begin{pmatrix} \varvec{f}(\varvec{x})+y\varvec{f}_1(\varvec{x},y) \\ yg(\varvec{x},y) \end{pmatrix},~~~~ \varvec{A}(\theta )= {\left\{ \begin{array}{ll} \varvec{A}^+(\theta ), ~~~~~~0 \le \theta \le T_1, \\ \varvec{A}^-(\theta ), ~~~~~~T_1 < \theta \le T. \end{array}\right. } \end{aligned}$$

(5.4)

Since ${\varvec{Z}^\top (\theta )}\varvec{Z}^\prime (\theta )=\mathbf{0}$, one has

$$\begin{aligned} \begin{aligned} \varvec{B}(\theta ,\varvec{h}) =&\varvec{Z}^\top (\theta ),\\ \varvec{f}_2(\theta ,\varvec{h}) =&{\varvec{Z}^\top (\theta )}[\tilde{\varvec{f}}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) -\tilde{\varvec{f}}(\varvec{U}(\theta ))-{\tilde{\varvec{f}}_ {\tilde{x}}} (\varvec{U}(\theta ))\varvec{Z}(\theta )\varvec{h}],\\ \varvec{A}(\theta ) =&{\varvec{Z}^\top (\theta )}{\tilde{\varvec{f}}_{\tilde{\varvec{x}}}} (\varvec{U}(\theta ))\varvec{Z}(\theta )= \begin{pmatrix} a(\theta ) &{} {\varvec{z}^\top (\theta )}f_1(\varvec{u}(\theta ),0) \\ 0 &{} g(\varvec{u}(\theta ),0) \end{pmatrix}. \end{aligned} \end{aligned}$$

By direct computation and Taylor Theorem, we get

$$\begin{aligned} \tilde{f}_1(\theta ,\varvec{h})= & {} \frac{1}{|\varvec{u}^\prime (\theta )|}({\varvec{v}^\top (\theta )}\varvec{f}_{\varvec{x}}(\varvec{u}(\theta )) \varvec{z}(\theta )\\&-\varvec{v}^\top (\theta )\varvec{z}^\prime (\theta ),\varvec{v}^\top (\theta )\varvec{f}_1(\varvec{u}(\theta ),0)){\varvec{h}}+O(|\varvec{h}|^2). \end{aligned}$$

Then we obtain (2.5) from (5.2).

For obtaining the expansion of $\varvec{f}_2(\theta ,\varvec{h})$, we set

$$\begin{aligned} \varvec{f}_2(\theta ,\varvec{h})= \begin{pmatrix} f_2^{(1)}(\theta ,\varvec{h}) \\ f_2^{(2)}(\theta ,\varvec{h}) \end{pmatrix}, ~~~ \tilde{\varvec{f}}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})= \begin{pmatrix} \tilde{\varvec{f}}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})) \\ \tilde{f}^{(2)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) \end{pmatrix}. \end{aligned}$$

Then using of (5.4) we have

$$\begin{aligned} \varvec{Z}^\top (\theta )\tilde{\varvec{f}}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})&= \begin{pmatrix} \varvec{z}^\top &{} 0 \\ \mathbf{0} &{} 1 \end{pmatrix} \begin{pmatrix} \tilde{\varvec{f}}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) \\ \tilde{f}^{(2)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) \end{pmatrix}\nonumber \\&=\begin{pmatrix} \varvec{z}^\top \tilde{\varvec{f}}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) \\ \tilde{f}^{(2)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) \end{pmatrix}. \end{aligned}$$

(5.5)

Note that

$$\begin{aligned} \varvec{f}_2(\theta ,0)=\varvec{0}~,~~~\frac{\partial \varvec{f}_2(\theta ,0)}{\partial \varvec{h}}=\varvec{0}. \end{aligned}$$

We can use Taylor Theorem to get

$$\begin{aligned} f_2^{(i)}(\theta ,\varvec{h}) = \frac{1 }{2}\varvec{h}^\top \frac{\partial ^2 f_2^{(i)}(\theta ,\varvec{0})}{\partial \varvec{h}^2}\varvec{h}+O(|\varvec{h}|^3),~~~~i=1,2, \end{aligned}$$

(5.6)

and in light of (5.5) and (5.6) we have

$$\begin{aligned} f_2^{(1)}(\theta ,\varvec{h})= \frac{1 }{2}\varvec{h}^\top \frac{\partial ^2 }{\partial \varvec{h}^2}[\varvec{z}^\top (\theta )\tilde{\varvec{f}}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}]\big |_{\varvec{h}=\varvec{0}}\varvec{h}+O(|\varvec{h}|^3). \end{aligned}$$

(5.7)

Then using of (5.6) we can write the first component of $\varvec{f}_2(\theta ,\varvec{h})$ as

$$\begin{aligned} f_2^{(1)}(\theta ,\varvec{h})&= \frac{1 }{2}\frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{0})}{\partial h_1{^2}}h_1^{2}+\frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{0})}{\partial h_1\partial h_2}h_1h_2+\frac{1 }{2}\frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{0})}{\partial h_2{^2}}h_2{^2}+O(|\varvec{h}|^3). \end{aligned}$$

(5.8)

Set

$$\begin{aligned} \tilde{\varvec{f}}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})= \begin{pmatrix} \tilde{f}_{1}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) \\ \tilde{f}_{2}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) \end{pmatrix}. \end{aligned}$$

Then the first component in (5.5) can be written as

$$\begin{aligned} \varvec{z}^\top \tilde{\varvec{f}}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})&= -v_2(\theta )\tilde{f}_{1}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})\\&\quad + v_1(\theta )\tilde{f}_{2}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}). \end{aligned}$$

Based on above analysis, we are going to compute the right of Eq. (5.8). Firstly,

$$\begin{aligned} \frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{h})}{\partial h_1{^2}}&= -v_2(\theta )\frac{\partial ^2 }{\partial h_1{^2}}\tilde{f}_{1}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}) + v_1(\theta )\frac{\partial ^2 }{\partial h_1{^2}}\tilde{f}_{2}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}). \end{aligned}$$

(5.9)

First of all, we compute $\frac{\partial ^2 }{\partial h_1{^2}}\tilde{f}_{1}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})$ in (5.9). Using of (5.4), we have

$$\begin{aligned} \frac{\partial ^2 }{\partial h_1{^2}}\tilde{f}_{1}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})&= \frac{\partial ^2 }{\partial h_1{^2}}[f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)+h_2f_{11}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})]\nonumber \\&= \frac{\partial ^2 }{\partial h_1{^2}}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)+h_2\frac{\partial ^2 }{\partial h_1{^2}}f_{11}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}). \end{aligned}$$

(5.10)

Transformation (2.4) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1=u_1(\theta )-v_2(\theta )h_1,\\ x_2=u_2(\theta )+v_1(\theta )h_1,\\ y=h_2, \end{array}\right. } \end{aligned}$$

hence

$$\begin{aligned} \frac{\partial x_1}{\partial h_1}=-v_2(\theta ),~~ \frac{\partial x_2}{\partial h_1}=v_1(\theta ),~~\frac{\partial y}{\partial h_2}=1, \frac{\partial x_1}{\partial h_2}=\frac{\partial x_2}{\partial h_2}=\frac{\partial y}{\partial h_1}=0. \end{aligned}$$

Firstly, we calculate the first item on the right of (5.10). Because of

$$\begin{aligned}&\frac{\partial }{\partial h_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\\&\quad = \frac{\partial }{\partial x_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\frac{\partial x_1}{\partial h_1}+\frac{\partial }{\partial x_2}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\frac{\partial x_2}{\partial h_1}\\&\quad = -v_2(\theta )\frac{\partial }{\partial x_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)+v_1(\theta )\frac{\partial }{\partial x_2}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1), \end{aligned}$$

we have

$$\begin{aligned}&\frac{\partial ^2}{\partial h_1^{2}}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\\&\quad = \frac{\partial }{\partial h_1} \left( \frac{\partial }{\partial h_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\right) \\&\quad =\frac{\partial }{\partial x_1} \left( \frac{\partial }{\partial h_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\right) \frac{\partial x_1}{\partial h_1} +\frac{\partial }{\partial x_2} \left( \frac{\partial }{\partial h_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\right) \frac{\partial x_2}{\partial h_1}\\&\quad = -v_2(\theta )\frac{\partial }{\partial x_1} \left( \frac{\partial }{\partial h_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\right) +v_1(\theta )\frac{\partial }{\partial x_2} \left( \frac{\partial }{\partial h_1}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\right) \\&\quad = v_2^{2}(\theta )\frac{\partial ^2}{\partial x_1^{2}}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1) -2v_1(\theta )v_2(\theta )\frac{\partial ^2 }{\partial x_1x_2}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\\&\qquad +v_1^{2}(\theta )\frac{\partial ^2 }{\partial x_2^{2}}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1). \end{aligned}$$

In light of similar analysis, we can obtain second coefficients on the right of (5.10). Namely,

$$\begin{aligned} \frac{\partial ^2 }{\partial h_1{^2}}f_{11}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})&= v_2^{2}(\theta )\frac{\partial ^2}{\partial x_1^{2}}f_{11}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})\\&\quad -2v_1(\theta )v_2(\theta )\frac{\partial ^2}{\partial x_1x_2}f_{11}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})\\&\quad +v_1^{2}(\theta )\frac{\partial ^2}{\partial x_2^{2}}f_{11}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h}). \end{aligned}$$

Therefore, for $\varvec{h}=\varvec{0}$, the left of the formula (5.10) is equal to

$$\begin{aligned} \frac{\partial ^2 }{\partial h_1{^2}}\tilde{f}_{1}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})\big |_{\varvec{h}=\varvec{0}}&= \frac{\partial ^2 }{\partial h_1{^2}}f_{01}(\varvec{u}(\theta )+\varvec{z}(\theta )h_1)\big |_{\varvec{h}=\varvec{0}}\\&=\varvec{z}^\top ({\theta })\begin{pmatrix} \frac{\partial ^2 f_{01}(\varvec{u}(\theta ))}{\partial x_1^2} &{} \frac{\partial ^2 f_{01}(\varvec{u}(\theta ))}{\partial x_1 \partial x_2} \\ \frac{\partial ^2 f_{01}(\varvec{u}(\theta ))}{\partial x_2 \partial x_1} &{} \frac{\partial ^2 f_{01}(\varvec{u}(\theta ))}{\partial x_2^2} \end{pmatrix}\varvec{z}(\theta ). \end{aligned}$$

Analogous to $\frac{\partial ^2 }{\partial h_1{^2}}\tilde{f}_{1}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})\big |_{\varvec{h}=\varvec{0}}$, for $\varvec{h}=\varvec{0}$ we deduce second coefficients on the right of (5.9)

$$\begin{aligned} \frac{\partial ^2 }{\partial h_1{^2}}\tilde{f}_{2}^{(1)}(\varvec{U}(\theta )+\varvec{Z}(\theta )\varvec{h})\big |_{\varvec{h}=\varvec{0}} =\varvec{z}^\top ({\theta }) \begin{pmatrix} \frac{\partial ^2 f_{02}(\varvec{u}(\theta ))}{\partial x_1^2} &{} \frac{\partial ^2 f_{02}(\varvec{u}(\theta ))}{\partial x_1 \partial x_2} \\ \frac{\partial ^2 f_{02}(\varvec{u}(\theta ))}{\partial x_2 \partial x_1} &{} \frac{\partial ^2 f_{02}(\varvec{u}(\theta ))}{\partial x_2^2} \end{pmatrix}\varvec{z}(\theta ). \end{aligned}$$

We can write $\frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{0})}{\partial h_1{^2}}$ in (5.8) as $-v_2(\theta )\varvec{z}^\top (\theta )f^{\prime \prime }_{01}(\varvec{u}(\theta ))\varvec{z}(\theta ) +v_1(\theta )\varvec{z}^\top (\theta ) f^{\prime \prime }_{02}(\varvec{u}(\theta ))\varvec{z}(\theta )$.

Similar argument as $\frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{h})}{\partial h_1{^2}}$ in (5.8), we can get

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{0})}{\partial h_1\partial h_2} =\varvec{z}^\top (\theta )\varvec{f}_{1\varvec{x}} (\varvec{u}(\theta ),\varvec{0})\varvec{z}(\theta ),~~~~ \frac{\partial ^2 f_2^{(1)}(\theta ,\varvec{0})}{\partial h_2{^2}} =2\varvec{z}^\top (\theta )\varvec{f}_{1y}(\varvec{u}(\theta ),\varvec{0}), \end{aligned} \end{aligned}$$

and the expanded formular of $f_2^{(2)}(\theta ,\varvec{h})$. Accordingly, it follows that

$$\begin{aligned} \varvec{f}_2(\theta ,\varvec{h})= \begin{pmatrix} \frac{1}{2}g_1(\theta )h^2_1+g_2(\theta )h_1h_2+\frac{1}{2}g_3(\theta )h^2_2+O(|\varvec{h}|^3) \\ g_{\varvec{x}}(\varvec{u}(\theta ),0)\varvec{z}(\theta )h_1h_2+g_y(\varvec{u}(\theta ),0)h^2_2+O(|h_2||\varvec{h}|^2) \end{pmatrix}. \end{aligned}$$

Hence, from (5.3) we obtain (2.6). The proof of Lemma  2 is completed. $\square$

The proof of Lemma 3

From the assumption that

$$\begin{aligned} (h^+_1(\theta ,m_1,m_2,\varepsilon ),h^+_2(\theta ,m_1,m_2,\varepsilon )),~~ 0 \le \theta \le T_1, \end{aligned}$$

is a solution of system (2.8) satisfying

$$\begin{aligned} (h^+_1(0,m_1,m_2,\varepsilon ),h^+_2(0,m_1,m_2,\varepsilon ))=(m_1,m_2), \end{aligned}$$

we have expansions below

$$\begin{aligned} \begin{aligned} h^+_1(\theta ,m_1,m_2,\varepsilon )&=A^+_1(\theta )m_1+A^+_2(\theta )m_2+A^+_3(\theta )\varepsilon \\&\quad +\,A^+_4(\theta )m^2_1+A^+_5(\theta )m_1m_2+A^+_6(\theta )m^2_2\\&\quad +\,A^+_7(\theta )m_1\varepsilon +A^+_8(\theta )m_2\varepsilon +A^+_9(\theta )\varepsilon ^2+O(|m_1,m_2,\varepsilon |^3),\\ h^+_2(\theta ,m_1,m_2,\varepsilon )&=B^+_1(\theta )m_2+B^+_2(\theta )\varepsilon +B^+_3(\theta )m_1m_2+B^+_4(\theta )m_1\varepsilon +B^+_5(\theta )m^2_2\\&\quad +\,B^+_6(\theta )m_2\varepsilon +B^+_7(\theta )\varepsilon ^2+O(|m_2,\varepsilon ||m_1,m_2,\varepsilon |^2), \end{aligned}\nonumber \\ \end{aligned}$$

(5.11)

where

$$\begin{aligned} A^+_1(0)= & {} 1,~~~B^+_1(0)=1,~~~A^+_i(0)=0,~~~B^+_j(0)=0,~~~~~i=2,\ldots ,9,~~~\\ j= & {} 2,\ldots ,7. \end{aligned}$$

The expressions of $A^{+}_i$ and $B^{+}_j$$(i=1,\ldots ,9,j=1,\ldots ,7)$ are similar to the expressions of $A_i$ and $B_j$$(i=1,\ldots ,9,j=1,\ldots ,7)$ in [16], namely,

$$\begin{aligned} B_1^+(\theta )&=e^{\int ^{\theta }_0b_1^+(s)ds}=e^{\int ^{\theta }_0g^+(\varvec{u}^+(s),0))ds},\nonumber \\ B_2^+(\theta )&=e^{\int ^{\theta }_0b_1^+(s)ds}{\int ^{\theta }_0e^{\int ^{s}_0g^+(\varvec{u}^+(\xi ),0) d\xi } Q^+(\varvec{u}^+(s),0,0)ds},\nonumber \\ A_1^+(\theta )&=e^{\int ^{\theta }_0a^+(s)ds} =exp\left( \int ^{\theta }_0\mathrm {tr}\varvec{f}^+_{\varvec{x}}(\varvec{u}^+(s))ds\right) |\varvec{f}^+(\varvec{u}^+(0))| /|\varvec{f}^+(\varvec{u}^+(\theta ))|\nonumber \\ A_2^+(\theta )&=e^{\int ^{\theta }_0a^+(s)ds}{\int ^{\theta }_0e^{-\int ^{s}_0a^+(\xi )d\xi } a_1^+(s)B_1^+(s)ds},\nonumber \\&=A_1^+(\theta )\int ^{\theta }_0 e^{\int ^{s}_0[g^+(\varvec{u}^+(\xi ),0) -\mathrm {tr}\varvec{f}^+_x(\varvec{u}^+(\xi ))]d\xi }\varvec{f}^+(\varvec{u}^+(s))\nonumber \\&\quad \wedge \varvec{f}^+_1(\varvec{u}^+(s),0)ds/|\varvec{f}^+(\varvec{u}^+(\theta ))|,\nonumber \\ A_3^+(\theta )&=A_1^+(\theta ){\int ^{\theta }_0e^{-\int ^{s}_0 a^+(\xi )d\xi }(a_1^+(s)B_2^+(s)+a_2^+(s))ds},\nonumber \\ A_4^+(\theta )&=A_1^+(\theta )\int ^{\theta }_0\tilde{a}_5^+(s)A_1^+(s)ds,\nonumber \\ B_3^+(\theta )&=B_1^+(\theta ){\int ^{\theta }_0\tilde{b}_5^+(s)A_1^+(s)ds},\nonumber \\ B_4^+(\theta )&=B_1^+(\theta ){\int ^{\theta }_0[\tilde{b}_3^+(s)A_1^+(s)+\tilde{b}_5^+(s) B_2^+(s)A_1^+(s)]e^{-\int ^{s}_0g^+(\varvec{u}^+(\xi ),0))d\xi } ds},\nonumber \\ B_5^+(\theta )&=B_1^+(\theta ){\int ^{\theta }_0[\tilde{b}_5^+(s) B_1^+(s)A_2^+(s)+\tilde{b}_6^+(s)(B_1^+(s))^2]e^{-\int ^{s}_0g^+(\varvec{u}^+(\xi ),0))d\xi }ds},\nonumber \\ B_6^+(\theta )&=B_1^+(\theta )\int ^{\theta }_0[\tilde{b}_3^+(s) A_2^+(s)+\tilde{b}_4^+(s)B_1^+(s)+\tilde{b}_5^+(s)(B_1^+(s)A_3^+(s)\nonumber \\&\quad +B_2^+(s)A_2^+(s))+2\tilde{b}_6^+(s)B_1^+(s)B_2^+(s)]e^{-\int ^{s}_0g^+(\varvec{u}^+(\xi ),0))d\xi }ds,\nonumber \\ B_7^+(\theta )&=B_1^+(\theta )\int ^{\theta }_0[\tilde{b}_3^+(s)A_3^+(s) +\tilde{b}_4^+(s)B_2^+(s)+\tilde{b}_5^+(s)B_2^+(s)A_3^+(s)\nonumber \\&\quad +\tilde{b}_6^+(s)(B_2^+(s))^2+\tilde{b}_7^+(s)]e^{-\int ^{s}_0g^+(\varvec{u}^+(\xi ),0))d\xi }ds,\nonumber \\ A_5^+(\theta )&=A_1^+(\theta )\int ^{\theta }_0[a_1^+(s)B_3^+(s) +2\tilde{a}_5^+(s)A_1^+(s)A_2^+(s)+\tilde{a}_6^+(s)A_1^+(s)B_1^+(s)] \nonumber \\&\quad \cdot e^{-\int ^{s}_0\mathrm {tr}\varvec{f}^+_{\varvec{x}}(\varvec{u}^+(\xi ))d\xi )}|\varvec{f}^+(\varvec{u}^+(s)))|/|\varvec{f}^+(\varvec{u}^+(0))|ds,\nonumber \\ A_6^+(\theta )&=A_1^+(\theta )\int ^{\theta }_0[a_1^+(s)B_5^+(s) +\tilde{a}_5^+(s)(A_2^+(s))^2\nonumber \\&\quad +\tilde{a}_6^+(s)A_2^+(s)B_1^+(s)+\tilde{a}_7^+(s) (B_1^+(s))^2]\nonumber \\&\quad \cdot e^{-\int ^{s}_0\mathrm {tr}\varvec{f}^+_{\varvec{x}}(\varvec{u}^+(\xi ))d\xi )}| \varvec{f}^+(\varvec{u}^+(s)))|/|\varvec{f}^+(\varvec{u}^+(0))|ds,\nonumber \\ A_7^+(\theta )&=A_1^+(\theta )\int ^{\theta }_0[a_1^+(s)B_4^+(s) +\tilde{a}_3^+(s)A_1^+(s)+2\tilde{a}_5^+(s)A_1^+(s)A_3^+(s)\nonumber \\&\quad +\tilde{a}_6^+(s)A_1^+(s)B_2^+(s)] \cdot e^{-\int ^{s}_0\mathrm {tr}\varvec{f}^+_{\varvec{x}}(\varvec{u}^+(\xi ))d\xi )}|\varvec{f}^+(\varvec{u}^+(s)))|/|\varvec{f}^+(\varvec{u}^+(0))|ds,\nonumber \\ A_8^+(\theta )&=A_1^+(\theta )\int ^{\theta }_0[a_1^+(s)B_6^+(s) +\tilde{a}_3^+(s)A_2^+(s)+\tilde{a}_4^+(s)B_1^+(s)\nonumber \\&\quad +2\tilde{a}_5^+(s)A_2^+(s)A_3^+(s)+\tilde{a}_6^+(s)(A_3^+(s)B_1^+(s)\nonumber \\&\quad +A_2^+(s)B_2^+(s))+2\tilde{a}_7^+(s)B_1^+(s)B_2^+(s)] (A_1^+(s))^{-1}ds,\nonumber \\ A_9^+(\theta )&=A_1^+(\theta )\int ^{\theta }_0[a_1^+(s)B_7^+(s) +\tilde{a}_3^+(s)A_3^+(s)+\tilde{a}_4^+(s)B_2^+(s)+\tilde{a}_5^+(s)(A_3^+(s))^2\nonumber \\&\quad +\tilde{a}_6^+(s)A_3^+(s)B_2^+(s)+\tilde{a}_7^+(s)(B_2^+(s))^2+\tilde{a}_8^+(s)](A_1^+(s))^{-1}ds. \end{aligned}$$

(5.12)

Analogously, for $T_1 < \theta \le T$, from the assumption that

$$\begin{aligned} (h^-_1(\theta ,n_1,n_2,\varepsilon ),h^-_2(\theta ,n_1,n_2,\varepsilon )) \end{aligned}$$

is a solution of system (2.8) satisfying

$$\begin{aligned} (h^-_1(T_1,n_1,n_2,\varepsilon ),h^-_2(T_1,n_1,n_2,\varepsilon ))=(n_1,n_2), \end{aligned}$$

we have two expansions as the following form

$$\begin{aligned} \begin{aligned} h^-_1(\theta ,n_1,n_2,\varepsilon )=&A^-_1(\theta )n_1+A^-_2(\theta )n_2+A^-_3(\theta )\varepsilon \\&+A^-_4(\theta )n^2_1+A^-_5(\theta )n_1n_2+A^-_6(\theta )n^2_2\\&+A^-_7(\theta )n_1\varepsilon +A^-_8(\theta )n_2\varepsilon +A^-_9(\theta )\varepsilon ^2+O(|n_1,n_2,\varepsilon |^3),\\ h^-_2(\theta ,n_1,n_2,\varepsilon )=&B^-_1(\theta )n_2+B^-_2(\theta )\varepsilon +B^-_3(\theta )n_1n_2+B^-_4(\theta )n_1\varepsilon +B^-_5(\theta )n^2_2\\&+B^-_6(\theta )n_2\varepsilon +B^-_7(\theta )\varepsilon ^2+O(|n_2,\varepsilon ||n_1,n_2,\varepsilon |^2), \end{aligned}\nonumber \\ \end{aligned}$$

(5.13)

where

$$\begin{aligned} A^-_1({T_1})= & {} 1,~~~B^-_1({T_1})=1,~~~A^-_i({T_1})=0,~~~B^-_j({T_1})=0,~~~~~i=2,\ldots ,9,~~~\\ j= & {} 2,\ldots ,7. \end{aligned}$$

The expressions of $A^{-}_i$ and $B^{-}_j$$(i=1,\ldots ,9,j=1,\ldots ,7)$ are similar to the expressions of $A_i^+$ and $B_j^+$$(i=1,\ldots ,9,j=1,\ldots ,7)$, so their expressions are omitted here.

Then applying (5.11) and (5.13) gives the succession functions of (2.8) as follows

$$\begin{aligned} \tilde{h}_1(m_1,m_2,\varepsilon )&=h^-_1(T,h^+_1(T_1,m_1,m_2,\varepsilon ),h^+_2(T_1,m_1,m_2,\varepsilon ),\varepsilon )-m_1\nonumber \\&=\bar{c}_1m_1+\bar{c}_2m_2+\bar{c}_3\varepsilon +\bar{c}_4m^2_1+\bar{c}_5m_1m_2+\bar{c}_6m^2_2+\bar{c}_7m_1\varepsilon \nonumber \\&\quad +\bar{c}_8m_2\varepsilon +\bar{c}_9\varepsilon ^2+O(|m_1,m_2,\varepsilon |^3),\nonumber \\ \tilde{h}_2(m_1,m_2,\varepsilon )&=h^-_2(T,h^+_1(T_1,m_1,m_2,\varepsilon ),h^+_2(T_1,m_1,m_2,\varepsilon ),\varepsilon )-m_2\nonumber \\&=\bar{d}_1m_2+\bar{d}_2\varepsilon +\bar{d}_3m_1m_2+\bar{d}_4m_1\varepsilon +\bar{d}_5m^2_2+\bar{d}_6m_2\varepsilon \nonumber \\&\quad +\bar{d}_7\varepsilon ^2+O(|m_2,\varepsilon ||m_1,m_2,\varepsilon |^2), \end{aligned}$$

(5.14)

where

$$\begin{aligned} \bar{c}_1&=A^-_1(T)A^+_1(T_1)-1,\nonumber \\ \bar{c}_2&=A^-_1(T)A^+_2(T_1)+A^-_2(T)B^+_1(T_1),\nonumber \\ \bar{c}_3&=A^-_1(T)A^+_3(T_1)+A^-_2(T)B^+_2(T_1)+A^-_3(T),\nonumber \\ \bar{c}_4&=A^-_1(T)A^+_4(T_1)+A^-_4(T)(A^+_1(T_1))^2,\nonumber \\ \bar{c}_5&=A^-_1(T)A^+_5(T_1)+A^-_2(T)B^+_3(T_1)+2A^-_4(T)A^+_1(T_1)A^+_2(T_1)\nonumber \\&\quad +A^-_5(T)A^+_1(T_1)B^+_1(T_1),\nonumber \\ \bar{c}_6&=A^-_1(T)A^+_6(T_1)+A^-_2(T)B^+_5(T_1)+A^-_4(T)(A^+_2(T_1))^2+A^-_5(T)A^+_2(T_1)B^+_1(T_1)\nonumber \\&\quad +A^-_6(T)(B^+_1(T_1))^2,\nonumber \\ \bar{c}_7&=A^-_1(T)A^+_7(T_1)+A^-_2(T)B^+_4(T_1)+2A^-_4(T)A^+_1(T_1)A^+_3(T_1)+A^-_7(T)A^+_1(T_1)\nonumber \\&\quad +A^-_5(T)A^+_1(T_1)B^+_2(T_1),\nonumber \\ \bar{c}_8&=A^-_1(T)A^+_8(T_1)+A^-_2(T)B^+_6(T_1)+2A^-_4(T)A^+_2(T_1)A^+_3(T_1)\nonumber \\&\quad +A^-_5(T)A^+_3(T_1)B^+_1(T_1)+A^-_5(T)A^+_2(T_1)B^+_2(T_1)+2A^-_6(T)B^+_1(T_1)B^+_2(T_1)\nonumber \\&\quad +A^-_7(T)A^+_2(T_1)+A^-_8(T)B^+_1(T_1),\nonumber \\ \bar{c}_9&=A^-_1(T)A^+_9(T_1)+A^-_2(T)B^+_7(T_1)+A^-_4(T)(A^+_3(T_1))^2+A^-_5(T)A^+_3(T_1)B^+_2(T_1)\nonumber \\&\quad +A^-_6(T)(B^+_2(T_1))^2+A^-_7(T)A^+_3(T_1)+A^-_8(T)B^+_2(T_1)+A^-_9(T),\nonumber \\ \bar{d}_1&=B^-_1(T)B^+_1(T_1)-1,\nonumber \\ \bar{d}_2&=B^-_1(T)B^+_2(T_1)+B^-_2(T),\nonumber \\ \bar{d}_3&=B^-_1(T)B^+_3(T_1)+B^-_3(T)A^+_1(T_1)B^+_1(T_1),\nonumber \\ \bar{d}_4&=B^-_1(T)B^+_4(T_1)+B^-_3(T)A^+_1(T_1)B^+_2(T_1)+B^-_4(T)A^+_1(T_1),\nonumber \\ \bar{d}_5&=B^-_1(T)B^+_5(T_1)+B^-_3(T)A^+_2(T_1)B^+_1(T_1)+B^-_5(T)(B^+_1(T_1))^2,\nonumber \\ \bar{d}_6&=B^-_1(T)B^+_6(T_1)+B^-_3(T)A^+_3(T_1)B^+_1(T_1)+B^-_3(T)A^+_2(T_1)B^+_2(T_1)\nonumber \\&\quad +B^-_4(T)A^+_2(T_1) +2B^-_5(T)B^+_1(T_1)B^+_2(T_1)+B^-_6(T)B^+_1(T_1),\nonumber \\ \bar{d}_7&=B^-_1(T)B^+_7(T_1)+B^-_3(T)A^+_3(T_1)B^+_2(T_1)+B^-_4(T)A^+_3(T_1)+B^-_2(T)(B^+_1(T_1))^2\nonumber \\&\quad +B^-_6(T)B^+_2(T_1)+B^-_7(T). \end{aligned}$$

(5.15)

Similar to (3.2), we obtain the bifurcation Eqs. (3.8) and (3.9). The proof is completed. $\square$