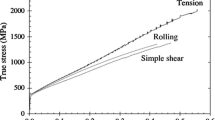
Abstract
This paper focuses on calibrating and modeling of distortional hardening behaviours in twinning induced plasticity steels. True stress-strain curves for uniaxial tension, plane strain tension, and pure shear specimens are inversely identified from corresponding load-displacement curves. The study reveals that accurately predicting the hardening behaviours of TWIP980 steel under plane strain tension and pure shear stress states is challenging with an isotropic hardening model, and a negative hydrostatic effect for TWIP980 is observed through shear testing. A novel distortional hardening model is proposed to simultaneously accommodate the three stress states on the contours of plastic work. Coefficients of the distortional hardening model are calibrated at discrete levels of plastic work and then interpolated to describe the distortion of the initial yield surface. The model is then expanded to consider the true stress-strain curves under uniaxial tension along 0, 45 and 90-degree directions, as well as under the plane strain tension along the 0-degree direction simultaneously. This expansion explicitly incorporates the three true stress-strain curves under uniaxial tension, with the curve of plane strain tension captured by an evolutionary exponent related to plastic work. The developed distortional hardening models demonstrate reasonable reproduction of load-displacement curves for TWIP980 steel under uniaxial tension, plane strain tension, and pure shear stress states.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Finite element analysis (FEA) has been widely employed in the metal forming industry to optimize the manufacturing process, thereby reducing costs and time during trial stages. The accuracy of simulation results heavily relies on constitutive models, including yield functions, work hardening laws, and flow rules. Phenomenological yield functions with the Cauchy stress components are commonly used to describe yielding in engineering. Once the yield function is calibrated, a hardening law is required to govern the evolution of the yield surface during plastic deformation, considering factors such as plastic strain, strain rate, and temperature. For example, the isotropic hardening law assumes uniform expansion of the initial yield surface, irrespective of the loading directions and stress states. However, this assumption is too simplistic for accurately describing complex hardening behaviours even under proportional loading cases.
Asymmetric hardening [1, 2], anisotropic hardening [3, 4], and differential hardening [5,6,7,8] have been proposed to improve the description of hardening behaviours. According to the above studies, anisotropic hardening represents the in-plane directionality of true stress-strain curves under stress states with the same stress triaxiality. On the other hand, differential hardening describes the stress triaxiality dependence of true stress-strain curves under stress states along the same loading direction. Thus, asymmetric hardening could be regarded as a special case of the so-called differential hardening.
The initial yield surface will undergo distortion during plastic deformation under proportional loading cases if the above hardening behaviours are observed, arising from the variation in loading directions and stress states. For example, due to the loading direction dependence of true stress-strain curves under uniaxial tension (UT), the initial yield surface expands non-uniformly [9, 10]. Experimental results have shown that the subsequent yield surfaces distorted for brass [11], steels [5, 6], aluminium alloys [12, 13], magnesium alloys [14], and titanium sheets [15] in proportional loadings.
The anisotropy parameters, stress ratios and the r-values, are generally not fixed during plastic deformation. The evolution of either or both stress ratios and the r-values has been considered in previous studies [16, 17]. Anisotropic coefficients of yield functions were then calibrated at the discrete levels of equivalent plastic strain or plastic work to describe the distortion of the yield surface. On the other hand, Stoughton and Yoon [9] analytically incorporated anisotropic hardening responses for AA5182-O along 0, 45 and 90-degree directions from the rolling direction (RD) and the equibiaxial tension (ET) into the normalized Hill48 criterion [18] using the non-associated flow rule. Lee et al. [19] proposed the coupled quadratic and non-quadratic (CQN) model by coupling the non-quadratic term, the Hosford yield function, with the S-Y2009 model [9]. Recently, Hu et al. [20] developed another coupled yield function using the Poly4 yield function [21] and the Hosford yield function, allowing for analytical descriptions of the hardening curves and r-values.
Aside from the anisotropic hardening mentioned the above, differential hardening is another significant factor that contributes to yield surface distortion. Hill and Hutchinson [5], as well as Hill et al. [6], observed progressive distortion of successive contours of plastic work in the biaxial stress area under stress states with arbitrary fixed principal stress ratios, indicating the influence of differential hardening. Kuwabara et al. [7] measured differential hardening in cold-rolled steel sheet using cruciform specimens and found that the Hill48 yield criterion overestimated the measured locus, particularly in the vicinity of ET. Differential hardening between UT and ET has also been reported by Ahn et al. [22], Stoughton and Yoon [9], and Ahn and Seo [23]. Notably, stress-strain curves for ET are often observed to be higher than those obtained from UT. As a special case of differential hardening, asymmetric hardening between proportional tensile and compressive tests have been documented in various works [1, 24].
While considerable efforts have been devoted to modeling initial yielding and hardening behaviors, many existing models are primarily characterized based on stress states like UT, ET, or uniaxial compression (UC). However, it has been recognized by several researchers that the yield locus near plane strain tension (PST) and pure shear (PS) states significantly influences the simulation results of sheet metals [25, 26]. Lee et al. [19] and Hu et al. [20] employed a coupling method with a non-quadratic term to flatten the locus to approximately capture the biaxial stress states. Others, such as Kuwabara et al. [12] and Pilthammar et al. [27], introduced yield functions with variable exponents, enhancing mathematical flexibility. Additionally, various interpolation-based yield criteria have been developed by Vegter and van den Boogaard [28], Peng et al. [29], and Hao and Dong [30]. Those yield criteria can account for the initial yield stresses at plane stress states with different stress triaxialities. However, modeling of the distinct work hardening behaviours at various stress states has rarely been reported. Recently, a stress invariant-based yield function considering stress states of UT, PST, and PS under isotropic hardening was proposed [31, 32]. Pham et al. [15] observed the distinct hardening curves between UT, PST, UC, and PS for a pure titanium grade-1 sheet in different directions. The UT, PST, and UC data were utilized to calibrate the yield functions at different levels of plastic work.
In the present study, a distortional hardening model is firstly developed to account for the initial yield stresses and the true stress-strain curves for UT, PST, and PS in the fixed loading direction. The true stress-strain curves for UT, PST, and PS specimens were obtained using an inverse experimental-numerical scheme. Note that for multiaxial stress states, von Mises stress is used as the “equivalent true stress”, and the true stress components can be easily calculated. Subsequently, a distortional hardening model considering the loading direction of UT is developed using the framework of CQN model [19]. This model accounts for the three true stress-strain curves under UT in the RD, diagonal direction (DD), and transverse direction (TD), as well as the true stress-strain curve under PST state along the RD. The load-displacement curves were reproduced from simulations to validate the distortional hardening models.
Experiment
A cold-rolled twinning induced plasticity (TWIP) steel sheet with an ultimate tensile strength up to 980 MPa was considered in this study. It was supplied by POSCO Ltd. (South Korea) with a chemical composition of Fe–18Mn–0.6 C–1.5Al (wt%). The stable microstructure is austenitic at room temperature with an average grain size of 2.2 μm.
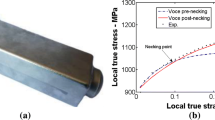
The proportional UT, PST, and PS tests were conducted with the specimens shown in Fig. 1. The specimen dimensions for the UT tests follow the ASTM E8 standard, while the dimensions for the PST tension tests follow those used by Lou and Huh [33]. The specimen dimensions for the shear test samples proposed by Merklein and Biasutti [34] was adopted as it is shown in Fig. 1c. The specimens were cut from the TWIP980 steel sheet with the thickness of 0.8 mm in the RD by waterjet cutting. An INSTRON 5967 was used with a crosshead speed of 2.28 mm/min for UT test, 0.5 mm/min for PST test and 0.21 mm/min for PS test to ensure the same quasi-static strain rate of 0.001/sec. The deformation of the specimens is measured by tracking the movement of the two markers on the surfaces of specimens using a video extensometer. The same distance of 20 mm between the two markers was selected for all specimens.
The load-displacement curves of the three loading cases in Fig. 2 show the repeatability of the tests. There is a large difference in the displacement at the sudden drop of load between tests. This may be caused by the imperfections along the gauge section. Since this study focuses on the yielding and work hardening behaviours rather than the fracture behaviour, the high variation in the measured sample fracture point will not affect this study.
To investigate the anisotropic hardening under the UT stress state, the uniaxial tension tests were conducted along the RD, DD, and TD directions. The comparisons of the load-displacement curves for these tests are shown in Fig. 3. To identify the anisotropic true stress-strain curves in each direction and model the anisotropic hardening behaviour is introduced in Section 5.
Isotropic hardening model
Under the isotropic hardening assumption, the yield surface maintains the initial shape and expands uniformly under all stress states for both isotropic and anisotropic yield function. The consistency condition during loading must be satisfied between yield function and hardening which is why the hardening is essential to accurately describe the full deformation process. Usually, the hardening curve can be obtained from the part of the true stress-strain curve of the uniaxial tension before localized necking. The hardening curve can be fitted with various hardening laws, or it can be obtained by using the inverse engineering method. In this section, both methods were adopted and validated by comparing the load-displacements data obtained from experiment and simulation.
The Swift-Voce hardening law, as shown in Eq. (1), is adopted to fit the true stress-strain curve of the uniaxial tension test, as shown in Fig. 4. \(K\), \({\epsilon }_{0}\), \(n\), \(A\), \(B\), and \(C\) in Eq. (1) are unknown coefficients that need to be identified. \(\stackrel{-}{\sigma }\) is effective stress and \({\stackrel{-}{\epsilon }}_{p}\) is equivalent plastic strain. The fitting results are listed in Table 1. Then, the von Mises function combined with the Swift-Voce hardening law is implemented into the ABAQUS User MATerials (UMAT) subroutine to predict the load-displacement response under UT, PST, and PS.
The load-displacements in Fig. 5 show that when using the isotropic hardening assumption, there is an obvious deviation between the experimental and the simulated load-displacement responses when the true stress-strain curve obtained from the UT test is used as the hardening curve to predict the load-displacement curves of the PST, and PS stress states. This phenomenon is caused by the stress triaxiality dependence of true stress-strain curves for the TWIP980 sheet metal. This suggests that the isotropic hardening law combined with one hardening function cannot account for the evolution of the true stresses at stress states with distinct stress triaxialities. To represent this the yield surface must be non-uniform to accommodate the different stress states simultaneously. Similar phenomena have been reported for other materials, AA7075 [31], for instance. Since the yield stresses under PST and PS have a significant impact on the sheet forming simulation, it is necessary to develop a hardening model to consider their individual evolutions during plastic deformation.
Distortional hardening modeling without considering the loading direction
Distortional hardening model without considering the loading direction
In order to accommodate the stress states at UT, PST, and PS simultaneously, an isotropic yield function is proposed. It is composed of the Hosford yield function \({\stackrel{-}{\sigma }}_{H}\) and the normal stress term \({\sigma }_{n}\), as shown in Eq. (2):
where parameters \(a\) and \(\mu\) are the constants for isotropic hardening, and \({\stackrel{-}{\sigma }}_{D}\) is the effective stress at the UT, PST and PS stress states, with
\({\sigma }_{1}\), \({\sigma }_{2}\), and, \({\sigma }_{3}\) in Eq. (3) are principal stresses, and \(m\) is the unknown parameter. The stress triaxiality is defined below:
where the von Mises stress, \({\stackrel{-}{\sigma }}_{vM}\), is given by
The Lode parameter is defined as
With Eqs. (5), (6), and (7), the principal stresses can be expressed by \({\stackrel{-}{\sigma }}_{vM}\), \(\eta\), and \(L\) as follows:
where \({\sigma }_{m}=({\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3})/3\), and \({s}_{1}\), \({s}_{2}\), and \({s}_{3}\) are the principal deviatoric stresses. By substituting the principal stresses, \({\sigma }_{1}\), \({\sigma }_{2}\), and \({\sigma }_{3}\) into Eqs. (3) and (4), Eq. (2) can be rewritten as
Then, at each \({\stackrel{-}{\sigma }}_{D}\), the corresponding \({\stackrel{-}{\sigma }}_{vM}\) with the same stress components can be calculated by Eq. (12):
For example, under the UT the corresponding von Mises stresses \({{\upsigma }}_{UT}\) at \({\stackrel{-}{\sigma }}_{D}\) can be calculated from Eq. (13):
The von Mises stresses under the PST and PS, \({{\upsigma }}_{PST}\) and \({{\upsigma }}_{PS}\), can be calculated in a similar way. It is pertinent to note that the stress triaxiality and Lode parameter in Eq. (12) have different values for each loading case. If \({{\upsigma }}_{UT}\), \({{\upsigma }}_{PST}\), and \({{\upsigma }}_{PS}\) at each \({\stackrel{-}{\sigma }}_{D}\) are known, the three unknown coefficients \(a\), \(\mu\), and \(m\) can be identified. More detail about the coefficients’ identification process is given in Section 4.2.
The true stress-strain curve of the UT test along the RD is selected as the hardening curve for Eq. (2), i.e., \({\stackrel{-}{\sigma }}_{D}={{\upsigma }}_{UT}={\sigma }_{11}\). Then Eq. (13) can be rewritten by Eq. (14):
Assuming isotropic hardening, the coefficients of the proposed isotropic yield function are constants. Yet, to accurately represent the distinct true stress-strain curves at UT, PST, and PS stress states, all coefficients must be updated to accommodate the three stress states simultaneously. This distinction characterizes the present distortional hardening model in contrast to the isotropic hardening model.
Calibration of the distortional hardening model
The previous section has shown that the true stress-strain curves at UT, PST, and PS are distinct under proportional loading. In order to calibrate the distortional hardening model, an inverse engineering method was adopted to obtain the true stress-strain curves for the UT, the PST, and the PS stress states. The inverse engineering method is an optimization process that minimizes the gap between the experimental and the simulated load-displacement curves by modifying the coefficients of the fitting functions of the true stress-strain curves until the results are satisfactory. Therefore, the advanced strain measure system is avoided, which is especially beneficial for conducting experiments for multiaxial stress states. During the optimization, the von Mises function was adopted, and the coefficients of the Swift-Voce hardening laws were modified iteratively. The results are listed in Table 1.
Figure 6 shows that the true stress-strain curve under UT obtained from the inverse engineering method is similar to the one obtained from the fitting method. This demonstrates the validity of the inverse engineering method for obtaining the true stress-strain curves. However, the true stress-strain curves for PST and PS specimens are quite different from that of UT. This illustrates the necessity to consider the differential hardening for stress states with distinct stress triaxialities. It also can be observed that the true stress-strain curves for the PST and the PS stress states are lower than that of the UT stress state. This is the reason why the load-displacement curves of Fig. 5b and 5c were overestimated when von Mises function and the hardening function fitted from the UT data were used in FEA.
The proposed function in Section 4.1 allows the identification of unknown parameters under UT, PST, and PS stress states explicitly. By updating the unknown parameters, the hardening behaviours for the different stress states can be captured. As for the state variable to describe the plastic deformation, either the accumulated equivalent plastic strain or the plastic work [12, 35] can be selected.
In this study, the plastic work is selected as the state variable. The plastic work increment can be calculated directly from the plastic strain increments and the stress components regardless of the definition of the yield functions. To measure and record the strain components and obtain the stress components, an advanced digital image correlation equipment is needed. According to the plastic work equivalence principle [36], the plastic work increment can be determined from the effective stress and its conjugated equivalent plastic strain increment, as shown in Eq. (15). If differential hardening is not considered, the effective stress and the conjugated equivalent plastic strain increment can have different values when calculated from the same stress and strain components by different yield functions and plastic potentials. In contrast, the values of effective stress and equivalent plastic strain increment are independent of the formulations of yield functions and the plastic potentials for the stress states (UT, PST, and PS) used in the calibration of the distortional hardening model. Therefore, if more true stress-strain curves from stress states under different stress triaxialities or loading directions are considered in the hardening modeling, errors stemming from the selection of constitutive models can be reduced.
where, \(dw\) is the plastic work increment. \({\stackrel{-}{\sigma }}_{D}\) is the effective stress of the distortional hardening model, and \(d{\stackrel{-}{\epsilon }}_{D}^{p}\) is the conjugated equivalent plastic strain increment to \({\stackrel{-}{\sigma }}_{D}\). \(d{\stackrel{-}{\epsilon }}^{p}\) is a general equivalent plastic strain increment conjugated to a general effective stress \(\stackrel{-}{\sigma }\).
Since the evolution of \({\sigma }_{UT}\), \({\sigma }_{PST}\), and \({\sigma }_{PS}\) with the reference plastic strain were obtained by the inverse engineering method, as shown in Fig. 6, they can uniquely define the size of the yield surface at the corresponding stress states. In other words, the true stress-strain curves shown in Fig. 6 are independent of the formulations of yield functions used in the inverse analysis. Then, it is possible to obtain their evolution laws with plastic work from Fig. 6 according to the plastic work equivalence principle, as is shown in Fig. 7. In this study the von Mises yield function was used in the inverse analysis. Thus, the ordinate values are von Mises stresses in Fig. 6 and Fig. 7. The inversely obtained von Mises stresses of UT, PST, and PS at the equivalent amounts of plastic work can be used to identify the unknown parameters. Since the UT true stress-strain curve is selected as the hardening curve for the distortional hardening model, i.e., \({\stackrel{-}{\sigma }}_{D}={\sigma }_{UT}={\sigma }_{11}\), the evolution laws of the parameters with plastic work can be further converted into the evolution laws with equivalent plastic strain \({\stackrel{-}{\epsilon }}_{D}^{p}\).
To identify \(a, \mu\) and \(m\), an object function is defined by Eq. (16) to minimize the difference between the von Mises stresses \({\sigma }_{UT}\), \({\sigma }_{PST}\), and \({\sigma }_{PS}\) calculated from Eq. (12) and the inversely obtained counterparts at several plastic work levels. The optimization was performed with the commercial software ISIGHT. During the optimization process, the theoretical values of the stress triaxiality \(\eta\) and the Lode parameter \(L\) for the three states were adopted.
The Hooke-Jeeves optimization algorithm was selected with a relative step size of 0.05. And the boundary for \(\mu\) was selected as \(\left[-0.5, 0.5\right]\). As for \(m\), it must be greater than or equal to 1 to ensure the convexity, although there is no concern about the violation of Drucker Postulate for plastic work contours. Iteration was stopped when \(err.<{10}^{-8}\).
The calibrated coefficients at several plastic work levels are shown in Table 2. The evolution of \(m\) and \(\mu\) with the accumulated plastic work is depicted in Fig. 8, using the piecewise linear interpolation method. The parameter \(a\) can be calculated from Eq. (14). Figure 9 illustrates the evolution of the yield surfaces with plastic work. The proposed distortional hardening model (denoted as ‘distor1’) successfully accommodates UT, PST, and PS stress states on the same contour during plastic deformation, as depicted by the red surfaces in Fig. 9.
The evolution of von Mises yield surface under the isotropic hardening assumption is also shown in Fig. 9. While the von Mises yield function accurately captures the evolution of the UT stress state (since UT is selected as the reference stress state to obtain the hardening function), it overestimates true stresses near PST and PS areas at each plastic work level. Consequently, the load-displacement of PST and PS are overestimated by the simulation when isotropic hardening is assumed, as shown in Fig. 5. Moreover, the negative pressure effect is observed for the TWIP980 sheet metal at large plastic work levels, which is captured by the negative values of \(\mu\), as shown in Fig. 8.
Prediction of load-displacement curves using the distortional hardening model
To validate the proposed distortional hardening model, it was implemented into the ABAQUS/UMAT interface to predict the load-displacement curves for the UT, PST, and PS stress states. The displacement output from the simulations represent the elongation between 2 nodes initially positioned 20 mm apart for the PST and PS specimens and 25 mm for the UT specimens, as shown in Fig. 10. The left side of the specimens are completed fixed, while concentrated loads are applied at the reference points at the right side. The von Mises stress distributions after simulations are shown in Fig. 11.
In the implementation of the distortional hardening model, equivalent plastic strain increments and stress components were obtained using the well-known cutting plane method. An efficient finite difference method [37] was adopted in the stress integration algorithm to reduce the computing cost. Subsequently, plastic work can be calculated to update the coefficients according to the evolution laws depicted in Fig. 8.
Figure 12 shows that the load-displacement curves are reasonably reproduced using the distortional hardening model. Significant improvement has been achieved compared with the prediction results shown in Fig. 5. This illustrates the advantage of the proposed distortional hardening model over any isotropic model. It’s noteworthy that the reasonable results were achieved with the assumption that the deformation of PST and PS specimens is uniform, considering the theoretical stress triaxiality and Lode parameter for the two stress states were used for calibrating the distortional hardening model.
Distortional hardening modeling considering the loading direction of UT
Distortional hardening model considering the loading direction of UT
The plane stress assumption is widely embraced in sheet forming simulations, although the consideration of the full stress condition becomes crucial in certain forming operations, such as ironing [38]. Most 3D anisotropic yield functions can be formulated using stress invariants or polynomial descriptions of all stress components. Among them, the Hill48 quadratic yield function [18] remains popular due to its simplicity, allowing for the analytical identification of material coefficients. The use of a non-associated flow rule allows the Hill48 yield function to capture both stress and r-value directionalities. By explicitly incorporating the loading direction-dependent true stress-strain curves, the Hill48 yield function can be analytically calibrated to describe anisotropic hardening [9]. As introduced in the introduction section, the CQN model proposed by Lee et al. [19] can describe the flatness at the plane strain tension area while keeping the advantages of the S-Y2009 model.
In this section, it is aimed to extend the distortional hardening model without considering the loading direction into a distortional hardening model that accounts for the loading direction of UT in the full stress space. This extension results in the development of a 3D evolutionary anisotropic yield function through the utilization of the coupling method. As formulated in Eq. (17), the deformation is defined to be elastic-plastic when \({\varphi }_{1}\left(\varvec{\sigma }\right)=1\). The distortional hardening model aims to account for the true stress-strain curves under the UT stress states in the RD, DD and TD, and that under PST stress state along the RD simultaneously. The pure shear state is not considered for the distortional hardening model in this section. A further discussion is given in Section 6.
In Eqs. (17),
where, \({\sigma }_{0}\left(w\right)\), \({\sigma }_{45}\left(w\right)\) and \({\sigma }_{90}\left(w\right)\) are the UT true stresses along the RD, the DD and the TD associated with the plastic work, and \({\sigma }_{ET}\left(w\right)\) is the true stress-strain function for the ET state. Due to the lack of ET data, \({\sigma }_{ET}\left(w\right)\) in this work it is determined by Eq. (20):
The plastic work \(w\) in \({\sigma }_{0}\left(w\right)\), \({\sigma }_{45}\left(w\right)\) and \({\sigma }_{90}\left(w\right)\) can be obtained by Eqs. (21),
Equation (17) adopts the framework of the CQN model but introduces an evolutionary exponent \({m}_{1}\) that varies with respect to plastic work, and it is determined by the PST state. \({m}_{1}\) is specified as a constant in the original CQN model [19], leading to a limitation in accurately capturing the evolution of true stress under PST in the presence of differential hardening.
Calibration of the distortional hardening model
In Section 3, the true stress-strain curves for UT, PST and PS in the RD have been obtained using the inverse engineering method. The true stress-strain curves for UT along the DD and TD directions can also be obtained with this method. The coefficients for the three curves are shown in Table 3. Accordingly, their evolution laws with plastic work can be obtained as described in Section 4.2 and shown in Fig. 13. In Fig. 13, the TWIP980 steel shows no significant anisotropic hardening for the UT stress state along the RD, DD and the TD. Since the capability to capture the directionality of UT has been well presented and verified by Lee et al. (2017), this study will focus on its improvement to describe the distinct true stress-strain curve at PST.
Under the plane stress condition, the stress states can be described by the stress components\(\left({\sigma }_{11},{\sigma }_{22},{\sigma }_{12}\right)\), where \({\sigma }_{11}\) and \({\sigma }_{22}\) are the yield stresses along the RD and the TD, and \({\sigma }_{12}\) is the in-plane shear stress. Since the von Mises stress has been inversely obtained, it is straightforward to calculate the theoretical stress components. The stress components for PST are \(\left(\frac{{2\sigma }_{PST}}{\sqrt{3}},\frac{{\sigma }_{PST}}{\sqrt{3}},0\right)\). For UT, the stress components are expressed as
where \(\theta\) is the loading direction of UT from the RD, and \({\sigma }_{UT\_\theta }\) is the corresponding effective stress.
The principal stresses are:
Similar to the calibration process of the distortional hardening model in Section 4, for the distortional hardening model considering the loading direction of UT, the coefficient \({m}_{1}\) can be identified at several selected plastic work levels of UT along the RD, DD and TD and of PST in the RD. The coefficient \({m}_{1}\) was identified by minimizing the difference between the calculated \({\varphi }_{1}\) and the theoretical counterpart at several plastic work levels. The optimization was conducted with the software ISIGHT, and the object function is described by Eq. (24). To calculate \({\varphi }_{1}\) in Eq. (17), the stress components in Eq. (22) and the principal stresses in Eq. (23) were inserted into Eq. (19) and Eq. (18), respectively. The theoretical value for \({\varphi }_{1}\) at yielding is 1.
During the calibration process, the Hooke-Jeeves optimization algorithm was selected with a relative step size of 0.05. \({m}_{1}\) must be greater than or equal to 1 to ensure the convexity. The iteration was stopped when \(err.<{10}^{-8}\) .
Figure 14 shows the evolution of the calibrated coefficient \({m}_{1}\) with the plastic work. It was interpolated with the piecewise linear functions before implemented into FEA. The evolution law of \({m}_{1}\) with plastic work can be further converted into the evolution law with equivalent plastic strain \({\stackrel{-}{\epsilon }}_{D}^{p}\), according to the work equivalence principle. Figure 15 shows that both the UT and PST stress states are well captured by the distortional hardening model (‘distor2’) at each plastic work level. However, the CQN model is unable to accurately predict the PST, and the von Mises yield function can only capture the evolution of the UT stress state along the RD.
Evolution of the yield surfaces with plastic work in space. The corresponding accumulated equivalent plastic strain of the plastic work can be found in Table 3
Prediction of load-displacement curves
To validate the proposed distortional hardening model, it was implemented into ABAQUS UMAT subroutine to predict the load-displacement curves of the PST and UT stress state. As shown in Fig. 16, the load-displacement under PST is well predicted, indicating the distortional hardening at PST is captured. Figure 17 shows the capability of the model to reproduce the load-displacement curves of the UT stress state in the RD, DD and TD. The results indicate that the anisotropic hardening of UT is well captured. In contrast, the distortional hardening model without considering the loading direction can only well predict the load-displacement curve of the UT stress state for the RD.
Discussion
It is commonly observed that when the stacking fault energy (SFE) falls in the narrow range of 15–45 mJ/m2 [39,40,41], TWIP steels deform mainly by dislocation glide and twinning. Twinning acts as an obstacle to dislocation glide, contributing to the high ductility and strength of TWIP steels. As reported by Kim et al. [42] and Kim and De Cooman [41], the TWIP steel used in the present study, Fe–18Mn–0.6 C–1.5Al, has a SFE value around 30 mJ/m2, ensuring the main deformation modes of dislocation glide and twinning at room temperature. Microstructural analysis of deformed samples after UT, PST, and ET revealed variations in twin volume fractions for different strain paths [43]. In addition, it was reported that the twin volume fraction in tension test is larger than in the other two states. The polycrystal plasticity approach, visco-plastic self-consistent (VPSC) model was also adopted to investigate the twinning behaviour, and similar results have been observed, which was considered as the result of texture development. These findings may explain the differential hardening phenomenon introduced in Section 4, as higher twinning tends to increase strain hardening [43].
A lower yield stress in compression is often observed in twin-driven HCP materials [44, 45]. A negative dependence on hydrostatic pressure for TWIP steels is first reported in this paper. A study on a high manganese steel (Fe–33Mn–2.93Al–3Si) has provided insights into the dependence of twinning on grain orientation for tension and compression stress states. This observation may offer an explanation for the negative hydrostatic pressure effect. More details can be found in the references [46, 47]. However, due to the lack of compression tests, the microstructure and texture evolution are unknown yet for the present TWIP980 metal sheets. This is worthy of further investigation.
The proposed distortional hardening model in Section 4 successfully describes a negative dependence on hydrostatic pressure in order to capture the relatively lower yield stresses and hardening rate at the pure shear stress state, as illustrated in Fig. 9. However, this is not the case for the distortional hardening model in Section 5, as shown in Fig. 15, because the pure shear state was not considered. To enable the distortional hardening model considering the loading direction of UT to capture the pure shear stress state, further improvement is necessary. One feasible method involves dividing the full stress space into two domains, each described by a 3D evolutionary anisotropic yield function based on the S-Y2009 model. This allows the functions to blend at the UT stress state, capturing anisotropic hardening under UT. The evolutionary coefficients in each part can be identified using either PST or PS stress state, thereby capturing the stress evolution at the two stress states. The detailed analysis and illustration of the yield surfaces blending method will be reported in future work.
Moreover, to enhance the model’s universality and applicability, the inclusion of additional stress states is recommended by introducing extra coefficients to the existing model. This extension allows the model to cover a broader range of stress triaxiality, and this enhancement has already been accomplished and is currently awaiting submission. In practical applications of the distortional hardening model in metal forming processes, the calibration of the model is particularly sensitive to the dominant stress states during plastic deformation, and these selected stress states may vary from case to case. For example, it’s suggested that ET, PST, UT, and PS should be selected when calibrating the distortional hardening model for the deep drawing of a cross-cup [48] whereas PST, plane strain compression should be considered in roll forming simulations.
Conclusions
In this study, the distinct true stress-strain curves under UT, PST and PS stress states for the TWIP980 steel were identified from the inverse engineering method and modeled by associating with one reference stress-strain curve. A distortional hardening model without considering the loading direction was proposed to explain the differential hardening among UT, PST and PS along a specific direction. Both the differential hardening between UT and PST and the anisotropic hardening under UT were modeled by the distortional hardening model considering the loading direction of UT. Both models were implemented into FEA and compared with the experimental results. The primary conclusions are summarized as follows:
-
(a)
Under proportional loading, variations in loading stress states and the loading directions contribute to the distortion of yield surfaces.
-
(b)
The TWIP980 steel sheet exhibits notable differential hardening behaviours, which cannot be explained by an isotropic hardening model. The proposed distortional hardening model effectively accommodate stress states of UT, PST and PS on the same plastic work contours during plastic deformation. Besides, a negative dependence on hydrostatic pressure is observed for TWIP980 sheet metal.
-
(c)
The distortional hardening model considering the loading direction of UT successfully represents loading direction-dependent true stress-strain curves under UT stress and stress triaxiality-dependent true stress-strain curves between UT and PST stress states along the RD for TWIP980 steel.
References
Ahn K (2020) Plastic bending of sheet metal with tension/compression asymmetry. Int J Solids Struct 204–205:65–80. https://doi.org/10.1016/j.ijsolstr.2020.05.022
Kumar MA, N’souglo KE, Hosseini N et al (2022) Theoretical predictions of dynamic necking formability of ductile metallic sheets with evolving plastic anisotropy and tension-compression asymmetry. Int J Mater Form 15:51. https://doi.org/10.1007/s12289-022-01696-2
Kuroda M, Tvergaard V (2000) Forming limit diagrams for anisotropic metal sheets with different yield criteria. Int J Solids Struct 37:5037–5059. https://doi.org/10.1016/S0020-7683(99)00200-0
Cauvin L, Raghavan B, Jin J et al (2022) Investigating the plastic anisotropy and hardening behavior of a commercial Zn–Cu–Ti alloy: experimental & modeling approach. Mech Mater 164:104103. https://doi.org/10.1016/j.mechmat.2021.104103
Hill R, Hutchinson JW (1992) Differential hardening in sheet metal under Biaxial Loading: a theoretical Framework. J Appl Mech 59:S1–S9. https://doi.org/10.1115/1.2899489
Hill R, Hecker SS, Stout MG (1994) An investigation of plastic flow and differential work hardening in orthotropic brass tubes under fluid pressure and axial load. Int J Solids Struct 31:2999–3021. https://doi.org/10.1016/0020-7683(94)90065-5
Kuwabara T, Ikeda S, Kuroda K (1998) Measurement and analysis of differential work hardening in cold-rolled steel sheet under biaxial tension. J Mater Process Technol 80–81:517–523. https://doi.org/10.1016/S0924-0136(98)00155-1
Wu K (2022) Ductile fracture with distortional hardening under the non-proportional loadings. PhD Thesis, Deakin University. https://doi.org/10.13140/RG.2.2.23684.71041
Stoughton TB, Yoon JW (2009) Anisotropic hardening and non-associated flow in proportional loading of sheet metals. Int J Plast 25:1777–1817. https://doi.org/10.1016/j.ijplas.2009.02.003
Chen Z, Wang Y, Lou Y (2022) User-friendly anisotropic hardening function with non-associated flow rule under the proportional loadings for BCC and FCC metals. Mech Mater 165:104190. https://doi.org/10.1016/j.mechmat.2021.104190
Tozawa Y (1978) Plastic deformation behavior under conditions of combined stress. In: Koistinen DP, Wang N-M (eds) Mechanics of sheet metal forming. Premium Publishing Corporation, New York, pp 81–110
Kuwabara T, Mori T, Asano M et al (2017) Material modeling of 6016-O and 6016-T4 aluminum alloy sheets and application to hole expansion forming simulation. Int J Plast 93:164–186. https://doi.org/10.1016/j.ijplas.2016.10.002
Iftikhar CMA, Li YL, Kohar CP et al (2021) Evolution of subsequent yield surfaces with plastic deformation along proportional and non-proportional loading paths on annealed AA6061 alloy: experiments and crystal plasticity finite element modeling. Int J Plast 143:102956. https://doi.org/10.1016/j.ijplas.2021.102956
Iftikhar CMA, Khan AS (2021) The evolution of yield loci with finite plastic deformation along proportional and non-proportional loading paths in an annealed extruded AZ31 magnesium alloy. Int J Plast 143:103007. https://doi.org/10.1016/j.ijplas.2021.103007
Pham QT, Lee MG, Suk Kim Y (2020) Distortional hardening behavior and strength different effect of pure Titanium Grade 1 sheets: experimental observation and constitutive modeling. IOP Conf Ser Mater Sci Eng 967:012052. https://doi.org/10.1088/1757-899X/967/1/012052
Yoshida F, Hamasaki H, Uemori T (2015) Modeling of anisotropic hardening of sheet metals including description of the Bauschinger effect. Int J Plast 75:170–188. https://doi.org/10.1016/j.ijplas.2015.02.004
Bandyopadhyay K, Basak S, Prasad KS et al (2019) Improved formability prediction by modeling evolution of anisotropy of steel sheets. Int J Solids Struct 156–157:263–280. https://doi.org/10.1016/J.IJSOLSTR.2018.08.024
Hill R (1948) A theory of the yielding and plastic flow of anisotropic metals. Proc R Soc Lond Math Phys Sci 193:281–297. https://doi.org/10.1098/rspa.1948.0045
Lee E-H, Stoughton TB, Yoon JW (2017) A yield criterion through coupling of quadratic and non-quadratic functions for anisotropic hardening with non-associated flow rule. Int J Plast 99:120–143. https://doi.org/10.1016/j.ijplas.2017.08.007
Hu Q, Yoon JW, Manopulo N, Hora P (2021) A coupled yield criterion for anisotropic hardening with analytical description under associated flow rule: modeling and validation. Int J Plast 136:102882. https://doi.org/10.1016/j.ijplas.2020.102882
Soare S, Yoon JW, Cazacu O (2008) On the use of homogeneous polynomials to develop anisotropic yield functions with applications to sheet forming. Int J Plast 24:915–944. https://doi.org/10.1016/j.ijplas.2007.07.016
Ahn DC, Yoon JW, Kim KY (2009) Modeling of anisotropic plastic behavior of ferritic stainless steel sheet. Int J Mech Sci 51:718–725. https://doi.org/10.1016/j.ijmecsci.2009.08.003
Ahn K, Seo M-H (2018) Effect of anisotropy and differential work hardening on the failure prediction of AZ31B magnesium sheet at room temperature. Int J Solids Struct 138:181–192. https://doi.org/10.1016/j.ijsolstr.2018.01.011
Hu Q, Yoon JW (2021) Analytical description of an asymmetric yield function (Yoon2014) by considering anisotropic hardening under non-associated flow rule. Int J Plast 140:102978. https://doi.org/10.1016/j.ijplas.2021.102978
Mattiasson K (2005) On the influence of the yield locus shape in the simulation of sheet stretch forming. In: AIP Conference Proceedings. AIP, pp 395–400
Flores P, Duchene L, Bouffioux C et al (2007) Model identification and FE simulations: Effect of different yield loci and hardening laws in sheet forming. Int J Plast 23:420–449. https://doi.org/10.1016/j.ijplas.2006.05.006
Pilthammar J, Banabic D, Sigvant M (2021) BBC05 with non-integer exponent and ambiguities in Nakajima yield surface calibration. Int J Mater Form 14:577–592. https://doi.org/10.1007/s12289-020-01545-0
Vegter H, van den Boogaard AH (2006) A plane stress yield function for anisotropic sheet material by interpolation of biaxial stress states. Int J Plast 22:557–580. https://doi.org/10.1016/j.ijplas.2005.04.009
Peng F, Dong X, Tian X et al (2015) An interpolation-type orthotropic yield function and its application under biaxial tension. Int J Mech Sci 99:89–97. https://doi.org/10.1016/j.ijmecsci.2015.05.008
Hao S, Dong X (2020) Interpolation-based plane stress anisotropic yield models. Int J Mech Sci 178:105612. https://doi.org/10.1016/j.ijmecsci.2020.105612
Lou Y, Zhang S, Yoon JW (2020) Strength modeling of sheet metals from shear to plane strain tension. Int J Plast 134:102813. https://doi.org/10.1016/j.ijplas.2020.102813
Zhang S, Lou Y, Yoon JW (2023) Earing prediction with a stress invariant-based anisotropic yield function under non-associated flow rule. Int J Mater Form 16:25. https://doi.org/10.1007/s12289-023-01749-0
Lou Y, Huh H (2013) Prediction of ductile fracture for advanced high strength steel with a new criterion: experiments and simulation. J Mater Process Technol 213:1284–1302. https://doi.org/10.1016/j.jmatprotec.2013.03.001
Merklein M, Biasutti M (2011) Forward and reverse simple shear test experiments for material modeling in forming simulations. In: Proceedings of the 10th International Conference on Technology of Plasticity, pp 702–707
Barlat F, Becker RC, Hayashida Y et al (1997) Yielding description for solution strengthened aluminum alloys. Int J Plast 13:385–401. https://doi.org/10.1016/S0749-6419(97)80005-8
Chung K, Lee M-G, Kim D et al (2005) Spring-back evaluation of automotive sheets based on isotropic-kinematic hardening laws and non-quadratic anisotropic yield functions. Int J Plast 21:861–882. https://doi.org/10.1016/j.ijplas.2004.05.016
Choi H, Yoon JW (2019) Stress integration-based on finite difference method and its application for anisotropic plasticity and distortional hardening under associated and non-associated flow rules. Comput Methods Appl Mech Eng 345:123–160. https://doi.org/10.1016/j.cma.2018.10.031
Yoshida F, Hamasaki H, Uemori T (2013) A user-friendly 3D yield function to describe anisotropy of steel sheets. Int J Plast 45:119–139. https://doi.org/10.1016/j.ijplas.2013.01.010
Jeong JS, Woo W, Oh KH et al (2012) In situ neutron diffraction study of the microstructure and tensile deformation behavior in Al-added high manganese austenitic steels. Acta Mater 60:2290–2299. https://doi.org/10.1016/j.actamat.2011.12.043
Shterner V, Molotnikov A, Timokhina I et al (2014) A constitutive model of the deformation behaviour of twinning induced plasticity (TWIP) steel at different temperatures. Mater Sci Eng: A 613:224–231. https://doi.org/10.1016/j.msea.2014.06.073
Kim J-K, De Cooman BC (2016) Stacking fault energy and deformation mechanisms in Fe-xMn-0.6 C-yAl TWIP steel. Mater Sci Eng: A 676:216–231. https://doi.org/10.1016/j.msea.2016.08.106
Kim J, Lee S-J, De Cooman BC (2011) Effect of Al on the stacking fault energy of Fe–18Mn–0.6 C twinning-induced plasticity. Scr Mater 65:363–366. https://doi.org/10.1016/j.scriptamat.2011.05.014
Weiss M, Mester K, Taylor A, Stanford N (2018) A critical assessment of deformation twinning and epsilon martensite formation in austenitic alloys during complex forming operations. Mater Charact 145:423–434. https://doi.org/10.1016/j.matchar.2018.09.003
Cazacu O, Plunkett B, Barlat F (2006) Orthotropic yield criterion for hexagonal closed packed metals. Int J Plast 22:1171–1194. https://doi.org/10.1016/j.ijplas.2005.06.001
Yoon JW, Lou Y, Yoon J, Glazoff MV (2014) Asymmetric yield function based on the stress invariants for pressure sensitive metals. Int J Plast 56:184–202. https://doi.org/10.1016/j.ijplas.2013.11.008
Meng L, Yang P, Xie Q et al (2007) Dependence of deformation twinning on grain orientation in compressed high manganese steels. Scr Mater 56:931–934. https://doi.org/10.1016/j.scriptamat.2007.02.028
Mohammadzadeh R (2019) Deformation characteristics of nanocrystalline TWIP steel under uniaxial tension and compression. Mech Mater 138:103147. https://doi.org/10.1016/j.mechmat.2019.103147
Brosius A, Küsters N, Lenzen M (2018) New method for stress determination based on digital image correlation data. CIRP Ann 67:269–272. https://doi.org/10.1016/j.cirp.2018.04.026
Acknowledgements
This work was supported by ARC Training Center of IC220100028 in Australia. Also, this work is partially supported by Basic and Applied Basic Research Foundation of Guangdong Province (2022A1515010363), and Shenzhen Science and Technology Program (JCYJ20210324122803009). The authors also would like to thank Prof. Qi Hu from Shanghai Jiaotong University for a valuable discussion on distortion hardening models.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no known financial or personal relationships with other people or organizations that could have appeared to inappropriately influence the work reported in this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wu, K., Zhang, S., Weiss, M. et al. Modeling of distortional hardening including plane strain tension and pure shear for a TWIP steel. Int J Mater Form 17, 37 (2024). https://doi.org/10.1007/s12289-024-01835-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12289-024-01835-x