1 Introduction

When initiating a turn, snowboarders lean their body weight over the edge of the snowboard, thus tilting it over and setting the carving angle. The concave sidecut geometry naturally engages the snowboard in the turn, intuitively setting the carving trajectory. Shorter sidecut radii tend to engage more rapidly in the turn, whereas longer radii lead to wider trajectories [1]. The sidecut line (geometry of the edge along the snowboard’s length) is often defined as the arc of a circle (referred to as “constant sidecut radius” geometry), with the idea of matching the carving trajectory [2]. However, bending and twist deformations of the structure during the turn lead to non-uniform deformations of the sidecut line, and must be accounted for. Besides, the underlying mechanics revealed the existence of contact pressure occurring at the interface between the snowboard edge and the snow, which is thought to be an important factor in the riding behaviour [3]. The pressure distribution directly relates to the sidecut geometry of the snowboard [4], among other factors like its camber profile [5] and stiffness distribution [6].

Determining the deformed state and the interface loads occurring on a snowboard during a carved turn poses a direct problem. Reciprocally, determining an initial geometry that leads to a specific interface loads corresponds to the inverse problem. In simple analytical representations, inversing the constitutive equation leads to elliptic integrals that can not be expressed in terms of elementary functions [4]. In numerical representations, methods involving discretization of the structure are often employed [7,8,9], where the inclusion of frictional contact requires iterative nonlinear solving procedures, also preventing access to derivative information.

In this perspective, optimizing the design variables of a snowboard undergoing the loading conditions of a carved turn is not straightforward. If information about the derivatives of the contact pressure function is unavailable, derivative-free algorithms might be employed to approach optimal solutions. Such methods include global search algorithms [10], evolutionary algorithms such as genetic algorithms [11], or direct search algorithms [12] such as the broadly used Nelder–Mead simplex method [13]. These iterative methods minimize an objective function that needs no explicit relationship to the input parameters. Through successive attempts, the algorithm travels down the map of the system response surface, converging towards an optimal solution. The flipside of such methods is that there exists no guarantee of finding a global optimum: following the path of steepest descent does not always lead to the bottom of the valley.

In this study, we considered the general inverse problem of determining the design parameters that lead to a pre-defined deformed state of a snowboard undergoing a carved turn. In particular, if a given contact pressure distribution between the edge and the snow is wished, how should the sidecut geometry be defined respectively? In previous work investigating a snowboard with constant sidecut radius geometry [8], strong discontinuities in the contact pressure distribution were observed, suggesting opportunities for improvement. These previous results were considered as a starting point for the optimization described in this study. As it is not yet established which pressure distribution provides an ideal riding experience, the particular case of a sidecut geometry leading to a uniform contact pressure along the sidecut line was investigated. In Sect. 2, the specimen considered is described together with the parametric representation of the sidecut geometry. Details about the finite element computations and the validation strategy are also provided. In Sect. 3, the optimization procedure conducted numerically is further described. In Sect. 4, the optimization results are presented along with the experimental results. Finally, the implications of the results are discussed and some conclusions are drawn.

2 Geometric modeling and structural analysis

2.1 Snowboard investigated

Fig. 1
figure 1

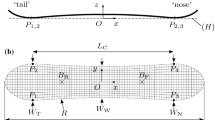
Geometrical representation of the snowboard investigated, defined as symmetric twin-tip. a Side view. b Top view. The description and value of each parameter is given in Table 1

Full size image

The simplified snowboard structure described in previous work [8] was considered (Table 1). The basis for the geometrical description involved additional conventions (naming of the points along the sidecut line) and is recalled in this section for clarity (Fig. 1). \(B_{\mathrm{R}}\) and \(B_{\mathrm{F}}\) indicate the position of the rear and front bindings, respectively. The geometry was defined as symmetric twin-tip (two planes of symmetry: xz-plane and yz-plane) and enforced a concave sidecut line such that the width was narrower at the waist than at the tips (\(W_{\mathrm{w}}<W_{\mathrm{t}}\)). The radius of the imaginary circle passing through T, M and N is referred to as the average sidecut radius \(R_{{\mathrm{avg}}}\). In previous work [8], a constant sidecut radius geometry was considered, such that the sidecut line described the arc of a circle. In this study, other types of curves were investigated (see Sect. 2.2). A flat camber profile was considered, such that T, M and N lied within the xy-plane.

Table 1 Geometrical parameters of the snowboard investigated, taken from [8]
Full size table

The structure of the snowboard consisted of a 5.55 mm constant thickness wood core made out of ash and poplar, sandwiched between two composite skins made out of epoxy reinforced tri-axial fiberglass (each 0.665 mm thick). No metallic edges were considered. Details on the stacking sequence and material properties are given in Online Resource 1.

2.2 Sidecut representation

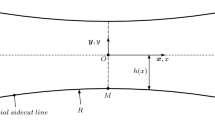
The sidecut line spanned between T and N and passed through M (Fig. 1). Since the board was defined as a symmetric twin-tip, the sidecut could be entirely described by the arc \(\overset{\frown }{TM}\). Typically, the sidecut line can follow the arc of a circle, but more advanced curvature distributions can be obtained using other mathematical representations of the sidecut line. This paper focuses on the study of polynomials [4], and particularly B-spline curves which are piecewise overlapping polynomial interpolation curves, defined by a set of n control points that do not necessarily lie on the curve. The position of these control points is rather interpolated by underlying basis functions, defined according to the Cox–de Boor recursion formula [14]. A higher degree of the basis polynomials describe more complex geometries, whereas an increasing number of control points provides a refined local control by “stitching” additional polynomials segments together. In parametric representations, local control implies reducing the inter-dependency between the design parameters, which smoothens the system response surface. This property makes B-splines particularly well suited for use in direct search optimization methods [15].

Fig. 2
figure 2

The B-spline describing the geometry of the sidecut arc (thick black line). The end-points T, M were fixed, and the curvature distribution was influenced by the position of the control points \(C_1\ldots C_5\). The control polygon is represented by the dashed line

Full size image

With regards to the study on the kinematics of a concave sidecut line deformed on a flat surface [4], the uniform quintic B-spline with clamped conditions was considered to represent the sidecut arc geometry with enough degree of flexibility. Seven control points are defined \(C_0=T\), \(C_1\ldots C_5\), \(C_6=M\), which position in the xy-plane was set by the nine design parameters \({\varvec{u}}=\lbrace {x_i\in {\mathbb {R}}\,|\,i=1,\ldots ,5}\rbrace \cup \lbrace {y_i\in {\mathbb {R}}\,|\,i=1,\ldots ,4}\rbrace\) as presented in Fig. 2. More details on the parametric equations of B-splines can be found in [14]. Note that, due to the symmetry condition and to preserve curvature continuity along the sidecut line, \(C_5\) and M were set to have the same vertical position, thus leading to a horizontal tangent at the mid-point M.

2.3 Finite element analysis

The snowboard geometry and structure were idealized in a finite element model representing the static conditions of a carved turn (Fig. 3). The model was based on previous work [8], and only the key details are summarised here. General-purpose shell elements (3 and 4 nodes) accounting for finite membrane strain were used to represent the composite structure. The laminated construction was captured in the element formulation such that each ply is represented independently. The mesh was generated automatically to account for the different sidecut geometries created along the optimization process. With an element size of about \(10\times 10\) mm, the model contained 4500 elements and about 30,000 degrees of freedom. The different materials were represented with linear elastic properties, detailed in Online Resource 1.

Fig. 3
figure 3

Static idealization of a carved turn. a Experimental set-up: the pressure measurement film inserted under the edge of the snowboard prior to the experiment is visible (white sheet on the picture, see Sect. 2.4). b Finite element model representation

Full size image

To compare the optimization outcome with existing results, the loading conditions of the static load bench developed in [8] were considered. In this previous work, the contact pressure was reported for a tilt angle \(\overline{\theta }=55^\circ\) (corresponding to a rotation about the x-axis introduced at the binding locations) and a vertical loading \(F=588.6\) N corresponding to 60 kg (Fig. 3). These parameters were, therefore, considered in this study, and introduced symmetrically via the two reference nodes \(R_{\mathrm{R}}\) and \(R_{\mathrm{F}}\) positioned relatively to the snowboard at the virtual center of mass of the experimental system. These reference nodes were coupled with the binding interface nodes via distributed coupling constraints, where the displacements and rotational degrees of freedom of the reference nodes were coupled to the mean displacements of the binding interface nodes, thus introducing the loading into the structure. A rigid body plate was considered to simulate the contact to the ground, and a friction coefficient of 0.4 [16] was assumed at the interface between the composite edge of the snowboard and the fixed aluminum plate (Fig. 3). The analysis was conducted with the finite element software Abaqus®  Academic Research release 6.13-2 on a 4-cores processor Intel® i7-6700 at 3.40 GHz platform with a maximum RAM memory of 16 GB.

2.4 Experimental validation

To validate the outcome of the optimization experimentally, an actual snowboard prototype similar to [8] was made in our laboratory. The only difference was the shape of the sidecut line, which described the optimized geometry rather than a constant sidecut radius. The outline was machined with a milling cutter, guided by a laser cut template (the repeat accuracy of the laser was \(\pm 0.05\) mm). The prototype was exposed to the aforementioned loading conditions of the static load bench (Fig. 3), where the interface contact pressure was measured with the use of a Prescale pressure measurement film [17] (pressure range 0.5–2.5 MPa) inserted between the edge of the snowboard and the aluminum contact plate. When pressure is applied, the measurement film turns red with the color intensity depending on the applied pressure. The resulting colored film was scanned and the color densities converted into pressure units for each pixel, according to a given scale. The values thus obtained were averaged over the y-direction, hence resulting in a scattered distribution along the x-direction. The measurement error of such films is reported to be approximately 10–15% for low contact pressure gradients [18], and is, therefore, recommended for qualitative estimations rather than quantitative assessments. The experiment was conducted three times with the same settings, to give an indication of the repeatability of the measurements and increase confidence in the results. Even though the loading was rapidly introduced during the experiment (the weight rings in Fig. 3 were positioned on the static load bench within a couple of seconds), the pressure measurement film imprints instantaneously, and the measurements, therefore, reflected the entire loading history (maximum values reached at a given location). For this reason, the finite element model was used to assess the evolution of the contact pressure distribution as the applied force progressively increased. The experimental results are shown together with the numerical predictions in Sect. 4.

3 Optimization strategy

The optimization described in this section was conducted numerically via the finite element model (see Sect. 2.3).

3.1 Design variables

The parameters that can be varied to improve the design are called design variables. In the present case, the design variables were the B-spline parameters describing the sidecut geometry (see Sect. 2.2). The design vector was denoted \({\varvec{u}}\) and was defined as the set of all B-spline parameters:

$$\begin{aligned} {\varvec{u}}=\lbrace {x_i\in {\mathbb {R}}\,|\,i=1,\ldots ,5}\rbrace \cup \lbrace {y_i\in {\mathbb {R}}\,|\,i=1,\ldots ,4}\rbrace . \end{aligned}$$
(1)

The target of the optimization process was to find the design vector \({\varvec{u^*}}\) that optimizes the interface contact pressure distribution. In the following, the term “optimum”, therefore, refers to the design leading to the best approximation of a uniform contact pressure, regardless to its carving performance on the mountain.

3.2 Objective function

The objective function \(f({\varvec{u}})\) is a mathematical function expressed in terms of the design vector \({\varvec{u}}\), which quantifies the performance of a given sample and allows to compare the different alternative designs. Let \({\varvec{p}}=\lbrace {p_i\in {\mathbb {R}}\,|\,i=1,\ldots ,k}\rbrace\) represent the set of results extracted from the finite element simulation of a given sample, where \(p_i\) is the nodal contact pressure and k the total number of nodes along the sidecut line. The deviation of the normalized pressure vector \({\varvec{{\hat{p}}}}\) to a constant profile was quantified by the root mean square error:

$$\begin{aligned} f({\varvec{u}})=\sqrt{\frac{1}{k}\sum _{i=1}^k{(\hat{p_i}-1)}^2}. \end{aligned}$$
(2)

Since the contact pressure is a positive scalar value, the normalized contact pressure was comprised between 0 and 1, and so was the value of the objective function. A value of \(f({\varvec{u}})=0\) would mean that the contact pressure reached a perfectly uniform distribution, whereas a value of \(f({\varvec{u}})=1\) quantifies the worst design. With the optimization procedure, the goal was, therefore, to minimize the objective function value.

3.3 Optimization procedure

Due to the variable width and thickness profiles along the snowboard’s length, structural bending stiffness and torsion generally consist of higher-order functions which can not be integrated analytically [4]. In numerical computations, the inclusion of frictional contact between the snowboard and the ground requires iterative nonlinear solving procedures, preventing direct access to derivative information. For these reasons, a derivative-free procedure was implemented to search the design space for an optimum sidecut configuration. The present optimization problem was formulated as follows:

Given

  • \({\varvec{u}}\) the design vector

  • \(f({\varvec{u}})\) the objective function.

Find \({\varvec{u}}^*\) such that

  • \({\varvec{u}}^* = \mathop {\mathrm {argmin}}\limits \limits _{{\varvec{u}}} f({\varvec{u}}).\)

The optimization was conducted without constraints, which means that the design variables were free to evolve outside the variation interval of the initial population. As a result, unfeasible designs such as self-intersecting sidecut geometries could emerge, possibly leading to non-convergence of the finite element analysis. A penalty strategy was, therefore, considered: whenever a design was considered unfeasible (non-invertible sidecut functions), a large number was assigned to the objective function value (\(f_{\mathrm{penalty}}>1.0\)) to artificially signalize a poor region of the design space, thus redirecting the algorithm towards feasible regions [19].

3.3.1 Initial population

Gradient-free optimization procedures require an initial guess as a starting point. Since the optimal sidecut configuration was supposedly unknown, the initial guess consisted in a sidecut line approximating the arc of a circle of radius \(R_{{\mathrm{avg}}}\). The method used to approximate the arc of a circle using B-Splines is documented in [20]. The design parameters of the initial guess were first varied within a given variation interval, to randomly create an initial population of 60 samples. The best candidates among the initial population were then fed to the optimization algorithm. The design variables of the initial guess and the chosen variation intervals are given in Table 2.

Table 2 Design vector \({\varvec{u}}_0\) of the initial guess, variation ranges for the initial population and optimum design vector \({\varvec{u^*}}\) (dimensionless)
Full size table

Latin Hypercube Sampling ensures an even distribution of the sampled points through the design space, filling a grid on the basis of equal probability size. It covers regions possibly important at the start of the optimization process [21]. Random shuffling of the input parameters is performed until the maximum correlation between each random vector falls below a given convergence threshold, thus ensuring statistical independence among the input variables.

3.3.2 Nelder–Mead algorithm

The Nelder–Mead simplex algorithm is a classical yet powerful local descent algorithm, making no use of the objective function derivatives [13]. A simplex is a geometrical figure defined, in m dimensions, by \((m+1)\) points \({\varvec{v}}_0,\ldots ,{\varvec{v}}_m\) called vertices. Each vertex represents a unique design vector (see Sect. 3.1) with a corresponding sidecut geometry. By evaluating the objective function at each vertex, a ranking is performed such that the “best” vertex features the lowest objective function value, while “worst” qualifies the vertex with the highest objective function value. Through a sequence of elementary geometric transformations (reflection, contraction, expansion and reduction), the Nelder–Mead algorithm endeavors to continuously improve the worst vertex based on the current simplex configuration, thus ultimately converging towards an optimum singularity. More details on the procedure and the effect of dimensionality are given in [22]. A termination criteria is implemented to stop the procedure after a given convergence threshold was reached, i.e. when the variation of each design variable and the improvement of the objective function value fell below 1%.

4 Results

The objective function value of the initial guess was \(f_{0}=0.880\). The average value over the initial population was \(\overline{f}_{{\mathrm{init}}}=0.729\), which already constituted an improvement of 17%. Along the optimization process, convergence was obtained after 439 analysis runs for a total computational time of 38 h. The objective function reached a minimum value of \(f_{{\mathrm{opt}}}=0.179\) for sample 435, which represents a final improvement of about \(80\%\) (Fig. 4).

Fig. 4
figure 4

Evolution of the objective function value along the optimization process

Full size image

The explored map of the system response surface was represented in the form of a colored scatter plot (Fig. 5). The optimum values of the design variables are reported in Table 2.

Fig. 5
figure 5

Optimum design geometry. The final sidecut arc is represented by the thick black line, along with the corresponding position of the control points. The underlying thin grey lines represent the various design geometries explored along the optimization process. The colored scatter plot illustrates the various positions of the control points investigated during the optimization process, together with their respective color-scaled objective function value \(f({\varvec{u}})\) (color figure online)

Full size image

The contact pressure per unit length resulting from optimum sample 435 was converted in surface pressure and is shown in Fig. 6, together with the numerical results of previous work [8] relating to a constant sidecut radius geometry. For comparison purpose, the optimization target corresponding to the uniform profile aimed for (\(\overline{p}_{{\mathrm{target}}}=0.819\) MPa) is also shown in Fig. 6.

Fig. 6
figure 6

Numerical results: optimum contact pressure distribution \({\varvec{p}}_{{\mathrm{opt}}}\) (blue line) and optimization target \({\varvec{p}}_{{\mathrm{target}}}\) (golden line). The pressure profile \({\varvec{p}}_{{\mathrm{init}}}\) resulting from a constant sidecut radius geometry [8] is shown for comparison (dotted red line) (color figure online)

Full size image

The history of the contact pressure distribution as the applied weight progressively increased is shown in Fig. 7 (numerical results). For intermediate loading, higher pressure peaks were observed close to the sidecut extremities, before the entire edge line contacted with the ground. The final envelope of the numerical results was, therefore, considered for the comparisons with the experimental measurements, shown in Fig. 8. For comparison purpose, the experimental measurements taken from previous work [8] relating to a constant sidecut radius geometry are also shown on Fig. 8, where a Prescale film with a higher pressure range was used (2–10 MPa).

Fig. 7
figure 7

Evolution of the contact pressure distribution with an increasing loading (finite element simulation results). To reflect the loading history, the experimental results were compared with the final envelope (filled in grey)

Full size image
Fig. 8
figure 8

Comparison of the experimental results (scatter plots for the three trials) with the numerical predictions (envelope over the entire loading history). The experimental results from previous work [8] relating to a constant sidecut radius geometry are also shown for comparison purpose

Full size image

5 Discussion

Considering the original constant sidecut radius geometry and the numerical results of the optimization, the maximum pressure peak dropped from \(p_{{\mathrm{init}}}^{{\mathrm{max}}}=5.287\) MPa to \(p_{{\mathrm{opt}}}^{{\mathrm{max}}}=0.947\) MPa (Fig. 6), which constitutes a reduction of 82%. The resulting pressure profile was not perfectly uniform and oscillated around the target value of \(\overline{p}_{{\mathrm{target}}}=0.819\) MPa with a standard deviation to a constant pressure profile of \(\sigma _p=0.112\) MPa \((\varepsilon _{\mathrm{std}}=13.7\%).\)

The three experimental measurements performed under identical conditions showed similar distributions and amplitudes of the interface contact pressure, suggesting the repeatability and thus increasing the confidence in the results. Some discontinuities were observed on the three imprints, where the pressure locally dropped below the measurement range of the Prescale film (0.5–2.5 MPa).

The numerical predictions and the experimental measurements were in the good overall agreement, showing similar order of magnitude of the interface contact pressure. Some deviations could be observed on the shape of the distributions, locally around the load introduction areas and at the sidecut extremities. These deviations can possibly be explained by the influence of the pressure measurement film during the experiment (altered frictional contact behaviour), the manufacturing precision of the prototype (see Sect. 2.4), and the accuracy of the stiffness estimation (material properties).

In Fig. 7, the history of the loading scenario displays the irregular deployment of the contact pressure with an increasing input force. The pressure distribution showed strong irregularities at lower loading, before it reached an almost constant distribution for the final loading \(F=588.6\) N. Similarly, the contact pressure also relates to the carving angle, and the optimization results are generally dependent on the load case considered. If it seems difficult to achieve a uniform pressure distribution for a wide range of loading parameters, one may identify a particular phase in the turn where a uniform pressure distribution is most beneficial, and perform the optimization accordingly. Alternatively, an objective function defined over the results of several configurations could also be foreseen in further work, to homogenize the contact pressure distribution over a wider range of loading parameters.

To put the sensitivity of the problem into perspective, it is noted that the maximum orthogonal distance between the optimum sidecut line and the original sidecut describing the arc of a circle was \(d_{\mathrm{max}}=1.4\) mm. This difference is barely perceptible to the naked eye on a full-scale geometry, and yet resulting in such a large difference in the contact pressure distribution. The system, therefore, demonstrated a strong sensitivity to small geometrical variations.

6 Conclusions

A novel approach to optimize the contact pressure occurring under the edge of a snowboard during a carved turn was introduced. Parametric B-Splines represented the sidecut geometry, and the contact pressure was assessed for a specific load case by means of finite element analysis. The optimization procedure, consisting in a derivative-free framework, could identify a sidecut geometry leading to near constant pressure distribution, predicting a \(82\%\) reduction of the maximum pressure value in comparison with a constant sidecut radius geometry. An actual snowboard prototype was made considering the numerical results, and validated experimentally with the use of a static load bench. If there exists no evidence that a uniform contact pressure relates to an ideal carving performance on the snow, the optimization process can be used to determine additional specific designs, and future work could be performed to assess the correlation with the riding behaviour. The applicability domain can generally be extended to the optimization of other geometric and structural variables, as long as the assumptions underlying the finite element formulation remain valid.