Mechanics of wedge turns in alpine skiing

Abstract

A simple approximate theory of snow machining is applied to modelling successive wedge turns of alpine skiing. The model involves predefined control functions describing skier’s control over the turns via angle of attack, edge angle and loading of the skis. To demonstrate the model’s potential, reasonable control functions with a small number of free parameters are designed and used in attempt to reproduce the data obtained in a previous field study by other researches. The results are in semi-quantitative agreement with the data. In particular, the model explains the nature of the abnormally high values for the “coefficient of friction” deduced in that study. Future field studies of wedge turns should aim at measuring the angle of attack, edge angle and loading of the skis. This will allow to determine the control functions from the experimental data and hence to conduct a more stringent verification of the model.

1 Introduction

A wedge turn is the first type of turns introduced to students in most schools of alpine skiing. In this turn, skis form a wedge pointing in the direction of motion (see Fig. 1). This increases the braking power of skis and hence allows to keep the speed of descent as low as needed for the students to feel safe and able to focus on improving their technique. The turning action is achieved by preferential loading one of the skis, which leads to turning in the opposite direction. For example, if the skier needs to turn right, then the left ski has to be loaded more than the right ski.

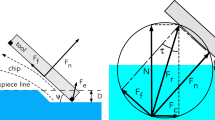
During a wedge turn, both skis are set at an angle to the direction of motion (the angle of attack). As a result, the motion of each ski is a combination of motions along the ski longitudinal axis and perpendicular to it. Moreover, the skis bases are set at an angle to the local slope surface (the edge angle) and the perpendicular motion involves removal of a top layer of snow.¹ Overall, the ski motion becomes very different from simple gliding over the snow surface.

This snow-removal action is similar to the removal of material in the manufacturing process of machining. In this process, the cutting tool is subject to a reaction force from the machined material, which can be considered as a combination of friction and pressure. The pressure force arises mostly at the rake face of the tool, where it pushes the chip out. Its component tangent to the machined surface is called the cutting force. In skiing, the role of the rake face is played by the ski base and hence the cutting force is perpendicular to the ski. It has a component which is opposed to the direction of motion and hence promotes braking. Moreover, it has a component which is perpendicular to the direction of motion, and this component is the reason behind the turning action of skis set at non-vanishing angle of attack.

The machining of snow and ice has been studied in laboratory [1,2,3,4,5]. These authors also derived empirical expressions for the snow reaction force and used them to model skidded ski turns. Moreover, Brown [6] applied to skiing the theory of metal cutting developed in [7] for the case of continuous (type-2) chips. However, snow and ice are highly brittle materials and instead of continuous chip their machining normally results in a spray of ice particles.

Fig. 1

Skier executing left wedge turn. The red line indicates the trajectory of motion (Image courtesy of Canadian Ski Instructors’ Alliance)

Recently, the work of Brown [6] was extended by Komissarov [8], where a simpler theory of snow machining was developed. The main assumptions of this theory are (1) the ski edge is perfectly sharp and (2) the Coulomb friction between the ski and the cut snow is negligibly small. The main advantage is the very simple analytical expressions for the turning and braking components of the cutting force, which in turn allow for rather simple mathematical models of ski manoeuvres involving side-slipping (skidding). In [9], this theory was applied to the side-slipping down the fall line, hockey stop and skidded traversing. The results agreed with skiing practice. Moreover, they allowed to explain the earlier results of the experimental study of traversing by Kaps et al. [10] without invoking of abnormally high, when compared to gliding, values of the kinetic coefficient of friction.

Even higher values for the coefficient of Coulomb friction were obtained by Sahashi and Ichino [11] in their investigation of skidded ski turns. Among several different types of such turns, they explored the wedge turn. This seems to be the only study of wedge turns published so far. Here we apply the theory of snow machining developed in [8] to wedge turns. Our main aim is to investigate whether this model can explain the data by Sahashi and Ichino [11] without resorting to abnormally strong Coulomb’s friction.

2 Methods

2.1 Basic equations

The key forces acting on a skier during a ski run are the gravity force, the snow friction, the snow reaction force, and the aerodynamic drag force. The snow friction is usually low, thanks to the slippery nature of ice, meltwater lubrication, and waxes. Hence, we will assume that the braking action due to the snow cutting component of the snow reaction force is much more important and will ignore the usual friction altogether. The aerodynamic drag force is also low because wedge turns are executed only at rather low speeds. Hence we will ignore the aerodynamic drag as well. As the result of these simplifications, the equation of motion reduces to

$$\begin{aligned} M \frac{{\text {d}} \varvec{v}}{{\text {d}} t} = M \varvec{g}+ \varvec{F}_{\text{r}}, \end{aligned}$$

(1)

where M is the skier mass, $\varvec{v}$ is the skiers velocity, $\varvec{g}$ is the gravitational acceleration vector, and $\varvec{F}_{\text{ r }}$ is the snow reaction force due to its machining by skis. Accounting for the contributions from both skis, we write

$$\begin{aligned} \varvec{F}_{\text{r}}=\varvec{F}_{\text{ r }}^{(l)}+\varvec{F}_{\text{ r }}^{(r)}, \end{aligned}$$

(2)

where “(l)” and “(r)” stand for the left and the right skis respectively. According to our theory of snow machining,

$$\begin{aligned} \varvec{F}_{\text{ r }}^{(i)}=N^{(i)}\tan \Psi ^{(i)}\, \hat{\varvec{n}}_{\text{ s }}^{(i)} +\varvec{N}^{(i)}, \end{aligned}$$

(3)

where $\varvec{N}^{(i)}=N^{(i)}\hat{\varvec{k}}$ is the normal component of the snow reaction force, $\hat{\varvec{k}}$ is the outgoing unit vector normal to the plane of the ski slope, $\hat{\varvec{n}}_{\text{ s }}^{(i)}$ is the unit vector in the plane of the slope which is normal to the edge of the i-th ski and points to the side opposite to the direction of side-slipping, and $\Psi ^{(i)}$ is the edge angle of ith ski [8]. For simplicity, we assume that both the skis and the skier centre of mass (CM) move with the same velocity and denote as $\hat{\varvec{m}}$ the unit vector in the direction of motion. Hence

$$\begin{aligned} \hat{\varvec{n}}_{\text{ s }}^{(i)} = \frac{(\varvec{\hat{\varvec{m}}} \!\times \! \varvec{\hat{\varvec{s}}}^{(i)})\times \hat{\varvec{s}}^{(i)}}{|\varvec{\hat{\varvec{m}}} \!\times \! \varvec{\hat{\varvec{s}}}^{(i)}|}, \end{aligned}$$

(4)

where $\hat{\varvec{s}}^{(i)}$ is the unit vector aligned with the i-th ski. Using Cartesian coordinates with the basis vectors $\hat{\varvec{k}}$ (normal to the ski slope), $\hat{\varvec{i}}$ (parallel to the fall line), and $\hat{\varvec{j}}$ (perpendicular to the other two), we can write

$$\begin{aligned} \nonumber \varvec{g}&=g\sin \alpha \hat{\varvec{i}}-g\cos \alpha \hat{\varvec{k}}\\ \nonumber \hat{\varvec{m}}&=\cos \beta \hat{\varvec{i}}+\sin \beta \hat{\varvec{j}}\\ \hat{\varvec{s}}^{(i)}&=\cos \left( \beta +\gamma ^{(i)}\right) \hat{\varvec{i}}+\sin \left( \beta +\gamma ^{(i)}\right) \hat{\varvec{j}}\\ \nonumber \hat{\varvec{n}}_{\text{ s }}^{(i)}&=\text{ sign }\,\gamma ^{(i)}\left( -\sin (\beta +\gamma ^{(i)})\hat{\varvec{i}}+\cos (\beta +\gamma ^{(i)})\hat{\varvec{j}}\right) , \end{aligned}$$

(5)

where $\alpha$ is the slope inclination angle, $\beta$ is the angle of traverse, and $\gamma$ is the angle of attack. Here we assume that both $\gamma$ and $\beta$ are measured in the counter-clockwise direction as seen from above the slope (see Fig. 2). The reference direction for $\beta$ is $\hat{\varvec{i}}$ and the reference direction for $\gamma$ is $\hat{\varvec{m}}$. Hence $\,\text{ sgn }\,{\gamma ^{(r)}}=+1$ and $\,\text{ sgn }\,{\gamma ^{(l)}}=-1$ (see Fig. 2).

Fig. 2

Key unit vectors and angles in the plane of the ski slope. $\hat{\varvec{i}}$ points in the direction of the fall line and the x axis, $\hat{\varvec{j}}$ is perpendicular to $\hat{\varvec{i}}$ and points in the direction of the y axis, $\hat{\varvec{m}}$ points in the direction of motion and hence the skier velocity $\varvec{v}$. $\beta$ is the angle between the fall line and the direction of motion, the angle of the traverse. $\hat{\varvec{s}}^{(l)}$ and $\hat{\varvec{s}}^{(r)}$ point along the edges of the left and right skis respectively, and $\gamma ^{(l)}$, $\gamma ^{(r)}$ are their angles of attack. $\hat{\varvec{n}}_{\text{ s }}^{(l)}$ is normal to $\hat{\varvec{s}}^{(l)}$ and points to the side opposite to the direction of side-slipping of this ski

If we ignore the up-and-down motion of skier’s CM, then $\hat{\varvec{k}}\cdot {\text {d}}\varvec{v}/{\text {d}}t = 0$, and projecting Eq. (1) on the direction of $\hat{\varvec{k}}$ we find

$$\begin{aligned} N=N^{(l)}+N^{(r)} = Mg\cos \alpha , \end{aligned}$$

(6)

where N is the total normal to the slope component of the snow reaction force, or the total load of the skis. Introducing $A^{(i)}_N=N^{(i)}/N$, the load distribution factor of the i-th ski, we can write

$$\begin{aligned} N^{(i)} = A^{(i)}_{N} Mg\cos \alpha . \end{aligned}$$

(7)

By this definition, $0\le A^{(i)}_N \le 1$ and

$$\begin{aligned} A^{(l)}_N+A^{(r)}_N=1. \end{aligned}$$

(8)

Projecting Eq. (1) onto the slope plane, we obtain

$$\begin{aligned} \frac{1}{g} \frac{{\text {d}} \varvec{v}}{{\text {d}} t} = \sin \alpha \hat{\varvec{i}}+ \cos \alpha \sum _{i=l,r}A^{(i)}_N \tan \Psi ^{(i)}\, \hat{\varvec{n}}_{\text{ s }}^{(i)}. \end{aligned}$$

(9)

Scalar multiplication of this equation with $\hat{\varvec{m}}$ yields the evolution equation for the skier speed

$$\begin{aligned} \frac{1}{g} \frac{{\text {d}} V}{{\text {d}} t} = \sin \alpha \cos \beta - \cos \alpha \sum _{i=l,r} A^{(i)}_N |\sin \gamma ^{(i)}| \tan \Psi ^{(i)}. \end{aligned}$$

(10)

One can also use Eq. (1) to find the evolution equation for the angle of traverse. To this end, we first note that because $\varvec{v}=V\hat{\varvec{m}}$

$$\begin{aligned} V\frac{{\text {d}} \hat{\varvec{m}}}{{\text {d}} t} = \frac{{\text {d}} \varvec{v}}{{\text {d}} t} - \hat{\varvec{m}}\frac{{\text {d}} V}{{\text {d}} t}. \end{aligned}$$

(11)

Substituting into this equation the above expressions for ${{\text {d}}\varvec{v}}/{{\text {d}}t}$ and ${{\text {d}}V}/{{\text {d}}t}$ and projecting the result onto the direction of $\hat{\varvec{i}}$ we obtain

$$\begin{aligned} \nonumber \frac{V}{g} \frac{{\text {d}} \beta }{{\text {d}} t} =&-\sin \alpha \sin \beta \\&+ \cos \alpha \sum _{i=l,r} A^{(i)}_N \,\text{ sgn }\,{\gamma ^{(i)}} \cos \gamma ^{(i)} \tan \Psi ^{(i)}. \end{aligned}$$

(12)

The skier trajectory is governed by the equations

$$\begin{aligned} \frac{{\text {d}} x}{{\text {d}} t} = V \cos \beta , \end{aligned}$$

(13)

and

$$\begin{aligned} \frac{{\text {d}} y}{{\text {d}} t} = V \sin \beta . \end{aligned}$$

(14)

So far, we have four scalar equations (10, 12, 13, and 14) determining the evolution of four dynamic variables: V(t), $\beta (t)$, x(t), and y(t). However, in addition to these variables, the equations involve six more parameters, $A^{(i)}_N$, $\gamma ^{(i)}$, and $\Psi ^{(i)}$, which also vary during ski runs. Their evolution is determined not so much by the laws of mechanics but rather by conscious actions of skiers, and for this reason they can be called control variables.

In the experiments run by Sahashi and Ichino [11], the skier was given a task of executing repetitive and symmetric turns. To achieve such turns, a skier has to aim at synchronising their actions with the variation of $\beta$ in general, and at terminating turns at some chosen extreme values of the angle of traverse $\pm \beta _{\text{ m }}$ in particular. Hence the control variables can be defined as functions of $\beta$. It also is important to differentiate between left and right turns. For example, when turning, a skier puts more weight on their outside ski, which is the left ski for a right turn and the right ski for a left turn. Hence, at the same angle of the traverse, $A^{(l)}_N(\beta )> A^{(r)}_N(\beta )$ for right turns and $A^{(l)}_N(\beta )< A^{(r)}_N(\beta )$ for left turns. Hence, there should be two sets of control functions, one per each turn direction.

This analysis invites to consider using $\beta$ as an independent variable, instead of t, because this simplifies the procedure of switching between the two sets of control functions. The required substitution can be done using Eq. (12) and it yields the equations,

$$\begin{aligned} \frac{{\text {d}} V}{{\text {d}} \beta } = V \,\frac{G}{F}, \end{aligned}$$

(15)

$$\begin{aligned} \frac{{\text {d}} t}{{\text {d}} \beta } = \frac{V}{g} \,\frac{1}{F}, \end{aligned}$$

(16)

$$\begin{aligned} \frac{{\text {d}} x}{{\text {d}} \beta } = \dfrac{V^2}{g}\, \dfrac{\cos \beta }{F}, \end{aligned}$$

(17)

$$\begin{aligned} \frac{{\text {d}} y}{{\text {d}} \beta } = \dfrac{V^2}{g} \dfrac{\sin \beta }{F}, \end{aligned}$$

(18)

where

$$\begin{aligned} G = \sin \alpha \cos \beta - \cos \alpha \sum _{i=l,r} A^{(i)}_N |\sin \gamma ^{(i)}| \tan \Psi ^{(i)}, \end{aligned}$$

(19)

and

$$\begin{aligned} \nonumber F=&-\sin \alpha \sin \beta + \\&+ \cos \alpha \sum _{i=l,r} A^{(i)}_N \,\text{ sgn }\,{\gamma ^{(i)}} \cos \gamma ^{(i)} \tan \Psi ^{(i)}. \end{aligned}$$

(20)

During a left turn, these equations are integrated into the positive direction of $\beta$ (towards the transition point $+\beta _{\text{ m }}$) using the control functions for left turns. At the transition point, the direction of integration is reversed, and the control functions are replaced with those for right turns. The values of V, t, x, and y found at the end of the previous turn become the initial conditions for the next turn. Hence the integration continues towards the transition at $-\beta _{\text{ m }}$, where the direction of integration and the control functions are swapped again, and so on until the desired number of turns is completed.

At the transition between turns, the ski/skier trajectory exhibits a smooth inflection [11]. Accordingly, we adopt the condition ${\text {d}}\beta /{\text {d}}t=0$ at $\beta =\pm \beta _{\text{ m }}$ and hence

$$\begin{aligned} F(\pm \beta _{\text{ m }})=0. \end{aligned}$$

(21)

This implies a singularity in Eqs. (15–18) at $\beta =\pm \beta _{\text{ m }}$. Provided $\pm \beta _{\text{ m }}$ is not a stationary (equilibrium) point and can be reached in finite time (which can be considered as a condition imposed on the control functions), this is only a minor technical disadvantage. The singularity can be avoided by starting and terminating the integration slightly off these extreme values of $\beta$.

Fig. 3

Left panel: The angle of attack function $A^{(l)}_\gamma (\beta )$ (left ski) as determined by Eqs. (24, 25). The arrows indicate the direction of evolution through turns. Right panel: Example of the load distribution functions $A^{(l)}_N$ (solid line) and $A^{(r)}_N$ (dash line) as determined by Eqs. (33, 34). The arrows show the direction of evolution through turns. In right turns $\beta$ decreases and in left turns it increases.

2.2 Control functions

As we have already discussed, the control functions close the dynamical equations of wedge turns by introducing the conscious actions of skiers aimed at controlling their descent down the ski slope. Hence they cannot be specified uniquely based on some general principles and may vary a lot from run to run and even during individual runs. Comprehensive experimental studies can establish these functions for the specific runs under investigation, and thereafter they can be entered into the model to see how well it captures these runs. In the absence of such data, which is the case here, we are forced to invent them. In this process, we are guided by the well established elements of the wedge turn technique.

According to Eq. (12), the turning action of ith ski is proportional to

$$\begin{aligned} A^{(i)}_N \text{ sign }\,\gamma ^{(i)} \cos \gamma ^{(i)} \tan \Psi ^{(i)}. \end{aligned}$$

Hence, it increases with the load of the ski $A^{(i)}_N$, its angle of attack $\gamma ^{(i)}$, and its edge angle $\Psi ^{(i)}$. For the left ski, $\gamma ^{(i)}<0$ and hence it promotes turning to the right (to position with smaller $\beta$). On the contrary, for the right ski $\gamma ^{(i)}>0$ and hence it promotes turning to the left. This conflict between the turning actions of left and right skis is the main difficulty of wedge turns, which has to be mitigated for better performance. The only way to do this is via reduction of the turning action of the inside ski (obstructing the currently executed turn), which can be done by reducing its load, angle of attack, and edge angle. Indeed, this seems to be a common feature of the wedge-turn technique as supported by openly available on YouTube video lessons by qualified ski instructors. Moreover, students are explicitly instructed to keep more weight on the outside ski. The lower angle of attack of the inside ski is also manifest in the data of Sahashi and Ichino [11]. These observations will be used below for designing suitable control functions.

2.2.1 Angle of attack

Throughout the wedge turn, the wedge angle between the skis, $\gamma _{\text{ w }}=\gamma ^{(r)}-\gamma ^{(l)}$, is usually kept approximately the same [e.g. 11]. Hence, it makes sense to put

$$\begin{aligned} \gamma ^{(l)} = -A^{(l)}_\gamma (\beta ) \gamma _{\text{ w }}, \quad \gamma ^{(r)} = A^{(r)}_\gamma (\beta ) \gamma _{\text{ w }}, \end{aligned}$$

(22)

where the functions $A^{(l)}$ and $A^{(r)}$ satisfy the constraint

$$\begin{aligned} A^{(r)}_\gamma (\beta ) +A^{(l)}_\gamma (\beta )= 1. \end{aligned}$$

(23)

According to the study of Sahashi and Ichino [11], the angle of attack of the inside ski is close to zero (in agreement with the analyses above) and hence the angle of attack of the outside ski is close to $\pm \gamma _{\text{ w }}$, with the sign $+$ for the right ski, and the sign − for the left ski. Moreover, the transition phase between turns is rather quick. Based on these observations, we adopt the following simple model:

$$\begin{aligned} A^{(l)}_\gamma (\beta ) = \dfrac{1}{2} - \dfrac{1}{2} \left( 1- \left( \dfrac{\beta }{\beta _{\text{ m }}}\right) ^2 \right) ^{1/2} \end{aligned}$$

(24)

for left turns, and

$$\begin{aligned} A^{(l)}_\gamma (\beta ) = \dfrac{1}{2} + \dfrac{1}{2} \left( 1- \left( \dfrac{\beta }{\beta _{\text{ m }}}\right) ^2 \right) ^{1/2} \end{aligned}$$

(25)

for right turns. One can see that $\gamma ^{(l)}= \gamma ^{(r)}=\gamma _{\text{ w }}/2$ for $\beta =\pm \beta _{\text{ m }}$, and hence at the transition point the ski wedge is symmetric with respect to their direction of motion. The graph of $A^{(l)}_\gamma (\beta )$ is shown in the left panel of Fig. 3.

2.2.2 Edge angle

In wedge turns, the angle between skier’s legs, $\Psi _{\text{ m }}$, is more or less constant. The basic geometrical consideration shows that, for straight legs, flat ski slope, and small wedge angle, $\Psi _{\text{ m }}\approx \Psi ^{(l)}+\Psi ^{(r)}$ (see the left panel of Fig. 4). Hence we may adopt the following model for the ski edging

$$\begin{aligned} \Psi ^{(l)} = A^{(l)}_\Psi (\beta ) \Psi _{\text{ m }}, \quad \Psi ^{(r)} = A^{(r)}_\Psi (\beta ) \Psi _{\text{ m }}, \end{aligned}$$

(26)

where

$$\begin{aligned} A^{(r)}_\Psi (\beta ) +A^{(l)}_\Psi (\beta )= 1. \end{aligned}$$

(27)

Unfortunately, Sahashi and Ichino [11] did not provide any information on the ski edging that could be used to specify the edging functions $A^{(i)}_\Psi (\beta )$. However, our analysis of the conflict between the turning actions of the inside and outside skis and the ways of its mitigation shows that the mitigation is most efficient when the attack and edge angles vary in unison. Hence we simply put

$$\begin{aligned} A^{(i)}_\Psi (\beta ) =A^{(i)}_\gamma (\beta ). \end{aligned}$$

(28)

In this model, (1) $\Psi ^{(l)}= \Psi ^{(r)}=\Psi _{\text{ m }}/2$ at the transition point between turns (at $\beta =\pm \beta _{\text{ m }}$), and (2) in the middle of the turn (at $\beta =0$) $\Psi = \Psi _{\text{ m }}$ for the outside ski and $\Psi =0$ for the inside ski.

To determine a reasonable range for $\Psi _{\text{ m }}$, let us suppose that ski’s head section (from the boot mounting point to the tip) is of the same length as skier’s leg. In the experiments by Sahashi and Ichino [11], the skis were 180 cm long, and the photograph of the skier shown in Figure 1 suggests that this assumption is quite reasonable. If we further assume that the ski tips touch each other, then the geometry of the problem implies $\Psi _{\text{ m }}\simeq \gamma _{\text{ w }}$ (see the middle and right panels of Fig. 4). In reality, the tips are usually kept somewhat apart (see Fig. 1 in [11]), resulting in a larger $\Psi _{\text{ m }}$ compared to $\gamma _{\text{ w }}$. Hence one can use as a guide

$$\begin{aligned} \Psi _{\text{ m }} = \kappa \gamma _{\text{ w }}, \end{aligned}$$

(29)

where $\kappa \gtrsim 1$.

Fig. 4

In these plots, the yellow bars depict skier’s legs and the red pointed planks depict the skis, and the ski slope is coloured in blue. Left panel: View from the front when the wedge angle vanishes. The dashed line is a normal to the ski slope and the ski bases are normal to the corresponding legs. In this case, the angle between the legs $\Psi _{\text{ m }}$ equals the sum of the edge angles $\Psi ^{(l)}+\Psi ^{(i)}$. Middle panel: View from above when the ski tips touch each other. From the equilateral triangle ABC, the distance |BC| between the ski mounting points B and C equals to $2a\sin (\gamma _{\text{ w }}/2)$. Right panel: View from the front when the ski tips touch each other. From the equilateral triangle BCD, the distance |BC| between the ski mounting points B and C equals to $2a\sin (\Psi _{\text{ m }}/2)$, provided the leg length equals to a.

2.2.3 Loading factor

Unfortunately, Sahashi and Ichino [11] did not provide any information on the ski loading too. When searching for suitable load distribution functions, one has to take into account that at the transition between turns ($\beta =\pm \beta _{\text{ m }}$), the angle of traverse function $\beta (t)$ takes extreme values and hence ${\text {d}}\beta /{\text {d}}t=0$. Combining this condition with equations (8, 12), one finds

$$\begin{aligned} A^{(l)}_N = {\left\{ \begin{array}{ll} A_m &{} \quad \text{ for }\quad \beta =\beta _m \\ 1-A_m &{} \quad \text{ for }\quad \beta =-\beta _m, \end{array}\right. } \,, \end{aligned}$$

(30)

where

$$\begin{aligned} A_m= \frac{1}{2}\left( 1- \dfrac{\tan \alpha \sin \beta _m}{\cos \dfrac{\gamma _{\text{ w }}}{2} \tan \dfrac{\Psi _m}{2}} \right) . \end{aligned}$$

(31)

These two equations are constraints of the load distribution function. More constraints appear if we want to control the load distribution elsewhere in the turn. For example, one can chose it to be the relative loading of the outside ski at $\beta =0$, the point where the skier moves in the direction of the fall line

$$\begin{aligned} A^{(l)}_N(0) = A_0. \end{aligned}$$

(32)

In general, three constraints allow to fully specify functions with three parameters, which suggest to approximate the loading function using quadratic polynomials, $A^{(l)}_N(\beta )=a\beta ^2+b\beta +c$. After solving the constraint equations for the coefficients of such polynomial, one finds

$$\begin{aligned} \nonumber A^{(l)}_N(\beta ) =&\left( A_0-\dfrac{1}{2}\right) \left( \dfrac{\beta }{\beta _m}\right) ^2 \\&+\left( A_m-\dfrac{1}{2}\right) \left( \dfrac{\beta }{\beta _m}\right) +1-A_0, \end{aligned}$$

(33)

for left turns, and

$$\begin{aligned} \nonumber A^{(l)}_N(\beta ) =&-\left( A_0-\dfrac{1}{2}\right) \left( \dfrac{\beta }{\beta _m}\right) ^2 \\&+\left( A_m-\dfrac{1}{2}\right) \left( \dfrac{\beta }{\beta _m}\right) +A_0 \end{aligned}$$

(34)

for right turns. This function was used in the simulations described in the next section. It is illustrated in the right panel of Fig. 3.

2.2.4 Suitability of control functions

In principle, a skier may decide to stop turning and continue their motion with a straight traverse. During such a traverse, the angle of traverse is constant and hence all its time derivatives vanish. Hence it is possible to choose such control functions that $\beta =\beta _{\text{ m }}$ is a stationary solution. In this case, other solutions will be able to reach $\beta _{\text{ m }}$ only asymptotically as $t\rightarrow \infty$.

The evolution equation for $\beta (t)$ (Eq. 12) has the form

$$\begin{aligned} \frac{{\text {d}} \beta }{{\text {d}} t} = K(\beta ), \end{aligned}$$

(35)

where $K(\beta ) = g F(\beta )/V(\beta )$ and hence vanishes at $\beta _{\text{ m }}$. If $K(\beta )$ was infinitely differentiable at $\beta _{\text{ m }}$ then all the higher order derivatives would vanish as well, implying that $\beta =\beta _{\text{ m }}$ is a stationary solution. For example,

$$\begin{aligned} \left. \frac{d^2 \beta }{d {t}^2}\right| _{\beta =\beta _{\text{ m }}} = K'(\beta _{\text{ m }}) K(\beta _{\text{ m }})=0 \end{aligned}$$

(36)

if $K'(\beta _{\text{ m }})$ is finite. Hence for $\beta =\beta _{\text{ m }}$ to be a point of transition between turns, $K(\beta )$ must not be infinitely differentiable at this point (The same applies to $\beta =-\beta _{\text{ m }}$.). In fact, such non-differentiability of $K(\beta )$ is ensured by our choice of the control functions for the angle of attack (Eqs. 24 and 25, and the left panel of Fig. 3). It is easy to see that their derivative diverges at $\pm \beta _{\text{ m }}$.

Expanding $K(\beta )$ in the vicinity of $\beta _{\text{ m }}$ in powers of $\zeta =1-\beta ^2/\beta ^2_{\text{ m }}$ leads to

$$\begin{aligned} \frac{{\text {d}} \beta }{{\text {d}} t} = K(\beta ) \simeq A\zeta ^{1/2}, \end{aligned}$$

where $A\ne 0$ is a constant. Integrating this equation with the initial condition $\beta (t_{\text{ m }})=\beta _{\text{ m }}$, one finds the asymptotic solution

$$\begin{aligned} \beta = \beta _m\sin (A(t-t_{\text{ m }})+\pi /2)\,, \end{aligned}$$

which confirms that $\beta _m$ is indeed not a stationary point and can be reached in finite time.

3 Results

In this section, it is investigated how well the above model of wedge turns can reproduce the results of the field study by Sahashi and Ichino [11]. Their experimental data are presented in the form of plots which show the trajectory of skis and the variation of some key parameters with the distance down the fall line—the angle of traverse for the midpoint of the ski wedge, the angles of attack for both the left and the right skis, the speed of the midpoint, “the curvature radius of ski track”, and the effective coefficient of snow friction. These data describe two consecutive turns of a single run.

The effective coefficient of friction was obtained on the basis of the observed acceleration of the midpoint and the model where it is attributed to the competition between the component of the gravity force along the direction of motion and the Coulomb friction. The way the radius of curvature is calculated is not described. Given the fact that in the wedge turn, skis leave a rather wide trail, this introduces a significant degree of uncertainty about this parameter.

The ski slope used in the study had the inclination $\alpha =7^\circ$. Based on the plots, the maximum angle of traverse $\beta _{\text{ m }}=40^\circ$, the wedge angle $\gamma _{\text{ w }} = 20^\circ$ and the skier speed $V\approx 3\,$m/s.

Given our selection of $\beta$ as an independent variable, the computations of the whole ski run split into computations of individual turns. During left turns, $\beta$ increases from $-\beta _{\text{ m }}$ to $+\beta _{\text{ m }}$ and during the right turns it decreases from $+\beta _{\text{ m }}$ to $-\beta _{\text{ m }}$. Because $F(\pm \beta _{\text{ m }})=0$, the integrated Eqs. (15)–(18) are singular at the turning points. To avoid the singularity, the numerical integrations of these equations begins and terminates at $\beta =\pm 0.9999\beta _{\text{ m }}$. The parameters found at the end of the previous turn determine the initial conditions for the next turn. The initial conditions for the whole run are $\beta =-0.9999\beta _{\text{ m }}$, $V=V_0=3\,$m/s, $x=0$, and $y=0$.

With $\beta _{\text{ m }}$, $\gamma _{\text{ w }}$, and $V_0$ immediately determined by the experimental data, the only other two model parameters which remain free are the relative loading of the outside ski at the fall line $A_0$ and the maximum edge angle as represented by the factor $\kappa$ in Eq. (29). The realistic ranges for this parameters are $A_0 \in (0.5,1)$ and $\kappa \in (1,2)$. Hence we explored this region of the parameter space, looking for a close similarity between the model and the experimental data.

As a first step, the loading parameter was set to $A_0=0.8$, and $\kappa$ was varied until there was no strong systematic variation of the skier speed V with x, like seen in the experimental data (after the short initial phase of skiing down the fall line during which the speed was growing). At the same point, the distance between two points corresponding to the same turn phase reached approximately the same value as in the experimental data, $\approx 4.5$ meters. This is rather surprising because, one would not expect a model to fit two independent sets of data by adjusting only one free model parameter. The obtained $\kappa =1.67$ corresponds to the reasonable ski edge angle $\Psi _{\text{ m }}=34^\circ$.

Fig. 5

Variation of the key parameters throughout consecutive wedge turns in the model with $A_0=0.8$ and $\kappa =1.67$

Figure 5 shows the variation of several kinematic parameters with the distance down the fall line obtained in the model with $A_0=0.8$ and $\kappa =1.67$. All these parameters were measured in the experiment and their actual variation is shown in Figure 3 of [11].

In the context of this study, the most important of these parameters is the effective coefficient of friction, defined as

$$\begin{aligned} \mu _{\text{ eff }} = \sum _{i=l,r} A^{(i)}_N |\sin \gamma ^{(i)}| \tan \Psi ^{(i)}. \end{aligned}$$

(37)

Using this definition, one can write Eq. (10) as

$$\begin{aligned} \frac{{\text {d}} V}{{\text {d}} t} = g (\sin \alpha \cos \beta - \mu _{\text{ eff }}\cos \alpha ), \end{aligned}$$

(38)

which looks exactly the same as in the model where the snow reaction force is replaced with Coulomb’s friction with the coefficient $\mu _{\text{ eff }}$. Like in the experimental plots, $\mu _{\text{ eff }}$ varies between 0.05 and 0.2. In the model, $\mu _{\text{ eff }}$ increases on approach to the fall line ($\beta =0^\circ$) and decreases after passing it. However, in the experimental data the peak is reached after the fall line.

Fig. 6

Superposition of the CM trajectory in the model with $A_0=0.8$ and $\kappa =1.67$, and the skis trajectories from [11]

The variation of the angle of traverse $\beta$ is similar to what is seen for the first turn in [11] but the transition between the first and the second turn of the experimental run is noticeably sharper. The speed plot shows qualitatively the same evolution as in the experiment, with maxima just before the fall line around the phase where the effective coefficient of friction is about half way between its extreme values. However, the amplitude of the speed variation is about half of that in the experimental data.

The largest difference between the model and the data is in the values of the curvature radius of the trajectory

$$\begin{aligned} R = \left| \frac{{\text {d}} \beta }{{\text {d}} l}\right| ^{-1} = V \left| \frac{{\text {d}} \beta }{{\text {d}} t}\right| ^{-1}, \end{aligned}$$

(39)

where l is the distance along the trajectory. While the shape and position of the theoretical curve are very similar to what is seen in the experimental curve, we find twice as lower radii at the minima. This is somewhat in conflict with the apparent similarity between our trajectory of the CM and the ski trajectories presented in [11]. To illustrate this point, we scanned their plot and superimposed it on our trajectory plot. The result is shown in Fig. 6. One can see that theoretical and the experimental trajectories agree. In fact, the theoretical curve traces the inside ski, as indeed is expected in the case where it runs flat, and hence the CM is located right above it (with the respect to the normal of the ski slope). Presumably, the explanation of the apparent conflict between the computed and measured curvature radii lies in the difference between their definitions. Unfortunately, Sahashi and Ichino [11] do not describe their procedure for measuring R.

Fig. 7

Critical wedge angle, above which wedge skidding down the fall line comes to a stop, as a function of the slope angle

Overall, the computed run is similar to the ski run presented in [11]. Without tabulated data, we cannot do a proper fitting of the theoretical model. Moreover, the experimental data describe only two turns, which are not identical, and hence the outcome of such a fitting would not provide any useful statistical information. Hence we opted not to proceed in this direction. Instead, we simply repeated our procedure with somewhat different values of $A_0$ to see if this would lead to a noticeably different outcome. This way we have found that for a higher $A_0$ a similar outcome can be obtained with lower value of $\kappa$, and the other way around. For example, the solutions corresponding to $A_0=0.7$ and $\kappa =1.78$, and $A_0=0.9$ and $\kappa =1.57$ are not much different from the reference solution described above.

We finish this section, by considering a simpler manoeuvre involving wedged skis that can also be used for experimental verification of our model. Namely we analyse the motion down the fall line. In this case, $\beta =0$, $A^{(l)}_N=A^{(r)}_N=1/2$, $\gamma ^{(l)}=\gamma ^{(r)}=\gamma _{\text{ w }}/2$, $\Psi ^{(l)}=\Psi ^{(r)}=\Psi _{\text{ m }}/2$, and Eq. (10) reads

$$\begin{aligned} \frac{1}{g} \frac{{\text {d}} V}{{\text {d}} t} = \sin \alpha - \cos \alpha \sin \left( \dfrac{\gamma _{\text{ w }}}{2}\right) \tan \left( \dfrac{\Psi _{\text{ m }}}{2}\right) \,. \end{aligned}$$

(40)

For travelling with constant speed, this equation implies

$$\begin{aligned} \tan \alpha =\sin \left( \dfrac{\gamma _{\text{ w }}}{2}\right) \tan \left( \dfrac{\Psi _{\text{ m }}}{2}\right) \,. \end{aligned}$$

(41)

For a larger wedge angle, the skier will decelerate and eventually stop. For smaller angles they will speed up. Figure 7 shows how the critical wedge angle depends on the slope inclination $\alpha$ when $\Psi _{\text{ m }}=\gamma _{\text{ w }}$. One can see that it grows rapidly at small $\alpha$ and reaches the appreciable value of $\gamma _{\text{ w }}=33^\circ$ already for slopes with $\alpha =5^\circ$. The even larger values of the wedge angle predicted for steeper slopes, with $\alpha >20^\circ$, require rather short skis in order to avoid their crossing.

4 Discussion

The complex movements of skier’s body performed during skiing are designed mostly to achieve the desired interaction between their skis and snow. This interaction allows skiers to make turns and control speed. Hence, a clear understanding of the ski-snow interaction is a primary objective for the theory of skiing. Here I focused on the case when skis are set on edge and sideslip during their motion on hard snow. This results in the removal of the top layer of snow, which makes the ski-snow interaction similar to the process of machining in manufacturing. The key force in this process is the snow reaction force normal to the ski base, which has both the braking and turning components².

In the theory of snow machining, the key parameters determining the turning and braking forces acting on the skis are their loading, angle of attack, and edge angle. How exactly skiers control these parameters is a topic of sports biomechanics and it is not addressed in this paper. Instead, these parameters are simply described as functions of the turn phase (the angle of traverse). This choice is convenient for modelling of repetitive ski runs (periodic or quasi-periodic solutions), which simplify studying the turn dynamics.

The theory requires proper verification via comparing its predictions with skiing practice. The main aim of this paper was to build a model that could be used in experimental studies of wedge turns. I used as a guide the study by Sahashi and Ichino [11], the only field study of wedge turns so far. Moreover, I wanted to explore if the strong braking force reported in this study could be attributed not to the abnormally high and variable coefficient of Coulomb friction, as done in [11], but to the cutting force of machining.

Unfortunately, the study gives no information on the ski loading and edging, and only rather limited graphic data on the angle of attack. Hence, I specified the control functions using as a guide the video recordings of wedge turns available on YouTube and my personal skiing experience. Admittedly, the videos reveal significant stylistic variety and hence the choice of control functions is far from unique.

To simplify the comparison between the model and the experiment, the control functions had only two free parameters, one adjusting the loading of the outside ski and another adjusting its edging. Although this reduced the flexibility of the model, it still succeeded in reproducing quite closely the wedge turns studied in [11], including the wedge angle, skier’s trajectory, and speed. Finally, the evolution of the effective coefficient of snow friction with the turn phase was also very similar to the one observed in the experiment, including the abnormally high values near the peak.

Unfortunately, Sahashi and Ichino [11] did not provide any information of the load distribution between the inside and outside skis and the skis edge angles. So, there remains a possibility of disagreement between the theory and experiment with regard to these parameters. Future experiments should aim at measuring them as well. In relation to this, the modelling has revealed a degeneracy in the plane of the parameters used to adjust the loading and edging functions—models with higher loading and lower edge angle of the outside ski yield similar results to models with lower loading and higher edge angle.

One small problem with experiments focused on repetitive ski runs is that in reality every individual turn is still somewhat different from other turns. Human errors and variations of terrain contribute to the inconsistency. However, the results of such imperfect runs can be analysed using a statistical approach.

The simpler is a ski manoeuvre, the easier it is to model and to analyse, and the more reliable can be conclusions on the ski-snow interaction. In this regard, skiing down the fall line in symmetric wedge configuration can be worthy of attention. In the theory, this motion is described by just one simple differential equation (40), which can be integrated analytically. In experiment, the skier is not required to repeat their movements turn after turn, but only to keep the position of their body and skis unchanged. Although such experiment cannot be used for studying the turning action of skidded skis, it is very suitable for investigation of their braking action.

The simplified theory of snow machining used in this study treats skis as flat plank with straight edge. In reality, most modern skis are shaped and do not have straight edge anyway. Moreover, due to their finite longitudinal and torsional stiffness, skis will bend and twist when interacting with snow [e.g. 2, 12]. As a result, the angle of attack becomes a function of the position along the ski edge [e.g. 2, 13]. For turns with large mean angle of attack, like the wedge turn, this is likely to be a secondary effect. However, for the aim of experimental verification of the basic machining theory, it is still preferable to use stiff skis with large sidecut radius.

For turns with small angle of attack, approaching pure carving, the bending and twisting of skis may become crucial for determining their braking power. Even a relatively small angle of attack at the skidding front section of the ski may be sufficient for the snow cutting force originated at this section to dominate Coulomb’s friction. Further investigation involving more complex models and computer simulations is needed to clarify this effect.

5 Conclusion

This paper described the first attempt to model consecutive wedge turns using a simplified theory of snow machining. The results are at least in a semi-quantitative agreement with previously published experimental data and are hence encouraging. In particular, the snow machining mechanism allows to explain the abnormally high and dependent on the turn phase values of the friction coefficient found in that field study. However, additional experiments, providing statistically sufficient information for a larger set of parameters, are required to make further advances in this area.