Abstract
Aerodynamic drag is the main resistive force in cycling at high speeds and on flat terrain. In wind tunnel tests or computational fluid dynamics simulations, the aerodynamic drag of cycling wheels is often investigated isolated from the rest of the bicycle, and sometimes in static rather than rotating conditions. It is not yet clear how these testing and simulating conditions influence the wheel aerodynamic performance and how the inclusion of wheel rotation influences the overall measured or computed cyclist drag. This study presents computational fluid dynamics simulations, validated with wind tunnel tests, that indicate that an isolated static spoked front wheel has a 2.2% larger drag area than the same wheel when rotating, and that a non-isolated static spoked front wheel has a 7.1% larger drag area than its rotating counterpart. However, rotating wheels are also subjected to the rotational moment, which increases the total power required to rotate and translate the wheel compared to static conditions where only translation is considered. The interaction with the bicycle frame and forks lowers the drag area of the front wheel by 8.8% for static and by 12.9% for the rotating condition, compared to the drag area of the isolated wheels. A different flow behavior is also found for static versus rotating wheels: large low-pressure regions develop from the hub for rotating wheels, together with a lower streamwise velocity region inside the circumference of the wheel compared to static wheels. The results are intended to help in the selection of testing/simulating methodologies for cycling spoked wheels.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Aerodynamic drag has a large impact on the cyclist overall resistance, up to 90% when riding on flat terrain at racing speeds [1, 2]. The aerodynamic drag is mainly caused by the cyclist body, which is responsible for between 60 and 82% of the total drag [2,3,4,5], whereas the remaining part is caused by the bicycle. Previous research reported that both wheels can be responsible for up to 10–15% of the total aerodynamic drag [6]. Reducing the aerodynamic drag and the rotational moment of the wheels is, therefore, important for improving the cyclist performance.
An overview on cycling wheel aerodynamics was provided in [7, 8], whereas specific wind tunnel (WT) and computational fluid dynamics (CFD) studies on cycling wheels are reported in Tables S1 and S2 in the supplementary material, respectively. The majority of these studies have been performed on isolated wheels and they focused on comparisons of the drag of different wheels [6, 9,10,11,12,13,14,15], on the aerodynamic drag reduction by adding external elements like claddings or splitter plates [16, 17], on the aerodynamic influence of the tire width to rim width ratio [18], the impact of wheel rotation on the aerodynamic drag [16, 19], the influence of the rotational moment on the total power required to move the wheel [11] and the influence of computational parameters and the type of wheel/ground contact modeling to the aerodynamics of spoked wheels [20,21,22]. Only a few studies have focused on the aerodynamics of non-isolated cycling wheels, including those by Godo et al. [23], Barry et al. [24] and Petrone et al. [25]. In addition, Kyle [26] mentioned that rear wheels had about 40% lower drag than front wheels, as rear wheels are situated partly in the wake of the rest of the bicycle. The main results of the studies on non-isolated wheels are briefly discussed below, with more details provided in the supplementary material.
Godo et al. [23] found that the computed wheel drag was only slightly influenced by the presence of a fork and the remaining bicycle components. Only the front part of a cut racing bicycle frame was included in the CFD simulations and that two deep-rim spoked wheels and a tri-spoke wheel were considered. Barry et al. [24] found that the drag behavior at yaw angles larger than zero was different for a bicycle tested with and without a cyclist mannequin. The drag values were also dependent on the type of the front wheel used, disc, tri-spoke and spoked wheels with shallow or deep rims. Petrone et al. [25] tested three sets of spoked wheels on a bicycle with a cyclist in a WT. The results were then used as input into a mathematical model which computed the time necessary to complete a flat but not straight track of 57 km. A cyclist pedaling at 350 W would save 154 s and 399 s choosing the most aerodynamic wheelset compared to the other two.
There seems to be no consensus in the scientific literature about the impact of wheel rotation on the resulting aerodynamic forces and moments on isolated wheels. Kyle [13, 27], reported a 22–25% drag increase at 13.41 m/s for two types of rotating spoked wheels compared to the same wheels when kept static in the WT. Kyle provided the results for the rotating wheels as the sum of the translational drag and an equivalent drag caused by the wheel rotational moment. Kyle [28] reported that the contribution of the rotational moment to the total drag of the rotating wheel ranged between 20 and 40%. This implies that the translational drag—thus excluding the rotational moment contribution to the total drag—of isolated static spoked wheels is comparable or higher than the same wheel rotating. Sayers and Stanly [16] reported a translational drag coefficient increase of up to 90% at a speed of 5 m/s for a commercially available wheel with aero-rim and 32 rounded spokes when rotating compared to a static condition, and a 15–25% translational drag coefficient increase at speeds between 10 and 20 m/s. Similarly, Karabelas and Markatos [19] computed a translational drag coefficient increase of about 18% for a rotating wheel compared to the same wheel but static. They performed unsteady simulations with a standard wall function approach for near wall modeling, which was found, together with the height of the first cell, to highly influence the results in other studies on cycling aerodynamics [29, 30]. Moreover, Karabelas and Markatos [19] performed WT tests only on a static wheel, and their CFD results underestimated the measured drag coefficient by 18–28%. Last, Crane and Morton [18] reported only a 3.9 ± 0.6% translation drag area increase for a rotating wheel compared to a static wheel over several trials, a discrepancy in the order of the experimental repeatability (2.3 ± 1.0%).
The information above indicated a lack of previous studies comparing the two most common methodologies to investigate wheel aerodynamics, i.e. isolated and non-isolated from the entire cyclist–bicycle system. In addition, substantial discrepancies could be noted among previous studies concerning the forces acting on a static and rotating wheel. Therefore, the present study compares the aerodynamics of a static and rotating wheel, both isolated and non-isolated from the remaining bicycle components and the cyclist, at zero degree yaw angle, and attempts to clarify discrepancies from previous studies.
2 Wind tunnel experiments
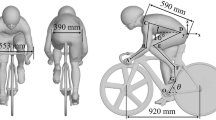
The WT experiments were performed in the closed-circuit WT of Eindhoven University of Technology in the Netherlands. The WT has a test section with a cross-section of 3 m width × 2 m height and a length of 27 m. The tests were performed using a full-scale time trial bicycle and cyclist mannequin wearing an aero-helmet (Fig. 1).
The mannequin was manufactured by CNC milling of high-density polyurethane based on a 3D scan of an elite cyclist. Afterwards a smooth surface treatment was applied. Rider consent was obtained for scanning and the procedure was approval by the Ethical Review Board of Eindhoven University of Technology with Nr. ERB2020BE_1859456_WT. No skinsuit or socks was used so a uniform roughness was present over the cyclist’s surface, except for the helmet and the shoes. The bicycle was equipped with aero-bars, a rear full disc wheel and a front spoked wheel with sixteen bladed spokes. The frontal area of the cyclist and the bicycle was 0.338 m2, yielding a blockage ratio of 5.6%. The bicycle and the cyclist were placed on a sharp-edged platform that included an embedded force sensor with an accuracy of about 0.1 N. The platform was elevated 0.1 m from the WT floor to limit the boundary layer development on the platform. The bicycle was fixed on the platform by a commercial Tacx system. The present supporting system did not enable the wheel rotation so static testing was performed. The drag force was sampled at 240 Hz for about 30 s. The measurement was conducted with a reference speed of about 15.0 m/s and repeated twenty times to obtain the mean value and standard deviation. The reference speed was measured by a cobra probe located about 0.15 m in front of the most forward point of the geometry of the cyclist-bicycle system, about 0.3 m above the cyclist upper point and 0.7 m laterally from the cyclist centerline. The approach-flow turbulence intensity was about 0.5%. The drag force of the support system was measured separately and deducted from the total measured drag to obtain the value pertaining to the cyclist and the bicycle alone. The drag area, \(C_{{\text{D}}} A\), is defined as follows:
where D is the wheel drag (N), ρ the air density (kg/m3), and U the speed measured by the cobra probe (m/s). Similarly, the wheel rotational moment area, \(C_{{\text{M}}} A\), is defined as follows:
where M is the wheel rotational moment (Nm) and r the wheel radius (m). The measured drag area was 0.231 ± 0.001 m2. The rotational moment was not measured in the WT experiments, but it is included in the computational part of the present study due to its importance in the wheel performance [11, 21, 28].
3 CFD simulations: settings and parameters
3.1 Isolated wheel
3.1.1 Geometry, computational domain and grids
The front wheel mounted on the bicycle described in Sect. 2 was selected for this part of the study. An Artec Eva 3D scanner [31] was used to acquire the main features of the wheel, from which the tire-rim profile and the hub profile were obtained using the software ANSYS/SpaceClaim. These profiles were revolved around the rotation axis to generate the entire wheel geometry, and later the spokes were added manually. Figure 2a–e shows the wheel shape, with details of the hub with quick-release bolts, the spoke cross-section, rim and tire. The tire was assumed to have a smooth surface without grooves. The tire and rim had a maximum width of about 24 and 29.5 mm, respectively. The combined tire and rim depth was about 80 mm. The external wheel diameter was about 680 mm. The computational domain (Fig. 2f) was based on the best practice guidelines for wind flow in the urban environment [32,33,34] and automotive external aerodynamics [35], as shown in Fig. 2f. A displacement height of 5 mm was present between the wheel and the ground, as suggested in Malizia and Blocken [21]. A moving reference frame (MRF) volume of elliptical shape was present around the spokes, the inner part of the hub and the inner part of the rim (Fig. 2e). The elliptical shape was used to allow the MRF volume to fit inside the bicycle forks, which were included in the simulations for the non-isolated case.
a Computational geometry of the spoked front wheel used in the wind tunnel tests, with close-up views of: b rim and tire cross-section; c spoke cross-section; d cross-section of hub and quick release bolts. e MRF volume shape with close-up view near the intersection with the rim and the hub. f Computational domain used for the isolated wheel study. Boundary condition symbols: V.I. = velocity inlet; P.O. = pressure outlet; Sym. = symmetry; Mov.Wall = moving no-slip wall
Four computational grids were created for the grid sensitivity analysis. Details of the computational grids are provided in Figs. 3 and 4. Two medium grids were created with a different spatial discretization on the spokes and different prismatic layer settings. For the first medium grid (IM1), the first cell height was of 0.08 mm and the number of prism layers was 12, whereas a 0.025 mm first cell height and 20 prism layers were used for the second medium grid (IM2). For both medium grids the last-ratio growth approach was used [36], and the last-ratio was set to 35%. External to the prism layers, tetrahedral cells were used to fill the domain, with pyramidal cells only used in the transition zones between the hexahedral cells and the tetrahedral cells used in the rest of the domain. The resulting grid sizes were 7.4 M (IC), 18.1 M (IM1), 24.3 M (IM2) and 45.6 M (IF). Further details about the grids are provided in the supplementary material. All the simulations in this paper are performed at zero degree yaw angle.
Three surface grids – coarse (IC), medium (IM2) and fine (IF) – for the grid sensitivity study of the isolated wheel. Total surface cell count was 293, 573, and 1066 k for coarse, medium and fine grid, respectively. a Wheel in side view. Close-up views of: b rim and tire; c intersection between the spoke and the rim; d hub and quick release bolts
3.1.2 Boundary conditions and rotation modeling approach
A uniform velocity U = 13.41 m/s, turbulence intensity TI = 0.5% and hydraulic diameter of 2.4 m were imposed at the inlet boundary. These values were used for consistency with the non-isolated wheel case (see Sect. 3.3). Zero static gauge pressure was imposed at the domain outlet. A symmetry boundary condition was applied on the lateral and top faces, whereas a moving no-slip wall boundary condition was applied on the ground, for both static and rotating wheel cases. The ground velocity was set to the same as the inlet velocity. The wheel rotation was modeled with the hybrid MRF–RW approach [rotating wall (RW)] [20]. The rotational velocity applied to the cells inside the MRF volume and on the wheel components outside this volume (tire, outer rim and outer hub) was equal to ω = U/r.
3.2 Non-isolated wheel
3.2.1 Geometry, computational domain and grids
The combined cyclist-bicycle setup described in Sect. 2 was considered. The wheels and the bicycle chain were first 3D scanned and then the remaining part of their geometry was reconstructed via CAD modeling. Two different computational domains were built, a low blockage domain (Fig. 5a) following the best practice guidelines mentioned in Sect. 3.1.1 and a WT based domain (Fig. 5b), with the same cross-section as the WT test section. The latter was used for validation, while the former was representative of non-confined conditions as in the field. The sharp-edged platform used during the measurements was also included in the WT based domain. A displacement height of 50 mm was present between the plate and the two wheels to resemble the actual experimental conditions. The wheel supports were not included.
For the low-blockage domain, three computational grids were built for the grid sensitivity analysis. The main characteristics of these grids are shown in Figs. 6 and 7. The same front wheel surface grid as in Sect. 3.1.1 is employed in this part of the work, for consistency and for a clear comparison between the isolated and non-isolated cases. The surface of the cyclist and bicycle, including the two wheels, was discretized with 687–1953 k surface cells. The volume grid was built for the three grids using prism layers near the walls of the domain, and tetrahedral cells in the rest of the domain. The total number of cells was 15.2 M (NC), 44.0 M (NM) and 82.4 M (NF) for the coarse (C), medium (M) and fine (F) non-isolated wheel grids, respectively. For the WT based domain, the surface grid used for the cyclist-bicycle system was built up in the same way as for the low-blockage domain. Further details about the grids can be found in the supplementary material.
3.2.2 Boundary conditions and rotation modeling approach
The rotation of the front wheel was modeled with the MRF–RW wheel rotation approach as in the isolated wheel case and with the same MRF volume for consistency. The rotation of the rear disc wheel was modeled with a RW approach, as this type of wheel is a body of revolution.
In the low blockage domain, the no-slip moving wall boundary condition was applied on the ground, whose velocity was the same as at the inlet face, 13.41 m/s, consistent with the WT speed. The inlet had a uniform velocity applied on it, with the turbulence intensity and hydraulic diameter based on the values measured in the WT test. The lateral and top faces had a symmetry boundary condition and at the outlet face zero static gauge pressure was imposed.
In the WT based domain, the velocity at the inlet was set to 14.5 m/s, with TI = 0.5% and hydraulic diameter of 2.4 m to resemble the experimental conditions. This inlet velocity was selected to obtain the same velocity at the position of the Cobra probe as in the WT test (13.41 m/s). Moreover, no Reynolds number sensitivity was observed in the speed range between 13.41 and 15.00 m/s. All the lateral faces of the test section region, the plate and the balance had a static no-slip wall boundary condition applied on them.
3.3 Solver settings
The commercial CFD code ANSYS/Fluent 2019 was used for the simulations [37]. The 3D RANS equations were solved with two turbulence models: the k-ω SST model and the k-ω SST intermittency model (γSST). Compared to the k-ω SST turbulence model [38], the latter includes an additional transport equation to model the laminar-to-turbulent transition [39]. These turbulence models had already been successfully employed to predict the aerodynamic forces in various cycling aerodynamics studies (e.g. [20, 29, 30, 40, 41]). The transitional SST turbulence model, widely used in cycling aerodynamics (e.g. [42,43,44]), could not be tested since it is not Galilean invariant: turbulence models should be Galilean invariant when either the MRF or the MRF–RW wheel rotation approaches are used [37].
The coupled algorithm was used for the pressure–velocity coupling, together with pseudo-transient under-relaxation. The pseudo-time step was computed following the approach for cases with rotational velocities [37]:
The gradient evaluation was performed with the Green-Gauss node-based method, second-order interpolation was used for the pressure and second-order schemes were used to discretize the remaining equations. The maximum values for the residuals were 7 × 10–4 for continuity, 5 × 10–6 for momentum, 1 × 10–3 for turbulent kinetic energy, 6 × 10–4 for the specific dissipation rate and 6 × 10–7 for intermittency. The forces and the moment were averaged over the last 8000 pseudo time steps from a total of 10,000.
4 Results
4.1 Isolated rotating wheel: grid sensitivity
The grid sensitivity analysis for both tested turbulence models, k–ω SST and γSST, pointed to the same wheel grid, IM2, to be retained for the grid sensitivity study of the non-isolated wheel. The differences in terms of CDA and CMA were max 1.3% compared to the finer grid (IF), while for the IM1 and IC grids these values were up to 5.0 and 8.4%, respectively.
For the front spoked wheel, the main contribution to the CMA for both turbulence models was given by the combined tire and rim (~ 70%) and the remaining by the sixteen spokes (~ 30%), whereas the hub did not significantly contribute to CMA (< 0.1%). The 16 spokes contributed less to the total CMA than the 16 spokes of a different spoked wheel (45 vs. 30% in the present study) which was simulated by Malizia and Blocken [21]: in this previous study, the spokes had a rectangular cross-section shape, whereas in the present study they had a rounded leading and trailing edge. The combined tire and rim was responsible for the largest absolute deviations in the results between the coarse/medium grids and the IF grid. In addition, the combined tire and rim represented about 60% of the total CDA and about 70% of CMA. The results for the quick releases were not included in the results above as their geometry was slightly different in the isolated versus the non-isolated wheel case.
Further details of the grid sensitivity analysis are given in the supplementary material.
4.2 Non-isolated rotating wheel: grid sensitivity
The grid sensitivity analysis for both tested turbulence models pointed to the same grid, NM, to be retained for the remainder of the study. The differences in terms of CDA and CMA were max 1.1% compared to the finer grid (IF), while for the IC grids these values were up to 8.8%.
The CMA contribution of the front wheel to the total CMA was about 60%. The different contribution of the two wheels to the total CMA should be mainly attributed to their different typology—spoked versus disc—rather than to their location in the bicycle—front versus rear. For example, Jermy et al. [11] measured the power needed for a wheel to overcome the rotational moment and found that the three tested disc wheels required 36–64% less (aerodynamic) power to rotate compared to the two tested spoked wheels.
4.3 Isolated wheel: CFD validation
In this study, the computational settings and the wheel/ground contact modeling approach were selected according to Malizia et al. [20] and Malizia and Blocken [21]. In the latter two studies, the CFD results for an isolated spoked wheel—although slightly different than the one in this study—were validated with WT tests by Tew and Sayers [15] and Greenwell et al. [6], respectively. Only the main results are reported here.
Malizia et al. [20] investigated the impact of computational parameters, such as the grid topology, wheel rotation modeling and turbulence modeling, on the aerodynamics of an isolated cycling wheel. The simulations did not include the ground to resemble the testing condition of the WT tests [15]. With a proper selection of these computations settings, a maximum discrepancy of 3.4% was found for the drag coefficient between the CFD results and the WT tests at zero degree yaw angle.
Similar computational settings were also used in Malizia and Blocken [21]. The aim of this study was to investigate the influence of the wheel/ground contact modeling approach on the wheel aerodynamics. The CFD results for a spoked rear-wheel in proximity with the ground were validated against literature available WT tests [6]. The computed drag coefficient values for two ground speeds (4.47, 8.94 m/s) were within the range of measured drag coefficient [6], whereas the computed drag coefficient at 13.41 m/s speed deviated only 0.3% from the minimum measured drag coefficient. Tew and Sayers [15] and Greenwell et al. [6] tested isolated wheels and measured the forces using force balances specifically intended for testing isolated wheels. For example, the balance accuracy was reported to be equal to 0.0005 in Tew and Sayers [15] in terms of CD, which was equivalent to 0.0002 m2 in terms of drag area CDA.
Given the good agreement between previous CFD results [20, 21] with available WT tests for spoked wheels available in the literature [6, 15], similar computational settings were considered appropriate in the present study.
4.4 Non-isolated wheel: CFD validation
The CFD validation was based on the WT tests with the mannequin described in Sect. 2. The wheels were static in the CFD simulations, to resemble the WT testing conditions. The velocity computed at the same position of the cobra probe used in the WT tests had about 0.7% difference with the measured one, and it was used as reference velocity to calculate the CDA. The total CDA was underestimated with 9.1 and 4.8% by the k–ω SST and the γSST model, respectively, compared to the WT value (for details, see Table S9 in supplementary material). While the WT tests only provided the total CDA, however, the CFD simulations revealed that the cyclist body, the static front wheel and the static rear wheel accounted for about 77, 4 and −0.5%, respectively, of the total CDA. For both turbulence models, the rear disc wheel had a negative CDA value, thus this component provided a small thrust to the system, reducing the total drag by about 0.5%. The best performing turbulence model, the γSST model, was chosen for the remainder of the study.
4.5 Isolated versus non-isolated wheel and static versus rotating wheel
Table 1 shows that the CDA of the isolated static wheel was 2.2% larger than the CDA of the same wheel but rotating. This difference arose by the increased CDA of the combined tire and rim (7.7%) for the static wheel, whereas the CDA of the spokes (8.0%) and the hub (−4.9%) decreased. For a rotating wheel, also a CMA is generated. The resulting sum of CDA and CMA for a static wheel was 28% lower than for a rotating wheel.
Figure 8 shows the pressure coefficient CP along the external tire centerline. For the isolated case, the static and rotating wheels had a similar CP profile for θ between −105° (255°) and 45°, thus for the most forward part of the tire and the top of the tire. At θ = 90°, thus near the ground, the CP profile of the static wheel did not show the peak that was present for the rotating wheel. A similar peak was already observed in Malizia and Blocken [21] for a different spoked wheel with the wheel/ground contact modeled with a gap, whereas a CP peak with values larger than one was found when the wheel/ground contact was modeled through a step. The CP behavior on the tire centerline in the wheel bottom/rear was influenced by the flow behavior around the wheel (Fig. 9). For the rotating wheel, a low-pressure region emerged at the hub and extended towards the ground (Fig. 9b), in contrast to the static wheel (Fig. 9a). This was also shown in Fig. 10a, b, e, f by means of contours of CP and normalized streamwise velocity in the wheel centerplane. For the static condition, the wake generated by the hub developed in the streamwise direction, which caused the oscillation in the CP profile near θ = 180° (Fig. 8, dash-dotted yellow line). For the rotating wheel, a low streamwise velocity region was present in the inside of the wheel, with two low pressure flow regions that developed behind the hub towards the ground, with a high-pressure region in between. This flow behavior caused the small peaks and dips in the CP profile in the rear-bottom of the wheel, at θ angles between 115° and 180° (Fig. 8, solid blue line). Moreover, the low streamwise velocity region inside the rotating wheel (Fig. 10f) and the lower CP in front of the rear section of the rim (Fig. 10b) compared to the static wheel (Fig. 10a, e) contributed to the lower CDA of the isolated rotating wheel with respect of the static wheel.
Contours of the pressure coefficient CP in the wheel centerplane for: a isolated static wheel; b isolated rotating wheel; c non-isolated static wheel; (d) non-isolated rotating wheel. Contours of the mean streamwise velocity component normalized by the reference velocity in the wheel centerplane for the: e isolated static wheel; f isolated rotating wheel; g non-isolated static wheel; h non-isolated rotating wheel
The non-isolated wheel case also showed a smaller CDA (6.6%) for the front wheel when the wheel was rotating rather than static, see Table 2. The rear static wheel had a more negative CDA value than when rotating, although its absolute value was small, reducing the total CDA by only 0.7%. A CDA increase was instead experienced for the bicycle (+ 0.1%) and the cyclist (+ 0.5%) due to the wheel rotation, causing a total CDA increase of 0.5% for the rotating case compared to the static one. The CDA distribution on the bicycle components was different for the static and rotating wheel conditions: for example, the CDA on the forks reduced by 1.9% for a rotating wheel compared to its static counterpart, see Table 3. Focusing on the front wheel component (Table 3), in the non-isolated configuration the CDA for the rotating wheel was 14.3% lower on the combined tire and rim, and 9.8 and 3.6% larger on the spokes and hub, respectively. The CMA contributed by 2.9% to the CDA and CMA sum for the non-isolated wheel case with rotating wheels, which rendered the CDA and CMA sum for the rotating wheel case 3.5% larger than with static wheels.
Both CP profiles for static and rotating non-isolated wheel showed a similar behavior for almost all θ than for the isolated spoked wheel (Fig. 8). A main difference occurs at θ = 245°–255°, where the tire was near the intersection between the head tube and the forks and between 180° and 245°, where the tire was in close proximity with the down tube. A high CP area occurred on the front of the head tube (Fig. 9c, d), which caused the CP peak at θ = 255°. The main differences in the CP and velocity streamwise contours between the static and rotating wheel cases for the non-isolated wheel were localized near the two wheels, and near the lower section of the bicycle and cyclist legs.
Comparing the isolated and the non-isolated case (Tables 1, 3), the CDA of the front wheel was 8.8 and 12.9% lower for the non-isolated wheel case compared to the isolated wheel case for the static and rotating conditions, respectively. In both conditions, all the wheel components experienced a CDA reduction in the non-isolated configuration: for instance, for the rotating wheel, the CDA on the tire-rim combination, the spokes and the hub was −19.0, −3.7 and −3.4% lower, respectively. In addition, the non-isolated wheel was also characterized by a −7.1% lower CMA compared to the isolated wheel: the combined tire and rim showed again the largest CMA reduction (−8.5%), whereas the spokes experienced a smaller CMA reduction (−4.1%).
5 Discussion and future work
The small drag area difference found in the present paper between static and rotating isolated wheels is in line with the results of Crane and Morton [18], although of opposite sign. In the present study, the rotating spoked wheel has a 2.2% lower drag area than its static counterpart, whereas a 3.9 ± 0.6% higher drag area was measured by Crane and Morton [18] for the rotating wheel. However, the wheels in these studies are different, and likely with a different tire mounted on it: the tire provides the largest contribution to the total drag area (~ 60% for both static and rotating wheels); therefore, differences in tire shape can partially explain these deviations. Moreover, rotating wheels are subjected to a rotational moment. The sum of the rotational moment area and drag area for the rotating wheel is 39% higher than the drag area of the static wheel in the present study: this difference is larger than the one measured by Kyle [13, 27], who reported a 22–25% increase. However, the rotational moment area contribution to this sum is in line with the 20–40% reported by Kyle [28] for a spoked wheel. A different drag behavior between static and rotating wheels was instead reported by Sayers and Stanley [16] and Karabelas and Markatos [19]. Both studies reported about 20% larger drag coefficients for rotating wheels compared to static wheels, at comparable speeds with the present study. Different causes might be responsible of this opposite behavior, among which the different wheel and tire considered in these studies. The WT tests by Sayers and Stanley [16] did not include the ground. Although Malizia and Blocken [21] found that the ground has only a small influence on the aerodynamic forces of a rotating wheel, this is not known for a static wheel yet. Moreover, in the CFD simulations by Karabelas and Markatos [19], the computed drag coefficient for a static wheel underestimated the measured drag coefficient for the same static wheel by 18–28%, whereas no WT tests were performed for the rotating wheel. The discrepancy between CFD and WT results for static wheels in Karabelas and Markatos [19] might partially explain the large deviations between these and the present results for static and rotating wheels.
Future work should extend this study by analyzing different shapes of spoked wheels and type of wheels, like tri-spoke and disc wheels. Increasing research efforts on the aerodynamics of different wheels and bicycles may also lead to establish relations on their mutual impact. Moreover, disc brakes are increasingly replacing caliper brakes on many bicycles, however, studies on their aerodynamic influence on the bicycle and wheel has not yet been reported in the scientific literature. The inclusion of crosswind in the analysis and additional WT tests, including velocity measurements in the wheel’s wake and pressure on the wheel surface, can also provide further insights.
6 Conclusions
The present paper compared, to the best of the authors’ knowledge for the first time, the aerodynamics of an isolated and non-isolated—including a time trial bicycle and a cyclist–cycling spoked wheel. Moreover, this paper further investigated the aerodynamic differences between static and rotating wheels, as several discrepancies were observed in the literature. Flow visualizations were also employed to identify the differences in the flow behavior between static and rotating wheels.
The static wheel had a larger CDA, both in the isolated (+ 2.2%) and non-isolated (+ 7.1%) configuration compared to the same wheel but rotating. However, the rotating wheel was also subjected to the rotational moment which influenced its aerodynamic performance. The sum of CDA and CMA was 38.9% and 3.5% higher for an isolated and non-isolated rotating wheel, respectively, compared to the same wheel but static. The CMA of both wheels also increased the sum of CDA and CMA for the whole cyclist-bicycle system by 2.9%.
The CDA for the non-isolated wheel was 8.8 and 12.9% lower than for the isolated wheel in static and rotating conditions, respectively. This was mainly caused by the interaction of the wheel with the down tube, forks and head tube on the rear and upper part of the wheel. Moreover, the CMA for the non-isolated wheel was 7.7% lower than that for the isolated one. The differences mainly originated from the combined tire and rim.
The flow behavior around static and rotating isolated wheels was different, although they had a similar drag area. The CP profile on the external tire centerline for static and rotating wheels was similar only in the front part of the wheel, whereas it displayed large differences near the ground and in the wheel rear section. Near the ground, the CP peak observed for the rotating wheel was not present for the static wheel. Moreover, a large low-pressure region emerged from the hub and reached the ground for both the isolated and the non-isolated rotating wheel, whereas this flow behavior was not observed for the static wheel. This low-pressure region could interact with the components of the bicycle located near the ground and with the feet and lower legs of the cyclist.
These results are intended to help researchers and manufacturers in choosing the most appropriate testing and simulating configurations for aerodynamic studies of cycling wheels.
References
Grappe F, Candau R, Belli A, Rouillon JD (1997) Aerodynamic drag in field cycling. Ergonomics 40:1299–1311
Kyle CR, Burke ER (1984) Improving the racing bicycle. Mech Eng 106:34–45
Barry N, Burton D, Sheridan J, Thompson M, Brown NAT (2015) Aerodynamic performance and riding posture in road cycling and triathlon. J Sport Eng Technol 229:28–38
Nonweiler T (1956) The air resistance of racing cyclists. Cranfield CERES 106:1–9
Defraeye T, Blocken B, Koninckx E, Hespel P, Carmeliet J (2010) Aerodynamic study of different cyclist positions: CFD analysis and full-scale wind-tunnel tests. J Biomech 43:1262–1268
Greenwell DI, Wood NJ, Bridge EKL, Addy RJ (1995) Aerodynamic characteristics of low-drag bicycle wheels. Aeronaut J 99:109–120
Crouch TN, Burton D, LaBry ZA, Blair KB (2017) Riding against the wind: a review of competition cycling aerodynamics. Sport Eng 20:81–110
Malizia F, Blocken B (2020) Bicycle aerodynamics: history, state-of-the-art and future perspectives. J Wind Eng Ind Aerodyn 200:104134
Godo MN, Corson D, Legensky SM (2009) An aerodynamic study of bicycle wheel performance using CFD. In: 47th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition, vol 12065, pp 1–21
Godo M, Corson D, Legensky S (2010) A comparative aerodynamic study of commercial bicycle wheels using CFD. In: 48th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition, vol 35, pp 1–31
Jermy M, Moore J, Bloomfield M (2008) Translational and rotational aerodynamic drag of composite construction bicycle wheels. J Sport Eng Technol 222:91–102
Knupe J, Farmer D (2009) Aerodynamics of high performance race bicycle wheels. Wing-light-de, Germany, pp 1–15
Kyle CR (2002) Selecting cycling equipment. In: Burke ER (ed) High tech Cycl, 2nd edn. Human Kinetics Books, Champaign, pp 1–48
Pogni M, Petrone N (2016) Comparison of the aerodynamic performance of five racing bicycle wheels by means of CFD calculations. Procedia Eng 147:74–80
Tew GS, Sayers AT (1999) Aerodynamics of yawed racing cycle wheels. J Wind Eng Ind Aerodyn 82:209–222
Sayers AT, Stanley P (1994) Drag force on rotating racing cycle wheels. J Wind Eng Ind Aerodyn 53:431–440
Zdravkovich MM (1992) Aerodynamics of bicycle wheel and frame. J Wind Eng Ind Aerodyn 40:55–70
Crane R, Morton C (2018) Drag and side force analysis on bicycle wheel-tire combinations. J Fluids Eng Trans ASME 140:1–8
Karabelas SJ, Markatos NC (2012) Aerodynamics of fixed and rotating spoked cycling wheels. J Fluids Eng 134:011102
Malizia F, Montazeri H, Blocken B (2019) CFD simulations of spoked wheel aerodynamics in cycling: Impact of computational parameters. J Wind Eng Ind Aerodyn 82:194
Malizia F, Blocken B (2020) CFD simulations of an isolated cycling spoked wheel: impact of the ground and wheel/ground contact modeling. Eur J Mech 82:21–38
Malizia F, Blocken B (2020) CFD simulations of an isolated cycling spoked wheel: the impact of wheel/ground contact modeling in crosswind conditions. Eur J Mech B 84:487–495
Godo MN, Corson D, Legensky SM, Manager FP, Analyst S, Park C, et al (2011) A practical analysis of unsteady flow around a bicycle wheel, fork and partial frame using CFD. In: 49th AIAA Aerospace sciences meeting including the new horizons forum and aerospace exposition, pp 1–25
Barry N, Burton D, Crouch T, Sheridan J, Luescher R (2012) Effect of crosswinds and wheel selection on the aerodynamic behavior of a cyclist. Procedia Eng 34:20–25
Petrone N, Giacomin M, Koptyug A, Bäckström M (2018) Racing wheels effect on drag/side forces acting on a cyclist at Sportstech-Miun wind tunnel. Project at Sports Tech Research Centre, Mid Sweden University, doi: https://doi.org/10.3390/proceedings2060210
Kyle CR (1990) Wind tunnel tests of bicycle wheels and helmets. Cycl Sci 2:27–30
Kyle CR (1991) New aero wheel tests. Cycl Sci 3:27–30
Kyle CR (1995) Aero wheel performance. Cycl Sci 6–9:20–21
Defraeye T, Blocken B, Koninckx E, Hespel P, Carmeliet J (2010) Computational fluid dynamics analysis of cyclist aerodynamics: performance of different turbulence-modelling and boundary-layer modelling approaches. J Biomech 43:2281–2287
Mannion P, Toparlar Y, Blocken B, Hajdukiewicz M, Andrianne T, Clifford E (2018) Improving CFD prediction of drag on Paralympic tandem athletes: influence of grid resolution and turbulence model. Sport Eng 21:123–135
Artec Europe. Artec Eva, 3D Scanners 2017. www.artec3d.com/3d-scanner/artec-eva. Accessed 22 May 2017
Blocken B (2015) Computational Fluid Dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build Environ 91:219–245
Franke J, Hellsten A, Schlünzen H, Carissimo B (2010) The best practise guideline for the CFD simulation of flows in the urban environment : an outcome of COST 732. In: Fifth internatinal symposium on computational wind engineering, p 1–10
Tominaga Y, Mochida A, Yoshie R, Kataoka H, Nozu T, Yoshikawa M et al (2008) AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J Wind Eng Ind Aerodyn 96:1749–1761
Lanfrit M (2005) Best practice guidelines for handling Automotive External Aerodynamics with FLUENT. Version 1.2. Fluent Deutschl GmbH Birkenweg 14a 64295 Darmstadt/Germany 2005, pp 1–14
ANSYS Inc (2019) ANSYS fluent user’s guide 2019R3—part II: meshing mode
ANSYS Inc (2019) ANSYS fluent—theory guide—v195 2019. ansyshelp.ansys.com.
Menter FR (1994) Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 32:1598–1605
Menter FR, Esch T, Kubacki S (2002) Transition modelling based on local variables. Elsevier, New York
Beaumont F, Taiar R, Polidori G, Trenchard H, Grappe F (2018) Aerodynamic study of time-trial helmets in cycling racing using CFD analysis. J Biomech 67:1–8
Giappino S, Omarini S, Schito P, Somaschini S, Belloli M, Tenni M (2018) Cyclist aerodynamics: a comparison between wind tunnel tests and CFD simulations for helmet design. In: Proceedings of the XV Conference of the Italian Association for Wind Engineering, IN-VENTO 2018, Naples
Blocken B, van Druenen T, Toparlar Y, Malizia F, Mannion P, Andrianne T et al (2018) Aerodynamic drag in cycling pelotons: new insights by CFD simulation and wind tunnel testing. J Wind Eng Ind Aerodyn 179:319–337
Blocken B, van Druenen T, Toparlar Y, Andrianne T (2018) Aerodynamic analysis of different cyclist hill descent positions. J Wind Eng Ind Aerodyn 181:27–45
Blocken B, van Druenen T, Toparlar Y, Andrianne T (2019) CFD analysis of an exceptional cyclist sprint position. Sport Eng 22:1–11
Acknowledgements
The activity presented in this paper is part of the Ph.D. research grant (dossier nr. IWT.141701) of the first author awarded by the Flemish Agency for Innovation and Entrepreneurship (VLAIO) in Belgium and also part of his work while he was afterwards appointed at Eindhoven University of Technology in the Netherlands. The authors acknowledge the partnership with professional Cycling Team Jumbo-Visma and with ANSYS CFD. This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative (Grant no. EINF-172).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary file2 (MP4 9527 KB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Malizia, F., van Druenen, T. & Blocken, B. Impact of wheel rotation on the aerodynamic drag of a time trial cyclist. Sports Eng 24, 3 (2021). https://doi.org/10.1007/s12283-021-00341-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s12283-021-00341-6