Advertisement

Sports Engineering

, 22:3 | Cite as

Impact of pilot and stoker torso angles in tandem para-cycling aerodynamics

  • Paul MannionEmail author
  • Yasin Toparlar
  • Bert Blocken
  • Magdalena Hajdukiewicz
  • Thomas Andrianne
  • Eoghan Clifford
Open Access
Original Article
First Online:

Abstract

The torso angle of a cyclist is a key element to consider when attaining aerodynamic postures. For athletes competing in the tandem para-cycling category as the pilot or stoker, the torso angles are similar to those adopted by able-bodied athletes. However, their aerodynamic interaction is not yet fully understood. To date, there has been no study to identify aerodynamically advantageous torso angles for tandem athletes. In this study, numerical simulations with computational fluid dynamics and reduced-scale wind tunnel experiments were used to study the aerodynamics of tandem cyclists considering 23 different torso angle combinations. The sagittal torso angle combination of the pilot and stoker that yielded the lowest overall drag area of 0.308 m2 (combined pilot, stoker and bicycle) was 25° for the pilot coupled with 20° for the stoker. The results suggest that higher torso angles for the pilot have a lower impact on the overall drag area than equivalent torso angles for the stoker. This study suggests that a slight relaxation of pilot torso angle (which may help increase power output) may not penalise aerodynamics, in low (< 25°) sagittal torso angle ranges.

Keywords

Aerodynamics Computational fluid dynamics Para-cycling Tandem Torso angle 

1 Introduction

Tandem para-cycling is a paralympic sport branch that features high speeds and unique aerodynamic considerations; two athletes in close proximity on a single tandem bicycle. Aerodynamic optimisation has become a key element of competitive cycling in recent years [1]. Numerous studies have been conducted to quantify and understand aerodynamic drag in cycling [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]. It has been shown for a competitive able-bodied cyclist that drag reductions in the order of 20% with respect to a traditional athlete’s posture can be obtained through refinements and adjustments of cycling positions/postures, while remaining within the boundaries of the rules set by the union cycliste internationale (UCI) [14]. The balance between power output and aerodynamics has become an important aspect of competitive cycling that can be unique to each athlete [15, 16, 17, 18, 19]. Two tandem athletes together contribute to the total power output, and both athletes along with the tandem bicycle experience aerodynamic drag forces. The aerodynamics of both athletes, the pilot and the stoker, need to be optimised both individually and simultaneously for a collective drag reduction, while keeping the power output at an optimal level. Recent research has shown that the aerodynamics of each tandem athlete is highly dependent on the other athlete [20, 21]. A supposed aerodynamic improvement to the pilot could have a negative effect on the stoker downstream, and thus a balance is required.

Competitive tandem para-cycling has received little attention in the literature by comparison to its able-bodied counterparts and tandem aerodynamics have only recently been investigated numerically and experimentally [20, 21]. Mannion et al. [20] demonstrated reliable numerical modelling of tandem aerodynamics requires careful grid generation and turbulence modelling. Mannion et al. [21] investigated four tandem setups along with the tandem athletes on solo bicycles to aid in understanding the aerodynamic interaction between the pilot and the stoker. The pilot was found to benefit aerodynamically by the presence of the stoker by up to 15.1%, while the stoker experienced up to 58.2% less drag than a solo cyclist. The unique frame-clench tandem setup [21] was found to yield the lowest drag area (CDA) from four setups tested.

Underwood et al. [22] investigated if a cyclist’s drag could be minimised with changes in torso and shoulder angles. Wind tunnel experiments at 40 km/h were conducted with three competitive track cyclists, using a custom handlebar setup for repeatability and measurability. The optimum torso angle for each athlete varied from 1.6° to 8.6° to the horizontal plane. Barry et al. [23] performed wind tunnel tests to investigate the effect of variations in body posture on aerodynamic performance. The torso angle of the athlete was also investigated in dropped positions. It was determined that the wake field behind the cyclist could be reduced by lowering the head and torso angle of a cyclist, resulting in a reduction of aerodynamic drag.

Computational fluid dynamics (CFD) has also been used to evaluate cyclist posture. Defraeye et al. [24] used both Reynolds-averaged Navier–Stokes (RANS) and large eddy simulation (LES). The lesser computational expense of the RANS method was deemed attractive over LES for the purpose of cycling posture analysis, with deviations from wind tunnel experiments of 11% and 7%, respectively. CFD has also been used to further the understanding of the underlying physics behind cycling aerodynamics. Two cyclists drafting in close proximity bears some resemblance to tandem cycling aerodynamics, and Blocken et al. [25] used CFD to find that the aerodynamics of the leading cyclist were significantly influenced by the trailing cyclist due to the subsonic upstream disturbance effect by the trailing cyclist. In this study, CFD simulations were performed considering 23 torso angle combinations for a tandem setup, to investigate their impact on aerodynamic drag.

2 Numerical methodology

2.1 Tandem geometrical models

The tandem geometry used in this study was based on the ‘dropped’ road race geometry utilised by Mannion et al. [20, 21]. This geometry used the same 3D scanned athlete for the pilot (front athlete) and stoker (rear athlete) to remove anthropometrical biases in the aerodynamic comparison between both athletes (Fig. 1). Sagittal torso angles are highlighted in red in Fig. 1, while the forearm angle (\(\alpha\)), elbow angle (\(\beta\)), shoulder angle (\(\gamma\)), hip angle (\(\delta\)), and knee angle (\(\varphi\)) are in blue. Subscripts for the angles denoted with Greek letters indicate the torso angle at which this anthropometric angle is achieved. For example, \({\beta _{25^\circ }}\) indicates the elbow angle when a torso angle of 25° is adopted. The sagittal torso angles (θ) of the pilot and stoker were set to 20°, 25°, 30°, 40° and 50° from the horizontal plane (Fig. 1). The torso angle was adjusted at the hip pivot point. No movement was allowed at the neck as the torso angle was adjusted. The forearms were hinged at the elbow locations and at the point of contact with the handlebars, and the shoulder joints were held static. Thus, the shoulder angle (\(\gamma\)) and knee angle (\(\varphi\)), as presented in Fig. 1, remained constant throughout all torso angles at 60° and 57°, respectively. 23 viable torso angle combinations for the tandem setup were obtained, with sagittal torso angles of 20°, 25°, 30°, 40° and 50° for the pilot and stoker. Two particular torso angle combinations of 40° and 50° for the pilot, coupled with 20° for the stoker, were not viable due to intersecting geometries. In addition, more aggressive dropped postures with a lower torso angle than the baseline torso angle of 20° (Fig. 1) were not viable due to geometry intersections, and would not have resulted in positions possible to attain on the tandem bicycle.

Open image in new windowFig. 1
Fig. 1

Side profile of the dropped tandem setup with the pilot and stoker at 20° sagittal torso angles, with the (\(\alpha\)) forearm angle, (\(\beta\)) elbow angle, (\(\gamma\)) shoulder angle, (\(\delta\)) hip angle, and (\(\varphi\)) knee angle for the five positions

The torso angle combinations are described as “Pilot angle-stoker angle” throughout the remainder of the manuscript. For example, the tandem setup with a pilot and stoker adopting angles of 40° and 30°, respectively, would be denoted as “40°–30°”.

2.2 Validation studies

The numerical simulations corresponding to the tandem setup with both the pilot and stoker at the baseline torso angle 20°–20° were validated with results from wind tunnel experiments as reported by Mannion et al. [20, 21]. The drag was measured individually and simultaneously on the pilot and the stoker whose geometry matched the corresponding CFD simulations. Drag force deviations between CFD and wind tunnel of 4.7% and 4.9% were reported for the pilot at 0° and 5° yaw, respectively [21]. Deviations of − 3.4% and − 3.4% were reported for the stoker at the same two yaw angles [21]. These experiments were also used for the grid sensitivity study and turbulence model evaluation as reported by Mannion et al. [20]. The SST k–\(\omega\) turbulence model (Menter 1994) was recommended, coupled with a grid sufficiently refined to yield an average y* (the non-dimensional wall distance) less than 1 at no-slip walls. The CFD simulations performed in the present study utilize the recommended, numerical settings as documented by Mannion et al. [20, 21], discussed briefly in Sects. 2.4 and 2.5.

2.3 Boundary conditions

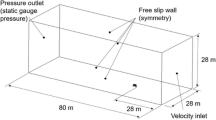
The fluid domain created for this study was developed according to guidelines by Franke et al. [26], Tominaga et al. [27] and Blocken [28]. The domain size was 28 × 28 × 80 m3, with the tandem geometry centred laterally and the midpoint of the geometry located 29 m from the inlet boundary (Fig. 2a). The maximum blockage ratio was 0.06%, occurring when a 50° torso angle was simulated by either the pilot or stoker, which was below the 3% maximum recommendation [26, 27, 28]. The tandem geometry was raised 0.02 m from the ground surface to ensure high grid quality where the wheel tyre would otherwise be tangent to the road surface. A free-slip wall was used for the ground surface. The tandem geometry was simulated using a no-slip wall with zero roughness. Symmetry conditions were applied to the side and top surfaces of the fluid domain. A velocity of 15 m/s (54 km/h) was applied to the inlet boundary with 0.2% turbulence intensity and a hydraulic diameter of 1 m. Zero static gauge pressure was applied to the outlet boundary condition.

Open image in new windowFig. 2
Fig. 2

a Domain size and shape for the tandem simulations (elevation and plan views). b1 Volume and surface grid density between pilot and stoker at torso angles of 5°–20° in a vertical centre-plane. b2 The prism layer grid (composed of 26 layers) on part of stoker geometry in a vertical centre-plane. b3 Volume and surface grid density for the front wheel and forks in a vertical centre-plane and in a horizontal plane

2.4 Numerical parameters

The commercial CFD solver ANSYS Fluent [29] was used for the simulations, which utilises the control volume method. The SST k–ω [30] turbulence model was used to achieve closure in the 3D reynolds-averaged Navier–Stokes (RANS) simulations. Second order pressure and second order discretisation schemes were used, along with the least-squares cell-based method to compute gradients. The coupled algorithm was used for the pressure–velocity coupling with the pseudo-transient solver. A pseudo time-step of 0.01 s was used and the aerodynamic drag was averaged over 4000 steps after an initialisation period of 5000 steps. The typical standard deviation measured for the total CDA (pilot, stoker and bicycle combined) was 0.005 m2.

2.5 Numerical grid

The grids generated in this study utilised the best-performing grid settings specified by the grid sensitivity study Mannion et al. [20], which were determined from systematic sensitivity studies. The first cell height was 2 × 10−5 m at the surfaces of the tandem geometry. 26 prism layers were used with a growth ratio of 1.2. The average y* was below 1. Additional volume grid refinements were placed between the athletes, where larger torso angles increased the separation distance between the stoker’s head and the pilot’s torso. Figure 2b1 illustrates the volume grid density between the pilot and stoker. The density of the prism layers on the athletes is illustrated in Fig. 2b2. The surface and volume grid density of the front wheel and forks of the tandem bicycle is highlighted in Fig. 2b3.

3 Results

The drag area (CDA) was used to describe and compare the aerodynamic drag as:
$${C_{\text{D}}}A=\frac{{{F_{\text{D}}}}}{{0.5\rho U_{{{\text{ref}}}}^{2}}},$$
(1)
$${C_{{\text{D:P}}}}A=\frac{{{F_{{\text{D:P}}}}}}{{0.5\rho U_{{{\text{ref}}}}^{2}}},$$
(2)
$${C_{{\text{D:S}}}}A=\frac{{{F_{{\text{D:S}}}}}}{{0.5\rho U_{{{\text{ref}}}}^{2}}},$$
(3)
where \({C_{\text{D}}}\) is the drag coefficient for the pilot, stoker and bicycle combined [–], \({C_{{\text{D:P}}}}\) the drag coefficient for the pilot only [–], \(~{C_{{\text{D:S}}}}\) the drag coefficient for the stoker only [–], \(A\) is the frontal area of the pilot, stoker and bicycle combined [m2], \(~{F_{\text{D}}}\) the total drag force [N], \(~{F_{{\text{D:P}}}}\) the pilot drag force [N], \(~{F_{{\text{D:S}}}}\) the stoker drag force [N], \(\rho\) the air density [kg/m3], and \({U_{{\text{ref}}}}\) the reference velocity of 15 m/s.

The CDA ranged between a minimum of 0.308 m2 (for the 25°–20° setup) and a maximum of 0.399 m2 (for the 20°–50°, 25°–50° and 50°–50° setup). Figure 3a shows the distribution of CDA over the range of torso angle combinations. The general trend was for CDA to increase as the torso angle of either the pilot or the stoker increased. However, there were a few exceptions. From 20°–20° to 25°–20°, the CDA decreased reaching its minimum at 25°–20°, suggesting that at this torso angle combination, it might be more favourable for the pilot to have a larger torso angle than the stoker as it can provide better aerodynamic shielding of the stoker. In the torso angle range from 20°–50° to 50°–50°, the CDA was reduced with increasing torso angle for the pilot from 20° to 40°, with a minimum CDA of 0.383 m2 at 40°–50°. This was opposite to the trends found at alternative stoker torso angles (Fig. 3a) and was attributed to the drafting benefit to the stoker from the pilot adopting a larger torso angle, which reduced the net drag until 40°–50°, after which the large drag experienced by the pilot resulted in an increase in CDA at 50°–50°.

Open image in new windowFig. 3
Fig. 3

CDA values for a the pilot, stoker and tandem bicycle combined, b the pilot individually, and c the stoker individually. *Torso angle combinations of 40° and 50° for the pilot, coupled with 20° for the stoker, were not viable due to intersecting geometries

The maximum drag for the pilot and the minimum drag for the stoker shared the same torso angle combination, at 50°–25° (Fig. 3b, c). CD:PA and CD:SA values of 0.230 m2 and 0.054 m2 were recorded for the pilot and the stoker, respectively, at 50°–25°; 65.4% and 15.3% of the total drag force, respectively. It was observed that the pilot and stoker both experienced larger drag forces as they increased their torso angle. However, for any set torso angle for the stoker, the stoker experienced a smaller drag force as the torso angle of the pilot increased (Fig. 3c). Notably, the same was often found to be true for the opposite case with the pilot. For any particular torso angle for the pilot, the pilot typically experienced less drag as the torso angle of the stoker increased (Fig. 3b), albeit on a smaller scale compared to the drag savings the stoker experienced from larger pilot torso angles. The maximum drag reduction found for the pilot as a result of changes to the stoker’s torso angle occurred between torso angle combinations of 20°–20° and 20°–50°, with a drag reduction of 5.5%. By comparison, the stoker experienced a 36.2% drag reduction between 20°–50° and 50°–50°.

At 20°–50°, the stoker experienced a larger drag force than the pilot. CD:PA and CD:SA values of 0.156 m2 and 0.177 m2 were recorded for the pilot and stoker, respectively, at 20°–50°; 39.1% and 44.4% of the total drag force at that torso angle combination. The same drag trend was also found at 25°–50°, with a CD:PA of 0.162 m2 and a CD:SA of 0.172 m2. At these torso angle combinations, it is indicated in Fig. 4a that the stoker experienced a large over-pressure region near the head and lower torso in addition to a large under-pressure region near the back. The pilot by comparison did not experience a large under-pressure region on the back at both 20°–50° and 25°–50° due to the subsonic upstream effect imparted by the stoker.

Open image in new windowFig. 4
Fig. 4

a Static pressure coefficient (CP) contours in a vertical centre-plane. b Normalised velocity (U/Uref) contours in a vertical centre-plane

Higher torso angles for the stoker were found to have a larger detrimental effect to the CDA than higher torso angles for the pilot. For comparative purposes, the torso angle combination 25°–25° was used as a baseline and torso angle combinations with 20° are not compared as the 40°–20° and 50°–20° positions were invalid due to geometry intersections. Thus, with 25°–25° as the baseline case, the 25°–50° combination increased drag by 23.9% (from a CDA of 0.322 m2 to 0.399 m2). However, a 9.3% increase from the 25°–25° torso angle combination was found for the 50°–25° torso angle combination by comparison, with CDA values of 0.322 m2 and 0.352 m2, respectively. Figure 4a contributes evidence as to why the drag for the 25°–50° case was higher than the 50°–25° case. Figure 4a depicts the static pressure coefficient in the vertical centre-plane. At the 25°–50° torso angle positions, both the pilot and the stoker were found to exhibit large over-pressure regions, whereas in the 50°–25° torso angle positions, only the pilot exhibits an over-pressure region. Figure 4b illustrates that the stoker was completely engulfed in the wake of the pilot for the 50°–25° torso angle combination. However, the stoker was partially removed from the wake of the pilot for the 25°–50° torso angle combination (Fig. 4b).

4 Discussion

A range of athlete torso angles were investigated for the pilot and stoker in tandem para-cycling with regards to aerodynamics. The sagittal torso angles investigated were 20°, 25°, 30°, 40° and 50° (Fig. 1), where the same athlete’s geometry was used for both the pilot and stoker in numerical simulation to remove anthropometric bias. This study found that torso angles within 20°–25° resulted in the lowest range of CDA values, with 0.322 m2 at 25°–25° and 0.308 m2 at 25°–20°, and 0.314 m2 at 20°–25° and 20°–20°. The pilot in this study could thus potentially benefit from a slightly more relaxed position at a torso angle of 25°, potentially affording greater power output, but crucially optimising the aerodynamic interaction between the pilot and stoker (if the stoker remained at 20°) to attain the lowest overall CDA. It is noted that the sagittal torso angles investigated in this study were discrete angles, and that the absolute optimum torso angle combination for the pilot and stoker may be between these discrete angles. Fintelman et al. [31] discussed that adopting extreme low torso angles may not benefit an athlete by compromising power output, and that a balance could be found between aerodynamics and power output. In able-bodied solo cycling, athletes are capable of attaining torso angles lower than the minimum of 20° from the horizontal plane investigated in this study, with torso angles as low as 0° [15, 31]. However, that case study was for a time-trial setup with elbow pads and aerobars, and similar low torso angles would be difficult to maintain on dropped handlebars in a road race setup. In addition, the optimal torso angle to balance power output and aerodynamics is often athlete-dependent, as demonstrated by Underwood et al. [22].

The proximity of the pilot and stoker can limit the torso angle range available to both athletes, with restrictions placed by the UCI on the dimensions of the tandem frame. The individual anthropometrics of the athletes also play a role in the torso angle range available. The relationship between power output and torso angle for a solo able-bodied athlete has some resemblance to the pilot of a tandem, who has a similar cockpit to that of a solo cyclist. However, the same relationship for the stoker is not well understood or investigated in the literature. The results from this research suggest that the stoker needs to maintain a torso angle equal to or less than the pilot for aerodynamic purposes, which might have a yet unknown negative impact on the power output of the stoker. Increasing torso angle for the stoker had a more detrimental effect on the CDA than increasing torso angle on the pilot (Fig. 3). A CDA of 0.329 m2 was found for the torso angle combination of 20°–30°, higher by 1.9% than 0.323 m2 found at 30°–20°, and 0.9% higher than 0.326 m2 found at 30°–25°. The 20°–25° torso angle combination resulted in the same CDA of 0.314 m2 found for 20°–20°, but was 1.9% higher than 0.308 m2 found at 25°–20°. The difference in power to maintain a velocity of 15 m/s between 25°–20° and 20°–20° was estimated at 12.4 W. Alternatively in another perspective, the 25°–20° torso angle combination could save 6.5 s over a 10 km race, compared to 20°–20°. The difference was greater between 25°–20° and 25°–25°, at 28.9 W and 15.0 s for both power and time comparisons, respectively. These calculations on time difference are conducted considering continuous power output throughout the course of the race distance. Furthermore, the clear aerodynamic advantage of lower torso angles for both the pilot and the stoker, suggests that the design of the tandem frame should accommodate the lowest possible athlete torso angles while remaining within the limits set by the UCI. A torso angle combination of 25°–20° was the optimum value found within this research for non-biased athletes; however, the result may be athlete dependant to some degree. A study that standardises athlete anthropometrics may yield further information to the preferable athlete anthropometric proportions for the pilot and stoker positioning for aerodynamics purposes. The UCI rules determine the dimensions for the tandem bicycle, which in turn, limit the positioning options for the athletes to some degree. The present study considers athletes placed on a road bicycle within the regulations; however, some athletes may prefer positions farther back or farther forwards on the saddle. Such individual and unique positioning may further expand or detract from the range of torso angles available to the stoker athlete. Furthermore, the anthropometrics of both athletes and in particular the vertical height of the stoker, have large impacts on the torso angle combinations achievable by the team. Athletes should consider where possible to adjust the tandem bicycle (saddle, seat tube, and handlebars) to allow for the lower torso angle combinations. For example, for particular tandem teams, it may be possible to achieve torso angles lower than those achieved in this study, and a new range of optimal torso angle combinations may be possible.

The individual drag trends of the pilot and stoker increased and decreased as the other athlete adopted smaller or larger torso angles, respectively (Fig. 3b, c), excluding the torso angle combination of 25°–20°. The drag experienced by the stoker followed the same trend for each fixed pilot torso angle and resulting variations in stoker’s torso angle (Fig. 3c). Higher drag forces were found on the stoker for increasing torso angle. As the pilot’s torso angle increased for fixed stokers’ torso angles, the typical trend across all fixed stoker torso angles was for the drag to decrease (Fig. 3c). However, the drag experienced by the stoker increased by 1.9% from 20°–30° to 25°–30°, and by 1.4% from 20°–40° to 25°–40°. The drag on the pilot increased with his increasing torso angle (Fig. 3b). The typical trend with increasing stoker’s torso angle was for the drag on the pilot to decrease. However, at fixed pilots’ torso angles of 20° and 40° there were variations to this trend, with the drag of the pilot increasing between torso angle combinations of 30°–30° to 30°–40°, and between 40°–30° and 40°–40°. These outliers from the general trends are associated with subtle aerodynamic interactions between the pilot and stoker. The CDA (Fig. 3a) broke from its typical trend of increasing with larger pilot torso angles when the torso angle of the stoker was fixed at 50°. Maximum CDA values of 0.399 m2 were measured for 20°–50°, 25°–50° and 50°–50°, with the minimum CDA value of 0.383 m2 at this fixed stoker torso angle occurring at 40°–50°.

Tandem cyclists are exposed to atmospheric wind conditions in outdoor events. The properties of the atmospheric wind conditions may impact the aerodynamics of the tandem cyclists and the optimal torso angle combination may not be applicable to all wind conditions. Mannion et al. [32] demonstrated that crosswinds can impact the drag distribution of the pilot and stoker. It was found that the drag of the pilot reduced from a 0° yaw angle to 15° yaw. In contrast, the drag of the stoker increased between the same yaw angles. This infers that a singular torso angle combination optimised for 0° yaw conditions, may not be the optimum choice in crosswind conditions. This holds greater significance in outdoor competitive events than indoor velodrome events, as crosswinds may be more prevalent in the former. Moreover, this study considered still air with a low turbulence intensity with no headwind, tailwind or crosswind. It is likely that in reality, turbulence intensity may be higher due to wind conditions which may impact the flow separation locations on the athletes, further impacting their aerodynamic drag.

There were several limitations and simplifications with this study. First, the study considered static geometries with no leg or wheel rotation. It is possible that the movement of the athletes’ legs may transfer some movement to the torso of the athlete. This may impact the aerodynamics, and thus the optimum torso angle combination. Second, all surfaces of the athletes and bicycle geometries were considered as smooth, with zero roughness. The roughness would vary from the skin to the skin suits, bicycle frame, tyres and other components in actual cycling conditions. The roughness of the athletes’ skinsuits coupled with the torso angle adopted by the athletes could impact the locations of flow separation on the torso surfaces of the athletes. This in turn could positively or negatively impact the drag of the athletes. Third, the head angle relative to the torso angle was not changed between torso angle variations. The head and helmet of the athlete were rotated with the torso for each increment. Athletes typically adjust their head angle to maintain forward visibility and for relaxation/comfort. The head angle would impact the orientation of the helmet which, typically, has aerodynamic considerations in its design. There may be an optimum head angle to minimise aerodynamic drag and this angle may be specific to unique helmet designs. Thus, further torso angle combination optimisation for tandem athletes should consider this variable within their analyses.

Future research could couple CFD and wind tunnel experiments, by utilising articulated mannequins in the wind tunnel to allow for precise adjustments of torso angles, while maintaining repeatability and preventing a bias between the anthropometrics of the pilot and the stoker. However, the effect of differing anthropometrics between the pilot and stoker is also of interest for future research. A pilot that is larger than the stoker may provide good aerodynamic shielding at a greater range of torso angles, allowing for more relaxed positions for the stoker to increase power output without negatively impacting the overall aerodynamics. Furthermore, the optimal choice of helmets and skin suits for tandem athletes may have a dependency on the postures adopted by the athletes. Finally, an investigation should be conducted to optimise the balance between power output and aerodynamics for the pilot and stoker in tandem para-cycling, with additional focus on the stoker.

5 Conclusions

Tandem para-cycling aerodynamics were investigated with respect to the pilot and stoker torso angles. The athletes’ sagittal torso angles were altered from 20° to 25°, 30°, 40° and 50° leading to a total of 23 viable torso angle combinations. CFD simulations were performed using computational settings based on prior solution verification and validation studies. Increasing the torso angle in excess of 25° for either athlete caused detrimental effects on the CDA of the tandem setup. However, it was found that a 5° increment from 20° to 25° for the pilot or stoker had only small effects on the CDA within a range of 1.9–4.5% (CDA range between 0.308 and 0.322 m2). Within this range, it might be possible that athletes can adopt a slightly more relaxed position if it gives greater power output than the aerodynamic losses from increased torso angles. It was found that larger adjustments to the torso angle of the stoker had more severe implications for the CDA than the equivalent torso angle adjustments for the pilot, indicating that there should be additional impetus on optimising the stoker’s posture to minimise the CDA.

The minimum CDA value were recorded at a torso angle combination of 25°–20° at 0.308 m2. The pilot experienced maximum and minimum aerodynamic drag at the torso angle combinations of 50°–25° and 20°–50°, respectively, and the stoker at 20°–50° and 50°–25° respectively. The drag of the pilot increased with increasing torso angle, but decreased with increasing torso angle of the stoker. The drag of the stoker decreased with increasing torso angle of the pilot, and increased with his (stoker’s) increasing torso angle.

Notes

Acknowledgements

The authors would like to thank Cycling Ireland, Paralympics Ireland and Sport Ireland Institute. The authors also thank the technical support team from the Department of the Built Environment at Eindhoven University of Technology: Stan van Asten, Geert-Jan Maas, and Jan Diepens; and for the support from the College of Engineering and Informatics at National University of Ireland, Galway. The authors wish to acknowledge the SFI/HEA Irish Centre for High-End Computing (ICHEC) for the provision of computational facilities and support, and also gratefully acknowledge the partnership with ANSYS CFD. Furthermore, the authors acknowledge and thank Corentin Cerutti and Thijs van Druenen for their assistance. This project did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors. This work was sponsored by NWO Exacte en Natuurwetenschappen (Physical Sciences) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organization for Scientific Research, NWO).

Compliance with ethical standards

Conflict of interest

The authors report no conflict of interest.

References

  1. 1.
    Haake SJ (2009) The impact of technology on sporting performance in Olympic sports. J Sports Sci 27:1421–1431.  https://doi.org/10.1080/02640410903062019 CrossRefGoogle Scholar
  2. 2.
    Blocken B, Toparlar Y, Andrianne T (2016) Aerodynamic benefit for a cyclist by a following motorcycle. J Wind Eng Ind Aerodyn 155:1–10.  https://doi.org/10.1016/j.jweia.2016.04.008 CrossRefGoogle Scholar
  3. 3.
    Blocken B, van Druenen T, Toparlar Y, Malizia F, Mannion P, Andrianne T, Marchal T, Maas G-J, Diepens J (2018) Aerodynamic drag in cycling pelotons: new insights by CFD simulation and wind tunnel testing. J Wind Eng Ind Aerodyn 179:319–337.  https://doi.org/10.1016/J.JWEIA.2018.06.011 CrossRefGoogle Scholar
  4. 4.
    Lukes RA, Chin SB, Haake SJ (2005) The understanding and development of cycling aerodynamics. Sports Eng 8:59–74.  https://doi.org/10.1007/BF02844004 CrossRefGoogle Scholar
  5. 5.
    Fintelman DM, Hemida H, Sterling M, Li F-X (2015) CFD simulations of the flow around a cyclist subjected to crosswinds. J Wind Eng Ind Aerodyn 144:31–41.  https://doi.org/10.1016/j.jweia.2015.05.009 CrossRefGoogle Scholar
  6. 6.
    Barry N, Burton D, Sheridan J, Thompson M, Brown NAT (2016) Flow field interactions between two tandem cyclists. Exp Fluids 57:1–14.  https://doi.org/10.1007/s00348-016-2273-y CrossRefGoogle Scholar
  7. 7.
    Blocken B, Toparlar Y (2015) A following car influences cyclist drag: CFD simulations and wind tunnel measurements. J Wind Eng Ind Aerodyn 145:178–186.  https://doi.org/10.1016/j.jweia.2015.06.015 CrossRefGoogle Scholar
  8. 8.
    Crouch TN, Burton D, LaBry ZA, Blair KB (2017) Riding against the wind: a review of competition cycling aerodynamics. Sports Eng 20:81–110.  https://doi.org/10.1007/s12283-017-0234-1 CrossRefGoogle Scholar
  9. 9.
    Crouch TN, Burton D, Brown NaT, Thompson MC, Sheridan J (2014) Flow topology in the wake of a cyclist and its effect on aerodynamic drag. J Fluid Mech 748:5–35.  https://doi.org/10.1017/jfm.2013.678 CrossRefGoogle Scholar
  10. 10.
    Griffith MD, Crouch T, Thompson MC, Burton D, Sheridan J (2014) Computational fluid dynamics study of the effect of leg position on cyclist aerodynamic drag. Am Soc Mech Eng J Fluids Eng 136:101105.  https://doi.org/10.1115/1.4027428 CrossRefGoogle Scholar
  11. 11.
    Defraeye T, Blocken B, Koninckx E, Hespel P, Carmeliet J (2010) Computational fluid dynamics analysis of cyclist aerodynamics: performance of different turbulence-modelling and boundary-layer modelling approaches. J Biomech 43:2281–2287.  https://doi.org/10.1016/j.jbiomech.2010.04.038 CrossRefGoogle Scholar
  12. 12.
    Oggiano L, Leirdal S, Sætran L, Ettema G (2008) Aerodynamic optimization and energy saving of cycling postures for international elite level cyclists. Eng Sport 7:597–604.  https://doi.org/10.1007/978-2-287-09411-8_70 CrossRefGoogle Scholar
  13. 13.
    García-López J, Rodríguez-Marroyo JA, Juneau C-E, Peleteiro J, Martínez AC, Villa JG (2008) Reference values and improvement of aerodynamic drag in professional cyclists. J Sports Sci 26:277–286.  https://doi.org/10.1080/02640410701501697 CrossRefGoogle Scholar
  14. 14.
    UCI (2017) Cycling regulations, part 16 para-cycling, version on 01/02/2017. http://www.uci.ch/mm/Document/News/Rulesandregulation/16/26/73/16-PAR-20170201-E_English.PDF
  15. 15.
    Fintelman DM, Sterling M, Hemida H, Li F-X (2015) The effect of time trial cycling position on physiological and aerodynamic variables. J Sports Sci 0414:1–8.  https://doi.org/10.1080/02640414.2015.1009936 CrossRefGoogle Scholar
  16. 16.
    Fintelman DM, Sterling M, Hemida H, Li FX (2016) Effect of different aerodynamic time trial cycling positions on muscle activation and crank torque. Scand J Med Sci Sport 26:528–534.  https://doi.org/10.1111/sms.12479 CrossRefGoogle Scholar
  17. 17.
    Grappe F, Candau R, Belli A, Rouillon JD (1997) Aerodynamic drag in field cycling with special reference to the Obree’s position. Ergonomics 40:1299–1311.  https://doi.org/10.1080/001401397187388 CrossRefGoogle Scholar
  18. 18.
    Heil DP, Derrick TR, Whittlesey S (1997) The relationship between preferred and optimal positioning during subsmaximal cycle ergometry. Eur J Appl Physiol Occup Physiol 75:160–165.  https://doi.org/10.1007/s004210050141 CrossRefGoogle Scholar
  19. 19.
    Underwood L, Jermy M (2013) Optimal handlebar position for track cyclists. Sports Eng 16:81–90.  https://doi.org/10.1007/s12283-013-0111-5 CrossRefGoogle Scholar
  20. 20.
    Mannion P, Toparlar Y, Blocken B, Hajdukiewicz M, Andrianne T, Clifford E (2018) Improving CFD prediction of drag on paralympic tandem athletes: Influence of grid resolution and turbulence model. Sports Eng 21:123–135.  https://doi.org/10.1007/s12283-017-0258-6 CrossRefGoogle Scholar
  21. 21.
    Mannion P, Toparlar Y, Blocken B, Clifford E, Andrianne T, Hajdukiewicz M (2018) Aerodynamic drag in competitive tandem para-cycling: road race versus time-trial positions. J Wind Eng Ind Aerodyn 179:92–101.  https://doi.org/10.1016/j.jweia.2018.05.011 CrossRefGoogle Scholar
  22. 22.
    Underwood L, Schumacher J, Burette-Pommay J, Jermy M (2011) Aerodynamic drag and biomechanical power of a track cyclist as a function of shoulder and torso angles. Sports Eng 14:147–154.  https://doi.org/10.1007/s12283-011-0078-z CrossRefGoogle Scholar
  23. 23.
    Barry N, Burton D, Sheridan J, Thompson M, Brown NAT (2015) Aerodynamic performance and riding posture in road cycling and triathlon. Proc Inst Mech Eng Part P J Sports Eng Technol 229:28–38.  https://doi.org/10.1177/1754337114549876 CrossRefGoogle Scholar
  24. 24.
    Defraeye T, Blocken B, Koninckx E, Hespel P, Carmeliet J (2010) Aerodynamic study of different cyclist positions: CFD analysis and full-scale wind-tunnel tests. J Biomech 43:1262–1268.  https://doi.org/10.1016/j.jbiomech.2010.01.025 CrossRefGoogle Scholar
  25. 25.
    Blocken B, Defraeye T, Koninckx E, Carmeliet J, Hespel P (2013) CFD simulations of the aerodynamic drag of two drafting cyclists. Comput Fluids 71:435–445.  https://doi.org/10.1016/j.compfluid.2012.11.012 CrossRefGoogle Scholar
  26. 26.
    Franke J, Hellsten A, Schlünzen H, Carissimo B (2007) Best practice guideline for the CFD simulation of flows in the urban environment. COST Action 732. In: Qual. Assur. Improv. Microscale Meteorol. Model, pp 1–52Google Scholar
  27. 27.
    Tominaga Y, Mochida A, Yoshie R, Kataoka H, Nozu T, Yoshikawa M, Shirasawa T (2008) AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J Wind Eng Ind Aerodyn 96:1749–1761.  https://doi.org/10.1016/j.jweia.2008.02.058 CrossRefGoogle Scholar
  28. 28.
    Blocken B (2015) Computational fluid dynamics for urban physics: importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build Environ 91:219–245.  https://doi.org/10.1016/j.buildenv.2015.02.015 CrossRefGoogle Scholar
  29. 29.
    ANSYS Fluent (2017) ANSYS fluent theory guide, release 18.2 documentation. ANSYS, Inc., Canonsburg, PAGoogle Scholar
  30. 30.
    Menter FR (1994) Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 32:1598–1605.  https://doi.org/10.2514/3.12149 CrossRefGoogle Scholar
  31. 31.
    Fintelman DM, Sterling M, Hemida H, Li F-X (2014) Optimal cycling time trial position models: Aerodynamics versus power output and metabolic energy. J Biomech 47:1894–1898.  https://doi.org/10.1016/j.jbiomech.2014.02.029 CrossRefGoogle Scholar
  32. 32.
    Mannion P, Toparlar Y, Clifford E, Hajdukiewicz M, Blocken B (2019) On the effects of crosswinds in tandem aerodynamics: an experimental and computational study. Eur J Mech B Fluids 74:68–80.  https://doi.org/10.1016/j.euromechflu.2018.11.001 CrossRefGoogle Scholar

Copyright information

© The Author(s) 2019

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • Paul Mannion
    • 1
    • 2
    • 4
    Email author
  • Yasin Toparlar
    • 2
  • Bert Blocken
    • 2
    • 3
  • Magdalena Hajdukiewicz
    • 1
    • 4
  • Thomas Andrianne
    • 5
  • Eoghan Clifford
    • 1
    • 4
  1. 1.Department of Civil Engineering, College of Engineering and InformaticsNational University of Ireland GalwayGalwayIreland
  2. 2.Department of the Built EnvironmentEindhoven University of TechnologyEindhovenThe Netherlands
  3. 3.Department of Civil EngineeringKU LeuvenLeuvenBelgium
  4. 4.Informatics Research Unit for Sustainable Engineering (IRUSE)GalwayIreland
  5. 5.Department of Aerospace and Mechanical EngineeringUniversity of LiègeLiègeBelgium

Personalised recommendations