The round-wheel compound bow model revisited: a new extension

Abstract

An extended offset-eccentric model of an archery twin-round-wheel compound bow is derived. Varying some parameters of the model, the respective effects on the calculated force–draw curve are considered. Two static quality coefficients for the compound bow are introduced. It was found that the twin-round-wheel compound bow can be designed to be more energetic with the help of the model. For a bow with some modifications 18.5% increment of energy was calculated. Also a theoretical limit for the force–draw curve of the compound bow is concluded.

1 Introduction

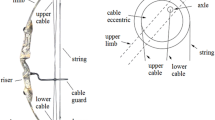
The force–draw relation of the archery bow is one of the main interests of the serious archer. Indeed, the force–draw (FD) curve of the bow not only determines the energy which is stored in the limbs and transferred mainly to the kinetic energy of the arrow, but also the experience of drawing, aiming and releasing the bow. Compared to conventional (or traditional) bows, the compound bow (a bow with pulley systems at the tips of the bow limbs) offers greater possibilities to manipulate the FD curve due to the more complex bow configuration. The simplest type of compound bows, the symmetric twin-round-wheel compound bow, is presented in Fig. 1.

Fig. 1

A typical twin-round-wheel compound bow in the initial position and its upper wheel system (Ref. [4], https://creativecommons.org/licenses/by/4.0/)

There are only a few researches concerning the compound bow. The first investigations of the compound bow including a model of the asymmetric single-cam compound bow were presented by Park [1, 2]. In [3] Zanevskyy has introduced an asymmetric model for a special type of compound bow with centric cable eccentrics. A model for a more usual round-wheel compound bow is presented in [4], and the static deformation of the limbs of this kind of bow is studied in [5]. A detailed model for the twin-cam compound bow is introduced in [6].

While the most effective compound bows nowadays in use have cam systems that differ markedly from circular, the compound bow with eccentrics has still a special role. Compared to non-round cams of the newest compound bows, the round eccentrics can be manufactured by simpler means. Although the mathematical model including round eccentrics (with or without the extension of this paper) is as well far from trivial, it is conceptually more simple and numerically more robust than models including non-round cams.

The aim of this paper is to develop the original round-wheel compound bow model of paper [4] further and to check the possibilities of improving the efficiency of the round-wheel compound bow. The idea of offset between the cable and the string eccentric centres is combined with the original model, as this offers more options to modify the FD curve of the bow. The round-wheel compound bow model with this extension may be called briefly as offset-eccentric model.

2 Offset-eccentric model

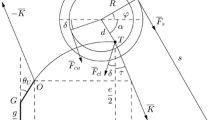
Let us consider the round-wheel compound bow in case of the cable and the string eccentrics of the upper wheel have different centres, as in Fig. 2. The respective upper part of the bow is presented in Fig. 3, from which we notice that

Fig. 2

The wheel system of the upper limb of the round-wheel compound bow with different eccentric centres when the bow is drawn. Note that $\varepsilon$ is here negative

Fig. 3

The upper part of the compound bow in the initial (1) and drawn (2) positions. Note that in position 2 $\varepsilon$ is negative. The cables and the cable eccentric are left out from the figure for clarity (Ref. [4], replaced symbols $d_\mathrm{R}$, $\varepsilon$ and $\varepsilon _0$, https://creativecommons.org/licenses/by/4.0/)

$$\begin{aligned} s= s_0+R(\varepsilon _{0}-\varepsilon )+R\varphi \nonumber \\= \frac{e_{0}}{2}-d_\mathrm{R}\sin \varepsilon _{0}+R(\varepsilon _{0}-\varepsilon )+R\varphi, \end{aligned}$$

(1)

where s is the length of the straight half-string, $s_0$ the value of s in the initial position, $\varepsilon$ the angle between the horizontal line and the line that connects the centre of the upper string eccentric and the upper axle point, $\varepsilon _0$ the value of $\varepsilon$ in the initial position, R the radius of the string eccentric, $e_0$ the distance between the upper and the lower axle point in the initial position, $d_\mathrm{R}$ the distance between the axle and the centre of the string eccentric, and $\varphi$ the angle between the horizontal line and the line that connects the centre of the upper string eccentric and the point where the string touches the upper string eccentric. Further, from Fig. 3 we also conclude that

$$\begin{aligned} s\cos \varphi =\frac{e}{2}-d_\mathrm{R}\sin \varepsilon +R\sin \varphi, \end{aligned}$$

(2)

where e is the distance between the upper and the lower axle point. From Eqs. (1) and (2) we get

$$\begin{aligned}&\left[ \frac{e_{0}}{2}-d_\mathrm{R}\sin \varepsilon _{0}+R(\varepsilon _{0}-\varepsilon +\varphi )\right] \cos \varphi -\frac{e}{2} \nonumber \\&\quad +d_\mathrm{R}\sin \varepsilon -R\sin \varphi =0. \end{aligned}$$

(3)

The cable and the string eccentrics are firmly attached to each other, so the rotating angle is the same for both eccentrics,

$$\begin{aligned} \varepsilon _0-\varepsilon =\alpha _0-\alpha, \end{aligned}$$

(4)

where $\alpha$ is the angle between the horizontal line and the line that connects the centre of the upper cable eccentric and the upper axle point, and $\alpha _0$ the value of $\alpha$ in the initial position. Now, with a fixed $\alpha$ the unknown $\varepsilon$ can be solved from Eq. (4), when $\varphi$ can be obtained from Eq. (3) with the Brent–Dekker method [7] for example. After this, s can be calculated from Eq. (1). Moreover, from Fig. 2 we see that the lever arms of the string and the cable tensions are

$$\begin{aligned} d_\mathrm{s}=R-d_\mathrm{R}\cos (\varphi -\varepsilon ), \quad \, d_{\mathrm{c}}=r+d\cos (\alpha -\delta ), \end{aligned}$$

(5)

where r is the radius of the cable eccentric, d the distance between the axle and the centre of the cable eccentric, and $\delta$ the angle between the horizontal line and the line that connects the centre of the upper cable eccentric and the point where the straight cable contacts the upper cable eccentric.

The draw is here defined as the distance from the midpoint of the string to the vertical line that connects the riser ends (or bottoms) of the upper and the lower limbs. According to Fig. 3, the draw is

$$\begin{aligned}D&=(1-A)L\sin \theta _{\mathrm{U}}+AL\sin \theta -d_\mathrm{R}\cos \varepsilon \nonumber \\&\quad +R\cos \varphi +s\sin \varphi, \end{aligned}$$

(6)

where L is the length of the limb (measured from the bottom of the limb to the axle point along the limb), A the ratio between the length of the supposed elastic portion of the limb with respect to L, $\theta$ the angle between the vertical line and the line that connects the upper axle point and the supposed hinge point of the limb, and $\theta _\mathrm{U}$ the angle between the undeflected bow limb and the vertical line.

The offset-eccentric model can now be formed from the original round-wheel model by replacing equations (8)–(11) and (13) of paper [4] with Eqs. (1)–(6). By choosing $d_\mathrm{R}=d$ and $\varepsilon _0=\alpha _0$ the offset-eccentric model is simplified into the original model.

3 Results

As one measure of evaluating the statics of the compound bow, Mullaney has suggested the ratio of stored energy to peak force [8]. This measure is quite usable when comparing some minor adjustment differences, or different bows with the same full draw. The drawback of this ratio is that it strongly depends on the full draw.

In [9] Kooi and Sparenberg have presented the static quality coefficient for traditional bows with or without recurved limbs. This quality coefficient is dimensionless and can also be used when comparing traditional bows with different full draws. However, in compound bows the force acting on the arrow at full draw is usually far from the maximum force.

On the other hand, when designing the compound bow, it seems reasonable to first search an eccentric system which produces the desired shape of the FD curve, and only after that consider the riser design. So there is also a need for evaluating the quality of the FD curve with a measure, which is independent of the value of D in the initial position. For these reasons, let us define two static quality coefficients for the compound bow,

$$\begin{aligned} q=\frac{\int _{D_{0}}^{D_\mathrm{F}} \! F(D) \, \mathrm {d}D}{(D_\mathrm{F}-h)F_{\mathrm{max}}}, \quad q_{\mathrm{F}}=\frac{\int _{D_{0}}^{D_\mathrm{F}} \! F(D) \, \mathrm {d}D}{(D_F-D_0)F_{\mathrm{max}}}, \end{aligned}$$

(7)

where F is the absolute value of the force acting on the arrow, $D_0$ the value of D in the initial position, $D_\mathrm{F}$ the full draw (here, the draw with the local minimum value of the force F), h the distance between the grip (handle) supporting point and the vertical line that connects the bottoms of the upper and the lower limbs (positive, when the grip supporting point is on the archer’s side from this line), and the peak force

$$\begin{aligned} F_{\mathrm{max}}=\max \{F(D)\} ,\quad D_0 \le D \le D_\mathrm{F}. \end{aligned}$$

(8)

We may call the measure q shortly as the static quality coefficient, whereas $q_{\mathrm{F}}$ may be called as the FD curve quality coefficient. The measures defined in Eq. (7) are dimensionless.

The value of h depends on the shape of the riser. With straight riser $h=0$. The riser is called “reflex” when $h>0$, and “deflex” when $h<0$. From Eq. (7) we notice that if $h=D_0$ and the FD curve is a perfect rectangle, $q=q_\mathrm{F}=1$. However, if $D_0-h$ is too small, the string will hit the bow hand when the bow is launched, and the clearance for the cables may also be a problem. Indeed, in practice $D_0-h$ is usually at least about 15 cm in compound bows, so $q<q_\mathrm{F}$. While the coefficient $q_\mathrm{F}$ is independent of h, for real bows the front part of the FD curve cannot be a vertical line, a fact we shall discuss later on. Hence, $q<q_\mathrm{F}<1$.

Now we shall study the effects of varying some bow parameters of the model. The calculations are done as described in Sect. 2 and in paper [4]. There are 12 initial bow parameters (and the supplemental parameter h) and innumerable ways to vary them. After preliminary testing it seems that the parameters related to the pulley system have the relatively greatest effects on the FD curve, which is our main interest, so we shall first limit our considerations on parameters d, $\alpha _{0}$, $d_\mathrm{R}$ and $\varepsilon _0$. Let us call the bow with parameter values of Table 1 in paper [4] as $B_1$, which has also a straight riser with $h=0$. The bow $B_1$ has the same centre for cable and string eccentrics, when $d_\mathrm{R}=d$ and $\varepsilon _0=\alpha _0$. The FD curve quality coefficient of $B_1$ is 0.619. In the following only the changed parameter values are mentioned, when the other parameter values needed in the model are the respective values of the bow $B_1$.

In case of round-wheel compound bow, it is usual that the force required to keep the bow in full draw position, where the force has a local minimum value, is about one-third of the maximum peak force. This reduction of force with respect to the maximum force is referred to as the bow’s let-off [10]. From Fig. 4 we notice that parameter d has a strong influence on the let-off.

Fig. 4

The force–draw curves of the bow $B_1$ with different values of parameter d

With the increased value of d the peak force increases but the local minimum force in full draw decreases, so that, for example with the value of $d = 16.7$ mm the let-off is about 80%, as seen from Fig. 4. While this large let-off may be desirable, it must be noted that in reality the value of $d = 16.7$ mm may already be out of reach in the viewpoint of material strength, for the radius of the cable eccentric of the bow $B_1$ is $r=19.9$ mm, and the axle has dimensions as well. With large let-off the coefficient $q_\mathrm{F}$ is also lower. For example, the bow of Fig. 4 with the value $d=16.7$ mm has $q_\mathrm{F}=0.589$.

Fig. 5

The force–draw curves of the bow $B_1$ with different values of parameter $d_\mathrm{R}$

While d had a quite straightforward effect to the minimum force value in full draw, it could be expected that the effect of $d_\mathrm{R}$ to the value of the peak force would be rather similar. However, the parameter $d_\mathrm{R}$ affects mostly on the placement of the peak force and the skewness of the FD curve, as can be seen from Fig. 5. The slopes of both the front and the rear parts of the curve seem to change in accordance with $d_\mathrm{R}$. Some differences on the peak force and the let-off can also be seen.

Fig. 6

The force–draw curves of the bow $B_1$ with different values of parameter $\alpha _0$

The value of $\alpha _{0}$ has also a clear effect on the FD curve of the compound bow, as can be seen from Fig. 6. With the value of $\alpha _{0}=0^{\circ }$ the peak force and the full draw are decreased, and the curve has become slightly skewed. With the value $\alpha _{0} =100^{\circ }$ the full draw and the force in full draw are increased, and the front part of the FD curve is a bit convex (downward), while the rear part of the curve is slightly concave. The peak force is then close to the original, and even if the let-off is only about 50%, the value of $q_\mathrm{F}$ is as large as 0.685.

Fig. 7

The force–draw curves of the bow $B_1$ with different values of parameter $\varepsilon _0$

From Fig. 7 we notice that parameter $\varepsilon _0$ affects both the height and the width of the peak of the FD curve from both sides. With the value $\varepsilon _0 =0^{\circ }$ the peak is wide and the FD curve quality coefficient as large as $q_\mathrm{F}=0.737$, albeit the let-off is less than 50%. With the value $\varepsilon _0=100^{\circ }$ the peak force has increased and the front part of the FD curve is convex, when the value of FD curve quality coefficient has decreased to the value of $q_\mathrm{F}=0.514$.

Earlier it was mentioned that in the view of maximizing the static quality coefficient the FD curve should be a rectangle. However, there is a limit for the FD curve of the compound bow, considering especially the front part of the curve. If we assume that

$$\begin{aligned} R=d_\mathrm{R}=0 \end{aligned}$$

(9)

the string is attached straight to the axle point, and the pulleys do not play any role. Our compound bow has thus simplified to a traditional one, and from Eq. (1) we get the length of the half-string of this traditional bow,

$$\begin{aligned} s_\mathrm{t} = \frac{e_0}{2}. \end{aligned}$$

(10)

Substituting Eqs. (9) and (10) into (6) we have the respective draw,

$$\begin{aligned} D_\mathrm{t}=(1-A)L\sin \theta _\mathrm{U}+AL\sin \theta +\frac{e_0}{2}\sin \varphi _\mathrm{t}. \end{aligned}$$

(11)

Further, substituting Eqs. (9) and (10) into (2) gives

$$\begin{aligned} e =e_0 \cos \varphi _\mathrm{t}, \end{aligned}$$

(12)

where $\varphi _\mathrm{t}$ is the angle between the vertical line and the half-string of this traditional bow. From Fig. 3 we also notice that

$$\begin{aligned} \frac{g}{2}+(1-A)L\cos \theta _{\mathrm{U}} =\frac{e}{2}-AL\cos \theta, \end{aligned}$$

(13)

where g is the distance between the bottoms of the upper and the lower limb. Now, substituting Eqs. (12) into (13) we may write for our traditional bow

$$\begin{aligned} e_0 \cos \varphi _\mathrm{t}=g+2(1-A)L\cos \theta _\mathrm{U}+2AL \cos \theta. \end{aligned}$$

(14)

For the round-wheel compound bow the absolute value of the force F acting on the arrow is [4]

$$\begin{aligned} F=\frac{2d_{\mathrm{c}}k(\theta -\theta _{\mathrm{U}})\sin \varphi }{d_{\mathrm{c}}\sin (\theta +\varphi )+2d_{\mathrm{s}}\sin \theta \cos \delta }, \end{aligned}$$

(15)

where k is the spring constant of the elastic portion of the limb, so for the respective traditional bow we get

$$\begin{aligned} F_\mathrm{t}=\frac{2k(\theta -\theta _\mathrm{U})\sin \varphi _\mathrm{t}}{\sin (\theta +\varphi _\mathrm{t})}.\end{aligned}$$

(16)

With given $\theta$, the angle $\varphi _\mathrm{t}$ can be solved from Eq. (14), when the FD curve of the respective traditional bow can be formed with the help of Eqs. (11) and (16). In the “Appendix” it is shown that this curve is indeed the limiting FD curve for any round-wheel compound bow with the same initial parameter values g, L, A, $\theta _\mathrm{U}$, k and $e_0$.

The minimum value of F in full draw has a close relation to the value of the lever arm of the cable tension $d_\mathrm{c}$. Considering Figs. 1 and 2, it also seems natural that in full draw, where the value of the force F has a (local) minimum value, the lever arm of the cable force $d_\mathrm{c}$ is also near its minimum value, when the cables take most of the load. More closely, from Eq. (15) we also notice that if $d_\mathrm{c} \rightarrow 0$ also $F \rightarrow 0$. On the other hand, for the minimum value of $d_\mathrm{c}$ the respective value of the prime variable can be judged from the right-side Eq. (5), it is $\alpha _{\mathrm{mi}n\{d_\mathrm{c}\}}=\delta _{\mathrm{min}\{d_\mathrm{c}\}}+180^{\circ }$. Usually $e/r \gg 1$, when $\delta _{\mathrm{min}\{d_\mathrm{c}\}}$ is quite small and approximately $\alpha _{\mathrm{min}\{d_\mathrm{c}\}} \approx 180^{\circ }$.

Instead, there is no similar “rule of thumb” for the relation between the peak force $F_{\mathrm{max}}$ and the lever arm of the string tension $d_\mathrm{s}$. Typically the peak force is achieved after the draw where $d_\mathrm{s}$ has its minimum, yet there are exceptions. The distance between the respective draws related to the peak force and to the minimum value of $d_\mathrm{s}$ may also be relatively great.

By modifying both the limbs and the wheels, we may find a more efficient FD curve without too drastic changes on the peak force, the initial value of draw, the full draw or the let-off. For example, let us choose two more virtual bows, $B_2$ and $B_3$. The initial parameters of the bows $B_1$, $B_2$ and $B_3$ are presented in Table 1.

Table 1 The initial parameters of the bows $B_1$, $B_2$ and $B_3$

The upper eccentric system of the bow $B_1$ in the initial position is quite the same as seen in Fig. 1. The upper eccentric systems of the bows $B_2$ and $B_3$ in the initial position with axle point as origin are presented in Figs. 8 and 9, where the bow riser leaves on the left side as in Fig. 1. Note that $B_2$ can be also treated with the earlier original round-wheel model without this paper. The calculated FD curves of $B_1$, $B_2$ and $B_3$ are presented in Fig. 10 with the before mentioned limiting FD curve for the bow $B_3$.

Fig. 8

The upper eccentric system of the bow $B_2$ in the initial position. The diameter of the axle is 4.75 mm

Fig. 9

The upper eccentric system of the bow $B_3$ in the initial position. The diameter of the axle is 4.75 mm

Fig. 10

The force–draw curves of the bows $B_1$, $B_2$ and $B_3$ with the limiting FD curve for the bow $B_3$

From Fig. 10 and from Table 2 we notice that the peak forces and the full draws of the bows $B_1$, $B_2$ and $B_3$ are quite the same. The forces in full draw are rather near each other, but the shapes of the curves differs distinctly, as can be seen from Fig. 10.

Table 2 The bows $B_1$, $B_2$ and $B_3$

It is interesting that the FD curve of the bow $B_3$ resembles the FD curves of some single-cam compound bows, as presented for example in [11].

According to q values of Table 2 the bow $B_3$ is the best, and also $B_2$ is a clear improvement when compared to the original bow $B_1$. The stored energy of the bow $B_3$ is 18.5% greater and the value of q 18.8% greater than the respective values of the bow $B_1$. Evidently it is possible to search such parameters that q is even greater, while the peak force, the let-off, the initial value of draw and also the full draw remain almost unchanged. With the model it is also easy to check for example that the maximum values of the static string and cable tensions are not too high. On the other hand, while the bow with appropriate limb and wheel modifications seems better, the model is static and does not take account of the possible effects of the modified wheel and limb masses or limb material on the dynamic performance of the bow.

The computations were checked as in [4] using the following two expressions for the energy stored in the bow,

$$\begin{aligned} V(D)=\int _{D_{0}}^D F(D) \, \mathrm {d}D \end{aligned}$$

(17)

and

$$\begin{aligned} V(\theta )=ALk(\theta ^{2}-\theta _{0}^{2}+2\theta _{0}\theta _{\mathrm{U}}-2\theta \theta _{\mathrm{U}}). \end{aligned}$$

(18)

One by one, the cubic spline function with the respective parameter values was fitted to the (D, F)-values of the bows of Table 2 and then integrated numerically. Using the draw from the initial position to the full draw and 2000 values for the prime variable $\alpha$, it was found that the differences between the calculations based on Eqs. (17) and (18) were greatest for the bow $B_3$, though also then $<10^{-6}$ J.

Another check was made by using the twin-cam model of paper [6]. The string and the cable cam radius were gained by cubic spline interpolation of the polar transformations of the known eccentrics of bows $B_1$, $B_2$ and $B_3$. Again, using the same draw domain and 2000 values for the prime variable, the procedure described in paper [6] was executed separately with every value of the prime variable, resulting also in the respective values of D and F. For comparing the force values with the same value of draw, the cubic spline function was fitted to the calculated (D, F)-values. The force differences between the offset-eccentric model and the twin-cam model with the same draw values were again greatest for the bow $B_3$, yet $<0.05$ N.

4 Conclusion

A model of the twin-round-wheel compound bow with offset between eccentric centres is introduced. It was found that the parameters related to the eccentrics have relatively the greatest effect on the FD curve. The internal consistency of the model was tested, and the model was also checked with the former twin-cam compound bow model.

Two static quality coefficients for the compound bow were introduced, $q_\mathrm{F}$ for the FD curve and q for the whole bow. A theoretical limit, which is independent of the pulley system, was also concluded for the FD curve of the compound bow.

It was demonstrated that also the original round-wheel model can be used for designing the round-wheel compound bow more effective, when with the help of the offset-eccentric model presented here, even more energetic compound bows with round eccentrics can be created. For an example commercial bow, 18.5% increment of energy and 18.8% increment of quality coefficient q is achievable by modifying only the eccentric systems and the spring constant k of the limbs. Finally, the reader is reminded that the model is static only, hence the dynamical performance of the bow must be estimated by other means.

Appendix: A limit for the FD curve

Let us first choose a traditional bow with the positive initial values g, L, A, $\theta _\mathrm{U}$, k and $e_0$, and with assumptions

$$\begin{aligned} 0< \theta< 180 ^{\circ }, \quad 0< \varphi _t < 90^{\circ } \end{aligned}$$

(19)

and

$$\begin{aligned} \varphi _t + \theta \le 180^{\circ }. \end{aligned}$$

(20)

The inequation (20) follows from the fact that if the line of the elastic portion of the limb is parallel to the line of the half-string, it is not sensible to draw the bow any more. The angle $\varphi _\mathrm{t}$, the draw $D_\mathrm{t}$ and the value of the force $F_\mathrm{t}$ with given $\theta$ can then be calculated from Eqs. (14), (11) and (16).

Let us now consider the round-wheel compound bow with the same initial values g, L, A, $\theta _\mathrm{U}$, k and $e_0$. We shall further make the assumptions

$$\begin{aligned} 0< \varphi< 90 ^{\circ },\quad 0< \delta < 90 ^{\circ } \end{aligned}$$

(21)

$$\begin{aligned} 0 \le d_\mathrm{R}< R, \quad 0 \le d < r. \end{aligned}$$

(22)

Then from Eq. (5) we notice that

$$\begin{aligned} d_\mathrm{s}>0, \quad d_\mathrm{c}>0. \end{aligned}$$

(23)

Let us suppose that the absolute value of the force acting on the arrow is equivalent to the force acting on the arrow for the before mentioned traditional bow with the same initial values and also the same values of $\theta$ and e. Then from Eqs. (15) and (16) we get

$$\begin{aligned} \frac{\sin \varphi }{\sin (\theta +\varphi )+\frac{2d_\mathrm{s}}{d_\mathrm{c}}\sin \theta \cos \delta }=\frac{\sin \varphi _\mathrm{t}}{\sin (\theta +\varphi _\mathrm{t})}. \end{aligned}$$

(24)

Fig. 11

The upper part of the round-wheel compound bow in drawn position with the respective traditional bow half-string of length $e_0/2$. Note that $\varepsilon$ is here negative

With Eqs. (19)–(23) we get from Eq. (24) after some trigonometric manipulation

$$\begin{aligned} \tan \varphi _\mathrm{t} =\frac{\sin \varphi }{\cos \varphi +\frac{2d_\mathrm{s}}{d_\mathrm{c}}\cos \delta } < \tan \varphi, \end{aligned}$$

(25)

so indeed $\varphi _\mathrm{t} < \varphi$, as shown in Fig. 11. The difference between the draws can be seen from Fig. 11, it is

$$\begin{aligned} D-D_\mathrm{t}=\frac{d_\mathrm{s}}{\cos \varphi }+\frac{e}{2} \tan \varphi - \frac{e}{2} \tan \varphi _\mathrm{t}. \end{aligned}$$

(26)

Remembering Eq. (25) and the assumptions $d_\mathrm{s}>0$ and $0< \varphi < 90^{\circ }$, the right side of Eq. (26) is always $>0$, so $D_\mathrm{t} < D$. In the initial position $\varphi =\varphi _\mathrm{t} =0$, when from Eq. (26) we notice that also then $D-D_\mathrm{t}>0$.

Thus, when a horizontal force is targeted to the midpoint of the string of the round-wheel compound bow, the draw of the respective traditional bow with the same limb and riser parameter values is always the least. It should also be noted that with minor changes a similar reasoning can be conducted with the twin-cam model of [6], resulting in the same outcome.