Skip to main content
SpringerLink
Log in

Movement of Dirac points and band gaps in graphyne under rotating strain

  • Research Article
  • Published:
Nano Research Aims and scope Submit manuscript

Abstract

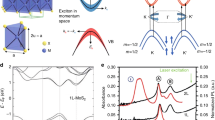
The introduction of lattice anisotropy causes Dirac cones to shift in response to the applied strain, leaving a pseudogap at the original Dirac points. Here, a group-theory analysis is combined with first-principles calculations to reveal the movement characteristics of Dirac points and band gaps in various graphynes under rotating uniaxial and shear strains. Graphene, where linear effects dominate, is different from α-, β-, and γ-graphynes, which generate strong nonlinear responses due to their bendable acetylenic linkages. However, the linear components of the electronic response, which are essential in determining material performance such as intrinsic carrier mobility due to electron–phonon coupling, can be readily separated, and are well described by a unified theory. The movement of the Dirac points in α-graphyne is circular under a rotating strain, and the pseudogap opening is isotropic with a magnitude of only 2% that in graphene. In comparison, the movement in β-graphyne is elliptical and the center is displaced from the origin. For γ-graphyne, three branches of gaps change with the applied strains with a sine/cosine dependence on the strain angle. The developed methodology is useful in determining the electronic response to various strains of Dirac materials and two-dimensional semiconductors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Avouris, P.; Chen, Z. H.; Perebeinos, V. Carbon-based electronics. Nature Nanotechnol. 2007, 2, 605–615.

    Article  Google Scholar 

  2. Enyashin, A. N.; Ivanovskii, A. L. Graphene allotropes. Phys. Status Solidi B 2011, 248, 1879–1883.

    Article  Google Scholar 

  3. Wang, J. Y.; Deng, S. B.; Liu, Z. F.; Liu, Z. R. The rare two-dimensional materials with Dirac cones. Natl. Sci. Rev. 2015, 2, 22–39.

    Article  Google Scholar 

  4. Novoselov, K. S.; Geim, A. K.; Morozov, S. V.; Jiang, D.; Zhang, Y.; Dubonos, S. V.; Grigorieva, I. V.; Firsov, A. A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669.

    Article  Google Scholar 

  5. Castro Neto, A. H.; Guinea, F.; Peres, N. M. R.; Novoselov, K. S.; Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162.

    Article  Google Scholar 

  6. Malko, D.; Neiss, C.; Viñes, F.; Görling, A. Competition for graphene: Graphynes with direction-dependent Dirac cones. Phys. Rev. Lett. 2012, 108, 086804.

    Article  Google Scholar 

  7. Baughman, R. H.; Eckhardt, H.; Kertesz, M. Structure property predictions for new planar forms of carbon: Layered phases containing sp 2 and sp atoms. J. Chem. Phys. 1987, 87, 6687–6699.

    Article  Google Scholar 

  8. Haley, M. M.; Brand, S. C.; Pak, J. J. Carbon networks based on dehydrobenzoannulenes: Synthesis of graphdiyne substructures. Angew. Chem., Int. Ed. 1997, 36, 836–838.

    Article  Google Scholar 

  9. Marsden, J. A.; Haley, M. M. Carbon networks based on dehydrobenzoannulenes. 5. Extension of two-dimensional conjugation in graphdiyne nanoarchitectures. J. Org. Chem. 2005, 70, 10213–10226.

    Article  Google Scholar 

  10. Yin, W.-J.; Xie, Y.-E.; Liu, L.-M.; Wang, R.-Z.; Wei, X.-L.; Lau, L.; Zhong, J.-X.; Chen, Y.-P. R-graphyne: A new twodimensional carbon allotrope with versatile Dirac-like point in nanoribbons. J. Mater. Chem. A 2013, 1, 5341–5346.

    Article  Google Scholar 

  11. Wang, X. Q.; Li, H. D.; Wang, J. T. Prediction of a new two-dimensional metallic carbon allotrope. Phys. Chem. Chem. Phys. 2013, 15, 2024–2030.

    Article  Google Scholar 

  12. Haley, M. M. Synthesis and properties of annulenic subunits of graphyne and graphdiyne nanoarchitectures. Pure Appl. Chem. 2008, 80, 519–532.

    Article  Google Scholar 

  13. Li, Y. J.; Xu, L.; Liu, H. B.; Li, Y. L. Graphdiyne and graphyne: From theoretical predictions to practical construction. Chem. Soc. Rev. 2014, 43, 2572–2586.

    Article  Google Scholar 

  14. Peng, Q.; Dearden, A. K.; Crean, J.; Han, L.; Liu, S.; Wen, X.; De, S. New materials graphyne, graphdiyne, graphone, and graphane: Review of properties, synthesis, and application in nanotechnology. Nanotechnol. Sci. Appl. 2014, 7, 1–29.

    Article  Google Scholar 

  15. Tahara, K.; Yamamoto, Y.; Gross, D. E.; Kozuma, H.; Arikuma, Y.; Ohta, K.; Koizumi, Y.; Gao, Y.; Shimizu, Y.; Seki, S. et al. Syntheses and properties of graphyne fragments: Trigonally expanded dehydrobenzo[12]annulenes. Chem.—Eur. J. 2013, 19, 11251–11260.

    Article  Google Scholar 

  16. Desroches, M.; Courtemanche, M.-A.; Rioux, G.; Morin, J.-F. Synthesis and properties of rhomboidal macrocyclic subunits of graphdiyne-like nanoribbons. J. Org. Chem. 2015, 80, 10634–10642.

    Article  Google Scholar 

  17. Cirera, B.; Zhang, Y.-Q.; Björk, J.; Klyatskaya, S.; Chen, Z.; Ruben, M.; Barth, J. V.; Klappenberger, F. Synthesis of extended graphdiyne wires by vicinal surface templating. Nano Lett. 2014, 14, 1891–1897.

    Article  Google Scholar 

  18. Li, G. X.; Li, Y. L.; Liu, H. B.; Guo, Y. B.; Li, Y. J.; Zhu, D. B. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010, 46, 3256–3258.

    Article  Google Scholar 

  19. Li, G. X.; Li, Y. L.; Qian, X. M.; Liu, H. B.; Lin, H. W.; Chen, N.; Li, Y. J. Construction of tubular molecule aggregations of graphdiyne for highly efficient field emission. J. Phys. Chem. C 2011, 115, 2611–2615.

    Article  Google Scholar 

  20. Zhou, J. Y.; Gao, X.; Liu, R.; Xie, Z. Q.; Yang, J.; Zhang, S. Q.; Zhang, G. M.; Liu, H. B.; Li, Y. L.; Zhang, J. et al. Synthesis of graphdiyne nanowalls using acetylenic coupling Reaction. J. Am. Chem. Soc. 2015, 137, 7596–7599.

    Article  Google Scholar 

  21. Gao, X.; Zhou, J. Y.; Du, R.; Xie, Z. Q.; Deng, S. B.; Liu, R.; Liu, Z. F.; Zhang, J. Robust superhydrophobic foam: A graphdiyne-based hierarchical architecture for oil/water separation. Adv. Mater. 2016, 28, 168–173.

    Article  Google Scholar 

  22. Zheng, J. J.; Zhao, X.; Zhao, Y.; Gao, X. Two-dimensional carbon compounds derived from graphyne with chemical properties superior to those of graphene. Sci. Rep. 2013, 3, 1271.

    Article  Google Scholar 

  23. Huang, H. Q.; Duan, W. H.; Liu, Z. R. The existence/absence of Dirac cones in graphynes. New J. Phys. 2013, 15, 023004.

    Article  Google Scholar 

  24. Li, Z. Z.; Wang, J. Y.; Liu, Z. R. Intrinsic carrier mobility of Dirac cones: The limitations of deformation potential theory. J. Chem. Phys. 2014, 141, 144107.

    Article  Google Scholar 

  25. Chen, J. M.; Xi, J. Y.; Wang, D.; Shuai, Z. G. Carrier mobility in graphyne should be even larger than that in graphene: A theoretical prediction. J. Phys. Chem. Lett. 2013, 4, 1443–1448.

    Article  Google Scholar 

  26. Ouyang, T.; Hu, M. Thermal transport and thermoelectric properties of beta-graphyne nanostructures. Nanotechnology 2014, 25, 245401.

    Article  Google Scholar 

  27. Bardeen, J.; Shockley, W. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 1950, 80, 72–80.

    Article  Google Scholar 

  28. Li, Y.; Jiang, X. W.; Liu, Z. F.; Liu, Z. R. Strain effects in graphene and graphene nanoribbons: The underlying mechanism. Nano Res. 2010, 3, 545–556.

    Article  Google Scholar 

  29. Yang, L.; Han, J. Electronic structure of deformed carbon nanotubes. Phys. Rev. Lett. 2000, 85, 154–157.

    Article  Google Scholar 

  30. Mohr, M.; Papagelis, K.; Maultzsch, J.; Thomsen, C. Twodimensional electronic and vibrational band structure of uniaxially strained graphene from ab initio calculations. Phys. Rev. B 2009, 80, 205410.

    Article  Google Scholar 

  31. Vozmediano, M. A. H.; Katsnelson, M. I.; Guinea, F. Gauge fields in graphene. Phys. Rep. 2010, 496, 109–148.

    Article  Google Scholar 

  32. Pereira, V. M.; Castro Neto, A. H. Strain engineering of graphene’s electronic structure. Phys. Rev. Lett. 2009, 103, 046801.

    Article  Google Scholar 

  33. Pereira, V. M.; Castro Neto, A. H.; Peres, N. M. R. Tightbinding approach to uniaxial strain in graphene. Phys. Rev. B 2009, 80, 045401.

    Article  Google Scholar 

  34. Farjam, M.; Rafii-Tabar, H. Uniaxial strain on gapped graphene. Phys. E 2010, 42, 2109–2114.

    Article  Google Scholar 

  35. Wang, J. Y.; Zhao, R. Q.; Yang, M. M.; Liu, Z. F.; Liu, Z. R. Inverse relationship between carrier mobility and bandgap in graphene. J. Chem. Phys. 2013, 138, 084701.

    Article  Google Scholar 

  36. Montambaux, G.; Piéchon, F.; Fuchs, J. N.; Goerbig, M. O. Merging of Dirac points in a two-dimensional crystal. Phys. Rev. B 2009, 80, 153412.

    Article  Google Scholar 

  37. Dvorak, M.; Wu, Z. G. Dirac point movement and topological phase transition in patterned graphene. Nanoscale 2015, 7, 3645–3650.

    Article  Google Scholar 

  38. Zhu, S.-L.; Wang, B. G.; Duan, L. M. Simulation and detection of Dirac fermions with cold atoms in an optical lattice. Phys. Rev. Lett. 2007, 98, 260402.

    Article  Google Scholar 

  39. Wunsch, B.; Guinea, F.; Sols, F. Dirac-point engineering and topological phase transitions in honeycomb optical lattices. New J. Phy. 2008, 10, 103027.

    Article  Google Scholar 

  40. Tarruell, L.; Greif, D.; Uehlinger, T.; Jotzu, G.; Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 2012, 483, 302–305.

    Article  Google Scholar 

  41. Hasegawa, Y.; Kishigi, K. Merging Dirac points and topological phase transitions in the tight-binding model on the generalized honeycomb lattice. Phys. Rev. B 2012, 86, 165430.

    Article  Google Scholar 

  42. Wang, L.; Fu, L. B. Interaction-induced merging of Dirac points in non-Abelian optical lattices. Phys. Rev. A 2013, 87, 053612.

    Article  Google Scholar 

  43. Ibañez-Azpiroz, J.; Eiguren, A.; Bergara, A.; Pettini, G.; Modugno, M. Self-consistent tight-binding description of Dirac points moving and merging in two-dimensional optical lattices. Phys. Rev. A 2013, 88, 033631.

    Article  Google Scholar 

  44. Wu, C. J.; Bergman, D.; Balents, L.; Das Sarma, S. Flat bands and wigner crystallization in the honeycomb optical lattice. Phys. Rev. Lett. 2007, 99, 070401.

    Article  Google Scholar 

  45. Yue, Q.; Chang, S. L.; Kang, J.; Qin, S. Q.; Li, J. B. Mechanical and electronic properties of graphyne and its family under elastic strain: Theoretical predictions. J. Phys. Chem. C 2013, 117, 14804–14811.

    Article  Google Scholar 

  46. Zhang, S. Q.; Wang, J. Y.; Li, Z. Z.; Zhao, R. Q.; Tong, L. M.; Liu, Z. F.; Zhang, J.; Liu, Z. R. Raman spectra and corresponding strain effects in graphyne and graphdiyne. J. Phys. Chem. C 2016, 120, 10605–10613.

    Article  Google Scholar 

  47. Lin, Z. R.; Liu, Z. R. Spin-1 Dirac-Weyl fermions protected by bipartite symmetry. J. Chem. Phys. 2015, 143, 214109.

    Article  Google Scholar 

  48. Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 1996, 6, 15–50.

    Article  Google Scholar 

  49. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab inito total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186.

    Article  Google Scholar 

  50. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561.

    Article  Google Scholar 

  51. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269.

    Article  Google Scholar 

  52. Perdew, J. P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868.

    Article  Google Scholar 

  53. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775.

    Article  Google Scholar 

  54. Cranford, S. W.; Buehler, M. J. Mechanical properties of graphyne. Carbon 2011, 49, 4111–4121.

    Article  Google Scholar 

  55. Peng, Q.; Ji, W.; De, S. Mechanical properties of graphyne monolayers: A first-principles study. Phys. Chem. Chem. Phys. 2012, 14, 13385–13391.

    Article  Google Scholar 

  56. Yang, Y. L.; Xu, X. M. Mechanical properties of graphyne and its family–A molecular dynamics investigation. Comput. Mater. Sci. 2012, 61, 83–88.

    Article  Google Scholar 

  57. Zhang, Y. Y.; Pei, Q. X.; Wang, C. M. Mechanical properties of graphynes under tension: A molecular dynamics study. Appl. Phys. Lett. 2012, 101, 081909.

    Article  Google Scholar 

  58. Couto, R.; Silvestre, N. Finite element modelling and mechanical characterization of graphyne. J. Nanomater. 2016, 2016, Article ID 7487049.

    Google Scholar 

  59. Cranford, S. W.; Brommer, D. B.; Buehler, M. J. Extended graphynes: Simple scaling laws for stiffness, strength and fracture. Nanoscale 2012, 4, 7797–7809.

    Article  Google Scholar 

  60. Liu, M. J.; Artyukhov, V. I.; Lee, H.; Xu, F. B.; Yakobson, B. I. Carbyne from first principles: Chain of C atoms, a nanorod or a nanorope. ACS Nano 2013, 7, 10075–10082.

    Article  Google Scholar 

  61. Gui, G.; Li, J.; Zhong, J. X. Band structure engineering of graphene by strain: First-principles calculations. Phys. Rev. B 2008, 78, 075435.

    Article  Google Scholar 

  62. Kim, B. G.; Choi, H. J. Graphyne: Hexagonal network of carbon with versatile Dirac cones. Phys. Rev. B 2012, 86, 115435.

    Article  Google Scholar 

  63. van Miert, G.; Juričić, V.; Smith, C. M. Tight-binding theory of spin-orbit coupling in graphynes. Phys. Rev. B 2014, 90, 195414.

    Article  Google Scholar 

  64. Kang, J.; Li, J. B.; Wu, F. M.; Li, S.-S.; Xia, J.-B. Elastic, electronic, and optical properties of two-dimensional graphyne sheet. J. Phys. Chem. C 2011, 115, 20466–20470.

    Article  Google Scholar 

  65. Lang, H. F.; Zhang, S. Q.; Liu, Z. R. Mobility anisotropy of two-dimensional semiconductors. Phys. Rev. B 2016, 94, 235306.

    Article  Google Scholar 

Download references

Acknowledgements

The authors thank Shuqing Zhang, Zeren Lin, and Ting Cheng for helpful discussions. The work was supported by the National Natural Science Foundation of China (No. 21373015).

Author information

Authors and Affiliations

  1. College of Chemistry and Molecular Engineering, Center for Nanochemistry, State Key Laboratory for Structure Chemistry of Unstable and Stable Species, and Beijing National Laboratory for Molecular Sciences (BNLMS), Peking University, Beijing, 100871, China

    Zhenzhu Li, Zhongfan Liu & Zhirong Liu

Authors
  1. Zhenzhu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhongfan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhirong Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhirong Liu.

Electronic supplementary material

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Z., Liu, Z. & Liu, Z. Movement of Dirac points and band gaps in graphyne under rotating strain. Nano Res. 10, 2005–2020 (2017). https://doi.org/10.1007/s12274-016-1388-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12274-016-1388-z

Keywords

Search

Navigation