Abstract
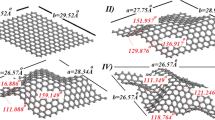
A tight-binding analytic framework is combined with first-principles calculations to reveal the mechanism underlying the strain effects on electronic structures of graphene and graphene nanoribbons (GNRs). It provides a unified and precise formulation of the strain effects under various circumstances-including the shift of the Fermi (Dirac) points, the change in band gap of armchair GNRs with uniaxial strain in a zigzag pattern and its insensitivity to shear strain, and the variation of the k-range of edge states in zigzag GNRs under uniaxial and shear strains which determine the gap behavior via the spin polarization interaction.

Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Geim, A. K.; Novoselov, K. S. The rise of graphene. Nat. Mater. 2007, 6, 183–191.
Cresti, A.; Nemec, N.; Biel, B.; Niebler, G.; Triozon, F.; Cuniberti, G.; Roche, S. Charge transport in disordered graphene-based low dimensional materials. Nano Res. 2008, 1, 361–394.
Yan, Q. M.; Huang, B.; Yu, J.; Zheng, F. W.; Zang, J.; Wu, J.; Gu, B. L.; Liu, F.; Duan, W. H. Intrinsic current-voltage characteristics of graphene nanoribbon transistors and effect of edge doping. Nano Lett. 2007, 7, 1469–1473.
Novoselov, K. S.; Geim, A. K.; Morozov, S. V.; Jiang, D.; Zhang, Y.; Dubonos, S. V.; Grigorieva, I. V.; Firsov, A. A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669.
Biel, B.; Blase, X.; Triozon, F.; Roche, S. Anomalous doping effects on charge transport in graphene nanoribbons. Phys. Rev. Lett. 2009, 102, 096803.
Pereira, V. M.; Neto, A. H. C. Strain engineering of graphene’s electronic structure. Phys. Rev. Lett. 2009, 103, 046801.
Ferralis, N.; Maboudian, R.; Carraro, C. Evidence of structural strain in epitaxial graphene layers on 6H-SiC(0001). Phys. Rev. Lett. 2008, 101, 156801.
Borysiuk, J.; Bozek, R.; Strupinski, W.; Wysmolek, A.; Grodecki, K.; Steapniewski, R.; Baranowski, J. M. Transmission electron microscopy and scanning tunneling microscopy investigations of graphene on 4H-SiC(0001). J. Appl. Phys. 2009, 105, 023503.
Sun, G. F.; Jia, J. F.; Xue, Q. K.; Li, L. Atomic-scale imaging and manipulation of ridges on epitaxial graphene on 6H-SiC(0001). Nanotechnology 2009, 20, 355701.
Jun, S. Density-functional study of edge stress in graphene. Phys. Rev. B 2008, 78, 073405.
Huang, B.; Liu, M.; Su, N. H.; Wu, J.; Duan, W. H.; Gu, B. L.; Liu, F. Quantum manifestations of graphene edge stress and edge instability: A first-principles study. Phys. Rev. Lett. 2009, 102, 166404.
Lee, C.; Wei, X. D.; Kysar, J. W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388.
Mohiuddin, T. M. G.; Lombardo, A.; Nair, R. R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D. M.; Galiotis, C.; Marzari, N.; Novoselov, K. S.; Geim, A. K.; Ferrai, A. C. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 205433.
Ni, Z. H.; Yu, T.; Lu, Y. H.; Wang, Y. Y.; Feng, Y. P.; Shen, Z. X. Uniaxial strain on graphene: Raman spectroscopy study and band-gap opening. ACS Nano 2008, 2, 2301–2305.
Kim, K. S.; Zhao, Y.; Jang, H.; Lee, S. Y.; Kim, J. M.; Kim, K. S.; Ahn, J. -H.; Kim, P.; Choi, J. -Y.; Hong, B. H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710.
Bao, W. Z.; Miao, F.; Chen, Z.; Zhang, H.; Jang, W. Y.; Dames, C.; Lau, C. N. Controlled ripple texturing of suspended graphene and ultrathin graphite membranes. Nat. Nanotechnol. 2009, 4, 562–566.
Lee, M. L.; Fitzgerald, E. A.; Bulsara, M. T.; Currie, M. T.; Lochtefeld, A. Strained Si, SiGe, and Ge channels for highmobility metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2005, 97, 011101.
Yang, L.; Han, J. Electronic structure of deformed carbon nanotubes. Phys. Rev. Lett. 2000, 85, 154–157.
Minot, E. D.; Yaish, Y.; Sazonova, V.; Park, J. Y.; Brink, M.; McEuen, P. L. Tuning carbon nanotube band gaps with strain. Phys. Rev. Lett. 2003, 90, 156401.
Teague, M. L.; Lai, A. P.; Velasco, J.; Hughes, C. R.; Beyer, A. D.; Bockrath, M. W.; Lau, C. N.; Yeh, N. C. Evidence for strain-induced local conductance modulations in single-layer graphene on SiO2. Nano Lett. 2009, 9, 2542–2546.
Chang, C. P.; Wu, B. R.; Chen, R. B.; Lin, M. F. Deformation effect on electronic and optical properties of nanographite ribbons. J. Appl. Phys. 2007, 101, 063506.
Gui, G.; Li, J.; Zhong, J. X. Band structure engineering of graphene by strain: First-principles calculations. Phys. Rev. B 2008, 78, 075435.
Farjam, M.; Rafii-Tabar, H. Comment on “Band structure engineering of graphene by strain: First-principles calculations”. Phys. Rev. B 2009, 80, 167401.
Gui, G.; Li, J.; Zhong, J. X. Reply to “Comment on ‘Band structure engineering of graphene by strain: First-principles calculations.’”. Phys. Rev. B 2009, 80, 167402.
Sun, L.; Li, Q. X.; Ren, H.; Su, H. B.; Shi, Q. W.; Yang, J. L. Strain effect on electronic structures of graphene nanoribbons: A first-principles study. J. Chem. Phys. 2008, 129, 074704.
Pereira, V. M.; Neto, A. H. C.; Peres, N. M. R. Tight-binding approach to uniaxial strain in graphene. Phys. Rev. B 2009, 80, 045401.
Mohr, M.; Papagelis, K.; Maultzsch, J.; Thomsen, C. Two-dimensional electronic and vibrational band structure of uniaxially strained graphene from ab initio calculations. Phys. Rev. B 2009, 80, 205410.
Hod, O.; Scuseria, G. E. Electromechanical properties of suspended graphene nanoribbons. Nano Lett. 2009, 9, 2619–2622.
Alam, K. Uniaxial strain effects on the performance of a ballistic top gate graphene nanoribbon on insulator transistor. IEEE Trans. Nanotechnol. 2009, 8, 528–534.
Pellegrino, F. M. D.; Angilella, G. G. N.; Pucci, R. Strain effect on the optical conductivity of graphene. Phys. Rev. B 2010, 81, 035411.
Choi, S. M.; Jhi, S. H.; Son, Y. W. Effects of strain on electronic properties of graphene. Phys. Rev. B 2010, 81, 081407.
Rasuli, R.; Rafii-Tabar, H.; Zad, A. I. Strain effect on quantum conductance of graphene nanoribbons from maximally localized Wannier functions. Phys. Rev. B 2010, 81, 125409.
Poetschke, M.; Rocha, C. G.; Torres, L. E. F. F.; Roche, S.; Cuniberti, G. Modeling graphene-based nanoelectromechanical devices. Phys. Rev. B 2010, 81, 193404.
Hossain, M. Z. Quantum conductance modulation in graphene by strain engineering. Appl. Phys. Lett. 2010, 96, 143118.
Lu, Y.; Guo, J. Band gap of strained graphene nanoribbons. Nano Res. 2010, 3, 189–199.
de Andres, P. L.; Verges, J. A. First-principles calculation of the effect of stress on the chemical activity of graphene. Appl. Phys. Lett. 2008, 93, 171915.
Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 1996, 6, 15–50.
Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775.
Perdew, J. P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation-energy. Phys. Rev. B 1992, 45, 13244–13249.
Harrison, W. A. Electronic structure and the properties of solids: The physics of the chemical bond; Dover Publications: New York, 1989.
Ribeiro, R. M.; Pereira, V. M.; Peres, N. M. R.; Briddon, P. R.; Neto, A. H. C. Strained graphene: Tight-binding and density functional calculations. New J. Phys. 2009, 11, 115002.
Castro Neto, A. H.; Guinea, F.; Peres, N. M. R.; Novoselov, K. S.; Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162.
Hasegawa, Y.; Konno, R.; Nakano, H.; Kohmoto, M. Zero modes of tight-binding electrons on the honeycomb lattice. Phys. Rev. B 2006, 74, 033413.
Son, Y. W.; Cohen, M. L.; Louie, S. G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803.
Saito, R.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M. S. Electronic-structure of chiral graphene tubules. Appl. Phys. Lett. 1992, 60, 2204–2206.
Mintmire, J. W.; Dunlap, B. I.; White, C. T. Are fullerene tubules metallic? Phys. Rev. Lett. 1992, 68, 631–634.
Zheng, F. W.; Liu, Z. R.; Wu, J.; Duan, W. H.; Gu, B. L. Scaling law of the giant Stark effect in boron nitride nanoribbons and nanotubes. Phys. Rev. B 2008, 78, 085423.
Wakabayashi, K.; Fujita, M.; Ajiki, H.; Sigrist, M. Electronic and magnetic properties of nanographite ribbons. Phys. Rev. B 1999, 59, 8271–8282.
Son, Y. W.; Cohen, M. L.; Louie, S. G. Half-metallic graphene nanoribbons. Nature 2006, 444, 347–349.
Zheng, F. W.; Zhou, G.; Liu, Z. R.; Wu, J.; Duan, W. H.; Gu, B. L.; Zhang, S. B. Half metallicity along the edge of zigzag boron nitride nanoribbons. Phys. Rev. B 2008, 78, 205415.
Fujita, M.; Wakabayashi, K.; Nakada, K.; Kusakabe, K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 1996, 65, 1920–1923.
Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M. S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954–17961.
Gunlycke, D.; Areshkin, D. A.; Li, J. W.; Mintmire, J. W.; White, C. T. Graphene nanostrip digital memory device. Nano Lett. 2007, 7, 3608–3611.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at Springerlink.com
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Li, Y., Jiang, X., Liu, Z. et al. Strain effects in graphene and graphene nanoribbons: The underlying mechanism. Nano Res. 3, 545–556 (2010). https://doi.org/10.1007/s12274-010-0015-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12274-010-0015-7