1 Introduction

Bandit Convex Optimization (BCO) is a type of Online Convex Optimization (OCO) in which we deal with partial information. In BCO, decisions are made between a player and an adversary repeatedly. In each iteration, the player selects a point from a fixed and known convex set. Then the adversary chooses a convex cost function. At the end of the iteration, the only available feedback for the player is the cost of the function at the selected point. In this framework, the player does not have any knowledge about the specific function nor the gradient [1]. The main emphasis of BCO in the machine learning community has been on rigorous theoretical performance analysis of algorithms. However, practical application of BCO algorithms still requires more attention.

BCO has two important advantages in wireless network communication. The first advantage is that the player only needs the cost function feedback of a given action, which facilitates practical implementation. Second, in BCO, the adversary is able to choose among a set of convex functions which can capture network dynamics such as changes in the number of nodes and channel conditions. We argue that since many wireless network optimization problems can be easily formulated as convex problems; BCO is appealing for the wireless networking community. Some potential applications of the convex optimization formulation are pulse shaping filter design, transmit beamforming, network resource allocation, MMSE precoder design for multi-access communication, robust beamforming and optimal linear decentralized estimation.

The main goal of this article is to evaluate the convergence rate of applying a bandit convex optimization algorithm to achieve proportional fair resource allocation in wireless networks. This approach can be implemented by the access point allowing learning of the optimal slot transmission probability only by monitoring the cost function to optimize, i.e., the throughput of the network. This research can help academia as well as practitioners to assess whether bandit convex optimization algorithms can be a practical solution for commercial use. The ultimate goal is to bring optimal channel allocation in WiFi to practice by addressing the limitations of traditional approaches that need to be fed with as well as track changes in network parameters (such as the packet size and data rate used by each node). In this article we perform a comprehensive evaluation of the algorithm, with the aim to assess its convergence rate. To do so, we have evaluated the sensitivity of the algorithm to different learning and network parameters as well as its response to nodes entering/leaving the network. We also evaluate the algorithm behavior when applied in practical settings, where estimates instead of the true value of throughput is fed to the algorithm. Additionally, we evaluate a solution to alleviate the effects of these noisy estimates.

This paper is organized as follows. We first describe the two building blocks needed for understanding the rest of the article. These are, first, the main background on proportional fair allocation in WiFi networks, which is described in Section 2. Second, we describe bandit convex optimization and the proposed algorithm in Section 3. The application of the algorithm to the WiFi setting is then presented in Section 4. After this, we describe the methodology used to evaluate the algorithm in Section 5. Then, Section 6 presents the performance results. Section 7 summarizes the related work in the area of WiFi network proportional fair optimization. Finally, in Section 8 some final remarks are given.

2 IEEE 802.11 background

In this section, we first describe the random back-off operation, then summarize proportional fairness throughput optimization in WiFi networks.

2.1 Random back-off operation

The IEEE 802.11 protocol consists of physical layer and media access control specifications for WLAN communications in various frequency bands ranging from 900 MHz to 60 GHz. The protocols that define WiFi regulations are based on the standards and amendments versions. The fundamental mechanism of the 802.11 protocol is known as the Distributed Coordination Function (DCF). It employs a Carrier Sense Multiple Access/Collision Avoidance (CSMA/CA) method with binary exponential back-off. The DCF default access technique is a two-way handshaking scheme called basic access mechanism, which consists of sending a data packet and waiting for the reception of an acknowledgment.

In DCF when a station wants to send a packet, it monitors the channel. If it senses the channel idle for a specific interval it starts a back-off countdown. This time interval is known as distributed inter-frame space (DIFS). Otherwise, if a station senses the channel busy, it continues to monitor the channel until it is sensed idle for a DIFS. After the channel is sensed idle for a DIFS, the back-off countdown timer starts. DCF operates in a discrete-time back-off scale. The time after each DIFS is slotted and each station is able to start a transmission only at the beginning of each slot time. The duration of this time slot (σ) is specified in the standard and accounts for the propagation delay. Each time a station starts the back-off procedure it initializes CW to CWmin and chooses a random number in (0,CW-1), where CW is the contention window. The back-off timer is then computed as CWσ and it decrements as long as the channel is sensed idle for a time slot. When a transmission is detected on the channel, this timer freezes. The back-off timer is reactivated when the channel is sensed idle for more than DIFS. The CW is doubled after each failed transmission (either due to channel errors or collisions with other simultaneous transmissions). The maximum value of the contention window is equal to \({2^{m} \text {CW}_{min}}\). The value m is the maximum back-off stage and it is a configurable parameter. Once a packet is transmitted, the sender waits for an ACK confirming the correct reception of the packet. If the station that started the transmission does not receive an ACK during the ACK timeout period, it understands that a collision has happened.Footnote 1 Therefore, the station retransmits the packet according to the back-off process. The packet is discarded if it experiences more collisions than the maximum retry limit.

2.2 Throughput optimization in WiFi networks

Throughput in the 802.11 standard depends on the number of active stations and the contention window used by each station. In particular, in multi-rate IEEE 802.11 WLANs, stations that use the DCF and transmit at lower transmission rates make use of the channel for longer periods of time to transmit the same amount of data compared to stations using higher transmission rates. This reduces the throughput of high-rate stations in the WLAN, since less time is available for transmission in the shared medium. This effect is known as performance anomaly. One solution to approach this problem is proportional fair allocation [2].

As done in [2], we formulate proportional fairness as a convex optimization problem whose objective is the sum of logs of throughput of the different stations, which will intrinsically capture fairness while trying to achieve high performance even in a multi-rate scenario. We assume that all the stations (n) are saturated (i.e., stations always have a packet to send) and generate uplink traffic to the network. The optimization problem defined in [2], as many others, considers no doubling of the contention window at each failed attempt, and assumes nodes use a fixed slot transmission probability (τ). Note that τ is then reciprocal of the CW. Let Si(τ) be the throughput of node i, then:

$$ {{S_{i}}(\tau)}=\frac{{P_{{\text{succ}},i}} D_{i}}{\sigma{{P_{\text{idle}}}} + {T_{c}}(1-P_{\text{idle}})}. $$
(1)

The average packet size of the ith station is defined by Di in bits. Psucc,i is the probability of a successful packet transmission of the ith station, i.e., the probability that only station i transmits a packet, and is given by \({P_{{\text {succ}},i}} = {\tau _{i}}{\prod }_{k=1,k\neq i}^{n}(1-\tau _{k})\). The term Pidle is the probability that the channel is idle. When none of the stations attempt to transmit a packet, the probability is defined as \(P_{\text {idle}} = {{\prod }_{k=1}^{n} (1-{\tau _{k}})}\). The term 1 − Pidle is the probability that the channel is busy due to the successful, unsuccessful (collisions) or other stations’ packet transmissions and it is defined by \(1-P_{\text {idle}} = 1 -{{\prod }_{k=1}^{n} (1-{\tau _{k}})}\). The time that the medium remains idle is of duration of an empty timeslot (σ) and the duration of a busy timeslot is denoted as Tc. Therefore, Eq. 1 is the amount of data transmitted at each successful slot over the average duration of a slot.

The duration of a busy timeslot (Tc) considers the mean duration of a successful or collided transmission of node i or other stations’ packet transmissions. A successful transmission includes a DIFS, the data transmission (of duration Tfra), a short inter-frame space (SIFS), which is the amount of time required before sending a response frame, and the transmission of the ACK (of duration Tack). For simplicity, we consider this duration equal for successful transmissions and collisions but the analysis can be easily extended to consider both [3]. Tc can be calculated as follows:

$$ {T_{c} = T_{\text{fra }}+ \text{SIFS} + T_{\text{ack}} + \text{DIFS} }. $$
(2)

In the following, it will be more useful to use the transformed variable \({{x_{i}} = \frac {{\tau _{i}}}{(1-{\tau _{i}})}}\) rather than τi, \({{x_{i}} \in [0,\infty )}\) for τi ∈ [0,1):

$$ {{{S_{i}}(x)}}=\frac{{x_{i}}}{{X(x)}}\frac{D_{i}}{T_{c}}, $$
(3)

where \({{X(x)}} = a+{\prod }_{k=1}^{n} (1+x_{k})-1\) with a = σ/Tc.

The proportional fair optimization problem can then be formulated as [2]:

$$ \begin{array}{@{}rcl@{}} \max.\quad \sum\limits_{i=1}^{n} {\tilde{S_{i}}(x)}, \\ s.t. {{\tilde{S_{i}}(x)}} \leq {\log} \frac{{x_{i}}{D_{i}}}{{X(x)}{T_{c}}}. \end{array} $$
(4)

The constraint certifies that the sum of logs of throughputs is feasible and sits in the rate region. Since the log-transformed rate region \( {\tilde Z}\) is strictly convex, there exists a unique solution that satisfies strong duality and Karush-Kuhn-Tucker (KKT) conditions, which implies a global maximum [2].

The optimization problem in Eq. 4 can be solved explicitly but our aim here is to formulate this problem in a bandit framework so that knowledge of the network parameters is no longer required. This facilitates practical implementation and can help towards the adoption of optimization approaches in commercial WiFi cards, where the selection of the CW used by the stations is generally static.

3 Bandit convex optimization

In bandit convex optimization (BCO) three steps are repeated between the player and the adversary. These three steps can be written for iteration t as:

  • The player chooses a point \({ x_{t}\in K \subseteq R^{d}}\).

  • The adversary chooses a cost function \( {f_{t}\in F\subseteq R^{k}} \).

  • The player observes ft(xt).

Here, xt is a point from a fixed and known convex set. K represents a convex subset of a d-dimensional Euclidean space (\({K \subseteq R^{d}} \)). In addition, all the functions in F are convex [4].

The aim of BCO algorithms is to achieve low regret:

$$ R_{T} = \sum\limits_{t=1}^{T} {{f_{t}}(x_{t})} -{{{\min}_{x\in K} \sum\limits_{t=1}^{T} {f_{t}}(x)}}. $$
(5)

This formulation is known as cumulative regret, which measures the difference between the cumulative loss that is revealed to the player and the best-fixed decision in hindsight after T iterations [1]. To achieve low regret most of the BCO algorithms use Online Gradient Descent (OGD) with estimations of the gradient. In fact, the main complication of BCO is to estimate the gradients of the cost functions. Therefore, many researchers in BCO have investigated methods for estimating these gradients and used their results in BCO algorithms [1].

Flaxman et al. [5] proposed a scheme that combined the estimated gradients with the OGD algorithm of Zinkevich [6], who showed that a simple gradient descent strategy for the player incurs an \({O(\sqrt {T})}\) regret bound [7]. The algorithm of Flaxman et al. uses point evaluations of convex functions to approximately estimate the gradient. The regret bound of this algorithm is shown to be O(T3/4). Agarwal et al. showed that in each round knowing the value of each cost function at two points is almost as useful as knowing the value of each function everywhere, therefore their algorithm has a regret bound of O(T2/3) improving the O(T3/4) bounds achieved by Flaxman et al. However, Flaxman et al. and Agarwal et al. approaches cannot be used in a practical implementation and realistic setting in wireless networks. First, in many settings it is impossible to query cost functions twice in one iteration. Second, the variance of the single point estimators in the approach of Flaxman et al. [5] is large; consequently, speed of convergence is not practical for wireless applications [4, 8].

3.1 Sequential multi-point gradient estimates

We use the multi-point BCO algorithm defined in [4] as it considers a simpler assumption than that of Agarwal [7]. This algorithm is called Online Gradient Descent with Sequential Multi-Point Gradient Estimates (OGD-SEMP) and combines queries from two consecutive iterations to estimate the gradient. The algorithm considers a sequence of auxiliary points y1,y2,... and updates gradient descent as follows:

$$ {{y_{k+1}}} = \prod\limits_{k} (y_{k} - \eta_{k}\tilde{g_{k}}), $$
(6)

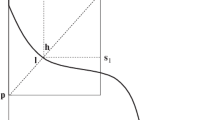
where \(\tilde {g_{k}}\) is the gradient estimate used to update yk+ 1. The parameter ηk is the gradient descent step size and η = {η1,η2,η3,...} is a sequence that shrinks over time. This coefficient affects the speed of convergence of gradient descent. To compute the gradient estimate (\(\tilde {g_{k}}\)), let’s consider yk as the kth point in a one-dimensional convex set within the interval [yk − 𝜖kδk,yk + 𝜖kδk], with 𝜖k a random number that can be either − 1 or 1 and δk a parameter that shrinks over time and determines the length of the interval (see Fig. 1). In the first step, we choose the point \(\bar {x_{t}}\) and obtain its cost function evaluation (\({g_{k}}^{+}\)) as:

$$ \begin{array}{@{}rcl@{}} \bar{x}_{t} &=& y_{k}+\epsilon_{k}\delta_{k},\\ {g_{k}}^{+} &=&{f_{t}(\bar x_{t})}. \end{array} $$
(7)
Fig. 1
figure 1

Sketch of OGD-SEMP

Full size image

In the second step, we choose \(\bar x_{t+1}\) and obtain its cost function evaluation (\({g_{k}}^{-}\)) as:

$$ \begin{array}{@{}rcl@{}} {\bar x_{t+1}} &=& y_{k}-\epsilon_{k}\delta_{k},\\ {g_{k}}^{-} &=& {f_{t+1}(\bar x_{t+1})}. \end{array} $$
(8)

The gradient can be then estimated as follows:

$$ {{\tilde{g_{k}}} = \frac{{g_{k}}^{+} - {g_{k}}^{-}}{2\epsilon_{k}\delta_{k}}}. $$
(9)

\(\tilde {g_{k}}\) is an unbiased estimator of the gradient.

4 Application of BCO to optimize WiFi networks

The Sequential Multi-Point Gradient Estimates algorithm presented in the previous section was applied in a wireless networking optimization use case in [4]. In that article the authors provided the theoretical analysis of this algorithm and evaluated its performance in an unlicensed LTE/WiFi fair coexistence use case. Here we aim to use this method for achieving proportional fair allocation of resources in an IEEE 802.11 network. Using this algorithm, we only need to know the throughput of each station, regardless of other parameters of Eq. 4, to achieve proportional fairness.

Let’s consider a WiFi network with a set of stations transmitting data to an access point in the uplink. Each station might be experiencing different conditions and serving different types of traffic and so its network access parameters (data rate, packet length, etc.) may differ. To optimize the network throughput considering fairness, the access point may select the value of the transmission attempt rate (controlled by the value of CW) of each station so that, as we previously described, proportional fairness is maximized.

To do so we apply the OGD-SEMP algorithm as follows. We assume homogeneous conditions for clarity of illustration. The access point at time t selects a point \(y_{t}=\frac {\tau _{t}}{(1-\tau _{t})}\), then computes xt (as described in Section 3.1),Footnote 2 it disseminates the corresponding CW value to the stations and observes the resulting throughput experienced by each station. It can then compute the cost function: \({f_{t}} ={\sum }_{i=1}^{n} {\tilde {S_{i}}(x_{t})}\). At t + 1 the access point selects xt+ 1 and computes \({f_{t+1}} ={\sum }_{i=1}^{n} {\tilde {S_{i}}(x_{t+1})}\) similarly.

In more detail, in each round t = {1,2,...,T}:

  • The WiFi access point chooses xt.

  • The WiFi network selects the parameters of Eq. 4 (ft), which represent the status of the network (n, Di and Tc).

  • The WiFi access point observes ft(xt).

Note that the notation can be easily extended to heterogeneous conditions by considering \({\bar x_{t} = \{x_{1},x_{2},...,x_{i}\}}\) a vector defining xi for all the stations at time t and \({\bar x_{t+1} = \{x_{1},x_{2},...,x_{i}\}}\) a vector defining xi for all the stations at time t + 1 instead of xt and xt+ 1.

5 Methodology

To evaluate the algorithm’s performance in the WiFi use case we have considered two simulation tools. In the first one we have implemented the algorithm in Matlab and used the true value of the cost function evaluation (Eq. 4) as feedback to the algorithm. This setup allows us to test the performance of our proposed method varying different parameters. Additionally, we have used a custom IEEE 802.11 network simulator to model more realistic situations in which the cost function is not directly available to the access point but needs to be measured.

The custom network simulator consists of two main parts: a channel and a node module. The node module includes a device model with physical, MAC, network and application layers. This simulator was previously used for evaluating OGD-SEMP performance in an unlicensed LTE/WiFi fair coexistence use case [4]. In this article we have extended the simulator to consider the particularities of the WiFi proportional fair use case. In particular, since the contention window values are discrete in our network simulator while the slot transmission probabilities in our model are continuous, we need to convert continuous values of contention window to the desired discrete ones in the simulator. To achieve this, we use CW1 for t1 seconds and CW2 for t2 seconds in a way that the average contention window matches that of the model. We set CW1 and CW2 to the immediately lower/higher allowed value in IEEE 802.11 and compute t1 and t2 accordingly. Recall that τ = 1/CW. The gradient descent algorithm is executed every Δ seconds, with Δ = c(t1 + t2), with c a positive integer. The throughput used by the algorithm as feedback is the average throughput during Δ seconds.

Note that the estimation of throughput in the network simulator is affected by noise caused by the random nature of the back-off and collision probabilities as well as the discretization of the slot transmission probability as described above. These errors are expected to decrease with longer sampling duration (Δ) at the cost of increasing the time of convergence of the bandit algorithm.

In both simulators we have used parameters according to the IEEE 802.11ac standard, we have considered:

$$ T_{\text{fra}}=T_{\text{plcp}}+ \left\lceil \frac{L_{\mathrm{s}} + n_{\text{agg}}(L_{\text{del}} + L_{\text{mac-h}} + D) + L_{\mathrm{t}}}{n_{\text{sym}}} \right\rceil T_{\text{sym}}, $$
(10)
$$ T_{\text{ack}}=T_{\text{plcp}}+\left\lceil \frac{L_{\mathrm{s}} + L_{\text{ack}} + L_{\mathrm{t}}}{n_{\text{sym}}} \right\rceil T_{\text{sym}}, $$
(11)

with physical and channel access parameters as listed in Table 1.

Table 1 Simulation parameters according to IEEE 802.11ac [9]
Full size table

We evaluate the performance of the algorithm using the individual throughput metric at time t (St). By comparing the evolution of throughput over time for different settings we evaluate the algorithm’s performance regarding the time to convergence to the optimum value.

6 Performance evaluation

In this section we present the results of the performance evaluation of the algorithm in the WiFi use case. As described in the previous section we have considered: (i) true cost function evaluations and (ii) noisy gradient estimates coming from an IEEE 802.11 network simulator. This has allowed us to evaluate the sensitivity of the algorithm to the learning parameters (gradient step size, exploration parameter and schedule), packet length, number of nodes and node dynamics as well as noisy cost function evaluations.

6.1 True cost function evaluations

We have set the gradient descent step size as ηk = η/k(3/4) and δk = ω/h(k), with ω as an input parameter and h(k) as some increasing function. We will refer to ω as the exploration parameter and h as the exploration schedule. We vary the number of stations in the network (n) with n = {5,20}. To evaluate the sensitivity of the algorithm to different exploration schedules, we also vary the increasing function h(k). We consider that stations always have a packet to transmit (nodes are saturated) and homogeneous stations (same packet size and transmission probability).

6.1.1 Sensitivity to the learning parameters

First, we evaluate the performance of the algorithm by changing the exploration parameter ω—observe that this parameter controls how far from yk we take the two cost function evaluations at consecutive iterations—and gradient descent step size (ηk). We set h(k) equal to k(3/4) which shrinks the exploration parameter as time goes by.

Figure 2 shows the results of the individual throughput for 5 nodes during 50 iterations. We repeat the same simulations for 30 runs to obtain more accurate results. Therefore, in the figures each color represents one simulation run. Optimal results from [2] are shown in Fig. 2 as straight lines. These results are obtained from the implementation of the algorithm in Matlab with cost function computed using Eq. 4 and IEEE 802.11ac parameters from [9]. We show results with different exploration parameter ω = {0.01,0.1,1} and gradient descent step size η = {0.1,1}.

Fig. 2
figure 2

Individual throughput for n = 5 using different ω, η and h(k) = k(3/4). a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image

Figure 2 illustrates that by fixing η and increasing parameter ω the rate of convergence increases. As we saw in Eq. 7 increasing the value of exploration parameter (ω), we take bigger steps towards the optimum. By fixing parameter ω and increasing η for the range of values considered, the rate of convergence increases as well since we also make larger steps with bigger gradient descent step sizes. It can be seen that for exploration parameter equal to {0.01,0.1,1} and gradient descent step size equal to 1, the algorithm converges to the optimum value after a few number of iterations (< 20).

6.1.2 Sensitivity to the number of nodes

Here we keep the algorithm setup same as above and increase the number of nodes. Figure 3 illustrates the individual throughput of a network of 20 nodes. By comparing Figs. 2 and 3, we observe, in case of η = 1, that for the same value of ω the algorithm converges to the optimum faster when more nodes are considered. The reason for this behavior is illustrated in Fig. 4. This figure shows the shape of the objective function for the different number of nodes. As it is shown, the more nodes in the network, the steeper the cost function, i.e., gradients are larger. Note that the difference between the minimum value of the convex function and its maximum is bigger for n = 20. This means that the algorithm makes larger steps at each iteration and reaches the optimum faster. For this case the algorithm converges in around 10 iterations or less for ω = {0.01,0.1,1} and η = 1.

Fig. 3
figure 3

Individual throughput for n = 20 using different ω, η and h(k) = k(3/4). a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image
Fig. 4
figure 4

Shape of the objective functions for a n = 5 and b n = 20

Full size image

6.1.3 Sensitivity to the exploration schedules

In this set of simulations we use the same setup as in the previous subsection but we change the exploration schedule to h(k) = k(1/2). The goal here is to evaluate the sensitivity of the algorithm to different exploration schedules. Similarly to Figs. 2 and 3, Figs. 5 and 6 show the individual throughput for different values of ω, η and h(k) = k(1/2). We can observe that with h(k) = k(1/2), the convergence speed is almost the same as with h(k) = k(3/4). Only for the case n = 5, ω = 1 and η = 1 (Fig. 2f and Fig. 5f), we observe that the convergence speed in Fig. 2f with h(k) = k(3/4) is slightly faster than in Fig. 5f with h(k) = k(1/2). These results show that the sensitivity of the algorithm to the exploration schedule is negligible for the exploration schedules considered.

Fig. 5
figure 5

Individual throughput for n = 5 using different ω, η and h(k) = k(1/2). a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image
Fig. 6
figure 6

Individual throughput for n = 20 using different ω, η and h(k) = k(1/2). a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image

This means that the impact of h(k) compared to the gradient descent step size η, exploration parameter ω and gradients is low. We also see, as before, that by increasing the number of nodes in the network, the individual throughput value converges to its optimum value faster, in general (see Fig. 6).

6.1.4 Sensitivity to the packet length

To evaluate the performance of the algorithm for different packet sizes, we keep the algorithm setup same as in Section 6.1.1 but we reduce the number of aggregated packets from nagg = 64 to nagg = 1, effectively reducing the packet size transmitted at each transmission attempt. Figure 7 illustrates the individual throughput for different values of ω and η. Note, by comparing Figs. 2 and 7, that the optimal individual throughput—depicted as a blue line—is now reduced from 45.37 to 10.23 Mbps, which is a common effect of reducing the packet size in WiFi. We can also observe, in general, that the convergence speed in Fig. 7 is slower than in Fig. 2. However, in the long run (for simulations of 500 iterations, not shown here due to space constraints) the throughput converges closer to the optimal value. The reason for this behavior may be the specific shape of the convex function (see Fig. 8), which for nagg = 64 (Fig. 8a) is steeper than that for nagg = 1 (Fig. 8b). From Fig. 7 it can be seen that even by decreasing the nagg value, the algorithm sensitivity to the exploration parameter does not change. This implies that, again, the algorithm sensitivity to ω changes is negligible compared to gradient step size changes.

Fig. 7
figure 7

Individual throughput for n = 5 using different ω, η and h(k) = k(3/4) with nagg= 1. a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image
Fig. 8
figure 8

Shape of the objective functions for n = 5 with a nagg = 64 and b nagg = 1

Full size image

6.1.5 Node dynamics

Here we keep the algorithm setup same as in Section 6.1.1 but we change the number of nodes in the network in runtime. During the first 20 iterations n = 5, for iteration 21 to 40, we set n = 20 and for the last 20 iterations n = 5. We show the results in Fig. 9. Note that the algorithm, for certain settings of parameters ω and η, is able to quickly adapt to the new configuration of the network. When η = 1, the algorithm is able to converge to the new optimal value—depicted as a blue line—in less than 10 iterations.

Fig. 9
figure 9

Individual throughput when the number of nodes changes using different ω, η and h(k) = k(3/4) with nagg= 64. a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image

6.2 Noisy gradient estimates

Here we evaluate the performance of the algorithm by having noisy estimates of the individual throughput instead of the true value of the cost function. To achieve this goal we implement the algorithm in the network simulator. We set the exploration parameter as ω = {0.01,1} and gradient descent step size as η = {0.01,0.1,1}. We set the gradient descent timer equal to Δ = 100 s and the value of contention window timer equal to (t1 + t2) = 0.1 s. The exploration schedule is set to k(3/4). Each simulation is again run 30 different times to achieve more accurate results.

Figure 10 shows that the algorithm still converges in less than 10 iterations for ω = 1 and η = 1. However, we see that the evolution of throughput is not following the desired convergence trend for ω = 0.01. We also see that convergence is worse for smaller values of the exploration parameter. The reason for this behavior is, we argue, the noise: the smaller ω, the less accurate the estimations of the gradient, making more probable for gradient descent to move in the opposite direction of the optimum.

Fig. 10
figure 10

Individual throughput for n = 5 using different ω, η and h(k) = k(3/4) (noisy estimates). a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image

6.2.1 Averaging gradient descent estimates

One solution to alleviate the effect of noise when using stochastic gradient descent is averaging gradient descent estimates [10, 11]. Here we apply an exponential moving average due to its simplicity to implement in practice, as it implies no need to store samples of the estimates at each iteration. Thus, we use \(\tilde {g_{k}} = \alpha \tilde {g_{k}} + (1-\alpha ) \tilde {g}_{k-1}\) at each iteration in which we compute the gradient. Figure 11 shows the results of the same setup above but using the exponential moving average just described with α = 0.2.Footnote 3 As can be observed, averaging the gradients allows to slightly alleviate the effect of noise in some cases (note the improvement in convergence rate for ω = 0.01 and η = 0.1). However, when η = 1, the convergence rate of the algorithm is now worsened (compare Fig. 10f with Fig. 11f). This result is to be expected as the higher η, the less relevant the past samples of the gradient. Thus, again, our conclusion is that care has to be taken when selecting the learning parameters of the algorithm, even when averaging of gradients is applied to reduce the effects of noise.

Fig. 11
figure 11

Individual throughput for n = 5 using different ω, η and h(k) = k(3/4) with exponential moving average (noisy estimates). a ω = 0.01, η = 0.1. b ω = 0.01, η = 1. c ω = 0.1, η = 0.1. d ω = 0.1, η = 1. e ω = 1, η = 0.1. f ω = 1, η = 1

Full size image

7 Related work

Key articles related to proportional fairness in WiFi networks include Checco et al. [2] and Patras et al. [3], which are similar in nature. Checco et al. [2] pioneered rigorous analysis of proportional fairness in IEEE 802.11 WLANs. They proved that a unique proportional fair rate allocation exists as the flow total air-time. This algorithm corrects previous works on air-time quantities and proves the IEEE 802.11 rate region as a log-convex. It satisfies per station fairness and per flow fairness. Patras et al. [3] extends previous work considering different packet sizes, data rates, and packet errors. Since then, proportional fairness in WiFi has been extensively studied. More recently, the focus has been on coexistence of WiFi networks collocated with other WiFi networks and/or other technologies, especially unlicensed LTE [12,13,14,15].

In general, in these approaches, throughput optimization is achieved in practice by inferring MAC parameters and network metrics, such as packet transmission duration, slot transmission probability, and average packet size of the stations. Then, the optimization problem is solved. These metrics can be estimated but estimation errors and network dynamics need to be addressed.

We base our algorithm on these rigorous approaches but without the need to know all parameters of the function to optimize. In this way, proportional fairness can be achieved without the need to infer and keep track of network parameters and only by estimating the individual throughput at each station, which can be achieved at the application layer in a commercial access point with minimal changes.

8 Conclusion

The main focus of this article is on achieving proportional fairness in WiFi networks by applying bandit convex optimization. We have applied the OGD-SEMP algorithm to the WiFi proportional fairness use case. Our results show that, with the appropriate setting of parameters, the algorithm converges to the optimum value in a few number of iterations for different configurations and settings, including node dynamics. However, the parameter of the algorithm that controls the degree of exploration has a significant impact on the algorithm’s performance, especially when we are faced with throughput estimation errors. We have seen that using averages of the gradient estimates can alleviate the effect of noise but that again, convergence depends on appropriate setting of the learning parameters. We conclude that the algorithm is a practical solution for wireless network optimization, but that care has to be taken when configuring the algorithm parameters.