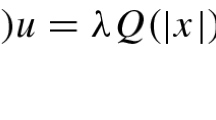Abstract
This paper is concerned with a planar Schrödinger–Poisson system involving Stein–Weiss nonlinearity
and its degenerate case
where \(\beta \ge 0,\) \(0<\mu <2\), \(2\beta +\mu <2\), \(V\in \mathcal {C}(\mathbb {R}^2,\mathbb {R})\) and f is of exponential critical growth. By combining variational methods, Stein–Weiss inequality and some delicate analysis, we derive the existence of ground state solution for the first system. Under some mild assumptions, we introduce the Pohozaev identity of the equivalent equation of the second system and use Jeanjean’s monotonicity method to achieve the existence of nontrivial solution for the second system.
Similar content being viewed by others
Data availability
Not applicable.
References
Ackermann, N.: On a periodic Schrödinger equation with nonlocal superlinear part. Math. Z. 248, 423–443 (2004)
Alves, C., Figueiredo, F.: Existence of positive solution for a planar Schrödinger–Poisson system with exponential growth. J. Math. Phys. 60, 1–14 (2019)
Alves, C., Cassani, D., Tarsi, C., Yang, M.: Existence and concentration of ground state solutions for a critical nonlocal Schrödigner equation in \({\mathbb{R} }^2\). J. Differ. Equ. 261, 1933–1972 (2016)
Berestycki, H., Lions, P.L.: Nonlinear scalar field equations. I. Existence of a ground state. Arch. Ration. Mech. Anal. 82, 313–345 (1983)
Biswas, R., Goyal, S., Sreenadh, K.: Quasilinear Choquard equations involving N-Laplacian and critical exponential nonlinearity. https://doi.org/10.48550/arXiv.2111.11134
Buffoni, B., Benci, V., Fortunato, D.: Abstract critical point theorems and applications to some nonlinear problems with “strong’’ resonance at infinity. Nonlinear Anal. 7, 981–1012 (1983)
Cao, D.: Nontrivial solution of semilinear elliptic equation with critical exponent in \({\mathbb{R} }^2\). Commun. Part. Differ. Equ. 17, 407–435 (1992)
Carvalho, J., Figueiredo, G., Furtado, M., Medeiros, E.: On a zero-mass \((N, q)\)-Laplacian equation in \({\mathbb{R} }^N\) with exponential critical growth. Nonlinear Anal. 213, 112488 (2021)
Cerami, G., Vaira, G.: Positive solutions for some non-autonomous Schrödinger–Poisson systems. J. Differ. Equ. 246, 521–541 (2010)
Chen, S., Tang, X.: Existence of ground state solutions for the planar axially symmetric Schrödinger–Poisson system. Discret. Contin. Dyn. Syst. Ser. B 24, 4685–4702 (2019)
Chen, S., Tang, X.: On the planar Schrödinger–Poisson system with the axially symmetric potentials. J. Differ. Equ. 268, 945–976 (2020)
Chen, L., Liu, Z., Lu, G., Tao, C.: Reverse Stein-Weiss inequalities and existence of their extremal functions. Trans. Am. Math. Soc. 370, 8429–8450 (2018)
Chen, L., Lu, G., Tao, C.: Existence of extremal functions for the Stein–Weiss inequalities on the Heisenberg group. J. Funct. Anal. 277, 1112–1138 (2019)
Cingolani, C., Weth, T.: On the planar Schrödinger–Poisson system. Ann. I. H. Poincaré 33, 169–197 (2016)
Dong, X., Mao, A.: Quasilinear Schrödinger–Poisson equations involving a nonlocal term and an integral constraint. Sci. China Math. 65, 2297–2324 (2022)
Du, M., Weth, T.: Ground states and high energy solutions of the planar Schrödinger–Poisson system. Nonlinearity 30, 3492–3515 (2017)
Du, L., Gao, F., Yang, M.: On elliptic equations with Stein–Weiss type convolution parts. Math. Z. 301, 2185–2225 (2022)
Figueiredo, G., Montenegro, M.: Fitzhugh–Nagumo system with zero mass and critical growth. Israel J. Math. 245, 711–733 (2021)
Figueiredo, D., Miyagaki, O., Ruf, B.: Elliptic equations in \({\mathbb{R} }^2\) with nonlinearities in the critical growth range. Calc. Var. Part. Differ. Equ. 3, 139–153 (1995)
Jeanjean, L.: Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. 28, 1633–1659 (1997)
Ji, C., Rădulescu, V.D.: Multi-bump solutions for the nonlinear magnetic Choquard equation with deepening potential well. J. Differ. Equ. 306, 251–279 (2022)
Jin, S., Seok, J.: Solitary waves for the nonlinear Schrödinger–Poisson system with positron–electron interaction. Calc. Var. Part. Differ. Equ. 62, 72 (2023)
Lieb, E.H.: Sharp constants in the Hardy–Littlewood–Sobolev and related inequalities. Ann. Math. 118, 349–374 (1983)
Lieb, E., Loss, M.: Analysis, Graduate Studies in Mathematics, vol. 14. American Mathematical Society, Province (1997)
Lin, X., Tang, X.: On concave perturbations of a periodic elliptic problem in \(\mathbb{R} ^2\) involving critical exponential growth. Adv. Nonlinear Anal. 12, 169–181 (2023)
Lions, P.: The concentration-compactness principle in the calculus of variations. The limit case. I. Rev. Mat. Iberoam. 1, 145–201 (1985)
Liu, Y., Li, X., Chao, J.: Multiplicity of concentrating solutions for a class of magnetic Schrödinger–Poisson type equation. Adv. Nonlinear Anal. 10, 131–151 (2021)
Liu, L., Rădulescu, V., Tang, T., Zhang, J.: Another look at planar Schrödinger–Newton systems. J. Differ. Equ. 328, 65–104 (2022)
Mattner, L.: Strict definiteness of integrals via complete monotonicity of derivatives. Trans. Am. Math. Soc. 349, 3321–3342 (1997)
Moser, J.: A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20, 1077–1092 (1970/1971)
Pankov, A.: On decay of solutions to nonlinear Schrödinger equations. Proc. Am. Math. Soc. 136, 2565–2570 (2008)
Qin, D., Tang, X.: On the planar Choquard equation with indefinite potential and critical exponential growth. J. Differ. Equ. 185, 40–98 (2021)
Ruiz, D.: The Schrödinger–Poisson equation under the effect of a nonlinear local term. J. Funct. Anal. 237, 655–674 (2006)
Stubbe, J.: Bound states of two-dimensional Schrödinger–Newton equations. http://arXiv.org/0807.4059
Sun, J., Ma, S.: Ground state solutions for some Schrödinger–Poisson systems with periodic potentials. J. Differ. Equ. 260, 2119–2149 (2016)
Tang, X.: Non-Nehari manifold method for asymptotically periodic Schrödinger equations. Sci. China Math. 58, 715–728 (2015)
Tang, X., Chen, S.: Ground state solutions of Nehari–Pohozaev type for Schrödinger–Poisson problems with general potentials. Discret. Contin. Dyn. Syst. 37, 4973–5002 (2017)
Trudinger, N.S.: On imbeddings into Orlicz spaces and some applications. J. Math. Mech. 17, 473–483 (1967)
Willem, M.: Minimax Theorem. Birkhäuser, Boston (1996)
Yang, C., Mills, R.: Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 96, 191 (1954)
Yang, M., Radulescu, V.D., Zhou, X.: Critical Stein-Weiss elliptic systems: symmetry, regularity and asymptotic properties of solutions. Calc. Var. Part. Differ. Equ. 61, 109 (2022)
Zhang, Y., Tang, X.: Large perturbations of a magnetic system with Stein–Weiss convolution nonlinearity. J. Geom. Anal. 32, 27 (2022)
Zhang, Y., Tang, X., Rădulescu, V.: Anisotropic Choquard problems with Stein–Weiss potential: nonlinear patterns and stationary waves. C. R. Math. Acad. Sci. Paris 359, 959–968 (2021)
Zhang, N., Tang, X., Chen, S.: Mountain-pass type solutions for the Chern–Simons–Schrödinger equation with zero mass potential and critical exponential growth. J. Geom. Anal. 33, 1–28 (2022)
Zhang, L., Tang, X., Chen, P.: On the planar Kirchhoff-type problem involving supercritical exponential growth. Adv. Nonlinear Anal. 11, 1412–1446 (2022)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Jin, P., Shu, M. & Wen, L. Groundstates for Planar Schrödinger–Poisson System Involving Convolution Nonlinearity and Critical Exponential Growth. J Geom Anal 34, 230 (2024). https://doi.org/10.1007/s12220-024-01671-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-024-01671-0