Abstract
We analyse the dynamics of the pullback of the map \(z \longmapsto z^m\) on the complex tori and toric varieties. We will observe that tropical objects naturally appear in the limit, and review several theorems in tropical geometry.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article, we employ several key ideas from tropical geometry to analyse the dynamics of the pullback of the map
as the positive integer \(m\rightarrow \infty .\) This analysis, in turn, lets us review certain aspects of tropical geometry from a dynamical standpoint. To start with, let us examine the case \(n=1.\) Observe that for any \(z\in \mathbb {C}^*,\) the family of sets \(\big \{\Phi _m^{-1}(z)\big \}\) converges towards a uniform distribution of points on the unit circle \(S^1\) as \(m\rightarrow \infty \). Formally, this observation can be formulated as the following equidistribution theorem: for any \(z \in \mathbb {C}^*,\)
where \(\delta _z\) is the Dirac measure at z, \(\mu (S^1)\) is the Haar measure on \(S^1,\) and the limit is in the weak sense of measures. Brolin’s remarkable theorem [12] is a generalisation of this observation: for any monic algebraic map of \(f: \mathbb {C}\longrightarrow \mathbb {C}\) of degree \(d\ge 2,\) there exists a (harmonic) measure \(\mu _f\), such that for any generic point \(z\in \mathbb {C}\),
where \(f^k:= f\circ \dots \circ f\) is the k-fold composition. This result was extended to \(\mathbb P^1\) for polynomials in [51] and for rational maps in [38]. Here the genericity of a point in \(\mathbb {C}\) and \(\mathbb P^1\) means that z is outside an invariant set of cardinality less than or equal to 1 and 2, respectively.
In complex dynamics, one naturally seeks the generalisation of Brolin’s theorem in higher dimensions and codimensions, and the question can be suitably formulated in the language of currents, where one explores weak limits of pullback of currents after a correct normalisation. Informally, currents on a complex smooth manifold X are continuous functionals acting on the space of smooth forms with compact support and of the appropriate (bi-)degree. For instance, an algebraic subvariety \(Z\subseteq X\) of dimension p defines an integration current [Z], which is of bidimension (p, p) and acts on the smooth forms with compact support of bidegree (p, p) by integration:
Generally, given a smooth algebraic variety X, \(f:X \longrightarrow X\) a holomorphic endomorphism of algebraic degree d, and \(Z \subseteq X\) an algebraic subvariety of dimension p, one is interested in analysing (the existence of) the weak limit of
as \(k \rightarrow \infty .\) We recall basic definitions in the theory of currents in Sect. 2.
On the tropical geometry side, algebraic subvarieties of the torus are degenerated to obtain their tropicalisation. For instance, a tropicalisation can be obtained by the logarithm map
Given an algebraic subvariety \(Z\subseteq (\mathbb {C}^*)^n\), the set \(\textrm{Log}(Z)\) is called the amoeba of Z. By Bergman’s theorem [9] there exists a close subset of \(\mathbb {R}^n\) such that
where the limit is in the Hausdorff metric in the compact sets of \(\mathbb {R}^n,\) and t is a complex parameter. It is further shown in tropical geometry that \(\mathcal {C}\) can be equipped with a structure of a tropical cycle; see Definition 3.1 and Sect. 5. With such an induced structure, we set \(\mathcal {C}\) to be the tropicalisation of Z, denoted by \(\textrm{trop}(Z)\).
Note that for any point \(z\in (\mathbb {C}^*)^n,\)
which corresponds to the above-mentioned equidistribution theorem. More generally, our first theorem shows how naturally tropical objects emerge as geometric objects in holomorphic dynamics.
Theorem A
Let \(Z\subseteq (\mathbb {C}^*)^n\) be an irreducible subvariety of dimension p, then

where  is the complex tropical current associated to \(\textrm{trop}(Z).\)
is the complex tropical current associated to \(\textrm{trop}(Z).\)
A complex tropical current  is a closed current of bidimension (p, p), associated to the tropical cycle \(\mathcal {C}\subseteq \mathbb {R}^n\) of pure dimension p, and with support \(\textrm{Log}^{-1}(|\mathcal {C}|).\) Here \(|\mathcal {C}|\) denotes the support of \(\mathcal {C}\) which is obtained by forgetting its polyhedral structure. Complex tropical currents were introduced in [5], and we recall their definition in Sect. 4.
is a closed current of bidimension (p, p), associated to the tropical cycle \(\mathcal {C}\subseteq \mathbb {R}^n\) of pure dimension p, and with support \(\textrm{Log}^{-1}(|\mathcal {C}|).\) Here \(|\mathcal {C}|\) denotes the support of \(\mathcal {C}\) which is obtained by forgetting its polyhedral structure. Complex tropical currents were introduced in [5], and we recall their definition in Sect. 4.
Noting that the pullback can be extended to more general currents, we introduce the following definition.
Definition 1.1
Let  be a closed positive current of bidimension (p, p) on \((\mathbb {C}^*)^n\). We define the dynamical tropicalisation of
be a closed positive current of bidimension (p, p) on \((\mathbb {C}^*)^n\). We define the dynamical tropicalisation of  as
as

when the limit exists.
Theorem A, therefore, states that the dynamical tropicalisation of an integration current along a subvariety of the torus yields the tropical current associated to the tropicalisation of that subvariety. Even though the preceding theorem is stated only in \((\mathbb {C}^*)^n,\) we require a passage to toric varieties to provide a proof. Recall that a toric variety is an irreducible variety X such that
-
(a)
\((\mathbb {C}^*)^n\) is a Zariski open subset of X, and
-
(b)
the action of \((\mathbb {C}^*)^n\) on itself extends to an action of \((\mathbb {C}^*)^n\) on X.
The action of \((\mathbb {C}^*)^n\) on X partitions X into orbits, and we will observe in Sect. 5 that the continuous extension of the endomorphism \(\Phi _m\) from \((\mathbb {C}^*)^n\) to X gives rise to an equidistribution theorem of points within each orbit; see Proposition 5.1. The above-mentioned tropicalisation corresponds to the tropicalisation with respect to the trivial valuation. In essence, this tropicalisation captures the (exponential) directions where a subvariety \(Z\subseteq (\mathbb {C}^*)^n\) approaches infinity, and there always exists a toric variety X that can contain those directions at infinity so that
-
(a)
the closure of Z in X is compact, and
-
(b)
the the boundary divisors \(X\setminus (\mathbb {C}^*)^n\) intersect the closure of Z in X properly.
This closure is called the tropical compactification of Z in X; see Definition 5.6. In Subection 7.1, we extend Theorem A to toric varieties:
Theorem B
Let \(Z\subseteq (\mathbb {C}^*)^n\) be a an irreducible subvariety of dimension p, and \(\bar{Z}\) be the tropical compactification of Z in the smooth projective toric variety X. Then,

where \(\Phi _m: X\longrightarrow X\) is the continuous extension of \(\Phi _m: (\mathbb {C}^*)^n \longrightarrow (\mathbb {C}^*)^n,\) and  is the extension by zero of
is the extension by zero of  to X.
to X.
Theorem B provides a vivid picture of dynamical tropicalisation which is illustrated in Fig.1. In Sect. 7.2, we observe that dynamical tropicalisation of Poincaré–Lelong equation, see Theorem 2.3, yields the following dynamical version of Kapranov’s theorem, which informally states that the tropicalisations of an algebraic hypersurface V(f) coincides with the tropical variety of the tropicalisation of the polynomial f:
Theorem C
Let \(V\subseteq (\mathbb {C}^*)^n,\) be an irreducible algebraic hypersurface, given as the variety of the polynomial \(f(z)= \sum _{\alpha } c_{\alpha } z^{\alpha }\in \mathbb {C}[z]\). We have that

where \(\mathfrak {q}= \max _{\alpha }\{ \langle -\alpha ,~\cdot ~ \rangle \}:\mathbb {R}^n \longrightarrow \mathbb {R},\) is the tropicalisation of f and \({V_{\textrm{trop}}(\mathfrak {q})}\) is the tropical variety associated to \(\mathfrak {q}\); see Definition 3.2.
In the beginning of the introduction, we mentioned the Brolin’s theorem and some generalisations. Let us now recall a equidistribution Conjecture of Dinh and Sibony, as well as some of the known special cases. This will allow for viewing Theorems A and B within the larger context of complex dynamics. For an overview of the current trends in Complex Dynamics in Higher Codimensions see Dinh’s ICM 2018 survey [23], and Dujardin’s ICM 2022 survey [31] on Geometric Methods in Holomorphic Dynamics.
Let  denote the set of holomorphic endomorphisms of degree d on \(\mathbb P^n,\) and assume that \(d\ge 2.\) The Green current of
denote the set of holomorphic endomorphisms of degree d on \(\mathbb P^n,\) and assume that \(d\ge 2.\) The Green current of  is defined by
is defined by

where \(\omega \) is the Fubini–Study form cohomologous to a hyperplane in \(\mathbb P^n.\)
Conjecture D
(Dinh–Sibony [23, 27]) For any  , any integer p with \(1 \le p\le n-1,\) and generic subvariety \(Z\subseteq \mathbb P^n\) of dimension p, we have the weak convergence of positive closed currents
, any integer p with \(1 \le p\le n-1,\) and generic subvariety \(Z\subseteq \mathbb P^n\) of dimension p, we have the weak convergence of positive closed currents

where  , is the \((n-p)\)-fold wedge product of the Green current of f, and in particular, the limit only depends on f.
, is the \((n-p)\)-fold wedge product of the Green current of f, and in particular, the limit only depends on f.
Here are the special known cases of the above conjecture.
-
(a)
The case \(p=0\) is shown by Fornæss and Sibony [36], Briend and Duval [11], Dinh and Sibony [24].
-
(b)
The case \(p=n-1\) by Fornæss and Sibony for generic maps [35], and by Favre and Jonsson for any map in dimension 2 in [34].
-
(c)
When \(p=n-1\) was proved by Dinh and Sibony in [25].
-
(d)
In any dimension for generic maps
 by Dinh and Sibony in [26].
by Dinh and Sibony in [26].
The above conjecture also predicts exponential rate of convergence which is studied in several works, see for instance [26, 48]. There are also non-archimedean versions of the Brolin’s theorem and we refer the reader to works Rivera-Letelier [66], Baker and Rumley [7], and to Johnsson’s comprehensive survey of results and references [49].
We remark further that
-
(a)
The map \(\Phi _d\) is not a generic map in
 in the sense of Item (d) above. Furthermore, comparing our result to the above conjecture implies that generic subvarieties of the projective space, up to the degree, have the same tropicalisation. This is not a contradiction, in fact, it is the main result of [67] for which we provide two other explanations in Sect. 7.3 and will observe that the Julia sets of \(\Phi _m\) relate to the support of Bergman fan of uniform matroids.
in the sense of Item (d) above. Furthermore, comparing our result to the above conjecture implies that generic subvarieties of the projective space, up to the degree, have the same tropicalisation. This is not a contradiction, in fact, it is the main result of [67] for which we provide two other explanations in Sect. 7.3 and will observe that the Julia sets of \(\Phi _m\) relate to the support of Bergman fan of uniform matroids. -
(b)
The map \(\Phi _m\) is indeed versatile. This map was already employed in [65] to find the logarithmic indicators of plurisubharmonic functions with logarithmic growth. Moreover, Fujino in [39] used \(\Phi _{m}\) to prove certain vanishing theorems on toric varieties;
-
(c)
In Sect. 7.2, we see that \(\Phi _m^*\), after a normalisation, applied to Lelong–Poincaré Eq. 2.3, yields a version of Kapranov’s theorem, where an analogue of Maslov dequantisation naturally appears; see Sect. 3. Finally, it is alluded in the proof of Theorem 6.1 that \(\Phi _m^*,\) after a normalisation preserves the Chow cohomology classes. We will gather further cohomological implications of the latter fact in a subsequent article [4].
In Sects. 2, 3, 4 and 5 of this manuscript, we provide the background required in proving our main theorems. The entirety of Sect. 6 is devoted to the proof of Theorem A. In Sect. 7 we prove Theorems B and C and discuss the implication of the Dinh–Sibony Conjecture in the case of the map \(\Phi _m\).
2 Preliminaries of the Theory of Currents
The content of this section is extracted from the Demailly’s book [20], which has always been generously publicly available.
Let X be a complex manifold of dimension n. For a non-negative integer k, we consider the space of smooth complex differential forms of degree k with compact support, denoted by  endowed with the inductive limit topology. The topological dual to
endowed with the inductive limit topology. The topological dual to  constitutes the space of currents of dimension k,
constitutes the space of currents of dimension k,

that is, the space of all continuous linear functionals on  . Hence, a current
. Hence, a current  acts on any form
acts on any form  and yields
and yields 
We note that when \(k=0,\) the space of k-currents is just the space of distributions as in the theory of partial differential equations. The support of  , denoted by
, denoted by  , is the smallest closed subset \(S\subseteq X,\) such that
, is the smallest closed subset \(S\subseteq X,\) such that  vanishes on its complement. A k-dimensional current
vanishes on its complement. A k-dimensional current  is the weak limit of a sequence of k-dimensional currents
is the weak limit of a sequence of k-dimensional currents  if
if

We say that  is a cluster value of a sequence
is a cluster value of a sequence  if
if  is the weak limit of a subsequence of
is the weak limit of a subsequence of 
Remark 2.1
Note that if  is the weak limit of the sequence
is the weak limit of the sequence  and the sets
and the sets  converge in the Hausdorff metric to the set S, then
converge in the Hausdorff metric to the set S, then  To see this, assume that \(z\notin S,\) then for any large \(i\gg 0,\)
To see this, assume that \(z\notin S,\) then for any large \(i\gg 0,\)  ’s vanish in a small neighbourhood of z, and therefore
’s vanish in a small neighbourhood of z, and therefore  . As an example for the strict inclusion
. As an example for the strict inclusion  for any \(z\in X,\) consider the weak limit
for any \(z\in X,\) consider the weak limit  We have
We have  and
and 
The exterior derivative of a k-dimensional current  is the \((k-1)\)-dimensional current
is the \((k-1)\)-dimensional current  defined by
defined by

The current  is called closed if
is called closed if  . The duality of currents and forms with compact support induces the following decompositions for the bidegree and bidimension
. The duality of currents and forms with compact support induces the following decompositions for the bidegree and bidimension

The space of smooth differential forms of bidegree (p, p) contains the cone of positive differential forms. By definition, a smooth differential (p, p)-form \(\varphi \) is positive if
A current  of bidimension (p, p) is positive if
of bidimension (p, p) is positive if

An important class of positive currents on X is obtained by integrating along the complex analytic subsets of X, giving rise to integration currents. More precisely, if Z is a p-dimensional complex analytic subset of X, then by Lelong’s theorem [20, Theorem III.2.7] the integration current along Z is the well-defined (p, p)-dimensional current given by

Remark 2.2
For simplicity, we only mention the notion of positive currents. To review weakly positive, positive and strongly positive forms and currents see [20].
Let us assume further that X is a Kähler manifold, with the Kähler form \(\omega \). One can check that all positive currents have signed measure coefficients. Accordingly, for a positive (p, p)-dimensional current  the trace measure of
the trace measure of  is defined as
is defined as  Note that the trace measure of any positive current is a positive measure. The local mass of
Note that the trace measure of any positive current is a positive measure. The local mass of  on a Borel set \(K\subseteq X,\) with respect to \(\omega ,\) is given by
on a Borel set \(K\subseteq X,\) with respect to \(\omega ,\) is given by

The differentials \(\partial , \bar{\partial }\) and the de Rham’s exterior derivative are defined on currents by duality and we also have \(d = \partial + \bar{\partial },\) and set \(d^c = \frac{\partial - \bar{\partial }}{2i\pi },\) to obtain \(dd^c = \frac{\partial \bar{\partial }}{i\pi }.\) An important family of \((n-1,n-1)\)-dimensional, or (1, 1)-bidegree, positive currents are currents of the form \(dd^c \psi \) where \(\psi \) is a plurisubharmonic function. Recall that a function \(\psi :\Omega \rightarrow [-\infty , \infty )\), for \(\Omega \subseteq \mathbb {C}^n\) an open set, is called plurisubharmonic if
-
(a)
\(\psi \) is not identically \(-\infty \) in any component of \(\Omega ;\)
-
(b)
\(\psi \) is upper semicontinuous;
-
(c)
for every complex line \(L\subseteq \mathbb {C}^n,\) \(\psi _{{\upharpoonright }_{\Omega \cap L}}\) is subharmonic on \(\Omega \cap L.\)
It is well-known that when \(u:\mathbb {R}^p \rightarrow \mathbb {R}\) is convex and increasing in each variable and \(\psi _1, \dots ,\psi _p\) are plurisubharmonic, then
is also a plurisubharmonic function. Moreover, for any holomorphic function \(f:\mathbb {C}^n \rightarrow \mathbb {C},\) \(\log |f|\) is plurisubharmonic, and one has the following equality of currents, for which we provide a tropical version in Sect. 7.2.1.
Theorem 2.3
(Lelong–Poincaré Equation) Let f be a non-zero meromorphic function on X, and let \(\sum m_j Z_j\) be the divisor of f. The function \(\log |f|\) is locally integrable on X, and
Given an analytic subset \(E\subseteq X\), and a positive closed (p, p)-current  in
in  it is important to know when
it is important to know when  can be extended by zero to a closed positive current
can be extended by zero to a closed positive current  The theorem of El Mir–Skoda asserts that this extension is possible if
The theorem of El Mir–Skoda asserts that this extension is possible if  has a finite mass in a neighbourhood of every point of E; see [20, III.2.3]. The pushforward and pullback of a current are defined as a dual operation to pullback and pushforward of differential forms, respectively. The pushforward of a form is defined by integrating along fibers: consider a submersion \(f:X\longrightarrow X'\) between the complex manifolds X and \(X'\) with respective complex dimensions m and n. Let \(\varphi \) be a differential form of degree k on X, with \(L^1_{\text {loc}}\) coefficients such that the restriction \(f{\upharpoonright }_{{\textrm{supp}(\varphi )}}\) is proper. Then,
has a finite mass in a neighbourhood of every point of E; see [20, III.2.3]. The pushforward and pullback of a current are defined as a dual operation to pullback and pushforward of differential forms, respectively. The pushforward of a form is defined by integrating along fibers: consider a submersion \(f:X\longrightarrow X'\) between the complex manifolds X and \(X'\) with respective complex dimensions m and n. Let \(\varphi \) be a differential form of degree k on X, with \(L^1_{\text {loc}}\) coefficients such that the restriction \(f{\upharpoonright }_{{\textrm{supp}(\varphi )}}\) is proper. Then,

In this situation, for  one defines
one defines  given by
given by

Note that for an analytic cycle Z, we have \(f^*[Z]= [f^{-1}(Z)]\). The set of seminorms

for all  , defines a topology on
, defines a topology on  With respect to this weak topology, the operations
With respect to this weak topology, the operations

are weakly continuous. See [20, Sect. I.2.C.3]. We finally recall that the wedge product or intersection of two positive closed currents is not always admissible, as we cannot always multiply measures. The leading theories are due to Bedford–Taylor [8] and Demailly [22] in codimension one, which we will use in Sect. 5. In higher dimensions, the theory has been developed in [2, 26, 28, 29],
3 Tropical Algebra and Tropical Cycles
Tropical geometry can be viewed as a geometry over max-plus or min-plus algebra. In this article, we choose \((\mathbb {T}, \otimes , \oplus ),\) where \(\mathbb {T}= \mathbb {R}\cup \{-\infty \},\) and \(\otimes \) and \(\oplus \) are the usual sum and maximum, respectively. These operations can be obtained from the following multiplication and addition through the Maslov dequantisation: for \(x,y \in \mathbb {R}\), let \(x \otimes _h y := x +y\) and \(x \oplus _h y := h \ln (\exp (x/h)+ \exp (y/h)),\) as \(h\rightarrow 0.\) See [55] for a survey of the topic touching on questions in thermodynamics, classical and quantum physics, and probability. See also [60, 61] and surveys [47, 72] on how Maslov dequantisation and degeneration of amoebas have played a fundamental role in application of tropical geometry to enumerative problems in algebraic geometry. In comparison to Maslov dequantisation, for \(z, w \in \mathbb {C}^*,\) we can consider \(\log |zw|= \log |z|+\log |w|,\) and apply \(\frac{1}{m} \Phi ^*_m\) to \(\log |z + w|\) to obtain:
in the sense of distributions or bidegree (0, 0) currents. We use this observation to derive a dynamical version of Kapranov’s theorem in Sect. 7.2. In these notes we follow [58] as our main reference of tropical geometry, and refer the reader to [40, 56, 57] for the recent scheme-theoretic development of tropical algebraic geometry.
3.1 Tropical Cycles
Recall that a linear subspace \(H\subseteq \mathbb {R}^n\) is called rational if it is spanned by a subset of \(\mathbb {Z}^n.\) A rational polyhedron in \(\mathbb {R}^n\) is an intersection of finitely many rational half-spaces which are defined by
A rational polyhedral complex is a complex with only rational polyhedra. The polyhedra in a polyhedral complex are also called cells. A fan is a polyhedral complex whose cells are all cones. If any cone of a fan \(\Sigma \) also belongs to another fan \(\Sigma ',\) then \(\Sigma \) is a subfan of \(\Sigma '\). The dimension of a polyhedron is the dimension of the affine subspace of minimal dimension containing it. All the fans and polyhedral complexes considered in this article are rational. For a given polyhedron \(\sigma \) let \(\text {aff}(\sigma )\) be the affine span of \(\sigma ,\) and \(H_{\sigma }\) be the translation of \(\text {aff}(\sigma )\) to the origin. Assume that \(\tau \) is a face of codimension one for the p-dimensional polyhedron \(\sigma ,\) and \(u_{\sigma / \tau }\) is the unique outward generator of the one dimensional lattice \((\mathbb {Z}^n \cap H_{\sigma })/(\mathbb {Z}^n \cap H_{\tau }).\)
Definition 3.1
(Balancing Condition and Tropical Cycles) Let \(\mathcal {C}\) be a rational polyhedral complex of pure dimension p. Assume that all the cells of \(\mathcal {C}\) of dimension p are weighted with positive integers. We say that \(\mathcal {C}\) satisfies the balancing condition at \(\tau \) if
where the sum is over all p-dimensional cells \(\sigma \) in \(\mathcal {C}\) containing \(\tau \) as a codimension 1 face, and \(w_{\sigma }\) is weight of \(\sigma \). A weighted complex is balanced if it satisfies the balancing condition at each of its codimension one cells. A tropical cycle or synonymously a tropical variety in \(\mathbb {R}^n\) is a balanced weighted complex with finitely many cells.
For a tropical variety \(\mathcal {C}\) we denote its support by \(|\mathcal {C}|,\) which is the underlying set of the \(\mathcal {C}\) as a polyhedral complex. In the tropical algebra, tropical polynomials are obtained by addition and multiplication of the variables and constants in the tropical semiring and we can associate to each tropical polynomial a tropical hypersurface:
Definition 3.2
For a tropical polynomial
where \(\alpha \in A\subseteq \mathbb {Z}^n_{\ge 0},\) \(|A|< \infty ,\) and \(c_{\alpha }\in \mathbb {R},\) the associated tropical variety to \(\mathfrak {q}\), denoted by \(V_{\textrm{trop}}(\mathfrak {q}),\) is defined by:
-
(a)
as a set
$$\begin{aligned} |V_{\textrm{trop}}(\mathfrak {q})| = \{x\in \mathbb {R}^n: \mathfrak {q}(x)\text {~is not differentiable at~} x\}; \end{aligned}$$ -
(b)
the weights on an \((n-1)\)-dimensional cell \(\sigma \) of \(|V_{\textrm{trop}}(\mathfrak {q})|\) is given by the lattice length of \(\alpha _1 - \alpha _2,\) where \( |\sigma | = \{x\in \mathbb {R}^n: \langle \alpha _1 , x \rangle +c_{\alpha _1} = \langle \alpha _2 , x \rangle +c_{\alpha _2} =\mathfrak {q}(x) \}.\)
Given a tropical polynomial \(\mathfrak {q},\) one can verify that \(V_{\textrm{trop}}(\mathfrak {q})\) is indeed balanced, [58, Proposition 3.3.2].
4 Complex Tropical Currents
Introduction of different notions of tropical currents as bridges between theory of currents and tropical geometry, to the author’s understanding, is indebted to [20, 63, 64]. In [63], Passare and Rullgård considered \((S^1)^n\)-invariant plurisubharmonic functions of the form \(\textrm{Log}_+^*f = f\circ \textrm{Log}_+\) for a convex continuous function \(f:\mathbb {R}^n \longrightarrow \mathbb {R},\) and
By Rashkovskii’s formula [65], one has
where \(\text {MA}(f)\) is the real Monge-Ampère measure of f and \(V \subseteq \mathbb {R}^n\) is a Borel set. Recall that when f is smooth, we have
where \(\mu \) is the Lebesgue measure in \(\mathbb {R}^n\) and the definition can be extended to the non-smooth case by continuity. Lagerberg in [53], introduced the theory of superforms and supercurrents where he could also decompose the real Monge–Ampère measures into bidegree (1, 1) components, \(dd^\sharp f\), to obtain
Moreover, Lagerberg introduced tropical supercurrents in codimension one, which were generalised by Gubler in [44] to higher codimensions. Chambert-Loir and Ducros in [17] followed by Gubler and Künnemann in [45] extended supercurrents to a fully-fledged theory on Berkovich spaces, and used them in application to Arakelov theory. Further, in [14], and in [59] intersection theory and Monge–Ampère operators were investigated; see also [15, 18, 30] for several far-reaching extensions of Rashkovskii’s formula. In [13], it was proved that the push-forward of the logarithm map can be defined in order to find a correspondence between a cone of certain \((S^1)^n\)-invariant closed positive currents on a complex toric variety and closed positive supercurrents on the tropicalisation of that toric variety. Moreover, one can lift, by the pull-back of the logarithm map, the tropical currents in [44] to complex tropical currents.
Complex tropical currents were introduced in [5] with a geometric representation which made it convenient for generalizing Demailly’s important example of an extremal current that is not an integration current along any analytic set. Recall that this current is given by  and equals the (complex) tropical current associated to the tropical line in \(\mathbb {R}^2\); see [21]. The extremality results in [5] were subsequently improved and extended to toric varieties by Huh and the author in [6], and tropical currents were used to find a non-trivial example of a positive closed current on a smooth projective toric variety which refutes a strong version of the Hodge conjecture for positive currents. Thereafter, Adiprasito and the author in [1] proposed a family of tropical currents which are counter-example to the aforementioned conjecture in any dimension and codimension greater than one. Moreover, tropical currents were also used in application to higher convexity problems and Nisse–Sottile conjecture [62], as well as finding a family of peculiar currents which cannot be regularised to obtain mollified currents with smooth boundaries; see [1, Theorem D].
and equals the (complex) tropical current associated to the tropical line in \(\mathbb {R}^2\); see [21]. The extremality results in [5] were subsequently improved and extended to toric varieties by Huh and the author in [6], and tropical currents were used to find a non-trivial example of a positive closed current on a smooth projective toric variety which refutes a strong version of the Hodge conjecture for positive currents. Thereafter, Adiprasito and the author in [1] proposed a family of tropical currents which are counter-example to the aforementioned conjecture in any dimension and codimension greater than one. Moreover, tropical currents were also used in application to higher convexity problems and Nisse–Sottile conjecture [62], as well as finding a family of peculiar currents which cannot be regularised to obtain mollified currents with smooth boundaries; see [1, Theorem D].
In all the above-mentioned works though, the notion of tropicalisation of integration currents along algebraic varieties was absent, which is the topic of this article.
4.1 Tropical Currents
In this subsection, we recall the definition of tropical currents, and their basic properties. We refer the reader to [5, 6] for more details. Let N be a finitely generated free abelian group, we define
Let \(\mathbb {C}^*\) be the group of nonzero complex numbers. As before, the logarithm map is the homomorphism
and the argument map is
For a rational linear subspace \(H \subseteq \mathbb {R}^n\) we have the following exact sequences:

where \({\mathbb {Z}^n(H)}:= \mathbb {Z}^n/(H \cap \mathbb {Z}^n).\) Moreover,

Define

One has
As a result, when H is of dimension p, the set \(\text {Log}^{-1}(H)\) is naturally foliated by copies of \(T_{H \cap \mathbb {Z}^n} \simeq (\mathbb {C}^*)^p.\)
Definition 4.1
Let H be a rational subspace of dimension p, and \(\mu \) be the Haar measure of mass 1 on \(S_{\mathbb {Z}^n(H)}\). We define a (p, p)-dimensional closed current  on \((\mathbb {C}^*)^n\) by
on \((\mathbb {C}^*)^n\) by

Example 4.2
It is instructive to explicitly understand the equations of the fibers of  where \(H\subseteq \mathbb {R}^n,\) is a rational hyperplane given by \(H=\{x\in \mathbb {R}^n: \langle \beta , x\rangle =0\}\) for some \( \beta \in \mathbb {Z}^n.\) The support of
where \(H\subseteq \mathbb {R}^n,\) is a rational hyperplane given by \(H=\{x\in \mathbb {R}^n: \langle \beta , x\rangle =0\}\) for some \( \beta \in \mathbb {Z}^n.\) The support of  is given by \(\textrm{Log}^{-1}(H).\) Let \(\beta = w_{H} \alpha ,\) where \(\alpha \in \mathbb {Z}^n\) is a primitive vector, i.e., its components have greatest common divisor equal to 1 and \(w_{H} \in \mathbb {Z}_{>0}\). In this case, each fiber \(\pi _H^{-1}(x)\) is given by the \((S^1)^n\)-translations of the toric set
is given by \(\textrm{Log}^{-1}(H).\) Let \(\beta = w_{H} \alpha ,\) where \(\alpha \in \mathbb {Z}^n\) is a primitive vector, i.e., its components have greatest common divisor equal to 1 and \(w_{H} \in \mathbb {Z}_{>0}\). In this case, each fiber \(\pi _H^{-1}(x)\) is given by the \((S^1)^n\)-translations of the toric set
where \(\alpha = \alpha ^+ - \alpha ^-,\) and \(\alpha ^{\pm }\in \mathbb {Z}^n_{\ge 0}.\)
We also note that the tangent space of the fiber \(\pi _{H}^{-1}(1)\) at \(w= (1, \dots , 1) \in (\mathbb {C}^*)^n\) is given by
It follows that if \(H, H'\subseteq \mathbb {R}^n\) are two hyperplanes intersecting transversely in \(\mathbb {R}^n,\) then all the fibers of  and
and  intersect transversely in \((\mathbb {C}^*)^n.\)
intersect transversely in \((\mathbb {C}^*)^n.\)
When A is an affine subspace of \(\mathbb {R}^n\) parallel to the linear subspace \(H= A - {a}\) for \(a \in A\), we define  by translation of
by translation of  Namely, we define the submersion \(\pi _{A}\) as the composition
Namely, we define the submersion \(\pi _{A}\) as the composition

For \(\sigma \) a p-dimensional (rational) polyhedron in \(\mathbb {R}^n,\) we denote
and for homogeneity, \(N(H):= \mathbb {Z}^n(H) = \mathbb {Z}^n /(H \cap \mathbb {Z}^n).\)
Definition 4.3
Let \(\mathcal {C},\) be a weighted polyhedral complex of dimension p. The tropical current  associated to \({\mathcal {C}}\) is given by
associated to \({\mathcal {C}}\) is given by

where the sum runs over all p-dimensional cells \(\sigma \) of \(\mathcal {C}.\)
Theorem 4.4
([5]) A weighted complex \(\mathcal {C}\) is balanced, if and only if,  is closed.
is closed.
The reminder of this section is devoted to proving the statements that will be useful in later sections. The idea of the following technical lemma is extensively used in the proof of Theorem 4.4 and extremality results in [5, 6]. For a measure \(\eta \) on the k-dimensional compact torus \((S^1)^k\) let us denote by \(\widehat{\eta }(\ell _1, \dots , \ell _k)\) its \((\ell _1, \dots , \ell _k)\)-th Fourier measure coefficients.
Proposition 4.5
For a p-dimensional affine plane A parallel to a rational linear space, assume that the current  is given by
is given by

for a positive measure \(\eta .\) Then, all the Fourier measure coefficients \(\widehat{\eta }(\nu ),\) for \(\nu \in \mathbb {Z}^n,\) can be determined by the action of the current  on the (p, p)-differential forms of type
on the (p, p)-differential forms of type
where \(I \subseteq [n],\) with \(|I|=p,\) \(\theta = (\theta _1, \dots , \theta _n)\) and \(r= (r_1, \dots , r_n)\) are polar coordinates, and \(\rho :\mathbb {R}^n \rightarrow \mathbb {R}\) is a smooth function with compact support.
Proof
(Sketch of Proof.) Without loss of generality, we can assume that A is a linear subspace of \(\mathbb {R}^n\). Let us choose \(\{w_1, w_2, \dots , w_p\}\) a \(\mathbb {Z}-\)basis for \(\mathbb {Z}^n \cap A \) and extend it to a \(\mathbb {Z}\)-basis of of \(\mathbb {Z}^n,\) \(B:=\{w_1, \dots , w_p, u_1, \dots , u_{n-p}\}.\) One can see that, compare to [5, Eq. (3.3.20)], with the right choice of \(\rho \),

where \(\text {det}_I\) is the minor of rows corresponding to \(I\subseteq [n],\) and
where \(A^{\perp }\) is the orthogonal complement of A in \(\mathbb {R}^n\) with respect to usual dot product. As B is a \(\mathbb {Z}\)-basis, the tuple \((\langle u_1, \nu \rangle , \dots , \langle u_{n-p}, \nu \rangle )\) can assume any value in \(\mathbb {Z}^{n-p}\) and therefore \(\eta \) can be fully understood. \(\square \)
We call a current on \((\mathbb {C}^*)^n\), \((S^1)^n-\)invariant if it is invariant under the induced action of multiplication by any \(x\in (S^1)^n.\) The following proposition is comparable to [13, Example 7.1.7]. See also [18, Theorem 3.6] for an interesting related result in codimension one.
Proposition 4.6
Assume that  is a closed positive \((S^1)^n\)-invariant current whose support is given by \(\textrm{Log}^{-1}(|\mathcal {C}|)\), for a polyhedral complex \(\mathcal {C}\subseteq \mathbb {R}^n\) of pure dimension p. Then
is a closed positive \((S^1)^n\)-invariant current whose support is given by \(\textrm{Log}^{-1}(|\mathcal {C}|)\), for a polyhedral complex \(\mathcal {C}\subseteq \mathbb {R}^n\) of pure dimension p. Then  is a tropical current.
is a tropical current.
Proof
By Demailly’s second theorem of support, [20, III.2.13], any positive current with support \(\textrm{Log}^{-1}(|\mathcal {C}|)\) can be presented as

for a unique complex measure \(\eta _{\sigma }\) for each \(\sigma \). We need to see that the measures \(\eta _{\sigma }\) are indeed Haar measures, but this is simple, since by definition of the fibers \(\pi _A\) each fiber of \(\pi _A\) is a translation of the kernel by the action of \((S^1)^n\), and if  is invariant under \((S^1)^n\) then each \(\eta _{\sigma }\) has to be invariant under the translation in the quotient \(S(N(H))= S_{\mathbb {Z}^n/(H\cap \mathbb {Z}^n)}.\) \(\square \)
is invariant under \((S^1)^n\) then each \(\eta _{\sigma }\) has to be invariant under the translation in the quotient \(S(N(H))= S_{\mathbb {Z}^n/(H\cap \mathbb {Z}^n)}.\) \(\square \)
Before ending this subsection let us recall the notion of refinement.
Definition 4.7
A p-dimensional weighted complex \(\mathcal {C}'\) is called a refinement of \(\mathcal {C},\) if \(|\mathcal {C}|= |\mathcal {C}'|,\) and each cell \(\sigma '\in \mathcal {C}'\) of dimension p (and non-zero weight) is contained in some p-dimensional cell \(\sigma \in \mathcal {C}\) with
It is easy to check that if \(\mathcal {C}\) and \(\mathcal {C}'\) have a common refinement then their tropical currents  and
and  coincide; see [6, Sect. 2.6].
coincide; see [6, Sect. 2.6].
5 The Toric Setting
5.1 The Multiplication Map on Toric Varieties
In this subsection, we intend to analyse the dynamics of \(\Phi _{m}\) on the points of toric varieties. The reader may consult [19] for a thorough and the notes [10] for a quick introduction to the theory of toric varieties. As before, let N be a free abelian group of rank n, \(M= \textrm{Hom}_{\mathbb {Z}}(N,\mathbb {Z}),\)
For a rational cone \(\sigma ,\) we let \(N_{\sigma }\) be the sublattice of N spanned by the points in \(\sigma \cap N,\) and \(N(\sigma )= N /N_{\sigma }.\) Moreover,
Let us fix a rational fan \(\Sigma \subseteq N_{\mathbb {R}},\) and recall that \(\Sigma \) defines a toric variety \(X_{\Sigma }\) which is obtained by gluing the affine varieties \(U_{\sigma }:= \textrm{Spec}~\mathbb {C}[\sigma ^{\vee } \cap M]\) according to the fan structure in \(\Sigma .\) There is a Cone-Orbit Correspondence between the cones in \(\Sigma \) and orbits of the continuous action of \(T_N\) on \(X_{\Sigma }.\) Namely, for any integer \(0\le p \le n,\)
Therefore, the \(T_N\)-orbits give rise to the partition
Each point of any affine piece \(U_{\sigma }\) corresponds to a semigroup homomorphism
where \(\mathbb {C}\) is considered as a semigroup under multiplication. The distinguished point \(z_{\sigma }\in \mathcal {O}(\sigma )\subseteq U_{\sigma },\) is then defined to be the unique point which corresponds to the semigroup homomorphism
The distinguished point of the open torus \((\mathbb {C}^*)^n,\) for instance, is just \((1,\dots , 1).\) We also have a Lie group isomorphism \(T_{N(\sigma )} \longrightarrow \mathcal {O}(\sigma )\), that can be understood by \(t~\longmapsto ~t \cdot z_{\sigma },\) and we can devise it to define the distinguished compact torus of \(\mathcal {O}(\sigma ),\) given by
Now, for any positive integer m, we consider the multiplication map
which induces the toric morphism (see [19, Definition 1.3.13]),
To justify the latter, note that in terms of semigroup homomorphisms the induced map \(\phi _m \otimes _{\mathbb {Z}} 1,\) is indeed
for any semigroup homomorphism \(\gamma : M \longrightarrow \mathbb {C}.\) As a result, when \(T_N= (\mathbb {C}^*)^n\), we obtain our familiar group endomorphism
We can also extend our multiplication map to \((\phi _m)_{\mathbb {R}}:N_{\mathbb {R}}\longrightarrow N_{\mathbb {R}},\) and note that it maps any cone \(\sigma \in \Sigma \) to itself, and as a result it induces a toric endomorphism, which we also denote by \(\Phi _{m}: X_{\Sigma }\longrightarrow X_{\Sigma };\) see [19, Theorem 3.3.4]. Since \(\sigma ^{\circ }\), the relative interior of \(\sigma \), is invariant under \((\phi _m)_{\mathbb {R}},\) every toric orbit \(\mathcal {O}(\sigma )\) also remains invariant under \(\Phi _m.\) In addition, \((\phi _{m})_{\mathbb {R}}^{-1}(\sigma ^{\circ }) = \sigma ^{\circ }\) implies that \(\Phi _m^{-1}(\mathcal {O}_{\sigma }) = \mathcal {O}_{\sigma }.\) Let us understand \(\Phi _m{\upharpoonright }_{\mathcal {O}(\sigma )}\) explicitly by observing that
Note that \(T_N \simeq \textrm{Hom}_{\mathbb {Z}}(M, \mathbb {C}^*),\) and \(\Phi _m\) is the continuous extension of \(t\in T_N \longmapsto t^m \in T_N,\) to \(X_{\Sigma }\longrightarrow X_{\Sigma }.\) Moreover, the isomorphism \(\mathcal {O}(\sigma )\simeq \textrm{Hom}_{\mathbb {Z}}(\sigma ^{\perp } \cap M, \mathbb {C}^*),\) implies that \(\mathcal {O}(\sigma )\) as a subset of \(U_{\sigma } = \textrm{Spec}~\mathbb {C}[\sigma ^{\vee }\cap M],\) is given by the set of semigroup homomorphisms satisfying
As a result, the map \(\Phi _m: T_N \longrightarrow T_N,\) \(\gamma \longmapsto \gamma ^m,\) extends continuously on \(\mathcal {O}(\sigma )~\longrightarrow ~\mathcal {O}(\sigma ),\) by \(\gamma \longmapsto \gamma ^m.\) Finally, we may write \(\gamma = t\cdot z_{\sigma },\) for some \(t\in T_{N(\sigma )},\) to obtain
Now we have gathered enough tools to show that we have a separate equidistribution theorem within each toric orbit:
Proposition 5.1
Let \(\Phi _{m}:X_{\Sigma } \longrightarrow X_{\Sigma }\) be the toric endomorphism induced by the multiplication map. For any \(z \in \mathcal {O}(\sigma ),\) we have the weak convergence
where \(\mu (S(\sigma ))\) is the normalised Haar measure on the distinguished compact torus \(S(\sigma )= S_{N(\sigma )}\cdot z_{\sigma } \subseteq \mathcal {O}(\sigma ).\)
Proof
We have observed that
Let
The fact that the pullbacks \(\xi ^*\) and \((\xi ^{-1})^*\) are continuous with respect to the weak topology of currents, see Sect. 2, implies that to prove the proposition it suffices to observe the weak convergence for the conjugate map instead:
for any \(z' \in T_{N(\sigma )},\) with \(z' = \xi ^{-1}(z).\) Let \(q= \dim (\mathcal {O}(\sigma ))= n-\dim (\sigma ).\) Note that the isomorphism \(N(\sigma ) \simeq \mathbb {Z}^q,\) induces an isomorphisms of Lie groups \(S_{N(\sigma )}\simeq (S^1)^q\), and a biholomorphism of complex manifolds
Consequently, by weak continuity of pullback morphisms, to prove the asserted convergence, it suffices to show the analogous statement on \((\mathbb {C}^*)^q.\) On \((\mathbb {C}^*)^q\), however, the induced map, which we also denote by \(\Phi _m,\) is given by
In this case, for any compactly supported smooth function \(f:(\mathbb {C}^*)^n \longrightarrow \mathbb {C}\), we have
as the left hand side is simply tending to the Riemann sum for the integral on the right hand side, since \(\mu \) is the Haar measure on \((S^1)^q\).
\(\square \)
Let us end this subsection with the following useful lemma, which can be also proved directly for any toric variety without the smoothness assumption.
Lemma 5.2
Let \(Z\subseteq (\mathbb {C}^*)^n\) be a subvariety, and \(\bar{Z}\) be the closure of Z in a smooth toric variety \(X_{\Sigma }.\) Then
Proof
When \(X_{\Sigma }\) is smooth, according to [32, Exercise 18.17], the finiteness property of \(\Phi _m\) implies that \(\Phi _m\) is flat. The assertion then follows from [42, Théorème 2.3.10].
\(\square \)
5.2 Tropical Compactifications
Let X be a smooth, projective toric variety and fix a torus equivariant projective embedding
Assume that \(\omega _0\) is the smooth positive (1, 1)-form on X, corresponding to \(\phi .\) We have that by Wirtinger’s theorem [41, Page 31], the closure of any closed algebraic variety \(Z\subset (\mathbb {C}^*)^n\) in X has a finite mass with respect to \(\omega _0\). We can therefore employ the El Mir–Skoda theorem, [20, Sect. III.2.A], and extend [Z] by zero to the closed positive current \(\overline{[Z]}\) on X. Similarly, any tropical current  can be extended by zero to any smooth projective toric variety, since any fiber \(\pi _{\text {aff}(\sigma )}^{-1}(x),\) for \(\sigma \in \mathcal {C},\) has a bounded normalised mass; see [6, Proposition 4.4] for more details where we also treat the tropical currents with non-positive weights. If, moreover, we demand that the support of \(\overline{[Z]}\) or the fibers of
can be extended by zero to any smooth projective toric variety, since any fiber \(\pi _{\text {aff}(\sigma )}^{-1}(x),\) for \(\sigma \in \mathcal {C},\) has a bounded normalised mass; see [6, Proposition 4.4] for more details where we also treat the tropical currents with non-positive weights. If, moreover, we demand that the support of \(\overline{[Z]}\) or the fibers of  intersect the torus-invariant divisors of \(X_{\Sigma }\) properly we need a certain compatibility with \(\Sigma \), which we present in Theorems 5.5 and 5.7 below, after recalling some important theorems from toric geometry. Recall that a p-dimensional cone \(\sigma = \text {cone}(\rho _1, \dots , \rho _p) \subseteq \mathbb {R}^n \simeq N_{\mathbb {R}}\) is called unimodular, if \(\{\rho _1, \dots , \rho _p \}\) can be completed to a \(\mathbb {Z}\)-basis of \(\mathbb {Z}^n.\)
intersect the torus-invariant divisors of \(X_{\Sigma }\) properly we need a certain compatibility with \(\Sigma \), which we present in Theorems 5.5 and 5.7 below, after recalling some important theorems from toric geometry. Recall that a p-dimensional cone \(\sigma = \text {cone}(\rho _1, \dots , \rho _p) \subseteq \mathbb {R}^n \simeq N_{\mathbb {R}}\) is called unimodular, if \(\{\rho _1, \dots , \rho _p \}\) can be completed to a \(\mathbb {Z}\)-basis of \(\mathbb {Z}^n.\)
Theorem 5.3
Let \(\Sigma \subseteq \mathbb {R}^n,\) be a fan. Then,
-
(a)
\(X_{\Sigma }\) is smooth, if and only if, \(\Sigma \) is unimodular, i.e., all cones in \(\Sigma \) are unimodular.
-
(b)
\(X_{\Sigma }\) is complete, if and only if, \(\Sigma \) is complete, i.e., \(|\Sigma | = \mathbb {R}^n.\)
-
(c)
\(X_{\Sigma }\) is projective, if and only if, \(\Sigma \) is projective, i.e., \(\Sigma \) is dual to a polytope.
Recall that, since our base field is the set of complex numbers, a variety is complete, if and only if, it is compact in the classical topology. Moreover, we do not require our varieties to be projective in this article, and have added Theorems 5.3.c and 5.4.c for completeness; see [19, Page 67] for the definition of a dual polytope. Further,
Theorem 5.4
-
(a)
The Toric Resolution of Singularities: any fan \(\Sigma \) can be refined to obtain a unimodular fan; [19, Theorem 11.1.9].
-
(b)
For any fan \(\Sigma \) there exists complete fan \(\Sigma '\) containing \(\Sigma \) as a subfan; [33, Theorem III.2.8].
-
(c)
The Toric Chow Lemma: every complete fan has a refinement that is projective; [19, Theorem 6.1.18].
Since our main objects in this article are differential forms and currents, we always need our ambient toric varieties to be smooth or equivalently their fan to be unimodular. When \(X_{\Sigma }\) is smooth, \(X_{\Sigma } \setminus (\mathbb {C}^*)^n\) is a simple normal crossing divisor, and the orbit closures \(D_{\sigma } := \overline{\mathcal {O}(\sigma )},\) for \(\sigma \in \Sigma ,\) are intersections of its irreducible components. As we mentioned in the introduction that \(\textrm{trop}(Z)\) as a set is given by the Hausdorff limit
Further, we know from the Structure Theorem in tropical geometry, [58, Theorem 3.3.5], that \(\textrm{trop}(Z)\) can be regarded as the support of a rational polyhedral complex. In the following paragraphs we recall how to endow a tropical structure on the set \(\textrm{trop}(Z),\) using the following theorem due to Tevelev and Sturmfels. Tevelev’s theorem below provides a condition for the closure of Z to be complete in a given toric variety, even when the toric variety is not complete. We also note that one significance of [71] is to consider the case where the compactification is flat, see [58, Sect. 6.4] for a definition, which we do not require in this article.
Theorem 5.5
Let \(Z \subseteq (\mathbb {C}^*)^n\) be an irreducible algebraic subvariety of dimension p, and \(\Sigma \subseteq N_{\mathbb {R}}\), a unimodular (rational) fan.
-
(a)
The closure \(\bar{Z}\) of Z in \(X_{\Sigma }\) is complete, if and only if, \(\textrm{trop}(Z) \subseteq |\Sigma |;\) see [71].
-
(b)
We have \(|\Sigma |= \textrm{trop}(Z)\), if and only if, for every \(\sigma \in \Sigma \) the intersection \( \mathcal {O}_{\sigma }\cap \bar{Z}\) is non-empty and of pure dimension \(p- \dim (\sigma );\) see [70].
For a subvariety \(Z\subseteq (\mathbb {C}^*)^n\), we can always find a unimodular fan \(\Sigma \) such that \(\textrm{trop}(Z)=|\Sigma |,\) this is a consequence of the toric resolution of singularities, Thereom 5.4.a. Suppose now that \(\Sigma '\) is a fan that contains \(\Sigma \) as a subfan. Then, the closure of Z in \(X_{\Sigma }= \bigcup _{\sigma \in \Sigma } \mathcal {O}(\sigma ) \) can be identified with the closure of Z in \(X_{\Sigma '} = \bigcup _{\sigma \in \Sigma '} \mathcal {O}(\sigma ).\) Applying the preceding theorem we obtain that for a p-dimensional cone \(\sigma \in \Sigma ',\) the intersection \(\mathcal {O}(\sigma ) \cap \bar{Z}\) is non-empty, if and only if, \(\sigma \in \Sigma ,\) and in this case, the intersection is of dimension \(p- \dim (\sigma );\) see also [58, Sect. 6.4] and [43]. Therefore, thanks to [20, Corollary 4.10], for any positive integer \(k\le p,\) if \(\tau = \text {cone}(\rho _1, \dots , \rho _k)\in \Sigma ,\) where \(\rho _i \in \Sigma \) are rays, the wedge product
is admissible, and yields a \((p-k, p-k)\)-closed positive current which can be considered in both \(X_{\Sigma }\) and \(X_{\Sigma '}\). When \(\dim (\sigma ) = p,\) the intersection is 0-dimensional, and we set
It is observed in tropical geometry that \(\textrm{trop}(Z)\) with the induced fan structure from \(\Sigma ,\) and the induced weights \(w_{\sigma }\) is a balanced fan; see [58, Theorem 6.7.7]. We also review this induced balancing condition as a consequence of our main convergence theorem by noting that the weak limit of a sequence of closed currents is indeed closed.
Definition 5.6
Suppose \(Z\subseteq (\mathbb {C}^*)^n\) is an irreducible subvariety, and \(\Sigma \) is a fan with \(|\Sigma | = \textrm{trop}(Z).\) The closure \(\bar{Z}\) of Z in the toric variety \(X_{\Sigma },\) or equivalently in any \(X_{\Sigma '},\) such that \(\Sigma '\) contains \(\Sigma \) as a subfan, is called a tropical compactification of Z.
Let us also investigate the situation for the tropical currents. Recall from Theorem 4.4 when a polyhedral complex \(\mathcal {C}\) satisfies the balancing condition, then  is closed.
is closed.
Theorem 5.7
Let \(\mathcal {C}, \Sigma \subseteq \mathbb {R}^n\) be two fans, and assume that \(\mathcal {C}\) is a p-dimensional tropical variety.
-
(a)
Let \(\tau \in \mathcal {C},\) \(\sigma \in \Sigma ,\) and \(\overline{\pi ^{-1}_{{\text {aff}(\tau )}}(x)}\) be the closure in \(U_{\sigma }.\) Then, the intersection
$$\begin{aligned} D_{\sigma } \cap \overline{\pi ^{-1}_{{\text {aff}(\tau )}}(x)}, \end{aligned}$$is non-empty, if and only if, \(\tau \) contains \(\sigma \) as a face and in this case the intersection is transverse; [6, Lemma 4.10.1].
-
(b)
If \(\sigma \in \mathcal {C}\cap \Sigma \) is cone of dimension p with weight \(w_{\sigma }\) in \(\mathcal {C}\), then

where
 is the extension by zero of
is the extension by zero of  in \(X_{\Sigma }\); [6, Theorem 4.7].
in \(X_{\Sigma }\); [6, Theorem 4.7].
The preceding theorem asserts that the wedge product \(\overline{[\pi _{\text {aff}(\sigma )}^{-1}(x)]} \wedge \, D_{\sigma },\) for any \(x\in S_{N(\sigma )}\) is a well-defined (0, 0)-dimensional current. Transversality implies that the intersection multiplicity is one, and Part (b) implies that averaging with respect to the Haar measure and multiplying with \(w_{\sigma }\) will indeed yield the total mass \(w_{\sigma }\).
Remark 5.8
Let \(Z\subseteq (\mathbb {C}^*)^n\) be an irreducible subvariety and consider \(\Sigma \) a unimodular fan with \(\textrm{trop}(Z)= |\Sigma |.\) Since, for any positive integer m
the sets \(\textrm{trop}(\Phi _m^{-1}(Z))\) coincide. As a result, by Theorem 5.5 all \(\overline{\Phi _m^{-1}(Z)}\)’s are simultaneously complete in \(X_{\Sigma },\) and intersect the toric invariant divisors of \(X_{\Sigma }\) properly. In consequence, the currents \(\big [\,\overline{\Phi _m^{-1}(Z)}\,\big ]\) carry no mass on \(X_{\Sigma }\setminus (\mathbb {C}^*)^n.\) And,
where \(\Phi _0^{-1}(Z):= Z.\) Finally, in view of Lemma 5.2, we conveniently obtain
5.3 Extended Tropicalisation
For any rational fan \(\Sigma \subseteq N_{\mathbb {R}},\) the logarithm map \(\textrm{Log}: T_N \longrightarrow N_{\mathbb {R}},\) can be continuously extended to
where \(N_{\Sigma }\) denotes the quotient \(X_{\Sigma }/S_{N(\{0\})};\) see [50, Sect. 3]. The tropical toric variety \(N_{\Sigma }\) can be regarded as the tropicalisation of toric variety \(X_{\Sigma }\) and it was studied in [3, 52, 64] and [58, Section 6.2]. The set \(N_{\Sigma }\) has a natural topology and it is straightforward to see that for a polyhedral complex \(\mathcal {C}\subseteq N_\mathbb {R}\subseteq N_{\Sigma },\)
By [50, Theorem A\('\)] for an algebraic subvariety \(Y \subseteq X_{\Sigma },\) the logarithmic tropicalisation also extends to \(X_{\Sigma }:\)
where \(\textrm{trop}(Y)\subseteq N_{\Sigma }\) is the tropicalisation of Y in \(N_{\Sigma }.\) Now assume that \(Z \subseteq T_N\) is an algebraic subvariety, and \(\bar{Z}\) is the closure of Z in \(X_{\Sigma },\) Theorem 6.2.18 in [58] implies that \(\textrm{trop}(\bar{Z})\) coincides with the closure of \(\textrm{trop}(Z)\subseteq N_{\mathbb {R}}\) in \(N_{\Sigma }.\) In consequence,
where the convergence is in the Hausdorff metric of compact sets of \(N_{\Sigma }\).
6 A Proof for Theorem A
We are now ready to prove the main theorem of this article. The reader may find viewing the figure in Sect. 7.1 instructive while following the steps of the proof.
Theorem 6.1
Let \(Z\subseteq (\mathbb {C}^*)^n\) be an algebraic variety of dimension p, then we have the weak convergence

in  Moreover, with the induced weights from any unimodular tropical compactification of Z, \(\textrm{trop}(Z)\) is balanced.
Moreover, with the induced weights from any unimodular tropical compactification of Z, \(\textrm{trop}(Z)\) is balanced.
Proof
We proceed in the following steps.
Step 1. The extention of the map \(\Phi _m\) to an endomorphism of \(\mathbb P^n\) has degree m, with respect to O(1). It is well-known that \(m^{p-n}\) is the correct normalisation factor for \(\Phi _m^*\) to preserve the normalised total mass of the closure of [Z] in \(\mathbb P^n\). Therefore, all the elements of the sequence \(\{m^{p-n}\Phi ^*_m[\bar{Z}] \}\) have an equal normalised total mass, and as a result of the Banach–Alaoglu theorem, the sequence is locally compact with respect to the weak topology of currents. In other words, it has a convergence subsequence in \(\mathbb P^n\), and by restriction on \((\mathbb {C}^*)^n.\)
Step 2. In Sect. 6.1 below, we prove that the support of any cluster value  of the sequence is given by \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\) Let \(\Sigma \) be a unimodular fan with \(|\Sigma |= \textrm{trop}(Z).\) Since
of the sequence is given by \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\) Let \(\Sigma \) be a unimodular fan with \(|\Sigma |= \textrm{trop}(Z).\) Since  is a positive closed current of bidimension (p, p), by Demailly’s second theorem of support, [20, III.2.13], it can be represented as
is a positive closed current of bidimension (p, p), by Demailly’s second theorem of support, [20, III.2.13], it can be represented as

for some positive measures \(\mathrm{{d}}\eta _{\sigma }.\)
Step 3. In Sect. 6.2 below, we show that for any cluster value  obtained in the above steps, the corresponding measures \(\mathrm{{d}}\eta _{\sigma }\) must be Haar measures. This, together with Proposition 4.6, implies that any cluster value
obtained in the above steps, the corresponding measures \(\mathrm{{d}}\eta _{\sigma }\) must be Haar measures. This, together with Proposition 4.6, implies that any cluster value  is indeed a tropical current with support \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\)
is indeed a tropical current with support \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\)
Step 4. Let  be a subsequence of \(m^{p-n}\Phi _m^*[Z]\) weakly convergent to the tropical current
be a subsequence of \(m^{p-n}\Phi _m^*[Z]\) weakly convergent to the tropical current  we show that in the toric variety \(X_{\Sigma },\) we have
we show that in the toric variety \(X_{\Sigma },\) we have  As in Step 2, the support of
As in Step 2, the support of  is given by \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\) Therefore
is given by \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\) Therefore

where in the first equality we have used a simple property of \(\textrm{Log}: X_{\Sigma } \longrightarrow N_{\Sigma },\) and the second equality is provided by [58, Theorem 6.2.18]. Assume now that  is a cluster value of
is a cluster value of  By Eq. ((I)) and Remark 2.1,
By Eq. ((I)) and Remark 2.1,  therefore
therefore

Since  the support of the positive closed (p, p)-dimensional current
the support of the positive closed (p, p)-dimensional current  is included in
is included in  where \(D_i\)’s are the torus invariant divisors of \(X_{\Sigma }.\) In view of Theorem 5.7,
where \(D_i\)’s are the torus invariant divisors of \(X_{\Sigma }.\) In view of Theorem 5.7,  has a Cauchy–Riemann dimension less than p, and by Demailly’s first theorem of support, [20, Theorem III.2.10], we have
has a Cauchy–Riemann dimension less than p, and by Demailly’s first theorem of support, [20, Theorem III.2.10], we have 
Step 5. Assume that  and
and  are two subsequences of \(m^{p-n}\Phi _m^*[Z]\) weakly convergent to the tropical currents
are two subsequences of \(m^{p-n}\Phi _m^*[Z]\) weakly convergent to the tropical currents  and
and  , respectively. We intend to show that
, respectively. We intend to show that  Applying Theorem 5.4.b, and the toric resolution of singularities Theorem 5.4.a, we can find a fan \(\Sigma '\) containing \(\Sigma \) as a subfan such that \(X_{\Sigma '}\) is a smooth projective toric variety. In view of Theorem 5.7.b, it only remains to show that for any p-dimensional cone \(\sigma \in \Sigma ',\)
Applying Theorem 5.4.b, and the toric resolution of singularities Theorem 5.4.a, we can find a fan \(\Sigma '\) containing \(\Sigma \) as a subfan such that \(X_{\Sigma '}\) is a smooth projective toric variety. In view of Theorem 5.7.b, it only remains to show that for any p-dimensional cone \(\sigma \in \Sigma ',\)

where the transversality of intersections are guaranteed by Step 2 and Theorem 5.7. For \(\sigma \in \Sigma ',\) let
We show that  , for any \(\sigma \in \Sigma '.\) By Step 4, in \(X_{\Sigma '}\)
, for any \(\sigma \in \Sigma '.\) By Step 4, in \(X_{\Sigma '}\)

By Remark 5.8,

Since \(\dim (\sigma )= p,\) we have \(\dim \big (\mathcal {O}(\sigma ) \big )=n-p.\) As a result, the restriction \(m^{p-n}\Phi ^*_{m}{{\upharpoonright }_{\mathcal {O}(\sigma )}}\) preserves the mass of zero dimensional integration currents in \(\mathcal {O}(\sigma ).\) Hence, for any positive integer m,
where we have used the invariance of \(D_{\sigma }\) under \(\Phi _m^{-1}\) in the latter equality. Now we can use [6, Proposition 4.12], which is heavily based on the Demailly’s regularisation theorem, to reduce the calculations of the above masses to intersection of cohomology classes. Namely, whenever  is a closed positive current such that
is a closed positive current such that  is admissible,
is admissible,

In the above formula,
\(\{~\}\) denotes the Dolbeault cohomology class in \(X_{\Sigma '},\)
\(D_{\sigma } = D_1 \cap \dots \cap D_p\), is the intersection of toric invariant divisors, and
\(\omega _1, \dots , \omega _p\) are the first Chern forms corresponding to \(D_1, \dots , D_p,\) respectively.
We note that we have chosen \(X_{\Sigma '}\) to be a smooth compact complex manifold in order to employ [6, Proposition 4.12]. Now, using the weak continuity of the cohomology class assignment, and the above formulas,

This concludes the proof of the main convergence theorem.
Step 6. Let us now observe that with the induced fan structure from \(\Sigma \) or \(\Sigma '\), and the induced weights, \(\textrm{trop}(Z)\) is balanced. The weak limit of a sequence of closed currents is a closed current, and Theorem 4.4 asserts that a tropical current associated to any weighted polyhedral complex is closed if and only if, the underlying weighted polyhedral complex is balanced. \(\square \)
6.1 Convergence of the Supports
In this subsection we show that for any p-dimensional subvariety \(Z \subseteq (\mathbb {C}^*)^n,\) the support of any cluster value of the sequence \(m^{p-n}\Phi _m^*[Z]\) is given by \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\) The inclusion in \( \textrm{Log}^{-1}(\textrm{trop}(Z))\) is easy but for the converse we need certain volume estimates. Notation-wise, it is slightly lighter to write the proofs of the following statements for the whole sequence rather than a subsequence, acknowledging that the proofs are identical.
Proposition 6.2
Assume that  is the weak limit of the sequence
is the weak limit of the sequence  Then,
Then,

We give a proof of the preceding proposition after the proof of Lemma 6.5.
Corollary 6.3
Assume that  is the weak limit of the sequence
is the weak limit of the sequence  then
then

in the Hausdorff metric of compact sets of \((\mathbb {C}^*)^n.\)
Proof
We note that by Bergman’s theorem and the definition of \(\Phi _m\)

in the Hausdorff metric and by Proposition 6.2,  \(\square \)
\(\square \)
Lemma 6.4
For any positive integer m sufficiently large, small \(\epsilon > 0,\) and \(b_m \in \Phi _m^{-1}(Z)\) we have
where \(\beta = dd^c \Vert z \Vert ^2,\) and C is a positive constant and independent of m.
Proof
Let \(b_m = (b_{m,1}, \dots , b_{m,n}), \, a_m= \Phi _m(b_m)=(a_{m,1}, \dots , a_{m,n})\in Z,\) and note that \(|b_{m,j}| = |a_{m,j}|^{1/m}\). For each \(j=1, \dots , n\), we set \({{\textbf {r}}}_{j} := (|b_{m,j}|-\frac{\epsilon }{\sqrt{2}})\) and \({{\textbf {R}}}_{j} := (|b_{m,j}|+\frac{\epsilon }{\sqrt{2}})\). For positive real numbers \({{\textbf {r}}}<{{\textbf {R}}}\), we will denote the annulus
We also set
which is a contractible open subset of \(C_{{{\textbf {r}}}, {{\textbf {R}}}}\). When m is large, \(\Phi _m(B_\epsilon (b_m))\) contains the multi-annulus given by
Let \(B_m^* = \prod _{j=1}^n C^*_{{{\textbf {r}}}^m_{j}, {{\textbf {R}}}^m_{j}}\). Since \(\Phi _m\) is a covering and \(B_m^*\) is contractible, we can partition \(\Phi _{m}^{-1}\bigl (B_m^*)\) into a disjoint union of open sets \(K_{m,1}, \dots , K_{m,m^n}\) such that for each \(i \in [m^n]: = \{1, \dots , m^n\},\)
is a homeomorphism. Each \(K_{m,i}\) can be parametrised in polar coordinates with \((0, {2\pi }/{m})^n \times \prod _{j\in [n]}({{\textbf {r}}}_j , {{\textbf {R}}}_j).\) For a fixed m, and any \(i\in [m^n]\),
We set \(Z_{i} = \Phi _m^{-1}(Z) \, \cap \, K_{m, i}\). Since by Lelong’s theorem [20, Theorem III.2.7], the singular set of Z does not charge any mass, we assume that Z is smooth and consider the parametrisation
for \(U \subseteq (\mathbb {R}^+)^p.\) Let \(\{ 1, \zeta , ...,\zeta ^{m-1}\}\) be all different m-th roots of unity, and for \(\ell = (\ell _1, \dots , \ell _n)\in \mathbb {Z}^n \cap [0,m-1]^n,\) define \(\lambda ^{\ell }(\zeta ):= (\zeta ^{\ell _1}, \dots , \zeta ^{\ell _n}).\) The component-wise multiplication \(\varvec{\tau }\cdot \lambda ^\ell (\zeta )\) for different \(\ell \) parametrises all the manifolds \(\Phi _m^{-1}(Z) \cap K_{m,i}\) for \(i=1, \dots , m^n.\) Therefore, the equality
implies that all \(Z_i\)’s have the same mass. We now claim that for each i
for a constant \(C_{i}.\) As we noted before, by Bergman’s theorem and the definition of \(\Phi _m\) we have  As a result, by shrinking \(\epsilon \), if necessary, there exists \(\sigma \in \textrm{trop}(Z),\) and a fiber \(\pi ^{-1}_{\sigma }(x)\) for some \( x\in (S^1)^{n-p},\) such that at a point \(w\in \pi _{\sigma }^{-1}(x),\) the projection \(\text {proj}: Z_i \longrightarrow T_w \pi _{\sigma }^{-1}(x)\) is surjective. It is crucial to note that, because of the Hausdorff convergence, for larger m’s we do not need to shrink \(\epsilon \) any further for such surjectivity to hold. Using this projection, we can find coordinates \(w= (w', w'')\) and polydiscs \(w'\in \Delta '\subseteq \mathbb {C}^p, w''\in \Delta ''\subseteq \mathbb {C}^{n-p}\) of radii \(r'=\frac{\epsilon }{\sqrt{2}}\) and \(r''\) with \(r'\le Cr''\) for \(C>0\) large, such that the projection \(\pi : Z_{i}\,\cap \big (\Delta ' \times \Delta '' \big )\longrightarrow \Delta '\) is also surjective. Therefore,
As a result, by shrinking \(\epsilon \), if necessary, there exists \(\sigma \in \textrm{trop}(Z),\) and a fiber \(\pi ^{-1}_{\sigma }(x)\) for some \( x\in (S^1)^{n-p},\) such that at a point \(w\in \pi _{\sigma }^{-1}(x),\) the projection \(\text {proj}: Z_i \longrightarrow T_w \pi _{\sigma }^{-1}(x)\) is surjective. It is crucial to note that, because of the Hausdorff convergence, for larger m’s we do not need to shrink \(\epsilon \) any further for such surjectivity to hold. Using this projection, we can find coordinates \(w= (w', w'')\) and polydiscs \(w'\in \Delta '\subseteq \mathbb {C}^p, w''\in \Delta ''\subseteq \mathbb {C}^{n-p}\) of radii \(r'=\frac{\epsilon }{\sqrt{2}}\) and \(r''\) with \(r'\le Cr''\) for \(C>0\) large, such that the projection \(\pi : Z_{i}\,\cap \big (\Delta ' \times \Delta '' \big )\longrightarrow \Delta '\) is also surjective. Therefore,
Since \(K_{m,i}\supseteq Z_{i}\) can be parametrised by \((0, {2\pi }/{m})^n \times \prod _{j\in [n]}({{\textbf {r}}}_j , {{\textbf {R}}}_j)\), we also can parametrise \(\Delta ',\) with \((0, {2\pi }/{m})^p \times (0, \frac{\epsilon }{\sqrt{2}})^p\), such that the Jacobian of the parametrisation does not depend on m. We have
We obtain Eq. ((II)), by taking into account that the change of coordinates \(z\mapsto w,\) contributes to the calculation of mass by multiplying a constant. Finally, to obtain the main assertion, we note that there are \(m^n\) components of \(K_{m,i},\) all with the same mass, and the normalising factor is \(m^{p-n}\).
\(\square \)
Lemma 6.5
For any positive integer m sufficiently large, small \(\epsilon > 0,\) and \(b_m \in \Phi _m^{-1}(Z)\) we have
where \(\beta = dd^c \Vert z \Vert ^2,\) and \(C'\) is a positive constant depending on \(b_m\).
Proof
Following the proof and the notation of Lemma 6.4, we find a lower bound for the mass of  in the ball \(B_{\epsilon }(b_m).\) Let \(b_m= (b_{m,1}, \dots , b_{m,n}).\) By previous lemma, the mass of
in the ball \(B_{\epsilon }(b_m).\) Let \(b_m= (b_{m,1}, \dots , b_{m,n}).\) By previous lemma, the mass of  in the multi-annulus \(A= \prod _{j=1}^n C_{{{\textbf {r}}}_{j}, {{\textbf {R}}}_{j}}\), is greater than \(C\epsilon ^{2p}.\) We can assume that \(|b_{m,j}| \gg \epsilon ,\) for all \(j=1,\dots , n.\) Note that for each j, the annulus in the j-th coordinate of the multi-annulus has an angle varying between 0 and \(2\pi ,\) which gives rise to the outer circumference of length \(2\pi (|b_j|+ \frac{\epsilon }{\sqrt{2}}).\) Therefore, in each coordinate, the angle corresponding to \(2\epsilon \) portion of the outer circumference can be approximated by
in the multi-annulus \(A= \prod _{j=1}^n C_{{{\textbf {r}}}_{j}, {{\textbf {R}}}_{j}}\), is greater than \(C\epsilon ^{2p}.\) We can assume that \(|b_{m,j}| \gg \epsilon ,\) for all \(j=1,\dots , n.\) Note that for each j, the annulus in the j-th coordinate of the multi-annulus has an angle varying between 0 and \(2\pi ,\) which gives rise to the outer circumference of length \(2\pi (|b_j|+ \frac{\epsilon }{\sqrt{2}}).\) Therefore, in each coordinate, the angle corresponding to \(2\epsilon \) portion of the outer circumference can be approximated by
We intend to estimate the portion of mass of  around \(b_m\) sliced within the angles \(\theta _1,\dots , \theta _n.\) Since the mass of
around \(b_m\) sliced within the angles \(\theta _1,\dots , \theta _n.\) Since the mass of  in A equals \(C\epsilon ^{2p},\) and components of
in A equals \(C\epsilon ^{2p},\) and components of  are divided symmetrically in A, we obtain the following lower bound
are divided symmetrically in A, we obtain the following lower bound
\(\square \)
Remark 6.6
As the above lemma suggests, the Lelong number of any tropical current at any point of its support is, in fact, zero. See [20, Sect. III.5] for a definition.
Proof of Proposition 6.2
We first show the inclusion  We note that if for any sufficiently large integer m, z has a neighbourhood that does not intersect
We note that if for any sufficiently large integer m, z has a neighbourhood that does not intersect  then
then  However, by Bergman’s theorem
However, by Bergman’s theorem
in the Hausdorff metric. Therefore, any point outside \(\textrm{Log}^{-1}\big (\textrm{trop}(Z)\big )\) is outside of  for any sufficiently large m. This implies that
for any sufficiently large m. This implies that  To prove the converse inclusion
To prove the converse inclusion  consider \(b\in \textrm{Log}^{-1}\big (\textrm{trop}(Z)\big ).\) We show that for any \(\epsilon >0\), there is a test form
consider \(b\in \textrm{Log}^{-1}\big (\textrm{trop}(Z)\big ).\) We show that for any \(\epsilon >0\), there is a test form  , such that its (compact) support contains the open ball of radius \(2\epsilon \) centered at b, \(B_{2\epsilon }(b),\) and
, such that its (compact) support contains the open ball of radius \(2\epsilon \) centered at b, \(B_{2\epsilon }(b),\) and

Let \(\beta =dd^c \Vert z \Vert ^2 = dd^c [|z_1|^2 + \dots + |z_n|^2].\) For any \(\epsilon >0,\) and sufficiently large m, there exists a point
such that \( \textrm{dist}\big (b_m,b) < \epsilon .\) This implies the inclusion \(B_{\epsilon }(b_m) \subseteq B_{2\epsilon }(b)\). By Lemma 6.5, we have that for any sufficiently large m, there exists a constant \(C_{b_m}:=\frac{C}{(4 \pi )^n |b_{m,1}\dots b_{m,n}|}>0\) such that

As \(b_m\rightarrow b,\) the sequence \(\big \{C_{b_{m}}\big \} \cup \{C_b\}\subseteq \mathbb {R}\) is compact and has a minimum value, say \(C',\) and we have

for all m. Now define the test-form \(\varphi := \chi \beta ^p,\) where \(\chi \) is a non-negative smooth function with compact support, equal to 1 in \(B_{2\epsilon }(b)\) and vanishing outside \(B_{3\epsilon }(b).\) As a result, the convergence of the complex sequence  , together with the above inequality implies that
, together with the above inequality implies that

\(\square \)
6.2 Any Cluster Value is a Tropical Current
In Lemma 6.2, we used the volume form \((dd^c\Vert z \Vert ^2)^p\) that adds the mass in different components \(K_{m,1}, \dots , K_{m,m^n}\). In contrast, in the following lemma we use the “Fourier differential forms” which are sensitive to the change of phases in polar coordinates, and we show that Fourier measure coefficients finally vanish at every non-zero degree.
Lemma 6.7
Let  be the weak limit of sequence
be the weak limit of sequence  then
then  is a tropical current.
is a tropical current.
Proof
By Proposition 6.2, the support of  has the form \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\) Let us set \(\mathcal {C}:= \textrm{trop}(Z).\) By Demailly’s second theorem of support, [20, III.2.13], there are measures \(\mathrm{{d}}\eta _{\sigma }\) such that
has the form \(\textrm{Log}^{-1}(\textrm{trop}(Z)).\) Let us set \(\mathcal {C}:= \textrm{trop}(Z).\) By Demailly’s second theorem of support, [20, III.2.13], there are measures \(\mathrm{{d}}\eta _{\sigma }\) such that

where By definition of tropical currents, we need to prove that all the non-zero degree Fourier coefficients of \(\eta _{\sigma }\) for all \(\sigma \in \Sigma \) vanish, and therefore are Haar measures. To see this we use Proposition 4.5. We prove this by showing that when m is sufficiently large,
for any fixed (p, p)-differential form \(\omega \) given in polar coordinates by
where \(\nu \in \mathbb {Z}^n \setminus \{0\},\) \(I \subseteq [n],\) with \(|I|=p,\) \(\theta = (\theta _1, \dots , \theta _n)\) and \(r= (r_1, \dots , r_n)\) are polar coordinates, and \(\rho :\mathbb {R}^n \rightarrow \mathbb {R}\) is a smooth and appropriately chosen, and \(\omega \) has the support given by \(\Phi _m^{-1}(B_{\epsilon }(a_m))\) for \(a_m \in Z.\) For convenience, we change the coordinates to have \(\omega _I = x^{\nu } \rho (r)~ \mathrm{{d}}r_{I} \wedge \mathrm{{d}}x_{I},\) with \((x, r) \in (S^1)^n \times (\mathbb {R}^+)^n \simeq (\mathbb {C}^*)^n.\) Let us recycle the notation in the proof of Lemma 6.4: \(b_m = (b_{m,1}, \dots , b_{m,n}),\, a_m= \Phi _m(b_m)=(a_{m,1}, \dots , a_{m,n})\in Z,\) and we partition \(\Phi _{m}^{-1}\bigl (B_m^*)\) into a disjoint union of open sets \(K_{m,1}, \dots , K_{m,m^n}.\) Since by Lelong’s theorem [20, Theorem III.2.7], the singular set of Z does not charge any mass, we assume that Z is smooth and consider the parametrisation
for \(U\subseteq (\mathbb {R}^+)^p.\) We let \(\{ 1, \zeta , ...,\zeta ^{m-1}\}\) be all different m-th roots of unity, and for \(\ell = (\ell _1, \dots , \ell _n)\in \mathbb {Z}^n \cap [0,m-1]^n,\) define \(\lambda ^{\ell }(\zeta ):= (\zeta ^{\ell _1}, \dots , \zeta ^{\ell _n}).\) The component-wise multiplication \(\varvec{\tau }\cdot \lambda ^\ell (\zeta )\) for different \(\ell \) parametrises all the manifolds \(\Phi _m^{-1}(Z) \cap K_{m,i}\) for \(i=1, \dots , m^n.\) We write
For each \(\ell =(\ell _1, \dots , \ell _n),\)
As a consequence, the term \(x^\nu \) in \(\omega _I\) discharges \(\zeta ^{\langle \ell , \nu \rangle },\) and \(dx_I\) produces \(\zeta ^{\langle \ell , \mathbb {1}_I \rangle },\) where \(\mathbb {1}_I\) is the characteristic vector of \(I\subseteq [n].\) We conclude
The final sum, however, vanishes for a fixed \(\nu = (\nu _1, \dots , \nu _n)\) and large m, since for  ,
,
\(\square \)
7 Applications
7.1 From Tori to Toric Varieties
Let us prove Theorem B of the introduction.
Theorem 7.1
Let \(Z\subseteq (\mathbb {C}^*)^n\) be an irreducible subvariety of dimension p, and \(\bar{Z}\) a tropical compactification of Z in the smooth projective toric variety \(X_{\Sigma }\). Then,

where \(\Phi _m: X_{\Sigma }\longrightarrow X_{\Sigma }\) is the extension of \(\Phi _m: (\mathbb {C}^*)^n \longrightarrow (\mathbb {C}^*)^n,\) and  is the extension by zero of
is the extension by zero of  to \(X_{\Sigma }.\)
to \(X_{\Sigma }.\)
Proof
Theorem A asserts that

As in Step 4 of the proof of Theorem 6.1,

Effectively, we only need to observe the equality
which is addressed in Remark 5.8. \(\square \)
Dynamical tropicalisation in \(\mathbb P^1 \times \mathbb P^1\). See the discussion following the proof of Theorem 7.1
Let us now elaborate on Fig. 1. The toric variety associated to the square is indeed \(\mathbb P^1 \times \mathbb P^1.\) The interior of the square corresponds to the two dimensional orbit \(\mathcal {O}(\{0\}),\) and the sides of the square to one dimensional orbit closures. On the left, the tropical compactification of a curve \(C\subseteq (\mathbb {C}^*)^2\) in \(\mathbb P^1 \times \mathbb P^1\) is considered. The closure \(\overline{C}\) intersects the one dimensional toric orbits properly and with multiplicity two at all the intersection points. All the toric orbits remain invariant under \(\Phi ^{-1}_m\), and under this application the points in each toric orbit move towards the compact torus above the corresponding distinguished points. By applying \(\Phi ^{-1}_m\) to the curve we obtain a local covering. Multiplying the integration current \(\frac{1}{\text {deg}(C)}[\Phi _m^{-1}(\overline{C})]\) by 1/m normalises the total mass, which is depicted by the thickness of the curves. The limit becomes the associated tropical current whose fibers are transverse to the toric orbits, where the weights account for the intersection multiplicity numbers. Accordingly, the intersection points of multiplicity two converge to the transverse (non-normalised) Haar measures on the distinguished circles with mass two.
7.2 Dynamical Kapranov Theorem
Kapranov’s theorem [58, Theorem 3.1.3] is a foundational result in tropical geometry for which we provide a dynamical version in the trivial valuation case. Let \(A\subseteq \mathbb {Z}_{\ge 0}^n\) be a finite set, and \(f(z) = \sum _{\alpha \in A} c_{\alpha } z^{\alpha } \in \mathbb {C}[z]\) be a complex polynomial. We set the tropicalisation of f to be
We have
Similar to the observation in the beginning of Sect. 3 we obtain
in \(L^1_{\text {loc}}(\mathbb {C}^n)\). See also [65, Theorem 3.4]. We note that the negative coefficient of \(\alpha \) in \(\textrm{trop}(f)\) is to compensate for using \(\textrm{Log}= -\log \otimes 1\) in the preceding formula. The (dynamical) Kapranov’s theorem asserts that the tropicalisation of the algebraic hypersurface V(f) coincides with the (tropical current of the) tropical variety of tropicalisation of f. Here is Theorem C of the introduction.
Theorem 7.2
Assume that \([V(f)]= dd^c \log |f|,\) is an integration current in  . Let \(\mathfrak {q}:= \textrm{trop}(f),\) defined as above. We have that,
. Let \(\mathfrak {q}:= \textrm{trop}(f),\) defined as above. We have that,

Proof
We have \(\Phi _m^*[V(f)]= \Phi _m^*(dd^c \log |f|) =dd^c (\Phi _m^* \log |f_t|).\) Dividing by m and taking the limit yields

For the above convergence, we have used Eq. ((III)) and the continuity differentials with respect to the weak limit, and for the latter equality we have used the tropical Lelong–Poincaré equation; see Proposition 7.4. \(\square \)
Remark 7.3
-
(a)
We have observed that the tropicalisation of the Lelong–Poincaré equation leads to a version of Kapranov’s theorem. It is therefore tempting to tropicalise the King’s formula [20, III.8.18], and wish to obtain a version of the Fundamental Theorem of Tropical Geometry, see [58, Sect. 3.2]. However, Monge–Ampère operators are not in general weakly continuous, see [16, 37, 54], and naively applying the dynamical tropicalisation to the King’s formula does not provide useful information.
-
(b)
Let \(W \subseteq \mathbb {C}^* \times (\mathbb {C}^*)^n\) be an irreducible subvariety of dimension \(p+1\) such that the projection of W onto the first factor is flat and surjective. We may therefore regard W as a one-parameter family of algebraic varieties \(W_t,\) where each \(W_t\) is the p-dimensional fiber above \(t \in \mathbb {C}^*.\) In tropical geometry, it is shown that the limit in the Hausdorff sense of
$$\begin{aligned} \frac{1}{\log |t|}\textrm{Log}(W_t), \quad \text {as }t\rightarrow \infty , \end{aligned}$$is a rational polyhedral complex which is balanced. See [63, 68] for the codimension one case, and [50] in any codimensions and the background on the evolution of proofs. The correct analogue of this statement in our setting seems to be proving that the sequence
$$\begin{aligned} \frac{1}{m^{n-p+1}}\Phi _m^* \big [(e^m,W_{e^m})\big ], \quad \text {as} m\rightarrow \infty , \end{aligned}$$converges to a tropical current. See also [5, Theorem 5.2.7] for a related result.
7.2.1 Tropical Lelong–Poincaré Equation
Chambert-Loir and Ducros in [17] proved the generalised Lelong–Poincaré equation for Lagerberg currents. We have the following theorem which also appeared in [5].
Proposition 7.4
For any tropical polynomial \(\mathfrak {q}:\mathbb {R}^n \rightarrow \mathbb {R}\),

in  .
.
Proof
On the one hand, \(\mathfrak {q}\) is a piece-wise linear function, and it is easy to see that the support of \(dd^c [\mathfrak {q} \circ \textrm{Log}]\) coincides with the set \(\textrm{Log}^{-1}(|V_{\textrm{trop}}(\mathfrak {q})|),\) on the other hand, \(dd^c [\mathfrak {q} \circ \textrm{Log}]\) is \((S^1)^n\) invariant. As a consequence of Proposition 4.6, \(dd^c [\mathfrak {q}\circ \textrm{Log}]\) is a tropical current. By Demailly’s first theorem of support, [20, Theorem III.2.10], we only need to verify the equality of these \((n-1,n-1)\)-dimensional currents on
Therefore, it only remains to see that the weights induced by \(dd^c [\mathfrak {q} \, \circ \, \textrm{Log}]\) on any \((n-1)\)-dimensional cone in \(V_{\textrm{trop}}(\mathfrak {q})\) coincides with the weights given in Definition 3.2.(b). We can assume, without loss of generality, that \(\sigma \) contains the origin. To prove the equality of the currents, it is sufficient to prove that for any ball B such that \(B \cap \textrm{Log}^{-1}(\sigma ^{\circ })\ne \varnothing ,~B \cap \partial \textrm{Log}^{-1}(\sigma ^{\circ }) = \varnothing ,\) and \(B\cap \textrm{Log}^{-1}\big ( |V_{\textrm{trop}}(\mathfrak {q})| -\sigma \big ) = \varnothing ,\)

Assume that \(\text {aff}(\sigma ) = \{x\in \mathbb {R}^n: \langle \beta _1 , x \rangle = \langle \beta _2 , x \rangle =\mathfrak {q}(x) \},\) for some \(\beta _1,\beta _2\in \mathbb {Z}^n.\) We have that

Therefore, it suffices to prove that

Recall by Definition 3.2, \(w_{\sigma }\) is defined to be the lattice length of \(\beta _1 - \beta _2.\) Let us write
where \(\alpha \) is a primitive vector and \(\alpha _{\pm }\in \mathbb {Z}^n_{\ge 0}.\) We have
Finally, to see that the masses of  and \(dd^c \max \{\langle \alpha _{+} ,~.~ \rangle , \langle \alpha _{-} , ~.~ \rangle \}\circ \textrm{Log}(z)\) coincide, we note that
and \(dd^c \max \{\langle \alpha _{+} ,~.~ \rangle , \langle \alpha _{-} , ~.~ \rangle \}\circ \textrm{Log}(z)\) coincide, we note that  is an average with respect to the Haar measure of the fibers, and it is enough to show that the mass of each fiber coincides with the mass of \(dd^c \max \{\langle \alpha _{+} ,~.~ \rangle , \langle \alpha _{-} , ~.~ \rangle \}\circ \textrm{Log}(z).\) By Example 4.2, for each \(x \in (S^1)^n,\) the integration current on each fiber is given by
is an average with respect to the Haar measure of the fibers, and it is enough to show that the mass of each fiber coincides with the mass of \(dd^c \max \{\langle \alpha _{+} ,~.~ \rangle , \langle \alpha _{-} , ~.~ \rangle \}\circ \textrm{Log}(z).\) By Example 4.2, for each \(x \in (S^1)^n,\) the integration current on each fiber is given by
where \(\bar{x} = x + S_{(H \cap \mathbb {Z}^n)}\) is the element in the quotient \(S_{\mathbb {Z}^n/(H \cap \mathbb {Z}^n)}\). Applying \(\frac{1}{m}\Phi ^*_m\) on both sides of this equation preserves the mass in any compactification of \((\mathbb {C}^*)^n\), but by Eq. ((III)) the left hand side becomes \(dd^c \max \{\langle \alpha _{+} ,~.~ \rangle , \langle \alpha _{-} , ~.~ \rangle \}\circ \textrm{Log}(z).\) \(\square \)
7.3 The Genericity Condition in \(\mathbb P^n\)
Comparing our convergence results to the conjecture of Dinh and Sibony, we need to verify that there all the generic algebraic subvarieties \(Z\subseteq \mathbb {P}^n\) of a given degree have the same tropicalisation. This implication, in fact, is the main result of main theorem of Römer and Schmitz in [67]. Roberto Gualdi has proposed a nice and intuitive explanation of this implication in codimension one: if we consider a homogeneous polynomial of degree d in \(\mathbb {P}^n,\) then all the coefficients are generically non-zero, which in turn, imposes the Newton polytope, hence the tropicalisation (with respect to trivial valuation). The genericity condition in dynamical systems usually amounts to avoiding certain invariant sets of low dimension. In Sect. 5, we observed that all the toric orbits are invariant under \(\Phi _m\) and \(\Phi _m^{-1},\) and the relation between the toric orbits and tropicalisation is already stated in the following proposition by Sturmfels and Tevelev.
Proposition 7.5
([70, Proposition 3.9]) Let \(\Sigma \) be a complete (rational) fan in \(N_{\mathbb {R}}\) and Z be a p-dimensional subvariety of \((\mathbb {C}^*)^n.\) Assume that the closure \(\bar{Z}\subseteq X_{\Sigma },\) does not intersect any of the toric orbits of \(X_{\Sigma }\) of codimension greater than p. Then, \(\textrm{trop}(Z)\) equals the union of all p-dimensional cones \(\sigma \in \Sigma \) such that \(\mathcal {O}_{\sigma }\) intersects \(\bar{Z}.\)
To deduce that the genericity condition for an algebraic subvariety of \(\mathbb P^n\) determines its tropicalisation, we will observe that the union of p-dimensional cones in \(\mathbb P^n\) is the support of a strongly extremal fan. Recall that
Definition 7.6
-
(a)
A tropical variety \(\mathcal {C}\) is called strongly extremal if the support of \(\mathcal {C}\) is can be uniquely weighted up to a multiple to become balanced. In other words, \(\mathcal {C}\) generates an extremal ray in the cone of positively weighted tropical varieties.
-
(b)
A current
 in the cone of positive closed currents of bidimension (p, p) on X is called extremal, if any decomposition
in the cone of positive closed currents of bidimension (p, p) on X is called extremal, if any decomposition  in this cone implies that
in this cone implies that  and
and 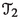 are positive multiples of
are positive multiples of  In other words,
In other words,  generates an extremal ray in the cone of positive closed currents of bidimension (p, p).
generates an extremal ray in the cone of positive closed currents of bidimension (p, p).
Lemma 7.7
Let \(\mathcal {C}, \tilde{\mathcal {C}}\) be two tropical varieties of same dimension such that \(\mathcal {C}\) is strongly extremal, and \(|\tilde{\mathcal {C}}|\subseteq |\mathcal {C}|.\) Then \(|\tilde{\mathcal {C}}|= |{\mathcal {C}}|.\)
Proof
There is a sufficiently large integer k, such that the tropical variety \(k \, \mathcal {C}-\tilde{\mathcal {C}}\) is a (positively weighted) tropical variety with support \(|\mathcal {C}|\). If \(|\tilde{\mathcal {C}}|\subsetneq |{\mathcal {C}}|,\) the weights on \(k \, \mathcal {C}-\tilde{\mathcal {C}}\) cannot be a multiple of the weights on \(\mathcal {C}.\)
\(\square \)
Essentially the same proof as above gives the following.
Lemma 7.8
Assume that \(\mathcal {C}, \tilde{\mathcal {C}}\) are two tropical varieties such that  is extremal among the tropical currents, and \(|\tilde{\mathcal {C}}|\subseteq |\mathcal {C}|.\) Then \(|\mathcal {C}|= |\tilde{\mathcal {C}}|.\)
is extremal among the tropical currents, and \(|\tilde{\mathcal {C}}|\subseteq |\mathcal {C}|.\) Then \(|\mathcal {C}|= |\tilde{\mathcal {C}}|.\)
For a given polyhedral complex \(\Sigma \), we denote by \(\Sigma (p)\) the union of all p-dimensional cells in \(\Sigma .\) We give two different proofs of the following:
Theorem 7.9
([67]) Let \(\Sigma \) be the fan of \(\mathbb P^n,\) and Z be any p-dimensional subvariety of \((\mathbb {C}^*)^n\) of degree d, and generic in the sense that \(\bar{Z}\subseteq \mathbb P^n\) does not intersect any of toric orbits of \(X_{\Sigma }=\mathbb P^n\) with codimension greater than p. Then, \(\textrm{trop}(Z)\) is independent of the choice of Z.
Proof
In view of Proposition 7.5 we have the inclusion \(|\textrm{trop}(Z)|\subseteq \bigcup _{\sigma \in \Sigma (p)} \sigma .\) By Lemma 7.7, to derive the converse inclusion it is sufficient to observe that the set \(\bigcup _{\sigma \in \Sigma (p)} \sigma \) is the support of a strongly extremal tropical variety. Let us justify the extremality in two ways by devising several strong theorems. See also [58, Exercise 6.8.11].
-
(a)
\(\bigcup _{\sigma \in \Sigma (p)} \sigma \) is the support of the Bergman fan of the uniform matroid \(U_{p+1, n+1}\); see [58, Example 4.2.13]. Therefore it is extremal by [46, Theorem 38] and the assertion follows from Lemma 7.7.
-
(b)
Let \(H\subseteq (\mathbb {C}^*)^n\) be a generic p-dimensional plane. Note that this genericity condition for H is equivalent to saying that all the maximal minors of the matrix of coefficients for any \(n-p\) linear equations defining H are non-zero. By [58, Example 4.2.13] for such a generic p-dimensional plane H, the set \(\textrm{trop}(H)\) is given by support of the Bergman fan of the uniform matroid: \(\bigcup _{\sigma \in \Sigma (p)} \sigma \). To see that \(\textrm{trop}(H)\) is extremal, we observe instead that the current
 is extremal among all \(\Phi _m\)-invariant currents. By Theorem A and [69, Proposition 6.1], for a generic H
is extremal among all \(\Phi _m\)-invariant currents. By Theorem A and [69, Proposition 6.1], for a generic H
where \(\omega \) is the normalised Fubini–Study form on \(\mathbb P^n.\) Finally, the bidimension (p, p) Green current of \(\Phi _m\), given by \(\lim _{m\rightarrow \infty }m^{p-n}\Phi ^*_m(\omega ^{n-p})\), is extremal among \(\Phi _m\)-invariant currents, [26, Theorem 1.0.1].
As a result, all generic closed p-dimensional algebraic varieties of \(\mathbb P^n\), up to the degree, have the same tropicalisation and,
\(\square \)
The support of the Green current of \(\Phi _m\) of bidimension (p, p) is called the Julia set of order p of \(\Phi _m,\) denoted by \(J_p\). Therefore, \(\textrm{Log}(J_p)\) coincides with the support of \(U_{p+1, n+1}\), i.e., the Bergman fan of uniform matroid of rank \(p+1\) on \(n+1\) points.
References
Adiprasito, Karim, Babaee, Farhad: Convexity of complements of tropical varieties, and ap- proximations of currents. Math. Ann. 373(1–2), 237–251 (2019)
Andersson, M., Eriksson, D., Kalm, H.S., Wulcan, E., Yger, A.: Global representation of Segre numbers by Monge-Ampère products. Math. Ann. 380(1–2), 349–391 (2021)
Ash, A., Mumford, D., Scholze, P., Rapoport, M., Tai, Y.: Smooth Compactifications of Locally Symmetric Varieties. Cambridge University Press, Smooth compactifications of locally Cambridge (2010)
Babaee, F.: Complex tropical currents, Ph.D. Thesis, Departments of Mathematics, Universities of Bordeaux and Padova (2014)
Briend, J.Y., Duval, J.: Deux caractérisations de la mesure d’équilibre d’un endo- morphisme de \({\rm P}^k({ {C}})\). Publ. Math. Inst. Hautes Études Sci. 93, 145–159 (2001)
Bergman, G.M.: The logarithmic limit-set of an algebraic variety. Trans. Am. Math. Soc. 157, 459–469 (1971)
Babaee, F., Gualdi, R.: Cohomological implications of dynamical tropicalisation, Work in Progress
Burgos Gil, J. I., Gubler, W., Jell, P., Küunnemann, K., Martin, F.: Differentiability of non-archimedean volumes and non-archimedean Monge-Ampère equations, Algebr. Geom. 7(2): 113–152. With an appendix by Robert Lazarsfeld (2020)
Burgos Gil, J. I., Gubler, W., Jell, P., Küunnemann, K., Martin, F.: A comparison of positivity in complex and tropical toric geometry, To appear in Mathematische Zeitschrift (2021)
Babaee, F., Huh, J.: A tropical approach to a generalized Hodge conjecture for positive currents. Duke Math. J. 166(14), 2749–2813 (2017)
Burgos Gil, J.I., Moriwaki, A., Moriwaki, P., Sombra, M.: Arithmetic positivity on toric varieties. J. Algebraic Geom. 25(2), 201–272 (2016)
Baker, M.H., Rumely, R.: Equidistribution of small points, rational dynamics, and potential theory. Ann. Inst. Fourier (Grenoble) 56(3), 625–688 (2006)
Brasselet, J.-P.: Introduction to toric varieties, Publicações Matemáticas do IMPA. [IMPA Mathematical Publications], Instituto de Matemática Pura e Aplicada (IMPA), Rio de Janeiro. \(23^{\text{o}}\) Colóquio Brasileiro de Matemática. [23rd Brazilian Mathematics Colloquium] (2001)
Brolin, H.: Invariant sets under iteration of rational functions. Ark. Mat. 6(1965), 103–144 (1965)
Bedford, E., Taylor, B.A.: A new capacity for plurisubharmonic functions. Acta Math. 149(1–2), 1–40 (1982)
Chambert-Loir, A., Ducros, A.: Formes différentielles réelles et courants sur les espaces de Berkovich. arXiv:1204.6277 (2012)
Cegrell, U.: Discontinuité de l’opérateur de Monge-Ampère complexe. C. R. Acad. Sci. Paris Sér. I Math. 1983(296), 869–871 (1983)
Coman, D., Guedj, V., Sahin, S., Zeriahi, A.: Toric pluripotential theory. Ann. Polon. Math. 123(1), 215–242 (2019)
Cox D. A., Little J. B., Schenck H. K.: Varieties Toric, Graduate Studies in Mathematics, vol. 124, American Mathematical Society, Providence, RI. MR2810322 (2012g:14094) (2011)
Demailly, J.P.: Courants positifs extrêmaux et conjecture de Hodge. Invent. Math. 69(3), 347–374 (1982)
Demailly, J.-P.: Regularization of closed positive currents and intersection theory. J. Algebraic Geom. 1(3), 361–409 (1992)
Demailly J.-P.: Complex analytic and differential geometry. Open Content Book, Version of June 21, https://www-fourier.ujf-grenoble.fr/~demailly/manuscripts/agbook.pdf (2012)
Ducros, A., Hrushovski, E., Loeser F.: Non-archimedean integrals as limits of complex integrals, arXiv preprint arXiv:1912.09162 (2019)
Dinh, T.-C.: Pluripotential theory and complex dynamics in higher dimension. In: Proceedings of the International Congress of Mathematicians—-Rio de Janeiro 2018. Vol. III. Invited lectures, pp. 1561–1581 (2018)
Dinh, T.-C., Nguyên, V.-A., Duc-Viet, V.: Super-potentials, densities of currents and number of periodic points for holomorphic maps. Adv. Math. 331, 874–907 (2018)
Dinh, T.C.: Dynamique des applications d’allure polynomiale,. J. Math. Pures Appl. 92(9), 367–432 (2003)
Dinh, T.-C., Sibony, N.: Equidistribution towards the Green current for holomor- phic maps. Ann. Sci. Éc. Norm. Supér. 4(41), 307–336 (2008)
Dinh, T.-C., Sibony, N.: Super-potentials of positive closed currents, intersection theory and dynamics. Acta Math. 1, 1–82 (2009)
Dinh, T.-C., Sibony, N.: Equidistribution speed for endomorphisms of projective spaces. Math. Ann. 347(3), 613–626 (2010)
Dinh, T.-C., Sibony, N.: Density of positive closed currents, a theory of non-generic intersections. J. Algebraic Geom. 27(3), 497–551 (2018)
Dujardin, R.: Geometric methods in holomorphic dynamics. In: To appear in the proceedings of the ICM 2022 (2021)
Eisenbud, D.: Commutative Algebra. Graduate Texts in Mathematics, vol. 150, Springer, New York. With a view toward algebraic geometry (1995)
Ewald, G.: Combinatorial Convexity and Algebraic Geometry. Graduate Texts in Mathematics, vol. 168. Springer, New York (1996)
Favre, C., Jonsson, M.: Brolin’s theorem for curves in two complex dimensions. Ann. Inst. Fourier (Grenoble) 53(5), 1461–1501 (2003)
Freire, A., Lopes, A., Mañe, R.: An invariant measure for rational maps. Bol. Soc. Brasil. Mat. 14(1), 45–62 (1983)
Fornæss, J. E., Sibony N.: Complex dynamics in higher dimensions, Complex potential theory (Montreal, PQ, 1993), pp. 131–186. Notes partially written by Estela A. Gavosto (1994)
Fornaess, J.E., Sibony, N.: Complex dynamics in higher dimension. II, Modern methods in complex analysis (Princeton, NJ, 1992), pp. 135–182 (1995)
Fornaess, J.E., Sibony, N.: Oka’s inequality for currents and applications. Math. Ann. 301(3), 399–419 (1995)
Fujino, Osamu: Multiplication maps and vanishing theorems for toric varieties. Math. Z. 257(3), 631–641 (2007)
Giansiracusa, J., Giansiracusa, N.: Equations of tropical varieties. Duke Math. J. 165(18), 3379–3433 (2016)
Griffiths, P., Harris J.: Principles of algebraic geometry, Wiley Classics Library. Wiley, New York, Reprint of the 1978 original (1994)
Gubler, W., Künnemann, K.: A tropical approach to nonarchimedean Arakelov geometry. Algebra Number Theory 11(1), 77–180 (2017)
Grothendieck, A.: Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV. Inst. Hautes Études Sci. Publ. Math. 32, 361 (1967)
Gubler W.: A guide to tropicalizations, Algebraic and combinatorial aspects of tropical geometry, pp. 125–189 (2013)
Gubler W.: Forms and current on the analytification of an algebraic variety (after Chambert-Loir and Ducros), Nonarchimedean and tropical geometry, pp. 1–30 (2016)
Huh, J.: Rota’s conjecture and positivity of algebraic cycles in permutohedral varieties. Ph.D. Thesis, Department of Mathematics, University of Michigan, (2014)
Itenberg, I., Mikhalkin, G.: Geometry in the tropical limit. Math. Semester. 59(1), 57–73 (2012)
Jonsson M.: Dynamics of Berkovich spaces in low dimensions, Berkovich spaces and applications, pp. 205–366 (2015)
Jonsson, M.: Degenerations of amoebae and Berkovich spaces. Math. Ann. 364(1–2), 293–311 (2016)
Kajiwara, T.: Tropical toric geometry. Toric Topol. 5, 197–207 (2008)
Lagerberg, Aron: Super currents and tropical geometry. Math. Z. 270(3–4), 1011–1050 (2012)
Lelong, P.: Discontinuité et annulation de l’opérateur de Monge-Ampère complexe, P. Lelong- P. Dolbeault-H. Skoda analysis seminar, 1981/1983, pp. 219–224 (1983)
Litvinov, G.L.: The Maslov dequantization, idempotent and tropical mathematics: a very brief introduction. Idempot Mathe. Math. Phys. 25, 1–17 (2005)
Ljubich, Ju.M.: Entropy properties of rational endomorphisms of the Riemann sphere. Ergodic Theory Dynam. Syst. 3(3), 351–385 (1983)
Mihatsch A.: On tropical intersection theory, arXiv preprint arXiv:2107.12067 (2021)
Mikhalkin, G.: Decomposition into pairs-of-pants for complex algebraic hypersurfaces. Topology 43(5), 1035–1065 (2004)
Mikhalkin, G.: Enumerative tropical algebraic geometry in \({\mathbb{R} }^2\). J. Am. Math. Soc. 18(2), 313–377 (2005)
Maclagan, D., Rincón, F.: Tropical ideals. Compos. Math. 154(3), 640–670 (2018)
Maclagan, D., Rincón, F.: Tropical schemes, tropical cycles, and valuated matroids. J. Eur. Math. Soc. (JEMS) 22(3), 777–796 (2020)
Maclagan, D., Sturmfels, B.: Introduction to tropical geometry, Graduate Studies in Mathematics, vol. 161. American Mathematical Society, Providence, RI (2015)
Nisse, M., Sottile, F.: Higher convexity for complements of tropical varieties. Math. Ann. 365(1–2), 1–12 (2016)
Payne, S.: Analytification is the limit of all tropicalizations. Math. Res. Lett. 16(3), 543–556 (2009)
Passare, M., Rullgård, H.: Amoebas, Monge-Ampère measures, and triangulations of the Newton polytope. Duke Math. J. 121(3), 481–507 (2004)
Rashkovskii, A.: Indicators for plurisubharmonic functions of logarithmic growth. Indiana Univ. Math. J. 50(3), 1433–1446 (2001)
Rivera-Letelier, J.: Espace hyperbolique p-adique et dynamique des fonctions rationnelles. Compos. Math. 138(2), 199–231 (2003)
Römer, T., Schmitz, K.: Generic tropical varieties. J. Pure Appl. Algebra 216(1), 140–148 (2012)
Russakovskii, A., Shiffman, B.: Value distribution for sequences of rational map- pings and complex dynamics. Indiana Univ. Math. J. 46(3), 897–932 (1997)
Rullgård, H.: Polynomial amoebas and convexity. Ph.D. Thesis, Department of Mathematics, Stockholm University (2001)
Sturmfels, B., Tevelev, J.: Elimination theory for tropical varieties. Math. Res. Lett. 15(3), 543–562 (2008)
Johan, T., Johan Ta in: Equidistribution speed towards the Green current for endomorphisms of \({\mathbb{P} }^k\). Adv. Math. 227(5), 2059–2081 (2011)
Tevelev, J.: Compactifications of subvarieties of tori. Am. J. Math. 129(4), 1087–1104 (2007)
Viro, O.: From the sixteenth Hilbert problem to tropical geometry. Jpn. J. Math. 3(2), 185–214 (2008)
Acknowledgements
I’m grateful to Nessim Sibony for his invitation and hospitality in Orsay in July 2018, as well as, accepting my invitation to visit Bristol for two weeks as a Heilbronn distinguished visitor in September 2020. A visit which was postponed to September 2022 due to the pandemic, and sadly could not take place. I’m grateful to Charles Favre for several insightful discussions and his comments the text. I’m thankful to Omid Amini for numerous encouraging discussions. I also thank Roberto Gualdi for reading the draft, and delightful and fruitful discussions. I cordially thank Tien Cuong Dinh, for his comments on the first arXiv version of this article. I finally thank the anonymous referee(s) for their comments which have led to improvement of mathematics and exposition of the text.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Babaee, F. Dynamical Tropicalisation. J Geom Anal 33, 74 (2023). https://doi.org/10.1007/s12220-022-01105-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-022-01105-9



 by Dinh and Sibony in [
by Dinh and Sibony in [ in the sense of Item (d) above. Furthermore, comparing our result to the above conjecture implies that generic subvarieties of the projective space, up to the degree, have the same tropicalisation. This is not a contradiction, in fact, it is the main result of [
in the sense of Item (d) above. Furthermore, comparing our result to the above conjecture implies that generic subvarieties of the projective space, up to the degree, have the same tropicalisation. This is not a contradiction, in fact, it is the main result of [
 is the extension by zero of
is the extension by zero of  in
in 
 in the cone of positive closed currents of bidimension (p, p) on X is called extremal, if any decomposition
in the cone of positive closed currents of bidimension (p, p) on X is called extremal, if any decomposition  in this cone implies that
in this cone implies that  and
and 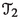 are positive multiples of
are positive multiples of  In other words,
In other words,  generates an extremal ray in the cone of positive closed currents of bidimension (p, p).
generates an extremal ray in the cone of positive closed currents of bidimension (p, p). is extremal among all
is extremal among all 