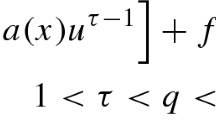(p, q)-Equations with Negative Concave Terms

Abstract

In this paper, we study a nonlinear Dirichlet problem driven by the (p, q)-Laplacian and with a reaction that has the combined effects of a negative concave term and of an asymmetric perturbation which is superlinear on the positive semiaxis and resonant in the negative one. We prove a multiplicity theorem for such problems obtaining three nontrivial solutions, all with sign information. Furthermore, under a local symmetry condition, we prove the existence of a whole sequence of sign-changing solutions converging to zero in $C^1_0(\overline{\Omega })$.

1 Introduction

Let $\Omega \subseteq \mathbb {R}^N$ be a bounded domain with a $C^2$-boundary $\partial \Omega$. In this paper, we study the following nonlinear Dirichlet problem

$$\begin{aligned} \begin{aligned} -\Delta _p u-\Delta _q u&= \vartheta (x) |u|^{\tau -2}u +f(x,u)&\text {in } \Omega , \\ u\big |_{\partial \Omega }&= 0, \quad 1<\tau<q<p,&\end{aligned} \end{aligned}$$

(1.1)

where $\Delta _r$ denotes the r-Laplacian for $r\in (1,\infty )$ given by

$$\begin{aligned} \Delta _r u=\mathop {\mathrm {div}}\limits \big (|\nabla u|^{r-2} \nabla u\big )\quad \text {for }u\in W^{1,r}_0(\Omega ). \end{aligned}$$

Problem (1.1) is driven by the sum of two such operators with different exponents called the (p, q)-Laplacian which is a nonhomogeneous operator. For such problems, we refer to the survey paper of Marano and Mosconi [13] and the references therein. In the right-hand side of (1.1), we have the combined effects of two distinct nonlinear terms. One term is the power function $s \rightarrow \vartheta (x) |s|^{\tau -2}s$ with $1<\tau <q$ and $0>-c_0\ge \vartheta (\cdot )\in L^{\infty }(\Omega )$ which is a concave contribution (so $(q-1)$-sublinear) to the reaction. The perturbation $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function, that is, $x\rightarrow f(x,s)$ is measurable for all $s\in \mathbb {R}$ and $s\rightarrow f(x,s)$ is continuous for a. a. $x\in \Omega$, which exhibits asymmetric growth as $s \rightarrow \pm \infty$. To be more precise, $f(x,\cdot )$ is $(p-1)$-linear in the negative semiaxis (as $s \rightarrow -\infty$) and can be resonant with respect to the principal eigenvalue of $(-\Delta _p,W^{1,p}_0(\Omega ))$. In the positive semiaxis (as $s\rightarrow +\infty$), $f(x,\cdot )$ is $(p-1)$-superlinear but without satisfying the Ambrosetti–Rabinowitz condition (AR-condition for short). Hence, problem (1.1) is partly resonant and partly a concave–convex problem. In addition to this lack of symmetric behavior, another feature which distinguishes our work here from earlier ones on nonlinear elliptic equations with concave terms, is the fact that the coefficient $\vartheta :\Omega \rightarrow \mathbb {R}$ of the concave term is x-dependent and negative. In the past, problems with a negative concave term were studied by Perera [22], de Paiva and Massa [3], Papageorgiou et al. [20] for semilinear equations and by Papageorgiou and Winkert [15] for nonlinear equations driven by the (p, 2)-Laplacian. From these works only the paper of Papageorgiou et al. [20] considers perturbations with asymmetric behavior as $s \rightarrow \pm \infty$. In the literature, papers dealing with equations with concave terms assume that the coefficient is a positive constant. This is the case in the classical concave–convex problems, see Ambrosetti et al. [2] for equations driven by the Laplacian and by García Azorero et al. [5] for equations driven by the p-Laplacian. The difficulty that we encounter when we deal with equations that have negative concave terms is that the nonlinear strong maximum principle is not applicable, see Pucci and Serrin [23].

2 Preliminaries

In this section, we will recall the basic facts about the function spaces, the properties of the operator and some results of Morse theory.

To this end, let $\Omega \subseteq \mathbb {R}^N$ be a bounded domain with a $C^2$-boundary $\partial \Omega$. For any $r\in [1,\infty ]$, we denote by $L^{r}(\Omega )=L^r(\Omega ;\mathbb {R})$ and $L^r(\Omega ;\mathbb {R}^N)$ the usual Lebesgue spaces with the norm $\Vert \cdot \Vert _r$. Moreover, the Sobolev space $W^{1,r}_0(\Omega )$ is equipped with the equivalent norm $\Vert \cdot \Vert =\Vert \nabla \cdot \Vert _r$ for $1<r<\infty$.

The Banach space

$$\begin{aligned} C^1_0(\overline{\Omega })= \left\{ u \in C^1(\overline{\Omega })\,:\, u\big |_{\partial \Omega }=0 \right\} \end{aligned}$$

is an ordered Banach space with positive cone

$$\begin{aligned} C^1_0(\overline{\Omega })_+=\left\{ u \in C^1_0(\overline{\Omega })\,:\, u(x) \ge 0 \text { for all } x \in \overline{\Omega }\right\} . \end{aligned}$$

This cone has a nonempty interior given by

$$\begin{aligned} \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right) =\left\{ u \in C^1_0(\overline{\Omega })_+: u(x)>0 \text { for all } x \in \Omega \text {, } \frac{\partial u}{\partial n}(x)<0 \text { for all } x \in \partial \Omega \right\} , \end{aligned}$$

where $n(\cdot )$ stands for the outward unit normal on $\partial \Omega$.

For $r\in (1,\infty )$, we denote by $\hat{\lambda }_{1}(r)$, the first eigenvalue of $(-\Delta _r,W^{1,r}_0(\Omega ))$. We know that $\hat{\lambda }_{1}(r)>0$ and

$$\begin{aligned} \hat{\lambda }_{1}(r)=\inf _{u\in W^{1,r}_0(\Omega )\setminus \{0\}} \frac{\Vert \nabla u\Vert _r^r}{\Vert u\Vert _r^r}. \end{aligned}$$

(2.1)

Furthermore, $\hat{\lambda }_{1}(r)$ is isolated, simple, and the infimum in (2.1) is achieved on the corresponding one-dimensional eigenspace, see Lê [10]. The elements of this eigenspace have fixed sign. By $\hat{u}_1(r)$, we denote the positive, $L^r$-normalized (that is, $\Vert \hat{u}_1(r)\Vert _r=1$) eigenfunction related to $\hat{\lambda }_{1}(r)$. The nonlinear regularity theory and the nonlinear Hopf maximum principle imply that $\hat{u}_1(r) \in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$.

We also use the weighted eigenvalue problem

$$\begin{aligned} \begin{aligned} -\Delta _p u&= \tilde{\lambda }\xi (x)|u|^{p-2}u \quad&\text {in } \Omega , \\ u&= 0&\text {on } \partial \Omega , \end{aligned} \end{aligned}$$

(2.2)

with eigenvalue $\tilde{\lambda }>0$ and $\xi \in L^{\infty }(\Omega )_+\setminus \{0\}$. We know that if $\xi _1(x)\le \xi _2(x)$ a. e. in $\Omega$ and $\xi _1\ne \xi _2$, then $\tilde{\lambda }_1(p,\xi _2)<\tilde{\lambda }_1(p,\xi _1)$, see Motreanu et al. [14, Proposition 9.47(d)].

Let $A_r:W^{1,r}_0(\Omega )\rightarrow W^{-1,r'}(\Omega )=W^{1,r}_0(\Omega )^*$ with $\frac{1}{r}+\frac{1}{r'}=1$ be the nonlinear operator defined by

$$\begin{aligned} \left\langle A_r(u),h\right\rangle =\int _{\Omega }|\nabla u|^{r-2}\nabla u \cdot \nabla h\,\mathrm {d}x\quad \text {for all } u,h\in W^{1,r}_0(\Omega ), \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ is the duality pairing between $W^{1,r}_0(\Omega )$ and its dual space $W^{1,r}_0(\Omega )^*$. This operator is bounded, continuous, strictly monotone, and of type $(\mathop {\mathrm {S}}\limits _+)$, that is,

$$\begin{aligned} u_n\rightharpoonup u \quad \text {in }W^{1,r}_0(\Omega ) \quad \text {and}\quad \limsup _{n\rightarrow \infty }\,\langle A_r(u_n),u_n-u\rangle \le 0 \end{aligned}$$

imply $u_n\rightarrow u$ in $W^{1,r}_0(\Omega )$, see Motreanu et al. [14, p. 40].

Let X be a Banach space, $\varphi \in C^1(X)$ and $c\in \mathbb {R}$. We introduce the following two sets

$$\begin{aligned} K_\varphi&=\left\{ u\in X\,:\, \varphi '(u)=0 \right\} \quad \text {and}\quad \varphi ^c=\left\{ u\in X \,:\, \varphi (u) \le c\right\} . \end{aligned}$$

If $(Y_1,Y_2)$ is a topological pair such that $Y_2\subseteq Y_1\subset X$ and $k\in \mathbb {N}_0$, then we denote by $H_k(Y_1,Y_2)$ the k-th singular homology group for the pair $(Y_1,Y_2)$ with integer coefficients. If $u\in K_\varphi$ is isolated, the k-th critical group of $\varphi$ at u is defined by

$$\begin{aligned} C_k(\varphi ,u)=H_k \left( \varphi ^c \cap U, \varphi ^c \cap U \setminus \{u\}\right) , \quad k\in \mathbb {N}_0, \end{aligned}$$

with $c=\varphi (u)$ and U being an open neighborhood of u such that $\varphi ^c\cap K_\varphi \cap U=\{u\}$. The excision property of singular homology implies that the definition of $C_k(\varphi ,u)$ is independent of the choice of the isolating neighborhood U, see Motreanu et al. [14]. The usage of critical groups allows us to distinguish between critical points of the energy functional.

We say that $\varphi \in C^1(X)$ satisfies the Cerami condition (C-condition for short) if every sequence $\{u_n\}_{n\in \mathbb {N}}\subseteq X$ such that $\{\varphi (u_n)\}_{n\in \mathbb {N}}\subseteq \mathbb {R}$ is bounded and $(1+\Vert u_n\Vert _X)\varphi '(u_n) \rightarrow 0$ in $X^*$ has a strongly convergent subsequence. This is a compactness-type condition on the functional $\varphi$ which compensates the fact that the ambient space X need not be locally compact.

For $s\in \mathbb {R}$, we set $s^{\pm }=\max \{\pm s,0\}$. If $u:\Omega \rightarrow \mathbb {R}$ is a measurable function, we define $u^{\pm }(x)=u(x)^{\pm }$ for all $x\in \Omega$. If $u\in W^{1,p}_0(\Omega )$, then $u^{\pm }\in W^{1,p}_0(\Omega )$ and $u=u^+-u^-$ as well as $|u|=u^++u^-$. If $u,v:\Omega \rightarrow \mathbb {R}$ are two measurable functions such that $u(x) \le v(x)$ for all $x\in \Omega$, then we define

Moreover, we denote by $\mathop {\mathrm {int}}\limits _{C^1_0(\overline{\Omega })}[u,v]$ the interior of $[u,v]\cap C^1_0(\overline{\Omega })$ in $C^1_0(\overline{\Omega })$. Finally, the critical Sobolev exponent of $p\in (1,\infty )$, denoted by $p^*$, is given by

$$\begin{aligned} p^*= {\left\{ \begin{array}{ll} \frac{Np}{N-p}&{}\text {if }p<N,\\ +\infty &{}\text {if } N\le p. \end{array}\right. } \end{aligned}$$

3 Multiple Solutions

In this section, we produce three nontrivial solutions of problem (1.1) where two of them have constant sign and one has changing sign.

Now we introduce the hypotheses on the data of problem (1.1).

$\hbox {H}_0$::

$\vartheta \in L^{\infty }(\Omega )$ and $\vartheta (x) \le -c_0 <0$ for a. a. $x\in \Omega$.

Remark 3.1

It is an interesting open question if the results in this paper remain valid under the weaker condition $\vartheta (x)<0$ for a. a. $x\in \Omega$.

$\hbox {H}_{1}$::

$f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function such that $f(x,0)=0$ for a. a. $x\in \Omega$ and it satisfies the following assumptions:

(i):

there exist $r\in (p,p^*)$ and $0\le a(\cdot )\in L^{\infty }(\Omega )$ such that

$$\begin{aligned} |f(x,s)| \le a(x) \left( 1+|s|^ {r-1}\right) \end{aligned}$$

for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$;

(ii):

if $F(x,s)=\int _0^sf(x,t)\,\mathrm {d}t$, then

$$\begin{aligned} \lim _{s\rightarrow +\infty } \frac{F(x,s)}{s^p}=+\infty \end{aligned}$$

uniformly for a. a. $x\in \Omega$ and there exists

$$\begin{aligned} \mu \in \left( (r-p)\max \left\{ \frac{N}{p},1\right\} ,p^*\right) \end{aligned}$$

such that

$$\begin{aligned} 0<\beta _0 \le \liminf _{s\rightarrow +\infty }\, \frac{f(x,s)s-pF(x,s)}{s^ \mu } \end{aligned}$$

uniformly for a. a. $x\in \Omega$;

(iii):

there exist $\beta _1\in L^{\infty }(\Omega )$ and $\beta _2>0$ such that

$$\begin{aligned} \hat{\lambda }_1(p) \le \beta _1(x)\quad \text {for a. a.}~x\in \Omega \end{aligned}$$

with $\beta _1 \not \equiv \hat{\lambda }_1(p)$ and

$$\begin{aligned} \beta _1(x) \le \liminf _{s\rightarrow -\infty } \frac{f(x,s)}{|s|^{p-2}s}\le \limsup _{s\rightarrow -\infty } \frac{f(x,s)}{|s|^{p-2}s} \le \beta _2 \end{aligned}$$

uniformly for a. a. $x\in \Omega$.

(iv):

there exists $\beta \in (1,\tau )$ such that

$$\begin{aligned} \lim _{s\rightarrow 0} \frac{f(x,s)}{|s|^{\beta -2}s}=0 \end{aligned}$$

uniformly for a. a. $x\in \Omega$,

$$\begin{aligned} \liminf _{s\rightarrow 0} \frac{f(x,s)}{|s|^{\tau -2}s}\ge \eta >\Vert \vartheta \Vert _\infty \end{aligned}$$

uniformly for a. a. $x\in \Omega$ and for every $\lambda >0$ there exists $\hat{\mu }(\lambda )\in (1,\beta )$ such that $\hat{\mu }(\lambda )\rightarrow \hat{\mu }\in (1,\beta )$ as $\lambda \rightarrow 0^+$ and

$$\begin{aligned} f(x,s)s\le \hat{c} \left( \lambda |s|^{\hat{\mu }(\lambda )}+|s|^r\right) -\tilde{c}|s|^\beta \end{aligned}$$

for a. a. $x\in \Omega$, for all $s\in \mathbb {R}$ with $\hat{c}, \tilde{c}>0$.

Remark 3.2

Hypotheses $\hbox {H}_{1}$ (ii) and $\hbox {H}_{1}$(iii) imply the asymmetric behavior of the perturbation $f(x,\cdot )$. Indeed, hypothesis $\hbox {H}_{1}$(ii) says that $f(x,\cdot )$ is $(p-1)$-superlinear as $s \rightarrow +\infty$ but need not satisfy the AR-condition, see, for example, Ghoussoub [6, p. 59]. Our condition is less restrictive and allows also nonlinearities with “slower” growth as $s \rightarrow +\infty$ which fail to satisfy the AR-condition. Here, we refer to a unilateral version of the condition since it concerns only the positive semiaxis $[0,\infty )$. Hypothesis $\hbox {H}_{1}$ (iii) says that $f(x,\cdot )$ is $(p-1)$-linear as $s \rightarrow -\infty$ and can be resonant with respect to the principal eigenvalue of $(-\Delta _p,W^{1,p}_0(\Omega ))$. Note that in hypothesis $\hbox {H}_{1}$ (i), we want $a\in L^{\infty }(\Omega )$ in order to be able to apply the regularity theory of Lieberman [12].

Example 3.3

The following function satisfies hypotheses $\hbox {H}_{1}$ but fails to satisfy the AR-condition:

$$\begin{aligned} f(x,s)= {\left\{ \begin{array}{ll} \gamma (x) \left( |s|^{p-2}s-|s|^{q-2}s\right) &{} \text {if } s<-1,\\[1ex] \eta (x)\left( |s|^{\tau -2}s-|s|^{\mu -2}s\right) &{}\text {if } -1\le s \le 1,\\[1ex] cs^{p-1} \ln (s) &{}\text {if }1<s, \end{array}\right. } \end{aligned}$$

with $\gamma \in L^{\infty }(\Omega )$, $\gamma (x)\ge \hat{\lambda }_1(q)$, $\gamma \not \equiv \hat{\lambda }_1(q)$ and $\eta \in L^{\infty }(\Omega )$, $\mathop {\mathrm {ess\,inf}}\limits _\Omega \eta >\Vert \vartheta \Vert _\infty$, $c>0$ and $p>\mu >\tau$.

Let $\varphi :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ be the energy functional corresponding to problem (1.1) defined by

$$\begin{aligned} \varphi (u)=\frac{1}{p} \Vert \nabla u\Vert _p^p +\frac{1}{q} \Vert \nabla u\Vert _q^q-\frac{1}{\tau } \int _{\Omega }\vartheta (x)|u|^\tau \,\mathrm {d}x-\int _{\Omega }F(x,u)\,\mathrm {d}x \end{aligned}$$

for all $u \in W^{1,p}_0(\Omega )$. It is clear that $\varphi \in C^1(W^{1,p}_0(\Omega ))$. Moreover, we introduce the positive and negative truncations of $\varphi$, namely, the $C^1$-functionals $\varphi _{\pm }:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ given by

$$\begin{aligned} \varphi _{\pm }(u)=\frac{1}{p} \Vert \nabla u\Vert _p^p+\frac{1}{q} \Vert \nabla u\Vert _q^q -\frac{1}{\tau } \int _{\Omega }\vartheta (x) \left( u^{\pm }\right) ^\tau \,\mathrm {d}x-\int _{\Omega }F\left( x,\pm u^{\pm }\right) \,\mathrm {d}x \end{aligned}$$

for all $u\in W^{1,p}_0(\Omega )$.

Our idea is to work with the truncated functionals $\varphi _{\pm }:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$.

Proposition 3.4

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then there exists $\hat{\varrho }>0$ such that

$$\begin{aligned} \varphi _{\pm }(u) \ge m >0 \quad \text {for all }u \in W^{1,p}_0(\Omega ) \text { with } \Vert u\Vert =\hat{\varrho }. \end{aligned}$$

Proof

From hypotheses H$_1$ (iv), we see that for given $\varepsilon >0$, we can find $c_1=c_1(\varepsilon )>0$ such that

$$\begin{aligned} F(x,s) \le \frac{\varepsilon -\tilde{c}}{\beta }|s|^\beta + c_1\left( \lambda |s|^{\hat{\mu }(\lambda )} + |s|^r\right) \quad \text {for a. a. }x\in \Omega \text { and for all }s\in \mathbb {R}. \end{aligned}$$

(3.1)

Using (3.1) and hypotheses $\hbox {H}_{0}$, we get for $u \in W^{1,p}_0(\Omega )$

$$\begin{aligned} \varphi _{\pm }(u) \ge \left( \frac{1}{p}-\lambda c_2 \Vert u\Vert ^{\hat{\mu }(\lambda )-p}-c_3\Vert u\Vert ^{r-p}\right) \Vert u\Vert ^p \end{aligned}$$

for some $c_2, c_3>0$.

Let

$$\begin{aligned} \xi _\lambda (t)=\lambda c_2 t^{\hat{\mu }(\lambda )-p}+c_3 t^{r-p}\quad \text {for }t>0. \end{aligned}$$

Since $\hat{\mu }(\lambda )<\beta<p<r$, we see that

$$\begin{aligned} \xi _\lambda (t)\rightarrow +\infty \quad \text {as }t\rightarrow 0^+ \text { and as } t\rightarrow +\infty . \end{aligned}$$

Therefore, we find a number $t_0 \in (0,\infty )$ such that

$$\begin{aligned} \xi _\lambda \left( t_0\right) =\inf _{t>0} \xi _\lambda (t). \end{aligned}$$

Thus, $\xi _\lambda '(t_0)=0$, and this implies

$$\begin{aligned} t_0=\left[ \frac{\lambda c_2(p-\hat{\mu }(\lambda ))}{c_3(r-p)}\right] ^{\frac{1}{r-\hat{\mu }(\lambda )}}. \end{aligned}$$

Since $\xi _\lambda (t_0)\rightarrow 0$ as $\lambda \rightarrow 0^+$, there exists $\lambda _0>0$ such that

$$\begin{aligned} \xi _\lambda (t_0)<\frac{1}{p}\quad \text {for all }\lambda \in (0,\lambda _0). \end{aligned}$$

Fix $\lambda \in (0,\lambda _0)$, then, for $\Vert u\Vert =t_0$, we have

$$\begin{aligned} \varphi _{\pm }(u)>0. \end{aligned}$$

Next, we show that $\varphi _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ satisfies the C-condition.

Proposition 3.5

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then the functional $\varphi _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ satisfies the C-condition.

Proof

Let $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}_0(\Omega )$ be a sequence such that

$$\begin{aligned}&\left| \varphi _+(u_n)\right| \le c_3 \quad \text {for some }c_3>0 \text { and for all }n\in \mathbb {N}, \end{aligned}$$

(3.2)

$$\begin{aligned}&\left( 1+\Vert u_n\Vert \right) \varphi _+'(u_n)\rightarrow 0 \quad \text {in }W^{-1,p'}(\Omega ). \end{aligned}$$

(3.3)

From (3.3), we get

$$\begin{aligned} \begin{aligned}&\left| \left\langle A_p(u_n),h\right\rangle +\left\langle A_q(u_n),h\right\rangle -\int _{\Omega }\vartheta (x)\left( u_n^+\right) ^{\tau -1}h\,\mathrm {d}x-\int _{\Omega }f\left( x,u_n^ +\right) h\,\mathrm {d}x\right| \\&\quad \le \frac{\varepsilon _n\Vert h\Vert }{1+\Vert u_n\Vert }\quad \text {for all }h\in W^{1,p}_0(\Omega ) \text { with }\varepsilon _n\rightarrow 0^+. \end{aligned} \end{aligned}$$

(3.4)

Choosing $h=-u_n^-\in W^{1,p}_0(\Omega )$ in (3.4) gives $\Vert u_n^ -\Vert ^p\le \varepsilon _n$ for all $n\in \mathbb {N}$ and so

$$\begin{aligned} u_n^- \rightarrow 0 \quad \text {in }W^{1,p}_0(\Omega ). \end{aligned}$$

(3.5)

Combining (3.2) and (3.5) yields

$$\begin{aligned} \left\| \nabla u_n^+\right\| _p^p+\frac{p}{q} \Vert \nabla u_n^+\Vert _q^q-\frac{p}{\tau } \int _{\Omega }\vartheta (x) \left( u_n^+\right) ^\tau \,\mathrm {d}x-\int _{\Omega }pF\left( x,u_n^+\right) \,\mathrm {d}x \le c_4 \end{aligned}$$

(3.6)

for some $c_4>0$ and for all $n\in \mathbb {N}$. Next, we take $h=u_n^+\in W^{1,p}_0(\Omega )$ in (3.4). We obtain

$$\begin{aligned} -\left\| \nabla u_n^+\right\| _p^p-\left\| \nabla u_n^+\right\| _q^q+\int _{\Omega }\vartheta (x)\left( u_n^+\right) ^\tau \,\mathrm {d}x+\int _{\Omega }f\left( x,u_n^+\right) u_n^+\,\mathrm {d}x \le \varepsilon _n \end{aligned}$$

(3.7)

for all $n \in \mathbb {N}$. Adding (3.6) and (3.7) and using hypotheses $\hbox {H}_{0}$ as well as $\tau<q<p$, we get

$$\begin{aligned} \int _{\Omega }\left( f\left( x,u_n^+\right) u_n^+-pF\left( x,u_n^+\right) \right) \,\mathrm {d}x\le c_5 \end{aligned}$$

(3.8)

for some $c_5>0$ and for all $n\in \mathbb {N}$.

Hypotheses $\hbox {H}_{1}$ (i) and $\hbox {H}_{1}$ (ii) imply that we can find $\hat{\beta }_0 \in (0,\beta _0)$ and $c_{6}>0$ such that

$$\begin{aligned} \hat{\beta }_0 s^\mu -c_{6} \le f(x,s)s-pF(x,s) \end{aligned}$$

(3.9)

for a. a. $x\in \Omega$ and for all $s\ge 0$. Using (3.9) in (3.8) leads to

$$\begin{aligned} \left\| u_n^+\right\| _\mu ^\mu \le c_{7} \quad \text {for some }c_{7}>0\text { and for all }n\in \mathbb {N}. \end{aligned}$$

Hence

$$\begin{aligned} \left\{ u_n^+\right\} _{n\in \mathbb {N}} \subseteq L^{\mu }(\Omega ) \text { is bounded}. \end{aligned}$$

(3.10)

First, assume that $p \ne N$. From hypothesis $\hbox {H}_{1}$ (ii) it is clear that we may assume that $\mu<r<p^*$. Then we can find $t\in (0,1)$ such that

$$\begin{aligned} \frac{1}{r}=\frac{1-t}{\mu }+\frac{t}{p^ *}. \end{aligned}$$

(3.11)

Using the interpolation inequality (see Papageorgiou and Winkert [18, p. 116]), we have

$$\begin{aligned} \left\| u_n^+\right\| _r \le \left\| u_n^+\right\| _\mu ^{1-t} \left\| u_n^+\right\| _{p^ *}^t\quad \text {for all }n\in \mathbb {N}. \end{aligned}$$

This combined with (3.10) results in

$$\begin{aligned} \left\| u_n^+\right\| _r^r \le c_{8} \left\| u_n^+\right\| ^{tr} \quad \text {for all }n\in \mathbb {N}\end{aligned}$$

(3.12)

with some $c_{8}>0$. Testing (3.4) with $h=u_n^+\in W^{1,p}_0(\Omega )$ we obtain

$$\begin{aligned} \left\| \nabla u_n^+\right\| _p^p \le \varepsilon _n +\int _{\Omega }f\left( x,u_n^+\right) u_n^+ \,\mathrm {d}x\quad \text {for all } n\in \mathbb {N}\end{aligned}$$

due to hypotheses $\hbox {H}_{0}$. Using $\hbox {H}_{1}$ (i), this implies

$$\begin{aligned} \left\| u_n^+\right\| ^p \le c_{9}\left( 1+\left\| u_n^+\right\| _r^r\right) \quad \text {for all } n\in \mathbb {N}\end{aligned}$$

with some $c_{9}>0$. Combining this with (3.12) yields

$$\begin{aligned} \left\| u_n^+\right\| ^p \le c_{10}\left( 1+\left\| u_n^+\right\| ^{tr}\right) \quad \text {for all } n\in \mathbb {N}\end{aligned}$$

(3.13)

for some $c_{10}>0$.

Recall that $p\ne N$. If $p>N$, then by definition we have $p^*=\infty$ and so

$$\begin{aligned} \frac{1}{r}=\frac{1-t}{\mu }, \end{aligned}$$

see (3.11), which implies, because of $\hbox {H}_{1}$ (ii), that $tr=r-\mu <p$. Then we conclude from (3.13) that

$$\begin{aligned} \left\{ u_n^+\right\} _{n\in \mathbb {N}} \subseteq W^{1,p}_0(\Omega ) \text { is bounded}. \end{aligned}$$

(3.14)

If $p<N$, then we have by definition $p^*=\frac{Np}{N-p}$. So from (3.11) and $\hbox {H}_{1}$ (ii), it follows

$$\begin{aligned} tr=\frac{p^*(r-\mu )}{p^*-\mu }=\frac{Np(r-\mu )}{Np-N\mu +\mu p}<\frac{Np(r-\mu )}{Np-N\mu +(r-p)\frac{N}{p} p}=p. \end{aligned}$$

Hence, (3.14) holds again in this case.

Finally, let $p=N$. Then by the Sobolev embedding theorem, we know that $W^{1,p}_0(\Omega ) \hookrightarrow L^{s}(\Omega )$ is continuous for all $1\le s<\infty$. Then, in the argument above, we need to replace $p^*$ by $s>r>\mu$. We choose $t\in (0,1)$ such that

$$\begin{aligned} \frac{1}{r}=\frac{1-t}{\mu }+\frac{t}{s}, \end{aligned}$$

which gives

$$\begin{aligned} tr=\frac{s(r-\mu )}{s-\mu }. \end{aligned}$$

(3.15)

Note that $\frac{s(r-\mu )}{s-\mu }\rightarrow r-\mu$ as $s\rightarrow +\infty$ and $r-\mu <p$, see $\hbox {H}_{1}$ (ii). We choose $s>r$ large enough such that

$$\begin{aligned} \frac{s(r-\mu )}{s-\mu }<p. \end{aligned}$$

Then, using (3.15), we have $tr<p$ and so $\{u_n^+\}_{n\in \mathbb {N}}\subseteq W^{1,p}_0(\Omega )$ is bounded. Combining this with (3.5), we obtain that $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}_0(\Omega )$ is bounded.

Then there exists a subsequence, not relabeled, such that

$$\begin{aligned} u_n\rightharpoonup u \quad \text {in }W^{1,p}_0(\Omega ) \quad \text {and}\quad u_n\rightarrow u \quad \text {in }L^{r}(\Omega ). \end{aligned}$$

(3.16)

If we use $h=u_n-u\in W^{1,p}_0(\Omega )$ in (3.4), pass to the limit as $n\rightarrow \infty$ and use (3.16), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty } \left( \left\langle A_p(u_n),u_n-u \right\rangle +\left\langle A_q(u_n),u_n-u \right\rangle \right) =0. \end{aligned}$$

By the monotonicity of $A_q$, we have

$$\begin{aligned} \left\langle A_q(u),u_n-u \right\rangle \le \left\langle A_q(u_n),u_n-u \right\rangle . \end{aligned}$$

Using this in the limit above, we obtain

$$\begin{aligned} \limsup _{n\rightarrow \infty } \left( \left\langle A_p(u_n),u_n-u \right\rangle +\left\langle A_q(u),u_n-u \right\rangle \right) \le 0. \end{aligned}$$

Hence, from the convergence properties in (3.16), we conclude that

$$\begin{aligned} \limsup _{n\rightarrow \infty } \left\langle A_p(u_n),u_n-u \right\rangle \le 0. \end{aligned}$$

The $(\mathop {\mathrm {S}}\limits _+)$-property of $A_p$ implies that $u_n\rightarrow u$ in $W^{1,p}_0(\Omega )$. This shows that $\varphi _+$ satisfies the C-condition.

Proposition 3.5 leads to the following existence result for problem (1.1).

Proposition 3.6

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$. Then problem (1.1) has at least one positive solution $u_0 \in C^1_0(\overline{\Omega })_+\setminus \{0\}$.

Proof

From Proposition 3.4, we know that

$$\begin{aligned} \varphi _+(0)=0<m\le \varphi _+(u)\quad \text {for all }u\in W^{1,p}_0(\Omega ) \text { with }\Vert u\Vert =\hat{\varrho }. \end{aligned}$$

(3.17)

Also, from Proposition 3.5, we know that

$$\begin{aligned} \varphi _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}\text { satisfies the C-condition}. \end{aligned}$$

(3.18)

Moreover, hypothesis $\hbox {H}_{1}$ (ii) implies that if $u \in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$, then

$$\begin{aligned} \varphi _+(tu)\rightarrow -\infty \quad \text {as }t\rightarrow +\infty . \end{aligned}$$

(3.19)

Then, (3.17), (3.18), and (3.19) permit the usage of the mountain pass theorem. Therefore, we can find $u_0\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} u_0 \in K_{\varphi _+} \quad \text {and}\quad \varphi _+(0)=0<m\le \varphi _+\left( u_0\right) . \end{aligned}$$

Hence, $u_0\ne 0$. From Ho et al. [7, Theorem 3.1], we know that $u_0\in L^{\infty }(\Omega )$. Then the nonlinear regularity theory of Lieberman [12] implies that $u_0 \in C^1_0(\overline{\Omega })_+\setminus \{0\}$.

Remark 3.7

Eventually, we will show that $u_0\in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$, see Corollary 3.12. However, at this point, due to the negative concave term, we cannot use the nonlinear Hopf maximum principle, see Pucci and Serrin [23, p. 120], and infer that $u_0\in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$.

Next, we are looking for a negative solution of problem (1.1). So, we work with the functional $\varphi _-:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$. For the functional $\varphi _-:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$, we have the following proposition.

Proposition 3.8

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then the functional $\varphi _-:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ satisfies the C-condition.

Proof

Let $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}_0(\Omega )$ be a sequence such that $\{\varphi _-(u_n)\}_{n\in \mathbb {N}}\subseteq \mathbb {R}$ is bounded and

$$\begin{aligned} \left( 1+\Vert u_n\Vert \right) \varphi _-'(u_n)\rightarrow 0 \quad \text {in }W^{-1,p'}(\Omega ). \end{aligned}$$

(3.20)

From (3.20), we have

$$\begin{aligned} \begin{aligned}&\left| \left\langle A_p(u_n),h\right\rangle +\left\langle A_q(u_n),h\right\rangle +\int _{\Omega }\vartheta (x)\left( u_n^-\right) ^{\tau -1}h\,\mathrm {d}x-\int _{\Omega }f\left( x,-u_n^-\right) h\,\mathrm {d}x\right| \\&\quad \le \frac{\varepsilon _n\Vert h\Vert }{1+\Vert u_n\Vert }\quad \text {for all }h\in W^{1,p}_0(\Omega ) \text { with }\varepsilon _n\rightarrow 0^+. \end{aligned} \end{aligned}$$

(3.21)

If we choose $h=u_n^+\in W^{1,p}_0(\Omega )$ in (3.21), we obtain $\Vert u_n^ +\Vert ^p\le \varepsilon _n$ for all $n\in \mathbb {N}$ which implies

$$\begin{aligned} u_n^+ \rightarrow 0 \quad \text {in }W^{1,p}_0(\Omega ). \end{aligned}$$

(3.22)

Suppose that $\Vert u_n^-\Vert \rightarrow \infty$ and let $y_n=\frac{u_n^-}{\Vert u_n^-\Vert }$. Then $\Vert y_n\Vert =1$ for all $n\in \mathbb {N}$. Therefore, we may suppose, for a subsequence if necessary, that

$$\begin{aligned} y_n\rightharpoonup y \quad \text {in }W^{1,p}_0(\Omega ) \quad \text {and}\quad y_n\rightarrow y\quad \text {in }L^{p}(\Omega ) \end{aligned}$$

(3.23)

for some $y\in W^{1,p}_0(\Omega )$ with $y\ge 0$. From (3.21) and (3.22), we obtain

$$\begin{aligned} \begin{aligned}&\left| \left\langle A_p(-y_n),h\right\rangle +\frac{1}{\Vert u_n^-\Vert ^{p-q}}\left\langle A_q(-y_n),h\right\rangle -\int _{\Omega }\frac{ \vartheta (x)}{\Vert u_n^-\Vert ^{p-\tau }}y_n^{\tau -1}h\,\mathrm {d}x\right. \\&\quad \left. -\int _{\Omega }\frac{f\left( x,-u_n^-\right) }{\Vert u_n^-\Vert ^{p-1}}h\,\mathrm {d}x\right| \le \varepsilon '_n\Vert h\Vert \quad \text {for all }h\in W^{1,p}_0(\Omega ) \text { with }\varepsilon '_n\rightarrow 0^+. \end{aligned} \end{aligned}$$

(3.24)

Choosing $h=y_n-y\in W^{1,p}_0(\Omega )$ in (3.24), passing to the limit as $n\rightarrow \infty$ and using the convergence properties in (3.23) gives

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\langle A_p(y_n), y_n-y\right\rangle =0. \end{aligned}$$

From the $(\mathop {\mathrm {S}}\limits _+)$-property of $A_p:W^{1,p}_0(\Omega )\rightarrow W^{-1,p'}(\Omega )=W^{1,p}_0(\Omega )^*$, we conclude that

$$\begin{aligned} y_n\rightarrow y \quad \text {in }W^{1,p}_0(\Omega ) \text { with }\Vert y\Vert =1 \text { and }y\ge 0. \end{aligned}$$

(3.25)

Note that from hypothesis $\hbox {H}_{1}$ (iii), we have

$$\begin{aligned} \frac{f(\cdot ,-u_n(\cdot )^-)}{\Vert u_n^-\Vert ^{p-1}}\rightarrow -\hat{\beta }(x)y^{p-1}\quad \text {in }L^{p'}(\Omega ) \end{aligned}$$

(3.26)

with $\hat{\beta }\in L^{\infty }(\Omega )$ and $\beta _1(x)\le \hat{\beta }(x)\le \beta _2$ for a. a. $x\in \Omega$, see Aizicovici et al. [1, proof of Proposition 16] and Motreanu et al. [14, Proof of Theorem 11.15, p. 317].

So, if we pass to the limit in (3.24) as $n\rightarrow \infty$ and use (3.25) as well as (3.26), we obtain

$$\begin{aligned} \left\langle A_p(-y),h\right\rangle =-\int _{\Omega }\hat{\beta }(x)y^{p-1}h\,\mathrm {d}x \quad \text {for all }h\in W^{1,p}_0(\Omega ). \end{aligned}$$

This means that

$$\begin{aligned} -\Delta _p y=\hat{\beta }(x)y^{p-1} \quad \text {in }\Omega , \quad y\big |_{\partial \Omega }=0. \end{aligned}$$

From (3.25), we know that $y\ne 0$ and

$$\begin{aligned} \tilde{\lambda }_1(p,\hat{\beta })<\tilde{\lambda }_1(p,\hat{\lambda }_1(p))=1, \end{aligned}$$

(3.27)

see (2.2). From (3.26) and (3.27), it follows that y must be sign-changing which is a contradiction to (3.25), see also Motreanu et al. [14, Proposition 9.47(b)]. Thus, $\{u_n^-\}\subseteq W^{1,p}_0(\Omega )$ is bounded; hence, $\{u_n\}\subseteq W^{1,p}_0(\Omega )$ is bounded, see (3.22). From this as in the proof of Proposition 3.5, we conclude that $\varphi _-:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ satisfies the C-condition.

On account of hypothesis $\hbox {H}_{1}$ (iii), we see that

$$\begin{aligned} \varphi _-(t\hat{u}_1(p)) \rightarrow -\infty \quad \text {as }t \rightarrow -\infty . \end{aligned}$$

(3.28)

Then (3.28), Proposition 3.8, and the mountain pass theorem lead to the following result.

Proposition 3.9

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then problem (1.1) has a negative solution $v_0 \in -C^1_0(\overline{\Omega })\setminus \{0\}$.

In what follows $\mathcal {S}_+$ (resp. $\mathcal {S}_-$) denote the set of positive (resp. negative) solutions to (1.1). From Propositions 3.6 and 3.9, we have

$$\begin{aligned} \emptyset \ne \mathcal {S}_+ \subseteq C^1_0(\overline{\Omega })_+ \setminus \{0\} \quad \text {and}\quad \emptyset \ne \mathcal {S}_- \subseteq \left( -C^1_0(\overline{\Omega })_+\right) \setminus \{0\}. \end{aligned}$$

Next, we are going to prove that $\mathcal {S}_+$ has a minimal element and $\mathcal {S}_-$ a maximal one. So we have extremal constant sign solutions, that is, there is a smallest positive solution $u_*$ and a largest negative solution $v_*$. These solutions will be useful in proving the existence of a sign-changing solution. Indeed, any nontrivial solution of problem (1.1) in the order interval $[v_*,u_*]$ distinct from $v_*$ and $u_*$ is necessarily sign-changing.

On account of hypotheses $\hbox {H}_{1}$ (i) and $\hbox {H}_{1}$ (iv), for a given $\varepsilon >0$, we can find $\hat{c}_1=\hat{c}_1(\varepsilon )>0$ such that

$$\begin{aligned} f(x,s)s\ge \left[ \eta -\varepsilon \right] |s|^{\tau }-\hat{c}_1|s|^r \end{aligned}$$

for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$. This implies

$$\begin{aligned} \vartheta (x)|s|^\tau + f(x,s)s\ge \left[ \eta -\varepsilon -\Vert \vartheta \Vert _\infty \right] |s|^{\tau }-\hat{c}_1|s|^r \end{aligned}$$

for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$. By hypothesis $\hbox {H}_{1}$ (iv), we have $\eta >\Vert \vartheta \Vert _\infty$. So, choosing $\varepsilon \in (0,\eta -\Vert \vartheta \Vert _\infty )$, we have

$$\begin{aligned} \vartheta (x)|s|^\tau + f(x,s)s\ge \hat{c}_2|s|^{\tau }-\hat{c}_1|s|^r \end{aligned}$$

(3.29)

for some $\hat{c}_2>0$, for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$. Then, (3.29) suggests that we consider the following Dirichlet (p, q)-equation

$$\begin{aligned} \begin{aligned} -\Delta _p u-\Delta _q u&=\hat{c}_{2} |u|^{\tau -2}u-\hat{c}_{1}|u|^{r-2}u&\text {in } \Omega , \\ u\big |_{\partial \Omega }&= 0, \ 1<\tau<q<p<r<p^*,&\end{aligned} \end{aligned}$$

(3.30)

Similarly to Proposition 4.1 of Papageorgiou and Winkert [17], we have the following existence and uniqueness result.

Proposition 3.10

Problem (3.30) has a unique positive solution $\overline{u} \in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$ and since problem (3.30) is odd, $\overline{v}=-\overline{u} \in -\mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$ is the unique negative solution of (3.30).

Proof

First, we show the existence of a positive solution of problem (3.30). To this end, let $\psi _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ be the $C^1$-functional defined by

$$\begin{aligned} \psi _+(u)=\frac{1}{p} \Vert \nabla u\Vert _p^p +\frac{1}{q}\Vert \nabla u\Vert _q^q+\frac{\hat{c}_{1}}{r} \left\| u^+\right\| _r^r-\frac{\hat{c}_{2}}{\tau } \left\| u^+\right\| _\tau ^\tau \end{aligned}$$

for all $u \in W^{1,p}_0(\Omega )$. Since $\tau<q<p<r$, it is clear that $\psi _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is coercive. Also, it is sequentially weakly lower semicontinuous. Therefore, there exists $\overline{u}\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \psi _+\left( \overline{u}\right) =\inf \left[ \psi _+(u)\,:\, u\in W^{1,p}_0(\Omega )\right] . \end{aligned}$$

(3.31)

Note that if $u \in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$ and $t\in (0,1)$ small enough, then $\psi _+(tu)<0$ since $\tau<q<p<r$ and so we have $\psi _+(\overline{u})<0=\psi _+(0)$. Thus, $\overline{u}\ne 0$.

From (3.31), we have $\psi _+'(\overline{u})=0$, that is,

$$\begin{aligned} \left\langle A_p\left( \overline{u}\right) ,h\right\rangle +\left\langle A_q\left( \overline{u}\right) ,h\right\rangle =\hat{c}_{2} \int _{\Omega }\left( \overline{u}^+\right) ^{\tau -1}h\,\mathrm {d}x-\hat{c}_{1}\int _{\Omega }\left( \overline{u}^+\right) ^{r-1}h\,\mathrm {d}x \end{aligned}$$

for all $h\in W^{1,p}_0(\Omega )$. Choosing $h=-\overline{u}^-\in W^{1,p}_0(\Omega )$ in the equality above shows that $\overline{u} \ge 0$ with $\overline{u}\ne 0$. Moreover, the nonlinear regularity theory of Lieberman [12] and the nonlinear strong maximum principle, see Pucci and Serrin [23, pp. 111 and 120], imply that $\overline{u}\in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$.

Next, we show the uniqueness of this positive solution. For this purpose, we introduce the functional $j:L^{1}(\Omega ) \rightarrow \mathbb {R}\cup \{\infty \}$ defined by

$$\begin{aligned} j(u)= {\left\{ \begin{array}{ll} \frac{1}{p} \left\| \nabla u^{\frac{1}{\tau }}\right\| _p^p+\frac{1}{q} \left\| \nabla u^{\frac{1}{\tau }}\right\| _q^q &{}\text {if } u\ge 0, \ u^{\frac{1}{\tau }}\in W^{1,p}_0(\Omega ),\\ +\infty &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

Let $\mathop {\mathrm {dom}}\limits j=\{u\in L^{1}(\Omega )\,:\, j(u)<\infty \}$ be the effective domain of $j:L^{1}(\Omega ) \rightarrow \mathbb {R}\cup \{\infty \}$. Using the ideas of Díaz and Saá [4] along with the fact that the function $s\mapsto s^{\frac{\hat{\eta }}{\tau }}$ for $\tau <\hat{\eta }$ is increasing and convex, we know that j is convex. Let $\overline{w}\in W^{1,p}_0(\Omega )$ be another positive solution of (3.30). As done before, we get $\overline{w}\in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$. From l’Hospital’s rule, we have

$$\begin{aligned} \frac{\overline{u}}{\overline{w}}\in L^{\infty }(\Omega )\quad \text {and}\quad \frac{\overline{w}}{\overline{u}}\in L^{\infty }(\Omega ). \end{aligned}$$

(3.32)

Let $h=\overline{u}^{\tau }-\overline{w}^\tau \in C^1_0(\overline{\Omega })$. From (3.32), we know that $\frac{\overline{w}^\tau }{\overline{u}^\tau } \le c$ with $c >0$ and so $-\overline{w}^\tau \ge - c\overline{u}^\tau$. Then, for |t| small enough, we have

$$\begin{aligned} \overline{u}^\tau +th =(1+t)\overline{u}^\tau -t\overline{w}^\tau \ge ((1+t)-tc)\overline{u}^c \ge 0. \end{aligned}$$

Clearly, $(\overline{u}^\tau +th)^{\frac{1}{\tau }}\in W^{1,p}_0(\Omega )$. Hence, $\overline{u}^\tau +th \in \mathop {\mathrm {dom}}\limits j$. Similarly, we can show that $\overline{w}^\tau +th\in \mathop {\mathrm {dom}}\limits j$.

Then the convexity of j implies that the directional derivative of j at $\overline{u}^\tau$ and at $\overline{w}^\tau$, respectively, in the direction h exists. Moreover, using the nonlinear Green’s identity, see Papageorgiou et al. [21, p. 35], we have

$$\begin{aligned} j'\left( \overline{u}^\tau \right) (h)&=\frac{1}{\tau }\int _{\Omega }\frac{-\Delta _p \overline{u}-\Delta _q \overline{u}}{\overline{u}^{\tau -1}}h\,\mathrm {d}x =\frac{1}{\tau } \int _{\Omega }\left[ \hat{c}_{2}-\hat{c}_{1}\overline{u}^{r-\tau }\right] h\,\mathrm {d}x,\\[1ex] j'\left( \overline{w}^\tau \right) (h)&=\frac{1}{\tau }\int _{\Omega }\frac{-\Delta _p \overline{w}-\Delta _q \overline{w}}{\overline{w}^{\tau -1}}h\,\mathrm {d}x =\frac{1}{\tau } \int _{\Omega }\left[ \hat{c}_{2}-\hat{c}_{1}\overline{w}^{r-\tau }\right] h\,\mathrm {d}x. \end{aligned}$$

The convexity of j implies the monotonicity of $j'$. So, we have

$$\begin{aligned} 0 \le \frac{\hat{c}_{1}}{\tau }\int _{\Omega }\left[ \overline{w}^{r-\tau }-\overline{u}^{r-\tau }\right] \left( \overline{u}^\tau -\overline{w}^{\tau }\right) \,\mathrm {d}x \le 0. \end{aligned}$$

Thus, $\overline{u}=\overline{w}$.

Since equation (3.30) is odd, $\overline{v}=-\overline{u} \in -\mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$ is the unique negative solution of (3.30).

Proposition 3.11

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then it holds $\overline{u} \le u$ for all $u\in \mathcal {S}_+$ and $v\le \overline{v}$ for all $v \in \mathcal {S}_-$, where $\overline{u}, \overline{v}$ are the unique nontrivial constant sign solutions of (3.30) given in Proposition 3.10.

Proof

Let $u \in \mathcal {S}_+$ and consider the Carathéodory function $l_+:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} l_+(x,s)= {\left\{ \begin{array}{ll} \hat{c}_{2}\left( s^+\right) ^{\tau -1}-\hat{c}_{1} \left( s^+\right) ^{r-1} &{}\text {if }s\le u(x),\\ \hat{c}_{2}u(x)^{\tau -1}-\hat{c}_{1} u(x)^{r-1} &{}\text {if }u(x)<s. \end{array}\right. } \end{aligned}$$

(3.33)

We set $L_+(x,s)=\int _0^s l_+(x,t)\,\mathrm {d}t$ and consider the $C^1$-functional $\sigma _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \sigma _+(u)=\frac{1}{p} \Vert \nabla u\Vert _p^p+\frac{1}{q}\Vert \nabla u\Vert _q^q-\int _{\Omega }L_+(x,u)\,\mathrm {d}x \end{aligned}$$

for all $u\in W^{1,p}_0(\Omega )$.

From the truncation in (3.33), it is clear that $\sigma _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is coercive. Moreover, it is also sequentially weakly lower semicontinuous. So, we can find $\tilde{u}\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \sigma _+\left( \tilde{u}\right) =\inf \left[ \sigma _+(u)\,:\,u\in W^{1,p}_0(\Omega )\right] . \end{aligned}$$

(3.34)

Since $\tau<q<p<r$, we see that $\sigma _+(\tilde{u})<0=\sigma _+(0)$. Hence, $\tilde{u}\ne 0$.

From (3.34), we have $\sigma _+'(\tilde{u})=0$. This gives

$$\begin{aligned} \left\langle A_p\left( \tilde{u}\right) ,h\right\rangle +\left\langle A_q\left( \tilde{u}\right) ,h\right\rangle =\int _{\Omega }l_+\left( x,\tilde{u}\right) h\,\mathrm {d}x \end{aligned}$$

(3.35)

for all $h\in W^{1,p}_0(\Omega )$. In (3.35) we first choose $h=-\tilde{u}^- \in W^{1,p}_0(\Omega )$ and obtain $\tilde{u}\ge 0$ and $\tilde{u}\ne 0$. Then we choose $h=(\tilde{u}-u)^+\in W^{1,p}_0(\Omega )$. This yields by applying (3.33) along with (3.29) and the fact that $u \in \mathcal {S}_+$

$$\begin{aligned}&\left\langle A_p\left( \tilde{u}\right) ,\left( \tilde{u}-u\right) ^+\right\rangle +\left\langle A_q\left( \tilde{u}\right) ,\left( \tilde{u}-u\right) ^+\right\rangle \\&\quad =\int _{\Omega }\left[ \hat{c}_{2} u^{\tau -1}-\hat{c}_{1} u^{r-1}\right] \left( \tilde{u}-u\right) ^+\,\mathrm {d}x\\&\quad \le \int _{\Omega }\left[ \vartheta (x)u^{\tau -1}+f(x,u)\right] \left( \tilde{u}-u\right) ^+\,\mathrm {d}x\\&\quad =\left\langle A_p\left( u\right) ,\left( \tilde{u}-u\right) ^+\right\rangle +\left\langle A_q\left( u\right) ,\left( \tilde{u}-u\right) ^+\right\rangle . \end{aligned}$$

Hence, $\tilde{u} \le u$. So we have proved that

$$\begin{aligned} \tilde{u}\in [0,u],\ \tilde{u} \ne 0. \end{aligned}$$

(3.36)

From (3.36), (3.33), and (3.35), it follows that $\tilde{u}$ is a positive solution of (3.30). Then $\tilde{u}=\overline{u}\in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$ and so $\overline{u} \le u$ for all $u\in \mathcal {S}_+$.

Similarly, we show that $v\le \overline{v}$ for all $v\in \mathcal {S}_-$.

We have the following corollary.

Corollary 3.12

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then

$$\begin{aligned} \emptyset \ne \mathcal {S}_+\subseteq \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right) \quad \text {and}\quad \emptyset \ne \mathcal {S}_-\subseteq -\mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right) . \end{aligned}$$

Now we are ready to produce extremal constant sign solutions.

Proposition 3.13

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then there exist solutions $u_*\in \mathcal {S}_+$ and $v_*\in \mathcal {S}_-$ such that

$$\begin{aligned} u_* \le u \quad \text {for all }u\in \mathcal {S}_+ \quad \text {and}\quad v\le v_* \quad \text {for all }v\in \mathcal {S}_-. \end{aligned}$$

Proof

From Papageorgiou et al. [19, Proposition 7], we know that $\mathcal {S}_+$ is downward directed. So, using Lemma 3.10 of Hu and Papageorgiou [8], we can find a decreasing sequence $\{u_n\}_{n\in \mathbb {N}}$ such that

$$\begin{aligned} \inf _{n\in \mathbb {N}} u_n = \inf \mathcal {S}_+. \end{aligned}$$

Since $u_n \in \mathcal {S}_+$, we have

$$\begin{aligned} \left\langle A_p\left( u_n\right) ,h\right\rangle +\left\langle A_q\left( u_n\right) ,h\right\rangle = \int _{\Omega }\vartheta (x) u_n^{\tau -1}h\,\mathrm {d}x+\int _{\Omega }f(x,u_n)h\,\mathrm {d}x \end{aligned}$$

(3.37)

for all $h\in W^{1,p}_0(\Omega )$. Evidently, the sequence $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}_0(\Omega )$ is bounded. So, we may assume that

$$\begin{aligned} u_n\rightharpoonup u_* \quad \text {in }W^{1,p}_0(\Omega ) \quad \text {and}\quad u_n\rightarrow u_* \quad \text {in }L^{r}(\Omega ). \end{aligned}$$

(3.38)

Choosing $h=u_n-u$ in (3.37), passing to the limit as $n\rightarrow \infty$, and using the convergence properties in (3.38), we obtain

$$\begin{aligned} \limsup _{n\rightarrow \infty } \left\langle A_p(u_n),u_n-u \right\rangle \le 0. \end{aligned}$$

Then, by the $(\mathop {\mathrm {S}}\limits _+)$-property of $A_p$, we get

$$\begin{aligned} u_n\rightarrow u_* \quad \text {in }W^{1,p}_0(\Omega ). \end{aligned}$$

(3.39)

Passing to the limit in (3.37) and using (3.39), we have

$$\begin{aligned} \left\langle A_p\left( u_*\right) ,h\right\rangle +\left\langle A_q\left( u_*\right) ,h\right\rangle = \int _{\Omega }\vartheta (x) u_*^{\tau -1}h\,\mathrm {d}x+\int _{\Omega }f(x,u_*)h\,\mathrm {d}x \end{aligned}$$

for all $h\in W^{1,p}_0(\Omega )$. From Proposition 3.11, we know that $\overline{u}\le u_*$. Hence, $u_*\in \mathcal {S}_+$ and $u_*\le u$ for all $u\in \mathcal {S}_+$.

Similarly, we produce $v_*\in \mathcal {S}_-$ such that $v \le v_*$ for all $v\in \mathcal {S}_-$. Note that $\mathcal {S}_-$ is upward directed.

Using the extremal constant sign solutions obtained in Proposition 3.13, we are going to prove the existence of a sign-changing solution. As explained earlier, we focus on the order interval $[v_*,u_*]$ and look for solutions in $[v_*,u_*]\setminus \{0,u_*,v_*\}$. Such a solution turns out to be sign-changing.

Implementing the approach just described, let $u_*\in \mathcal {S}_+$ and $v_*\in \mathcal {S}_-$ be the extremal constant sign solutions from Proposition 3.13 and consider the truncation functions $k_1,k_2:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} k_1(x,s)= {\left\{ \begin{array}{ll} \vartheta (x)|v_*(x)|^{\tau -2}v_*(x)&{}\text {if }s<v_*(x),\\ \vartheta (x)|s|^{\tau -2}s&{}\text {if }v_*(x)\le s \le u_*(x),\\ \vartheta (x)u_*(x)^{\tau -1}&{}\text {if }u_*(x)<s, \end{array}\right. } \end{aligned}$$

(3.40)

and

$$\begin{aligned} k_2(x,s)= {\left\{ \begin{array}{ll} f(x,v_*(x))&{}\text {if }s<v_*(x),\\ f(x,s)&{}\text {if }v_*(x)\le s \le u_*(x),\\ f(x,u_*(x))&{}\text {if }u_*(x)<s. \end{array}\right. } \end{aligned}$$

(3.41)

It is clear that both are Carathéodory functions. We set

$$\begin{aligned} k(x,s)=k_1(x,s)+k_2(x,s). \end{aligned}$$

(3.42)

Furthermore, we introduce the positive and negative truncations of $k(x,\cdot )$, namely the Carathéodory functions

$$\begin{aligned} k_{\pm }(x,s)=k_1\left( x,\pm s^{\pm }\right) +k_2\left( x,\pm s^{\pm }\right) . \end{aligned}$$

(3.43)

We set

$$\begin{aligned} K_1(x,s)&=\int _0^s k_1(x,t)\,\mathrm {d}t,\quad&K_2(x,s)&=\int _0^s k_2(x,t)\,\mathrm {d}t,\\ K(x,s)&= K_1(x,s) + K_2(x,s),\quad&K_{\pm }(x,s)&=\int _0^s k_{\pm }(x,t)\,\mathrm {d}t \end{aligned}$$

and consider the $C^1$-functionals $\zeta , \zeta _{\pm }:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \zeta (u)&=\frac{1}{p} \Vert \nabla u\Vert _p^p +\frac{1}{q}\Vert \nabla u\Vert _q^q -\int _{\Omega }K(x,u)\,\mathrm {d}x\quad \text {for all }u\in W^{1,p}_0(\Omega )\\ \zeta _{\pm }(u)&=\frac{1}{p} \Vert \nabla u\Vert _p^p +\frac{1}{q}\Vert \nabla u\Vert _q^q -\int _{\Omega }K_{\pm }(x,u)\,\mathrm {d}x\quad \text {for all }u\in W^{1,p}_0(\Omega ),\nonumber \end{aligned}$$

(3.44)

Applying (3.40), (3.41), (3.42), and (3.43), we check easily that

$$\begin{aligned} K_\zeta \subseteq [v_*,u_*]\cap C^1_0(\overline{\Omega }), \ K_{\zeta _+}\subseteq [0,u_*]\cap C^1_0(\overline{\Omega })\quad \text {and}\quad K_{\zeta _-}\subseteq [v_*,0]\cap \left( -C^1_0(\overline{\Omega })\right) . \end{aligned}$$

Due to the extremality of $u_*$ and $v_*$, we conclude that

$$\begin{aligned} K_\zeta \subseteq [v_*,u_*]\cap C^1_0(\overline{\Omega }), \ K_{\zeta _+}=\{0,u_*\} \quad \text {and}\quad K_{\zeta _-}=\{0,v_*\}. \end{aligned}$$

(3.45)

Proposition 3.14

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then $u_*\in \mathcal {S}_+$ and $v_*\in \mathcal {S}_-$ are local minimizers of $\zeta :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$.

Proof

Because of (3.40), (3.41), and (3.43), it is clear that $\zeta _+:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is coercive and it is also sequentially weakly lower semicontinuous. Hence, we find $\tilde{u}_* \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \zeta _+\left( \tilde{u}_*\right) =\inf \left[ \zeta _+(u)\,:\,u\in W^{1,p}_0(\Omega )\right] <0=\zeta _+(0), \end{aligned}$$

(3.46)

since $\tau<q<p$, for $t\in (0,1)$ small enough, we have by using $\hbox {H}_{1}$ (iv) and choosing $\varepsilon \in (0,\eta -\Vert \vartheta \Vert _\infty )$

$$\begin{aligned} \zeta _+\left( tu_*\right) \le t^p\frac{\Vert \nabla u_*\Vert _p^p}{p} +t^q\frac{\Vert \nabla u_*\Vert _q^q}{q} +t^\tau \frac{1}{\tau }\left( \int _{\Omega }\left[ \Vert \vartheta \Vert _\infty -(\eta -\varepsilon )\right] u_*^\tau \,\mathrm {d}x\right) <0. \end{aligned}$$

Due to (3.46), we know that $\tilde{u}_* \in K_{\zeta _+}$ and so $\tilde{u}_*=u_*$, see (3.45). Let $\varrho >0$ and

$$\begin{aligned} \overline{B}_\varrho ^{C^1_0} =\left\{ u\in C^1_0(\overline{\Omega })\,:\, \Vert u-u_*\Vert _{C^1_0(\overline{\Omega })}\le \varrho \right\} . \end{aligned}$$

Since $\zeta \mid _{C^1_0(\overline{\Omega })_+}=\zeta _+ \mid _{C^1_0(\overline{\Omega })_+}$, we obtain for $u\in \overline{B}_\varrho ^{C^1_0}$

$$\begin{aligned} \begin{aligned} \zeta (u)-\zeta (u_*)&=\zeta (u)-\zeta _+(u_*)\\&\ge \zeta (u)-\zeta _+(u)\\&= \int _{\Omega }\left[ K_+(x,u)-K(x,u)\right] \,\mathrm {d}x\\&=\int _{\Omega }-K_1\left( x,-u^-\right) \,\mathrm {d}x+\int _{\Omega }-K_2\left( x,-u^-\right) \,\mathrm {d}x. \end{aligned} \end{aligned}$$

(3.47)

We write as abbreviation

$$\begin{aligned} \{-u^-<v_*\}&:=\{x\in \Omega \,:\,-u^-(x)<v_*(x)\},\\ \{v_*\le -u^-\}&:=\{x\in \Omega \,:\,v_*(x)\le -u^-(x)\}. \end{aligned}$$

Then, for the first integral on the right-hand side in (3.47), we have

$$\begin{aligned} \begin{aligned}&\int _{\Omega }-K_1\left( x,-u^-\right) \,\mathrm {d}x\\&\quad =\int _{\{-u^-<v_*\}} \left( - \frac{\vartheta (x)}{\tau } |v_*|^{\tau } - \vartheta (x)\left[ |v_*|^{\tau -2}v_*(-u^--v_*)\right] \right) \,\mathrm {d}x\\&\qquad +\int _{\{v_* \le -u^-\}}\frac{-\vartheta (x)}{\tau }(u^-)^\tau \,\mathrm {d}x\\&\quad \ge \int _{\{v_* \le -u^-\}}\frac{- \vartheta (x)}{\tau }(u^-)^\tau \,\mathrm {d}x. \end{aligned} \end{aligned}$$

(3.48)

From H$_1$ (iv), for given $\varepsilon >0$, we can find $\hat{c}_{11}=\hat{c}_{11}(\varepsilon )>0$ such that

$$\begin{aligned} F(x,s) \le \frac{\varepsilon -\tilde{c}}{\beta }|s|^\beta + \hat{c}_{11}\left( \lambda |s|^{\hat{\mu }(\lambda )} + |s|^r\right) \end{aligned}$$

(3.49)

for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$. Using (3.49), the second integral on the right-hand side in (3.47) can be estimated by (see also the proof of Proposition 3.4)

$$\begin{aligned} \begin{aligned}&\int _{\Omega }-K_2\left( x,-u^-\right) \,\mathrm {d}x\\&\quad =\int _{\{-u^-<v_*\}} -\left[ F(x,v_*)+f(x,v_*)(-u^--v_*)\right] \,\mathrm {d}x\\&\qquad -\int _{\{v_* \le -u^-\}}F\left( x,-u^-\right) \,\mathrm {d}x\\&\quad \ge \int _{\{-u^-<v_*\}} -\left[ F(x,v_*)+f(x,v_*)(-u^--v_*)\right] \,\mathrm {d}x\\&\qquad -\int _{\{v_* \le -u^-\}} \xi _\lambda \left( \left\| u^-\right\| _\infty \right) \left( u^-\right) ^p \,\mathrm {d}x. \end{aligned} \end{aligned}$$

(3.50)

Combining (3.47), (3.48), (3.50) and applying hypotheses $\hbox {H}_{0}$, we obtain

$$\begin{aligned} \begin{aligned}&\zeta (u)-\zeta (u_*)\\&\quad \ge \int _{\{-u^-<v_*\}} -\left[ F(x,v_*)+f(x,v_*)(-u^--v_*)\right] \,\mathrm {d}x\\&\qquad +\int _{\{v_* \le -u^-\}} \left( \frac{- \vartheta (x)}{\tau }(u^-)^\tau -\xi _\lambda \left( \left\| u^-\right\| _\infty \right) \left( u^-\right) ^p\right) \,\mathrm {d}x\\&\quad \ge \int _{\{-u^-<v_*\}} -\left[ F(x,v_*)+f(x,v_*)(-u^--v_*)\right] \,\mathrm {d}x\\&\qquad +\int _{\{v_* \le -u^-\}} \left( \frac{1}{\tau }c_0 \left( u^-\right) ^\tau -\xi _\lambda \left( \left\| u^-\right\| _\infty \right) \left( u^-\right) ^p\right) \,\mathrm {d}x. \end{aligned} \end{aligned}$$

(3.51)

Recall that $u_* \in C^1_0(\overline{\Omega })_+\setminus \{0\}$ and $u\in \overline{B}_\varrho ^{C^1_0}$. Hence, we have

$$\begin{aligned} \left\| u^-\right\| _{\infty }\rightarrow 0 \quad \text {as }\varrho \rightarrow 0^+. \end{aligned}$$

Thus, $|\{-u^-\le v_*\}|_N\rightarrow 0$ as $\varrho \rightarrow 0^+$ and $|\{v_*\le -u^-\}|_N>0$ for $\varrho >0$ small enough and it is also decreasing in $\varrho$. Then, for $\lambda$ small and for $\varrho >0$ small enough, from (3.51), it follows that $u_*$ is a local $C^1_0(\overline{\Omega })$-minimizer of $\zeta$ and from Papageorgiou and Rădulescu [16], we deduce that $u_*$ is a local $W^{1,p}_0(\Omega )$-minimizer of $\zeta$.

Similarly, working with $\zeta _-$ instead of $\zeta _+$, we can show the result for $v_*\in \mathcal {S}_-$.

Now we are ready to generate a sign-changing solution for problem (1.1).

Proposition 3.15

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then problem (1.1) has a sign-changing solution $y_0 \in [v_*,u_*]\cap C^1_0(\overline{\Omega })$.

Proof

We assume that $K_\zeta$ is finite, otherwise on account of (3.45), (3.40), and (3.41), we would have infinity smooth sign-changing solutions. Moreover, we assume that $\zeta (v_*) \le \zeta (u_*)$. The analysis is similar if the opposite inequality holds. From Proposition 3.14, we know that $u_*$ is a local minimizer of $\zeta$. Recall that the functional $\zeta$ is coercive. So, it satisfies the C-condition, see, for example, Papageorgiou et al. [21, p. 369]. So, using Theorem 5.7.6 of Papageorgiou et al. [21], we can find $\rho \in (0,1)$ small enough such that

$$\begin{aligned} \zeta (v_*) \le \zeta (u_*)<\inf \left[ \zeta (u)\,:\,\Vert u-u_*\Vert =\rho \right] =:m_\rho \quad \text {and}\quad \Vert v_*-u_*\Vert >\rho . \end{aligned}$$

Therefore, we can use the mountain pass theorem and find $y_0\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} y_0\in K_\zeta \subseteq [v_*,u_*]\cap C^1_0(\overline{\Omega }), \end{aligned}$$

(3.52)

see (3.45), and

$$\begin{aligned} \zeta (v_*) \le \zeta (u_*)<m_\rho \le \zeta (y_0). \end{aligned}$$

(3.53)

From (3.53), we see that $y_0 \not \in \{v_*,u_*\}$. Moreover, Theorem 6.5.8 of Papageorgiou et al. [21] implies that

$$\begin{aligned} C_1\left( \zeta ,y_0\right) \ne 0. \end{aligned}$$

(3.54)

On the other hand, the presence of the concave term and the $C^1$-continuity of critical groups imply that

$$\begin{aligned} C_k(\zeta ,0)=0 \quad \text {for all }k \in \mathbb {N}_0, \end{aligned}$$

(3.55)

see Leonardi and Papageorgiou [11, Proposition 6] and Papageorgiou et al. [21, Proposition 6.3.4]. Comparing (3.54) and (3.55), we infer that $y_0\ne 0$. Taking (3.52) into account, we conclude that $y_0$ is a smooth sign-changing solution of problem (1.1).

Summarizing this, we can state the following multiplicity theorem for problem (1.1).

Theorem 3.16

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{1}$ be satisfied. Then problem (1.1) has at least three nontrivial smooth solutions

$$\begin{aligned} u_0\in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right) , \quad v_0 \in - \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right) \end{aligned}$$

and

$$\begin{aligned} y_0 \in \left[ v_0,u_0\right] \cap C^1_0(\overline{\Omega }) \quad \text {being sign-changing}. \end{aligned}$$

4 Infinitely Many Nodal Solutions

In this section, under a local symmetry condition on $f(x,\cdot )$, we prove the existence of a whole sequence of nodal solutions converging to 0 in $C^1_0(\overline{\Omega })$.

The new conditions on the perturbation $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ are the following ones:

$\hbox {H}_2$::

$f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function such that $f(x,\cdot )$ is odd for a. a. $x\in \Omega$ in $[-\gamma ,\gamma ]$ with $\gamma >0$ and it satisfies the following assumptions:

(i):

there exist $r\in (p,p^*)$ and $0\le a(\cdot )\in L^{\infty }(\Omega )$ such that

$$\begin{aligned} |f(x,s)| \le a(x) \left( 1+|s|^ {r-1}\right) \end{aligned}$$

for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$;

(ii):

if $F(x,s)=\int _0^sf(x,t)\,\mathrm {d}t$, then

$$\begin{aligned} \lim _{s\rightarrow +\infty } \frac{F(x,s)}{s^p}=+\infty \end{aligned}$$

uniformly for a. a. $x\in \Omega$ and there exists

$$\begin{aligned} \mu \in \left( (r-p)\max \left\{ \frac{N}{p},1\right\} ,p^*\right) \end{aligned}$$

such that

$$\begin{aligned} 0<\beta _0 \le \liminf _{s\rightarrow +\infty }\, \frac{f(x,s)s-pF(x,s)}{s^ \mu } \end{aligned}$$

uniformly for a. a. $x\in \Omega$;

(iii):

there exist $\beta _1\in L^{\infty }(\Omega )$ and $\beta _2>0$ such that

$$\begin{aligned} \hat{\lambda }_1(p) \le \beta _1(x)\quad \text {for a. a.} \ x\in \Omega \end{aligned}$$

with $\beta _1 \not \equiv \hat{\lambda }_1(p)$ and

$$\begin{aligned} \beta _1(x) \le \liminf _{s\rightarrow -\infty } \frac{f(x,s)}{|s|^{p-2}s}\le \limsup _{s\rightarrow -\infty } \frac{f(x,s)}{|s|^{p-2}s} \le \beta _2 \end{aligned}$$

uniformly for a. a. $x\in \Omega$.

(iv):

there exists $\beta \in (1,\tau )$ such that

$$\begin{aligned} \lim _{s\rightarrow 0} \frac{f(x,s)}{|s|^{\beta -2}s}=0 \end{aligned}$$

uniformly for a. a. $x\in \Omega$ and

$$\begin{aligned} \liminf _{s\rightarrow 0} \frac{f(x,s)}{|s|^{\tau -2}s}\ge \eta >\Vert \vartheta \Vert _\infty \end{aligned}$$

uniformly for a. a. $x\in \Omega$ and for every $\lambda >0$ there exists $\hat{\mu }(\lambda )\in (1,\beta )$ such that $\hat{\mu }(\lambda )\rightarrow \hat{\mu }\in (1,\beta )$ as $\lambda \rightarrow 0^+$ and

$$\begin{aligned} f(x,s)s\le \hat{c} \left( \lambda |s|^{\hat{\mu }(\lambda )}+|s|^r\right) -\tilde{c}|s|^\beta \end{aligned}$$

for a. a. $x\in \Omega$, for all $s\in \mathbb {R}$ with $\hat{c}, \tilde{c}>0$.

Recall that the functional $\zeta :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is given by

$$\begin{aligned} \zeta (u)&=\frac{1}{p} \Vert \nabla u\Vert _p^p +\frac{1}{q}\Vert \nabla u\Vert _q^q -\int _{\Omega }K(x,u)\,\mathrm {d}x\quad \text {for all }u\in W^{1,p}_0(\Omega ), \end{aligned}$$

see (3.44), where the difference is that, due to the local oddness of $f(x,\cdot )$, we truncate in (3.40), (3.41) above at ${\text {int}}\left( C^1_0(\overline{\Omega })_+\right) \ni \hat{\eta } <\min \{\gamma ,u_*\}$ instead of $u_*$ and below at $-{\text {int}}\left( C^1_0(\overline{\Omega })_+\right) \ni \left( -\hat{\eta }\right) >\max \{-\gamma ,v_*\}$ instead of $v_*$. Let $V\subseteq W^{1,p}_0(\Omega )\cap L^{\infty }(\Omega )$ be a finite-dimensional subspace.

Proposition 4.1

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{2}$ be satisfied. Then there exists $\rho _V>0$ such that

$$\begin{aligned} \sup \left[ \zeta (u)\,:\,u\in V,\, \Vert u\Vert =\rho _V\right] <0. \end{aligned}$$

Proof

On account of hypothesis $\hbox {H}_{2}$ (iv), for a given $\varepsilon >0$, there exists $\delta =\delta (\varepsilon ) >0$ such that

$$\begin{aligned} F(x,s) \ge \frac{1}{\tau } \left( \eta -\varepsilon \right) |s|^\tau \end{aligned}$$

(4.1)

for a. a. $x\in \Omega$ and for all $|s|\le \delta$.

Since V is finite dimensional, all norms are equivalent. Therefore, we can find $\rho _V>0$ such that

$$\begin{aligned} u\in V\text { and } \Vert u\Vert \le \rho _V \text { imply } |u(x)| \le \delta \text { for a.\,a.\,}x\in \Omega . \end{aligned}$$

(4.2)

Applying (4.1) and (4.2), we have for $\Vert u\Vert \le \rho _V$

$$\begin{aligned} \zeta (u) \le \frac{1}{p}\Vert \nabla u\Vert ^p+\frac{1}{q}\Vert \nabla u\Vert ^q -\frac{1}{\tau } \int _{\Omega }\left( \eta -\varepsilon -\Vert \vartheta \Vert _\infty \right) |u|^\tau \,\mathrm {d}x, \end{aligned}$$

see the truncations in (3.40) and (3.41). Recalling that $\eta >\Vert \vartheta \Vert _\infty$, we choose $\varepsilon \in (0,\eta -\Vert \vartheta \Vert _\infty )$. Then, using once more the fact that on V all norms are equivalent, we obtain

$$\begin{aligned} \zeta (u) \le \frac{1}{p}\Vert \nabla u\Vert ^p+\frac{1}{q}\Vert \nabla u\Vert ^q -\hat{c}_1\Vert u\Vert ^\tau \end{aligned}$$

for some $\hat{c}_1>0$.

Since $\tau<q<p$, choosing $\rho _V\in (0,1)$ even smaller if necessary, we have

$$\begin{aligned} \sup \left[ \zeta (u)\,:\,u\in V,\, \Vert u\Vert =\rho _V\right] <0. \end{aligned}$$

Now we are ready for the new multiplicity theorem for problem (1.1) under $\hbox {H}_{2}$.

Theorem 4.2

Let hypotheses $\hbox {H}_{0}$ and $\hbox {H}_{2}$ be satisfied. Then problem (1.1) has a whole sequence of distinct nodal solutions $\{u_n\}_{n\in \mathbb {N}}$ such that $u_n\rightarrow 0$ in $C^1_0(\overline{\Omega })$.

Proof

Evidently, the functional $\zeta :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is even, $\zeta (0)=0$ and it is bounded below and satisfies the C-condition being coercive due to (3.40) as well as (3.41). Then it satisfies the PS-condition as well, see Papageorgiou et al. [21, Proposition 5.1.14]. On account of Proposition 4.1, we can apply Theorem 1 of Kajikiya [9] and obtain a sequence $\{u_n\}_{n\in \mathbb {N}} \subseteq W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} u_n\in K_\zeta \quad \text {for all }n\in \mathbb {N}\quad \text { and }\quad u_n\rightarrow 0 \quad \text {in } W^{1,p}_0(\Omega ). \end{aligned}$$

Note that $u_n\in L^{\infty }(\Omega )$ (see, for example Ho et al. [7, Theorem 3.1]). Then, from the nonlinear regularity theory due to Lieberman [12, p. 320], there exist $\alpha \in (0,1)$ and $M>0$ such that

$$\begin{aligned} u_n\in C^{1,\alpha }_0(\overline{\Omega }) \quad \text {and}\quad \Vert u_n\Vert _{C^{1,\alpha }_0(\overline{\Omega })}\le M. \end{aligned}$$

Using the compactness of $C^{1,\alpha }_0(\overline{\Omega })$ into $C^{1}_0(\overline{\Omega })$ gives

$$\begin{aligned} u_n \in C^1_0(\overline{\Omega })\quad \text {for all }n\in \mathbb {N}\quad \text { and }\quad u_n\rightarrow 0 \quad \text {in } C^1_0(\overline{\Omega }). \end{aligned}$$

Since $\mathop {\mathrm {int}}\limits _{C^1_0(\overline{\Omega })} [v_*,u_*] \ne \emptyset$ (recall that $v_*\in -\mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right) , u_*\in \mathop {\mathrm {int}}\limits \left( C^1_0(\overline{\Omega })_+\right)$), it follows that $\{u_n\}_{n\ge n_0}\subseteq [v_*,u_*]$ for some $n_0\in \mathbb {N}$. These are nodal solutions of (1.1).

Remark 4.3

It will be interesting to extend the results of this paper to anisotropic equations. We believe that this is feasible. However, concerning possible extensions to double-phase problems with unbalanced growth, we doubt that this is possible due to the lack of a global regularity theory for such problems.