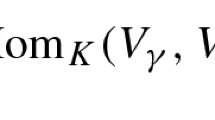Abstract
In this article, we study the stability problem for the Einstein–Hilbert functional on compact symmetric spaces following and completing the seminal work of Koiso on the subject. We classify in detail the irreducible representations of simple Lie algebras with Casimir eigenvalue less than the Casimir eigenvalue of the adjoint representation and use this information to prove the stability of the Einstein metrics on both the quaternionic and Cayley projective plane. Moreover, we prove that the Einstein metrics on quaternionic Grassmannians different from projective spaces are unstable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Perhaps the most interesting mathematical insight gained from studying general relativity is that the Einstein metrics g on a compact-connected manifold M can be characterized variationally as critical points of the Einstein–Hilbert or total scalar curvature functional
on the set \({ {M}}_+\,:=\,\Gamma (\, {Sym}^2_+T^*M\,)\) of Riemannian metrics on M under volume-preserving variations. Here, \( {scal}_g\) denotes the scalar curvature of the metric g. By construction, the functional \({ {S}}\) is invariant \({ {S}}[\,\varphi ^*g\,]\,=\,{ {S}}[\,g\,]\) under the right action of the diffeomorphism group \( {Diff}\,M\) on the set \({ {M}}_+\) via pull back, for this reason, the second variation of the Einstein–Hilbert functional in a critical point will have an infinite-dimensional space of null directions.
Factoring out the action of the connected component \( {Diff}^\circ M\, \subseteq \, {Diff}\,M\) of the identity, we may consider instead the reduced Einstein–Hilbert functional \({ {S}}:\,{ {M}}_+^V/ {Diff}^\circ M\longrightarrow { {R}}\) on the set of marked isometry classes of Riemannian metrics \(g\,\in \,{ {M}}^V_+\) of volume \(V\,=\, {Vol}[\,g\,]\) on a compact manifold M of dimension \(m\,\in \,{ {N}}\). It is technically easier though to use the equivalent functional \({ {S}}^V\) on the quotient of the set \({ {M}}_+\) of all Riemannian metrics by the extended group \({ {R}}^+\times {Diff}^\circ M\) acting on the right by pull back and constant rescaling

For every Einstein metric g of volume \( {Vol}[\,g\,]\,=\,V\) on M different from a round metric on \(S^m\) the formal tangent space to \(g\,\in \,{ {M}}_+\) decomposes into the direct sum [2, Lemma 4.57]
where \(D^*:\,\Gamma (\, {Sym}^2T^*M\,)\longrightarrow \Gamma (\,TM\,),\,h\longmapsto D^*h,\) is the formally adjoint differential operator to the Lie derivative \(D:\,\Gamma (\,TM\,)\longrightarrow \Gamma (\, {Sym}^2T^*M\,),\,X\longmapsto {Lie}_Xg\). Both differential operators factorize over \(\nabla \) and can be written as sums over local orthonormal bases:
The subspace \({ {R}}\,g\,\oplus \, {im}\,D\,\oplus \,\{\,0\,\}\,\subseteq \, \Gamma (\, {Sym}^2T^*M\,)\) defined in terms of the decomposition (1) is equal to the tangent space to the \({ {R}}^+\times {Diff}^\circ M\)-orbit of the Einstein metric g in \({ {M}}_+\). Choosing the subspace \(C^\infty (\,M\,)_\circ \,\subseteq \,C^\infty (\,M\,)\) of functions with zero integral as a linear complement to the constants \({ {R}}\,\subseteq \,C^\infty (\,M\,)\), we get a suitable description of the formal tangent space
to the marked isometry class \([\,g\,]\) of the Einstein metric in the quotient \({ {M}}^V_+/ {Diff}^\circ M\). Under this identification of the formal tangent space to the marked isometry class of the Einstein metric g, the Hessian \({ {S}}{ }\) of the reduced Einstein–Hilbert functional becomes the following quadratic form for tuples \(f\,\oplus \,h\) formed by a zero integral function f and a so-called tt-tensor, a trace and divergence-free symmetric 2-tensor \(h\,\in \,\ker \,D^*\,\cap \,\Gamma (\, {Sym}^2_\circ T^*M\,)\)
see [2, Theorem 4.60]. In this formula \(\Delta _L\) denotes the Lichnerowicz Laplacian:
The interested reader may find more details on \(\Delta _L\) and \(q(\,R\,)\) in [16]. The original definition of Lichnerowicz spelled out the curvature term \(q(\,R\,)\) in the form:

where \( {Der}_ {Ric}\) acts on 2-tensors by \((\, {Der}_ {Ric}h\,)(\,X,\,Y\,) \,{:=}\,h(\, {Ric}\,X,\,Y\,)\,{+}\,h(\,X,\, {Ric}\,Y\,)\) and:

The explicit formula (3) of the Hessian \({ {S}}{ }\) of the reduced Einstein–Hilbert functional highlights again the special role of the round spheres in the decomposition (1): According to the Theorem of Lichnerowicz–Obata [6], the Laplace–Beltrami operator satisfies \(\Delta \,>\,\frac{ {scal}}{m-1}\) on the subspace \(C^\infty (\,M\,)_\circ \, \subseteq \,C^\infty (\,M\,)\) of zero integral functions for all compact Einstein manifolds M of scalar curvature \( {scal}\,\in \,{ {R}}\) and dimension \(m\, \,3\) except for the round spheres. In consequence, the Hessian \({ {S}}{ }\) of the reduced Einstein–Hilbert functional is positive definite on the subspace \(C^\infty (\,M\,)_\circ \) tangential to conformal, volume-preserving variations of g.
En nuce the stability problem for compact Einstein manifolds M is the question, whether the Hessian \({ {S}}{ }\) of the reduced Einstein–Hilbert functional is negative definite on the complementary subspace \(\ker \,D^* \,\cap \,\Gamma (\, {Sym}^2_\circ T^*M\,)\) of tt-tensors. Following the seminal work of Koiso, we call an Einstein metric g stable, if its Hessian \({ {S}}{ }\) is negative definite on the space of tt-tensors; in the same vein, we call g unstable provided that there are tt-tensor directions on which \({ {S}}{ }\) is positive definite [10, Definition 2.7]. The kernel of \({ {S}}{ }\) agrees with the space of infinitesimal Einstein deformations characterized by the linearized Einstein equation:
Stability of Einstein metrics with respect to the Einstein–Hilbert functional \({ {S}}\) has been extensively studied for example in [4, 10] and [11]. In [10] Koiso essentially classified the stable symmetric spaces of compact type. More precisely Koiso’s result stipulates that the Einstein metrics on simply connected irreducible symmetric spaces of compact type are stable unless the spaces belong to one of the following three categories with \(n\, \,3;\,r,\,s\, \,2\):

In the work of Koiso, the complex quadric \( {Gr}^{ {or}}_2{ {R}}^5\,=\, {SO}(5)/ {SO}(3)\times {SO}(2)\) in \({ {C}}P^4\) was actually overlooked as remarked by Cao & He [3]; however, it is unstable according to results by Gasqui & Goldschmidt [7]. The stability status of the quaternionic and Cayley projective plane \({ {H}}P^2\) and \({ {O}}P^2\,=\, {F}_4/ {Spin}(9)\), and the quaternionic Grassmannians \( {Gr}_r{ {H}}^{r+s}\,=\, {Sp}(r+s)/ {Sp}(r)\times {Sp}(s)\) with \(r,\,s\, \,2\), remained undecided by Koiso. Apparently this question has not been settled since. In the recent work of Cao & He [3, Table 2], for example, the stability status of these spaces is listed as unknown. Our main result fills this gap and clarifies the stability status for the remaining symmetric spaces of compact type:
Theorem 1.1
(Stability of Quaternionic and Cayley Projective Plane) The Cayley projective plane \({ {O}}P^2\,=\, {F}_4/ {Spin}(9)\) is stable in the sense of Koiso. The quaternionic Grassmannians \( {Gr}_r{ {H}}^{r+s}\,=\, {Sp}(r+s) / {Sp}(r)\times {Sp}(s)\) of quaternionic subspaces of dimension r in \({ {H}}^{r+s}\) are unstable in the sense of Koiso for all parameters \(r,\,s\, \,2\), for \(r\,=\,1\) or \(s\,=\,1\); however, they are stable. In particular, \({ {H}}P^2\,=\, {Gr}_1{ {H}}^3\) is stable.
It should be pointed out that Koiso identified the Lichnerowicz Laplacian on symmetric spaces with a suitably normalized Casimir operator \( {Cas}\) and used this information to compute the first eigenvalue of \(\Delta _L\) on the space \(\Gamma (\, {Sym}^2_\circ T^*M\,)\) of trace-free symmetric 2-tensors. The first eigenvalues \(\frac{2(r+s)}{(r+s+1)}\,\frac{ {scal}}{m}\) and \(\frac{4}{3}\,\frac{ {scal}}{m}\) Koiso obtained for the quaternionic Grassmannians \( {Gr}_r{ {H}}^{r+s}\) and the Cayley projective plane \({ {O}}P^2\) are both below the critical value \(2\,\frac{ {scal}}{m}\). Our contribution to the classification of Koiso solves the question, whether the corresponding trace-free eigentensors \(h\,\in \,\Gamma (\, {Sym}^2_\circ T^*M\,)\) of the Lichnerowicz Laplacian \(\Delta _L\) can be chosen to be divergence-free \(D^*h\,=\,0\) as well or not.
Besides Koiso’s notion, there actually exists a weaker notion of stability of Einstein metrics, the so-called \({ {S}}\)-linear stability (cf. [17, 18]), which allows for the presence of infinitesimal deformations. More precisely an Einstein metric is called \({ {S}}\)-linearly stable, if \({ {S}}{ }\) is non-positive on the space of tt-tensors. According to the classification of Koiso, the only two symmetric spaces of compact type with infinitesimal deformations and subcritical eigenvalues on \(\Gamma (\, {Sym}^2_\circ T^*M\,)\) are \( {SU}(\,n\,)\) and \( {E}_6/ {F}_4\). In a forthcoming paper based on our approach, Schwahn [15] shows that both symmetric spaces are \({ {S}}\)-linearly stable, because their subcritical eigenvalues are not realizable by tt-tensors.
In Sect. 2, we discuss the left regular representation on sections of homogeneous vector bundles and use the Frobenius reciprocity to associate a family of linear maps, the prototypical differential operators, to every left invariant differential operator. The prototypical divergence operators associated to \(D^*\) allow us to translate the stability problem into a problem in finite-dimensional linear algebra. In Sect. 3, we provide the details of the classification of the critical representations by Koiso to identify the subcritical eigenspaces for the quaternionic and Cayley projective plane and the quaternionic Grassmannians. In Sects. 4 and 5, we decide for the Cayley projective plane \({ {O}}P^2\) and the quaternionic Grassmannians, respectively, whether the subcritical eigenvalues can be realized by tt-tensors or not.
2 Prototypical Differential Operators
Analysis on homogeneous spaces or Harmonic Analysis is a subtopic of differential geometry of particular elegance, because many of its problems can be translated into equivalent problems of linear algebra by means of an extensive dictionary of rules and prescriptions. In this section, we focus on a particular concept in this dictionary, the prototypical differential operators, in order to formulate the linear algebra equivalent of the stability problem for compact symmetric spaces in Corollary 2.3. Of particular importance in Sects. 4 and 5 is the formula (14) for the prototypical divergence operator \(D^*_R\). Below we will discuss this operator in a form geared to be easily accessible and self-contained.
Let us recall that a homogeneous space is a manifold M endowed with a transitive smooth action \(G\times M\longrightarrow M,\,(\,g,\,p\,) \longmapsto g\, \,p,\) of a Lie group G with the associated group homomorphism \(\mu :\,G\longrightarrow {Diff}\;M,\,g\longmapsto \mu _g,\) of left multiplication \(\mu _g(\,p\,)\,:=\,g p\). A homogeneous vector bundle over a homogeneous space is a vector bundle VM over the manifold M endowed with a smooth action \(\star :\,G\times VM\longrightarrow VM,\,(\,g,\,v\,)\longmapsto g\,\star \,v,\) on its total space, which covers the action of G on M and is linear on fibers. Every homogeneous vector bundle VM over M gives rise to the infinite-dimensional left regular representation:
of the group G on the vector space \(\Gamma (\,VM\,)\) by means of \((\,L_gv\,)(\,p\,)\,:=\,g\,\star \,v(\,g^{-1} p\,)\). Every tensor bundle – or more generally every natural vector bundle VM on a homogeneous space M – is automatically a homogeneous vector bundle; the characteristic smooth action \(\star :\,G\times VM\longrightarrow VM\) on its total space VM is implicitly defined by stipulating the identity
for all \(g\,\in \,G\). The rather unexpected change \(g g^{-1}\) in this identity is mandated by the contravariance \((\varphi \,\circ \,\psi )^* \,=\,\psi ^*\,\circ \,\varphi ^*\) of the pull back of sections of natural vector bundles. A left invariant differential operator on a homogeneous space M is a differential operator
between the sections of homogeneous vector bundles VM and WM over M, which is in addition equivariant \(D(\,L_gv\,)\,=\,L_g(\,Dv\,)\) under G for all \(v\,\in \,\Gamma (\,VM\,)\) and \(g\,\in \,G\).
The fiber of a homogeneous vector bundle VM in a chosen base point \(p\,\in \,M\) is naturally a representation \(V_pM\) of the stabilizer or isotropy subgroup \(K\,:=\,\{\;k\,\in \,G\;|\;k\, \,p\,=\,p\;\} \,\subseteq \,G\) by restricting the smooth action \(\star \) to the submanifold \(K\times V_pM\,\subseteq \,G\times VM\). In terms of this representation the evaluation map \( {ev}_p:\,\Gamma (\,VM\,)\longrightarrow V_pM,\,v\longmapsto v(\,p\,)\) is equivariant under the stabilizer subgroup \(K\,\subseteq \,G\) due to the trivial identity \((\,L_kv\,)(\,p\,)\,=\, k\,\star \,v(\,p\,)\) for all \(k\,\in \,K\) and \(v\,\in \,\Gamma (\,VM\,)\). Postcomposition with \( {ev}_p\), thus, induces a linear map
for every finite-dimensional representation \((\,R,\,\star _R\,)\) of the group G. The well-known Frobenius reciprocity asserts that this linear map is a vector space isomorphism, whose inverse
reads \((\,F^ {ext}r\,)(\,g p\,)\,=\,g\,\star \,F(\,g^{-1}\star _Rr\,)\) for all \(r\,\in \,R\) and \(g\,\in \,G\). Using Frobenius reciprocity, we can break up a left invariant differential operator \(D:\,\Gamma (\,VM\,)\longrightarrow \Gamma (\,WM\,)\) into more manageable pieces, the prototypical differential operators \(D_R\) associated to D and a finite-dimensional representation R of the group G by means of the commutative diagram

where the upper arrow is equal to postcomposition with D and the vertical arrows are the Frobenius reciprocity isomorphisms. Prototypical differential operators are used frequently in harmonic analysis, for example, to calculate the spectra of elliptic left invariant differential operators on compact homogeneous spaces. In order to reduce both statements of our main Theorem 1.1 to a statement about prototypical differential operators we formulate a representation theoretic concept akin to the concept of characteristic subgroups in group theory:
Definition 2.1
(Characteristic Subspaces of Representations). A G–characteristic subspace of the vector space \(\Gamma (VM)\) of sections of a homogeneous vector bundle VM is a G–invariant subspace \(R \subseteq \Gamma (VM)\) under the left regular representation, which contains the image \(F(R) \subseteq R\) of every G–equivariant linear map \(F : R \longrightarrow \Gamma (VM)\).
Lemma 2.2
(Kernels of Left Invariant Differential Operators) Consider a left invariant differential operator \(D:\,\Gamma (\,VM\,) \longrightarrow \Gamma (\,WM\,)\) between sections of homogeneous vector bundles VM and WM over a homogeneous space M under a transitive smooth action \(G\times M\longrightarrow M\) of a compact Lie group G. A finite-dimensional G-characteristic subspace \(R\,\subseteq \, \Gamma (\,VM\,)\) intersects the kernel of D trivially \(R\,\cap \,\ker \,D \,=\,\{\,0\,\}\), if and only if the prototypical differential operator associated to D and R is injective:
Proof
Assuming for the moment that the prototypical differential operator \(D_R\) associated to D and R is injective, we observe that the kernel of the left invariant differential operator \(D:\,\Gamma (\,VM\,)\longrightarrow \Gamma (\,WM\,)\) is necessarily a G-invariant subspace \(\ker \,D\,\subseteq \,\Gamma (\,VM\,)\). The intersection \(R\,\cap \,\ker \,D\,\subseteq \,R\) is, thus, a G-invariant subspace of the finite-dimensional representation R of the compact group G so that there exists a surjective G-equivariant projection \(P:\,R\longrightarrow R\,\cap \,\ker \,D\). Interpreting P as a G-equivariant linear map \(P:\,R\longrightarrow \Gamma (\,VM\,)\) we obtain an element P of the kernel of postcomposition with the differential operator D:
Postcomposition with D, however, is conjugated to the injective prototypical differential operator \(D_R\) via the commutative diagram, and so we conclude \(P\,=\,0\) and in turn \(R\,\cap \,\ker \,D\,=\,\{\,0\,\}\) due to the surjectivity of P. Conversely let us assume that R and \(\ker \,D\) intersect trivially \(R\,\cap \,\ker \,D\,=\,\{\,0\,\}\) and let \(F:\,R \longrightarrow \Gamma (\,VM\,)\) be the G-equivariant linear map Frobenius reciprocal to a linear map \( {ev}_p\,\circ \,F\,\in \,\ker \,D_R\) in the kernel of the prototypical differential operator \(D_R\). With \(D\,\circ \,F\,=\,0\) vanishing the image of F is contained in \(\ker \,D\); moreover, \(F(\,R\,)\, \subseteq \,R\) for the G-characteristic subspace R. In consequence \(F(\,R\,)\,\subseteq \,R\,\cap \,\ker \,D\,=\,\{\,0\,\}\) leading to \(F\,=\,0\) and in turn to \(\ker \,D_R\,=\,\{\,0\,\}\).
In the context of Theorem 1.1, we are interested in compact-connected Riemannian symmetric spaces M and the G-invariant subspace \(R\,\subseteq \,\Gamma (\, {Sym}^2_\circ T^*M\,)\) given by the direct sum of all eigenspaces of the Lichnerowicz Laplacian (4) restricted to trace-free symmetric 2-tensors
for the eigenvalues below the critical value \(2\,\frac{ {scal}}{m}\). Here, \( {scal}\) and m denote the scalar curvature and the dimension of M, respectively. Elliptic regularity [12] enjoyed by the elliptic differential operators of Laplace type like \(\Delta _L\) ensures that \(R\,\subseteq \,\Gamma (\, {Sym}^2_\circ T^*M\,)\) is a finite-dimensional G-invariant subspace. In order to verify that R is a G-characteristic subspace, we observe that the Lichnerowicz Laplacian \(\Delta _L\) is a special case of the standard Laplace operator \(\Delta \) defined in [16] and, thus, agrees on every symmetric space M with the Casimir operator of G. More precisely let \( {Cas}\,\in \,{ {U}}{ {g}}\) be the Casimir operator with respect to the unique invariant scalar product \(B:\,{ {g}}\times { {g}}\longrightarrow { {R}}\) on the Lie algebra \({ {g}}\) of the group G, which makes the orbit map \(G\longrightarrow M,\,g\longmapsto g p,\) through a point \(p\,\in \,M\) a Riemannian submersion. The image of \( {Cas}\,\in \,{ {U}}{ {g}}\) under the left regular representation L on \(\Gamma (\, {Sym}^2_\circ T^*M\,)\) satisfies
for every G-equivariant linear map \(F:\,R\longrightarrow \Gamma (\, {Sym}^2_\circ T^*M\,)\). According to equation (11) every finite direct sum \(R\,\subseteq \,\Gamma (\, {Sym}^2_\circ T^*M\,)\) of eigenspaces of \(\Delta _L\) is G-characteristic, because every G-equivariant linear map \(F:\,R\longrightarrow \Gamma (\, {Sym}^2_\circ T^*M\,)\) maps R necessarily into the direct sum of eigenspaces of \(\Delta _L\) for the eigenvalues the Casimir operator \( {Cas}\) assumes on R:
Corollary 2.3
(Stability of Einstein Metrics on Symmetric Spaces) Consider a compact irreducible Riemannian symmetric space M of dimension m and scalar curvature \( {scal}\) as a homogeneous space under the transitive action \(G\times M\longrightarrow M\) of its isometry group G. The direct sum of all eigenspaces of the Lichnerowicz Laplacian \(\Delta _L\) for the eigenvalues below the critical value \(2\,\frac{ {scal}}{m}\) is a finite-dimensional G-characteristic subspace \(R\,\subseteq \,\Gamma (\, {Sym}^2_\circ T^*M\,)\). In particular, the symmetric Einstein metric on M is stable
if and only if the prototypical differential operator associated to the divergence \(D^*\) is injective:
For Riemannian symmetric spaces, the critical value \(2\,\frac{ {scal}}{m}\) has a rather direct interpretation in terms of the Casimir operator \( {Cas}\). In order to establish this interpretation, we remark that the standard Laplace operator \(\Delta \) is defined in [16] for every natural vector bundle over a Riemannian manifold M, not only for \( {Sym}^2_\circ T^*M\), in particular, the version of \(\Delta \) defined on the tangent bundle appears in the following identity for Killing vector fields \(X\,\in \,\Gamma (\,TM\,)\):
For a Riemannian symmetric space M, the fundamental vector field map
maps \({ {g}}\) to the Lie algebra of Killing vector fields and so equations (11) and (12) imply:
Remark 2.4
(Casimir Eigenvalue of Adjoint Representation) The eigenvalue of the Casimir operator \( {Cas}\,\in \,{ {U}}{ {g}}\) on the adjoint representation \({ {g}}\) of the isometry group G of an irreducible Riemannian symmetric space M of dimension m is equal to
provided the Casimir operator \( {Cas}\,\in \,{ {U}}{ {g}}\) is defined with respect to the unique invariant scalar product on \({ {g}}\), which makes the orbit map \(G\longrightarrow M,\,g\longmapsto g p,\) a Riemannian submersion.
Corollary 2.3 and Remark 2.4 reduce Theorem 1.1 in essence to a simple and straightforward problem in linear algebra. In order to make this reduction effective, however, we need to calculate the prototypical differential operators \(D^*_R\) associated to the divergence operator \(D^*:\,\Gamma (\, {Sym}^2_\circ T^*M\,)\longrightarrow \Gamma (\,TM\,)\) of equation (2) restricted to trace-free symmetric 2-tensors. For this purpose, we recall that the Lie derivative of a section \(v\,\in \,\Gamma (\,VM\,)\) of a tensor bundle VM along \(X\,\in \,\Gamma (\,TM\,)\) can be written in terms of the connection:
induced on VM from a connection \(\nabla \) on the tangent bundle, where \(\nabla ^{ {op}}_YX\,:=\,\nabla _XY\,-\,[X,Y]\) denotes the connection opposite to \(\nabla \) and \(\star \) the infinitesimal representation of the Lie algebra bundle \( {End}\,TM\) on VM. For the torsion-free Levi–Civita connection and the fundamental vector field \(X^M\,:=\, \frac{d}{dt} _0\mu _{e^{tX}}\,\in \,\Gamma (\,TM\,)\) associated to \(X\,\in \,{ {g}}\), this formula becomes
In contrast to general Riemannian homogeneous spaces, the Lie algebra \({ {g}}\) of the isometry group G of a Riemannian symmetric space M splits naturally into the direct sum \({ {g}}\,=\,{ {k}}\,\oplus \,{ {m}}\) of the Lie subalgebra \({ {k}}\,\subseteq \,{ {g}}\) of the stabilizer \(K\,\subseteq \,G\) of a chosen base point \(p\,\in \,M\) and the subspace \({ {m}}\) of transvections. The latter space corresponds to the Killing vector fields which are parallel, i.e., in the case of symmetric spaces, the complement \({ {m}}\) allows the description
in p. Choosing a basis \(E_1,\,\ldots ,\,E_m\,\in \,{ {m}}\) with orthonormal values in \(T_pM\) we, thus, find
for every given argument \(F\,\in \, {Hom}_K(\,R,\, {Sym}^2_\circ T^*_pM\,)\) with Frobenius reciprocal extension \(F^ {ext}:\,R\longrightarrow \Gamma (\, {Sym}^2_\circ T^*M\,)\) by using \((\,\nabla E^M_\mu \,)_p\,=\,0\) and equation (5) in the last line. Note that the equality \((\,D^*h\,)_p\,=\,-\sum (\,E^M_\mu \, \,\nabla _{E^M_\mu }h\,)^\sharp _p\) requires orthonormality of the local basis \(E^M_1,\,\ldots ,\,E^M_m\) in the point \(p\,\in \,M\) only, because \(X\, \, \nabla _Yh\) depends \(C^\infty (\,M\,)\)-bilinearly on X and Y. By construction \(F^ {ext}\) is G-equivariant with \(L_{e^{-tE_\mu }}F^ {ext}(\,r\,)\,=\,F^ {ext}(\,e^{-tE_\mu }\star _Rr\,)\) so that we can summarize our arguments for all \(F\,\in \, {Hom}_K(\,R,\, {Sym}^2_\circ T^*_pM\,)\) in the form:
3 Critical Representations of Simple Lie Algebras
On a compact irreducible Riemannian symmetric space M of dimension m and scalar curvature \( {scal}\) the direct sum of all eigenspaces of the Lichnerowicz Laplacian \(\Delta _L\) on trace-free symmetric 2-tensors with eigenvalues below the critical value \(2\,\frac{ {scal}}{m}\) is a characteristic subspace \(R\,\subseteq \,\Gamma (\, {Sym}^2_\circ T^*M\,)\) under the isometry group G. Being a characteristic subspace R is equal to the direct sum of all isotypical components of \(\Gamma (\, {Sym}^2_\circ T^*M\,)\) corresponding to irreducible representations of G with Casimir eigenvalues below the Casimir eigenvalue \( {Cas}_{ {g}}\,=\,2\,\frac{ {scal}}{m}\), i.e., the eigenvalue of the adjoint representation \({ {g}}\) according to Remark 2.4:
Definition 3.1
(Critical Representation) An irreducible finite-dimensional representation R of a simple Lie algebra \({ {g}}\) is a critical representation with respect to the stability problem of Einstein metrics provided its Casimir eigenvalue \( {Cas}_R\) is at most equal to the Casimir eigenvalue \( {Cas}_{ {g}}\) of the adjoint representation:
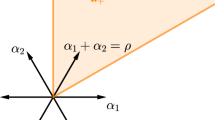
In order to classify the critical representations of a simple complex Lie algebra \({ {g}}\) of rank n, we choose a maximal torus \({ {t}}\,\subseteq \,{ {g}}\), an ordering of roots in form of a system \(\alpha _1,\,\ldots ,\,\alpha _n\,\in \, { {t}}^*\) of simple roots and a Weyl invariant scalar product \(b:\,{ {t}}^*\times { {t}}^* \longrightarrow { {C}}\), which is positive definite on the real subspace spanned by the (simple) roots. The geometry of the system of simple roots is encoded in the Dynkin diagram of the simple Lie algebra \({ {g}}\) [5], and this geometry determines the fundamental weights \(\omega _1,\,\ldots ,\, \omega _n\,\in \,{ {t}}^*\) by means of the identity
valid for all \(r,\,s\,=\,1,\ldots ,n\), where \(\delta _{rs}\) denotes the Kronecker delta which casts the boolean expression \(r\,=\,s\) to 1 or 0. A detailed tabulation of the systems of fundamental weights for all simple complex Lie algebras can be found in a number of references, for example in [5], and we will freely use this information in the sequel. Up to isomorphism every irreducible finite-dimensional representation \(R\,=\,R^\lambda \) is characterized by its highest weight, an element
of the additive semigroup of \({ {t}}^*\) generated by the fundamental weights with \(\lambda _1,\,\ldots ,\,\lambda _n\,\in \,{ {N}}_0\). According to Freudenthal’s formula for the Casimir eigenvalues [5] the Casimir operator \( {Cas}\,\in \,{ {U}}{ {g}}\) can be normalized in such a way that the Casimir eigenvalue of every irreducible representation \(R\,=\,R^\lambda \) is equal to the Casimir constant \( {Cas}_R\,=\, {Cas}_\lambda \) of its highest weight \(\lambda \):
By construction the highest weights of the form (15) form an additive semigroup \(\Lambda ^+\,\subseteq \,{ {t}}^*\). Addition in this semigroup corresponds to the Cartan product of irreducible representations, in other words the Cartan product of two irreducible representations \(R^\lambda \) and \(R^{{\hat{\lambda }}}\) of highest weights \(\lambda \) and \({\hat{\lambda }}\) is some irreducible representation \(R^{\lambda \,+\,{\hat{\lambda }}}\,=\,R^\lambda R^{{\hat{\lambda }}}\) of highest weight \(\lambda \,+\,{\hat{\lambda }}\). The Casimir eigenvalue of the Cartan product is equal to the sum of Casimir eigenvalues
plus an additional term \(b(\,\lambda ,\,{\hat{\lambda }}\,)\). Both highest weights \(\lambda \) and \({\hat{\lambda }}\) pertain to the Weyl chamber, the real cone in \({ {t}}^*\) generated by the fundamental weights \(\omega _1,\,\ldots ,\,\omega _n\), and so the additional term is strictly positive \(b(\,\lambda ,\,{\hat{\lambda }}\,) \,>\,0\) unless \(\lambda \,=\,0\) or \({\hat{\lambda }}\,=\,0\). Thought of as a map \( {Cas}:\,\Lambda ^+\longrightarrow { {R}},\,\lambda \longmapsto {Cas}_\lambda ,\) the Casimir eigenvalue is, thus, superadditive in the sense \( {Cas}_{\lambda + {\hat{\lambda }}}\, \, {Cas}_\lambda \,+\, {Cas}_{{\hat{\lambda }}}\), hence the equality (15) converts into the linear lower bound
for the Casimir eigenvalue of a highest weight \(\lambda \,\in \,\Lambda ^+\) with equality, if and only if \(\lambda \) is itself a fundamental weight or zero. This linear lower bound is of course rather weak, after all the Casimir eigenvalue is the quadratic polynomial (16) in \(\lambda \), nevertheless it suffices to select a short list of candidates for critical representations for every simple Lie algebra \({ {g}}\).
Let us discuss this procedure for the sequence of special linear Lie algebras \( {sl}(n+1,{ {C}})\) for all \(n\, \,1\), which correspond to the Dynkin diagrams of type \(A_n\). The weights \(\varepsilon _1,\,\ldots ,\,\varepsilon _{n+1}\) of the defining representation \(V\,:=\,{ {C}}^{n+1}\) generate the dual \({ {t}}^*\) of the maximal torus \({ {t}}\,\subseteq \, {sl}(n+1,{ {C}})\) of diagonal matrices and are subject only to the characteristic trace zero constraint
which is reflected by the following Weyl invariant scalar product \(b:\,{ {t}}^*\times { {t}}^*\longrightarrow { {C}}\) on \({ {t}}^*\):
Due to the trace zero constraint the generating weights \(\varepsilon _1,\,\ldots , \,\varepsilon _{n+1}\) are linearly dependent, nevertheless the scalar product \(b(\,\lambda ,\,{\hat{\lambda }}\,)\) of two linear combinations \(\lambda , \,{\hat{\lambda }}\,\in \,{ {t}}^*\) of \(\varepsilon _1,\,\ldots ,\,\varepsilon _{n+1}\) is readily calculated by first pretending that \(\varepsilon _1,\,\ldots ,\,\varepsilon _{n+1}\) is an orthonormal basis of \({ {t}}^*\) and then subtracting the product of the two coefficient sums of \(\lambda \) and \({\hat{\lambda }}\) respectively divided by \(n+1\). For a suitable ordering of roots the simple roots and fundamental weights read
in particular \(2\,\rho \,=\,2n\,\varepsilon _1\,+\,2(n-1)\,\varepsilon _2\,+\,\cdots \,+\,2\,\varepsilon _n\) has coefficient sum equal to \(n(n+1)\). The adjoint representation of \({ {g}}\,=\, {sl}(n+1,{ {C}})\) is isomorphic to the Cartan product \(V^* V\) of the irreducible representations for \(\omega _n\) and \(\omega _1\) of highest weight \(\varepsilon _1-\varepsilon _{n+1}\) resulting in
The irreducible representation corresponding to the fundamental weight \(\omega _r\) is equal to the exterior power \(\Lambda ^rV\,\cong \,\Lambda ^{n+1-r}V^*\) of the defining representation V with Casimir eigenvalue:
Considered as a quadratic polynomial in r the Casimir eigenvalue has zeroes in \(r\,=\,0,\,n+1\), hence it is symmetric about \(r\,=\,\frac{n+1}{2}\) and strictly monotonely increasing for \(r\,\in \,[\,0,\,\frac{n+1}{2}\,]\):
In passing, we observe that there are fewer different fundamental weights than shown in this diagram for \(n\, \,4\). The classification of all possible critical representations of the Lie algebras \( {sl}(n+1,{ {C}})\) with \(n\, \,1\) follows from the lower linear estimate (17), the inequality
valid for all \(n\, \,1\) and two additional inequalities valid for \(n\, \,3\) and \(n\, \,7\), respectively:
According to the inequalities (19) and (20) the highest weight \(\lambda \) of every critical representation for \( {sl}(n+1,{ {C}})\) is the sum of at most two fundamental weights, the first inequality in (21) ensures in turn that \(\lambda \) is either zero, a fundamental weight or the sum \(2\,\omega _1\), \(\omega _1+\omega _n\) or \(2\,\omega _n\) of two fundamental weights in \(\{\,\omega _1,\,\omega _n\,\}\). Moreover, the second inequality in (21) excludes the fundamental weights \(\omega _3,\,\ldots ,\, \omega _{n-2}\) for all \(n\, \,7\) from consideration, while the two sums \(2\,\omega _1\) and \(2\,\omega _n\) have to be discarded by hand for all \(n\, \,2\) by verifying for those n:
In consequence, the trivial representation \({ {C}}\), the adjoint representation \(V^* V\) and the four fundamental representations \(V,\,\Lambda ^2V,\,\Lambda ^2V^*\) and \(V^*\) of \( {sl}(n+1,{ {C}})\) are critical representations, and they comprise all possible critical representations of \( {sl}(n+1,{ {C}})\) unless \(n\,=\,5\) or \(n\,=\,6\), in which case \(\Lambda ^3V\) and \(\Lambda ^3V^*\) are critical representations of \( {sl}(n+1,{ {C}})\) as well.
Repeating the preceding discussion for the other three series of classical simple Lie algebras, we recall first of all that the Dynkin diagrams of type \(B_n\) with \(n\, \,2\) are represented by the odd-dimensional orthogonal Lie algebras \( {so}(2n+1,{ {C}})\) of rank \(n\,\in \,{ {N}}\). The weights \(\pm \varepsilon _1,\, \ldots ,\,\pm \varepsilon _n\) and 0 of the defining representation \(V\,:=\,{ {C}}^{2n+1}\) of \( {so}(2n+1,{ {C}})\) form an orthonormal basis \(\varepsilon _1,\,\ldots ,\,\varepsilon _n\) of the dual \({ {t}}^*\) of a maximal torus with respect to the Weyl invariant scalar product \(b:\,{ {t}}^*\times { {t}}^*\longrightarrow { {C}}\) of choice. For a suitable ordering of roots the simple roots and fundamental weights of the Lie algebras of type \(B_n\) read
Using \(2\,\rho \,=\,(2n-1)\,\varepsilon _1\,+\,(2n-3)\,\varepsilon _2\,+\,\cdots \,+\,\varepsilon _n\), we can calculate the Casimir eigenvalues
for the exterior powers \(\Lambda ^rV\) of the defining representation V, which are irreducible representations of highest weight \(\omega _r\) for \(r\,=\, 1,\,\ldots ,\,n-1\). In the same vein the Casimir eigenvalue of the spinor representation, the irreducible representation \(\Sigma \) of the highest weight \(\omega _n\) is equal to
The Casimir eigenvalue of the adjoint representation \(\Lambda ^2V\) of \( {so}(2n+1,{ {C}})\) is equal to \(2\,(2n-1)\) even in the exceptional case \(n\,=\,2\), where the highest weight of \(\Lambda ^2V\) is equal to \(2\,\omega _2\,=\,\varepsilon _1+\varepsilon _2\). Discussing the roots of the quadratic polynomial \( {Cas}_{\omega _r}\,=\,r\,(2n+1-r)\) in r, we conclude
Taking these inequalities together with the lower bound (17) and the auxiliary inequalities
valid for all \(n\, \,2\) and \(n\, \,3\), respectively, we conclude that the highest weight \(\lambda \,\in \,{ {t}}^*\) of a critical representation for \( {so}(2n+1,{ {C}})\) is either zero or a fundamental weight for all \(n\, \,3\), interestingly \(2\,\omega _2\) is the highest weight of the critical adjoint representation \( {so}(5,{ {C}})\,=\,\Lambda ^2V\) in the exceptional case \(n\,=\,2\). Due to the inequalities (22) combined with \( {Cas}_{\omega _2}\,=\, {Cas}_{ {g}}\) the fundamental weights \(\omega _3,\,\ldots ,\,\omega _{n-1}\) cannot be critical for \(n\, \,3\), in consequence classification of the critical irreducible representations of \( {so}(2n+1,{ {C}})\) centers on the candidates \({ {C}},\,V,\,\Lambda ^2V\) and the spinor representation \(\Sigma \), the latter, however, is critical only for \(n\,=\,2,\,\ldots ,\,6\).
Let us now turn to the symplectic Lie algebras \({ {g}}\,=\, {sp}(2n,{ {C}})\) of rank \(n\,\in \,{ {N}}\) and Dynkin diagrams of type \(C_n\) under the assumption \(n\, \,2\). The weights \(\pm \varepsilon _1,\,\ldots ,\,\pm \varepsilon _n\) of the defining representation \(V\,=\,{ {C}}^{2n}\) of the symplectic Lie algebras form a basis \(\varepsilon _1,\,\ldots ,\,\varepsilon _n\) of the dual \({ {t}}^*\) of a maximal torus \({ {t}}\), which is actually an orthonormal basis for the Weyl invariant scalar product \(b:\,{ {t}}^*\times { {t}}^*\longrightarrow { {C}}\) of our choice. In terms of this orthonormal basis the simple roots associated to a suitable ordering of roots and the corresponding fundamental weights is equal to
and so \(2\,\rho \,=\,2n\,\varepsilon _1\,+\,2(n-1)\,\varepsilon _2\,+\,\cdots \,+\,2\,\varepsilon _n\). In consequence the Casimir eigenvalue of the fundamental representation \(\Lambda ^r_\circ V\) corresponding to the fundamental weight \(\omega _r\) is equal to
for \(r\,=\,1,\,\ldots ,\,n\). In analogy to the inequalities (19) and (22), we establish the inequalities:
The adjoint representation of \({ {g}}\,=\, {sp}(2n,{ {C}})\) is isomorphic to the second symmetric power \( {sp}(2n,{ {C}})\,=\, {Sym}^2V\) of the defining representation V, its Casimir eigenvalue is equal to
The sequence of inequalities (23) together with the auxiliary inequalities
valid for all \(n\, \,2\) and all \(n\, \,4\), respectively, tell us that the highest weight \(\lambda \) of a critical representation of \( {sp}(2n,{ {C}})\) is either zero \(\lambda \,=\,0\), the highest weight \(\lambda \,=\,2\,\omega _1\) of the adjoint representation or one of the two fundamental weights \(\lambda \,=\,\omega _1\) or \(\lambda \,=\,\omega _2\) unless \(n\,=\,3\), where \(\lambda \,=\,\omega _3\) is an additional possibility. The critical representations of the symplectic Lie algebras \( {sp}(2n,{ {C}})\) are, thus, \({ {C}},\,V,\, {Sym}^2V\) and \(\Lambda ^2_\circ V\) with \(\Lambda ^3_\circ V\) being critical only for \(n\,=\,3\).
The last sequence \(D_n\) of irreducible Dynkin diagrams is represented by the even dimensional orthogonal Lie algebras \( {so}(2n,{ {C}})\) of rank \(n\, \,3\), the classification of their critical representation, thus, follows the discussion of the odd dimensional orthogonal Lie algebras closely. The weights \(\pm \varepsilon _1,\,\ldots ,\,\pm \varepsilon _n\) of the defining representation \(V\,:=\,{ {C}}^{2n}\) form again an orthonormal basis \(\varepsilon _1,\,\ldots ,\,\varepsilon _n\) of the dual \({ {t}}^*\) of a maximal torus with respect to our preferred Weyl invariant scalar product \(b:\,{ {t}}^*\times { {t}}^*\longrightarrow { {C}}\). Simple roots and fundamental weights read
for a suitable ordering of roots. The Casimir eigenvalues for the exterior powers \(\Lambda ^rV\) is equal to
for all \(r\,=\,1,\,\ldots ,\,n-2\) due to \(2\,\rho \,=\,(2n-2)\,\varepsilon _1\,+\, (2n-4)\,\varepsilon _2\,+\,\cdots \,+\,2\,\varepsilon _{n-1}\). The Casimir eigenvalues of the two half spinor representations \(\Sigma ^-\) and \(\Sigma ^+\) of \( {so}(2n,{ {C}})\) of highest weight \(\omega _{n-1}\) and \(\omega _n\) agree due to the existence of the exterior automorphism \(+\varepsilon _n\, \,-\varepsilon _n\):
In consequence, the Casimir eigenvalue of the adjoint representation \(\Lambda ^2V\) of \( {so}(2n,{ {C}})\) is equal to \(2\,(2n-2)\) even in the exceptional case \(n\,=\,3\), where the highest weight of \(\Lambda ^2V\) equals \(\omega _2+\omega _3\,=\,\varepsilon _1+\varepsilon _2\). The sequence of inequalities between the Casimir eigenvalues
established by considering \( {Cas}_{\omega _r}\,=\,r(2n-r)\) as a quadratic polynomial in r together with
for all \(n\, \,3\) and \(n\, \,4\), respectively, imply that the highest weight \(\lambda \) of a critical representation is either zero or a fundamental weight different from \(\omega _3,\,\ldots ,\,\omega _{n-2}\) unless \(n\,=\,3\), in which case \(\omega _2+\omega _3\,=\,\varepsilon _1+\varepsilon _2\) is equal to the highest weight of the critical adjoint representation \(\Lambda ^2V\) of \( {so}(6,{ {C}})\,\cong \, {sl}(4,{ {C}})\). Leaving aside this special case already discussed above, we conclude that the only candidates for critical representations are \({ {C}},\,V,\,\Lambda ^2V\) and the two half spinor representations \(\Sigma ^+\) and \(\Sigma ^-\), the latter, however, are critical only for \(n\,=\,3,\,\ldots ,\,7\).
For the convenience of the reader, we summarize the preceding classification of the critical representations of the classical simple Lie algebras of types A to D in the following table, in which the column denoted by Casimir is reserved for the relative Casimir eigenvalue \(\frac{ {Cas}_\lambda }{ {Cas}_{ {g}}}\):
Algebra | Weight | Representation | Casimir | Constraints |
|---|---|---|---|---|
\( {sl}(\,n+1,\,{ {C}}\,)\) | 0 | \({ {C}}\) | 0 | for all \(n\, \,1\) |
\(\omega _1\) | V | \(\frac{n(n+2)}{2(n+1)^2}\) | for all \(n\, \,1\) | |
\(\omega _n\) | \(V^*\) | \(\frac{n(n+2)}{2(n+1)^2}\) | for all \(n\, \,2\) | |
\(\omega _2\) | \(\Lambda ^2V\) | \(\frac{(n-1)(n+2)}{(n+1)^2}\) | for all \(n\, \,3\) | |
\(\omega _{n-1}\) | \(\Lambda ^2V^*\) | \(\frac{(n-1)(n+2)}{(n+1)^2}\) | for all \(n\, \,4\) | |
\(\omega _3\) | \(\Lambda ^3V\) | \(\frac{7}{8},\;\frac{48}{49}\) | for \(n\,=\,5,\,6\) | |
\(\omega _4\) | \(\Lambda ^3V^*\) | \(\frac{48}{49}\) | for \(n\,=\,6\) | |
\(\omega _1+\omega _n\) | \(V^* V\) | 1 | for all \(n\, \,1\) | |
\( {so}(\,2n+1,\,{ {C}}\,)\) | 0 | \({ {C}}\) | 0 | for all \(n\, \,1\) |
\(\omega _1\) | V | \(\frac{2n}{2(2n-1)}\) | for all \(n\, \,1\) | |
\(\omega _2\) | \(\Lambda ^2V\) | 1 | for all \(n\, \,2\) | |
\(\omega _n\) | \(\Sigma \) | \(\frac{2n(2n+1)}{16(2n-1)}\) | for \(n\,=\,1,\,\ldots ,\,6\) | |
\( {sp}(\,2n,\,{ {C}}\,)\) | 0 | \({ {C}}\) | 0 | for all \(n\, \,1\) |
\(\omega _1\) | V | \(\frac{2n+1}{4(n+1)}\) | for all \(n\, \,1\) | |
\(\omega _2\) | \(\Lambda ^2_\circ V\) | \(\frac{4n}{4(n+1)}\) | for all \(n\, \,2\) | |
\(\omega _3\) | \(\Lambda ^3_\circ V\) | \(\frac{15}{16}\) | for \(n\,=\,3\) | |
\(2\,\omega _1\) | \( {Sym}^2V\) | 1 | for all \(n\, \,1\) | |
\( {so}(\,2n,\,{ {C}}\,)\) | 0 | \({ {C}}\) | 0 | for all \(n\, \,3\) |
\(\omega _1\) | V | \(\frac{2n-1}{2(2n-2)}\) | for all \(n\, \,3\) | |
\(\omega _2\) | \(\Lambda ^2V\) | 1 | for all \(n\, \,3\) | |
\(\omega _{n-1} \) | \(\Sigma ^-\) | \(\frac{2n(2n-1)}{16(2n-2)}\) | for \(n\,=\,3,\,\ldots ,\,7\) | |
\(\omega _n \) | \(\Sigma ^+\) | \(\frac{2n(2n-1)}{16(2n-2)}\) | for \(n\,=\,3,\,\ldots ,\,7\) |
The classification of the critical representations of the exceptional simple Lie algebras of types \(E_6,\,E_7,\,E_8\) and \(F_4,\,G_2\) is significantly simpler, because all the Casimir eigenvalues are explicit rational numbers and the highest weights of the adjoint representations \({ {g}}\) are all fundamental weights. Moreover, all Casimir eigenvalues of the fundamental weights turn out to be greater than or equal to \(\frac{1}{2}\) so that the highest weights of all non-trivial critical representations are necessarily fundamental weights. The resulting classification reads
Algebra | Representation | Casimir | Algebra | Representation | Casimir |
|---|---|---|---|---|---|
\({ {e}}_6\) | \({ {C}}\) | 0 | \({ {e}}_8\) | \({ {C}}\) | 0 |
\([\,27\,]\) | \(\frac{13}{18}\) | \([\,248\,]\) | 1 | ||
[ 27 ]\(^*\) | \(\frac{13}{18}\) | \({ {f}}_4\) | \({ {C}}\) | 0 | |
\([\,78\,]\) | 1 | \( {Im}\;{ {A}}\) | \(\frac{2}{3}\) | ||
\({ {e}}_7\) | \({ {C}}\) | 0 | \([\,52\,]\) | 1 | |
\([\,56\,]\) | \(\frac{19}{24}\) | \({ {g}}_2\) | \({ {C}}\) | 0 | |
\([\,133\,]\) | 1 | \( {Im}\;{ {O}}\) | \(\frac{1}{2}\) | ||
\([\,14\,]\) | 1 |
In these tables, we have indicated the non-trivial critical irreducible representations by their dimensions only in order to avoid any ambiguity caused by the rather arbitrary enumeration of simple roots and fundamental weights of the exceptional Lie algebras. The two exceptions are the two critical representations of \( {G}_2\) and \( {F}_4\) arising from the octonions \({ {O}}\) and the 27-dimensional Albert algebra \({ {A}}\), which will be studied in detail in Sect. 4.
4 Geometry of the Cayley Projective Plane
In order to prove the stability of the Cayley projective plane \({ {O}}P^2\), we will study the Albert algebra \({ {A}}\) of hermitian \(3\times 3\)-matrices over the octonions \({ {O}}\) to describe the unique non-trivial critical representation \(R\,=\, {Im}\,{ {A}}\) of its automorphism group \( {F}_4\,=\, {Aut}\,{ {A}}\). Using the machinery of prototypical differential operators introduced in Sect. 2 and our description of R, we will proceed to prove the injectivity of the associated prototypical divergence operator \(D^*_R\) and conclude that the Einstein metric on \({ {O}}P^2\) is stable in the sense of Koiso. A detailed introduction to the octonions and the Albert algebra can be found in [1] or the book [8].
Working with the algebra \({ {O}}\) of Cayley numbers or octonions is hampered by the fact that many different constructions and definitions of \({ {O}}\) exist in the literature, it can hardly be called obvious that all these constructions lead to the same algebra. Perhaps the most direct construction of \({ {O}}\) is via the Cayley–Dickson process, in this construction octonions are tuples \((\,a,\,\alpha \,)\,\in \,{ {H}}\oplus { {H}}\) of quaternions with the multiplication, conjugation and algebra unit:
All our subsequent calculations are independent from the question, which construction of the octonions is to be preferred; they only rely on four characteristic properties of the algebra \({ {O}}\), which the reader may easily verify in her or his favorite model for the octonions:
-
The algebra \({ {O}}\) of octonions is an algebra with unit \( {1}\,\in \,{ {O}}\) which decomposes into the vector space direct sum \({ {O}}\,=\,{ {R}}\,\oplus \, {Im}\,{ {O}}\) of the line generated by \( {1}\) and the subspace \( {Im}\,{ {O}}\,\subseteq \,{ {O}}\) of imaginary octonions spanned by all the square roots of \(- {1}\) in \({ {O}}\).
-
The involutive linear map \({ {O}}\longrightarrow { {O}},\,A\longmapsto \overline{A},\) with eigenspaces \({ {R}}\) and \( {Im}\,{ {O}}\) for the eigenvalues \(+1\) and \(-1\), respectively, is an algebra antiautomorphism \(\overline{AB}\,=\,{\overline{B}}\,{\overline{A}}\).
-
Every two octonions \(A,\,B\,\in \,{ {O}}\) lie in a common associative subalgebra of \({ {O}}\) together with the unit \( {1}\,\in \,{ {O}}\) and in consequence \({\overline{A}}\,=\,2( {Re}\,\,A) {1}\,-\,A\) as well as \({\overline{B}}\). In particular, there is no need to indicate parentheses in expressions like \(A{\overline{A}}B\) or \(BA\overline{A}\).
-
The expression \(g_{ {O}}(A,B)\,:=\, {Re}\,({\overline{A}}\,B)\) defines a positive definite scalar product on \({ {O}}\). In the same vein, \(\Omega (A,B,C) \,:=\, {Re}\,(ABC)\) is well defined for all \(A,\,B,\,C\,\in \,{ {O}}\) independent of the way we evaluate it and defines a cyclically invariant 3-form \(\Omega \).
In the Cayley–Dickson construction of the octonions for example the 3-form \(\Omega \) reads
and is, thus, cyclically invariant, it becomes an alternating 3-form only after restriction to the subspace \( {Im}\,{ {O}}\,\subseteq \,{ {O}}\) of imaginary octonions. The four properties formulated above in particular imply the fundamental identity \(\overline{A}A\,=\,|\,A\,|^2_{ {O}}\, {1}\) for all \(A\,\in \,{ {O}}\), which is needed in the verification of essentially all the formulas stipulated below. The Albert algebra is the commutative algebra \({ {A}}\) of all hermitian \(3\times 3\)-matrices with coefficients in \({ {O}}\)
under the symmetrized matrix multiplication \({ {A}}\,*\, {{\hat{A}}}\,=\,\frac{1}{2}(\,{ {A}}\, {{\hat{A}}}\,+\, {{\hat{A}}}\,{ {A}}\,)\) or equivalently under:
Let us point out two subspaces of the Albert algebra, the vector and the spinor subspace
with parameters \(A_0\,\in \,{ {R}}\) and \(A_1,\,\alpha _2,\,\alpha _3\,\in \,{ {O}}\). The vector space underlying the Albert algebra \({ {A}}\) decomposes into the internal direct sum of V and \(\Sigma \) as well as the two real lines
spanned by the algebra unit \( {1}\,\in \,{ {A}}\) and the auxiliary trace-free element \(\Gamma \,\in \,{ {A}}\) defined by
Most importantly the multiplication in the Albert algebra can be written completely in terms of the decomposition (26) and the spin geometry of the euclidean vector space V, namely
for all \(a,\,\underline{a}\,\in \,{ {R}}\), \(A\,\in \,V\) and \(\alpha \,\in \,\Sigma \). In this spinorial description of the multiplication in the Albert algebra the notation \(g_V:\,V\times V\longrightarrow { {R}}\) and \(g_\Sigma :\,\Sigma \times \Sigma \longrightarrow { {R}}\) refers to the standard positive definite scalar products on \(V\,\cong \,{ {R}}\,\oplus \,{ {O}}\) and \(\Sigma \,\cong \,{ {O}}\,\oplus \,{ {O}}\), respectively
while \(\bullet :\,V\times \Sigma \longrightarrow \Sigma \) refers to the Clifford multiplication of V on its spinor module \(\Sigma \):
Last but not least \(\diamond :\,\Sigma \times \Sigma \longrightarrow V\) denotes the symmetric bilinear spinor multiplication:
The verification of the formula (28) for the multiplication in \({ {A}}\) is a slightly tedious, but otherwise straightforward exercise in expanding definitions. In the same vein the identities
are easily verified for all \(A\,\in \,V\) and \(\alpha \,\in \,\Sigma \) by expanding definitions and using the cyclic invariance of \(\Omega \). It is the first of these two identities of course which allows us to think of \(\bullet \) as the multiplication of the Clifford algebra \( {Cl}(\,V,\, -g_V\,)\,\cong \, {Mat}_{16\times 16}({ {R}}\,\oplus \,{ {R}})\) on its irreducible module \(\Sigma \,\cong \,{ {R}}^{16}\). The cyclic invariance of \(\Omega \) is needed as well to establish the identity
for all \(A\,\in \,V\) and \(\alpha ,\,\beta \,\in \,\Sigma \), which tells us in particular that the symmetric spinor multiplication \(\diamond \) is completely determined by the Clifford multiplication \(\bullet \) and, thus, by the spin geometry of V. In consequence, the spin group \( {Spin}(\,V,\,-g_V\,)\) acts by automorphisms on \({ {A}}\)
for all \(F\,\in \, {Spin}(\,V,-g_V\,)\,\subseteq \, {Cl}(\,V,\,-g_V\,)\), where \( {Ad}_F\,\in \, {SO}(\,V,\,-g_V\,)\,=\, {SO}(\,V,\,+g_V\,)\) denotes the restriction of the conjugation by F to the subspace \(V\,\subseteq \, {Cl}(\,V,\,-g_V\,)\). The full automorphism group of \({ {A}}\), however, is much larger due to the presence of the derivations
for the multiplication (28) parametrized by an arbitrary spinor \(\xi \,\in \,\Sigma \). The full automorphism group of the Albert algebra \({ {A}}\) turns out to be generated by \( {Spin}(\,V,\,-g_V\,)\) and the exponentials of the derivations (31), in particular the automorphism group of \({ {A}}\) equals the compact simple Lie group \( {F}_4\,:=\, {Aut}\,{ {A}}\) of dimension 52 [1] with \({ {Z}}_2\)-graded Lie algebra
in the sense that the commutator \([\, _\xi ,\, _{{\hat{\xi }}}\,] \,\in \, {so}(\,V,\,g_V\,)\) of two of the derivations (31) lies in \( {so}(\,V,\,g_V\,)\). The symmetric space corresponding to this \({ {Z}}_2\)-graded Lie algebra is the Cayley projective plane \({ {O}}P^2\), which can be defined for example as the orbit of the element \(\Gamma \,\in \,{ {A}}\) defined in equation (27) under the automorphism group \( {F}_4\) of the Albert algebra \({ {A}}\).
For the purpose of this article, the most important conclusion of the preceding discussion is that the 26-dimensional subspace \(R\,:=\, {Im}\,{ {A}}\,\subseteq \,{ {A}}\) of trace-free albertions represents the unique non-trivial critical irreducible representation of the simple Lie group \( {F}_4\,=\, {Aut}\,{ {A}}\) found in Sect. 3, in fact all other non-trivial irreducible representations of \( {F}_4\) have strictly larger dimensions. In particular, R decomposes under the stabilizer subgroup \( {Spin}(\,V,\,-g_V\,)\,\cong \, {Spin}(\,9\,)\) of the base point \(\Gamma \,\in \, {Im}\,{ {A}}\) of the Cayley plane \({ {O}}P^2\) into
According to decomposition (32), the isotropy representation of the Cayley projective plane \({ {O}}P^2\) equals the spinor representation \(\Sigma \) parametrizing the derivations (31) of the Albert algebra, we may, thus, assume that the Riemannian metric on \({ {O}}P^2\) is induced by \(g_\Sigma \). Second symmetric and exterior powers of spinor representations \(\Sigma ^*\,\cong \, \Sigma \) decompose into exterior powers of the vector representation V, in the case at hand this decomposition reads
According to equations (33) and (34) and the Lemma of Schur both homomorphism spaces
are one-dimensional, in particular the Frobenius reciprocal extension \(F^ {ext}\) of every non-zero
identifies R with the only eigenspace of the Lichnerowicz Laplacian \(\Delta _L\) on the trace-free symmetric 2-tensors on \({ {O}}P^2\) with eigenvalue below \(2\,\frac{ {scal}}{16}\). In light of Corollary 2.3, we need to verify that the prototypical divergence operator \(D^*_R\) associated to R is injective
in order to prove that the Cayley projective plane \({ {O}}P^2\) is stable. A suitable non-zero element \(F\,\in \, {Hom}_{ {Spin}(V,-g_V)}(\,R,\, {Sym}^2_\circ \Sigma ^*\,)\) is provided by the symmetric spinor multiplication \(\diamond \)
where \(\{\,\xi _\mu \,\}\) is some basis of the isotropy representation \(\Sigma \) and \(\{\,d\xi _\mu \,\}\) denotes the dual basis of \(\Sigma ^*\). Using the musical isomorphism \(\sharp :\,\Sigma ^*\longrightarrow \Sigma \) with respect to \(g_\Sigma \), we calculate
and conclude that the composition \( {tr}_g\,\circ \,F\) is effectively a \( {Spin}(\,V,\,-g_V\,)\)-invariant and, thus, vanishing linear functional on the irreducible representation V. In consequence, the linear map \(F:\,R\longrightarrow {Sym}^2_\circ \Sigma ^*\) takes values in the trace-free symmetric 2-forms as claimed and
Before proceeding to calculate \(D^*_RF\), we want to point out the following identity in \(\alpha ,\,\beta \,\in \,\Sigma \)
which is a partial polarization of the identity \((\alpha \diamond \alpha ) \,\bullet \,\alpha \,=\,g_\Sigma (\alpha ,\alpha )\,\alpha \) mentioned above. Specifically, we replace \(\alpha \) in equation (29) by the expression \(\beta +t\alpha \) and take the derivative of the resulting identity in \(t\,=\,0\) using trilinearity and the symmetry of \(\diamond \) and \(g_\Sigma \). Tracing the partially polarized identity over \(\beta \) with a view on equation (36), we conclude
In light of the decomposition (32), the subspace \(\Sigma \,\subseteq \,{ {f}}_4\) of the Lie algebra of \( {F}_4\,=\, {Aut}\,{ {A}}\) acts on the Albert algebra \({ {A}}\) and its invariant subspace \(R\,\subseteq \,{ {A}}\) by the derivations (31), to wit \(\xi \,\star \,=\, _\xi \) for all \(\xi \,\in \,\Sigma \). In consequence the general description (14) of the prototypical divergence operator associated to the finite dimensional representation R becomes
where we have used \(g_V(\,A,\,\xi _\mu \diamond \xi _\nu \,)\,=\,g_\Sigma (\,A\bullet \xi _\mu ,\,\xi _\nu \,)\) and the trace (37) in the last line. In particular the prototypical divergence operator (35) is injective and the Cayley projective plane \({ {O}}P^2\) is stable in the sense of Koiso as stipulated in Theorem 1.1.
5 Einstein Deformations of the Grassmannians
In analogy to our discussion of the stability of the Cayley projective plane \({ {O}}P^2\) in Sect. 4, we analyze the stability of the family of quaternionic Grassmannians \( {Gr}_r{ {H}}^{r+s}\) of r-dimensional quaternionic subspaces in \({ {H}}^{r+s}\) in this section for all parameters \(r,\,s\, \,1\). Needless to say this family includes the quaternionic projective spaces \({ {H}}P^s\,=\, {Gr}_1{ {H}}^{s+1}\) and \(S^4\,=\,{ {H}}P^1\), whose stability had been settled by Koiso except for the case \(s\,=\,2\). Calculating the prototypical divergence operator, we will show that the quaternionic Grassmannians \( {Gr}_r{ {H}}^{r+s}\) are stable, if and only if they are quaternionic projective spaces in the sense \(r\,=\,1\) or \(s\,=\,1\).
For the time being, we interpret the unitary symplectic groups \( {Sp}(n)\) as the groups of unitary \(n\times n\)-matrices with coefficients in the quaternions \({ {H}}\), which act naturally on the spaces \({ {H}}^n\) of column vectors considered as right vector spaces over \({ {H}}\,=\, {Mat}_{1\times 1}{ {H}}\) by right matrix multiplication. For all \(r,\,s\, \,1\) the induced action of \( {Sp}(r+s)\) on the Grassmannian
of r-dimensional subspaces of \({ {H}}^{r+s}\) is transitive as well with stabilizer in the base point \({ {H}}^r\,\subseteq \,{ {H}}^{r+s}\) given by the diagonal subgroup \( {Sp}(r)\,\times \, {Sp}(s)\,\subseteq \, {Sp}(r+s)\). Under restriction to the stabilizer of the base point the defining representation \(V\,:=\,{ {H}}^{r+s}\) decomposes into the direct sum \(V\,=\,H\,\oplus \,E\) of the defining representations \(H\,:=\,{ {H}}^r\) and \(E\,:=\,{ {H}}^s\) of \( {Sp}(r)\) and \( {Sp}(s)\). In general, we will consider V as a complex vector space via the obvious inclusion \({ {C}}\,\subseteq \,{ {H}}\) endowed with the \( {Sp}(r+s)\)-equivariant, conjugate linear map \(C:\,V\longrightarrow V\) of right multiplication with j satisfying \(C^2\,=\,- {id}_V\); analogous remarks apply to both H and E. The adjoint representation of the symplectic Lie groups equals the second symmetric power of its defining representation, in turn the decomposition \(V\,=\,H\,\oplus \,E\) implies
so that \(H\otimes E\,\cong \,T_{{ {H}}^r}M\,\otimes _{ {R}}{ {C}}\) equals the complexified isotropy representation of the irreducible symmetric space \(M\,:=\, {Gr}_r{ {H}}^{r+s}\). Its trace-free second symmetric power decomposes into
En nuce the all important difference between the projective spaces with \(\min \{\,r,\,s\,\}\,=\,1\) and the general Grassmannians with \(r,\,s\, \,2\) derives from this decomposition, after all \(\Lambda ^2_\circ H\,=\,\{\,0\,\}\) or \(\Lambda ^2_\circ E\,=\,\{\,0\,\}\) vanish for \(r\,=\,1\) or \(s\,=\,1\), respectively.
According to the classification of critical representations of the symplectic Lie algebras \( {sp}(2n,{ {C}})\,=\, {sp}(n)\otimes _{ {R}}{ {C}}\) in Sect. 3 the only critical irreducible representations of \( {sp}(r+s)\) besides the trivial and adjoint representations are V, \(\Lambda ^2_\circ V\) together with \(\Lambda ^3_\circ V\) for \(r+s\,=\,3\). In light of the decomposition (38) the Frobenius reciprocity (7) ensures that neither V nor \(\Lambda ^3_\circ V\) occurs in the trace-free symmetric 2-tensors \(\Gamma (\, {Sym}^2_\circ T^*M\,)\), and so we are left with
as the only candidate, where \(R\,\subseteq \,\Lambda ^2_\circ V\) equals the subspace of real elements with respect to the equivariant real structure. Using Schur’s Lemma, we conclude from (38) and (39) that

have dimension 2 and 1, respectively, unless M is a quaternionic projective space. In consequence the prototypical divergence operator associated to the critical representation \(\Lambda ^2_\circ V\)
cannot be injective in general, because its domain has dimension 2 and is range dimension 1. According to Corollary 2.3 the Einstein metrics on the quaternionic Grassmannians \( {Gr}_r{ {H}}^{r+s}\) with parameters \(r,\,s\, \,2\) are, thus, unstable in the sense of Koiso.
In order to study the prototypical divergence operator \(D^*_{\Lambda ^2_\circ V}\) in somewhat more detail, we recall that H and E come along with complex bilinear, invariant symplectic forms \(\sigma _H\) and \(\sigma _E\), respectively, which give rise to the musical isomorphisms \(\flat :\,H\longrightarrow H^*,\, h\longmapsto \sigma _H(\,h,\,\cdot \,)\) and \(\sharp \,:=\,\flat ^{-1}\) as well as the analogous musical isomorphisms \(\flat \) and \(\sharp \) for E. Choosing pairs of dual bases \(\{\,h_\alpha \,\}\), \(\{\,dh_\alpha \,\}\) and \(\{\,e_\mu \,\}\), \(\{\,de_\mu \,\}\) for H and E, we define the two linear maps
from \(\Lambda ^2H\) and \(\Lambda ^2E\), respectively, to \( {Sym}^2(H\otimes E)^*\). Both maps are evidently equivariant under \( {Sp}(r)\,\times \, {Sp}(s)\) and send the bivectors \(\sum _\alpha dh^\sharp _\alpha \wedge h_\alpha \) and \(\sum _\mu de^\sharp _\mu \wedge e_\mu \) to zero. In essence, they, thus, factorize through linear maps \(\Lambda ^2_\circ H\longrightarrow {Sym}^2_\circ (H\otimes E)^*\) and \(\Lambda ^2_\circ E\longrightarrow {Sym}^2_\circ (H\otimes E)^*\), which we may precompose with the corresponding projections in (39) to linear maps
which generate the domain \( {Hom}_{ {Sp}(r)\times {Sp}(s)}(\,\Lambda ^2_\circ F, \, {Sym}^2_\circ (H\otimes E)^*\,)\) of \(D^*_{\Lambda ^2_\circ V}\) due to the decomposition (38). Needless to say the special case \(\min \{\,r,\,s\,\}\,=\,1\) of quaternionic projective spaces is reflected by \(F^H\,=\,0\) or \(F^E\,=\,0\) for \(r\,=\,1\) or \(s\,=\,1\). Without loss of generality, we may assume that the symplectic forms \(\sigma _H\) and \(\sigma _E\) are normalized to make their tensor product agree with the Riemannian metric \(g\,=\,\sigma _H\otimes \sigma _E\) in the base point \({ {H}}^r\,\in \,M\) so that
holds true for every orthonormal basis \(\{\,E_\lambda \,\}\) of \(T_{{ {H}}^r}M\,\otimes _{ {R}}{ {C}}\,\cong \,H\otimes E\). Replacing the sum over the orthonormal basis \(\{\,E_\lambda \,\}\) in formula (14) by the sum on the right-hand side of this identity, we calculate in a first step
due to the antisymmetry \(\sum dh^\sharp _\alpha \otimes h_\alpha \,=\,-\sum h_\alpha \otimes dh^\sharp _\alpha \) and the definition of the representation \(\star _{\Lambda ^2_\circ V}\) of the Lie algebra \( {sp}(r+s)\otimes _{ {R}}{ {C}}\,=\, {Sym}^2V\). Using this intermediate result, we conclude
The completely analogous calculation for the linear map \(F^E\) results in
where the sign change is effectively caused by the reversed order of the product \(e_\mu \wedge f\) compared to \(a\wedge h_\alpha \) in the formula for \((\,h_\alpha \otimes e_\mu \,)\,\star _{\Lambda ^2_\circ V}\,(\,a\wedge f\,)\). In consequence the prototypical divergence operator (40) always has maximal rank for all \(r,\,s\, \,1\), in particular \(D^*_{\Lambda ^2_\circ V}\) is injective for \(r\,=\,1\) or \(s\,=\,1\) proving the stability of the Einstein metric on all quaternionic projective spaces including \(S^4\,=\,{ {H}}P^1\) and \({ {H}}P^2\) in the sense of Koiso.
References
Baez, J.: The octonions. Bull. Am. Math. Soc. (N. S.) 39(2), 145–205 (2002)
Besse, A.: Einstein Manifolds. Ergebnisse der Mathematik und ihrer Grenzgebiete 3rd Series, vol. 10. Springer, Berlin (1987)
Cao, H.-D., He, C.: Linear stability of Perelman’s \(\nu \)-entropy on symmetric spaces of compact type. J. Reine Angew. Math. 709, 229–246 (2015)
Dai, X., Wang, X., Wei, G.: On the stability of Riemannian manifold with parallel spinors. Invent. Math. 161(1), 151–176 (2005)
Fulton, W., Harris, J.: Representation Theory: A First Course. Graduate Texts in Mathematics, vol. 129. Springer, New York (1991)
Gallot, S.: Équations différentielles caractéristiques de la sphére. Ann. Sci. École Norm. Sup. (4) 12(2), 235–267 (1979)
Gasqui, J., Goldschmidt, H.: Radon transforms and spectral rigidity on the complex quadrics and the real Grassmannians of rank two. J. Reine Angew. Math. 480, 1–69 (1996)
Harvey, F.R.: Spinors and Calibrations. Perspectives in Mathematics, vol. 9. Academic Press Inc., Boston (1990)
Heil, H., Moroianu, A., Semmelmann, U.: Killing and conformal Killing tensors. J. Geom. Phys. 106, 383–400 (2016)
Koiso, N.: Rigidity and stability of Einstein metrics—the case of compact symmetric spaces. Osaka J. Math. 17(1), 51–73 (1980)
Kröncke, K.: On the stability of Einstein manifolds. Ann. Glob. Anal. Geom. 47(1), 81–98 (2015)
Lawson, H.B., Michelsohn, M.L.: Spin Geometry. Princeton University Press, New Jersey (1989)
Lichnerowicz, A.: Géométrie des groupes de transformations. Travaux et Recherches Mathematiques, vol. III. Dunod, Paris (1958)
Obata, M.: Conformal Changes of Riemannian Metrics on a Euclidean Sphere, Differential Geometry (in honor of Kentaro Yano), pp. 347–353. Kinokuniya, Tokyo (1972)
Schwahn, P.: Stability of Einstein metrics on irreducible symmetric spaces of compact type, preprint, (2020)
Semmelmann, U., Weingart, G.: The standard Laplace operator. Manuscr. Math. 158(1–2), 273–293 (2019)
Semmelmann, U., Wang, C., Wang, M.: On the linear stability of nearly Kähler 6-manifolds. Ann. Glob. Anal. Geom. 57(1), 15–22 (2020)
Wang, C.: Stability of Riemannian manifolds with Killing spinors. Int. J. Math. 28(1), 1750005 (2017)
Acknowledgements
The first author acknowledges the support received by the Special Priority Program SPP 2026 Geometry at Infinity funded by the Deutsche Forschungsgemeinschaft DFG. Likewise the second author expresses his gratitude for the funding received as a SNI member from the Consejo Nacional de Ciencia y Tecnología CONACyT.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Semmelmann, U., Weingart, G. Stability of Compact Symmetric Spaces. J Geom Anal 32, 137 (2022). https://doi.org/10.1007/s12220-021-00838-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-021-00838-3