Stitching Data: Recovering a Manifold’s Geometry from Geodesic Intersections

Abstract

Let (M, g) be a Riemannian manifold with boundary. We show that knowledge of the length of each geodesic, and where pairwise intersections occur along the corresponding geodesics allows for recovery of the geometry of (M, g) (assuming (M, g) admits a Riemannian collar of a uniform radius). We call this knowledge the ‘stitching data’. We then pose a boundary measurement problem called the ‘delayed collision data problem’ and apply our result about the stitching data to recover the geometry from the collision data (with some reasonable geometric restrictions on the manifold).

1 Introduction

Let (M, g) be a Riemannian manifold with boundary. Imagine each geodesic of M is a string of a length determined by the metric. Now, suppose that for each pair of intersecting geodesics, you know where they intersect and how intersection points on the first geodesic correspond to intersection points on the second. With this information, one could imagine gluing all of the strings together in the right places to reconstruct the manifold. The image that comes to mind is that of stitching a collection of threads together to form a piece of fabric. Thus, we will call the information described above the ‘stitching data’. With reasonable geometric constraints, we will show that knowledge of the stitching data does indeed allow us to recover the geometry of the manifold it came from. In particular, we note that this result allows for non-compact manifolds, unbounded manifolds and manifolds with empty boundary.

Additionally, when every geodesic intersects the boundary, we can think of the stitching data as a type of boundary data, and we can place this in the broader setting of boundary rigidity problems. We describe a geometric data set called the delayed collision data which encodes when two particles fired from different points on the boundary at different times will first collide (if they collide at all). We show that the delayed collision data determines the stitching data, and hence the geometry of the manifold (again, with reasonable geometric assumptions). As with the stitching data, this result applies to potentially non-compact and unbounded manifolds. However, the boundary must not be empty, of course.

2 The Stitching Data

Let (M, g) be a Riemannian manifold with boundary. Let $X_g$ be the geodesic vector field on TM. Then for each vector $v\in TM$, there is an integral curve $\hat{\gamma }_v :I_v\rightarrow TM$, where $\hat{\gamma }_v(0)=v$, and $I_v$ is the maximal domain.

In general, $I_v$ could be any type of interval (closed, open, infinite, half-open, etc.). Additionally, $I_v$ could be the singleton set $\{0\}$. We let $\gamma _v:I_v\rightarrow M$ be the projection of $\hat{\gamma }_v$ onto the base space M. (i.e. $\gamma _v=\pi \circ \hat{\gamma }_v$ where $\pi :TM\rightarrow M$ is the usual surjection).

Let $SM\subset TM$ denote the unit sphere bundle. For $v,w\in SM$, write $v\sim _{SM} w$ if there exists $t\in I_v$ such that $w=\hat{\gamma }_v(t)$ or $w=-\hat{\gamma }_v(t)$. Then it is easy to verify that $\sim _{SM}$ is an equivalence relation on SM. Thus, $\sim _{SM}$ partitions SM into equivalence classes. Let $[v]\subset SM$ denote the equivalence class containing v. We let $\mathcal {G}= SM/\sim _{SM}$. $\mathcal {G}$ represents the space of geodesics.

We are now able to formally define the geodesic data described in the introduction:

Definition 2.1

Let (M, g) be a Riemannian manifold with boundary. Let $(\mathscr {G}, m_\bullet ,\mathscr {C}_{\bullet ,\bullet })$ be a triple where $\mathscr {G}$ is a set, $m_\alpha$ is an interval for each $\alpha \in \mathscr {G}$, and $\mathscr {C}_{\alpha ,\beta }:m_\alpha \rightarrow 2^{m_\beta }$ is a set-valued ifunction for each $\alpha ,\beta \in \mathscr {G}$. We say $(\mathscr {G},m,\mathscr {C})$ is a stitching data for (M, g) if there exists a function $f:\mathscr {G}\rightarrow SM$ satisfying

• 1. $\alpha \mapsto [f(\alpha )]$ is surjective from $\mathscr {G}$ to $\mathcal {G}$.

• 2. For each $\alpha \in \mathscr {G}$, $m_\alpha =I_{f(\alpha )}$.

• 3. For $\alpha ,\beta \in \mathscr {G}$, then $t\in \mathscr {C}_{\alpha ,\beta }(s)$ if and only if $\gamma _{f(\alpha )}(s)=\gamma _{f(\beta )}(t)$.

In such a case, we call $\mathscr {G}$ the geodesic index set, we call $m_\bullet$ the interval function, and $\mathscr {C}_{\bullet ,\bullet }$ the crossover map.

Let (M, g) be a Riemannian manifold with boundary, and $(\mathscr {G},m,\mathscr {C})$ be a stitching data for (M, g). Intuitively, each element of $\mathscr {G}$ corresponds to a geodesic of (M, g). Since the function f in the above definition must be surjective, multiple elements of $\mathscr {G}$ may correspond to the same geodesic. For $\alpha \in \mathscr {G}$, the interval $m_\alpha$ tells us how the geodesic may be parameterized. Finally, for two elements $\alpha ,\beta \in \mathscr {G}$, the crossover map $\mathscr {C}_{\alpha ,\beta }$ tells us which points in the images of the two corresponding geodesics coincide.

Definition 2.2

Let $(M_i,g_i)$ be Riemannian manifolds with boundary for $i=1,2$. For each $i=1,2$, let $(\mathscr {G}^i,m^i,\mathscr {C}^i)$ be a stitching data for $(M^i,g^i)$. If there exists a bijection $\Psi :\mathscr {G}^1\rightarrow \mathscr {G}^2$ such that

• 1. $m^2_{\Psi (\alpha )}=m^1_\alpha$ for all $\alpha \in \mathscr {G}^1$.

• 2. $\mathscr {C}_{\Psi (\alpha ),\Psi (\beta )}(t)=\mathscr {C}_{\alpha ,\beta }(t)$ for all $\alpha ,\beta \in \mathscr {G}^1$ and $t\in m^1(\alpha )=m^2_{\Psi (\alpha )}$.

then we say that $\Psi$ conjugates the two stitching data, and we say that the stitching data are equivalent.

We note here that equivalent stitching data are essentially just relabelings of each other.

We recall that, for each $x\in M$, there is an exponential function, $\exp _x$, defined on a subset of $T_xM$ taking values in M. We call this subset $\text {dom}(\exp _x)\subset T_xM$ and define it as follows: for $v\in T_xM$, we write $v\in \text {dom}(\exp _x)$ if $[0,1]\subset I_v$. This lets us define $\exp _x:\text {dom}(\exp _x)\rightarrow M$ by $\exp _x(v)=\gamma _v(1)$.

When x is in the interior of M (i.e. $x\in M\setminus \partial M$) the exponential map is a local diffeomorphism. Specifically there exists $\varepsilon >0$ such that $B_\varepsilon (0)\subset \text {dom}(\exp _x)$ and $\exp _x:B_\varepsilon (0)\rightarrow M$ is a diffeomorphism onto its image (where $B_\varepsilon (0)=\{v\in T_xM| |v|_g\le \varepsilon \}$). We let $\text {inj}_x$ be the supremum over all such $\varepsilon$. Note that $\text {inj}_x$ may be infinite.

For a full review of the exponential map, we refer readers to [1].

The following definition is adapted from [2].

Definition 2.3

Let (M, g) be a Riemannian manifold with boundary. For $x\in \partial M$, let $\nu _x$ be the inward pointing unit normal vector at x. Let $r_C>0$. If the map $K:(x,t)\mapsto \exp _x(t\nu _x)$ from $\partial M\times [0,r_C)\rightarrow M$ is defined and is a diffeomorphism onto its image, we say that $r_C$ is a collar radius for (M, g). If there exists a collar radius for (M, g), we say that (M, g) is collarable.

We also include manifolds with empty boundary to be collarable. If $r_C$ is a collar radius for (M, g), we let $N(r_C)$ denote the image $K(M\times [0,r_C))$. We call the coordinates $(x,t)\mapsto K(x,t)$ boundary normal coordinates for $N(r_C)$.

We are now able to state our main result, which is that the geometry of a manifold is determined by a stitching data.

Theorem 2.4

Let $(M^i,g^i)$ be collarable Riemannian manifolds with (possibly empty) boundary for $i=1,2$. For $i=1,2$, let $(\mathscr {G}^i,m^i,\mathscr {C}^i)$ be a stitching data for $(M^i,g^i)$. If the two stitching data are equivalent, then there exists an isometry $\varphi :M^1\rightarrow M^2$.

We restate Theorem 2.4 as follows.

Theorem 2.5

Let (M, g) be a collarable Riemannian manifold with (possibly empty) boundary. Then a stitching data for (M, g) determines the isometry class of (M, g).

When (M, g) is a compact manifold with boundary, there are always boundary normal coordinates. Thus, we obtain the following corollary.

Corollary 2.6

Let (M, g) be a compact Riemannian manifold with boundary. Then a stitching data for (M, g) determines its isometry class.

We pause here to discuss possible proofs of Theorem 2.4. First, one could argue directly according to the definitions. To do this, we would take two Riemannian manifolds with boundary with equivalent stitching data and use the conjugating bijection to show that there is an isometry between the two manifolds.

Alternatively, if we wish to work with a single manifold rather than two equivalent manifolds, we have the following proof strategy: use the stitching data to construct a metric space $(X,d_X)$ which is isometric to $(M,d_g)$. By “construct”, we mean to write the set X and the distance function $d_X$ directly in terms of the objects in the triple that make up the stitching data. This yields a proof of Theorem 2.4 in the following way. Suppose we have two manifolds $(M^i,g^i)$ with equivalent stitching data. One can construct metric spaces $(X^i,d_{X^i})$ out of each stitching data. Since the two stitching data are just relabelings of eachother, it follows that the two metric spaces will be isometric. Thus $(M^1,d_{g^1})$ is isometric to $(X^1,d_{X^1})$, which is isometric to $(X^2,d_{X^2})$, which is isometric to $(M^2,d_{g^2})$. By composing the isometries, we find that $(M^1,d_{g^1})$ is isometric to $(M^2, d_{g^2})$.

3 Proof of Main Result

We prove Theorem 2.4 in two parts. In the first part, we put a length structure on M where admissable curves are piecewise geodesic. We show that the distance function induced by this length structure is equal to $d_g$. For an overview of length spaces and length structures, we refer readers to [3].

In the second part, we use the stitching data to construct a length space X. We then show that the constructed length space is isomorphic to the piecewise geodesic length space from the first part. If $d_X$ is the distance function on X induced by the constructed length space, it follows that $(X,d_X)$ is isometric to $(M,d_g)$. In addition, since the induced metric can be constructed in terms of the length structure, and the length structure can be constructed in terms of the stitching data, we conclude that the metric space $(X,d_X)$ can be constructed in terms of the stitching data.

3.1 The Piecewise Geodesic Length Structure

Let $(M,L_g,\mathcal {A})$ be the standard length structure for (M, g). In particular, a continuous curve $\eta :[a,b]\rightarrow M$ is in $\mathcal {A}$ if and only if $\eta$ is piecewise smooth. Additionally, its length is defined by $L_g(\eta )=\int _a^b|\dot{\eta }(t)|_g\mathrm{{d}}t$.

For $x,y\in M$, we denote the set of piecewise smooth curves which begin at x and end at y by $\mathcal {A}_{x,y}$. The length structure induces a distance function

$$\begin{aligned} d_g(x,y)=\inf \limits _{\eta \in \mathcal {A}_{x,y}}L_g(\eta ) \end{aligned}$$

which is the standard Riemannian distance.

Definition 3.1

Let (M, g) be a Riemannian manifold with boundary. We say a continuous curve $\eta :[a,b]\rightarrow M$ is piecewise geodesic if there exists a partition $\{x_1,\ldots ,x_n\}$ of [a, b], vectors $\{v_1,\ldots ,v_{n-1}\}\subset SM$, and smooth functions $\{s_1,\ldots ,s_{n-1}\}$ such that

• 1. $v_k\in T_{\eta (x_k)}M$.

• 2. $s_k:[x_k,x_{k+1}]\rightarrow I_{v_k}$

• 3. $\eta \big |_{[x_k,x_{k+1}]}(t)=\gamma _{v_k}(s_k(t))$ for all $t\in [a,b]$.

For such a curve, we write $\eta \in \mathcal {A}^{p.g.}$.

We call the length structure $(M,L_g,\mathcal {A}^{p.g.})$ the piecewise geodesic length structure. This length structure induces the piecewise geodesic distance

$$\begin{aligned} d_{p.g.}(x,y)=\inf \limits _{\eta \in \mathcal {A}^{p.g.}_{x,y}}L_g(\eta ) \end{aligned}$$

The goal of this section is to prove the following

Theorem 3.2

Let (M, g) be a collarable Riemannian manifold with (possibly empty) boundary. Then $d_g=d_{p.g.}$.

Since $\mathcal {A}^{p.g.}\subset \mathcal {A}$ and the distance functions are defined by taking the infimum over the corresponding sets of admissable curves, we easily obtain $d_g\le d_{p.g.}$. Thus, we wish to show the opposite inequality. Specifically, we claim that $d_{p.g.}\le d_g$. We will need a handful of lemmas to prove Theorem 3.2.

First, we show that piecewise smooth curves are Lipschitz with respect to the distance function $d_g$.

Lemma 3.3

Let $\eta \in \mathcal {A}$. Then $\eta$ is Lipschitz.

Proof

Let $\eta :[a,b]\rightarrow M$ be in $\mathcal {A}$. We must show that there exists $N>0$ such that $d_g(\eta (s),\eta (t))\le N|s-t|$ for all $s,t\in [a,b]$.

Let $\{x_1,\ldots ,x_n\}$ be a partition of [a, b] such that $\eta \big |_{[x_k,x_{k+1}]}$ is smooth. Let $\eta _k=\eta \big |_{[x_k,x_{k+1}]}$. Then $|\dot{\eta }_k|$ is continuous for each k. Thus, by the extreme value theorem, there exists $N_k>0$ such that $|\dot{\eta }_k|\le N_k$ on $[x_k,x_{k+1}]$. Let $N=\max \{N_1,\ldots ,N_{n-1}\}$. Then

$$\begin{aligned} d_g(\eta (s),\eta (t))&\le L_g(\eta \big |_{[s,t]})\\&\le \int _s^t|\dot{\eta }(r)|_g\mathrm{{d}}r\\&\le \int _s^t N\mathrm{{d}}r\\&\le N|s-t| \end{aligned}$$

as required. $\square$

Next, we show that if a piecewise smooth curve is contained in the interior of M, then there is a piecewise geodesic curve with the same endpoints whose length is no greater than the original curve.

Lemma 3.4

Let (M, g) be a Riemannian manifold with boundary. Let $x,y\in M\setminus \partial M$ and $\eta :[a,b]\rightarrow M\setminus \partial M$ be in $\mathcal {A}_{x,y}$. Then there exists $\tilde{\eta }\in \mathcal {A}^{p.g.}_{x,y}$ such that $L_g(\tilde{\eta })\le L_g(\eta )$.

Proof

Let $(M,g),x,y,\eta$ be as stated. Our strategy will be to find a partition $\{t_k\}_{k=1}^n$ of [a, b] such that there is a minimizing geodesic between $\eta (t_k)$ and $\eta (t_{k+1})$. Then we will form $\tilde{\eta }$ by concatenating the minimizing geodesic segments.

From [4] Proposition 10.18, the injectivity radius on a manifold without boundary is continuous. It follows from this that the injectivity radius is continuous on $M\setminus \partial M$. Thus, by the extreme value theorem the function $\text {inj}_{\eta (t)}$ achieves a positive minimum on [a, b]. Let $0<r<\inf \limits _{t\in [a,b]}\text {inj}_{\eta (t)}$. This implies that there is a unique unit speed, minimizing geodesic from $\eta (t)$ to $\eta (s)$ whenever $d_g(\eta (t),\eta (s))\le r$.

By Lemma 3.3, there exists $N>0$ such that $d_g(\eta (s),\eta (t))\le N|s-t|$. In particular, if $|s-t|<\frac{r}{N}$, then there is a minimizing geodesic segment from $\eta (s)$ to $\eta (t)$ [1].

Thus, let $\{t_1,\ldots ,t_n\}$ be a partition of [a, b] such that $|t_k-t_{k+1}|<\frac{r}{N}$ for $k=1,\ldots ,n-1$. For each such k, let $\eta _k:[0,d_g(\eta (t_k),\eta (t_{k+1})]\rightarrow M$ be the minimizing geodesic segment connecting $\eta (t_k)$ to $\eta (t_{k+1})$. We form $\tilde{\eta }$ by concatenating all of the $\eta _k$.

It is clear that $\tilde{\eta }\in \mathcal {A}^{p.g.}_{x,y}$ by construction. Additionally, since the $\eta _k$ are minimizing, $L_g(\eta _k)\le L_g(\eta \big |_{[t_k,t_{k+1}]})$ for all $k=1,2,\ldots ,n-1$. Thus, $L_g(\tilde{\eta })\le L_g(\eta )$ as required. $\square$

In the following lemma, we construct a family of smooth maps field to push curves away from the boundary.

Lemma 3.5

Let (M, g) be a collarable Riemannian manifold with boundary. Then, there exists a smooth one parameter family of maps $\varphi _\bullet :[0,\infty )\times M\rightarrow M$ (i.e. for $t\in [0,\infty )$ we have $\varphi _t:M\rightarrow M$) such that

• 1. $\varphi _0$ is the identity.

• 2. For all $t>0$, $\varphi _t(x)\in M\setminus \partial M$.

• 3. For all $x\in M$, and all $s>0$, the curve $t\mapsto \varphi _t(x)$ from $[0,s]\rightarrow M$ is either stationary or a parameterization of a geodesic segment whose length is less than or equal to s.

Proof

Let $r_C>0$ be a collar radius for (M, g). Let $X_\nu$ be the vector field on $N(r_C)$ which is given by $\partial _t$ in the boundary normal coordinates $(x,t)\mapsto \exp _x(t\nu _x)$. Let $\chi :[0,r_C)\rightarrow [0,1]$ be a non-negative smooth function which is identically one on $[0,\frac{r_C}{3}]$, non-zero on $[0, 2\frac{r_C}{3})$, and identically zero on $[\frac{2r_C}{3},r_C)$. Let $V(x,t)=\chi (t)X_\nu (x,t)$. Then V extends to a smooth vector field which is identically zero on $M\setminus N(\frac{2r_C}{3})$. Let $\varphi _t$ be the flow generated by V. We claim that $\varphi _\bullet$ has the desired properties.

The fact that $\varphi _0$ is the identity is a property of all flows generated by vector fields, so $\varphi _\bullet$ has property 1.

Now, we prove that $\varphi _\bullet$ has property 2. Let $x\in M$. Then either $x\in N(\frac{2r_C}{3})$ or $x\notin N(\frac{2r_C}{3})$. If $x\notin N(\frac{2r_C}{3})$, then $V(x)=0$ by construction, so the integral curve is stationary. Thus, $\varphi _t(x)=x\in M\setminus N(\frac{2r_C}{3})\subset M\setminus \partial M$.

If $x\in N(\frac{2r_C}{3})$, then let $x=(x',s)$ in boundary normal coordinates. Let f solve the initial value problem ${\left\{ \begin{array}{ll} f'=\chi \\ f(0)=s\end{array}\right. }$. In particular, $\chi >0$ on $N(\frac{2r_C}{3})$ so f is increasing. Additionally, by construction $\varphi _t(x)=(x',f(t))$, so for $t>0$ we have $f(t)>0$ and $(x',f(t))\notin \partial M$. This proves that $\varphi _\bullet$ has property 2.

Finally, we show that $\varphi _\bullet$ has property 3. Let $x\in M$. Again, there are two possibilities. Either $x\in N(\frac{2r_C}{3})$ or $x\notin N(\frac{2r_C}{3})$. As before, if $x\notin N(\frac{2r_C}{3})$, then $\varphi _\bullet (x)$ is stationary.

If $x\in N(\frac{2r_C}{3})$, then we have that $\varphi _t(x)=(x',f(t))$ in boundary normal coordinates as before. This is a reparameterization of the unit speed geodesic $t\mapsto (x',t)$. It follows from properties of boundary normal coordinates that $|\frac{d}{dt}\varphi _t(x)|_g=|f'(t)|$. Since $f'(t)=\chi (t)\le 1$, we have that the length of $\varphi _t(x)\big |_{[0,s]}$ is at most s as required. $\square$

Next, we show that we can push a curve away from the boundary in a controlled way.

Lemma 3.6

Let (M, g) be a collarable Riemannian manifold with boundary. Let $x,y\in M$, $\eta \in \mathcal {A}_{x,y}$, and $\varepsilon >0$. Then there exists $x',y'\in M\setminus \partial M$ and $\tilde{\eta }\in \mathcal {A}_{x',y'}$ such that

• 1. $d_{p.g.}(x,x')+d_{p.g.}(y',y)\le \varepsilon$

• 2. The image of $\tilde{\eta }$ is contained in $M\setminus \partial M$.

• 3. $L_g(\tilde{\eta })\le L_g(\eta )+\varepsilon$

Proof

We use the flow constructed above to prove Lemma 3.6. Let $x,y,\eta ,\varepsilon$ be as stated. Let $0<r_C<\varepsilon$ be a collar radius for (M, g) and let $\varphi _\bullet$ be the flow constructed in Lemma 3.5.

For $\delta \ge 0$, let $\eta _\delta (t)=\varphi _\delta (\eta (t))$. Then $\eta _\delta \in \mathcal {A}_{\varphi _\delta (x),\varphi _\delta (y)}$. Since $\varphi _\bullet$ is smooth, we have that $\delta \mapsto L_g(\eta _\delta )$ is continuous and equal to $L_g(\eta )$ when $\delta = 0$. Thus, there exist $\delta '>0$ such that if $\delta <\delta '$, then $L_g(\eta _\delta )\le L_g(\eta )+\varepsilon$.

Additionally, from the property 3 of $\varphi _\bullet$, we have that $\varphi _\bullet (x)\big |_{[0,\delta ]}$ and $\varphi _\bullet (y)\big |_{[0,\delta ]}$ are piecewise geodesic, and $L_g(\varphi _\bullet (x)\big |_{[0,\delta ]}),L_g(\varphi _\bullet (y)\big |_{[0,\delta ]})\le \delta$. Thus, $d_{p.g.}(x,\varphi _\delta (x))+d_{p.g.}(y,\varphi _\delta (y))\le 2\delta$. Choose $\delta <\min \{\varepsilon /2,\delta '\}$. Let $x'=\varphi _\delta (x),y'=\varphi _\delta (y)$ and $\tilde{\eta }=\eta _\delta$. Then, $d_{p.g.}(x,x')+d_{p.g.}(y',y)\le \varepsilon$ as required.

Finally, from property 2 of $\varphi _\bullet$, we have that the image of $\tilde{\eta }$ is contained in $M\setminus \partial M$ as required. $\square$

Finally, we use Lemmas 3.4 and 3.6 to prove Theorem 3.2

Proof of Theorem 3.2

Let (M, g) be a collarable Riemannian manifold with boundary. Let $x,y\in M$ and $\eta \in \mathcal {A}_{x,y}$. Let $\varepsilon >0$. Then by Lemma 3.6 there exists $x',y'\in M\setminus \partial M$ and $\eta _1\in \mathcal {A}_{x',y'}$ such that

• 1. $d_{p.g.}(x,x')+d_{p.g.}(y',y)\le \frac{\varepsilon }{3}$

• 2. The image of $\eta _1$ is contained in $M\setminus \partial M$.

• 3. $L_g(\eta _1)\le L_g(\eta )+\frac{\varepsilon }{3}$.

From Lemma 3.4, there exists $\eta _2\in \mathcal {A}^{p.g.}_{x',y'}$ such that $L_g(\eta _2)\le L_g(\eta _1)$.

From the definition of $d_{p.g.}$, there exists $\eta _3\in \mathcal {A}^{p.g.}_{x,x'}$ and $\eta _4\in \mathcal {A}^{p.g.}_{y',y}$ such that $L_g(\eta _3)\le d_{p.g.}(x,x')+\frac{\varepsilon }{6}$ and $L_g(\eta _4)\le d_{p.g.}(y',y)+\frac{\varepsilon }{6}$. Combining this with (1.) above, we obtain $L_g(\eta _3)+L_g(\eta _4)\le 2\frac{\varepsilon }{3}$.

Thus, let $\tilde{\eta }\in \mathcal {A}^{p.g.}_{x,y}$ be obtained by concatenating $\eta _3$, $\eta _2$ and $\eta _4$. Then we have that

$$\begin{aligned} L_g(\tilde{\eta })&=L_g(\eta _3)+L_g(\eta _2)+L_g(\eta _4)\\&\le 2\frac{\varepsilon }{3} + L_g(\eta _2)\\&\le 2\frac{\varepsilon }{3} + L_g(\eta )+\frac{\varepsilon }{3}\\&\le L_g(\eta )+\varepsilon \end{aligned}$$

Thus, we have shown that for all $\varepsilon >0$, there exist $\tilde{\eta }\in \mathcal {A}^{p.g.}_{x,y}$ such that $L_g(\tilde{\eta })\le L_g(\eta )+\varepsilon$. From this, it follows that $d_{p.g.}(x,y)\le d_g(x,y)$.

Combining this with the trivial inequality that $d_g(x,y)\le d_{p.g.}(x,y)$, we get the desired equality $d_g(x,y)=d_{p.g.}(x,y)$. $\square$

3.2 Constructing an Isomorphic Length Space

In the previous section, we showed that $d_{p.g.}=d_g$ if (M, g) is collarable. In this section, we show that knowledge of the stitching data allows us to form a length space that is isomorphic to $(M,L_g,\mathcal {A}^{p.g.})$. From this it follows that knowledge of the length space allows us to construct a metric space which is isometric to $(M,d_g)$.

As before, let (M, g) be a Riemannian manifold with boundary, and let $(\mathscr {G},m,\mathscr {C})$ be a stitching data for M. We form the stitching space by taking the disjoint union $\mathcal {S}=\sqcup _{\alpha \in \mathscr {G}} m_\alpha$. For points in $\mathcal {S}$, we use subscripts to make it explicit which $m_\alpha$ they come from. For instance, we would write $a_\alpha \in m_\alpha \subset \mathcal {S}$.

In the following, we construct a length space $(X,L_X,\mathcal {A}^X)$. It is important to note that we do this without reference to M; all of the information required to carry out the construction is contained in the stitching data.

Construction 3.7

Write $a_\alpha \sim _\mathcal {S}b_\beta$ if $\mathscr {C}_{\alpha ,\beta }(a_\alpha )\ni b_\beta$ This forms an equivalence relation on $\mathcal {S}$. Let $\langle a_\alpha \rangle \subset \mathcal {S}$ denote the equivalence class containing $a_\alpha$. Let $X=\mathcal {S}/\sim _\mathcal {S}$.

For $\eta :[c,d]\rightarrow X$, write $\eta \in \mathcal {A}^X$ if there exists a partition $\{x_1,\ldots ,x_n\}$ of [c, d], a subset $\{\alpha _1,\ldots ,\alpha _{n-1}\}\subset \mathscr {G}$, and smooth curves $\{\eta _1,\ldots ,\eta _{n-1}\}$ such that

• 1. $\eta _k:[x_k,x_{k+1}]\rightarrow m_{\alpha _k}$, for $k=1,2,\ldots ,n-1$.

• 2. $\eta \big |_{[x_k,x_{k+1}]}(t)=\langle \eta _k(t)\rangle$, for $k=1,2,\ldots ,n-1$

• 3. $\langle \eta _k(x_{k+1})\rangle = \langle \eta _{k+1}(x_{k+1})\rangle$ for $k=1,2,\ldots ,n-2$.

For $\eta \in \mathcal {A}^X$, with $\{\eta _1,\ldots ,\eta _{n-1}\}$ as above, define

$$\begin{aligned} L_X(\eta )=\sum _1^{n-1} L(\eta _k) \end{aligned}$$

where $L(\eta _k)=\int _{x_k}^{x_{k+1}}|\eta _k'(s)|ds$

Lemma 3.8

The relation $\sim _\mathcal {S}$ defined in Construction 3.7 is in fact an equivalence relation.

Proof

We must show that $\sim _\mathcal {S}$ is reflexive, symmetric and transitive. Let $f:\mathscr {G}\rightarrow SM$ satisfy the hypotheses of Definition 2.1.

First, we show that $\sim _\mathcal {S}$ is reflexive. Let $a_\alpha \in m_\alpha \subset \mathcal {S}$. Then $\gamma _{f(\alpha )}(a_\alpha )=\gamma _{f(\alpha )}(m_\alpha )$, so $a_\alpha \in \mathscr {C}_{\alpha ,\alpha }(a_\alpha )$. Thus, $a_\alpha \sim _\mathcal {S}a_\alpha$ as required.

Now, we show that $\sim _\mathcal {S}$ is symmetric. Let $a_\alpha ,b_\beta \in \mathcal {S}$. Suppose $a_\alpha \sim \mathcal {S}b_\beta$. Then, $b_\beta \in \mathscr {C}_{\alpha ,\beta }(a_\alpha )$. Thus, $\gamma _{f(\alpha )}(a_\alpha )=\gamma _{f(\beta )}(b_\beta )$. This implies that $a_\alpha \in \mathscr {C}_{\beta ,\alpha }(b_\beta )$, so $b_\beta \sim _\mathcal {S}a_\alpha$ as required.

Finally, we show that $\sim _\mathcal {S}$ is transitive. Let $a_\alpha ,b_\beta ,c_\zeta \in \mathcal {S}$. Suppose that $a_\alpha \sim _\mathcal {S}b_\beta$ and $b_\beta \sim _\mathcal {S}c_\zeta$. Then it follows that $\gamma _{f(\alpha )}(a_\alpha )=\gamma _{f(\beta )}(b_\beta )=\gamma _{f(\zeta )}(c_\zeta )$. Thus, $c_\zeta \in \mathscr {C}_{\alpha ,\zeta }(a_\alpha )$. This implies that $a_\alpha \sim _\mathcal {S}c_\zeta$ as required. $\square$

Definition 3.9

Let $(Y_i,L_i,\mathcal {A}^i)$ be length spaces for $i=1,2$. We say that the length spaces are isomorphic if there exists a bijection $\varphi :Y_1\rightarrow Y_2$ such that

• 1. The map $\eta \mapsto \eta \circ \varphi$ is a bijection from $\mathcal {A}^1\rightarrow \mathcal {A}^2$

• 2. $L_2(\eta \circ \varphi )=L_1(\eta )$ for all $\eta \in \mathcal {A}^1$.

Clearly the metric spaces generated by isomorphic length spaces are isometric. Thus, we wish to show the following:

Theorem 3.10

The length structure $(X,L_X,\mathcal {A}^X)$ is isomorphic to $(M,L_g,\mathcal {A}^{p.g.})$.

To prove Theorem 3.10 we will need the following two facts, which follow directly from basic properties of the geodesic flow:

Lemma 3.11

Let (M, g) be a Riemannian manifold with boundary. Suppose $v,w\in SM$ and $v\sim _{SM}w$. Then, there exists an isometry $s:I_v\rightarrow I_w$ such that $\hat{\gamma }_v=\hat{\gamma }_w\circ s$, and $\gamma _v=\gamma _w\circ s$.

Lemma 3.12

Let (M, g) be a Riemannian manifold with boundary. Suppose $v\in SM$ and $\eta :[a,b]\rightarrow I_v$ is smooth. Let $\mu :[a,b]\rightarrow M$ be defined by $\mu (t)=\gamma _v(\eta (t))$. Then $|\eta '(t)|=|\dot{\mu }(t)|_g$.

Proof of Theorem 3.10

Let $(\mathscr {G},m,\mathscr {C})$ be the stitching data for (M, g) from which $(X,L_X,\mathcal {A}^X)$ was constructed. Then, there exists $f:\mathscr {G}\rightarrow SM$ satisfying the constraints of Definition 2.1.

Let $\tilde{\varphi }:\mathcal {S}\rightarrow M$ be defined by $\tilde{\varphi }(a_\alpha )=\gamma _{f(\alpha )}(a_\alpha )$. If $\langle a_\alpha \rangle =\langle b_\beta \rangle$, then $\gamma _{f(\alpha )}(a_\alpha )=\gamma _{f(\beta )}(b_\beta )$. Thus, $\tilde{\varphi }(a_\alpha )=\tilde{\varphi }(b_\beta )$, so $\tilde{\varphi }$ is constant on the equivalence classes of $\sim _\mathcal {S}$. This implies that $\tilde{\varphi }$ passes to the quotient space. Specifically, there exists $\varphi :X\rightarrow M$ satisfying $\varphi (\langle a_\alpha \rangle )=\tilde{\varphi }(a_\alpha )$. We claim that $\varphi$ satisfies the constraints of Definition 3.9.

First, we show that $\varphi$ is surjective. Let $y\in M$. We must show that there exists $\langle a_\alpha \rangle \in X$ such that $\varphi (\langle a_\alpha \rangle )= y$. Let $v\in S_yM$. Since $\alpha \mapsto [f(\alpha )]$ is surjective, there exists $\alpha \in \mathscr {G}$ such that $[f(\alpha )]=[v]$. By the definition of $\sim _{SM}$, there exists $a_\alpha \in I_{f(\alpha )}=m_\alpha$ such that $\gamma _{f(\alpha )}(a_\alpha )=y$. Thus, $\tilde{\varphi }(a_\alpha )=y$, so $\varphi (\langle a_\alpha \rangle )=y$ as required.

Next, we show that $\varphi$ is injective. Let $\langle a_\alpha \rangle ,\langle b_\beta \rangle \in X$. Suppose $\varphi (\langle a_\alpha \rangle )=\varphi (\langle b_\beta \rangle )$. We must show that $a_\alpha \sim _\mathcal {S}b_\beta$. The fact that $\varphi (\langle a_\alpha \rangle )=\varphi (\langle b_\beta \rangle )$ implies that $\gamma _{f(\alpha )}(a_\alpha )=\gamma _{f(\beta )}(b_\beta )$. Thus, $b_\beta \in \mathscr {C}_{\alpha ,\beta }(a_\alpha )$, so $a_\alpha \sim _\mathcal {S}b_\beta$ as required. Thus, we have that $\varphi$ is surjective and injective, so it is a bijection.

Let $\Phi :\mathcal {A}^X\rightarrow \mathcal {A}^{p.g.}$ be defined by $\Phi (\eta )=\eta \circ \varphi$. We claim that $\Phi$ is a bijection.

First, we show that $\Phi$ is surjective. Let $\tilde{\eta }:[a,b]\rightarrow M$ be a piecewise geodesic path. We must show that there exists $\eta \in \mathcal {A}^X$ such that $\Phi (\eta )=\tilde{\gamma }$. Since $\tilde{\eta }$ is piecewise geodesic, there exists a partition $\{x_1,\ldots ,x_n\}$ of [a, b] such that $\tilde{\eta }\big |_{[x_k,x_{k+1}]}(t)=\gamma _{v_k}(s_k(t))$ for $v_k\in SM$ and $s_k:[x_k,x_{k+1}]\rightarrow I_{v_k}$ smooth.

There exists $\{\alpha _1,\ldots ,\alpha _{n-1}\}\subset \mathscr {G}$ such that $[f(\alpha _k)]=[v_k]$, since $\alpha \mapsto [f(\alpha )]$ is surjective. Let $\tilde{s}_k:I_{v_k}\rightarrow m_{\alpha _k}$ be the isometry guaranteed in Lemma 3.11. Then, let $\gamma _k:[x_k,x_{k+1}]\rightarrow m_{\alpha _k}$ be defined by $\gamma _k(t)=\langle \tilde{s}_k(s_k(t))\rangle$.

Observe that $\varphi (\eta _k(t))=\gamma _{f(\alpha _k)}(s_k(t))=\tilde{\eta }\big |_{[x_k,x_{k+1}]}(t)$. Thus, if we form $\eta$ by concatenating the $\eta _k$, we get that $\tilde{\eta }=\Phi (\eta )$ as required.

Now, we show that $\Phi$ is injective. Suppose $\eta _1,\eta _2\in \mathcal {A}^X$, and $\Phi (\eta _1)=\Phi (\eta _2)$. We must show that $\eta _1=\eta _2$. This follows from the fact that $\varphi$ is injective. Thus, we have that $\Phi$ is a bijection.

Finally, we wish to show that $\Phi$ preserves lengths. Let $\eta \in \mathcal {A}^X$. Suppose $\eta :[a,b]\rightarrow X$, $\{x_1,\ldots ,x_n\}$ is a partition of [a, b], and $\{\alpha _1,\ldots ,\alpha _{n-1}\} \subset \mathscr {G}$ such that $\eta \big |_{[x_k,x_{k+1}]}(t)=\langle \eta _k(t)\rangle$ for paths $\eta _k:[x_k,x_{k+1}]\rightarrow m_{\alpha _k}$. Let $\mu _k(t)=\gamma _{f(\alpha _k)}(\eta _k(t))=\varphi (\langle \eta _k(t)\rangle )$. Then by Lemma 3.12

$$\begin{aligned} L_X(\eta )&=\sum \limits _{k=1}^{n-1}L(\eta _k)\\&=\sum \limits _{k=1}^{n-1}\int _{x_k}^{x_{k+1}}|\eta _k'(s)|\mathrm{{d}}s\\&=\sum \limits _{k=1}^{n-1}\int _{x_k}^{x_{k+1}}|\mu _k'(s)|\mathrm{{d}}s\\&=\sum \limits _{k=1}^{n-1}L_g(\Phi (\eta )\big |_{[x_k,x_{k+1}]})\\&= L_g(\Phi (\eta )) \end{aligned}$$

as required. $\square$

We summarize our prior constructions in the proof of our first main theorem.

Proof of Theorem 2.4

Let (M, g) be a collarable Riemannian manifold with (possibly empty) boundary. Fix a stitching data $(\mathscr {G},m,\mathscr {C})$ for (M, g). We claim that we can provide a sequence of sets and mathematical objects starting with $(\mathscr {G},m,\mathscr {C})$ and ending with $(X,d_X)$ such that each object can be written directly in terms of the objects before it. It follows from Theorems 3.10 and 3.2 that $(M,d_g)$ is isometric to $(X,d_X)$. Thus, as discussed at the end of Sect. 2, such a sequence would constitute a proof of Theorem 2.4.

First, we provide the sequence, then we make explicit the relationship described in each arrow.

$$\begin{aligned} (\mathscr {G},m,\mathscr {C})\implies \mathcal {S}\implies \sim _\mathcal {S}\implies X \implies \mathcal {A}^X\implies L_X\implies (X, d_X) \end{aligned}$$

[$\implies \mathcal {S}$:

] $\mathcal {S}$ can be written in terms of $\mathscr {G}$ and m as the disjoint union $\mathcal {S}=\bigsqcup \nolimits _{\alpha \in \mathscr {G}}m_\alpha$.

[$\implies \sim _\mathcal {S}$:

] For $a_\alpha \in m_\alpha \subset \mathcal {S}$ and $b_\beta \in m_\beta \subset \mathcal {S}$, then $a_\alpha \sim _\mathcal {S}b_\beta$ if and only if $b_\beta \in \mathscr {C}_{\alpha ,\beta }(a_\beta )$.

[$\implies X$:

] X is just the quotient $\mathcal {S}/\sim _\mathcal {S}$.

[$\implies \mathcal {A}^X$:

] We break up the description of $\mathcal {A}^X$ into a few parts. First, observe that the set

$$\begin{aligned} A=\{\eta :[a,b]\rightarrow m_\alpha |a\le b,\eta _k\text { is smooth}, \alpha \in \mathscr {G}\} \end{aligned}$$

can be written in terms of m and $\mathscr {G}$. Then, observe that the set

$$\begin{aligned} B=\{\tilde{\eta }:[a,b]\rightarrow X|\tilde{\eta }(t)=\langle \eta (t)\rangle \text { for some }\eta \in A\} \end{aligned}$$

can be written in terms of A and $\sim _\mathcal {S}$. Next, for two curves $\eta _1:[a,b]\rightarrow X$ and $\eta _2:[c,d]\rightarrow X$, we can form their concatenation $(\eta _1 \& \eta _2):[a,b+d-c]\rightarrow X$ by

$$ \begin{aligned} (\eta _1 \& \eta _2)(t)= {\left\{ \begin{array}{ll} \eta _1(t)&{} t\in [a,b]\\ \eta _2(t+c-b)&{} t\in [a,b+d-c] \end{array}\right. } \end{aligned}$$

whenever $\eta _1(b)=\eta _2(c)$. This condition, where the end of one curve is equal to the beginning of another curve is just the property of being able to identify when two elements of a set. Thus, it is describable in terms of X. Finally, we may write $\mathcal {A}^X$ in the following way

$$ \begin{aligned} \mathcal {A}^X=\{(\eta _1 \& \eta _2 \& \cdots \& \eta _N)|\eta _k\in B\text { }\forall k=1,2,\ldots ,N\\ \text { and the right endpoint of } \eta _k \text { is compatible }\\ \text { with the left end point of } \eta _{k+1}\text { }\forall k=1,2,\ldots ,N-1\} \end{aligned}$$

[$\implies L_X$:

] Fix $\eta \in \mathcal {A}^X$. We will show that we can describe $L_X(\eta )$ in terms of the previous sets and mathematical objects. As described in the previous section, $\eta$ is the concatenation of curves of the form $t\mapsto \langle \eta _k(t)\rangle$ where $\eta _k:[a,b]\rightarrow m_\alpha$ is smooth. The particular decomposition of $\eta$ into such segments is describable in terms of $\eta$ itself, m, $\mathscr {G}$ and $\sim _\mathcal {S}$. Thus, we may identify the $\eta _k:[a_k,b_k]\rightarrow m_{\alpha _k}$. Once this is done, we simply have

$$\begin{aligned} L_X(\eta )=\sum \limits _{k=1}^N\int _{a_k}^{b_k}|\eta _k'(s)|\mathrm{{d}}s \end{aligned}$$

[$\implies d_X$:

] For $p,q\in X$, $d_X(p,q)=\inf \limits _{\eta \in \mathcal {A}^X_{p,q}} L_X(\eta )$

Thus, we have constructed a metric space isometric to $(M,d_g)$ as required. $\square$

4 Review of Boundary Measurement Problems

Many seismic and medical imaging problems can be framed as taking measurements of a geometric system from the boundary and trying to recover the interior geometry from these measurements. Thus, we would like to frame the stitching data in these terms. Before we do this, we review two of the standard boundary measurement inverse problems: boundary rigidity and lens rigidity, and two boundary measurement problems that are directly related to geodesic intersections: broken scattering rigidity and internal scattering rigidity.

For all of the following problems, the given measurements do not change under an isometry that fixes the boundary. We call this the ‘natural obstruction’.

For a more complete review of current results on boundary measurement problems, we refer readers to [5].

4.1 Boundary Rigidity

Distance is perhaps the simplest geometric quantity. Thus, the first boundary measurement we will discuss is the distance between boundary points. Seismically, this corresponds to measuring how long it takes an earthquake wave to propagate from the earthquake epicenter to different seismometers set up around the globe. Mathematically, let (M, g) be a Riemannian manifold with boundary. Suppose we are given $(\partial M,d_g\big |_{\partial M\times \partial M})$. The boundary rigidity problem is to determine when this information allows us to recover (M, g) up to the natural obstruction.

Let $\mathscr {M}$ be a class of Riemannian manifolds with boundary. We say that $\mathscr {M}$ is boundary rigid if the following holds: For all pairs of manifolds $(M_1,g_1),(M_2,g_2)\in \mathscr {M}$ such that there exists a diffeomorphism of the boundaries $\varphi ^\partial :\partial M_1\rightarrow \partial M_2$ satisfying $d_{g_2}(\varphi ^\partial (x),\varphi ^\partial (y))=d_{g_1}(x,y)$ for all $x,y\in \partial M_1$, then $\varphi ^\partial$ extends to a diffeomorphism $\varphi :M_1\rightarrow M_2$ such that $g_1=\varphi ^*g_2$.

Not all classes of Riemannian manifolds are boundary rigid. Consider the class of compact Riemannian manifolds with boundary. One can construct a compact Riemannian manifold with boundary (M, g) that has an open subset $U\subset M$ such that no distance-minimizing geodesics between boundary points pass through U. Thus, $g\big |_U$ is invisible to the boundary distance data. In particular, we can perturb g on U such that the boundary distances remain the same, but the isometry class of M is altered. For a specific example, take the round sphere and remove an open geodesic disk properly contained in one of the hemisphere.

One class of manifolds that avoids the above issue is simple manifolds. A compact, connected Riemannian manifold is simple if $\partial M$ is strictly convex (i.e. the second fundamental form on the boundary is everywhere positive definite), and pairs of distinct points are connected by a unique geodesic; furthermore, all geodesics are minimizing. In [6], Michel conjectured that the class of simple manifolds is boundary rigid. It is not known whether the entire class of simple manifolds is boundary rigid, however the following subclasses are known to be boundary rigid:

• 1. Simple 2-dimensional manifolds [7]

• 2. Simple subspaces of Euclidean space [8]

• 3. Simple subspaces of an open 2-dimensional hemisphere [9]

• 4. Simple subspaces of symmetric spaces of constant negative curvature [10]

4.2 Lens Rigidity

In the previous subsection, an issue arose when there was an open subset through which no length-minimizing geodesics between boundary points pass. We addressed this issue by restricting to a class of manifolds for which this does not occur. Alternatively, one might hope to address this issue by considering geodesics which are not length-minimizing. In the current subsection, and the two subsections that follow, we consider geometric data object that, in principle, contain information about every part of a connected manifold with non-empty boundary.

Let (M, g) be a compact Riemannian manifold with boundary which is a codimension 0 subspace of a complete Riemannian manifold without boundary $(\tilde{M},\tilde{g})$. In other words, $M\subset \tilde{M}$ and $\tilde{g}\big |_M= g$. Define the exit time function $\tau : SM\rightarrow [0,\infty ]$ by $\tau (v)=\infty$ if $\gamma _v(t)\in M$ for all $t\ge 0$, otherwise $\tau (v)=\inf \{t\ge 0|\gamma _v(t)\in \tilde{M}\setminus M\}$. We note that the values of $\tau$ on SM do not depend on the specific extension of M to a manifold $\tilde{M}$. Intuitively $\tau (v)$ is the first time that $\gamma _v$ exits the manifold M. When $\tau (v)\ne \infty$ for all $v\in \partial SM$, we say (M, g) is non-trapping.

If $\tau (v)\ne \infty$, define $\Sigma (v)=\dot{\gamma }_v(\tau (v))$. Intuitively, $\Sigma (v)$ is the direction that $\gamma _v$ is traveling when it exits the manifold M. If $\tau (v)=\infty$, we leave $\Sigma (v)$ undefined. Thus, we obtain a partially defined function $\Sigma :SM\rightarrow SM$. We call $\Sigma$ the scattering relation, and the pair $(\partial SM,\Sigma \big |_{\partial SM})$ is the scattering data.

If, in addition to the scattering relation, we are given the exit times, what we have is the lens data. Specifically, the lens data is the triple $(\partial SM,\Sigma \big |_{\partial SM},\tau \big |_{\partial SM})$. Observe that, when M is connected with non-empty boundary, every point in M has a geodesic which passes through it and originates at the boundary. Thus, in principle the lens data may contain information about portions of the manifold which are invisible to the boundary distance data.Note that if $v\in S_xM$ is outward pointing (i.e. $\langle v,\nu _x\rangle <0)$, then $\tau (v)=0$ and $\Sigma (v)=v$. In most of the literature, the scattering and exit time relation are initially defined only for inward pointing directions, and then extended to be defined on all of $\partial SM$. For expositional simplicity, we will stick with our definition. While this definition differs from the extensions in the literature, one can be obtained from the other, so all of the results are equivalent. As with the boundary rigidity, we say a class of manifolds is lens rigid if the lens data determines the metric up to an isometry which fixes the boundary.

The lens data determine the boundary distance data, and when the manifold is simple, they are equivalent [6]. Thus, one may ask if the additional information contained in the lens data provides us with anything useful in the non-simple case.

Guillarmou, Mazzucchelli and Tzou showed in [11] that the class of non-trapping, oriented compact Riemannian surfaces is boundary rigid. This class is larger than the class of simple 2-dimensional Riemannian manifolds, since it replaces the convex restriction with a non-trapping restriction, and simple manifolds are already non-trapping.

In [12], Lassas, Sharafutdinov, and Uhlmann show that the boundary distances for a simple Riemannian manifold (and hence the lens data) determine the jets of the metric at the boundary in boundary normal coordinates. In [13], Stefanov and Uhlmann extend this result to manifolds without conjugate points (thus, lifting the convex boundary assumption).

In [14], Stefanov, Uhlmann, and Vasy show that manifolds which satisfy a convex foliation condition are lens rigid.

4.3 Broken Scattering Rigidity

Let (M, g) be a compact Riemannian manifold with boundary. A piecewise geodesic curve that starts and ends at the boundary is a curve $\eta :[0,L_g(\eta )]\rightarrow M$ such that

$$\begin{aligned} \eta (t)= {\left\{ \begin{array}{ll} \gamma _v(t)&{} t\in [0,s]\\ \gamma _w(t-s)&{} t\in (s,L_g(\eta )] \end{array}\right. } \end{aligned}$$

For some $v\in \partial SM$ and $w\in SM$, such that $\gamma _v(s)=\pi (w)$ and $\eta (L_g(\eta ))\in \partial M$. The broken scattering relation for (M, g) is the set

$$\begin{aligned} R_g=\{(v,\Sigma (w),L_g(\eta ))|\text {there exists }v,w,\eta \text { as above}\}\subset \partial SM\times \partial SM\times [0,\infty ) \end{aligned}$$

Physically, one can think of the broken scattering relation as measuring the input directions, output directions, and travel times of a particle moving through a diffuse medium that gets scattered one time in an arbitrary direction.

In [15], Kurylev, Lassas, and Uhlmann consider the problem of recovering the geometry of a manifold from its broken scattering relation. They show that the broken scattering relation of a compact Riemannian manifold with non-empty boundary determines the isometry class of the manifold, as long as the manifold is at least three-dimensional.

In [16], de Hoop, Ilmavirta, and Saksala extend the broken scattering relation from Riemannian manifolds to Finsler manifolds. They prove that two Finsler manifolds with broken scattering relations that conjugate via a diffeomorphism of the boundary, and a diffeomorphism of the tangent bundle restricted to the boundary are isometric, provided

• both manifolds admit a particular foliation by convex hypersurfaces

• both finsler functions are reversible

• the manifolds are at least three-dimensional

4.4 Internal Scattering Rigidity

Let (M, g) be a Riemannian manifold with boundary. For $x\in M$, define

$$\begin{aligned} \text {star}(x)=\{v\in \partial SM| \exists w\in S_pM \text { and } t\in [0,\infty )\cap I_w \text { such that } v=\hat{\gamma }_w(t)\} \end{aligned}$$

Intuitively, $\text {star}(x)$ is the set of exit directions (or glancing directions) of geodesics emanating from x. One can flip this around and say that if $w\in \partial SM$, then $(-w)\in \text {star}(x)$ if and only if $\gamma _{w}(t)=x$ for some $t\ge 0$, to consider entering directions that pass through x. Define the collection of sets

$$\begin{aligned} \text {STAR}_g=\{\text {star}(x)\}_{x\in M} \end{aligned}$$

We will call the pair $(\partial M,\text {STAR}_g)$ the internal scattering data. In [17], Lassas, Saksala, and Zhou consider the problem of recovering the geometry of a Riemannian manifold with boundary. They show that for a particular generic class of (M, g) satisfying

• (M, g) is non-trapping

• $\partial M$ is strictly convex

the internal scattering data allows for recovery of the isometry class of the manifold.

5 The Delayed Collision Data

Now, we develop a boundary measurement type problem from which we will recover the stitching data.

Imagine, for each point in on the boundary of M, we can choose an inward pointing direction and shoot a particle at unit speed along the geodesic in that direction. Imagine further, that at another point on the boundary, you can wait any amount of time from when the first particle was released, and fire another particle at unit speed along a geodesic in any inward pointing direction. Then, you can detect whether the two fired particles collide and how long it took for the collision to occur.

In this section, we formalize the data set described above and show that it determines the stitching data (and hence the geometry of the manifold) under reasonable geometric assumptions.

To encode the geodesic information described above as boundary data, we would like all geodesics to reach the boundary in at least one direction. The following definition captures this idea

Definition 5.1

Let (M, g) be a Riemannian manifold with boundary. If the map $v\mapsto [v]$ from $\overline{\partial _+SM}$ to $\mathcal {G}$ is surjective, we say that (M, g) is semi-nontrapping.

where

$$\begin{aligned} \partial _+SM&=\bigcup \limits _{x\in \partial M}\{v\in S_xM|\langle \nu _x,v\rangle > 0\}\\ \overline{\partial _+SM}&=\bigcup \limits _{x\in \partial M}\{v\in S_x M|\langle \nu _x,v\rangle \ge 0\} \end{aligned}$$

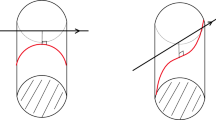
Let (M, g) be a Riemannian manifold with boundary. Let $v,w\in \partial _+SM$ and $D\ge 0$. If $\gamma _v(t)\ne \gamma _w(t+D)$ for all $t\ge 0$, then write $\mathbb {D}(v,w,D)=\infty$, otherwise write $\mathbb {D}(v,w,D)=\inf \{t\in I_v|\gamma _v(t)=\gamma _w(t+D)\}$. We call $\mathbb {D}$ the delayed collision operator. We define the delayed collision data $\mathcal {D}=\{(v,w,s,D)\in \overline{\partial _+SM}\times \overline{\partial _+SM}\times I_v\times [0,\infty ) | \mathbb {D}(v,w,D)=s\}$. Intuitively $(v,w,s,D)\in \mathcal {D}$ if we fire a particle in direction w, wait D units of time, then fire a particle in direction v and the first collision occurs after s more units of time. See Fig. 1 for an illustration of this.

Fig. 1

(a) $(v,w,s,D)\in \mathcal {D}$ (b) One intersection point is ‘hiding’ another, because both geodesic segments have length r

5.1 Relation to Lens Data

We briefly discuss the relationship between the delayed collision data and the lens data. Namely, that the delayed collision data is stronger than the lens data.

Let $v\in \partial SM$. We start by dealing with the edge case $\Sigma (v)=v$ (i.e. v is outward pointing or tangent to the boundary at a convex point such that the geodesic $\gamma _v$ immediately exits M). This occurs if and only if all collisions with $\gamma _v$ occur at $\gamma _v(0)$. Specifically, that $\{s>0|(v,w,s,D)\in \mathcal {D}\text { for some }w,s,d\}=\varnothing$. Thus, the delayed collision data allows us to identify the set $\Sigma (v)=v$. Thus, in what follows, we will assume that if $\Sigma (v)=w$, then $v\ne w$.

Let $v\in \partial _+SM$ and $\Sigma (v)=w$. Then $\gamma _v$ and $\gamma _{-w}$ are parameterizations of the same geodesic but in opposite directions. In particular, there are a continuum of intersection points between $\gamma _v$ and $\gamma _{-w}$. All of these points will show up in the delayed collision data: if $\gamma _v(s)=\gamma _{-w}(t)$ and $s\le t$, then $(v,-w,s,t-s)\in \mathcal {D}$.

Conversely, if $\Sigma (v)\ne w$ then $\gamma _v$ and $\gamma _{-w}$ intersect at discrete points. Thus, we have $\Sigma (v)=w$ if and only if the set $\{s|(v,-w,s,D)\in \mathcal {D}\text { or }(w,-v,s,D)\in \mathcal {D}\}$ contains an interval. Thus, the delayed collision data determines the scattering relation.

Now, we wish to recover the exit times. Observe that $\tau (v)=\infty$ if and only if there does not exist any w such that $\Sigma (v)=w$. Thus, we restrict our attention to non-trapped geodesics. Suppose that $\Sigma (v)=w$. Then, observe that $\tau (v)=D$ if and only if $\sigma (v,-w,0,D)\in \mathcal {D}$. Thus, the delayed collision data determines the exit times.

5.2 Relation to Broken Scattering Data

Let us now discuss the relationship between the delayed collision data and the broken scattering data. Of course, in three and higher dimensions, the broken scattering relation determines the entire geometry, and thus is at least as strong as the delayed collision data. In the other direction, we show that the delayed intersection data determines the broken scattering relation when (M, g) is simple. For the remainder of this subsection, we will assume (M, g) is simple.

For simple manifolds, all entry directions of geodesics are elements of $\partial _+SM$ and all exit directions are elements of $\partial _-SM=\{-v|v\in \partial _+SM\}$. Thus, if $(v,w,l)\in R_g$, then we have $v\in \partial _+SM$ and $w\in \partial _-SM$. We will show that we can identify whether or not (v, w, l) is an element of $R_g$ from the delayed collision data. We will break this analysis up into two lemmas. In the first case, we consider when $\pi (v)=\pi (w)$, and in the second, we consider when $\pi (v)\ne \pi (w)$.

Lemma 5.2

Let (M, g) be a simple Riemannian manifold with boundary. Let $v\in \partial _+ SM$, $w\in \partial _-SM$ and $l\in [0,\infty )$ be such that $\pi (v)=\pi (w)$. Then $(v,w,l)\in R_g$ if and only if $w=-v$ and $l\le 2\tau (v)$.

Proof

First, we note that this “if and only if” constraint can be written in terms of the delayed collision data, since we showed in the previous subsection that the exit time function can be written in terms of the delayed collision data.

Next, we recall one of the primary properties of simple manifolds: between any two points there is a unique minimizing geodesic. Thus, if a broken geodesic enters and exits at the same point, the only way for this to occur is if it enters the manifold in one direction and leaves it in the opposite direction (i.e., it travels for some time, then gets scattered in the opposite direction and travels back along the same geodesic segment in reverse).

Finally, observe that the geodesic can be broken at any point, and then travel back along the same geodesic. Thus, any length between 0 and $2\tau (v)$ is possible. $\square$

Next, we consider the situation where $\pi (v)\ne \pi (w)$.

Lemma 5.3

Let (M, g) be a simple Riemannian manifold with boundary. Let $v\in \partial _+SM$, $w\in \partial _-SM$ and $l\in [0,\infty )$ be such that $\pi (v)\ne \pi (w)$. Then $(v,w,l)\in R_g$ if and only if there exists $s,D\ge 0$ such that $l=2s+D$ and one of the following hold

• 1. $(v,-w,s,D)\in \mathcal {D}$

• 2. $(-w,v,s,D)\in \mathcal {D}$

Proof

Let $v\in \partial _+SM$, $w\in \partial _-SM$ and $l\in [0,\infty )$ be such that $\pi (v)\ne \pi (w)$. First, suppose that $(v,w,l)\in R_g$. Let $\eta :[0,l]\rightarrow M$ be defined by

$$\begin{aligned} \eta (t)= {\left\{ \begin{array}{ll} \gamma _v(t)&{} t\in [0,t^*]\\ \gamma _z(t)&{} t\in (t^*,l] \end{array}\right. } \end{aligned}$$

be a broken geodesic that corresponds to (v, w, l). Observe then, that $\gamma _v(t^*)=\gamma _{-w}(l-t^*)$. If $t^*\ge l-t^*$, then let $s=l-t^*$ and $D=t^*-s$. It follows that $\gamma _v(s+D)=\gamma _{-w}(s)$, and $l=2s+D$. It follows straightforwardly from the fact that any two points have a unique geodesic connecting them, that two intersecting geodesics either intersect at a single point or are reparameterizations of eachother. Since $\pi (v)\ne \pi (w)$, we have that $\gamma _v$ either intersects $\gamma _{-w}$ at a single point or $\gamma _v$ is the “reverse” of $\gamma _{-w}$ (i.e. the same geodesic, but in the opposite direction. Thus, it follows that the equation

$$\begin{aligned} \gamma _v(x+D)=\gamma _{-w}(x) \end{aligned}$$

has exactly one solution $x=s$. Thus, $(-w,v,s,D)\in \mathcal {D}$.

Similarly, if $t^*<l-t^*$, let $s=t^*$ and $D=(l-t^*)-t^*$. Then $l=2s+D$ and $(v,-w,s,D)\in \mathcal {D}$.

Conversely, suppose that there exists $s,D \ge 0$ such that $(v,-w,s,D)\in \mathcal {D}$, and $l=2s+D$ (the analysis of the $(-w,v,s,D)\in \mathcal {D}$ will be nearly identical, so we will not include it). Since (M, g) is simple, we know that two intersecting geodesics intersect at a single point or have identical images. It follows that the infimum in the definition in $\mathcal {D}$ is saturated. Thus, $\gamma _{-w}(s+D)=\gamma _v(s)$. Let $z=-\hat{\gamma }_{-w}(s+D)$. Then $\Sigma (z)=w$. It follows that $\eta :[0,l]\rightarrow M$ defined by

$$\begin{aligned} \eta (t)= {\left\{ \begin{array}{ll} \gamma _v(t)&{} t\in [0,s]\\ \gamma _z(t-s)&{} t\in (s,l] \end{array}\right. } \end{aligned}$$

is a broken geodesic corresponding to (v, w, l). Thus, $(v,w,l)\in R_g$ as required. $\square$

We note here that the fact that the delayed collision data determines the broken scattering relation when (M, g) is simple also follows from Theorem 5.10. However, the relationship is less clear when one uses Theorem 5.10 as an intermediate. We also note that it is certainly plausible that the delayed collision data determines the broken scattering relation in settings that are more general than simple manifolds.

5.3 Relation to Internal Scattering Data

In this subsection, we show that the delayed collision data determines the internal scattering data when (M, g) is simple. As in the previous subsection, we assume that (M, g) is simple for the entirety of this subsection. For $x\in \partial M$, observe that $\text {star}(x)=\Sigma (S_x M)$. Thus, since the delayed collision data determines $\Sigma$, we are able to identify all such sets. Thus, we restrict our attention to identifying when a set $S\subset \partial SM$ is a star set $\text {star}(x)$ for some $x\in M\setminus \partial M$.

Observe that for all such sets, the fact that geodesics between distinct points are unique implies that there is exactly one element of $\text {star}(x)$ based at each point in $\partial M$. Additionally, it follows from the properties of simple manifolds that all exit directions of geodesics which start on the interior are strictly outward directions (i.e. elements of $\partial _-SM$).

Lemma 5.4

Let (M, g) be a simple Riemannian manifold with boundary. Let $S\subset \partial _-SM$ be such that $\pi : S\rightarrow \partial M$ is a bijection. Then $S=\text {star}(x)$ for some $x\in M\setminus \partial M$ if and only if there exists $v_0\in S$ and $r_0>0$ such that for all $w\in S\setminus \{v_0\}$ one of the following hold.

• 1. $(-v_0,-w, r_0,D)\in \mathcal {D}$ for some $D\ge 0$

• 2. $(-w,-v_0, s, r_0-s)\in \mathcal {D}$ for some $s\ge 0$.

Proof

Let $S\subset \partial _-SM$ be such that $\pi :S\rightarrow \partial M$ is a bijection. First, suppose $S=\text {star}(x)$ for $x\in M\setminus \partial M$. Let $v_0\in S$ be arbitrary and let $r_0=d_g(\pi (v_0),x)$. Then $\gamma _{-v_0}(r_0)=x$. Let $w\in S\setminus \{v_0\}$. If $d_g(\pi (w),x)\ge r_0$, then let $D=r_0-d_g(\pi (w),x)$. It follows that $\gamma _{-w}(r_0+D)=x$. Thus, by a similar argument as in Lemma 5.3, we have that $(-v_0,-w,r_0,D)\in \mathcal {D}$.

If $d_g(\pi (w),x)<r_0$, let $s=r_0-d_g(\pi (w),x)$. Then similar to the argument above, we get $(-w,-v_0,s,r_0-s)\in \mathcal {D}$.

Conversely, suppose that there exists $v_0\in S$ and $r_0>0$ such that for all $w\in S\setminus \{v_0\}$ (1.) or (2.) holds. We claim that $S=\text {star}(\gamma _{-v_0}(r_0))$. Let $w\in S\setminus \{v_0\}$. We must show that $\gamma _{-w}$ passes through $\gamma _{-v_0}(r_0)$. First, suppose that (1.) is satisfied. Since $(-v_0,-w,r_0,D)\in D$, we know that $\gamma _{-v_0}(r_0)=\gamma _{-w}(r_0+D)$, so $\gamma _{-w}$ passes through $\gamma _{-v_0}(r_0)$. If (2.) is satisfied, then $\gamma _{-w}(s)=\gamma _{-v_0}(s+r_0-s)=\gamma _{-v_0}(r_0)$ as required. $\square$

Just as with the broken scattering relation, it is certainly plausible that the delayed collision data determines the internal scattering data.

5.4 Recovery of Stitching Data

In this subsection, we show that the delayed collision data determines a stitching data, and hence the geometry, if the manifold (M, g) is what we will call ‘generically delayed’ and ‘semi-nontrapping’.

As an intermediate between the delayed collision data and stitching data, we define the stitching boundary relation to be the set $\mathcal {B}=\{(v,w,s,t)\in \overline{\partial _+SM}\times \overline{\partial _+SM}\times [0,\infty )\times [0,\infty )|\gamma _v(s)=\gamma _w(t)\}$. The stitching boundary relation is essentially a repackaged stitching data where the index set, $\mathscr {G}$, is just $\overline{\partial _+SM}$.

Lemma 5.5

Let (M, g) be semi-nontrapping. Then, the stitching boundary relation determines a stitching data for (M, g).

Proof

We let $\mathscr {G}=\overline{\partial _+SM}$. Then let $f:\overline{\partial _+SM}\rightarrow SM$ be the obvious injection. Since (M, g) is semi-nontrapping, f is surjective. For $v\in \mathscr {G}$, we define $m_v=\{t\ge 0|\exists w\in \mathscr {G},s\in \mathbb {R}\text { such that }(v,w,t,s)\in \mathcal {B}\}$. It is clear that $m_v=I_v$.

Finally, we define $\mathscr {C}_{v,w}(s)=\{t\in m_w|(v,w,s,t)\in \mathcal {B}\}$. $\square$

We would like to recover the stitching boundary relation from the delayed collision data. Observe that, a sufficient condition for $\gamma _v(s)=\gamma _w(t)$ is that $t\ge s$ and $(v,w,s,t-s)\in \mathcal {D}$ (or if $t\le s$ then $(w,v,t,s-t)\in \mathcal {D}$). However, this is not a necessary condition. In particular if $\gamma _v(s)=\gamma _w(t)$ and $t\ge s$, but $(v,w,s,t-s)\notin \mathcal {D}$, then there exists $t'\ge s'$ and $r>0$ such that $(v,w,s',t'-s')\in \mathcal {D}$ and $t=t'+r$, $s=s'+r$. Geometrically, this occurs when two geodesics have an intersection point, and then you travel the same length along each geodesic to reach another intersection point. Intuitively, this means that any delayed pair of particles that “would” collide at the second intersection point, collide at the first intersection point instead. This situation should be rare, since the length between intersection points measured along both geodesics would have to be exactly the same.

Definition 5.6

Let (M, g) be a Riemannian manifold with boundary. A pair of vectors $(v,w)\in \overline{\partial _+SM}$ is generically delayed if $\gamma _v(s)=\gamma _w(t)$ implies $(v,w,s,t-s)\in \mathcal {D}$ or $(w,v,t,s-t)\in \mathcal {D}$.

When (v, w) are not generically delayed, we have one intersection point ‘hiding’ intersection points past it. If the ‘hidden’ intersection points can be reached by a third geodesic which does not have the original issue, we can overcome this obstruction. This third geodesic is confirming the existence of the hidden intersection points. The following definition formalizes this.

Definition 5.7

Let (M, g) be a Riemannian manifold with boundary. We say that (M, g) confirms intersections (or that it is intersection-confirming) if for all $(v,w,s,t)\in \mathcal {B}$, there exists $z\in \overline{\partial _+SM}$ such that

• 1. $\gamma _z$ passes through $\gamma _v(s)$

• 2. (v, z) and (w, z) are generically delayed.

In such a case, we say that z confirms the intersection (v, w, s, t).

Lemma 5.8

Let (M, g) be a semi-nontrapping Riemannian manifold that confirms intersections. Then $(v,w,s,t)\in \mathcal {B}$ if and only if there exists $z\in \overline{\partial _+SM}$ and $r\in I_z$ such that

• 1. $(z,v,r,s-r)\in \mathcal {D}$ or $(v,z,s,r-s)\in \mathcal {D}$.

• 2. $(z,w,r,t-r)\in \mathcal {D}$ or $(w,z,t,r-t)\in \mathcal {D}$.

Proof

First, suppose that $(v,w,s,t)\in \mathcal {B}$. Suppose z confirms the intersection (v, w, s, t). This implies that $\gamma _z$ passes through $\gamma _v(s)=\gamma _w(t)$ and that (v, z), (w, z) are generically delayed. Let $r\in I_z$ be such that $\gamma _z(r)=\gamma _v(s)=\gamma _w(t)$. By the definition of generically delayed we have that

• 1. $(z,v,r,s-r)\in \mathcal {D}$ or $(v,z,s,r-s)\in \mathcal {D}$.

• 2. $(z,w,r,t-r)\in \mathcal {D}$ or $(w,z,t,r-t)\in \mathcal {D}$.

as required.

Conversely, suppose that there exists $z\in \overline{\partial _+SM}$ and $r\in I_z$ such that

• 1. $(z,v,r,s-r)\in \mathcal {D}$ or $(v,z,s,r-s)\in \mathcal {D}$.

• 2. $(z,w,r,t-r)\in \mathcal {D}$ or $(w,z,t,r-t)\in \mathcal {D}$.

Then (1.) implies that $\gamma _z(r)=\gamma _v(s)$, and (2.) implies that $\gamma _z(r)=\gamma _w(t)$. Thus, by transitivity $\gamma _v(s)=\gamma _w(t)$, so $(v,w,s,t)\in \mathcal {B}$ as required. $\square$

As a direct corollary of Lemmas 5.8 and 5.5 we obtain

Theorem 5.9

Let (M, g) be a semi-nontrapping Riemannian manifold that confirms intersections. Then the delayed collision data determines a stitching data for (M, g).

Since a stitching data allows for the construction of a metric space which is isometric to $(M,d_g)$ we obtain

Theorem 5.10

Let (M, g) be a semi-nontrapping Riemannian manifold that confirms intersections. Then the delayed collision data determines the isometry class of (M, g).

6 Discussion

A stitching data is quite a lot of information. It contains very detailed knowledge of all intersections of all geodesics. Thus, it allows for recovery of the geometry in a very general setting. We do not view the stitching data as an inverse problem on its own, but more as a target for geodesic inverse problems in general. In other words, rather than trying to recover the metric g directly as a tensor field on a manifold, it seems logical that trying to construct a stitching data may be an easier path if your starting point is a geodesic data set. The delayed collision data was chosen to demonstrate this strategy.

In addition to demonstrating the strategy of constructing a stitching data from geodesic boundary data, it seems reasonable that the delayed collision data could yield a practical experiment. To find an application of the delayed collision data, one should consider a non-linear PDE where information can be propagated along geodesics. The non-linearity would be essential to measure if two packets of information propagating along different geodesics interact or not. A similar strategy was employed in [18] where four waves are propagated to produce a non-linear interaction that can be measured to recover information about the structure of a spacetime.