Abstract
We prove that if an ALE Ricci-flat manifold (M, g) is linearly stable and integrable, it is dynamically stable under Ricci flow, i.e. any Ricci flow starting close to g exists for all time and converges modulo diffeomorphism to an ALE Ricci-flat metric close to g. By adapting Tian’s approach in the closed case, we show that integrability holds for ALE Calabi–Yau manifolds which implies that they are dynamically stable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider a complete Riemannian manifold \((M^n,g)\) without boundary endowed with a Ricci-flat metric g. As such, it is a fixed point of the Ricci flow and therefore, it is a natural problem to study the stability of such a metric with respect to the Ricci flow. Whether the manifold is compact or noncompact makes an essential difference in the analysis. In both cases, if \((M^n,g)\) is Ricci-flat, the linearized operator is the so-called Lichnerowicz operator acting on symmetric 2-tensors. Nonetheless, the \(L^2\) approach differs drastically in the noncompact case. Indeed, even in the simplest situation, that is the flat case, the spectrum of the Lichnerowicz operator is not discrete anymore and 0 belongs to the essential spectrum. In this paper, we consider Ricci-flat metrics on noncompact manifolds that are asymptotically locally Euclidean (ALE for short), i.e. that are asymptotic to a flat cone over a space form \({\mathbb {S}}^{n-1}/\Gamma \) where \(\Gamma \) is a finite group of \(\mathrm{SO}(n)\) acting freely on \({\mathbb {R}}^n\setminus \{0\}\).
If \((M^n,g_0)\) is an ALE Ricci-flat metric, we assume furthermore that it is linearly stable, i.e. the Lichnerowicz operator is nonpositive in the \(L^2\) sense and that the set of ALE Ricci-flat metrics close to \(g_0\) is integrable, i.e. has a manifold structure of finite dimension: see Sect. 2.1.
The strategy we adopt is given by Koch and Lamm [18] that studied the stability of the Euclidean space along the Ricci flow in the \(L^{\infty }\) sense. The quasi-linear evolution equation to consider here is
where \((M^n,g_0)\) is a fixed background ALE Ricci-flat metric and \({{\mathscr {L}}}_{V(g,g_0)}(g)\) is the so-called DeTurck’s term. Equation (1) is called the Ricci–DeTurck flow: its advantage over the Ricci flow equation is to be a strictly parabolic equation instead of a degenerate one. Koch and Lamm managed to rewrite (1) in a clever way to get optimal results regarding the regularity of the initial condition: see Sect. 3.
Our main theorem is then:
Theorem 1.1
Let \((M^n,g_0)\) be an ALE Ricci-flat space. Assume it is linearly stable and integrable. Then for every \(\epsilon >0\), there exists a \(\delta >0\) such that the following holds: for any metric \(g\in {\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\delta )\), there is a complete Ricci–DeTurck flow \((M^n,g(t))_{t\ge 0}\) starting from g converging to an ALE Ricci-flat metric \(g_{\infty }\in {\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\epsilon )\).
Moreover, the \(L^{\infty }\) norm of \((g(t)-g_0)_{t\ge 0}\) is decaying sharply at infinity:
As far as we know, this theorem is the first stability result for nonflat and noncompact Ricci-flat manifolds under Ricci flow.
Schnürer et al. [29] have proved the stability of the Euclidean space for an \(L^2\cap L^{\infty }\) perturbation as well. The decay obtained in Theorem 1.1 sharpens their result. Indeed, the proof shows that if \((M^n,g_0)\) is isometric to \(({\mathbb {R}}^n,\mathrm{eucl})\) then the \(L^{\infty }\) decay holds on the whole manifold. This \(L^{\infty }\) decay on Euclidean space was also recently shown in [2] by a different approach.
Remark 1.2
It is an open question whether the decay in time obtained in Theorem 1.1 holds on the whole manifold with an exponent \(\alpha \) less than or equal to n/4.
One of the main difficulties in proving Theorem 1.1 is to establish a uniform-in-time \(L^2\) bound on the difference of the metrics \(g(t)-g_0(t)\) for nonnegative time t and a suitable family of Ricci-flat reference metrics \(g_0(t)\) . To prove such a bound in case the background metric \(g_0\) is flat, [2, 29] use a direct integration by parts. In our setting, this approach does not work for mainly two reasons: the kernel of the Lichnerowicz operator might be nontrivial and the curvature terms from the linearized operator cannot be treated as error terms. Therefore, the strategy is to work orthogonally to the kernel of the Lichnerowicz operator in order to apply a delicate notion of strict positivity for the Lichnerowicz operator that enables us to absorb the curvature terms. This leads us in turn to a very delicate choice of a reference metric \(g_0(t)\) which makes the analysis trickier: see Sect. 3.3.
Now, from the physicist point of view, the question of stability of ALE Ricci-flat metrics is of great importance when applied to hyperkähler or Calabi–Yau ALE metrics: Hyperkähler ALE metrics (also called gravitational instantons) are of great importance in theoretical physics: see for instance [1, 10] and the references therein. In this context, the Ricci flow serves as a first-order approximation of the renormalization group flow and admits deep connections with it, see [11].
In the hyperkähler or Calabi–Yau case, the Lichnerowicz operator is always a nonnegative operator because of the special algebraic structure of the curvature tensor shared by these metrics. It turns out that they are also integrable: see Theorem 2.18 based on the fundamental results of Tian [33] in the closed case. In particular, it gives us plenty of examples to which one can apply Theorem 1.1.
Another source of motivation comes from the question of continuing the Ricci flow after it reached a finite time singularity on a 4-dimensional closed Riemannian manifold: the works of Bamler and Zhang [7] and Simon [32] show that the singularities that can eventually show up for Ricci flows with bounded scalar curvature are orbifold singularities and thus modelled over ALE Ricci-flat metrics. A strong connection between the appearance of such singularities and the stability of their blow-up limits is expected. However, there is no classification available for such metrics in dimension 4 at the moment, except Kronheimer’s classification for hyperkähler metrics [22].
Finally, we would like to discuss some related results especially regarding the stability of closed Ricci-flat metrics. There have been basically two approaches. On one hand, Sesum [30] has proved the stability of integrable Ricci-flat metrics on closed manifolds: in this case, the convergence rate is exponential since the spectrum of the Lichnerowicz operator is discrete. On the other hand, Haslhofer–Müller [16] and the second author [21] have proved Lojasiewicz inequalities for Perelman’s entropies which are monotone under the Ricci flow and whose critical points are exactly Ricci-flat metrics and Ricci solitons, respectively. The analysis in the proof of Theorem 1.1 differs substantially from these two previous approaches as these tools and features are not available in our setting.
The paper is organized as follows. Section 2.1 recalls the basic definitions of ALE spaces together with the notions of linear stability and integrability of a Ricci-flat metric. Sect. 2.2 gives a detailed description of the space of gauged ALE Ricci-flat metrics: see Theorem 2.7 and Theorem 2.11. Sect. 2.3 investigates the integrability of Kähler Ricci-flat metrics: this is the content of Theorem 2.18. Section 3 is devoted to the proof of the first part of Theorem 1.1. Sect. 3.1 discusses the structure of the Ricci–DeTurck flow. Section 3.2 establishes pointwise and integral short-time estimates. The core of the proof of Theorem 1.1 is contained in Sect. 3.3: a priori uniform-in-time \(L^2\) estimates are proved with the help of a suitable notion of strict positivity for the Lichnerowicz operator developed for Schrödinger operators by Devyver [14]. The infinite time existence and the convergence aspects of Theorem 1.1 are then proved in Sect. 3.4. Finally, Sect. 4 proves the last part of Theorem 1.1: the decay in time is verified with the help of a Nash–Moser iteration.
2 ALE Spaces
2.1 Analysis on ALE Spaces
We start by recalling a couple of definitions.
Definition 2.1
A complete Riemannian manifold \((M^n,g_0)\) is said to be asymptotically locally Euclidean (ALE) with one end of order \(\tau >0\) if there exists a compact set \(K\subset M\), a radius R and a diffeomorphism such that : \(\phi :M\setminus K\rightarrow ({\mathbb {R}}^n\setminus B_R)/\Gamma \), where \(\Gamma \) is a finite group of \(\mathrm{SO}(n)\) acting freely on \({\mathbb {R}}^n\setminus \{0\}\), such that
holds on \(({\mathbb {R}}^n\setminus B_R)/\Gamma \).
The linearized operator we will focus on is the so-called Lichnerowicz operator whose definition is recalled below:
Definition 2.2
Let (M, g) be a Riemannian manifold. Then the operator \(L_g:C^{\infty }(S^2T^*M)\rightarrow C^{\infty }(S^2T^*M)\), defined by
is called the Lichnerowicz Laplacian acting on the space of symmetric 2-tensors \(S^2T^*M\).
In this paper, we consider the following notion of stability:
Definition 2.3
Let \((M^n,g_0)\) be a complete ALE Ricci-flat manifold. \((M^n,g_0)\) is said to be linearly stable if the (essential) \(L^2\) spectrum of the Lichnerowicz operator \(L_{g_0}:=\Delta _{g_0}+2\mathrm{Rm}(g_0)*\) is in \((-\infty ,0]\).
Equivalently, this amounts to say that \(\sigma _{L^2}(-L_{g_0})\subset [0,+\infty )\). By a theorem due to Carron [12], \(\ker _{L^2}L_{g_0}\) has finite dimension. Denote by \(\Pi _c\) the \(L^2\) projection on the kernel \(\ker _{L^2}L_{g_0}\) and \(\Pi _s\) the projection orthogonal to \(\Pi _c\) so that \(h=\Pi _ch+\Pi _sh\) for any \(h\in L^2(S^2T^*M)\).
Let \((M,g_0)\) be an ALE Ricci-flat manifold and \({\mathcal {U}}_{g_0}\) the set of ALE Ricci-flat metrics with respect to the gauge \(g_0\), that is:
endowed with the \(L^2\cap L^{\infty }\) topology coming from \(g_0\).
Definition 2.4
\((M^n,g_0)\) is said to be integrable if \({\mathcal {U}}_{g_0}\) has a smooth structure in a neighbourhood of \(g_0\). In other words, \((M^n,g_0)\) is integrable if the map
is a local diffeomorphism at \(g_0\).
If \((M,g_0)\) is ALE and Ricci-flat, it is a consequence of [8, Theorem 1.1] that it is already ALE of order \(n-1\). Moreover, if \(n=4\) or \((M,g_0)\) is Kähler, it is ALE of order n. This is due to the presence of Kato inequalities, [8, Corollary 4.10] for the curvature tensor. We will show in Theorem 2.7 that by elliptic regularity, all \(g\in {\mathcal {U}}_{g_0}\) are ALE of order \(n-1\) with respect to the same coordinates as \(g_0\).
In order to do analysis of partial differential equations on ALE manifolds, one has to work with weighted function spaces which we will define in the following. Fix a point \(x\in M\) and define a function \(\rho :M\rightarrow {\mathbb {R}}\) by \(\rho (y)=\sqrt{1+d(x,y)^2}\). For \(p\in [1,\infty )\) and \(\delta \in {\mathbb {R}}\), we define the spaces \(L^p_{\delta }(M)\) as the closure of \(C^{\infty }_{0}(M)\) with respect to the norm
and the weighted Sobolev spaces \(W^{k,p}_{\delta }(M)\) as the closure of \(C^{\infty }_{0}(M)\) under
The weighted Hölder spaces are defined as the set of maps \(u\in C^{k,\alpha }_{loc}(M)\), \(\alpha \in (0,1)\) such that the following quantity
is finite. Here \(\tau _x^y\) denotes the parallel transport from x to y along the shortest geodesic joining x and y. All these spaces are Banach spaces, the spaces \(H^k_{\delta }(M):=W^{k,2}_{\delta }(M)\) are Hilbert spaces and their definition does not depend on the choice of the base point defining the weight function \(\rho \). All these definitions extend to Riemannian vector bundles with a metric connection in an obvious manner.
In the literature, there are different notational conventions for weighted spaces. We follow the convention of [9]. The Laplacian \(\Delta _g\) is a bounded map \(\Delta _g:W^{p,k}_{\delta }(M)\rightarrow W^{p,k-2}_{\delta -2}(M)\) and there exists a discrete set \(D\subset {\mathbb {R}}\) such that this operator is Fredholm for \(\delta \in {\mathbb {R}}\setminus D\). This is shown in [9] in the asymptotically flat case and the proof in the ALE case is the same up to minor changes. We call the values \(\delta \in D\) exceptional and the values \(\delta \in {\mathbb {R}}\setminus D\) nonexceptional. If \(\delta \in (2-n,0)\), the operator is even an isomorphism [27, p. 151]. The Fredholm properties also hold for elliptic operators of arbitrary order acting on vector bundles supposed that the coefficients behave suitable at infinity [24, Theorem 6.1]. The isomorphism properties also hold with the same range of \(\delta \) for connection Laplacians on arbitrary tensor bundles. We will use these facts frequently in this paper.
2.2 The Space of Gauged ALE Ricci-Flat Metrics
Fix an ALE Ricci-flat manifold \((M,g_0)\). Let \({\mathcal {M}}\) be the space of smooth metrics on the manifold M. For \(g\in {\mathcal {M}}\), let \(V=V(g,g_0)\) be the vector field defined intrinsically by (3) and locally given by \(g^{ij}(\Gamma (g)^k_{ij}-\Gamma (g_0)_{ij}^k)\) where \(\Gamma (g)_{ij}^k\) denotes the Christoffel symbols associated to the Riemannian metric g. We call a metric g gauged, if \(V(g,g_0)=0\). Let
be the set of stationary points of the Ricci–DeTurck flow. In local coordinates, Eq. (4) can also be written as
see [31, Lemma 2.1]. By defining \(h=g-g_0\), this equation can be again rewritten as
where we used that \(g_0\) is Ricci-flat. The linearization of this equation at \(g_0\) is given by

A proof of this fact can be found for instance in [5, Chapter 3].
We recall the well-known fact that the \(L^2\)-kernel of the Lichnerowicz operator consists of transverse traceless tensors:
Lemma 2.5
Let \((M^n,g)\) be an ALE Ricci-flat manifold and \(h\in \ker _{L^2}(L_{g_0})\). Then \(\mathrm{tr}_{g_0} h=0\) and \(\mathrm{div}_{g_0} h=0\).
Proof
Straightforward calculations show that \(\mathrm{tr}_{g_0}\circ L_{g_0}=\Delta _{g_0}\circ \mathrm{tr}_{g_0}\) and \(\mathrm{div}_{g_0}\circ L_{g_0}=\Delta _{g_0}\circ \mathrm{div}_{g_0}\). Therefore, \(\mathrm{tr}_{g_0} h\in \ker _{L^2}(\Delta _{g_0})\) and \(\mathrm{div}_{g_0} h\in \ker _{L^2} (\Delta _{g_0})\) which implies the statement of the lemma. \(\square \)
The next proposition ensures that ALE steady Ricci solitons are Ricci-flat:
Proposition 2.6
Let \((M^n,g,X)\) be a steady Ricci soliton, i.e. \(\mathrm{Ric}(g)={\mathcal {L}}_X(g)\) for some vector field X on M. Then \(\lim _{+\infty }|X|_g=0\) implies \(X=0\). In particular, any steady soliton in the sense of (4) that is ALE with \(\lim _{+\infty }V(g,g_0)=0\) is Ricci-flat.
Proof
By the contracted Bianchi identity, one has
Therefore, \(\Delta _gX+\mathrm{Ric}(g)(X)=0\). In particular,
which establishes that \(|X|_g^2\) is a subsolution of \(\Delta _X:=\Delta _g+X\cdot \). The use of the maximum principle then implies the result in case \(\lim _{+\infty }|X|=0\). \(\square \)
Theorem 2.7
Let \((M^n,g_0)\) be an ALE Ricci-flat manifold with order \(\tau >0\). Let \(g\in {\mathcal {F}}\) be in a sufficiently small neighbourhood of \(g_0\) with respect to the \(L^2\cap L^{\infty }\)-topology. Then g is an ALE Ricci-flat manifold of order \(n-1\) with respect to the same coordinates as \(g_0\).
Remark 2.8
-
(i)
If \(n=4\) or \(g_0\) is Kähler, it seems likely that \(g\in {\mathcal {F}}\) is ALE of order n with respect to the same coordinates as \(g_0\). However, we don’t need this decay for further considerations.
-
(ii)
A priori, Proposition 2.7 does not assume any integral or pointwise decay on the difference tensor \(g-g_0\) or on the curvature tensor of g. The assumptions on g can be even weakened as follows: If \(\left\| g-g_0\right\| _{L^p(g_0)}\le K<\infty \) for some \(p\in [2,\infty )\) and \(\left\| g-g_0\right\| _{L^{\infty }(g_0)}<\epsilon =\epsilon (g_0,p,K)\), then the conclusions of Theorem 2.7 hold.
Proof of Theorem 2.7
The first step consists in applying a Moser iteration to the norm of the difference of the two metrics: \(\vert h\vert _{g_0}:=|g-g_0|_{g_0}\). Indeed, recall that h satisfies (5) which can also be written as
In particular,
Therefore, as \(\Vert h\Vert _{L^{\infty }(g_0)}\le \epsilon \) where \(\epsilon >0\) is a sufficiently small constant depending on n and \(g_0\), we get
As \(|\mathrm{Rm}(g_0)|\in L^{n/2}(M)\) and \(h\in L^2(S^2T^*M)\), Lemma 4.6 and Proposition 4.8 of [8] tell us that \(|h|^2=\textit{O}(r^{-\tau })\) at infinity for any positive \(\tau <n-2\), i.e. \(h=\textit{O}(r^{-\tau })\) for any \(\tau <n/2-1\). Here, r denotes the distance function on M centred at some arbitrary point \(x\in M\).
The next step is to show that \(\nabla ^{g_0} h=\textit{O}(r^{-\tau -1})\) for \(\tau <n/2-1\). Assume \(p\ge 2\). We first proceed with a chain of inequalities as follows:
Here, the first inequality follows from elliptic regularity for weighted Sobolev spaces, see [25, Theorem 4.21]. The second inequality uses Eq. (5) and the third inequality follows from an interpolation inequality for weighted spaces, see Lemma 2.9 below. This implies
for all \(p\in (n,\infty )\) and \(\tau +\epsilon <\frac{n}{2}-1\) provided that the \(L^{\infty }\)-norm is small enough. Here, the first inequality follows from weighted Sobolev embedding, see [27, Remark 6.9]. The second inequality follows from the above and the third inequality follows from the weighted Hölder inequality (see e.g. [27, Lemma 6.7]) applied to h and the weight function itself. Consequently,
In the following we will further improve the decay order and show that \(h=\textit{O}(r^{-n+1})\). As a consequence of elliptic regularity for weighted Hölder spaces ([25, Theorem 4.21]), we will furthermore get \(\nabla ^{g_0,k}h=\textit{O}(r^{-n+1-k})\) for any \(k\in {\mathbb {N}}\). To prove these statements we adapt the strategy in [8, pp. 325–327].
As \(\mathrm{Rm}(g_0)=\textit{O}(r^{-n-1})\), \(h=\textit{O}(r^{-\tau })\) and \(\nabla ^{g_0} h=\textit{O}(r^{-\tau -1})\) for some fixed \(\tau \) slightly smaller than \(\frac{n}{2}-1\), Eq. (5) implies that \(\Delta _{g_0} h=\textit{O}(r^{-2\tau -2})\). Thus, \(\Delta _{g_0} h=\textit{O}(r^{-\mu })\) for some \(\mu \) slightly smaller than n.
Let \(\varphi : M\setminus B_R(x)\rightarrow ({\mathbb {R}}^n\setminus B_R)/\Gamma \) be coordinates at infinity with respect to which \(g_0\) is ALE of order \(n-1\). Let furthermore \(\Pi :{\mathbb {R}}^n\setminus B_R\rightarrow ({\mathbb {R}}^n\setminus B_R)/\Gamma \) be the projection map. From now on, we consider the objects on M as objects on \({\mathbb {R}}^n\setminus B_R\) by identifying them with the pullbacks under the map \(\Pi \circ \varphi ^{-1}\). To avoid any confusion, we denote the pullback of \(\Delta _{g_0}\) by \(\Delta \). The operator \(\Delta _0\) denotes the Euclidean Laplacian on \({\mathbb {R}}^n\setminus B_R\).
Let \(r_0=|z|\) be the euclidean norm as a function on \({\mathbb {R}}^n\setminus B_R\). Then we have, for any \(\beta \in {\mathbb {R}}\),
Let \(u=h_{ij}\) for any i, j. For any constant \(A>0\), we have
If we choose \(\beta >0\) so that \(\beta +2<\mu <n\), we can choose A so large that
The strong maximum principle then implies that \(u=\textit{O}(r_0^{-\beta })\) and we also get \(\Delta u=\textit{O}(r_0^{-\beta -2})\). By elliptic regularity, \(u\in W^{2,p}_{-\beta }({\mathbb {R}}^n\setminus B_R)\) for all \(p\in [1,\infty )\). We now claim that we can (5) to prove \(\Delta _0 u\in L^{p}_{-2\beta -2}({\mathbb {R}}^n\setminus B_R)\). To do so, we first compute
Here \(\partial \) denotes the coordinate derivative on \({\mathbb {R}}^n\). We rewrite (5) schematically as
A combination of these two formulas combined with standard estimates yields
and the right-hand side is finite because \(g_0-\delta =O(r^{-n+1})\), \(\Gamma (g_0)=O(r^{-n})\), \(\partial \Gamma (g_0)=O(r^{-n-1})\), \(\mathrm{Rm}(g_0)=O(r^{-n-1})\) and \(\beta <n-2\). This proves the claim.
Recall that a weight parameter \(\delta \in {\mathbb {R}}\) is called exceptional if \(k\notin {\mathbb {Z}}\setminus \left\{ -1,-2,\ldots ,3-n\right\} \). Now for all nonexceptional values \(-\gamma \), [9, Theorem 1.7] implies that the Euclidean Laplacian is an isomorphism as a map
Thus for all nonexceptional values \(-\gamma \) satisfying \(\gamma<2\beta <2(n-2)\), there exists a function \(v^{\gamma }_{ij}\in W^{2,p}_{-\gamma }({\mathbb {R}}^n\setminus B_R)\) such that \(\Delta _0v^{\gamma }_{ij}=\Delta _0h_{ij}\). By the expansion of harmonic functions on \({\mathbb {R}}^n\), we have
Here, \(z=(z_1,\ldots ,z_n)\) denotes the coordinates on \({\mathbb {R}}^n\) so that \(|z|=r_0\). Sobolev embedding implies \(v^{\gamma }_{ij}\in C^{1,\alpha }_{1-n}({\mathbb {R}}^n\setminus B_R)\). Therefore,
We now can use Proposition 2.6 to improve this decay rate slightly by getting rid of the \(A_{ij}\). In fact, the proposition implies that the equations \(\mathrm {Ric}(g)=0\) and \(V(g,g_0)=0\) hold individually. Therefore,
which implies that \(A_{ij}=0\) and thus, \(h=\textit{O}(r^{-n+1})\). As \(h_{ij}=v^{\gamma }_{ij}+\textit{O}(r_0^{-n+1})\) with \(v^{\gamma }_{ij}\in W^{2,p}_{-\gamma }({\mathbb {R}}^n\setminus B_R)\) and an harmonic remainder term, Sobolev embedding and elliptic regularity imply that \(h_{ij}\in C^{1,\alpha }_{1-n}({\mathbb {R}}^n\setminus B_R)\), so that \(\nabla ^{g_0} h=\textit{O}(r^{-n})\). Elliptic regularity for weighted Hölder spaces ([25, Theorem 4.21] again) implies that \(\nabla ^{g_0,k} h=\textit{O}(r^{-n+1-k})\) for all \(k\in {\mathbb {N}}\). \(\square \)
Lemma 2.9
Let \(p\in [2,\infty )\), \(\tau \in {\mathbb {R}}\) and a fixed ALE metric be given. Let h be a section in a Riemannian vector bundle with connection. If \(h\in L^{\infty }\) with \(\nabla h\in W^{1,p}_{\tau +1}\), we have \(|\nabla h|^2\in L^p_{\tau }\) and the weighted interpolation inequality
Proof
By density, we may assume that h is compactly supported. To avoid differentiability issues at 0, we introduce the quantity \(|h|_{\delta }=(\langle h,h\rangle +\delta )^{1/2}\). Recall that \(\rho \) is the weight function on the manifold. Then we compute
where we used that \(|\nabla \rho |\) is bounded in the last step. By letting \(\delta \rightarrow 0\), we obtain
By the Young inequality,
Therefore,
Let us choose \(\epsilon <\frac{1}{2C}\). Then we obtain, by subtracting the first term on the right-hand side and by dividing by a constant
Taking the p-th root yields, with a new constant C:
Inserting \(\alpha =-\tau p-n\) yields the desired inequality. \(\square \)
Remark 2.10
The proof of the above theorem also applies to \(h\in \ker _{L^2}(L_{g_0})\) with the only difference that the first equality in (7) is replaced by the formula \(0=\mathrm{div}_{g_0}h-\frac{1}{2}\nabla ^{g_0}\mathrm{tr}_{g_0} h\) but which admits the same asymptotic expansion. This formula in turn holds because h is a TT-tensor due to Proposition 2.5. Therefore we can conclude that \(h=\textit{O}_{\infty }(r^{-n+1})\) if \(h\in \ker _{L^2}(L_{g_0})\).
Theorem 2.11
Let \((M,g_0)\) be an ALE Ricci-flat metric and \({\mathcal {F}}\) as above. Then there exists an \(L^2\cap L^{\infty }\)-neighbourhood \({\mathcal {U}}\) of \(g_0\) in the space of metrics and a finite-dimensional real-analytic submanifold \({\mathcal {Z}}\subset {\mathcal {U}}\) with \(T_{g_0}{\mathcal {Z}}=ker_{L^2}(L_{g_0})\) such that \({\mathcal {U}}\cap {\mathcal {F}}\) is an analytic subset of \({\mathcal {Z}}\). In particular if \(g_0\) is integrable, we have \({\mathcal {U}}\cap {\mathcal {F}}={\mathcal {Z}}\).
Proof
Let \(\Phi :g\mapsto -2\mathrm{Ric}(g)+{{\mathscr {L}}}_{V(g,g_0)}(g)\) and \({\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\epsilon )\) be the \(\epsilon \)-ball with respect to the \(L^2\cap L^{\infty }\)-norm induced by \(g_0\) and centred at \(g_0\). By Theorem 2.7, we can choose \(\epsilon >0\) be so small that any \(g\in {\mathcal {F}}\cap {\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\epsilon )\) satisfies the condition \(g-g_0=\textit{O}_{\infty }(r^{-n+1}\)) so that \(\left\| g-g_0\right\| _{H^k_{\delta }}<\infty \) for any \(k\in {\mathbb {N}}\) and \(\delta >-n+1\).
Suppose now in addition that \(k>n/2+2\) and \(\delta \le -n/2\) and let \({\mathcal {V}}\) be a \(H^k_{\delta }\)-neighbourhood of \(g_0\) with \({\mathcal {V}}\subset {\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\epsilon _1)\). Then the map \(\Phi \), considered as a map \(\Phi : H^k_{\delta }(S^2T^*M)\supset {\mathcal {V}}\rightarrow H^{k-2}_{\delta -2}(S^2T^*M)\) is a real-analytic map between Hilbert manifolds. If \(\delta \) is nonexceptional, the differential \(\mathrm{d}\Phi _{g_0}=L_{g_0}: H^k_{\delta }(S^2T^*M)\rightarrow H^{k-2}_{\delta -2}(S^2T^*M)\) is Fredholm. By [20, Lemma 13.6], there exists (possibly after passing to a smaller neighbourhood) a finite-dimensional real-analytic submanifold \({\mathcal {W}}\subset {\mathcal {V}}\) with \(g_0\in {\mathcal {W}}\) and \(T_{g_0}{\mathcal {W}}=\ker _{H^k_{\delta }}(L_{g_0})\) such that \({\mathcal {V}}\cap \Phi ^{-1}(0)\subset {\mathcal {W}}\) is a real-analytic subset.
By the proof of Theorem 2.7, we can choose an \(L^2\cap L^{\infty }\)-neighbourhood \({\mathcal {U}}_{g_0}\subset {\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\epsilon )\) of \(g_0\) so small that \({\mathcal {U}}_{g_0}\cap {\mathcal {F}}\subset {\mathcal {V}}\) (provided that \({\mathcal {V}}\) is small enough). Then the set \({\mathcal {Z}}={\mathcal {U}}_{g_0}\cap {\mathcal {W}}\) fulfils the desired properties because \(T_{g_0}{\mathcal {Z}}=T_{g_0}{\mathcal {W}}=\ker _{H^k_{\delta }}(L_{g_0})=\ker _{L^2}(L_{g_0})\) due to the asymptotics of elements in \(\ker _{L^2}(L_{g_0})\) shown in Proposition 2.7 and Remark 2.10. \(\square \)
Proposition 2.12
Let \((M^n,g_0)\) be an ALE Ricci-flat manifold and let \(k>n/2+1\) and \(\delta \in (-n+1, -n/2]\) nonexceptional. Then there exists a \(H^k_{\delta }\)-neighbourhood \({\mathcal {U}}^k_{\delta }\) of \(g_0\) in the space of metrics such that the set
is a smooth manifold. Moreover, for any \(g\in {\mathcal {U}}_{\delta }^k\), there exists a unique diffeomorphism \(\varphi \) which is \(H^{k+1}_{\delta +1}\)-close to the identity such that \(\varphi ^*g\in {\mathcal {G}}_{\delta }^k\).
Proof
Let \({\mathcal {U}}\) be a \(H^{k}_{\delta }\)-neighbourhood of \(g_0\) in the space of metrics such that the map \(V:H^k_{\delta }(S^2T^*M)\supset {\mathcal {U}}\rightarrow H^{k-1}_{\delta -1}(TM)\), given by \(V(g)^l=V(g,g_0)^l=g^{ij}(\Gamma (g)_{ij}^l-\Gamma (g_0)_{ij}^l)\) is well-defined. Linearization at \(g_0\) yields the map \(F:H^k_{\delta }(S^2T^*M)\rightarrow H^{k-1}_{\delta -1}(TM)\), defined by \(F(h)=(\mathrm {div}_{g_0}h)^{\sharp }-\frac{1}{2}\nabla ^{g_0}\mathrm {tr}_{g_0}h\). To prove the theorem, it suffices to prove that F is surjective and that the decomposition
holds (here, \({{\mathscr {L}}}_X(g_0)\) denotes the Lie-Derivative of \(g_0\) along X). In fact, a calculation shows that \(F\circ {{\mathscr {L}}}(g_0)= \Delta _{g_0}+\mathrm{Ric}(g_0)(\cdot )=\Delta _{g_0}\) since \(g_0\) is Ricci-flat. Since the map \(\Delta _{g_0}:H^{k+1}_{\delta +1}(\Lambda ^1M)\rightarrow H^{k-1}_{\delta -1}(\Lambda ^1M)\) is an isomorphism, it follows that F is surjective and \(\ker F\cap {{\mathscr {L}}}(g_0)(H^{k+1}_{\delta +1}(TM))=\left\{ 0\right\} \). To show that
let \(h\in H^k_{\delta }(S^2T^*M)\) and \(X\in H^{k+1}_{\delta +1}(TM)\) the unique solution of \(F(h)=\Delta _{g_0} X=F( {{\mathscr {L}}}_X(g_0))\). Then \(h=(h-{{\mathscr {L}}}_X(g_0))+{{\mathscr {L}}}_X(g_0)\) is the desired decomposition. By surjectivity of F, \({\mathcal {G}}_{\delta }^k\) is a manifold. The second assertion follows because the map
is a local diffeomorphism around \(g_0\) due to the implicit function theorem and the above decomposition. \(\square \)
Remark 2.13
The construction in Proposition 2.12 is similar to the slice provided by Ebin’s slice theorem [15] in the compact case. The set \({\mathcal {F}}\) is similar to the local premoduli space of Einstein metrics defined in [20, Definition 2.8]. In contrast to the compact case, the elements in \({\mathcal {F}}\) close to \(g_0\) can all be homothetic. In fact, this holds for the Eguchi–Hanson metric, see [28]. More generally, any four-dimensional ALE hyperkähler manifold (M, g) admits a three-dimensional subspace of homothetic metrics in \({\mathcal {F}}\): see [34, p. 52–53].
2.3 ALE Ricci-Flat Kähler Spaces
Lemma 2.14
(\(\partial {\bar{\partial }}\)-Lemma for ALE manifolds) Let (M, g, J) be an ALE Kähler manifold, \(\delta +2\le -n/2+2\) nonexceptional, \(k\ge 1\) and \(\alpha \in H^k_{\delta }(\Lambda ^{p,q}M)\). Suppose that
-
\(\alpha =\partial \beta \) for some \(\beta \in H^{k+1}_{\delta +1}(\Lambda ^{p-1,q}M)\) and \({\bar{\partial }}\alpha =0\) or
-
\(\alpha ={\bar{\partial }}\beta \) for some \(\beta \in H^{k+1}_{\delta +1}(\Lambda ^{p,q-1}M)\) and \({\partial }\alpha =0\).
Then there exists a form \(\gamma \in H^{k+2}_{\delta +2}(\Lambda ^{p-1,q-1}M)\) such that \(\alpha =\partial {\bar{\partial }}\gamma \). Moreover, we can choose \(\gamma \) to satisfy the estimate \(\left\| \gamma \right\| _{H^{k+2}_{\delta +2}}\le C\cdot \left\| \alpha \right\| _{H^{k}_{\delta }}\) for some \(C>0\).
Proof
This follows along the lines of Lemma 5.50 in [4], except that we have to replace the standard Sobolev spaces by weighted ones to capture the ALE condition. Let \(d=\partial \) or \(d={\bar{\partial }}\) and \(\Delta =\Delta _{\partial }=\Delta _{{\bar{\partial }}}\). Consider \(\Delta \) as an operator \(\Delta :H^{k+2}_{\delta +2}(\Lambda ^{*}M)\rightarrow H^{k}_{\delta }(\Lambda ^{*}M)\). Because of the assumption on \(\delta \), it is Fredholm and we have the \(L^2\)-orthogonal decomposition
for \(\delta \in [-n+1,-n/2)\) [17, Theorem 8.4.1]. Moreover, Fredholm properties of elliptic operators on ALE manifolds (see e.g. [27, Sect. 10]) imply that \(\Delta \) is a Fredholm map of index zero on these spaces. Thus, we can define the Green’s operator G which is zero on \(\ker _{L^2}(\Delta )\) and the inverse of \(\Delta \) on \(\ker _{L^2}(\Delta )^{\perp }\). This defines a continuous linear operator \(G:H^{k}_{\delta }(\Lambda ^{*}M)\rightarrow H^{k+2}_{\delta +2}(\Lambda ^{*}M)\). By Hodge theory and because \(d+d^* :H^{k+1}_{\delta +1}(\Lambda ^{*}M)\rightarrow H^{k}_{\delta }(\Lambda ^{*}M)\) is also Fredholm,
and it is straightforward to see that G is self-adjoint and commutes with d and \(d^*\). As in Ballmann’s book, one shows that \(\gamma =-G\partial ^*{\bar{\partial }}^*G\alpha \) does the job in both cases. The estimate on \(\gamma \) follows from construction. For \(\alpha \in H^k_{\delta }(\Lambda ^{p,q}M)\) with \(\delta \le -n+1\), we get \(\gamma \in H^{k+2}_{\delta '+2}(\Lambda ^{p,q}M)\) for any \(\delta '> -n+1\). But as in [17, Theorem 8.4.4], the fact that \(\alpha =\partial {\bar{\partial }}\gamma \) allows us to deduce \(\gamma \in H^{k+2}_{\delta +2}(\Lambda ^{p,q}M)\). \(\square \)
Let (M, g, J) be a Kähler manifold. An infinitesimal complex deformation is an endomorphism \(I:TM\rightarrow TM\) that anticommutes with J and satisfies \({\bar{\partial }}I=0\) and \({\bar{\partial }}^*I=0\). By the relation \(IJ+JI=0\), I can be viewed as a section of \(\Lambda ^{0,1}M\otimes T^{1,0}M\).
Theorem 2.15
Let \((M^n,g,J)\) be an ALE Kähler manifold with a holomorphic volume form, \(k>n/2+1\), \(\delta \le -n/2\) nonexceptional and \(I\in H^k_{\delta }(\Lambda ^{0,1}M\otimes T^{1,0}M)\) such that \({\bar{\partial }}I=0\) and \({\bar{\partial }}^*I=0\). Then there exists a smooth family of complex structures J(t) with \(J(0)=J\) such that \(J(t)-J\in H^k_{\delta }(T^*M\otimes TM)\) and \(J'(0)=I\).
Proof
The proof follows along the lines of Tian’s proof by the power series approach [33]: We write \(J(t)=J(1-I(t))(1+I(t))^{-1}\), where \(I(t)\in H^k_{\delta }(\Lambda ^{0,1}M\otimes T^{1,0}M)\) and I(t) has to solve the equation
where [., .] denotes the Frölicher–Nijenhuis bracket. If we write I(t) as a formal power series \(I(t)=\sum _{k\ge 1} I_kt^k\), the coefficients have to solve the equation
inductively for all \(N\ge 2\). As \(\Lambda ^{n,0}M\) is trivial, there is a natural identification of the bundles \(\Lambda ^{0,1}M\otimes T^{1,0}M=\Lambda ^{n-1,1}M\) by using the holomorphic volume form and we now think of the \(I_k\) as being \((n-1,1)\)-forms. Initially, we have chosen \(I_1\in H^k_{\delta }(\Lambda ^{0,1}M\otimes T^{1,0}M)\), given by \(I=2I_1J\). By the multiplication property of weighted Sobolev spaces [13, p. 538], \([I_1,I_1]\in H^{k-1}_{\delta -1}(\Lambda ^{n-1,2}M)\). Using \(\partial I_1=0\) and \({\bar{\partial }}^*I_1=0\), one can now show that \({\bar{\partial }}[I_1,I_1]=0\) and \([I_1,I_1]\) is \(\partial \)-exact. The \(\partial {\bar{\partial }}\)-lemma now implies the existence of a \(\psi \in H^{k+1}_{\delta +1}(\Lambda ^{n-2,1}M)\) such that
and so, \(I_2=\partial \psi \in H^{k}_{\delta }(\Lambda ^{n-1,1}M)\) does the job. Inductively, we get a solution of the equation
by the \(\partial {\bar{\partial }}\)-lemma since the right-hand side is \({\bar{\partial }}\)-closed and \(\partial \)-exact (which in turn is true because \(\partial I_k=0\) for \(1\le k\le N-1\)). Now we can choose \(I_N=\partial \psi \in H^{k}_{\delta }(\Lambda ^{n-1,1}M)\).
Let us prove the convergence of the above series: Let \(D_1\) be the constant in the estimate of the \(\partial {\bar{\partial }}\)-lemma and \(D_2\) be the constant such that
Then one can easily show by induction that
for \(N\ge 1\), where C(N) is the sequence defined by \(C(1)=1\) and \(C(N)=\sum _{i=1}^{N-1}C(i)\cdot C(N-i)\) for \(N>1\). By defining \(D:=2/(D_1\cdot D_2)\) and \(s=\frac{1}{2}D_1\cdot D_2\cdot \left\| I_1\right\| _{H^{k}_{\delta }}\cdot t\), we get
if \(s<1/4\) which shows that the series converges. Thus \(I(t)\in H^{k}_{\delta }(\Lambda ^{n-1,1}M)\) and \(J(t)-J=-2JI(t)(1+I(t))^{-1}\in H^{k}_{\delta }(\Lambda ^{n-1,1}M)\cong H^{k}_{\delta }(\Lambda ^{0,1}M\otimes T^{1,0}M)\). \(\square \)
The proof of the above theorem provides an analytic immersion \(\Theta :H^{k}_{\delta }(\Lambda ^{0,1}M\otimes T^{1,0}M)\cap \ker _{L^2}(\Delta )\supset U\rightarrow H^{k}_{\delta }(T^*M\otimes TM)\) whose image is a smooth manifold of complex structures which we denote by \({\mathcal {J}}^k_{\delta }\) and whose tangent map at J is just the injection.
Proposition 2.16
Let \((M,g_0,J_0)\) be an ALE Calabi–Yau manifold, \(\delta <2-n\) nonexceptional and \({\mathcal {J}}^k_{\delta }\) be as above. Then there exists a \(H^{k}_{\delta }\)-neighbourhood \({\mathcal {U}}\) of J and a smooth map \(\Phi :{\mathcal {J}}^k_{\delta }\cap {\mathcal {U}}\rightarrow {\mathcal {M}}^k_{\delta }\) which associates to each \(J\in {\mathcal {J}}^k_{\delta }\cap {\mathcal {U}}\) sufficiently close to \(J_0\) a metric g(J) which is \(H^k_{\delta }\)-close to \(g_0\) and Kähler with respect to J. Moreover, we can choose the map \(\Phi \) such that
Proof
We adapt the strategy of Kodaira and Spencer [19, Sect. 6]. Let \(J_t\) be a family in \({\mathcal {J}}^k_{\delta }\) and define \(J_t\)-hermitian forms \(\omega _t\) by \(\Pi ^{1,1}_{t}\omega _0(X,Y)=\frac{1}{2}(\omega _0(X,Y)+\omega _0(J_tX,J_tY))\). Let \(\partial _t,{\bar{\partial }}_t\) the associated Dolbeaut operators and \(\partial _t^*,{\bar{\partial }}_t^*\) their formal adjoints with respect to the metric \(g_t(X,Y):=\omega _t(X,J_tY)\). We now define a forth-order linear differential operator \(E_t:H^k_{\delta }(\Lambda ^{p,q}_tM)\rightarrow H^{k-4}_{\delta -4}(\Lambda ^{p,q}_tM)\) by
It is straightforward to see that \(E_t\) is formally self-adjoint and strongly elliptic. Moreover, \(\alpha \in \ker _{H^k_{\delta }}(E_t)\) if and only if \(\partial _t\alpha =0\), \({\bar{\partial }}_t\alpha =0\) and \({\bar{\partial }}^*_t\partial _t^*\alpha =0\), i.e. \(d\alpha =0\) and \({\bar{\partial }}^*_t\partial _t^*\alpha =0\) hold simultaneously. If \(\delta \) is nonexceptional, \(E_t\) is Fredholm which allows us to define for each t its Greens operator \(G_t:H^{k-4}_{\delta -4}(\Lambda ^{p,q}_tM)\rightarrow H^k_{\delta }(\Lambda ^{p,q}_tM)\). As in [19, Proposition 7], one now shows that
is an \(L^2(g_t)\) orthogonal decomposition. The dimension of \(\ker _{L^2}(E_t)\cap H^k_{\delta }(\Lambda ^{1,1}_tM)\) is constant for small t which implies that \(G_t\) depends smoothly on t. The proof of this fact is exactly as in [19, Proposition 8].
Now observe that \(E_t\omega _t\in H^{k-4}_{\delta -4}(\Lambda ^{1,1}_tM)\) if \(\omega _t\) and \(J_t\) are \(H^k_{\delta }\)-close to \(\omega _0\) and \(J_0\), respectively. This allows us to define
where \(u_t\in H^{k+2}_{\delta +2}(M)\) is a smooth family of functions such that \(u_0=0\) which will be defined later. Clearly,
As \({\bar{\omega }}_t\) is \(H^k_{\delta }\)-close to \(\omega _0\), \(\nabla ^{g_t}{\bar{\omega }}_t\in H^{k-1}_{\delta -1}(g_t)\), since \(\omega _0\) is \(g_0\)-parallel. Therefore, \(\nabla ^{g_t}{\bar{\omega }}_t=\textit{O}(r^{-\alpha -1}) \) and \(\nabla ^{g_t,2}\bar{\omega _t}=\textit{O}(r^{-\alpha -2})\) for any \(\alpha <-\delta \). Thus, if we choose the nonexceptional value \(\delta \) so that \(\delta <-n+2\), integration by parts implies that
Therefore, \({\bar{\omega }}_t\) and hence also \({\tilde{\omega }}_t\) is closed. Differentiating at \(t=0\) yields
Because \(d{\tilde{\omega }}_t=0\), we have \(d{\tilde{\omega }}'_0=0\) and since \(J_0'\) is an infinitesimal complex deformation, \(E_0\omega '_0=0\) and \(d\omega '_0=0\) which implies that
Let now \( v\in H^{k+2}_{\delta +2}(M) \) so that \(\partial _0{\bar{\partial }}_0v=G_0(E_0'\omega _0).\) Then define \(u_t\in H^{k+2}_{\delta +2}(M) \) by
By this choice, \( {\tilde{\omega }}_0'=\omega '_0\) and the assertion for \(\mathrm{d}\Phi _{J_0}(J'_0)={\tilde{g}}_0'\) follows immediately. Finally, \({\tilde{g}}_t(X,Y):={\tilde{\omega }}_t(X,J_tY)\) is a Riemannian metric for t small enough and it is Kähler with respect to \(J_t\). \(\square \)
Remark 2.17
Let \(J_t\) is a smooth family of complex structures in \({\mathcal {J}}^k_{\delta }\cap {\mathcal {U}}\) and \(g_t=\Phi (J_t)\). Then the construction in the proof above shows that \(I=J'_0\) and \(h=g'_0\) are related by
Before we state the next theorem, recall the notation \({\mathcal {G}}_{\delta }^k\) we used in Proposition 2.12.
Theorem 2.18
Let \((M^n,g_0,J_0)\) be an ALE Calabi–Yau manifold and \(\delta \in (1-n,2-n)\) nonexceptional. Then for any \(h\in \ker _{L^2}(L_{g_0})\), there exists a smooth family g(t) of Ricci-flat metrics in \({\mathcal {G}}^k_{\delta }\) with \(g(0)=g_0\) and \(g'_0=h\). Each metric g(t) is ALE and Kähler with respect to some complex structure J(t) which is \(H^k_{\delta }\)-close to \(J_0\). In particular, \(g_0\) is integrable.
Proof
We proceed similarly as in [3, Chapter 12], except the fact that we use weighted Sobolev spaces. Given a complex structure J close to \(J_0\) and a J-(1, 1)-form \(\omega \) which is \(H^{k}_{\delta }\)-close to \(\omega _0\), we seek a Ricci-flat metric in the cohomology class \([\omega ]\in {\mathcal {H}}^{1,1}_J(M)\). As the first Chern class vanishes, there exists a function \(f_{\omega }\in H^{k}_{\delta }(M)\) such that \(i\partial {\bar{\partial }}f_{\omega }\) is the Ricci form of \(\omega \). If \({\bar{\omega }}\in [\omega ]\) and \({\bar{\omega }}-\omega \in H^{k}_{\delta }(\Lambda ^{1,1}_{J}M)\), the \(\partial {\bar{\partial }}\)-lemma implies that there is a \(u\in H^{k+2}_{\delta +2}(M)\) such that \({\bar{\omega }}=\omega +i\cdot \partial {\bar{\partial }}u\). Ricci-flatness of \({\bar{\omega }}\) is now equivalent to the condition
Let \({\mathcal {J}}^k_{\delta }\) be as above and \(\Delta _J\) the Dolbeaut Laplacian of J and the metric g(J). Then all the \((L^2_{\delta })\)-cohomologies \({\mathcal {H}}^{1,1}_{J,\delta }(M)=\ker _{L^2_{\delta }}(\Delta _J)\cap L^2_{\delta }(\Lambda ^{1,1}M)\) are isomorphic for \(J\in {\mathcal {J}}^k_{\delta }\) if we choose \({\mathcal {J}}^k_{\delta }\) is small enough: We have \({\mathcal {H}}^2_{\delta }(M)={\mathcal {H}}^{2,0}_{J,\delta }(M)\oplus {\mathcal {H}}^{1,1}_{J,\delta }(M)\oplus {\mathcal {H}}^{0,2}_{J,\delta }(M)\). The left-hand side is independent of J and the metric g(J) is provided by Proposition 2.16. The spaces on the right-hand side are kernels of J-dependent elliptic operators whose dimension depends upper-semicontinuously on J. However the sum of the dimensions is constant and so the dimensions must be constant as well.
Thus, there is a natural projection \(pr_{J}:\ker _{L^2}(\Delta _{J_0})\rightarrow \ker _{L^2}(\Delta _{J})\) which is an isomorphism. We now want to apply the implicit function theorem to the map
where \(\omega (J)(X,Y):=g(J)(JX,Y)\) and g(J) is the metric constructed in Proposition 2.16. We have \(G(J_0,0,0)=0\) and the differential restricted to the third component is just given by \(\Delta :H^{k+2}_{\delta +2}(M)\rightarrow H^{k}_{\delta }(M)\) (cf. [3, p. 328]), which is an isomorphism. Therefore we find a map \(\Psi \) such that \(G(J,\kappa , \Psi (J,\kappa ))=0\).
Let now \(h\in \ker _{L^2}(L_{g_0})\) and let \(h=h_H+h_A\) its decomposition into a \(J_0\)-hermitian and a \(J_0\)-anti-hermitian part. We want to show that h is tangent to a family of Ricci-flat metrics. We have seen in Theorem 2.7 together with Remark 2.10 that \(h\in H^k_{\delta }(S^2T^*M)\) for all \(\delta >1-n\) and we can define \(I\in H^k_{\delta }(T^*M\otimes TM)\) and \(\kappa \in H^k_{\delta }(\Lambda ^{1,1}_{J_0})(M)\) by
It is easily seen that I is a symmetric endomorphism satisfying \(IJ_0+J_0I=0\) and thus can be viewed as \(I\in H^k_{\delta }(\Lambda ^{0,1}M\otimes T^{1,0}M)\). Moreover, because \(h_A\) is a TT-tensor, \({\bar{\partial }} I=0\) and \({\bar{\partial }}^*I=0\). In addition \(\kappa \in {\mathcal {H}}^{1,1}_{J_0}(M)\). The proof of this facts is as in [20]. Let \(J(t)=\Theta (t\cdot I)\) be a family of complex structures tangent to I and \({\tilde{\omega }}(t)={\tilde{\Phi }}(J(t))\) be the associated family of Kähler forms. We consider the family \(\omega (t)={\tilde{\omega }}(t)+pr_{J(t)}(t\cdot \kappa )+i\partial {\bar{\partial }} \Psi (J(t),t\cdot \kappa )\) and the associated family of Ricci-flat metrics \({\tilde{g}}(t)(X,Y)=\omega (t)(X,J(t)Y)\). It is straightforward that \({\tilde{g}}'(0)=h\). By Proposition 2.12, there exist diffeomorphisms \(\varphi _t\) with \(\varphi _0=id\) such that \(g(t)=\varphi _t^*{\tilde{g}}(t)\in {\mathcal {G}}^k_{\delta }\). We obtain \(g'(0)=h+{{\mathscr {L}}}_{X}g_0\) for some \(X\in H^{k+1}_{\delta +1}(TM)\). Since h is a TT-tensor due to Lemma 2.5, \(h\in T_{g_0}{\mathcal {G}}_{\delta }^{k}\). On the other hand, \(g'(0)\in T_{g_0}{\mathcal {G}}_{\delta }^{k}\) as well which implies that \(g'(0)=h\) due to the decomposition in Proposition 2.12.
By Theorem 2.11, the set of stationary solutions of the Ricci–DeTurck flow \({\mathcal {F}}\) close to \(g_0\) is an analytic set contained in a finite-dimensional manifold \({\mathcal {Z}}\) with \(T_{g_0}{\mathcal {Z}}=\ker _{L^2}(L_{g_0})\). The above construction provides a smooth map \(\Xi :\ker _{L^2}(L_{g_0})\supset {\mathcal {U}}\rightarrow {\mathcal {F}}\subset {\mathcal {Z}}\) whose tangent map is the identity. Therefore, there exists a \(L^2\cap L^{\infty }\)-neighbourhood \({\mathcal {U}}\) of \(g_0\) in the space of metrics such that \({\mathcal {F}}\cap {\mathcal {U}}={\mathcal {Z}}\cap {\mathcal {U}}\). \(\square \)
Let \(h\in C^{\infty }(S^2T^*M)\) and \(h_H,h_A\) its hermitian and anti-hermitian part, respectively. The hermitian and anti-hermitian part are preserved by \(L_{g_0}\). Let \(I=I(h_A)\) and \(\kappa =\kappa (h_H)\) be defined as in (8). Then we have the relations \(I(L(h_A))=\Delta _C(I(h_A))\) and \(\kappa (L(h_H) )=\Delta _H(\kappa (h_H))\), where \(\Delta _C\) and \( \Delta _H\) are the complex Laplacian and the Hodge Laplacian acting on \(C^{\infty }(\Lambda ^{0,1}M\otimes T^{1,0}M)\) and \(C^{\infty }(\Lambda ^{1,1}_{J_0}M)\), respectively. For details see [20] and [3, Chap. 12]. As a consequence, we get
Theorem 2.19
(Koiso) If \((M,g_0,J_0)\) is an ALE Ricci-flat Kähler manifold, it is linearly stable.
3 Ricci Flow
Our main result of this section is the following
Theorem 3.1
Let \((M^n,g_0)\) be an ALE Ricci-flat manifold. Assume it is linearly stable and integrable. Then for every \(\epsilon >0\), there exists a \(\delta >0\) such that the following holds: For any metric \(g\in {\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\delta )\), there is a complete Ricci–DeTurck flow \((M^n,g(t))_{t\ge 0}\) starting from g converging to an ALE Ricci-flat metric \(g_{\infty }\in {\mathcal {B}}_{L^2\cap L^{\infty }}(g_0,\epsilon )\).
3.1 An Expansion of the Ricci Flow
Let us fix an ALE Ricci-flat manifold \((M^n,g_0)\) once and for all. Recall the definition of the Ricci flow
where h is a symmetric 2-tensor on M (denoted by \(h\in S^2T^*M\)) such that g(0) is a metric. The Ricci–DeTurck flow is given by
where \(V(g(t),g_0)\) is a vector field defined locally by \(V^k=g(t)^{ij}(\Gamma (g(t))_{ij}^k-\Gamma (g_0)_{ij}^k)\) and globally by
Following [31, Lemma 2.1], the Ricci–DeTurck flow can be written in coordinates as
For our purposes, we calculate a different expansion: Let \({\bar{g}}\) and g two Riemannian metrics on a given manifold and \(h:=g-{\bar{g}}\). Then a careful computation shows that in local coordinates,
where \(g^{uv},{\bar{g}}^{uv}\) are the inverse matrices of \(g_{uv},{\bar{g}}_{uv}\), respectively. For a calculation, see for instance [5, p. 15]. Furthermore, if a background metric \(g_0\) is fixed and if \(V=V(g,g_0)\) is defined as above, then we have the expansion
Thus for \(V=V(g,g_0)\) and \({\bar{V}}=V({\bar{g}},g_0)\), we have
Now if \({\bar{g}}\) is a Ricci-flat metric that additionally satisfies \({\bar{V}}=0\), we can write the Ricci–DeTurck flow as an evolution of the difference \(h(t):=g(t)-{\bar{g}}\) for which we get
where \(\langle h,\Gamma ({\bar{g}})-\Gamma (g_0)\rangle ^k=h_{pq}{\bar{g}}^{pi}{\bar{g}}^{qj}(\Gamma ({\bar{g}})_{ij}^k-\Gamma (g_0)_{ij}^k)\) and \(*\) denotes a linear combination of tensor products and contractions with respect to the metric \({\bar{g}}\). The tensors F and G depend on \(g^{-1}\) and \(\Gamma (g_0)\).
3.2 Short-Time Estimates and an Extension Criterion
In this subsection we recall the short-time estimates of \(C^k\)-norms and an extension criterion for the Ricci–DeTurck flow. In addition, we prove some new Shi-type estimates for \(L^2\)-type Sobolev norms. For the sake of simplicity, all covariant derivatives and norms in this subsection are taken with respect to \(g_0\).
Lemma 3.2
(A priori short-time \(C^k\)-estimates) Let \((M,g_0)\) be a complete Ricci-flat manifold of bounded curvature. Then there exist constants \(\epsilon >0\) and \(\tau \ge 1\) such that if g(0) is a metric satisfying
there exists a Ricci–DeTurck flow \((g(t))_{t\in [0,\tau ]}\) with initial metric g(0) which satisfies the estimates
Moreover, \((g(t))_{t\in [0,\tau )}\) is the unique Ricci–DeTurck flow starting at g(0) which satisfies
In particular, this implies the following: if \((g(t))_{t\in [0,\infty )}\) is a Ricci–DeTurck flow and such that it is in \({\mathcal {B}}_{L^{\infty }}(g_0,\epsilon )\) for all time, then there exist constants such that
Proof
The same statement is given in [6, Proposition 2.8] for the case of negative Einstein metrics. The proof is standard and translates easily to the present situation. For more details, see e.g. [5, Sect. 3.7]. \(\square \)
Lemma 3.3
(A priori short-time \(L^2\)-estimate) Let \((M,g_0)\) be an ALE Ricci-flat manifold. Then there exists an \(\epsilon =\epsilon (n,g_0)>0\) with the following property: Suppose that \((g(t))_{t\in [0,T_{max})}\) is a Ricci–DeTurck flow such that \(h(t)=g(t)-g_0\) satisfies \(\Vert h(t)\Vert _{L^{\infty }}<\epsilon \) for all \(t\in [0,T_{max})\) and \(\Vert h(0)\Vert _{L^2}<\infty \). Then \(\Vert h(t)\Vert _{L^2}<\infty \) for all \(t\in (0,T_{max})\) and there exists a constant \(C=C(n,g_0)\) such that
Proof
By (10), we can rewrite the Ricci–DeTurck flow with gauge \(g_0\) in the schematic form
For each \(R>0\), let \(\eta _R:[0,\infty )\) be a function such that \(\eta _R(r)=1\) for \(r\le R\), \(\eta _R(r)=0\) for \(r\ge 2R\) and \(|\nabla \eta _R|\le 2/R\). For \(x\in M\), let \(\phi _{R,x}(y)=\eta _R( d(x,y))\). Then \(\phi _{R,x}\equiv 1\) on \(B_R(x)\), \(\phi _{R,x}\equiv 0\) on \(M\setminus B_{2R}(x)\) and \(|\nabla \phi _{R,x}|\le 2/R\). For notational convenience, we write \(\phi =\phi _{R,x}\) in the following. By (11), we obtain
for an appropriate choice of \(\delta \). Define
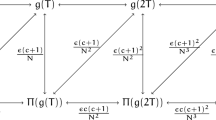
As \((M,g_0)\) is ALE, there exists a constant \(N=N(n)\) such that each ball on M of radius 2R can be covered by N balls of radius R. Thus, by integration in time,
Consequently,
and by the Gronwall inequality,
The assertion follows from letting \(R\rightarrow \infty \). \(\square \)
Lemma 3.4
(A priori short-time \(H^k\)-estimates) Let \((M,g_0)\) be an ALE Ricci-flat manifold. Then there exists an \(\epsilon =\epsilon (n,g_0)>0\) with the following property: Suppose that \((g(t))_{t\in [0,T_{max})}\) is a Ricci–DeTurck flow such that \(h(t)=g(t)-g_0\) satisfies
Then for each \(T\in (0,T_{max})\) and \(k\in {\mathbb {N}}\) there exist constants \(C_k=C_k(n,g_0,T)\) such that if \(\Vert h(t)\Vert _{L^2}\le K\) for all \(t\in [0,T]\), we get
In particular, if \((g(t))_{t\in [0,T_{max})}\) is a Ricci flow satisfying \(\Vert h(t)\Vert _{L^{\infty }}<\epsilon \) and \(\Vert h(t)\Vert _{L^2}<K\) as long as \(t\in [0,T_{max})\), then there exist constants \(C_k=C_k(n,g_0)\) such that
Proof
The proof follows from a delicate argument involving a sequence of cutoff functions. By differentiating (11), we get
Let \(\phi \) be a cutoff function as in the proof of Lemma 3.3. Then
Let us consider each of these terms separately. Then we get
and
In the estimates of the higher order terms, we use the property \(\Vert \nabla ^k h\Vert _{L^{\infty }}\le C_k t^{-k/2}\epsilon \), which follows from Lemma 3.2. It also implies \(\Vert \nabla ^k F\Vert _{L^{\infty }}\le C\cdot t^{-k/2}\) and \(\Vert \nabla ^k G\Vert _{L^{\infty }}\le C\cdot t^{-k/2}\) for \(t\in (0,T]\) and \(k\in {\mathbb {N}}\).
For the last term, we first perform integration by parts:
The first of these terms is estimated by
where we used the Peter–Paul inequality \(ab\le \delta a^2+\frac{1}{4\delta }b^2\). For the second of these terms, we estimate
where we again used the Peter–Paul inequality. Summing up, we get
Assuming that \(\epsilon ,\delta >0\) are small enough, we therefore get
In the following, let \(x\in M\) and \(\phi _l:M\rightarrow [0,1]\), \(0\le l\le k\) a sequence of cutoff functions with the following properties:
Obviously, we get \(\phi _l\le \phi _{l-1}\) for \(1\le l\le k\) and, if \(R\ge 2\), \(|\nabla \phi _l|\le \phi _{l-1}\) for \(1\le l\le k\). We now define a function \(F_k:[0,T]\rightarrow {\mathbb {R}}\) as
where \(A_l\) are some positive constants we will choose later. Then we can compute
Note that we used the properties \(\phi _l\le \phi _{l-1}\) and \(|\nabla \phi _l|\le \phi _{l-1}\) in the above estimate. Now if we choose \(A_k,A_{k-1},\ldots A_0\) inductively such that
for all \(t\in [0,T]\), then
so that we get \(F_k(t)\le C(g_0,k,T)\cdot \sup _{t\in [0,T]} \int _M |h|^2\,\mathrm{d}\mu \) for all \(t\in [0,T]\). The result now follows from letting \(R\rightarrow \infty \). \(\square \)
We conclude this section with some very general result due to [29] giving a criteria for ensuring infinite time existence.
Theorem 3.5
(Criteria for infinite time existence) Let \((M^n,g_0)\) be a complete Riemannian manifold such that \(\Vert \mathrm{Rm}(g_0)\Vert _{L^{\infty }}=:k_0<+\infty \). Then there exists a positive constant \({\tilde{\delta }}={\tilde{\delta }}(n,k_0)\) such that the following holds. Let \(0<\beta <\delta \le {\tilde{\delta }}\). Then every metric g(0) \(\beta \)-close to \(g_0\) has a \(\delta \)-maximal solution \(g(t)_{t\in [0,T(g(0)))}\) with T(g(0)) positive and \(\Vert g(t)-g_0\Vert _{L^{\infty }}<\delta \) for all \(t\in [0,T(g(0)))\). The solution is \(\delta \)-maximal in the following sense. Either \(T(g(0))=+\infty \) and \(\Vert g(t)-g_0\Vert _{L^{\infty }}<\delta \) for any nonnegative time t or we can extend \((g(t))_t\) to a solution on \(M^n\times [0,T(g(0))+\tau )\), for some positive \(\tau =\tau (n,k_0)\) and \(\Vert g(T(g(0)))-g_0\Vert _{L^{\infty }}=\delta .\)
3.3 A Local Decomposition of the Space of Metrics
In order to prove convergence of a Ricci–DeTurck flow g(t) to a Ricci-flat metric \(g_{\infty }\), we have to construct a family \(g_0(t)\) of Ricci-flat reference metrics. For the proof of the main theorem, it is necessary to construct \(g_0(t)\) in such a way that \(\partial _t g_0= \textit{o}((g-g_0)^2)\). This section is devoted to this construction. For this purpose, let \({\mathcal {F}}\) again be given by
If \(g_0\) satisfies the integrability condition, then there exists an \(L^2\cap L^{\infty }\)-neighbourhood \({\mathcal {U}}\) of \(g_0\) in the space of metrics such that
is a manifold and for all \(g\in \widetilde{{\mathcal {F}}}\), the equations \(\mathrm{Ric}(g)=0\) and \({{\mathscr {L}}}_{V(g,g_0)}g=0\) hold individually by Proposition 2.6. Linearization of these two conditions shows that the tangent space \(T_g\widetilde{{\mathcal {F}}}\) is given by the kernel of the map
where \(\langle h,\Gamma (g)-\Gamma (g_0)\rangle ^k=g^{ik}g^{lj}h_{kl}(\Gamma (g)_{ij}^k-\Gamma (g_0)_{ij}^k)\) and \(L_g\) is the Lichnerowicz Laplacian of g.
The next lemma ensures that the kernels \(\ker L^*_{g,g_0}\) all have the same dimension when g is an ALE Ricci-flat metric sufficiently close to \(g_0\):
Lemma 3.6
Let \((M^n,g_0)\) be a linearly stable ALE Ricci-flat manifold which is integrable. Furthermore, let \(\widetilde{{\mathcal {F}}}\) be as in (12). Then there exists an \(L^2\cap L^{\infty }\)-neighbourhood \({\mathcal {U}}\) of \(g_0\) in the space of metrics such that \(\dim \ker _{L^2} L^*_{g,g_0}=\dim \ker _{L^2} L_{g_0}\) for all \(g\in \widetilde{{\mathcal {F}}}\).
Proof
First, we claim that elements in the kernel of \(L_{g,g_0}\) have decay rate \(-(n-1)\). This follows along the lines of the proof of Theorem 2.7 and we are able to establish (6) if \(h\in \ker _{L^2}L_{g,g_0}\). To improve the decay, we use the special algebraic structure of the operator \(L_{g,g_0}\) by considering the divergence and the trace with respect to g of \(L_{g,g_0}h\):
which implies the following relation:
Since the vector field \(\mathrm{div}_gh-\frac{\nabla ^g\mathrm{tr}_gh}{2}-\langle h,\Gamma (g)-\Gamma (g_0)\rangle \) goes to 0 at infinity, the maximum principle ensures that
An asymptotic expansion of this equation analogous to (7) shows that \(h=\textit{O}(r^{-(n-1)}).\) In particular, the previous claim implies that
where \(\delta \in (-n+1,-n/2]\) is a nonexceptional weight and k can be any natural number.
Now, \(L_{g_0}=L_{g_0,g_0}\) is Fredholm as a map from \(H^k_{\delta }(S^2T^*M)\) to \(H^{k-2}_{\delta -2}(S^2T^*M)\) with Fredholm index 0. The same holds for \(L_g\) with \(g\in {\mathcal {F}}\) in a sufficiently small neighbourhood of \(g_0\). Observe that \(L_{g,g_0}-L_g\) is a bounded operator as a map from \(H^k_{\delta }(S^2T^*M)\) to \(H^{k-2}_{\delta -2}(S^2T^*M)\), with arbitrarily small norm operator. Therefore, by the openness of the set of Fredholm operators with respect to the operator norm, \(L_{g,g_0}\) has the same index as \(L_{g_0,g_0}\), which is 0. Therefore we get
\(\square \)
Now we claim that if \({\mathcal {U}}\) is small enough, every metric \(g\in {\mathcal {U}}\) can be decomposed uniquely as \(g={\bar{g}}+h\) where \({\bar{g}}\in \widetilde{{\mathcal {F}}}\) and \(h\in \overline{L_{{\bar{g}},g_0}(C^{\infty }_{0}(S^2T^{*}M))}\) (where the closure is taken with respect to \(L^2\cap L^{\infty }\)). Indeed, this follows from the implicit function theorem applied to the map
where \(\left\{ e_1({\bar{g}}),\ldots e_m({\bar{g}})\right\} \) is an \(L^2({\bar{g}})\) orthonormal basis of \(\ker _{L^2}(L_{{\bar{g}},g_0}^*)\) which can be chosen to depend smoothly on \({\bar{g}}\) by Lemma 3.6.
Let now \((g(t))_{t\in [0,T)}\) be a Ricci–DeTurck flow in \({\mathcal {U}}\) and \((g_0(t))_{t\in [0,T)}\in \widetilde{{\mathcal {F}}}\) be the family of Ricci-flat metrics such that
Writing \(h(t)=g(t)-g_0\) and \(h_0(t)=g_0(t)-g_0\), we see that \(h(t)-h_0(t)=g(t)-g_0(t)\) admits the expansion
where the connection is now with respect to \(g_0(t)\).
Before stating the next lemma, we need to recall the Hardy inequality for Riemannian manifolds with nonnegative Ricci curvature and positive asymptotic volume ratio due to Minerbe [26, Theorem 2.23]:
Theorem 3.7
(Minerbe) Let \((M^n,g)\) be a Riemannian manifold with nonnegative Ricci curvature and Euclidean volume growth, i.e.
for some (and hence all) \(x\in M\). Then
where \(r_x(y)=\mathrm{d}(x,y)\).
The next lemma controls the time derivative of \(h_0\) in the \(C^k\) topology in terms of the \(L^2\) norm of the gradient of \(h-h_0\).
Lemma 3.8
Let \({\mathcal {U}}\) be an \(L^2\cap L^{\infty }\)-neighbourhood of \(g_0\) such that the above decomposition holds. Let \((g(t))_{t\in [0,T)}\) be a Ricci–DeTurck flow in \({\mathcal {U}}\) and let \(g_0(t)\), h(t), \(h_0(t)\) be defined as above for \(t\in [0,T)\). Then we have the following estimate that holds for \(t\in (0,T)\):
Proof
Let \(\left\{ e_1(t),\ldots e_m(t)\right\} \) be a family of \(L^2(\mathrm{d}\mu _{g_0(t)})\)-orthonormal bases of \(\ker _{L^2}\left( {L}_{g_0(t),g_0}^*\right) \). Note that \(\partial _te_i(t)\) depends linearly on \(\partial _th_0(t)\). We can write
for some \(k(t_0)\in \overline{L_{g_0(t_0),g_0}(C^{\infty }_{0}(S^2T^{*}M))}=:N\). Note that by this condition on \(k(t_0\)), we have \((k(t_0),e_i(t_0))_{L^2}=0\) for all \(i\in \left\{ 1,\ldots m\right\} \). Therefore, differentiating at time \(t_0\) yields
where A depends linearly on both entries. Let us split this expression into \(A=A_{\widetilde{{\mathcal {F}}}}+A_{N}\) according to the decomposition \(T_{g_0(t_0)}\widetilde{{\mathcal {F}}}\oplus N\). If we also split \(h'=h'_{\widetilde{{\mathcal {F}}}}+h'_{N}\), we get
By inverting, we conclude that
Note that the orthogonal projection \(\Pi :T_{g_0(t_0)}\widetilde{{\mathcal {F}}}\rightarrow \ker _{L^2}\left( {L}_{g_0(t_0),g_0}^*\right) \) is an isomorphism. Because \(\partial _th={L}_{g_0(t),g_0}(h-h_0)+R[h-h_0]\) and by elliptic regularity,
We used the Hardy inequality (Theorem 3.7) and the fact that \(r\nabla ^{g_0(t)} e_i\) is bounded by elliptic regularity in the last step. \(\square \)
Before proving Theorem 3.1, we start by recalling a result by Devyver [14, Definition 6] adapted to our context:
Theorem 3.9
(Strong positivity of \(L_{g_0}\)) Let \((M^n,g_0)\) be an ALE Ricci-flat space that is linearly stable. Then the restriction of \(-L_{g_0}\) to the orthogonal of \(\ker _{L^2}(L_{g_0})\) is strongly positive, i.e. there exists some positive \(\alpha _{g_0}\in (0,1]\) such that
Sketch of proof
The proof is as in [14] with some minor modifications we point out here. Write \(-L_{g_0}=-\Delta _{g_0}+R_+-R_-\) where \(R_+\) and \(R_-\) correspond to the positive (resp. nonpositive) eigenvalues of \(Rm(g_0)*\). Let \(H=-\Delta _{g_0}+R_+\) and \(A:L^2(S^2T^*M)\rightarrow L^2(S^2T^*M)\) be defined by \(A=H^{-1/2}R_-H^{-1/2}\). The operator A is compact [12, Corollary 1.3] Because \(-L_{g_0}\) is nonnegative, all eigenvalues of A lie in [0, 1]. It can be shown that \(H^{1/2}\) maps \(\ker _{L^2}(L_{g_0})\) isomorphically to \(\ker _{L^2}(1-A)\). As A is a compact operator, we get the condition
for some \(\epsilon >0\) which in turn is equivalent to
\(\square \)
Theorem 3.10
Let \((M^n,g_0)\) be a linearly stable ALE Ricci-flat manifold which is integrable. Furthermore, let \(\widetilde{{\mathcal {F}}}\) be as in (12). Then there exists a constant \(\alpha _{g_0}>0\) such that
for all \(g\in \widetilde{{\mathcal {F}}}\) and \(h\in L_{g_0(t),g_0}(C^{\infty }_{0}(S^2T^{*}M))\) provided that \(\widetilde{{\mathcal {F}}}\) is chosen small enough.
Proof
By Theorem 3.9, there exists a constant \(\alpha _0>0\) such that
for any compactly supported \(h\in \ker _{L^2}(L_{g_0})^{\perp }\). Now by Taylor expansion, with \(k=g-g_0\)

for some \(\sigma \in (0,1)\). To justify the last inequality, we use elliptic regularity and Sobolev embedding as in the proof of Theorem 2.7 to obtain
with \(\sigma =1-\frac{2}{p}\) and \(p>n\). This can be combined with the Hardy inequality (3.7) to obtain
which yields the estimate of the theorem for \(h\in \ker _{L^2}(L_{g_0})^{\perp }\), provided that \(\left\| k\right\| _{L^{\infty }(g_0)}\) is small enough. To pass to \(h\in \ker _{L^2}({L}_{g,g_0}^*)^{\perp }\), we note that an isomorphism between \(\ker _{L^2}(L_{g_0})^{\perp }\) and \( \ker _{L^2}({L}_{g,g_0}^*)^{\perp }\) is given by \(\Phi _g:h\mapsto h-\sum _i(h,e_i(g))_{L^2(g)}\cdot e_i(g)\) where the tensors \(e_i(g)\) are an orthonormal basis of \(\ker _{L^2}({L}_{g,g_0}^*)\). At first, we have
from which we conclude, using integration by parts
The first inequality here can be proven as follows: Because \(e_i=\textit{O}(r^{-n+1})\) as \(r\rightarrow \infty \) (cf. Theorem 2.7), we have
due to the Hardy inequality The same argument also yields
because \(\Delta _ge_i=\textit{O}(r^{-n-1})\) as \(r\rightarrow \infty \) (cf. Theorem 2.7 again). This justifies the first inequality from above. For the second inequality, we write
and \((\Gamma (g_0)-\Gamma (g))=\textit{O}(r^{-n})\), see Theorem 2.7. Again by the Hardy inequality,
Here, we use the smallness of \(\left\| g-g_0\right\| _{L^{\infty }(g_0)}\) to compare the corresponding \(L^2\)-norms. To finish the proof, it remains to show that the inequality
holds for some constant \(C>0\). We compute
where we also used the Sobolev inequality and elliptic regularity. \(\square \)
3.4 Existence for all Time and Convergence
Proposition 3.11
Let \((M,g_0)\) be a linearly stable ALE Ricci-flat manifold which satisfies the integrability condition. Then there exists an \(\epsilon >0\) with the following property: If \((g(t))_{t\in [0,T]}\) is a Ricci–DeTurck flow and T a time such that \(\left\| g(t)-g_0\right\| _{L^{\infty }}<\epsilon \) for all \(t\in [0,T]\), then there exists a constant such that the evolution inequality

holds.
Proof
We know that
where
Thanks to Theorem 3.10 and Lemma 3.8,
which proves the desired estimate. \(\square \)
Proof of Theorem 3.1
Let \(\epsilon >0\) be so small that Proposition 3.11 holds, provided that \(\left\| h\right\| _{L^{\infty }(g_0)}<\epsilon \). By Lemma 3.2, we can find \(\delta _1>0\) so small that the above \(\epsilon \)-bound holds as long as \(h\in {\mathcal {B}}_{L^2\cap L^{\infty }}(0,\delta _1)\). Now let \(\delta _2>0\) be so small that \(h(1)\in {\mathcal {B}}_{L^2\cap L^{\infty }}(0,\delta _1)\) if \(h(0)\in {\mathcal {B}}_{L^2\cap L^{\infty }}(0,\delta _2)\) where \(\delta _2=\delta _2(\epsilon )\) will be chosen below. Suppose that \(T_{max}\ge 1\) is the first time where h(t) leaves \({\mathcal {B}}_{L^2\cap L^{\infty }}(0,\epsilon )\). By Lemma 3.8, Proposition 3.11 and elliptic regularity,
Furthermore by Proposition 3.11,
Again by Proposition 3.11, Lemma 3.2 and interpolation,
with \(\alpha =\frac{n}{n+2}\).
By the triangle inequality,
provided that \(\delta _1>0\) was chosen small enough. We now have proven that such a \(T_{max}\) can not exist and that \(h(t)\in {\mathcal {U}}\) for all \(T>0\).
Moreover, because
and since
by Lemma 3.4, we get
and \(h_0(t)\) converges in \(L^2\) to some limit \(h_0(\infty )\). Due to elliptic regularity, \((h_0(t))_{t\ge 0}\) converges to \(h_0(\infty )\) as t goes to \(+\infty \) with respect to all Sobolev norms. We are going to show now that \((g(t))_{t\ge 0}\) converges to \(g_0+h_0(\infty )=: g_{\infty }\) as t goes to \(+\infty \) with respect to all \(W^{k,p}\)-norms with \(p>2\). For this purpose, it suffices to show that \((h(t)-h_0(t))_{t\ge 0}\) converges to 0 as t goes to \(+\infty \) with respect to all these norms. At first, by the Euclidean Sobolev inequality,
which implies that \(\lim _{t\rightarrow +\infty }h-h_0=0\) in \(L^p\) for all \(p\in (2,\infty )\) by interpolation and due to smallness in \(L^2\cap L^{\infty }\). Moreover, for \(j\in {\mathbb {N}}\) arbitrary, by interpolation inequalities,
as \(t\rightarrow +\infty \) with \(\alpha =\frac{jp}{mp+n}\) and \(m\in {\mathbb {N}}\) so large that \(\alpha <1\). Due to Sobolev embedding, convergence also holds for \(p=\infty \). \(\square \)
4 Nash–Moser Iteration at Infinity
In this section, we prove a decay of the \(L^{\infty }\) norm of the difference between an immortal solution to the Ricci–DeTurck flow with gauge an ALE Ricci-flat metric \(g_0\) and the metric \(g_0\) itself. More precisely, one has the following theorem:
Theorem 4.1
Let \((M^n,g_0)\) be a complete Riemannian manifold endowed with a Ricci-flat metric with quadratic curvature decay at infinity, i.e.
for some positive constant C and some point \(x_0\in M\). Let \((M^n,g(t))_{t\ge 0}\) be an immortal solution to the Ricci–DeTurck flow with respect to the background metric \(g_0\) such that
for some positive universal \(\epsilon \). Then, for any positive time t, and radius \(r<\sqrt{t}\),
In particular, if \(\sup _{t\ge 0}\Vert g(t)-g_0\Vert _{L^2(M)}\le C<+\infty \), then
Remark 4.2
Notice that \(P(x_0,t,r)\) is the parabolic neighbourhood of a point at infinity on the manifold M.
Before starting the proof of this theorem, we remark that by combining Theorems 3.1 and 4.1 leads to Theorem 1.1.
Proof of Theorem 4.1
Recall that \((g(t))_{ t\ge 0}\) (or similarly \(h(t):=g(t)-g_0\)) satisfies the following partial differential equation:
In particular,
Since \(\Vert h(t)\Vert _{L^{\infty }(M)}\le \epsilon \) for any positive time t:
if \(\epsilon \le \epsilon (n)\). Define \(u:=|h|_{g_0}^2\) and multiply the previous differential inequality by \(pu^{p-1}\) for some real \(p\ge 2\) to get:
Take any smooth space-time cutoff function \(\psi \) and multiply the previous differential inequality by \(\psi ^2u^p\) and integrate by parts as follows:
for any \(t'\in (t-r^2,t].\)
Now, by integrating by parts once and using the pointwise Young inequality:
for some universal positive constant c, and where we used the smallness of \(\Vert h(t)\Vert _{L^{\infty }(M)}\) for all time t. Going back to (14) and (15), one gets by absorbing terms appropriately:
Finally, by integrating by parts with respect to time:
We need to control the integral involving the potential \({{\mathcal {R}}}(g_0)\). By assumption, on the quadratic curvature decay at infinity:
Let \(\tau , \sigma \in (0,+\infty )\) such that \(\tau +\sigma \le r\). Define momentarily,
Notice that \(s_1<s_2\) implies \(P(x_0,t,r,s_1)\subset P(x_0,t,r,s_2).\)
Now, choose two smooth functions \(\phi :{\mathbb {R}}_+\rightarrow [0,1]\) and \(\eta :{\mathbb {R}}_+\rightarrow [0,1]\) such that
Define \(\psi (y,s):=\phi (d_{g_0}(x_0,y))\eta (s)\), for \((y,s)\in M\times (0,+\infty )\). Then
for some uniform positive constant c.
In particular, thanks to claim (16) applied to this cutoff function \(\psi \) previously defined, one has:
which implies in particular that
Now, by Hölder inequality, for \(s\ge 0\),
Therefore, to sum it up, if \(\alpha _n:=1+2/n\), by using (17) in the third line,
Define the following sequences:
Then, \(\lim _{i\rightarrow +\infty }\tau _i= r/2\) and, for any \(i\ge 0\),
i.e.
since \(P(x_0,t,r,r/2)=P(x_0,t,r/2)\). It remains to estimate the previous infinite product:
i.e.
To get a bound depending on the \(L^1\) norm of u, one can proceed as in [23] (the so-called Li–Schoen’s trick) by iterating (18) appropriately. \(\square \)
Change history
12 August 2021
A Correction to this paper has been published: https://doi.org/10.1007/s12220-021-00732-y
References
Anselmi, D., Billó, M., Fré, P., Zaffaroni, A., Girardello, L.: ALE manifolds and conformal field theories. Int. J. Mod. Phys. A 9(17), 3007–3057 (1994)
Appleton, A.: Scalar curvature rigidity and Ricci DeTurck flow on perturbations of Euclidean space. Calc. Var. Partial Differ. Equ. 57(5), 23 (2018). Art. 132
Arthur, L.: Besse. Einstein Manifolds. Classics in Mathematics. Springer, Berlin (2008). Reprint of the 1987 edition
Ballmann, W.: Lectures on Kähler Manifolds. ESI Lectures in Mathematics and Physics. European Mathematical Society (EMS), Zürich (2006)
Bamler, R.H.: Stability of Einstein Metrics of Negative Curvature. ProQuest LLC, Ann Arbor, MI (2011). Thesis (Ph.D.). Princeton University, Princeton
Bamler, R.H.: Stability of hyperbolic manifolds with cusps under ricci flow. Adv. Math. 263, 412–467 (2014)
Bamler, R.H., Zhang, Q.S.: Heat kernel and curvature bounds in Ricci flows with bounded scalar curvature. Adv. Math. 319, 396–450 (2017)
Bando, S., Kasue, A., Nakajima, H.: On a construction of coordinates at infinity on manifolds with fast curvature decay and maximal volume growth. Invent. Math. 97(2), 313–349 (1989)
Bartnik, R.: The mass of an asymptotically flat manifold. Commun. Pure Appl. Math. 39(5), 661–693 (1986)
Bertolini, M., Campos, V.L., Ferretti, G., Fré, P., Salomonson, P., Trigiante, M.: Supersymmetric 3-branes on smooth ALE manifolds with flux. Nuclear Phys. B 617(1–3), 3–42 (2001)
Carfora, M.: Renormalization group and the Ricci flow. Milan J. Math. 78(1), 319–353 (2010)
Carron, G.: \(L^2\)-cohomologie et inégalités de Sobolev. Math. Ann. 314(4), 613–639 (1999)
Choquet-Bruhat, Y.: General Relativity and the Einstein Equations. Oxford Mathematical Monographs. Oxford University Press, Oxford (2009)
Devyver, B.: A Gaussian estimate for the heat kernel on differential forms and application to the Riesz transform. Math. Ann. 358(1–2), 25–68 (2014)
Ebin, D.G.: The manifold of Riemannian metrics. In: Global Analysis (Proceedings of Symposia in Pure Mathematics, Vol. XV, Berkeley, CA, 1968), pp. 11–40. American Mathematical Society, Providence, RI (1970)
Haslhofer, R., Müller, R.: Dynamical stability and instability of Ricci-flat metrics. Math. Ann 360, 547–553 (2014)
Joyce, D.D.: Compact Manifolds with Special Holonomy. Oxford Mathematical Monographs. Oxford University Press, Oxford (2000)
Koch, H., Lamm, T.: Geometric flows with rough initial data. Asian J. Math. 16(2), 209–235 (2012)
Kodaira, K., Spencer, D.C.: On deformations of complex analytic structures. III. Stability theorems for complex structures. Ann. Math. (2) 71, 43–76 (1960)
Koiso, N.: Einstein metrics and complex structures. Invent. Math. 73(1), 71–106 (1983)
Kröncke, K.: Stability and instability of Ricci solitons. Calc. Var. Partial Differ. Equ. 53(1–2), 265–287 (2015)
Kronheimer, P.B.: A Torelli-type theorem for gravitational instantons. J. Differ. Geom. 29(3), 685–697 (1989)
Li, P., Schoen, R.: \(L^p\) and mean value properties of subharmonic functions on Riemannian manifolds. Acta Math. 153(3–4), 279–301 (1984)
Lockhart, R.B., McOwen, R.C.: Elliptic differential operators on noncompact manifolds. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 12(3), 409–447 (1985)
Marshall, S.: Deformations of special Lagrangian submanifolds. PhD thesis, University of Oxford, (2002). http://people.maths.ox.ac.uk/joyce/theses/MarshallDPhil.pdf
Minerbe, V.: Weighted Sobolev inequalities and Ricci flat manifolds. Geom. Funct. Anal. 18(5), 1696–1749 (2009)
Pacini, T.: Desingularizing isolated conical singularities: uniform estimates via weighted Sobolev spaces. Commun. Anal. Geom. 21(1), 105–170 (2013)
Page, D.N.: A physical picture of the k3 gravitational instanton. Phys. Lett. B 80(1), 55–57 (1978)
Schnürer, O.C., Schulze, F., Simon, M.: Stability of hyperbolic space under Ricci flow. Commun. Anal. Geom. 19(5), 1023–1047 (2011)
Sesum, N.: Linear and dynamical stability of Ricci-flat metrics. Duke Math. J. 133(1), 1–26 (2006)
Shi, W.-X.: Deforming the metric on complete Riemannian manifolds. J. Differ. Geom. 30(1), 223–301 (1989)
Simon, M.: Extending four dimensional Ricci flows with bounded scalar curvature (2015). ArXiv e-prints
Tian, G.: Smoothness of the universal deformation space of compact Calabi–Yau manifolds and its Petersson–Weil metric. In: Mathematical Aspects of String Theory (San Diego, CA, 1986). Advances in Mathematical Physics, vol. 1, pp. 629–646. World Sci. Publishing, Singapore (1987)
Viaclovsky, J.A.: Critical Metrics for Riemannian Curvature Functionals (2014). ArXiv e-prints
Acknowledgements
This work was carried out while the authors were supported by the National Science Foundation under Grant No. DMS-1440140 while in residence at the Mathematical Sciences Research Institute (MSRI) in Berkeley, California, during the Spring 2016 semester. They wish to thank MSRI for their excellent working conditions and hospitality during this time.
Funding
Open access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deruelle, A., Kröncke, K. Stability of ALE Ricci-Flat Manifolds Under Ricci Flow. J Geom Anal 31, 2829–2870 (2021). https://doi.org/10.1007/s12220-020-00376-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-020-00376-4