Introduction

Fluids and space exploration have always been interconnected, with a critical relevance in manned missions. The reduced gravity environment of most space missions changes substantially the way fluids interact with their surroundings and respond to external forces or other variations in their conditions. In microgravity, surface tension is a major (if not exclusive) restoring force, favoring minimum surface energy interfaces. In this scenario, contact forces may cause a confined liquid to wet adjacent boundaries, while small external accelerations (Weislogel and Ross 1990), known as g-jitter, can drive large-scale motion of its center of mass (Salgado Sánchez et al. 2019b). Indeed, the absence of gravity has a profound impact not only in fluid systems and associated phenomena, but affects other fundamental processes like plant growth (Kordyum 2014) or gene expression (Hammond et al. 1999).

In the field of vibrated fluids, some interfacial phenomena are significantly enhanced under reduced gravity conditions. These include, among others, the vibroequilibria effect (Lyubimov et al. 1997; Beyer et al. 2001; Gavrilyuk et al. 2004; Fernández et al. 2017; Salgado Sánchez et al. 2019a) and the frozen wave instability (Lyubimov and Cherepanov 1986; Wunenburger et al. 1999; Gandikota et al. 2014; Gligor et al. 2020; Troitiño et al. 2020), which generates columnar patterns with interfaces oriented nearly perpendicular to the vibrational axis, upon which Faraday waves (Benjamin and Ursell 1954) can be excited as a secondary instability (Salgado Sánchez et al. 2019b; Gandikota et al. 2014; Shevtsova et al. 2016; Lyubimova et al. 2019; Labrador et al. 2021; Torres et al. 2023). Furthermore, g-jitter perturbations, which are characterized by constant and low-frequency accelerations (between 0.1 and \(1 \, \text {Hz}\)), can easily couple with fluid resonances and excite sloshing, a phenomenon that has attracted the attention from scientists and engineers since the 1960s, due to its importance in numerous terrestrial and space applications (Ibrahim 2001). For instance, sloshing behavior is observed in tanks of offshore extraction plants (Ueda et al. 2016), spacecrafts (Bourdelle et al. 2019; Govindan and Dreyer 2023), unmanned aerial vehicles (Ahmed et al. 2022) and road trucks (Cheli et al. 2012). Even on ground, the effects of gravity can be negligible for relatively small fluid systems with a characteristic size similar to the capillary length. One representative example is found on the dynamics of small vibrated droplets (Vukasinovic et al. 2007; Ivantsov et al. 2023), which are entirely selected by the applied vibrational forcing, with gravity playing little to no role.

Since the seminal work of Abramson (1966), the knowledge on sloshing phenomena has been vastly extended, simultaneously aiming to develop more precise mathematical models of sloshing motion (Faltinsen and Timokha 2009), along with the development of strategies to mitigate its (generally) adverse effects on fluid systems and, no less important, structural mechanics; see Faltinsen and Timokha (2009), Ibrahim et al. (2001) for more insight. Strategies to reduce sloshing and, in general, control fluids have long-standing relevance for both terrestrial and space applications, though they are expected to play a critical role on the latter. This control may simply involve an adequate system design or the deliberate use of certain phenomena to promote or suppress others (Porter et al. 2021).

Nowadays, several control strategies have been researched, although most of them base their performance on viscous effects for increased damping. In this regard, adding passive dampers (baffles) (Wang et al. 2019) increases the effective area of boundary layers and, by extension, viscous dissipation. Moreover, if strategically placed within the container, they interfere with the fluid bulk flow and potentially shift sloshing resonances to higher frequencies. As a direct consequence, the coupling with g-jitters or other (low-frequency) accelerations is reduced. Other strategies include leveraging contact properties (Utsumi 2017): the (viscous) friction work due to the contact angle hysteresis increases the damping ratio, although its effectiveness is limited to reduced-gravity environments.

Fig. 1
figure 1

(a, b) CAD views of the ThermoSlosh experiment: (a) experiment cell, (b) complete experiment set-up, including the optical (camera, lens and LED panel) and vibrational subsystems (base plate attached to a stepper motor). (c) Sample image of the free surface obtained with a ground prototype. Adapted from Salgado Sánchez et al. (2023)

Full size image

Additional studies have advanced the knowledge on baffle-based sloshing mitigation by analyzing the optimal shape, size, and placement of dampers in various container geometries; see Belakroum et al. (2010); Demirel and Aral (2018); Peromingo et al. (2023) and references therein. The work of Wang et al. (2019), for instance, analyzed the optimal positioning of annular dampers in cylindrical containers, achieving a maximum sloshing reduction of 76%. Similarly, Kim et al. (2018, 2020) proposed the use of a matrix of small air-trapping dampers along the container side walls, resulting in effective sloshing reductions ranging from 20% to 80%. Albeit passive baffles still remain as one of the most widespread sloshing mitigation strategies, other researchers have explored actively controlled dampers as well. The recent work of Xie and Zhao (2021) investigated the effect of two motion-controlled baffles and optimized the system using reinforcement learning, achieving an 80% reduction in sloshing.

Despite their effectiveness and simplicity, baffles can significantly increase the mass and/or volume of the fluid system, posing a significant challenge for space applications. Other strategies, however, remain relatively unexplored. The idea of using magnetic fields for sloshing control was first proposed in the 1960s and has been recently revisited by Romero-Calvo et al. (2020, 2021), demonstrating that ferrofluid-based fuels can be an effective alternative. Besides sloshing control, this approach has been also envisaged for reigniting liquid fuel engines during the secondary stages of rockets (Romero-Calvo et al. 2023) and has found applications, not only in fuel management, but also in phase separation and electrolysis (Romero-Calvo et al. 2022) in microgravity, where passive magnets are used to force the motion of bubbles generated during these processes, increasing overall efficiency.

More recently, Gligor et al. (2022a, b) discussed the use of the thermocapillary effect to control the steady and low-frequency dynamics of a free surface in microgravity, and evaluate its effectiveness for sloshing reduction in a real microgravity scenario considering a reboosting maneuver of the International Space Station (ISS). Compared to passive dampers, this thermocapillary-based strategy entails the main drawback of being active and requiring a power source, but it is this active nature that offers adaptability, particularly when implemented with feedback. Furthermore, it is relatively simple compared to active baffles, which may require complex mechanical designs with moving parts. Compared to magnetic-based management, thermocapillary controllers are more versatile, as they can be used with a wide range of fluids as long as suitable contact properties are present (Gligor et al. 2022b).

Furthermore, this thermocapillary control can be easily implemented in combination with baffles (Peromingo et al. 2023) or other control strategies like the use of vibrations (Salgado Sánchez et al. 2019a, 2020; Porter et al. 2021); the interaction of thermocapillary flows with vibrational excitation was also considered by Gligor et al. (2022a). Note that, on their own, vibrations generate various important interfacial phenomena, including harmonic and subharmonic waves — Faraday (Benjamin and Ursell 1954; Kumar and Tuckerman 1994) or cross-waves (Miles and Henderson 1990; Salgado Sánchez et al. 2016) —, frozen waves (Lyubimov and Cherepanov 1986; Talib et al. 2007), and vibroequilibria (Fernández et al. 2017; Salgado Sánchez et al. 2020; Porter et al. 2021). In microgravity, vibrations are also known to mimic certain gravity effects in phase transitions and convection (Beysens 2006), and the vibroequilibria effect can be viewed from this perspective too (Porter et al. 2021; Salgado Sánchez et al. 2019a, 2020).

In this context, the “Thermocapillary-based control of a free surface in microgravity" (ThermoSlosh) experiment (Salgado Sánchez et al. 2023) was recently presented to the 1st edition of the “International Space Science and Scientific Payload" competition, securing the second position (silver medal) in the competition final. ThermoSlosh proposes to explore the effectiveness of the thermocapillary effect and supplemental vibrations for fluid control in microgravity and related applications. The heart of the experiment is a cylindrical cell partially filled with liquid and subjected to controlled temperatures and accelerations. Figure 1(a, b) illustrates CAD views of the experiment cell and the complete set-up, respectively. Figure 1(c) shows a sample image of the free surface obtained with a ground prototype.

This work can be understood as a natural continuation of the ThermoSlosh project. Here, we present a detailed numerical analysis of the interfacial dynamics driven by thermal excitation and supplemental vibrations in a two-dimensional cylindrical cell holding different liquids in microgravity. Various silicone oils and a fluorinert are used due to their significance to previous microgravity research (Fernández et al. 2017; Salgado Sánchez et al. 2019a).

The structure of the manuscript is as follows. In Section 2, the governing equations and boundary conditions of the model, as well as the characteristics of the numerical simulations and initial conditions are detailed. Sections 3 and 4 present the results for fixed thermal gradient simulations with both static and dynamic contact angle models, and with supplemental vibrations, respectively. Then, interface positioning simulations that consider a classical proportional-integral-derivative controller are investigated in Section 5. Finally, in Section 6, we present conclusions and suggest lines of future research.

Mathematical Formulation

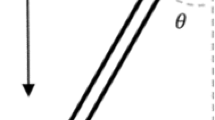
The two-dimensional dynamics of a cylindrical cell containing equal volumes of liquid and air in microgravity are investigated. A temperature difference \(\Delta T\) is applied between its lateral walls, whose temperatures are asymmetric deviations from the mean value \(T_0 = 25 ^{\circ }\)C. Additionally, vibrations directed along the local x-axis — referred to as horizontal vibrations, for simplicity — are applied. The interface between the air and the liquid moves in response to these excitations. Figure 2 shows a general sketch of the system.

Hereafter, the mathematical formulation used to describe the dynamics is introduced, starting with the governing equations and boundary conditions. For further details about the mathematical model, including mesh convergence tests and validation, the reader is referred to Gligor et al. (2022a, b), Salgado Sánchez et al. (2023).

Governing Equations and Boundary Conditions

Laminar and incompressible flow is considered. Thus, the conservation of mass, momentum, and energy in the fluids (liquid and air) can be described by the Navier-Stokes equations (Landau and Lifshitz 1987):

$$\begin{aligned} \nabla \cdot \textbf{u}_j = 0, \end{aligned}$$
(1a)
$$\begin{aligned} \rho _j \left( \frac{\partial \textbf{u}_j}{\partial t} + \textbf{u}_j \cdot \nabla \textbf{u}_j\right) = -\nabla p_j + \mu _j \, \Delta \textbf{u}_j&+ \rho _j \, \textbf{a}(t), \end{aligned}$$
(1b)
$$\begin{aligned} \rho _j \, c_{pj} \left( \frac{\partial T_j}{\partial t} + \textbf{u}_j \cdot \nabla T_j\right) = k_j \, \Delta T_j, \end{aligned}$$
(1c)

where the subscript j = 1, 2 refers to the liquid and air, respectively. These equations are characterized by the velocity, pressure, and temperature fields, \(\textbf{u}_j\), \(p_j\), \(T_j\), and by the density, dynamic viscosity, specific heat at constant pressure, and thermal conductivity of both fluids, \(\rho _j\), \(\mu _j\) = \(\rho _j \, \nu _j\), \(c_{pj}\), and \(k_j\).

Fig. 2
figure 2

Sketch of the two-dimensional numerical model: a cylindrical cell, holding equal volumes of liquid and air in microgravity, and subjected to a temperature difference \(\Delta T\) between its side walls and horizontal vibrations of magnitude \(A\omega\)

Full size image

The volumetric force \(\rho _j \, \textbf{a}(t)\) is included in Eq. (1b) to capture the effect of the applied horizontal vibrations:

$$\begin{aligned} \textbf{a}(t) = A\omega ^2 \cos \omega t \, \textbf{e}_x, \end{aligned}$$
(2)

where A and \(\omega\) are the vibrational amplitude and frequency, and (\(\textbf{e}_x, \, \textbf{e}_y\)) refer to the Cartesian basis.

At the liquid-air interface, \(F(\textbf{x}, \, t) = 0\), the balance between pressure, viscous stresses, and surface tension \(\sigma\) (Gligor et al. 2022b; Salgado Sánchez et al. 2023) reads:

$$\begin{aligned} \begin{aligned} (p_2 - p_1) \, \textbf{n} - \sigma \left( \nabla _s \cdot \textbf{n} \right) \, \textbf{n} + \nabla _s \, \sigma = \quad&\\ \left[ \mu _2\left( \nabla \textbf{u}_2 + \nabla \textbf{u}_2^T\right) - \mu _1\left( \nabla \textbf{u}_1 + \nabla \textbf{u}_1^T\right) \right]&\cdot \textbf{n}, \end{aligned} \end{aligned}$$
(3)

where \(\textbf{n}\) = \({\nabla F}/{|\nabla F |}\) is the unit vector normal to the interface, \(\nabla _s\) = \((\textbf{I} - \textbf{n}\,\textbf{n}^T) \nabla\) the surface gradient, \(\textbf{I}\) the identity matrix, and the following additional kinematic conditions apply:

$$\begin{aligned} \textbf{u}_2 - \textbf{u}_1 = 0, \end{aligned}$$
(4a)
$$\begin{aligned} \frac{\partial F}{\partial t} + \textbf{u}_1 \nabla F = 0. \end{aligned}$$
(4b)

The thermocapillary effect is described by the linearized dependence of \(\sigma\) on T:

$$\begin{aligned} \sigma = \sigma _0 - \gamma \, (T-T_0), \end{aligned}$$
(5)

where \(\gamma\) = \(|{\partial \sigma } / {\partial T} |\) is the thermocapillary coefficient at the reference temperature \(T_0\). This variation in \(\sigma\) generates thermocapillary flow, which carries the fluid along the interface from hotter regions with lower \(\sigma\) to colder regions with higher \(\sigma\).

On the inner (circular) boundary of the cell, the movement of contact points is allowed to preserve the contact angle \(\beta\) by imposing:

$$\begin{aligned} \textbf{u}_j \cdot \textbf{n}_w = 0, \end{aligned}$$
(6a)
$$\begin{aligned} \textbf{n} \cdot \textbf{n}_w = \cos \beta , \end{aligned}$$
(6b)

where \(\textbf{n}_w\) is the (inner) wall normal.

Table 1 Thermo-physical properties of 2, 5 and 20 cSt silicone oils and the fluorinert FC-40 at \(T_0 = 25 ^{\circ }\); extracted from Someya and Munakata (2005)
Full size table

Within the (aluminum) body of the cell of (external) dimensions \(L \times L\), the temperature field is described by a heat equation analogous to (1c), except for the convective term:

$$\begin{aligned} \rho _a \, c_{pa} \frac{\partial T_a}{\partial t} = k_a \, \Delta T_a, \end{aligned}$$
(7)

where \(\rho _a\), \(c_{pa}\), and \(k_a\) are the density, specific heat at constant pressure, and thermal conductivity of aluminum.

As detailed in each section, different boundary conditions for T are applied to the external walls of the cell. The temperature field in the cell is coupled with that of the fluids assuming continuity at the inner circular boundary:

$$\begin{aligned} T_j = T_a \; \; \; \text {at} \; \; \left( x-L/2\right) ^2 + \left( y-L/2\right) ^2 = R^2. \end{aligned}$$
(8)

Numerical Simulations

The results presented in this work have been obtained for an aluminum cell with an inner radius of \(R = 15 \, \text {mm}\) and dimensions \(L \times L = 40 \times 40 \, \text {mm}^2\) (Salgado Sánchez et al. 2023). The material properties of aluminum are \(\rho _a = 2700 \, \text {kg/m}^3\), \(k_a = 155 \, \text {W/(m K)}\), and \(c_{pa}\) = 1025 J/(kg K). As mentioned above, the cell contains equal volumes of liquid and air, with properties \(\rho _2\) = 1.225 kg/m\(^3\), \(\nu _2 = 1.5 \times 10^{-5} \, \text {m}^2/\text {s}\), \(k_2 = 0.024 \, \text {W/(m K)}\) and \(c_{p2} = 1006 \, \text {J/(kg K)}\). The liquids used in the analysis are 2, 5, and 20 \(\text {cSt}\) silicone oils as well as the fluorinert FC-40. The properties of these liquids have been extracted from the work of Someya and Munakata (2005) and are summarized in Table 1.

Following the work of Gligor et al. (2022a, b), we reduce the analysis to two-dimensional dynamics. From an experimental perspective, achieving two dimensional dynamics is possible with an appropriate cell design, where the third dimension is kept small (Salgado Sánchez et al. 2019b). In addition, previous two-dimensional simulations of interfacial dynamics have shown excellent agreement with microgravity experiments on vibrated immiscible liquids (Salgado Sánchez et al. 2019b, 2020).

In line with these simplifications, the temperature dependency of \(\rho _j\), \(\nu _j\) and \(k_j\) is neglected as well (Gligor et al. 2022a, b). In particular, neglecting the temperature dependence of density (i.e., thermal expansion) disables any potential effect of the generalized Boussinesq approach on the fluid dynamics and, by extension, the effect of thermovibrational convection (Birikh et al. 1993, 1994). In general, thermovibrational convection would fully develop at a timescale larger than the characteristic time of the free surface reorientation considered here (\(\sim 10\) s). Besides, the oscillatory (rotational) motion of the free surface until reaching the steady state has two additional effects: upon reorienting the free surface, the thermal gradient within the liquid bulk is no longer \(\Delta T\), but (a lower) one determined by the heat diffusion equation on the cell circular walls; the same reorientation drives some liquid region in direct contact to the aluminum walls to switch alternatively between hot and cold sides, and thus prevents them to develop a large thermal gradient buildup during the early stages of the reorientation motion; the reader is referred to Section 3 and (the supplementary material of) Salgado Sánchez et al. (2023) for further details. Due to these combined effects, we would expect thermovibrational convection to play a role only at timescales larger than that of the free surface reorientation and therefore, its contribution is neglected.

The commercial software COMSOL Multiphysics is used to resolve the formulation described in Section 2.1 in dimensional variables using the finite element method. The liquid-air interface dynamics is solved using a standard moving mesh scheme. The scheme follows the Arbitrary Lagrangian-Eulerian formulation, where the equations from Section 2.1 are written in mesh coordinates. These mesh coordinates are uniquely mapped to spatial coordinates in the fluid domains and are deformed using the Yeoh smoothing technique (Yeoh 1993) with a stiffness factor of 1000. This deformation follows the constraints imposed at the fluid domain boundaries: zero normal displacement at the circular wall and a mesh velocity \(\textbf{u}_{mesh} = \textbf{u}_1\) at the interface (Salgado Sánchez et al. 2023). A triangular mesh is employed with a maximum element size of \(R/15 \simeq 1 \ \text {mm}\), featuring minimum and mean element qualities of 0.62 and 0.88, respectively.

The contact angle \(\beta\) is considered both statically and dynamically. In this latter case, we follow the (implicit) dynamic model proposed by Kistler (1993):

$$\begin{aligned} \beta _{\infty ,D} = f\left[ \textrm{Ca} + f^{-1}\left( \beta _\infty \right) \right] , \end{aligned}$$
(9a)
$$\begin{aligned} \cos f = 1 - 2 \tanh \left[ {5.16} \left( \frac{x}{1+{1.31}x^{0.99}} \right) ^{0.706} \right] , \end{aligned}$$
(9b)

because its applicability to low viscosity fluids similar to those used in this research. Here, \(\textrm{Ca} = \mu \, u/\sigma _0\) is the capillary number, with u being the characteristic velocity of the contact line.

The initial conditions for temperature and velocity are \(T_1 = T_2 = T_a = T_0 = 25\, ^\circ\)C and \(\textbf{u}_1 = \textbf{u}_2 = 0\), respectively. For initialization purposes, we use the following smoothed (\(C^2\)-class) Heaviside function (Gligor et al. 2022b):

$$\begin{aligned} \mathcal {H}(t) = \left\{ \begin{matrix} 0, &{} t < 0, \\ \frac{t}{\tau } - \frac{1}{2\pi } \sin \left( \frac{2\pi t}{\tau }\right) , &{} \quad 0 \le t \le \tau , \\ 1, &{} t > \tau , \end{matrix} \right. \end{aligned}$$
(10)

where \(\tau\) is the initialization time. Simulations start with a completely flat interface at a 90\(^\circ\) contact angle that gradually reaches \(\beta _\infty\) by writing:

$$\begin{aligned} \beta (t) = 90^\circ + \left( \beta _\infty - 90^\circ \right) \mathcal {H}(t), \end{aligned}$$
(11)

where \(\beta _\infty\) is either the static or dynamic contact angle (9a) of the liquid, and \(\tau = 2\) s. For simplicity, we will refer to \(\beta _\infty\) as \(\beta\). Similarly, the temperature difference \(\Delta T\) and vibrational forcing \(A \omega\) are initialized sequentially once \(\beta\) is settled by writing \(\mathcal {H}( t - \tau _0)\), with \(\tau _0 = 2, \, 4\) s, respectively.

Finally, temporal integration is performed using a backward differentiation formula (BDF) scheme (Süli and Mayers 2003). BDF schemes constitute a family of implicit linear multistep methods used to numerically integrate ordinary differential equations. In the present formulation, this scheme is used along with streamline (Harari and Hughes 1992) and crosswind (Codina 1993) stabilization techniques. The maximum time step is \(0.1 \ \text {s}\), with smaller steps automatically used by the numerical scheme when the Courant-Friedrichs-Levy condition requires it. Recall that for further details about mesh convergence tests and validation, the reader is referred to Gligor et al. (2022a, b), Salgado Sánchez et al. (2023).

Results are presented hereafter. These are organized in: fixed thermal forcing, combined thermal and vibrational forcing, and interface positioning with feedback control simulations.

Fixed Thermal Forcing

In this section, we analyze the interface response when subjected to a constant \(\Delta T\) applied between the lateral walls of the cell. The upper and lower walls of the cell are considered adiabatic, as sketched in Fig. 2. The influence on the dynamics of the applied \(\Delta T\), the liquid viscosity \(\nu\), and contact angle \(\beta\) are investigated.

Fig. 3
figure 3

Time evolution of the free surface orientation for the 5 cSt silicone oil with \(\beta = 70^\circ\) and \(\Delta T = 5\) K. The response is characterized using the angle of the right contact point \(\Theta = \theta - \theta _0\). The figure indicates the first crossing time \(t_0\), stabilization time \(t_\infty\), stabilization angle \(\Theta _{\infty }\), and relative overshoot \(\mathcal {O} =\Theta _\textrm{max} - \Theta _\infty\)

Full size image

In Fig. 3, we provide an example of the temporal evolution of the interface orientation for the 5 cSt silicone oil with \(\beta = 70^\circ\) when subjected to \(\Delta T = 5\) K. This response is measured using \(\theta\), as indicated in Fig. 2, with respect to its initial value \(\theta _0\), selected by the initial hydrostatic equilibrium set by \(\beta\). Note that we have removed the initial transient associated to the initilization of \(\beta\); the actual start time is considered at the initialization of \(\Delta T\).

Five quantities are used to characterize the response: the rise time \(t_0\), the stabilization time \(t_\infty\), the final steady angle \(\Theta _\infty = \theta _\infty - \theta _0\), the overshoot \(\Theta _{\text {max}}-\Theta _\infty\), and the oscillation period \(\mathcal {P}\). Insets showing the free surface location, temperature fields in the cell and the liquid, and streamlines (black lines) in the liquid are included to help understand the evolution.

The applied \(\Delta T\) modifies the initial equilibrium. Note that, given the high value of k of aluminum, this \(\Delta T\) is effectively transferred to the fluids, modifying the contact point temperatures and creating a thermal gradient at the free surface. It is evident, however, that a small time interval is necessary for the thermal gradient to reach the cell interior via thermal conduction. Once this occurs, the associated thermocapillary effect draws liquid from the warmer region of lower \(\sigma\) to the cooler region of higher \(\sigma\). Initially, since the liquid is located in the lower part of the cell, a counterclockwise rotation of the interface is generated, reflected in the increasing value of \(\Theta = \theta -\theta _0\).

At \(t_0\), the free surface reaches, for the first time, an average orientation perpendicular to the applied \(\Delta T\), i.e., \(\Theta = 90^\circ\). Note that \(t_0\) quantifies the responsiveness of the system. As time passes, \(\Theta\) continues increasing due to inertia. However, as \(\Theta > 90^\circ\), the thermal gradient is effectively inverted and the thermocapillary effect then acts to decelerate the rotation. Eventually, \(\Theta\) reaches its maximum value \(\Theta _\textrm{max}\) (overshoot) and starts decreasing; the free surface then rotates in a clockwise sense. Cycles of alternating clock and counterclock-wise rotations, associated with temperature differences at the contact points of alternating sign, are repeated around \(\Theta = 90^\circ\). The amplitude of successive maxima and minima in \(\Theta\) decreases with time due to viscous dissipation, as it does the effective temperature graduient at the free surface, until a final steady state perpendicular to the applied \(\Delta T\) is reached with \(\Theta = \Theta _\infty = 90^\circ\). Following classical control theory, we consider this stabilization time \(t_\infty\) when the overshoot amplitude is within \(\pm 3\%\) of \(\Theta _\infty\) (blue shaded region in the figure).

Effect of the Applied Thermal Gradient

Note that, despite the effective thermal gradient at the free surface is time-dependent, it is driven by that applied at the cell walls, which sets an upper bound for the thermocapillary force and selects the subsequent system response. From an experimental perspective, controlling the external wall temperatures is relatively simple compared to attempt this same control at the contact points. For these reasons, we analyze here the system dynamics in terms of the applied temperature difference, which is varied within the range \(\Delta T \in (0, 25]\) K.

Fig. 4
figure 4

Effect of the applied temperature difference \(\Delta T\) (upper), viscosity \(\nu\) (central), and static contact angle \(\beta\) (lower) on the free surface dynamics

Full size image

The upper panel of Fig. 4 illustrates the temporal evolution of \(\Theta\) for the 5 cSt silicone oil with \(\beta = 70^\circ\) when subjected to \(\Delta T = 2.5\), 5 and 10 K. It is observed that, as \(\Delta T\) increases, the system response becomes faster, significantly reducing the values of \(t_0\) and \(t_\infty\). Additionally, the frequency of the response increases as well, leading to a decrease in \(\mathcal {P}\). The overshoot, surprisingly, is only weakly dependent on \(\Delta T\).

Effect of Viscosity

Another important parameter in defining the response is the viscosity of the liquid (Gligor et al. 2022b). We investigate the influence of \(\nu\) by considering commercial silicone oils of 2, 5, and 20 cSt, which share similar physical properties while differing substantially in their viscosities; see Table 1.

The central panel of Fig. 4 illustrates the evolution of \(\Theta\) for these silicone oils with \(\beta = 70^\circ\) when subjected to \(\Delta T = 5\) K. Increasing \(\nu\) has several effects on the response. First, the period of oscillations \(\mathcal {P}\) increases, slowing down the fluid back-and-forth motion around \(\Theta _\infty\), as one would expect. In line with this, the system responsiveness decreases slightly, measured by slightly increasing values of \(t_0\).

Effect of the Contact Angle

We analyze now the difference between working with \(\beta = 70^\circ\) and an ideal static contact angle of \(\beta = 90^\circ\). The lower panel of Fig. 4 illustrates the temporal evolution of \(\Theta\) for the 5 cSt silicone oil with \(\beta = 90^\circ\) when subjected to \(\Delta T = 2.5, \, 5\) and 10 K. Note that it also illustrates the effect of \(\Delta T\) in ideal configurations with \(\beta = 90^\circ\).

At low applied \(\Delta T\), the system displays a slightly underdamped response with some overshoot. As \(\Delta T\) increases, the associated response becomes faster over time, with decreasing values of \(t_0\) and \(t_\infty\). After surpassing a certain \(\Delta T\), the system begins to exhibit oscillations, whose amplitude are somewhat proportional to the applied thermal gradient. Beyond this point, \(\mathcal {P}\) decreases with \(\Delta T\), while the overshoot increases. As mentioned above, \(t_0\) and \(t_\infty\) continue to decrease in this large \(\Delta T\) regime.

Fig. 5
figure 5

Effect of the dynamic contact angle (DCA) on the free surface dynamics. (Upper) Time evolution of \(\Theta\) for the 5 cSt silicone oil with a DCA \(\beta = 70^\circ\) when subjected to \(\Delta T = 5\) K; the associated evolution for a static \(\beta = 70^\circ\) (dashed curve) is included for visual comparison. (Lower) Time evolution of \(\Theta\) for 2 and 5 cSt silicone oils and different applied \(\Delta T\)

Full size image

In addition, we investigate the effect of using a dynamic contact angle (DCA) instead; see Eq. (9). The upper panel of Fig. 5 illustrates the interface response for the 5 cSt silicone oil with a DCA \(\beta = 70^\circ\) when subjected to \(\Delta T = 5 \; {\text {K}}\) (solid line); the associated response with the static model (dashed line) is included for visual comparison. The main conclusion is that considering hysteresis at the contact line entails increased damping (Utsumi 2017). Indeed, the system response becomes overdamped. Furthermore, despite the system responsiveness decreases, as measured by a larger value of \(t_0\), the stabilization time shows a weak dependence since there is no overshoot and oscillations around \(\Theta _\infty\).

The effect of \(\Delta T\) and \(\nu\) is illustrated in the lower panel of Fig. 5. The time evolution of \(\Theta\) for the 2 and 5 cSt silicone oils with a DCA \(\beta = 70^\circ\) and \(\Delta T = 2.5\), 10 and 25 K are illustrated. Again, one can observe the damping effect of viscosity, evident in the slower response exhibited by the 5 cSt silicone oil, and the opposite effect of the applied \(\Delta T\), which acts increasing the system responsiveness, as measured by a faster (smaller) \(t_\infty\).

Summary of Results

All the above-mentioned results are summarized in Fig. 6. The panels show the system response as \(\Delta T\) is varied for \(\beta = 70 ^{\circ }\) (left) and \(\beta = 90 ^{\circ }\) (right) and all the fluids explored in this work; see Table 1.

Regarding the stabilization angle \(\Theta _{\infty }\), we observe a consistent interface reorientation in a counterclockwise sense and perpendicular to the imposed thermal gradient, regardless of the fluid properties and \(\beta\). As described above, this result can be easily understood by the temperature distribution shown in the snapshots of Fig 3. In the limit of weak thermal forcing \(\Delta T < 5\) K, in particular, a visible divergence in the values of \(\Theta _{\infty }\) around \(90^\circ\) is observed, as the reduced strength of the thermocapillary-driven flow is not large enough to counteract viscous dissipation at large times.

Fig. 6
figure 6

Summary of fixed \(\Delta T\) simulations for \(\beta = 70^\circ\) (left) and \(\beta = 90^\circ\) (right), showing the stabilization angle \(\Theta _\infty\), first crossing time \(t_0\), stabilization time \(t_\infty\), overshoot \(\mathcal {O}\) (in %), and oscillation period \(\mathcal {P}\). The inset included in the left panel of \(t_\infty\) depicts a comparison between static and DCA models with \(\beta = 70^\circ\)

Full size image

The first crossing time, \(t_0\), exhibits a potential decaying trend with respect to the applied \(\Delta T\). For \(\beta = 70^\circ\), we observe here a similar behavior for all fluids with minor differences. In the silicone oils family, the increase in \(\nu\) leads to larger values of \(t_0\). For FC-40, whose density is about twice that of silicone oils, inertia plays a significant role in the dynamics, resulting in larger \(t_0\) despite its lower \(\nu\). Comparing the values of \(t_0\) for \(\beta = 70^\circ\) and \(90^\circ\), the overall response of the fluid system is slower in this latter case. This can be explained following the work of Gligor et al. (2022b) and looking at the velocity induced at the free surface: for \(\beta = 90^\circ\), this velocity is perfectly perpendicular to the aluminum wall, while it has a tangential component otherwise (see sketch in Fig. 2), contributing to a faster rotation of the liquid. For the ideal \(\beta = 90^\circ\) case, therefore, the most influencing parameter seems to be the liquid viscosity, which has a direct effect on the induced thermocapillary flow.

The stabilization time, \(t_\infty\), also displays a potential decaying trend with \(\Delta T\), except for the 2 cSt silicone oil, where a more irregular behavior when transitioning from lower to larger applied \(\Delta T\) is observed. This silicone oil is characterized by an intermediate density value and low \(\nu\), resulting in relatively low fluid inertia and dissipation, respectively. For \(\Delta T \lessapprox 2.5\) K, the driven flow is not vigorous enough to drive a rapid rotation of the liquid, and this motion rapidly vanishes leaving a steady-state error in \(\Theta _{\infty }\) with respect to \(90^\circ\). The net effect on \(t_\infty\) is to reduce it. For moderate \(\Delta T \approx 5\) K, the larger thermocapillary force drives a faster interface motion that, together with lower dissipation, results in a relatively large value of \(t_\infty\). For larger \(\Delta T\), \(t_\infty\) decreases, supported by the stabilizing effect of the applied \(\Delta T\).

The overall trend and observed values of \(t_\infty\) are similar for both \(\beta = 70^\circ , \, 90^\circ\). Note that, despite the fluid system with \(\beta = 90^\circ\) generally displays a slower response, as measured by \(t_0\), the associated overshoot is also smaller, allowing \(t_\infty\) to be very similar in both scenarios. Regarding the influence of the DCA on \(t_\infty\), one can see its effect in the inset. These results are consistent with the upper panel of Fig. 5, showing that the hysteresis at the contact points has a non-negligible influence on \(t_\infty\), which can be as important as ordinary viscous damping in microgravity conditions; see Utsumi (2017) for further details.

The overshoot, \(\mathcal {O} = \Theta _\textrm{max}/\Theta _\infty - 1\), shows a weak dependency on \(\Delta T\) for \(\beta = 70^\circ\). For the ideal value \(\beta = 90^\circ\), in contrast, \(\mathcal {O}\) is significantly affected both by the applied temperature gradient itself and by fluid properties. Following again the work of Gligor et al. (2022b), one can attribute this difference to the masking effect of the free surface velocity projections perpendicular and parallel to the inner circular wall; that is, if there is an effective parallel component (\(\beta \ne 90^\circ\)), the system response achieves almost a constant overshoot regardless of the applied \(\Delta T\). We also note here that for small \(\Delta T < 5\) K and large \(\nu\) — thus weaker thermocapillary-driven flow — no overshoot is observed; see pink markers in Fig. 6.

Finally, as the system response resembles an exponentially decaying oscillatory function, we can also measure the associated period \(\mathcal {P}\). Again, we observe a potential decaying trend for \(\mathcal {P}\). A direct comparison between both \(\beta\) values allows us to confirm once again that the system response is quantitatively slower in the ideal case, which is also consistent with the argument based on the projection of the free surface velocity: the larger the tangential component is, the faster the system response and thus it oscillates faster with respect to the equilibrium (Gligor et al. 2022b). This effect is especially significant for the 20 cSt silicone oil, which has large \(\nu\) and exhibits oscillatory behavior for \(\beta = 70^\circ\), whereas no oscillations are observed for \(\beta = 90^\circ\). Besides the 20 cSt silicone oil, for \(\beta = 90^\circ\), the other studied fluids exhibit a vertical asymptote for a certain thermal gradient \(\Delta T\), which decreases with \(\nu\). This behavior is consistent with the non-oscillating behavior if the thermal gradient is not large enough to overcome viscous dissipation. We also note that this vertical asymptote coincides (approximately) with the minimum \(\mathcal {O}\) for each fluid, as expected.

Fig. 7
figure 7

Effect of the applied vibrational forcing on the free surface dynamics. Results are shown for the 5 cSt silicone oil with \(\beta = 70^\circ\), when subjected to vibrations of \(A = 2\) mm and \(\omega /(2\pi ) = 20\) Hz. The streamlines depict the time-averaged fluid flow over one forcing period. The dashed line depicts the free surface shape prior to the vibrational forcing initialization

Full size image

Combined Thermal and Vibrational Forcing

We analyze now the free surface dynamics under combined thermal and vibrational forcing.

As anticipated above, vibrations alone can generate a wide variety of interfacial phenomena and instabilities in microgravity — see Porter et al. (2021) for a detailed review — or interact with thermocapillary flows by affecting the instability modes and their onsets, as presented in the linear stability analysis of Lyubimova (2017). The vibroequilibria effect (Fernández et al. 2017; Apffel et al. 2021; Salgado Sánchez et al. 2023), in particular, can be used in advance for controlling liquids, since fluid interfaces tend to reorient themselves perpendicular to the direction of the applied vibrations. In the context of the ThermoSlosh project, therefore, vibrations can be used to enhance (or suppress) the effect of the applied thermal excitation, if introduced parallel (or perpendicular) to the applied \(\Delta T\). In the remainder of this manuscript, we restrict the analysis to the 5 cSt silicone oil with a static \(\beta = 70^\circ\). In this section, supplemental horizontal vibrations of frequency \(\omega /(2\pi ) = 5 \; {\text {Hz}}\) are applied.

As described in Section 2, we initialize the thermal forcing just after the settling of \(\beta\), and then, after 2 s, the vibrational forcing. The rationale behind this “stepped” initialization lies on the vibroequilibria effect, which would cause, in the absence of thermal forcing, a symmetric deformation of the initial interface (Fernández et al. 2017), as depicted in Fig. 7. This deformation is characterized by the rise of both contact points, which could eventually lead to the break-up of the liquid domain into two separate portions with interfaces approximately perpendicular to the vibrational axis. To avoid this scenario, \(\Delta T\) is initialized first to drive the interface rotation and break the time-averaged reflection symmetry that the vibrational problem would present otherwise.

Fig. 8
figure 8

Effect of the applied vibrational amplitude A on the free surface dynamics. Results are shown for the 5 cSt silicone oil with \(\beta = 70^\circ\), \(\Delta T = 5\) K and \(\omega /(2\pi ) = 5 \; {\text {Hz}}\). The light red curve presents the complete response with small oscillations, while the other curves show the time-averaged response over \((2 \pi )/\omega\)

Full size image

We consider first an applied \(\Delta T = 5\) K and increasing values of A. Figure 8 shows the time evolution of \(\Theta\) for A = 0, 0.3 and 0.6 mm. The observed dynamics are analogous to that discussed in Section 3. Initially, the interface rotates counterclockwise. At the rise time \(t_0\), the free surface reaches for the first time a perpendicular orientation with respect to \(\Delta T\), corresponding to \(\Theta = 90^\circ\). From this point onward, the response is characterized by alternating clockwise and counterclockwise rotations around \(\Theta = 90^\circ\), which last until a final steady state with \(\Theta _\infty = 90^\circ\) is reached.

Supplemental vibrations, however, significantly increase the responsiveness of the system, as reflected in the reduced values of \(t_0\) and \(t_\infty\). As one would expect, the larger the vibrational forcing applied, the faster the system stabilizes at \(\Theta _\infty\). Interestingly, results suggest that the overshoot depends only weakly on the applied vibrations; see the peak values in Fig 8.

Fig. 9
figure 9

Summary of thermal-vibrational simulations for the 5 cSt silicone oil with \(\beta = 70^\circ\): rise time \(t_0\), stabilization time \(t_\infty\), and relative overshoot \(\mathcal {O}\). Results are shown as functions of: (left) A with \(\Delta T = 5\) K, (right) \(\Delta T\) with \(A = 0.3\) mm (dotted lines) and without supplemental vibrations (lighter solid lines). Adapted from Salgado Sánchez et al. (2023)

Full size image

Results for combined thermal and vibrational forcing are summarized in Fig. 9 for varying A and \(\Delta T = 5\) K (left panels) and varying \(\Delta T\) and \(A = 0.3\) mm (right panels). As mentioned above, the applied vibration significantly reduces the values of \(t_0\) and \(t_\infty\) without notably affecting the relative overshoot over the explored range of A and \(\Delta T\). Compared to Section 3.4, the influence of varying \(\Delta T\) is weaker in this case, which suggests that the free surface dynamics is essentially controlled by the applied vibrations. This result is consistent with the vibroequilibria effect and its stabilizing (gravity-like) effect.

In addition, for large \(\Delta T\), the results with supplemental vibrations (dashed lines) and the ones only with thermal forcing converge, suggesting that both excitations have a similar influence on the interface positioning: the effect of a thermal gradient of \(\sim\)20 K is equivalent to the applied vibrations. From these results, we observe that constant vibrational forcing seems to keep the relevant parameters more bounded, as measured by \(\mathcal {O}\) and \(t_\infty\) as \(\Delta T\) is varied. The influence of the thermal gradient on these parameters is thus weaker, suggesting that the vibrational forcing (if applied) drives to a larger extent the interface reorientation.

The first crossing time \(t_0\), on the other hand, exhibits a similar trend with and without vibrations. This effect can be easily explained in terms of the sequential initialization described above. Note that this initialization leads to the fluid being exclusively influenced by \(\Delta T\) during the early stages of the evolution, affecting notably \(t_0\). Increasing \(\Delta T\) ensures that the system has already acquired a rotational motion by the time the vibrational forcing starts, and thus its “accelerating” effect may remain masked for the small value of \(A = 0.3\) mm considered here.

For further analyses on the interaction of thermocapillary and vibrational effects, the reader is referred to the recent work of Gligor et al. (2022a, b).

Interface Positioning with Feedback Control

Following the preliminary results of Salgado Sánchez et al. (2023), we further develop the concept of a classical controller to perform custom interface reorientations (maneuvers) using thermocapillary flows.

A standard proportional-integral-derivative (PID) controller is considered, characterized by its proportional, integral and derivative gains: \(K_P, K_I, K_D\). The error signal of this controller is the difference between the actual (measured) interface orientation \(\Theta\) and the desired interface orientation \(\Theta _d\). From an experimental perspective, the orientation of the free surface could be obtained in (near) real-time via image processing of the images acquired by a simple optical subsystem, such as the image shown in Fig. 1(c).

Based on this error signal, the controller produces a thermal modulation \(\Delta T (t)\) that orients the free surface to its desired state (\(\Theta _d\)) via the following control law:

$$\begin{aligned} \begin{aligned} \Delta T&= -K_P\, (\Theta -\Theta _d) -K_I\int _0^t (\Theta -\Theta _d)\textrm{d}t \\&- K_D\,\frac{\textrm{d}(\Theta -\Theta _d)}{\textrm{d}t}. \end{aligned} \end{aligned}$$
(12)

Given that the aluminum cell has four external walls whose temperatures can be controlled separately to potentially reach any value of \(\Theta _d\), the actual application of \(\Delta T\) should consider the relative orientation of each wall and \(\Theta _d\). Accounting for this, \(\Delta T\) is introduced at each wall as follows:

$$\begin{aligned} \Delta T_w = \Delta T \cos {(\Theta _w-\Theta )}\,\mathcal {H}(t-\tau _0), \end{aligned}$$
(13)

where \(\Theta _w = 0^\circ , 90^\circ , 180^\circ\) and \(270^\circ\) refers to the (outward normal vectors) orientations of the right, top, left and bottom walls, respectively. The cosine term ensures a minimum temperature output at the most ineffective walls (i.e., if the interface is completely horizontal, heating/cooling the top and bottom walls would have no effect at all) and minimizes power consumption. As introduced in Section 2, we also use the function \(\mathcal {H}\) with \(\tau _0 = 2\) s to introduce the control signal just after the settling of \(\beta\). Remark that this control law is just an early concept that may be subject of future analysis.

Regarding controller gains, we use as reference the values \(K^*_P = 3582\) K/m, \(K^*_D = 852\) K s/m presented in the work of Gligor et al. (2022a), and scale them by the radius R to have consistent units: \(K_{P,\,\text {ref}} = K^*_P\, R = 53.73\) K and \(K_{D,\,\text {ref}} = K^*_D\, R = 12.78\) K s. Note that \(K_I\) is removed from the controller due to its destabilizing effect.

In the remainder of this section, we refer \(K_P\) and \(K_D\) to these reference values and introduce the following dimensionless gains for the analysis:

$$\begin{aligned} \left( \hat{k}_p, \, \hat{k}_d \right) = \left( \frac{ K_P}{K_{P,\,\text {ref}}}, \, \frac{ K_D}{K_{D,\,\text {ref}}} \right) . \end{aligned}$$
(14)

Reference Maneuver

To evaluate the PD controller performance, we define a reference maneuver that considers a controlled liquid rotation from \(\Theta = 0^\circ\) to \(\Theta _d = 90^\circ\), which can be directly compared to the natural evolution of the system when subjected to a fixed \(\Delta T\); see Section 3.1. One would expect the PD controller to achieve the same final equilibrium position more efficiently from the perspective of the commanded temperatures. Figure 10 depicts the time evolution of \(\Theta\) for the 5 cSt silicone oil with a fixed \(\Delta T = 5\) K (black curve) and four selected combinations of \(( \hat{k}_p, \, \hat{k}_d )\). Different types of dynamics can be observed.

Fig. 10
figure 10

Time evolution of the interface orientation \(\Theta\) for the 5 cSt silicone oil with an applied \(\Delta T = 5\) K and four selected (\(\hat{k}_p,\hat{k}_d\)) combinations for the reference maneuver from \(\Theta = 0^\circ\) to \(90^\circ\)

Full size image

For (\(\hat{k}_p,\hat{k}_d\)) = (0.05, 3.5), the interface orientation exhibits a response very similar to an overdamped system. Although stable, the response becomes excessively slow and the stabilization time remains very similar to the fixed \(\Delta T\) case. By increasing \(\hat{k}_p\) and reducing \(\hat{k}_d\), a significant improvement in the system dynamics is observed, consistent with the results of Gligor et al. (2022a). The red curve corresponding to (\(\hat{k}_p,\hat{k}_d\)) = (0.1, 2) does not yet exhibit any oscillation around \(\Theta _d\), while \(t_\infty\) is now significantly lower and, therefore, the system response is relatively faster. For these values of (\(\hat{k}_p,\hat{k}_d\)), one may argue that the system exhibits a critically damped response (or close to it). Compared to the fixed \(\Delta T = 5\) K case, the PD controller provides a significantly faster response from the early stages of the evolution.

Further increase in \(\hat{k}_p\) and decrease in \(\hat{k}_d\) leads to an underdamped behavior. For the selected combination (\(\hat{k}_p,\hat{k}_d\)) = (0.15, 1), the overshoot is not excessive and \(t_\infty\) is not significantly penalized compared to the critically damped case.

The tendency shown for increasing (decreasing) \(\hat{k}_p\) (\(\hat{k}_d\)) is interrupted by unstable behavior; see pink curve in Fig. 10. For (\(\hat{k}_p,\hat{k}_d\)) = (0.2, 0), the response exhibits a stable amplitude oscillation around the desired (commanded) angle \(\Theta _d\). Note that this scenario lacks of practical interest from a fluid positioning perspective and, therefore, we restrict subsequent analyses to \(\hat{k}_d > 0\) to prevent this type of dynamics.

The system sensitivity to the controller gains makes an adequate selection of (\(\hat{k}_p,\hat{k}_d\)) critical in a hypothetical microgravity experiment. When properly selected, the PD controller provides an improved system response.

Optimization of the Controller

As suggested by these preliminary results, it may be possible to select a combination of (\(\hat{k}_p,\hat{k}_d\)) that minimizes \(t_\infty\), while not causing unstable oscillatory dynamics. Considering the work of Gligor et al. (2022a), we propose an analogous multi-objective optimization based on the following criteria (objective functions).

The first objective is directly based on \(t_\infty\). From an experimental perspective, performing a larger number of maneuvers in a fast manner is highly desirable, especially if there is limited microgravity time available. Put in other words, \(t_\infty\) should be minimum.

Fast-responding dynamics, however, are associated to vigorous thermocapillary flow and larger thermal forcing. This, in turn, is related to a certain “cost” on the physical interface that transforms the control signal to the boundary temperatures. The ThermoSlosh experiment (Salgado Sánchez et al. 2023) foresees the use of Peltier modules, which are able to cool or heat the cell walls by applying an adequate current circulation, for this temperature control. For simplicity, the present numerical results address this cost using the following function:

$$\begin{aligned} \begin{aligned} \mathcal {C}&= \int _{0}^{t_\infty } \left[ (T_b - T_0)^{2} + (T_u - T_0)^{2} + \right. \\ {}&\left. (T_l - T_0)^{2} + (T_r - T_0)^{2} \right] \, \textrm{d} t, \end{aligned} \end{aligned}$$
(15)

which considers the temperature modulations commanded to the bottom, upper, left and right aluminum walls; denoted by the subscripts \(b,\,u,\,l,\,r\), respectively. A more precise estimate of power consumption would require a complete dynamic model of Peltier modules; see, e.g., Huang and Duang (2000). This is suggested below as a line for future research.

In order to prevent a badly-conditioned optimization problem, we refer \(t_\infty\) and \(\mathcal {C}\) to the associated values for fixed \(\Delta T = 5\) K, \(\mathcal {C}^* = 1495\) K\(^2\,\)s and \(t_\infty ^* = 119.6\) s, and define the dimensionless objective functions:

$$\begin{aligned} \left( \kappa , \, \upsilon \right) = \left( \frac{\mathcal {C}}{\mathcal {C}^*}, \, \frac{t_\infty }{t_\infty ^*} \right) . \end{aligned}$$
(16)

An extensive set of simulations for different combinations of \((\hat{k}_p,\hat{k}_d)\) is performed to obtain maps of \((\kappa ,\upsilon )\); these are presented in the upper-left and upper-right panels of Fig. 11, respectively. Simulations were also restricted to \(\hat{k}_p \ge 0.05\) given that only the proportional contribution can initially trigger interface motion when starting from a hydrostatic equilibrium with \(\Theta = \dot{\Theta } = 0\). Put in other words, adding a small proportional gain ensures that the interface reorientation starts immediately after the controller is initialized at \(\tau _0 = 2\) s.

Fig. 11
figure 11

(Upper panels) Contour maps showing the relative cost \(\kappa\) (left) and stabilization time \(\upsilon\) (right) as functions of (\(\hat{k}_p,\hat{k}_d\)) for the reference maneuver. Red, green and blue markers correspond to (\(\hat{k}_p,\hat{k}_d\)) = (0.05, 1.5), (0.1, 2) and (0.15, 2) selected from the Pareto front. (Lower panel) Pareto front of the multi-objective \(\kappa\)-\(\upsilon\) optimization

Full size image

Regarding \(\upsilon\), \(\hat{k}_d\) is the most effective gain as evidenced by the predominantly horizontal contour levels at small \(\hat{k}_d\) values — see the upper-right panel of Fig. 11. However, larger \(\hat{k}_d\) can eventually lead to the stagnation of the free surface close to \(\Theta _d\) and penalize \(t_\infty\). Such behavior was already anticipated in Fig. 10 (green curve), where an excessively large derivative gain ultimately led to an overdamped response, associated to larger \(t_\infty\). This type of overdamped behavior would also lead to small time derivatives of the error signal and reduced cost. Remark also that \(\upsilon\) exhibits a clear minimum, contrary to \(\kappa\).

Using this data, we can obtain the Pareto front for the simultaneous minimization of \((\kappa ,\upsilon )\); this is shown in the lower panel of Fig. 11. The Pareto front, together with the associated contours, evidences the following conclusions.

Starting from the lowest relative cost (large \(\hat{k}_d\), overdamped response), a reduction in \(t_\infty\) can be achieved without increasing \(\kappa\) by simply reducing \(\hat{k}_d\), i.e., moving along the left axis on the upper panels of Fig. 11 (red marker). This transition is presented on the Pareto front as a very steep line with nearly constant \(\kappa\), corresponding to the transition from an overdamped system to a slightly underdamped one. A further decrease in \(\upsilon\) requires to increase \(\hat{k}_p\) and so it does the associated cost (green marker). The last point of the Pareto front coincides with the local minimum of \(\upsilon\), highlighted with a cyan marker.

Fig. 12
figure 12

(Upper panel) Time evolution of \(\Theta\) for the (\(\hat{k}_p,\hat{k}_d\)) combinations selected from the Pareto front of the reference maneuver. (Lower panels, I-III) Time evolution of the commanded temperatures

Full size image

Based on the Pareto front, we select three \((\hat{k}_p,\hat{k}_d)\) combinations corresponding to low cost, moderate stabilization time (red marker), intermediate cost and stabilization time (green marker), and maximum cost, lowest stabilization time (cyan marker). For these values, we illustrate the time evolution of \(\Theta\) and the commanded wall temperatures in Fig. 12.

As anticipated above, the black curve exhibits an underdamped, or perhaps close to critically damped, response. The commanded temperatures are significantly low, with a maximum (minimum) peak of approximately \(\pm 3\) K and \(t_\infty \simeq 19.8\) s. Compared to the stabilization time \(t^*_\infty = 119.6\) s of the fixed \(\Delta T = 5\) K case, the controller performance makes the reorientation notably faster with a much lower cost; see panel I in Fig. 12.

The other two \((\hat{k}_p,\hat{k}_d)\) combinations exhibit an underdamped response, albeit no oscillations are observed likely due to a still large damping value. The larger commanded temperatures, despite increasing the cost, reduce further the stabilization time; see panels II and III of Fig. 12.

Other Maneuvers

The reference maneuver from \(\Theta = 0^\circ\) to \(90^\circ\) can be regarded as representative for the physical characterization of the system. However, the present controller, able to act on each wall temperature, can (theoretically) drive the reorientation of the free surface toward any desired \(\Theta _d\). In this sense, the most critical maneuvers should be those that position the interface at \(\Theta _d = 45^\circ ,\,135^\circ ,\,225^\circ\) and \(315^\circ\), which are the “furthest” ones from the orientations that can be directly achieved by imposing a constant temperature gradient at opposing cell walls. Besides, from a thermal perspective, the time required for a thermal modulation to reach the fluid interface would be a bit longer in these cases, due to a slightly longer thermal diffusion path. To analyze these scenarios, we explore maneuvers toward \(\Theta _d = 45^\circ\) and \(135^\circ\) hereafter.

Fig. 13
figure 13

Time evolution of \(\Theta\) in maneuvers toward \(\Theta _d = 45^\circ\) (upper) and \(135^\circ\) (lower) with the optimal (\(\hat{k}_p,\hat{k}_d\)) combinations selected from the Pareto front of the reference maneuver. For each maneuver, two representative snapshots show the early and final interface orientation. Negative (positive) steady-state error is observed for \(\Theta _d = 45^\circ\) (\(135^\circ\))

Full size image

The results for these maneuvers with the optimal controller gains of Section 5.1 are summarized in Fig. 13. Both panels show a relatively good behavior although displaying a steady-state error of approximately \(5^\circ\) and \(8^\circ\) for \(\Theta _d = 45^\circ\) and \(135^\circ\), respectively. We note that the steady-state error (slightly) decreases as \(\hat{k}_p\) increases, an expected result since the induced thermal modulation is (precisely) proportional to this gain. The induced thermal modulation at large times, however, is not large enough to counteract viscosity and the liquid remains quiescent close to \(\Theta _d\).

From these considerations, we may wonder whether further increases in \(\hat{k}_p\) would reduce the steady-state error, albeit with increasing cost. In this regard, future work can be directed toward a multi-objective optimization that considers together \(\kappa\), \(\upsilon\) and the steady-state error, and provides a global solution for these three characteristic maneuvers. The results obtained from such a study could be applicable to any other value of \(\Theta _d\).

Effect of the Integral Gain

Derived from classical control theory, the integral gain \(K_I\) is often useful to reduce steady-state errors. So far in this manuscript, we have not considered \(K_I\) due to the destabilizing effect it has on the physical system presented (Gligor et al. 2022a). However, the presence of the steady-state error observed for the \(45^\circ\) and \(135^\circ\) maneuvers motivates to explore the use of \(K_I\) in more detail. The integral contribution should be able to reduce it at the cost of making our system more prone to oscillatory behavior.

Fig. 14
figure 14

Time evolution of \(\Theta\) for a PID controller with (\(\hat{k}_p,\hat{k}_d\)) = (0.2, 2) and \(K^*_I =\) 1 K/s applied to a reorientation maneuver toward \(\Theta _d= 135^\circ\). Compared to Fig. 13, the averaged steady-state error vanishes at the cost of steady small-amplitude oscillations around \(\Theta _d\)

Full size image

We consider a small arbitrary value \(K_I = 1\) K/s that is applied only 6 s after commanding the desired orientation. This prevents, during the early stages of the maneuver, the build-up of an excessively large integral error that destabilizes the system. The associated controller performance is illustrated in Fig. 14, where one can observe that the averaged steady-state error has been effectively suppressed at the cost of small oscillations around \(\Theta _d\) of roughly \(5^\circ\) amplitude.

Another possible solution to suppress the steady-state error and minimize this long-standing oscillatory behavior could be based on the definition of two PID controllers: one that acts during the initial stages of the maneuver when the error \(\Theta -\Theta _d\) is large, and another one, tuned for small error signal, that aims to suppress the steady-state error in the lowest time possible, without penalizing the controller cost significantly.

Conclusions and Future Work

We presented here an extensive numerical analysis of the interfacial dynamics driven by the thermocapillary effect and horizontal vibrations in a two-dimensional cylindrical cell containing equal volumes of liquid and air under microgravity conditions. Various silicone oils of different viscosity and a type of fluorinert were analyzed due to their significance in microgravity experiments and applications (Salgado Sánchez et al. 2019a). Building upon recent studies in thermocapillary flow (Salgado Sánchez et al. 2023; Gligor et al. 2022a, b), an initial static contact angle of \(\beta = 70^\circ\) was primarily considered, although the ideal angle of \(\beta = 90^\circ\) and the implementation of a dynamic contact angle (DCA) were also investigated.

In Section 3, the response of the interface to a constant thermal excitation was analyzed first. The interface dynamics were characterized by the temporal evolution of the right contact point angle, \(\Theta\). Parameters such as the steady-state value \(\Theta _{\infty }\), first crossing time \(t_0\), stabilization time \(t_{\infty }\), overshoot \(\mathcal {O}\), and oscillation period \(\mathcal {P}\), were obtained and provided a complete picture to evaluate the response.

The results strongly suggested that thermocapillary flows can be used to control the interface position within the cell. The applied thermal gradient significantly influenced the response, accelerating it. Viscosity, on the other hand, delayed fluid motion. Furthermore, when an ideal \(\beta = 90^\circ\) was implemented, the system responsiveness decreased, although this effect was counterbalanced by the decrease in \(\mathcal {O}\), and \(t_{\infty }\) remained similar to the associated evolution with \(\beta = 70^\circ\). A DCA model to account for hysteresis at the contact line was also implemented, showing a delayed response associated to an additional effect similar to ordinary viscous damping (Utsumi 2017).

In Section 4, constant thermal excitation was combined with vibrations. It was demonstrated that the use of supplemental horizontal vibrations significantly accelerates the system response. Both \(t_0\) and \(t_{\infty }\) were substantially reduced without notably affecting \(\mathcal {O}\). Additionally, the influence of the thermal gradient on the response was diminished for the system with supplemental vibrations. This suggested that the interface dynamics were primarily controlled by the vibrational excitation, consistent with the vibroequilibria phenomenon and its stabilizing effect (Salgado Sánchez et al. 2019a, b, 2020).

Continuing the analysis, a classical PID controller was implemented in Section 5. The controller acted on the temperatures of the four external walls of the aluminum cell. Initially, the integral gain \(K_I\) was not considered due to its destabilizing effect. First, the effect of the proportional and derivative gains, \(K_P\) and \(K_D\), were analyzed by defining a reference maneuver that rotates the interface by \(90^\circ\). A parametric study was conducted within a wide range of \((K_P, \, K_D)\) and contour diagrams were constructed to characterize the response. To assess the effectiveness of each gain, a relative stabilization time \(\upsilon\) and cost \(\kappa\) were defined, allowing for a multi-objective optimization to obtain the Pareto front. Efficient solutions on this front lied in intermediate values of \(K_D\) and a wide range of \(K_P\). Systems with shorter stabilization times in the Pareto front entailed higher cost.

Three optimal \((K_P, \, K_D)\) combinations were selected from the Pareto front, and maneuvers to rotate the interface by \(45^\circ\) and \(135^\circ\) were analyzed. For each case, the controller effectively stabilized the free surface at the commanded position in a relatively short time, albeit with a significant steady-state error. To compensate for this error, we introduced a small value of \(K_I\) at the cost of long-standing small-amplitude oscillations around the desired interface position. In a real-world scenario, these oscillations might not occur due to friction with the walls or the damping effect of the dynamic contact angle.

Overall, the present results clearly highlighted the potential of the thermocapillary effect for fluid control in microgravity. Strategies of this nature may be of vital importance in the development of space exploration, such as lunar constructions or the future colonization of Mars, with direct application in propulsion or life support systems. Furthermore, this technology has direct relevance to certain terrestrial applications: controlling sloshing is crucial in tanks of offshore extraction plants or unmanned aerial vehicles, among other possibilities.

Several lines for future research are proposed. First, an extended analysis of the interface response to oscillatory thermal excitation is suggested. It may be also worthwhile to incorporate some type of restoring force that helps maintain a preferred initial equilibrium position. Examples of possible solutions include the use of vertical vibrations or magnetic fields in combination with ferro-fluids, and the modification of the cell geometry to an elliptical shape, stretching the container along its vertical axis so that the initial position becomes the one of minimum surface energy.

Second, it will be important to conduct more realistic three-dimensional simulations and implement dynamic modeling of the thermal control devices (i.e., Peltier element modules). This would allow to consider not only operational limitations, such as a maximum applied thermal gradient or delays in the control actuation, but can also lead to the development and (numerical) testing of more advanced control schemes.

Finally, experiments are required to definitely test these results. On ground, these could be approached by aligning gravity with the third dimension of the cell, selecting a sufficiently small container depth and using two fluids with similar densities to reduce inertial effects. For microgravity experiments, the development of a fully functional experiment prototype would be necessary in a more advanced phase of the ThermoSlosh project. An extensive ground test campaign would provide a precise estimate of the required on-orbit resources. Additionally, conducting a conceptual analysis of potential space applications of this control strategy, as well as its potential transfer to terrestrial applications, would be of interest.