Experimental Investigation of Liquid Interface Stability During the Filling of a Tank in Microgravity

Abstract

The storage of propellants in space as well as the transfer and filling of spacecraft tanks is a prerequisite for future long-term space exploration missions. In this work, the vented filling of a partially filled tank, which is envisioned as a spacecraft tank, was investigated experimentally under compensated gravity in the Bremen Drop Tower. Experiments were performed with a partially filled tank and a test liquid HFE-7500. The drop tower provides 9 s of compensated gravity. The shape of the free liquid surface inside a right circular cylinder changes from the normal gravity configuration to a free fall configuration during the test. The filling was initiated after 3.5 s and continued until the end at 9 s. The interaction of the incoming liquid jet with the liquid interface was studied for different volumetric flow rates. A stable, but not steady liquid interface was characterized by a deformation due to the incoming liquid jet and the formation of a geyser. The growth of the geyser and the following disintegration into liquid droplets indicated an unstable liquid interface. Subcritical, critical and supercritical regimes of the volumetric flow rates were identified to classify stable and unstable liquid interfaces. The critical Weber number was found to be 1.04, which corresponds to a critical volumetric flow rate of 1.30 mL s^-1. This critical Weber number was compared with the existing literature. Additionally, the behaviour of the liquid interface during the reorientation of the liquid inside the tank was observed.

Introduction

Long-range crewed space missions require storage and transfer of propellants in space. Storage of propellants can be envisioned by a propellant space depot, from which the propellants can be transferred to the spacecraft tanks, when the spacecraft docks to the propellant depot. Propellant management devices can be used to ensure the separation of liquid and gaseous phases in the acceleration environment of the spacecraft system on-orbit. As capillary forces are dominant in microgravity, the free surface shape changes and it becomes important to determine the position of the liquid inside the tank. Vented and no-vent filling are the methods employed in filling spacecraft tanks. Heat transfer from the surroundings results in the self-pressurization of the spacecraft tanks. Vented filling helps to control the tank pressure. However, repeated venting may lead to propellant loss, if the gas phase cannot be separated from the liquid phase at the gas port of the tank. Therefore, the determination of a stability criteria of the liquid interface during filling is required.

State of the Art

The transfer of liquids under microgravity conditions has been investigated in various studies conducted at the Lewis Research Center. Symons et al. (1968) investigated the interface stability during liquid inflow into an empty hemispherical-ended cylindrical tank under microgravity conditions. In this study, a non-dimensional number called Weber number was defined, as shown in Eq. 1. The Weber number is defined as the ratio of stagnation pressure to capillary pressure. An approximation of the capillary pressure $p_c$ is the ratio between the surface tension of the liquid and the characteristic length $l_c$: $p_c = \sigma / l_c$. The Weber number is the criterion that delineates the regions of interface stability. Symons et al. (1968) determined the critical Weber number for the filling of an initially empty tank to be $\mathrm {We_1}$ = 1.3. The critical value of the Weber number was also confirmed in a study conducted with larger tanks and larger inlet radii by Symons (1970).

$$\begin{aligned} \mathrm {We_1} = \frac{1}{2}\frac{\rho \ v_{I}^2 \ R_{I} }{ \sigma } \end{aligned}$$

(1)

The study of Symons et al. (1968) was then extended to a partially filled tank with different initial fill heights and different liquids in Symons (1969). Stable and unstable regions of the interface were noticed and the critical inflow velocity was determined. Symons and Staskus (1971) reported the effect of the velocity profile of the incoming liquid jet and initial liquid height on the critical inflow velocity. Weber numbers for different inlet velocity profiles of the liquid jet were defined for the filling into a partially filled tank, as shown in Eq. 2 for a uniform velocity profile

$$\begin{aligned} \mathrm {We_2} = \frac{1}{2}\frac{\rho \ v_{I}^2 \ R_{I} }{ \sigma }\frac{R_I}{R_J} \end{aligned}$$

(2)

and Eq. 3 for a parabolic velocity profile

$$\begin{aligned} \mathrm {We_3} = \frac{2}{3}\frac{\rho \ v_{I}^2 \ R_{I} }{ \sigma }\frac{R_I}{R_J} \end{aligned}$$

(3)

The radius of the liquid jet at the liquid interface $R_J$ is equal to the inlet radius $R_I$ for an initially empty tank, ($R_J = R_I$) and the term $R_I/R_J$ in Eqs. 2 and 3 becomes unity. The radius of the liquid jet at the liquid interface $R_J$ is dependent on the spreading angle of the liquid jet in the bulk liquid.

Aydelott (1979) conducted drop tower experiments on axial jet mixing of ethanol in a cylindrical tank and observed four different geyser flow patterns. Dominick and Tegart (1981) demonstrated propellant transfer between supply and receiver tanks using vane devices for different liquids under microgravity conditions. The critical Weber number for a bare tank was $\mathrm {We_1}$ = 7, while the interface remained stable for the baffled tank even at $\mathrm {We_1}$ = 34. Dominick and Driscoll (1993) discussed the results of the three vented fill tests, which were conducted as part of the Fluid Acquisition and Resupply Experiment (FARE-I) on board the space shuttle STS 53. A spherical tank, that contained a screen channel propellant management device (PMD) and a perforated baffle near the inlet was used to study the stability regime of the liquid interface. A disturbed interface was observed for $\mathrm {We_1}$ = 5.2. It was also reported that having the vent tube positioned at the centre of the tank would increase the final fill level of the tank. FARE-II experiments were conducted on board the space shuttle STS 57 and the results are reported in Dominick and Tegart (1994). In the FARE-II experiment, a standpipe was fitted into the receiver tank and 8 radial vanes were attached to the standpipe. An abrupt transition from stable to unstable flow was observed during the vented fill tests of FARE-II. It was demonstrated that for a stable liquid inflow, the gas can be vented out without any loss of liquid, due to the presence of vanes.

Bentz et al. (1997) demonstrated the pressure reduction of the tank with the help of an axial jet mixing of the refrigerant R-113. Three space shuttle experiments were conducted as part of the Tank Pressure Control Experiment (TPCE), in which it was shown that the liquid jet completely penetrates the ullage for $\mathrm {We_2} \ge {}{3}{}$ with an initial liquid fill level of 39 %, and $\mathrm {We_2}>$ 5 for an initial fill level of 83 %. Chato and Martin (2006) illustrated the flight test results of Vented Tank Resupply Experiment (VTRE), where refrigerant 113 was transferred between two tanks and liquid-free venting was accomplished for the tested flow rates. The results of Zero Boil-Off Tank experiment (ZBOT-1) are reported in Kassemi et al. (2018). The results of tank ullage penetration by an axial jet at different inflow velocities and different fill levels under microgravity conditions to control the tank pressure were presented and compared with the numerical simulation results. Breon et al. (2020) demonstrated new technologies to store and transfer cryogenic liquids on-orbit during the Robotic Refueling Mission-3 (RRM3). However, due to the malfunction of the cryocooler in the source dewar, the transfer of liquid methane to the receiver dewar could not be accomplished on-orbit. Lei et al. (2023) discussed the design and development of the Tianzhou cargo spacecraft, that has demonstrated the orbital refuelling by providing propellant supplement to the Chinese space station Tiangong.

Several numerical studies modelled the jet-induced geyser formation under microgravity, as observed in the experiments of Aydelott (1979). The mixing of cryogenic propellants induced by a jet in low-gravity was predicted numerically by Hochstein et al. (1984). Dominick and Tegart (1990) used the Flow-3D software to predict the liquid behaviour during the filling of tanks in low-gravity. The computational models were validated with the existing experimental data and were also extended to real-scale tanks. Wendl et al. (1991) simulated the four geyser patterns using the ECLIPSE code and compared it with experiments from Aydelott (1979). Thornton and Hochstein (2001) improved the correlations from Aydelott (1979) for the geyser height prediction of turbulent jets. However, these new correlations were again amended by Simmons et al. (2005) by performing numerical simulations. Marchetta and Benedetti (2010) performed three-dimensional numerical simulations of the jet-induced geysers using ANSYS Fluent and compared the dimensionless geyser height with the experimental data of Aydelott (1979). Different turbulence models were tested and the jet spread rate was found to have an influence on the geyser height prediction.

Breisacher and Moder (2015) studied the dynamics of the liquid-vapour interface by carrying out numerical simulations using the Flow-3D software. Ullage shape and movement caused by the jet penetration were qualitatively analysed and compared with the images from the TPCE. Kartuzova and Kassemi (2019) validated the ANSYS Fluent CFD models with ZBOT-1 experiments for predicting the jet-induced mixing and ullage interaction. It was noticed that the jet tilt angle and orientation influence the jet-ullage interaction the most. It was also shown that the ullage shape and position during the jet mixing is predicted well by the LES model better than the RANS model.

The liquid reorientation inside the tank under microgravity has been investigated by carrying out drop tower experiments and numerical simulations by Li et al. (2013). Li et al. (2018) conducted drop tower experiments with two types of partially filled cylindrical tubes and compared the experiment results of the centre point evolution and the oscillation frequency of the liquid interface with the numerical simulation results. Li et al. (2020) performed numerical analyses of the liquid sloshing inside the storage tanks with different fill ratios by considering the dynamic contact angle. Friese et al. (2019) described the theory of reorientation and axial sloshing of liquids inside cylindrical tanks under microgravity conditions. Some isothermal experiments were conducted to study the free surface behaviour under microgravity, and the centre point and wall point progressions were plotted to understand the reorientation of liquid inside the tank. For a perfectly wetting liquid with an initial fill height of $H_L$, the final equilibrium position of the centre point of the liquid interface $z_{c,0g}$ in microgravity was defined by Eq. 4, where $R_T$ is the radius of the tank.

$$\begin{aligned} z_{c,0g} = H_L - \frac{R_T}{3} \end{aligned}$$

(4)

The time required for the liquid-vapour interface to reach its equilibrium under microgravity conditions is reported in Siegert et al. (1964). The first time, when the centre point of the interface crosses the final equilibrium position in microgravity, is called the equilibrium time $t_{s}$. It is defined in Eq. 5 for a cylindrical tank. It was found that the equilibrium time is dependent on the liquid properties and tank dimensions. This study helps in predicting the time after which the liquid inflow into a pre-filled tank can be started in microgravity.

$$\begin{aligned} t_{s} = 0.4 \, \left[ \frac{\rho \, R_T^{3}}{\sigma } \right] ^{1/2} \end{aligned}$$

(5)

Theoretical Background

The reduction of gravitational acceleration causes the liquid to undergo a reorientation inside a pre-filled tank, and the interface shape changes from flat to hemispherical. Tanks can be filled with liquid under microgravity with or without venting the gas. During the vented filling of a tank under microgravity conditions, the gas-free liquid is filled into the tank and the gas is vented from the tank.

Fig. 1

Geyser flow patterns as reported in Hochstein et al. (2008)

One of the common liquid injection techniques is to create a jet using an inlet pipe. The liquid jet that enters the tank interacts with the liquid interface and forms a geyser. The four different geyser flow patterns, as reported in Hochstein et al. (2008), are shown in Fig. 1. Though they correspond to a no-vent filling of a tank, the patterns I, II and III are also relevant for the vented filling of a tank. As the liquid jet enters the tank, it exchanges momentum with the already present bulk liquid and travels towards the liquid interface. In pattern I, the liquid jet does not disturb the interface. The liquid jet penetrates through the interface and creates a geyser in pattern II, if the incoming momentum of the jet is higher than the capillary pressure of the interface. In pattern III, this geyser moves towards the top part of the tank and circulates there. In case of a vented filling, this geyser may reach the vent port and this may lead to a liquid propellant loss. In case of a no-vent filling, the liquid jets help in cooling the tank down during self-pressurization. Pattern IV is only applicable for a no-vent filling and it occurs, when the liquid flows back along the tank wall and mixes with the bulk liquid. Therefore, it is important to determine the Weber number, at which the liquid interface becomes unstable. If the stagnation pressure is much lower than the capillary pressure, the liquid jet does not disturb the interface and its momentum is dissipated in the bulk liquid. This results in a nearly unperturbed and stable liquid interface. If the stagnation pressure is in the same order as the capillary pressure, the jet perturbs the interface and a geyser is formed. As long as the geyser remains intact and does not disintegrate into droplets, the liquid interface remains stable. If the stagnation pressure exceeds the capillary pressure, the geyser breaks into droplets, new surfaces are created, and the liquid interface becomes unstable.

The generic drawing of an axis-symmetric cylindrical tank considered for the interface stability study is shown in Fig. 2. The tank has an inner radius $R_T$ and height $H_T$. The tank has an outlet port of radius $R_{O}$. A circular plate (also called a velocity control plate (VCP)) of radius ${R_{VP}}$ is fitted inside the tank. A hole of radius $R_{I}$ is drilled on the circular plate and an inlet pipe of radius $R_{I}$ is connected to it. Because of using the circular plate, two types of liquid injection into the tank are possible. The primary liquid inlet is the centre hole of the VCP. The secondary liquid inlet is the annular gap between the tank wall and the VCP. In this work, only the liquid filling through the primary inlet is considered. The length of the primary inlet pipe $L_{I}$ is selected according to Eq. 6 for laminar flow from White (2011), such that the velocity profile of the liquid jet at the exit of the inlet pipe is fully developed.

$$\begin{aligned} L_{I} = 0.12 \; \textrm{Re}_{1} \, R_{I} \end{aligned}$$

(6)

The tank coordinate system is at the centre of the primary inlet orifice, denoted by a dot in Fig. 2. The initial fill height of the liquid $H_L$ and the height of the tank $H_T$ are measured from the axis. $H_I$ is the height of the liquid interface in microgravity at the start of liquid filling. $\eta _c$ is the centre point of the liquid interface, whose location is marked in Fig. 2 by a solid square in normal gravity and by a solid triangle in microgravity. The mean velocity of the liquid at the inlet is $v_{I}$.

Fig. 2

Generic drawing of the experiment tank. The length of the inlet pipe $L_I$ is not shown

Dimensional Analysis

Dimensional analysis is carried out to scale the filling process of the tank shown in Fig. 2. The penetration of the liquid interface by an incoming liquid jet can be described using the Weber number. The liquid jet that enters the tank through the inlet spreads in the bulk liquid before reaching the liquid interface. As the spreading angle of the liquid jet in the bulk liquid could not be measured in our experiments, the Weber number definition according to Eq. 3 could not be considered for this study. Therefore, the Weber number according to Eq. 1 is considered for this study. The liquid interface remains stable as long as the capillary pressure balances the stagnation pressure. It becomes unstable when the liquid jet momentum is notably higher than the capillary pressure. This results in the penetration of the interface, the formation of a geyser and the disintegration of the geyser into droplets. We repeat the Weber number here and denote it as our first $\Pi$-parameter, which is the Weber number at the tank inlet.

$$\begin{aligned} \mathrm {We_{1}} = \Pi _0 = \frac{1}{2}\frac{\rho v_{I}^2 R_{I} }{\sigma } \end{aligned}$$

(7)

The initial fill height of the liquid inside the tank is expressed in dimensionless form as a ratio with the inlet radius in $\mathrm {\Pi _1}$.

$$\begin{aligned} \mathrm {\Pi _1} = \frac{H_L}{R_I} \end{aligned}$$

(8)

The ratio $\mathrm {\Pi _2}$ is formed by relating the radius of the inlet $R_{I}$ to the radius of the tank $R_{T}$.

$$\begin{aligned} \mathrm {\Pi _2} = \frac{R_{I}}{R_T} \end{aligned}$$

(9)

The mean velocity at the inlet is defined as the ratio of the volumetric flow rate and the inlet cross-sectional area.

$$\begin{aligned} v_{I} = \frac{Q_L}{A_{I}} \end{aligned}$$

(10)

The cross-sectional area of the inlet can be calculated using $A_I = \pi R_I^2$. The displacement of the centre point of the liquid interface due to the penetration of the liquid interface is governed by the maximum velocity (also called the centreline velocity) of the incoming liquid jet. This maximum velocity is determined by the shape of the velocity profile of the liquid jet at the exit of the inlet pipe. Therefore, another dimensionless number $\mathrm {\Pi _3}$ is formed, which characterizes the velocity profile of the liquid jet.

$$\begin{aligned} \mathrm {\Pi _3} = \frac{v_{max}}{v_I} \end{aligned}$$

(11)

In order to compare the critical Weber number from this study with the existing literature, another dimensionless number $\mathrm {\Pi _4}$ is introduced in Eq. 12.

$$\begin{aligned} \mathrm {\Pi _4} = \frac{H_I}{R_I} \end{aligned}$$

(12)

The initial height $H_I$ is the surface elevation above the inlet at the beginning of the filling in microgravity. This differs from $H_L$ due to the reorientation of the liquid surface upon the step reduction of the acceleration. The Reynolds number predicts the flow pattern by comparing the inertial and viscous forces. The inlet Reynolds number is calculated using the radius of the inlet $R_{I}$ and the mean velocity of the liquid at the inlet $v_{I}$.

$$\begin{aligned} \mathrm {Re_{1}} = \Pi _5 = \dfrac{2 \rho v_{I} R_{I} }{\mu } \end{aligned}$$

(13)

Our final $\Pi _6$-parameter is a combination of $\Pi _0$ and $\Pi _3$, which is the centreline Weber number at the exit of the inlet pipe (tank inlet).

$$\begin{aligned} \Pi _6 = \Pi _0 \, \Pi _3^2 = \dfrac{\rho R_{I} v_{max}^2}{2 \sigma } \end{aligned}$$

(14)

Experimental Setup

An experimental setup was built and assembled into a drop capsule, as used in the Bremen Drop Tower. The drop capsule consisted of five platforms, as shown in Fig. 3. The uppermost platform 1 housed the camera recorder. The two platforms in the middle of the capsule were the experiment platforms, which were named as tank platform (platform 2) and pump platform (platform 3). The tank platform was placed at a height of 470 mm from the pump platform, in order to accommodate the long primary inlet pipe for the experiment tank. The fluid loop components assembled on the platforms 2 and 3 are also shown in Fig. 3. The bottom two platforms (4 and 5) were allotted for the power distribution unit and capsule control system (CCS).

Fig. 3

The drop capsule of the experiment setup with five platforms. The fluid loop components assembled on the platforms 2 and 3 are also shown

Experiment Tank

The experiment tank is the main test article of the experimental setup. An axis-symmetric drawing of the experiment tank is shown in Fig. 4. The drawing consists of 20 points and the r- and z-coordinates of these points are listed in Table 1. The points 2-11 represent the secondary inlet, where the liquid enters the tank through an annular gap. The secondary inlet is not considered in this work. The experiment tank was made up of polymethyl methacrylate (PMMA) material and has a cylindrical cross-section with height $H_T = {94\,\mathrm{\text {m}\text {m}}}$ and inner radius $R_T = {30\,\mathrm{\text {m}\text {m}}}$. The total empty volume of the experiment tank is 265 mL. An outlet port was provided at the top of the tank to vent the gas.

A circular velocity control plate (VCP) with radius ${R_{VP}} = {25\,\mathrm{\text {m}\text {m}}}$ and thickness 1 mm was mounted inside the experiment tank, so that two inlet configurations could be tested. However, in this work, only the primary inlet is used to study the interface stability. The liquid enters the experiment tank directly from the bottom through the primary inlet. The inlet and outlet radii are $R_I$ = $R_O$ = 2 mm. The length of the primary inlet pipe is $L_I = {220\,\mathrm{\text {m}\text {m}}}$, which was chosen based on Eq. 6 for laminar flow.

Fig. 4

Axis-symmetric drawing of the experiment tank. The inlet and outlet radii are $R_I$ = $R_O$ = 2 mm and the tank radius is $R_T$ = 30 mm

Table 1 List of points and their position in axial and radial coordinates. These points describe the axis-symmetric model of the experiment tank, as shown in Fig. 4

Fluid Loop

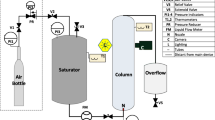
The fluid loop of the experimental setup is shown in Fig. 5. It consists of phase separator (PS), liquid reservoir (LR), experiment tank (ET), bladder tank (BT), storage tank (ST), fluid pump (FP) and flow meter (FM). Totally 6 solenoid valves V1 to V6 from the company SMC were used in the setup to control the flow. Valve V2 was normally open and all the other valves were normally closed. The in-house built PS, which was also made up of PMMA, contained two sections with a screen in between. The porous screen element Dutch twilled weave (DTW) 200$\times$1400 was selected, which has an outer diameter of 90 mm. The screen blocks the gas and allows only liquid to pass through between the sections, until the bubble point pressure of the screen is not exceeded. The concept of phase separation using a screen element was demonstrated in the experiments conducted by Conrath and Dreyer (2012) and Hartwig (2016). Bisht and Dreyer (2020) also used the same PS in the parabolic flight experiments. Thereby, the gas-free liquid was withdrawn from the PS and filled into the experiment tank. The total volume of the PS is 445 mL. The top section of the PS has a gas vent line, through which the gas collected in the gas side of the PS was vented manually before every drop tower experiment. The gas vent line is shown in Fig. 5. The liquid reservoir (LR) was pre-filled and the liquid side of the PS was connected to the LR through valve V6. Any gas bubbles trapped in the liquid side of the PS were removed by opening valve V6.

The liquid from the PS was pumped in a closed loop, which consists of FP, FM and valve V2. The gear pump GA-T23 from the company Micropump, Inc. was used to deliver the required flow rate. SIKA VG 0,02 VA was the flow meter used to measure the volumetric flow rate of the liquid. The accuracy of the flow meter specified by the manufacturer is $\pm 0.3\%$ of the measured value. However, the flow meter was calibrated in-house and the calibration measurements showed a maximum deviation of $\pm 1 \%$ to the measured mean value.

The absolute pressure was measured in the fluid loop using Analogue Pressure Transmitter (ATM) pressure sensor (P1) from the company TetraTec Instruments GmbH. The pressure sensor has an accuracy of ± 12.5 mbar and measures absolute pressure between 0 bar and 2.5 bar. PCA-type PT100 sensors from JUMO GmbH & Co. KG were used to measure the temperatures at three locations in the setup, which are marked as T1, T2 and T3 in Fig. 5. All the sensors recorded data at a sampling rate of 1000 Hz in the experiments. There were two inlet lines to the experiment tank, which are the primary and the secondary inlet. Each inlet line consisted of a valve and a temperature sensor. The experiment tank was connected to the bladder tank (BT), which was used to collect any gas that escaped through the outlet port of the experiment tank. Moreover, during the landing of the drop capsule, the BT also helped to collect any liquid that entered the outlet port of the experiment tank. In case of an overfill of the initial fill height, the excess liquid was drained from the experiment tank into the storage tank (ST).

Fig. 5

The fluid loop of the experimental setup. PI denotes the primary inlet and SI denotes the secondary inlet. The fluid loop consists of liquid reservoir (LR), phase separator (PS), fluid pump (FP), flow meter (FM), experiment tank (ET), bladder tank (BT), storage tank (ST), valves (V1, V2, V3, V4, V5, V6), temperature sensors (T1, T2, T3) and pressure sensor (P1)

Optics

Two high-speed camera heads CAM1 and CAM2 from Photron FASTCAM MC2 were used to record the images at a frame rate of 500 frames per second. The images have a resolution of 512$\times$512 pixels and the recording time was 16.4 s. The recorded images were stored in the camera recorder, also from Photron, which was placed in the uppermost platform of the drop capsule.

CAM1 was equipped with a lens type ${}{2.1}{}/{}{6}{}-{}{0901}{}$ and CAM2 with a lens type ${}{1.4}{}/{}{8}{}-{}{0902}{}$. Both the lenses were from the company Schneider Kreuznach. The cameras CAM1 and CAM2 were placed perpendicular to each other. CAM1 focused on the total view of the experiment tank, while CAM2 captured the ullage region. Two LED panels from the company Stemmer Imaging AG were used as light sources and were placed at a distance of 5 mm behind the experiment tank. Both LED panels emit red light with a wavelength of 635 nm. For diffusing the light, a white sheet was attached to the walls of the experiment tank facing the LED panels. A black and white ruler was pasted on the two sides of the experiment tank, in order to measure the liquid fill height inside the tank. The experiment tank along with the LED panels, cameras and bladder tank were placed on the tank platform of the drop capsule.

Test Liquid

The test liquid chosen for the experiments is the storable liquid 3M Novec Engineering Fluid HFE-7500. It is a perfectly wetting liquid having a contact angle of 0${}^{\circ }$ with the tank wall. Due to the experience and knowledge gained from using this liquid in the previous experiments conducted at ZARM, it was chosen for this set of experiments as well. The properties of the test liquid are listed in Table 2.

Table 2 Properties of the test liquid HFE-7500, as reported in Bisht and Dreyer (2020)

Experimental Procedure

15 drop tower experiments were conducted in three campaigns between December 2020 and August 2021 in the Bremen Drop Tower. According to Könemann (2022), the drop tower offers two modes of operation: the drop mode with 4.7 s and the catapult mode with 9.3 s of microgravity time. The experiments were divided into two categories as reorientation and filling experiments. Three tests were used to observe the reorientation of the liquid interface under microgravity. The remaining 12 tests were performed to study the interface stability using the primary inlet of the experiment tank, in which each flow rate was tested twice. An overview of the drop tower test matrix of these 15 tests is shown in Table 3.

Table 3 Test matrix for the drop tower experiments. Tests F15, F17 and F31 are reorientation tests without filling. The remaining 12 tests correspond to the study of interface stability during the filling of the experiment tank. Test F15 is a drop test. All the other tests are catapult tests. The flow regime for the filling experiments is also listed. The initial fill height is $H_L = (30 \pm {}{0}{}.1) \, {\text {m}\text {m}}$

It can be noticed from Table 3 that the measured liquid temperature $T_L$ varies for each test. However, the mean of the liquid temperature from all the tests is $T_L$ = 25.1 ${}^{\circ }\text {C}$. Therefore, the experiments are considered to be performed under isothermal conditions and the liquid properties corresponding to $T_L$ = 25 ${}^{\circ }\text {C}$ have been chosen from Table 2 for calculating the dimensionless numbers $\mathrm {Re_1}$ and $\mathrm {We_1}$ in Table 3.

As the first step, the liquid reservoir was filled manually by opening the lid. By opening valve V6, the PS was filled from the liquid reservoir. Then, the fluid pump was operated to establish the flow in the closed loop. The desired flow rate was obtained by setting the input set value of the gear pump between 0 V to 10 V. Then, valve V3 was operated to fill the experiment tank to a fill height of $H_L$ = 33 mm. A higher fill level was required to account for any liquid loss due to evaporation inside the experiment tank, while the drop tower is being prepared for the catapult test. When valve V3 was opened, valve V1 was also opened and valve V2 was closed, such that PS does not get depressurized due to the removal of liquid from it. Valve V1 was exposed to ambient pressure inside the capsule. Any air bubbles in the loop were blocked by the screen and collected in the gas side of the PS, which was removed manually by opening the gas vent line. The liquid reservoir was refilled to a certain fill level and then the capsule was taken into the drop tower.

The fill level was adjusted to $H_L$ = 30 mm by operating valve V5 and removing the liquid from the experiment tank and purging it into the storage tank, shortly before the catapult launch or drop of the capsule. In all the experiments, the initial fill height of the liquid inside the tank was set to $H_L = (30 \pm {}{0.1}{}) \, {\text {m}\text {m}}$. An initial fill height of $H_L$ = 30 mm was chosen in such a way that it is equivalent to the tank radius $R_T$ ($H_L / R_T = {}{1}{}$). The desired flow rate was obtained by setting the corresponding input voltage value to the pump. The cameras were set to record ready. The operation of the experiment was programmed in LabVIEW. The catapult launch or drop of the capsule was triggered by pressing the drop sequence switch on the LabVIEW program user interface.

The beginning and end of the drop tower experiments were synchronized with the beginning and end of the microgravity time, although the experiment data were logged for a longer duration. In the filling experiments, from $t = {0\,\mathrm{\text {s}}}$ to $t = {3.5\,\mathrm{\text {s}}}$ in microgravity, the liquid was pumped in the closed loop, where valve V2 remained open. During this time, the reorientation of the pre-filled liquid inside the experiment tank took place and the liquid interface approached its final equilibrium configuration in microgravity. At $t = {3.5\,\mathrm{\text {s}}}$, the filling of the experiment tank commenced by opening valves V3 and V1 and closing valve V2. The filling continued until the end of the microgravity time. At the end of microgravity, valves V3 and V1 were closed and valve V2 was opened to pump the liquid again in the closed loop. The flow meter measured the volumetric flow rate for the whole duration of the experiment. For the reorientation experiments, the pump was stopped after the initial liquid fill height was set in the experiment tank. Therefore, there was no flow of liquid in the fluid loop during the reorientation experiments. The timeline of the drop tower experiments is presented in Table 4.

Table 4 Timeline of the drop tower experiments

Data Evaluation

Image Processing

Two images of the experiment tank in normal gravity before the catapult launch are shown in Fig. 6 for both cameras CAM1 and CAM2. CAM1 captures the total view of the experiment tank and CAM2 focuses on the ullage view. The point of interest is the centre point of the liquid interface on the z-axis (r = 0). Its position is measured from the origin of the experiment tank, which is located at the centre of the inlet orifice, as shown on the left side of Fig. 6.

Fig. 6

The camera views of the experiment tank in 1g with $H_L = (30 \pm {}{0.1}{}) \, {\text {m}\text {m}}$. CAM1 captures the total view (left) and CAM2 captures the detailed view (right)

The images recorded from CAM1 were chosen for the image processing of the reorientation experiment, because the oscillation of the centre point of the liquid interface was completely captured in the total view. The images from CAM2 were used to detect the centre point position in the filling experiments. An image processing function was created in MATLAB, which reads the image as a matrix and processes it. The images were cropped according to the regions of interest. The free surface was detected using the Sobel edge detection algorithm with an accuracy of $\pm 1$ pixel.

The lowermost edge on the z-axis was detected in the liquid reorientation experiment, which corresponds to the centre point of the liquid interface, as shown in Fig. 7a. The uppermost edge on the z-axis was detected for the filling experiment. This is due to the penetration of the interface by the incoming liquid jet and the formation of a geyser. This can be noticed in Fig. 7b. The raw pixel values corresponding to the detected edge were then converted to length scale using the transformation functions obtained from the calibration tests of the cameras. The transformation functions are given in the appendix section A. The image resolution on the z-axis for CAM1 is 4 pixel per millimetre and 5.5 pixel per millimetre for CAM2.

Due to the refraction of light, these transformed length scale values had to be corrected using two correction factors. An extensive ray tracing method, as described in Kulev (2020), was carried out. The ray tracing method, that was applied to correct the measured centre point of the interface, is described in detail in the appendix section B. The initial fill height of the liquid $H_L$ inside the experiment tank in normal gravity was also obtained from the CAM1 images. The correction of the initial fill height is explained in the appendix section C. The measurement error of the centre point of the interface for CAM1 is $\pm {0.3\,\mathrm{\text {m}\text {m}}}$ and $\pm {0.2\,\mathrm{\text {m}\text {m}}}$ for CAM2.

Fig. 7

Detection of the centre point of the liquid interface. A drawing depicting the centre point detection is on the left and the image from the experiment is on the right

Acceleration Measurement

An inertial measurement unit (IMU) from the company iMAR Navigation GmbH was mounted in the drop capsule to measure the acceleration with a sampling rate of 400 Hz, as reported in Könemann (2022). Figure 8 shows the z-axis acceleration of the drop capsule for the test F19. The beginning and end of microgravity are marked by vertical dashed lines in Fig. 8. The capsule experiences a high acceleration of about 310 m s^-2 during the catapult launch, which lasts for approximately 0.3 s. During the landing in the deceleration chamber at the end of microgravity, the capsule is again subjected to a high acceleration of about 410 m s^-2.

Fig. 8

z-axis acceleration of the drop capsule for the catapult test F19. The first vertical dashed line denotes the beginning of microgravity and the second vertical dashed line denotes the end of microgravity. The z-axis acceleration profile before and after the beginning of microgravity is shown in the inset

Flow Rate Measurement

The flow meter was calibrated in-house and the volumetric flow rate as a function of the voltage output of the flow meter was obtained. This function was later used to convert the flow meter voltage output from the experiments to the volumetric flow rate. A moving average with an interval of 100 was performed on the original experiment data, which has a sampling rate of 1000 Hz. These moving averages of volumetric flow rate are plotted over time in Fig. 9 for four different tests. The flow rates are plotted from $t = {0\,\textrm{s}}$ to $t = {9\,\textrm{s}}$ in microgravity. The vertical dashed line indicates the opening of valve V3 to fill the experiment tank. The valve operation causes fluctuations in the flow rate and these fluctuations dampen after $t = {5\,\textrm{s}}$. Therefore, the time-averaged volumetric flow rate is calculated between $t = {5\,\textrm{s}}$ and $t = {9\,\textrm{s}}$. This is the mean volumetric flow rate $Q_L$ considered for the calculation of the dimensionless numbers. The mean volumetric flow rates from the experiments were compared with the calibrated values and the deviation was found to be under 3%.

Fig. 9

$Q_L$ progression over time in microgravity. The vertical dashed line indicates the start of the liquid filling into the experiment tank

Pressure Measurement

The absolute pressure was measured in the filling line to the experiment tank using the pressure sensor P1. The absolute pressure values from two tests are plotted in Fig. 10. The first vertical dashed line from the left represents the start of microgravity at $t = {0\,\mathrm{\text {s}}}$. The second and third vertical dashed lines represent the operation of valves V1 and V3, respectively. A sudden peak in the pressure before $t = {0\,\mathrm{\text {s}}}$ is due to the catapult launch of the drop capsule, where the hypergravity causes an increase in pressure in the fluid loop. When the capsule enters microgravity, this high pressure relaxes and remains above 1 bar.

We observed the penetration of the liquid interface by the incoming jet and the break-up into droplets immediately after valve V3 was operated at $t = {3.5\,\mathrm{\text {s}}}$ in tests F08, F10, F11 and F12. This rapid penetration of the liquid interface was caused by the high pressure in the fluid loop which remained above 1 bar and dropped to 1 bar only after the operation of valve V3, as shown in Fig. 10 for the test F12. This effect was later mitigated in all the other filling tests by operating valve V1 at $t = {3\,\mathrm{\text {s}}}$, 0.5 s prior to the opening of valve V3. This relaxed the pressure to around 1 bar before the filling of the experiment tank began.

This effect is compared between tests F12 and F28 in Fig. 11. Some liquid droplets can be seen moving towards the tank outlet in test F12, whereas in test F28, this was not observed. The mean volumetric flow rate was $Q_L =$ 1.20 mL s⁻¹ in both the tests F12 and F28. Some fluctuations in the pressure can be observed at $t = {3.5\,\mathrm{\text {s}}}$, when the valve V3 is operated and the filling begins. A constant pressure value is maintained in the filling line to the experiment tank after $t = {4\,\mathrm{\text {s}}}$.

Fig. 10

The measurement of the absolute pressure in the filling line. The first vertical dashed line indicates the start of microgravity. The second vertical dashed line indicates the operation of valve V1 to relax the pressure in the test F28. The third vertical dashed line represents the start of the liquid filling into the experiment tank

Fig. 11

a The liquid jet penetrates the liquid interface and breaks into droplets due to the pressure rise in test F12. b The liquid jet penetrates the liquid interface but does not break into droplets in test F28. Both images correspond to the microgravity time of $t = {4\,\textrm{s}}$ and the volumetric flow rate was $Q_L = {1.20\,\mathrm{\text {mL}\ {s}^{-1}}}$ in both tests

Temperature Measurement

The liquid temperature $T_L$ measured in the primary inlet line by the temperature sensor T1 and the outer wall temperature of the experiment tank $T_{ET}$ measured by the temperature sensor T3 are plotted in Figs. 12 and 13 for the whole microgravity duration of 9 s. The temperatures are plotted for four different tests. The plots are created after a moving average with an interval of 100 is performed on the experiment data, which was originally sampled at 1000 Hz. A smooth decline in the liquid temperature $T_L$ is observed after $t = {5\,\textrm{s}}$ for all the tests in Fig. 12. However, the maximum deviation in the liquid temperature $T_L$ is less than 1 ${}^{\circ }\text {C}$ in all the tests. The temperature inside the drop capsule as well as the backlight from the LED panels influence the outer wall temperature of the experiment tank $T_{ET}$. The outer wall temperature of the experiment tank $T_{ET}$ remained constant throughout the test duration, as can be seen in Fig. 13. Therefore, it can be confirmed that the drop tower experiments were performed under isothermal conditions.

Fig. 12

The liquid temperature $T_L$ measured in the primary inlet line under microgravity for four different tests. The vertical dashed line indicates the start of the liquid filling into the experiment tank

Fig. 13

The outer wall temperature of the experiment tank $T_{ET}$ measured under microgravity for four different tests. The vertical dashed line indicates the start of the liquid filling into the experiment tank

Results

The data from 15 tests, as listed in Table 3, are considered for the analysis. The experiment results are divided into two sections:

• 1. Liquid reorientation

• 2. Filling of the tank

Liquid reorientation

In order to observe the reorientation of the liquid interface inside the tank and also to determine the starting time of the liquid filling into the experiment tank under microgravity condition, three tests were carried out without filling the experiment tank. One test was a drop test with a microgravity time of 4.6 s and the other two tests were catapult tests with a longer microgravity time of 9 s. As soon as the capsule enters microgravity, the liquid meniscus rises along the tank wall, due to the completely wetting behaviour and the contact angle of 0${}^{\circ }$ of the test liquid HFE-7500. There is a capillary wave, that propagates from the tank wall towards the centre axis and the centre point of the liquid interface begins to move downwards. This leads to an axial sloshing of the liquid inside the tank and the interface becomes hemispherical. The reorientation of liquid under microgravity at different time steps is shown in Fig. 15 for the catapult test F31. The flat interface of the liquid with some vibrations can be observed at t = 0 s in Fig. 15a. The vibrations are caused due to the launch of the catapult system. Then, the interface changes from a gravity-dominated shape to a capillary-dominated shape in microgravity and this leads to a hemispherical shape of the interface, as seen in Fig. 15b. At t = 9 s, the interface reaches its equilibrium position in microgravity.

Based on the procedure explained in the appendix section B.1, the measured centre point of the interface was corrected. The first correction factor $\Delta z_1$ was calculated using Eq. 20 for every time frame and was found to be in the order of 2.3 mm. Then, the first correction factor $\Delta z_1$ was added to the measured centre point of the interface. The position of the centre point of the liquid interface ($z_c$), corrected with the first correction factor $\Delta z_1$, is plotted against time for the test F31 in Fig. 14. The plot is created by applying a moving average of 50 to the processed data from the images. The initial and final positions of the centre point are marked with dashed horizontal lines. The solid vertical line represents the start of microgravity at t = 0 s. As it can be seen from Fig. 14, the centre point undergoes an oscillation, that dampens with time. For an initial liquid fill height of $H_L = {30\,\mathrm{\text {m}\text {m}}}$, the final equilibrium position of the centre point of the liquid interface in microgravity is determined to be $z_{c,0g} = {20\,\mathrm{\text {m}\text {m}}}$ using Eq. 4.

After applying the first correction factor $\Delta z_1$ to the detected centre point, the final equilibrium position of the centre point of the interface under microgravity condition at $t = {9\,\mathrm{\text {s}}}$ measured for the test F31 is found to be $z_c = {19.3\,\mathrm{\text {m}\text {m}}}$. The measurement accuracy is in the order of $\pm 0.3$ mm. The second correction factor was manually calculated as $\Delta z_2 = {0.6\,\mathrm{\text {m}\text {m}}}$ for the final centre point position at $t = {9\,\mathrm{\text {s}}}$. Due to its complexity, the second correction factor $\Delta z_2$ was only determined for the final centre point position at $t = {9\,\mathrm{\text {s}}}$ and not for all the time frames. It is assumed that the second correction factor $\Delta z_2$ will have its maximum value at $t = {9\,\mathrm{\text {s}}}$. Therefore, the corrected final equilibrium position of the centre point of the liquid interface at $t = {9\,\mathrm{\text {s}}}$ after applying both the correction factors is found to be $z_c = 19.9 \pm 0.3 {\,\mathrm{\text {m}\text {m}}}$.

The equilibrium time in microgravity is calculated using Eq. 5. It is $t_s = {0.68\,\mathrm{\text {s}}}$ for the test F31, which is marked with a dot in Fig. 14. The experimental value matches well with the predicted value of $t_s = {0.67\,\mathrm{\text {s}}}$ from Eq. 5. As the centre point of the liquid interface completes its first period of oscillation and is closer to its final equilibrium position at $t = {3.5\,\mathrm{\text {s}}}$ in microgravity, the liquid inflow was started at $t_{fs} = {3.5\,\mathrm{\text {s}}}$ in microgravity for all the filling tests.

Fig. 14

The centre point oscillation during the reorientation test F31. The initial fill level in normal gravity and the final equilibrium position in microgravity are marked by the horizontal dashed lines. The solid vertical line indicates the start of microgravity. The first vertical dashed line represents the time at which the centre point crosses the final equilibrium position for the first time. The second vertical dashed line shows the time, when the liquid filling into the experiment tank was started in the filling experiments

Fig. 15

Liquid reorientation inside the tank under microgravity for the catapult test F31. The vibrations on the liquid interface at $t = {0\,\mathrm{\text {s}}}$ are caused due to the launch of the catapult system

Filling of the tank

Totally 12 catapult tests were conducted to investigate the stability of the liquid interface perturbed by an incoming liquid jet during the filling of the tank. The liquid jet enters the tank through the primary inlet and momentum exchange takes place with the bulk liquid, as it passes through the bulk liquid. If the momentum of the incoming liquid jet is higher than the capillary pressure of the liquid interface, the jet deforms the liquid interface and a geyser is formed. This geyser then either remains at its position or grows continuously over time. It disintegrates into droplets due to the instability of the liquid column. The geyser flow patterns observed in this work are similar to the patterns I, II and III reported in Aydelott (1979).

The flow regimes can be classified into three categories as subcritical, critical and supercritical regimes. A subcritical flow regime occurs when the incoming liquid jet deforms the liquid interface and forms a geyser, but this geyser does not grow with time. The geyser height is defined as the vertical distance between the origin and the highest point of the liquid interface, as shown in Fig. 7b. If the geyser height increases continuously over time and the geyser starts to disintegrate into droplets, it can be called the critical flow regime. In the supercritical flow regime, the liquid jet completely penetrates the liquid interface and moves rapidly towards the outlet port of the tank.

Due to a longer microgravity time in the catapult tests, the formation and development of geysers could be observed more clearly. The experiments were carried out for volumetric flow rates in the range ${1.0\,\mathrm{\text {mL}\ {s}^{-1}}} \le Q_L \le {1.50\,\mathrm{\text {mL}\ {s}^{-1}}}$. Each flow rate was tested twice. The images recorded by camera CAM2 are shown in Fig. 16 for 6 different tests at a microgravity time of $t = {9\,\mathrm{\text {s}}}$.

The incoming liquid jet only deforms the interface for $Q_L = {1.0\,\mathrm{\text {mL}\ \text {s}^{-1}}}$, creating only a small bulge. A small geyser is formed for $Q_L = {1.10\,\mathrm{\text {mL}\ {s}^{-1}}}$, which remains at its height throughout the microgravity time. The geyser height increases, as the flow rate is increased to $Q_L = {1.20\,\mathrm{\text {mL}\ {s}^{-1}}}$. As the geyser grows for $Q_L = {1.20\,\mathrm{\text {mL}\ {s}^{-1}}}$, oscillations are observed. The flow rates ${1.0\,\mathrm{\text {mL}\ {s}^{-1}}} \le Q_L \le {1.20\,\mathrm{\text {mL}\ {s}^{-1}}}$ can be classified as subcritical flow rates, because the geyser height does not increase with time. The flow rate $Q_L = {1.30\,\mathrm{\text {mL}\ {s}^{-1}}}$ is the critical flow rate, where the geyser starts to grow with time and also breaks into droplets, as seen in Fig. 16d. These droplets reach the outlet port of the tank. The flow rates of $Q_L > {1.30\,\mathrm{\text {mL}\ {s}^{-1}}}$ belong to the supercritical flow regime. In this regime, the incoming liquid jet penetrates the interface and directly travels towards the outlet port of the tank, as observed in Fig. 16e, f.

Fig. 16

Still images from the filling experiments showing the interaction of the incoming liquid jet with the liquid interface under microgravity at $t = {9\,\mathrm{\text {s}}}$ for different volumetric flow rates $Q_L$

We present the images from five different tests with flow rates of $Q_L = {1.10\,\mathrm{\text {m}\text{L}\;\text {s}^{-1}}}$, ${1.20\,\mathrm{\text {m}\text {L}\;\text{s}^{-1}}}$, ${1.30\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$, ${1.38\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$ and ${1.50\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$ in Fig. 20. The images are shown at four different time instants in microgravity. The flow rates of $Q_L = {1.10\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$ and ${1.20\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$ can be considered as subcritical flow rates, as the geyser height does not grow with time. The geyser begins to grow for $Q_L = {1.30\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$. The geyser disintegrates at $t = {5.5\,\mathrm{\text {s}}}$ and the detachment of a droplet can be seen in Fig. 20j. With time, more droplets are generated and move towards the tank outlet. This is the critical domain, where the geyser pattern is very sensitive to the flow rate. As the flow rate is increased to $Q_L = {1.38\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$, the height of the geyser becomes prominent. The instability of the liquid column leads to a frequent detachment of droplets. For $Q_L = {1.50\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$, a long column of liquid jet is formed, which moves rapidly towards the tank outlet. This can be seen in Fig. 20q to t. The flow rates of $Q_L = {1.38\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$ and $Q_L = {1.50\,\mathrm{\text {m}\text {L}\;\text {s}^{-1}}}$ belong to the supercritical flow regime.

The recorded images were processed to measure the height of the geyser versus time. The position of the centre point of the liquid interface, which defines the geyser height, is plotted versus time between $t = {3\,\mathrm{\text {s}}}$ and $t = {9\,\mathrm{\text {s}}}$ in Fig. 17 for different volumetric flow rates $Q_L$. The plot is created after the first correction factor is taken into account, and a moving average of 50 data points (at a recording frequency of 500 frames per second) is applied. The accuracy of the image processing procedure is $\pm {0.2\,\mathrm{\text {m}\text {m}}}$. The second correction factor is estimated manually to be in the order of $< {0.05\,\mathrm{\text {m}\text {m}}}$. The vertical line represents the start of the liquid filling into the tank in Fig. 17. For flow rates ${1.30\,\mathrm{\text {mL}\ {s}^{-1}}} \le Q_L \le {1.50\,\mathrm{\text {mL}\ {s}^{-1}}}$, the curves are plotted only until the time, when the first detachment of a droplet occurs. It can be seen, that the height of the geyser increases with increasing flow rate. For subcritical flow rates ${1.0\,\mathrm{\text {mL}\ {s}^{-1}}} \le Q_L \le {1.20\,\mathrm{\text {mL}\ {s}^{-1}}}$, the geyser height does not grow continuously with time and fluctuations in the height can be seen. A significant growth could be observed for $Q_L = {1.30\,\mathrm{\text {m}\text {L}\text {s}^{-1}}}$. This is the critical flow rate found in our study. The corresponding critical Weber number is $\left( \mathrm {We_1}\right) _{cr} = 1.04 \pm 0.03$, calculated from Eq. 7. A sharp increase in the geyser height can be noticed for higher flow rates. The higher the flow rate gets, the faster the liquid column disintegrates into droplets.

Fig. 17

The evolution of the centre point of the interface over time during microgravity for different $Q_L$

We compare our data for the critical Weber number (test F24) with the existing literature from Symons et al. (1968), Symons (1969), Symons (1970) and Symons and Staskus (1971). Symons (1969) and Symons and Staskus (1971) do not report the initial liquid fill height $H_L$ in normal gravity. They use the height of the liquid interface $H_I$ at the start of the liquid injection in microgravity. Therefore, we use the dimensionless number $\mathrm {\Pi _4} = H_I/R_I$ instead of $\mathrm {\Pi _1}$ for our analysis.

The data points are given in Table 6. All data points in Table 6 correspond to an unstable interface. We have compiled the mean inlet velocity $v_I$ for the critical Weber number together with the dimensionless numbers $\Pi _0, \Pi _5, \Pi _2, \Pi _3$ and $\Pi _4$. The dimensionless number $\Pi _3$ has the limits $1 \le \Pi _3 \le 2$. A uniform velocity profile has $\Pi _3 = {1.0}$, a parabolic (fully developed) profile leads to $\Pi _3 = {2.0}$. Symons et al. (1968), Symons (1969) and Symons (1970) mention partially parabolic profile without a specific definition. Therefore, we assign the value of $\Pi _3 = {1.5}$ in Table 6.

Three test liquids are used in the comparison, and their properties are listed in Table 5. The properties of the test liquids ethanol and trichlorotrifluoroethane (TCTFE) are given for the liquid temperature of $T_L = {20\,\mathrm{{{}^{\circ }\text {C}}}}$, the properties for HFE-7500 correspond to the liquid temperature of $T_L = {25\,\mathrm{{{}^{\circ }\text {C}}}}$.

Table 5 Properties of the test liquids used in this study and in the literature

Table 6 Comparison of dimensionless numbers between experiment F24 and literature data. All data points correspond to an unstable interface. The definitions for the $\Pi$-numbers are repeated for convenience: $\Pi _0 = \rho v_I^2 R_I/2 \sigma$, $\Pi _5 = 2 \rho v_I R_I/\mu$, $\Pi _2 = R_I/R_T$, $\Pi _3 = v_{max}/v_I$, $\Pi _4 = H_I/R_I$

In order to observe the influence of the velocity profile of the liquid jet on the instability of the interface, the inlet Weber number $\Pi _0$ is multiplied by the square of the dimensionless number $\Pi _3$ to get $\Pi _6 = \Pi _0 \, \Pi _3^2 = \rho v_{max}^2 R_I / (2 \sigma )$. This creates a Weber number based on the centreline velocity of the incoming liquid jet. This Weber number is plotted against the dimensionless liquid height $\Pi _4 = H_I/R_I$ in Fig. 18 for three test liquids and different dimensionless numbers $\mathrm {\Pi _2}$. The data from the experiment F24 is marked as a dot in Fig. 18. Each data point in Fig. 18 is annotated by its corresponding position in Table 6.

The centreline Weber number of our experiment (point 1 in Fig. 18) is higher than other tests with comparable $\mathrm {\Pi _4}$. The maximum velocity for a parabolic-shaped velocity profile occurs on the centreline, and it is twice as high as the mean velocity. A nearly linear trend can be observed for TCTFE and $\mathrm {\Pi _4} \ge 8$. Moreover, the centreline Weber number for TCTFE with $\mathrm {\Pi _2} = {0.10}$ is higher than ethanol, when the tank is initially pre-filled with liquid. The centreline Weber number for ethanol with $\mathrm {\Pi _2} = {0.10}$ varies between 2 and 3, when the tank is initially pre-filled with liquid.

A cluster of points can be noticed for initially empty tanks for both test liquids ethanol and TCTFE. This is caused by the different inlet Reynolds numbers, which characterize the flow behaviour. The centreline Weber number as a function of inlet Reynolds number $\mathrm {\Pi _5 = Re_1}$ is shown in Fig. 19. The distinction of each data point can be identified in this Fig. 19. Even though a direct comparison of the experiment data (F24) with the literature is not possible, Figs. 18 and 19 help to understand the effect of all the dimensionless numbers on the interface stability.

Fig. 18

Comparison of the centreline Weber number $\Pi _6 = \Pi _0 \, \Pi _3^2$ against the dimensionless liquid height $\Pi _4 = H_I/R_I$ for different test liquids and different $\Pi _2 = R_I/R_T$. Each data point is annotated by its corresponding position in Table 6. The point 1 is from the drop tower test F24 of this study. Points 2-16 represent initially empty tanks, and points 17-32 represent pre-filled tanks. The data points correspond to the cases, where the interface becomes unstable

Fig. 19

Comparison of the centreline Weber number $\Pi _6 = \Pi _0 \, \Pi _3^2$ against the inlet Reynolds number $\mathrm {\Pi _5 = Re_1}$ for different test liquids and different $\mathrm {\Pi _2} = R_I/R_T$. Each data point is annotated by its corresponding position in Table 6. The point 1 is from the drop tower test F24 of this study. Points 2-16 represent initially empty tanks, and points 17-32 represent pre-filled tanks. The data points correspond to the cases, where the interface becomes unstable

Fig. 20

Time series of the geyser patterns observed in microgravity. The five rows from top to bottom correspond to $Q_L$ = 1.10 mL s$^{-1}$, 1.20 mL s$^{-1}$, 1.30 mL s$^{-1}$, 1.38 mL s$^{-1}$ and 1.50 mL s$^{-1}$

Conclusion

We report the experimental results of the vented filling of a tank in microgravity. The experiments were performed in the Bremen Drop Tower, which offers approximately 9 s of microgravity time. The initial liquid fill height in the tank was set to $H_L = (30 \pm {}{0}{}.1) \, {\text {m}\text {m}}$ for all tests. The tests were divided into two categories: the reorientation of the free surface, and the liquid injection into the experiment tank through the primary inlet.

Three tests were conducted to study the reorientation of the bulk liquid inside the experiment tank under microgravity condition. An oscillation of the centre point of the liquid interface was observed, which begins to damp after $t = {3.5\,\mathrm{\text {s}}}$ in microgravity. The final equilibrium position of the centre point of the interface was found to be at $z_c = ({}{19.9}{} \pm {}{0}{}.3) \, {\text {m}\text {m}}$ for the test F31. The reorientation tests helped to define the start time of the liquid injection into the experiment tank.

The stability of the liquid interface during the filling of the experiment tank under microgravity was investigated for different volumetric flow rates in the range of ${1.0\,\mathrm{\text {mL}\ {s}^{-1}}} \le Q_L \le {1.50\,\mathrm{\text {mL}\ {s}^{-1}}}$. In these tests, the liquid jet entered the experiment tank from the bottom through the primary inlet pipe. The liquid inflow was started at $t = {3.5\,\mathrm{\text {s}}}$ in microgravity. The longer microgravity time provided in the catapult tests enables us to observe the development of different geyser patterns. Three distinct flow regimes were identified based on the formation and growth of a geyser. These regimes can be categorized in terms of volumetric flow rates.

A stable geyser is formed in the subcritical flow regime ${1.0\,\mathrm{\text {mL}\ {s}^{-1}}} \le Q_L \le {1.20\,\mathrm{\text {mL}\ {s}^{-1}}}$, which does not grow with time. The geyser starts to grow in the critical flow regime around $Q_L = {1.30\,\mathrm{\text {mL}\ {s}^{-1}}}$ and disintegrates into droplets. In the supercritical flow regime of $Q_L > {1.30\,\mathrm{\text {mL}\ {s}^{-1}}}$, a rapid growth of the geyser was observed, which also becomes unstable and results in frequent detachment of droplets. These droplets reach the top of the tank.

The geyser height was evaluated and plotted over time with the help of image processing tools. This helped to identify the critical volumetric flow rate and its corresponding Weber number, where the liquid interface becomes unstable. The critical Weber number was found as $\left( \mathrm {We_1}\right) _{cr} = 1.04 \pm 0.03$. The comparison of this critical Weber number with the existing literature revealed that the velocity profile of the incoming liquid jet plays an important role in the stability criterion of the interface. We conclude that the centreline velocity is responsible for the instability of the free liquid surface. A constant flow profile leads to a higher critical Weber number $\left( \mathrm {We_1}\right) _{cr}$ than a parabolic flow profile. We have tried to make the data comparable by using the centreline Weber number $\Pi _6$ instead of the mean velocity Weber number $\Pi _0$. Differences still exist, because the flow problem is governed by other dimensionless numbers as well, such as the Reynolds number of the incoming jet $\Pi _5 = 2 \rho v_I R_I/\mu$, the aspect ratio of the inlet radius to the tank radius $\Pi _2 = R_I/R_T$, and the aspect ratio of the interface height in microgravity to the inlet radius $\Pi _4 = H_I/R_I$.

Appendices

Appendix A. Transformation of Pixels to Millimetre

The images from both cameras were calibrated in the laboratory and transformation functions as second-order polynomials were derived, in order to convert the detected pixels to millimetre. The transformation functions for CAM1 are given in Eqs. 15 and 16. The images recorded by the camera CAM2 were processed for the filling experiments. The transformation function for CAM2 is given in Eq. 17. The centre point of the interface was detected as an edge using the Sobel algorithm in MATLAB. The pixel value of the centre point of the interface is denoted as $z_{pix}$ in Eqs. 15, 16 and 17. For the reorientation experiment, the Eq. 15 was used for transforming the pixel to millimetre. For the filling experiments, the pixels were transformed to millimetre using Eq. 17. The initial fill height of the liquid inside the experiment tank in 1g was detected at the tank wall ($r = R_T$) from CAM1 and the pixels were converted to millimetre from Eq. 16. After transformation, $z_{cu}$ is the position of the centre point of the interface in millimetre.

$$\begin{aligned} (z_{cu})_{r=0} = ({}{-2E-05}{} \, z_{pix}^2 ) - (0.2423 \, z_{pix}) + 104.62 \end{aligned}$$

(15)

$$\begin{aligned} (z_{cu})_{r=R_T} = ({}{-4E-05}{} \, z_{pix}^2 ) - (0.1924 \, z_{pix}) + 95.62 \end{aligned}$$

(16)

$$\begin{aligned} (z_{cu})_{r=0} = ({}{-6E-06}{} \, z_{pix}^2 ) - (0.1775 \, z_{pix}) + 100.07 \end{aligned}$$

(17)

Appendix B. Correction of the Centre Point

Appendix B.1 Reorientation experiment

The light rays from the LED panels get refracted as they travel through the media of liquid, solid and air to reach the cameras. Due to the bending of light, the detected centre point of the interface has to be corrected. The path of a single light ray is traced from the centre axis of the experiment tank (z-axis) to the lens of the camera CAM1 in Fig. 21. The real centre point of the interface is indicated by a black dot on the z-axis in Fig. 21. Due to the hemispherical shape of the interface in microgravity, the light ray does not pass through the centre point of the interface. Instead, it passes as a tangent through a point on the hemispherical interface. This point is projected to the z-axis and is called the apparent centre point, which is marked as a black square in Fig. 21. The camera perceives the light ray to travel in a straight line without any bending. Therefore, the centre point detected by the camera is marked as a black triangle in Fig. 21. This uncorrected centre point ($z_{cu}$) has to be corrected using two correction factors $\Delta z_1$ and $\Delta z_2$.

Fig. 21

Generic drawing depicting the ray tracing for the reorientation experiment

The refractive index of the test liquid HFE-7500 is $n_l = {}{1.29}{}$, as reported in Tang et al. (2009). The solid medium is the experiment tank wall, which is made up of PMMA material. The refractive index of PMMA is $n_s = {}{1.49}{}$, as reported in Beadie et al. (2015) and the refractive index of air is $n_a = {}{1}{}$. The angle of refraction $\alpha$ in the air was calculated from Eq. 18. In Eq. 18, $H_{c1}$ denotes the height of the camera lens from the origin of the experiment tank and $L_{c1}$ is the distance of the camera lens from the experiment tank outer wall. The thickness of the experiment tank wall is $t_w$ = 10 mm. For CAM1, $H_{c1}$ = 52 mm and $L_{c1}$ = 126 mm. The other angles of refraction in solid medium ($\beta$) and liquid medium ($\gamma$) were calculated from Eq. 19 by applying the corresponding indices of refraction. Then, the first correction factor $\Delta z_1$ was calculated using Eq. 20. The first correction factor for the test F31 was estimated to be in the order of $\Delta z_1$ = 2.3 mm.

$$\begin{aligned} \alpha = \tan ^{-1} \left( \frac{H_{c1} - z_{cu}}{R_T + t_w + L_{c1}} \right) \end{aligned}$$

(18)

$$\begin{aligned} n_a \sin \alpha = n_s \sin \beta = n_l \sin \gamma \end{aligned}$$

(19)

$$\begin{aligned} \Delta z_1 = (R_T + t_w) \tan \alpha - t_w \tan \beta - R_T \tan \gamma \end{aligned}$$

(20)

The second correction factor $\Delta z_2$ was found out manually by geometrically constructing a tangent to the hemispherical interface. The starting point of the tangent is the position of the lens of CAM1. The interface shape was assumed to be hemispherical with its real centre point at $z_c$ = 20 mm. The tangent was extended to the centre axis (z-axis) and the height difference between the apparent centre point and the real centre point was measured. Because of its complexity, the determination of the second correction factor $\Delta z_2$ was only done for the image corresponding to microgravity time of t = 9 s. For the reorientation test F31, $\Delta z_2$ = 0.6 mm. Applying both the correction factors, the real position of the centre point of the interface at t = 9 s was found using Eq. 21. For all the other time instants, the second correction factor was assumed as $\Delta z_2 = {}{0}{}$ in Eq. 21.

$$\begin{aligned} z_c = z_{cu} + \Delta z_1 + \Delta z_2 \end{aligned}$$

(21)

Appendix B.2 Filling experiment

The images from CAM2 were processed for the filling experiments F10, F11, F12, F24, F30, and F23. Sobel algorithm was used to detect the edge of the liquid interface as pixel values. The image frame, in which the liquid jet hits the liquid interface, was identified manually for each experiment. In all the frames before that, the centre point of the liquid interface was detected as the lowermost edge of the liquid interface on the z-axis. After the perturbation of the liquid interface by the liquid jet, the centre point was detected as the uppermost edge of the geyser on the z-axis. The detected edges as pixel values were then transformed to millimetre using Eq. 17. In the experiments F24, F30, and F23, the edges were detected only until the image frame, when the first droplet detaches from the geyser.

The first correction factor $\Delta z_1$ was determined following the same method as shown in section B.1 for the frames, where the liquid interface was not penetrated by the liquid jet. However, the height of the camera CAM1 ($H_{c1}$) was replaced by the height of the camera CAM2 ($H_{c2}$) in Eq. 18. For CAM2, $H_{c2}$ = 54.5 mm. The distance of the camera lens of CAM2 from the experiment tank wall is the same as the camera CAM1. $L_{c1}$ = $L_{c2}$ = 126 mm.

Fig. 22

Generic drawing depicting the ray tracing for the filling experiment. The shaded part is the liquid film at the wall

The thickness of the liquid film at the experiment tank wall should also be known, for the frames, where a geyser is formed. This was required for finding the first correction factor $\Delta z_1$, as the light ray from the geyser travels through four media (ullage, HFE-7500, PMMA and air) before it reaches the camera, as shown in Fig. 22. For a given pixel value of the centre point of the geyser, the outermost edge in the radial direction from the tank wall (r = $R_T$) was detected as the liquid film boundary near the wall. The thickness of the liquid film was found by counting the pixels between the tank wall and the liquid film boundary. Then, these pixels were converted to millimetre by multiplying them by a factor of 0.25. This factor comes from the calibration images of CAM2, where 1 pixel = 0.25 mm in the radial direction (r) near the tank wall. Finally, the first correction factor $\Delta z_1$ was determined using Eq. 22, where $t_l$ is the thickness of the liquid film and $\delta$ is the angle of refraction of the light ray in the ullage. The refractive index of the ullage is assumed to be the same as the refractive index of air ($n_a$ = 1). In the filling experiments, the first correction factor $\Delta z_1$ was found to be in the range 0.2 mm $\le \Delta z_1 \le$ 0.9 mm.

$$\begin{aligned} \begin{aligned} \Delta z_1&= (R_T + t_w) \tan \alpha - t_w \tan \beta \\&\quad - t_l \tan \gamma - (R_T - t_l) \tan \delta \end{aligned} \end{aligned}$$

(22)

In the filling experiment F30, the first correction factor $\Delta z_1$ was calculated using Eq. 23, for the image frames, where the uncorrected centre point of the geyser is above the camera height ($z_{cu} > H_{c2}$). In all the other frames, where a geyser is formed, the first correction factor $\Delta z_1$ was calculated using Eq. 22.

$$\begin{aligned} \begin{aligned} \Delta z_1&= t_w \tan \beta + t_l \tan \gamma + (R_T - t_l) \tan \delta \\&\quad - (R_T + t_w) \tan \alpha \end{aligned} \end{aligned}$$

(23)

The second correction factor $\Delta z_2$ for the filling experiments was manually calculated to be in the order of 0.02 mm. Therefore, only the first correction factor was considered in the correction of the centre point of the geyser, as shown in Eq. 24.

$$\begin{aligned} z_c = z_{cu} + \Delta z_1 \end{aligned}$$

(24)

Appendix C. Correction of the Initial Fill Height

The initial fill height of the liquid ($H_L$) inside the experiment tank in 1g was determined by processing the images of the camera CAM1. The liquid meniscus in 1g was detected at the experiment tank wall ($r=R_T$) as pixel values. The pixel values were then converted to millimetre using Eq. 16. The first correction factor $\Delta z_1$ was calculated by tracing the light ray from the tank wall to the camera lens, as shown in Fig. 23. The trigonometry and Snell’s law were applied only for two media of PMMA and air. The first correction factor $\Delta z_1$ was found using Eq. 25. The order of magnitude of the first correction factor was estimated as $\Delta z_1$ = 0.6 mm in 1g. The corrected liquid fill height in 1g was determined using Eq. 26.

$$\begin{aligned} \Delta z_1 = t_w \tan \alpha - t_w \tan \beta \end{aligned}$$

(25)

$$\begin{aligned} z_c = (z_{cu})_{r=R_T} + \Delta z_1 \end{aligned}$$

(26)

Fig. 23

Generic drawing depicting the ray tracing for measuring the initial fill height in 1g