Stability and Bifurcation Analysis of Two-Immiscible Liquids Film Down an Inclined Slippery Solid Substrate

Abstract

In this work, the dynamic behavior of linear and nonlinear waves propagating at the separating surface between two thin layers of viscous Newtonian fluids is studied in the presence of the effect of insoluble surface surfactant. The two liquids are confined between two infinite rigid parallel plates and assumed to have different densities and viscosities. The equations of evolution for surface-wave elevation and concentration of surfactant are derived using the lubrication approximation. In the linear stage, by utilizing the normal mode approach, we have derived the dispersion relation that relates the wave angular frequency to the wave number and other parameters that is solved numerically to inspect the influences of some selected parameters on the stability criteria of the fluid flow. Also, analytical expressions for the growth rate as well as its maximum value with corresponding wave number are obtained in the special case of long-wave limiting. It is concluded that the Marangoni number $\text {Ma}$ has acquired a significant stabilizing influence on the fluid flow, whereas the inverse of the slippery length of substrate plate $\beta$, resorts to the destabilize the motion of the interfacial waves. Consequently, both of the Marangoni number and the substrate slippy coefficient can be utilized to control the film flow regime, where they preserve the film laminar flow and tend to prevent the film breakdown. These can be useful in many industrial applications such as coating processes, heat exchangers, cooling microelectronic devices, chemical reactors, food processing, thermal protection design of combustion chambers in rocket engines and operation of Laser cutting and heavy casting production processes.

Introduction

The phenomenon of falling films in a wide range of industrial and applications has received much attention from many authors, for example, Chang (1994), Oron et al. (1997), Weinstein and Ruschak (2004), Craster and Matar (2009), Zakaria (2012), Kalliadasis et al. (2013), Batchvarov et al. (2021) and others. The open-flow systems under the influence of various factors are encountered in many industrial fields, like coating processes as reported by Alekseenko et al. (1994), heat exchangers by Salvagnini and Taqueda (2004), cooling microelectronic devices by Squires and Quake (2005), chemical reactors by Bender et al. (2017), food processing and thermal protection design of combustion chambers in rocket engines by Shine and Nidhi (2018). Many practical experiences have been made continually by researchers to validate and complement the theoretical studies on falling liquid films, for examples, Liu et al. (1994), Alekseenko et al. (2005), Kharlamov et al. (2015), Adebayo et al. (2017), Charogiannis et al. (2017) and Charogiannis and Markides (2019).

Insoluble surfactants are surface active agents that have been shown to influence the surface tension of fluids Chang and Franses (1995). Some experimental measurements of Song et al. Song et al. (2006) for equilibrium surface tension have evidenced that the surface tension is reduced in response to the surfactant concentration in the fluid bulk. The influence of insoluble surfactants on a falling film was first studied theoretically by Benjamin (1964) and Whitaker (1967). They remarked that the increase of the critical Reynolds number when surface elasticity is included, concluding that there was a stabilizing effect of surfactants, which was qualitatively in agreement with many experimental observations (Stirba and Hurt 1955; Tailby and Portalski 1961; Blyth and Pozrikidis 2004 and others) identified a new Marangoni mode when surfactants are present where a stabilizing effect of surfactants is remarked. According the perturbation theory, Oron and Edwards (1993) derived a nonlinear evolution equation for the free-surface displacement of the liquid film in the presence of interfacial viscous stress. Pereira and Kalliadasis (2008) studied the problem of moved liquid film in both linear and nonlinear regimes. In linear instability, they solved the Orr-Sommerfeld eigenvalue problem and obtained three different modes, where they stated that the Marangoni stress caused by surfactants reduces the domain of film instability. Using the weighted residual model (WRM), they found that the amplitude and velocity of travelling waves on the film are decreased by the Marangoni effect. The linear stability Couette-Poiseuille flow with insoluble surfactants is studied by Frenkel and Halpern (2002) in zero gravity environment and obtained asymptotic long-wave expressions for the growth rates. They found a caused destabilization by the interfacial surfactant. Halpern and Frenkel (2003) studied linear instability of creeping Couette-Poiseuille flow for a two-layer system with a monolayer of an insoluble surfactant in the Stokes approximation. They demonstrated that the unstable waves are not necessarily much longer than the smaller of the two layer thicknesses, there are parametric regimes for which the instability has a mid-wave character and the flow being stable at both sufficiently large and small wavelengths and unstable in between. Frenkel and Halpern (2017) investigated the Couette flow of a horizontal channel of two-layer system subject to vertical gravitational forces and with insoluble interfacial surfactants. They introduced linear and nonlinear instability of the inertialess long-wave with surfactant and gravity dependent using the lubrication approximation which leads to coupled nonlinear evolution equations. In their study, the effect of density stratification included in the system to examine the interacting effects of gravity and Marangoni forces. Linear stability regime of an immiscible bounded two-layer plane Couette flow film in the presence of an insoluble surfactant monolayer along the interface and the boundary parallel plates moving at a constant relative velocity to each other is produced by Frenkel et al. (2019). The impact of insoluble surfactant on the instability of interfacial waves between a thin film and a much thicker fluid has been analyzed in the studies of Bassom et al. (2010), Kalogirou et al. (2012), Kalogirou and Papageorgiou (2016) and Kalogirou (2018) through analysis and numerical computations of a system of evolution equations that includes a non-local contribution from the thicker fluid. The effect of slippery boundary condition of substrate on the dynamics of overlying liquid film flow is discussed by many anthers, for example, Pascal (1999), Samanta et al. (2011), Zakaria (2012), Bhat and Samanta (2018), Sani et al. (2020) and Samanta (2020). Pascal investigated the linear stability of a fluid flowing down an inclined permeable plane by studying the evolution in time of infinitesimal disturbances of long wavelength. He assumed a flow through the porous medium which is governed by Darcy’s law, with producing critical conditions for the onset of instability. Also, Pascal remarked that increasing the permeability of the inclined plane destabilizes the flow of the fluid layer flowing above. Samanta et al. (2011) considered the gravity-driven film flow on a slippery inclined plane within the framework of long-wave and boundary layer approximations. They observed the non-trivial effect for Navier slip condition at the wall on the primary instability. Also, the observed role of Navier slip condition on the behavior of backflow phenomenon in the capillary region of the solitary waves. Zakaria studied the linear and nonlinear instability for the evolution of superposed layers of fluid flowing down inside an inclined permeable channel using the Kármán-Pohlhausen method through a long-wave approximation. Bhat & Samanta studied The linear stability analysis of a fluid flow down a slippery inclined plane when the free surface of the fluid is contaminated by a monolayer of insoluble surfactant. According to their analysis, wall slip exhibits a stabilizing effect on the surface mode as opposed to the result in the long-wave regime, while the insoluble surfactant exhibits a stabilizing effect on the surface mode as in the result of the long-wave regime at moderate Reynolds number. At high Reynolds number, both wall slip and insoluble surfactant exhibit a stabilizing effect. The both surface and shear modes compete with each other to dominate the primary instability in case of sufficiently small inclination angle. Sani et al. analyzed the linear instability of a surfactant-laden two-layer falling film over an inclined slippery wall under the influence of external shear stress the top free surface. They found that the overall stabilization of the surface mode by wall velocity slip for the stratified two-fluid flow is contrary to that of the single fluid case in the presence of strong imposed shear. Samanta studied the temporal and spatial disturbance growths for three-dimensional viscous incompressible fluid flows with slippery walls. He investigated that for a free surface flow over a slippery inclined substrate, the maximum temporal energy amplification increases in severity with the effect of wall slip for the spanwise perturbation, but it attenuates with the wall slip for both streamwise and spanwise wavenumbers. The aim of present manuscript is to study the linear and nonlinear instability with the bifurcation view for an overlying two-layer plane Couette flow with different densities, viscosities, thicknesses and insoluble interfacial surfactants on inclined fixed substrate which satisfies the slippery condition and bounded by an upper moved solid wall. The rest of this manuscript is organized as follows: Mathematical equations are posed in section "Mathematical Formulation". Lubrication approximation for the considered problem is discussed in section "Lubrication Approximation". The evolution equations are explored in section "Evolution Equations". Section "Linear Instability Analysis" is devoted for linear instability thorough the growth rate and neutral curves is in investigated. In section "Weakly Nonlinear Analysis of Surface Resonated Waves", Weakly nonlinear analysis of surface resonated waves is browsed through the bifurcation view. The concluding remarks are presented in section "Conclusion".

Mathematical Formulation

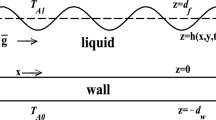
Consider a two-dimensional system $(x^{*},z^{*})$ film of two- liquids with different densities, viscosities past a slippery inclined substrate. The film is bounded by a parallel plate which is moved at a constant velocity $U_2$ with $U_2=\mathcal {V}^*$ at a distance $z^{*}=\mathcal {Z}^*$ as shown in Fig. 1. The $z^{*}$-axis is the spanwise, coordinate perpendicular to the two plates with the substrate located at $z^{*}=0$ where $z^{*}=d$ defines the location of the unperturbed liquid-liquid interface. The symbol $*$ indicates a dimensional quantity.

Fig. 1

Skeleton of the problem

At the interface, the surface tension, $\sigma ^{*}$ depends on the concentration of the insoluble surfactant monolayer, $\varGamma ^{*}$. The basic flow is driven by the combination of the steady motion of the the upper plate and the inclination of substrate.

In the base state, the interface is flat, and the surfactant concentration is uniform.

Once disturbed, the surface tension and surfactant concentration are no longer uniform and the deflection of the liquid-liquid interface is represented by the function $H^*(x^*,t^*)$ where $t^*$ represents the time.

The continuity equation and the Navier–Stokes equations govern the fluid film motion in the two layers (with $j = 1$ for the lower liquid layer and $j = 2$ for the upper liquid layer). They are

$$\begin{aligned} \nabla ^*\cdot {\textbf {v}}_j^* = 0, \end{aligned}$$

(1)

$$\begin{aligned} \rho _j(\partial _{t^*}+{\textbf {v}}_j^*\cdot \nabla ^*){\textbf {v}}_j^*=-\nabla ^*p_j^*+\rho _jg\{\text {sin}\theta ,-\text {cos}\theta \}+\mu _j\nabla ^{*2}{} {\textbf {v}}_j^*, \end{aligned}$$

(2)

where $\rho _j$ is the density, ${\textbf {v}}_j^*=\{u_j^*,w^*_j\}$ is the fluid velocity vector; $p^*_j$ is the pressure, $\mu _j$ is the viscosity; g is the gravity and $\theta$ is the inclination angle of the substrate.

The interfacial boundary conditions will be as follows. The velocity must be continuous:

$$\begin{aligned}{}[{\textbf {v}}^*]^2_1= 0, \end{aligned}$$

(3)

where $[f]^2_1=f_2-f_1$ denotes the jump in f across the interface, $z^* =H^*(x^*,t^*)$.

We assume the dependence of surface tension on the surfactant concentration given by the Langmuir isotherm relation (Edwards et al. 1991), which becomes the linear Gibbs isotherm when the surfactant concentration $\varGamma ^*$

$$\begin{aligned} \sigma ^*= \sigma _0-Ee(\varGamma ^*[x^*,t^*]-\varGamma _0), \end{aligned}$$

(4)

where $\sigma _0$ and $\varGamma _0$ are the basic surface tension and surfactant and Ee is the elasticity parameter. Here we have considered dilute surfactant concentrations only, and therefore a linear equation of state is expected to be valid.

According to the gradient of surface tension, the interfacial balances of the tangential and normal stresses are given by, respectively,

$$\begin{aligned}{}[\mu \left( 1-H^{*2}_{x^*}\right) \left( u^*_{z^*}+w^*_{x^*}\right) +\mu H^*_{x^*}\left( w^*_{z^*}-u^*_{x^*}\right) ]^2_1=-\sigma ^*_{x^*}\mathcal {H}, \end{aligned}$$

(5)

and

$$\begin{aligned}{}[p^*-\dfrac{2\mu }{\mathcal {H}^2}\left( H^{*2}_{x^*}u^*_{x^*}-H^*_{x^*}\left( u^*_{z^*}+w^*_{x^*}\right) +w^*_{z^*}\right) ]^2_1=\sigma ^*\mathcal {H}^{-3}, \end{aligned}$$

(6)

where $\mathcal {H}=\left( 1+H^{*2}_{x^*}\right) ^{1/2}$. The kinematic interfacial condition is

$$\begin{aligned} w^*=H^{*}_{t^*}+H^{*}_{x^*}u^*. \end{aligned}$$

(7)

Surface concentration value of the insoluble surfactant on the interface, $\varGamma ^*[x^*,t^*]$, obeys the following transport equation (Blyth and Pozrikidis 2004 and Frenkel and Halpern 2017)

$$\begin{aligned} \partial _{t^*}\left( \mathcal {H}\varGamma ^*\right) +\partial _{x^*}\left( \mathcal {H}\varGamma ^*u^*\right) =D_s\partial _{x^*}\left( \mathcal {H}^{-1}\varGamma ^*_{x^*}\right) , \end{aligned}$$

(8)

where $D_s$ is the diffusivity constant for the interfacial surfactant. The surface tension gradient in the tangential stress balance Eq. (5) emerges due to local changes in the surfactant concentration and give rise to Marangoni forces.

At the slippery substrate, $z^*=0$, the lower layer fluid velocity satisfies Navier-slip and no penetration boundary conditions (Pascal 1999; Samanta 2020)

$$\begin{aligned} \beta ^*u^*_1=u^*_{1,z^*}, \end{aligned}$$

(9)

where $\beta ^*$ is the inverse dimensional sliplength. At the upper plate, we have

$$\begin{aligned} u^*_2=U^*_2. \end{aligned}$$

(10)

The deriving of the evolution equation will be made wherein the sum of the flow rates of two-layers Q, is held constant where

$$\begin{aligned} Q^*=\int _0^{H^*}u^*_1dz^*+\int _{H^*}^{\mathcal {Z}^*}u^*_2dz^*. \end{aligned}$$

(11)

The governing equations with their boundary conditions are normalized by introducing the following dimensionless variables:

$$\begin{aligned} & (x,z,H)=(x^*/\lambda ,z^*/d,H^*/d);~t= (U/\lambda )t^*;\\&~(u_j,w_j)=(u^*_j,(d/\lambda ) w^*_j)/U;~ \varGamma =\varGamma ^*/\varGamma _0;~\\&\sigma =\sigma ^*/\sigma _0;~ p_j=d^2p^*_j/(\lambda \mu _1 U),\end{aligned}$$

(12)

where U is the characteristic velocity scale and $U=\dfrac{d^2g\rho _1\text {sin}\theta }{\mu _1}$, d is the thickness of lower layer and $\lambda$ is the typical wavelength.

Lubrication Approximation

The interest of this work is to follow the temporal evolution of a given perturbation at the interface, and in particular to explore the effects of surfactants, the slippery of the substrate and film thickness on the emerging linear and nonlinear developments on the interface. In what follows we assume that the wavelength of the disturbance is much larger than the film thickness, which suggests a parameter $\epsilon (=d/\lambda )\ll 1$. The evolution of long waves can be described efficiently working under the lubrication approximation. Under these conditions, the Navier–Stokes equation is greatly simplified by assuming that the fluids are in a state of nearly unidirectional motion (Blyth and Pozrikidis 2004; Bassom et al. 2010; Frenkel and Halpern 2017; Zakaria and Sirwah 2018; Frenkel et al. 2019 and others). The lubrication approximation was used by Halpern and Frenkel (2008), Kalogirou (2018) and Kalogirou and Blyth (2020) to build a model valid for interfacial deformations of the same order as the film thickness.

Considering a weak inclination and Reynolds number Re, the inertial effects are negligible and thereby we can apply the concept of lubrication approximation theory. For apply this, we consider $\text {cot}\theta =\mathcal {S}/\epsilon$ and Reynolds number is assumed to be $\mathcal {O}(\epsilon )$ Mavromoustaki et al. (2010); Zakaria and Sirwah (2018). Substitution of the normalizations in (12) into the governing equations and boundary conditions, taking into acount the concept of lubrication theory, yields the following set of leading order equations:

$$\begin{aligned} \begin{aligned} p_{j,x}-\mu ^{j-1} u_{j,\text {zz}}-\rho ^{j-1}&=0, \\ p_{j,z}+\mathcal {S} \rho ^{j-1}&=0, \\ \mu u_{2,z}-u_{1,z}-\tilde{\text {Ma}} \Gamma _x=0~~\text {at}~~z&=H, \\ p_1-p_2+\frac{H_{\text {xx}}}{\tilde{\text {Ca}}}=0~~\text {at}~~z&=H, \\ \Gamma _t+u_1 \Gamma _x+\Gamma u_{1,x}=\frac{\Gamma _{\text {xx}}}{\tilde{\text {Pe}}}~~\text {at}~~z&=H,\\ u_1-u_2=0~~\text {at}~~z&=H, \\ w=H_t+H_xu~~\text {at}~~z&=H, \\ u_{1,z}=\beta u_1~~\text {at}~~z=0;~~u_2=\mathcal {V}~~\text {at}~~z&=\mathcal {Z}, \end{aligned} \end{aligned}$$

(13)

where $\text {Ma}= \frac{\Gamma _0 \text {Ee} }{\mu _1 U}=\epsilon ^{-1}\tilde{\text {Ma}}$, $\text {Ca}=\frac{\mu _1 \text {U}}{\gamma _0}= \epsilon ^{3}\tilde{\text {Ca}}$, $\text {Pe}=\frac{U d}{\text {Ds}}= \epsilon \tilde{\text {Pe}}$ are the Marangoni, capillary and Péclet numbers. The parameter scalings considered here are in order to retain gravity, surface tension and Marangoni contributions in the leading-order dynamics and are similar to those applied in Kalogirou and Blyth (2020).

Evolution Equations

Using the leading-order normal stress balance, the solution of the pressure perturbation namely

$$p_1=-\mathcal {S} z+\text {C}(x,t),$$

$$p_2=-\mathcal {S} (\rho z-H (\rho -1))+\frac{H_{xx}}{\text {Ca}}+C(x,t).$$

Using the solutions of the pressure and the boundary conditions, the momentum equations in (13) can be integrated in z twice to give

$$\begin{aligned} u_1&=C_x(x,t)(\frac{z^2}{2}-\frac{\mathcal {A}_2(H) (\beta z+1)}{2 \mathcal {U}_0(H)})+\frac{\text {Ma} (H-\mathcal {Z}) \Gamma _x (\beta z+1)}{\mathcal {U}_0(H)} \\ &\quad-\frac{(\rho -1) \mathcal {S} H_x (H-\mathcal {Z})^2 (\beta z+1)}{2 \mathcal {U}_0(H)}-\frac{H_{\text {xxx}} (H-\mathcal {Z})^2 (\beta z+1)}{2 \mathcal {U}_0(H)}+\frac{\mathcal {A}_1(H) (\beta z+1)}{2 \mathcal {U}_0(H)}-\frac{z^2}{2}, \end{aligned}$$

$$\begin{aligned} u_2=&\frac{\text {Ma} (\beta H+1) (z-\mathcal {Z}) \Gamma _x{}^{(1,0)}(x,t)}{\mathcal {U}_0(H)}+C_x(x,t)(-\frac{\mathcal {Z} \mathcal {A}_7(H)}{2 \mu \mathcal {U}_0(H)}\\&-\frac{\beta z \mathcal {A}_2(H)}{2 \mu \mathcal {U}_0(H)}+\frac{z^2}{2 \mu }) +\frac{\mathcal {Z} \mathcal {A}_4(H)}{2 \mu \mathcal {U}_0(H)}-\frac{\beta \mathcal {V} \mathcal {Z}}{\mathcal {U}_0(H)}\\&+\mathcal {S} H_x (-\frac{(\rho -1) \mathcal {Z} \mathcal {A}_6(H)}{2 \mu \mathcal {U}_0(H)}-\frac{(\rho -1) z \mathcal {A}_5(H)}{2 \mu \mathcal {U}_0(H)}+\frac{(\rho -1) z^2}{2 \mu })\\&+H_{\text {xxx}} (\frac{\mathcal {A}_8(H)}{2 \mu \mathcal {U}_0(H)} -\frac{z \mathcal {A}_5(H)}{2 \mu \mathcal {U}_0(H)}+\frac{z^2}{2 \mu })+\frac{z \mathcal {A}_3(H)}{2 \mu \mathcal {U}_0(H)}+\mathcal {V}-\frac{\rho z^2}{2 \mu }, \end{aligned}$$

where C(x, t) is the constant of the integration. Finally, the leading-order kinematic equation and leading-order transport equation for interfacial surfactant are given by

$$\begin{aligned} H_t+q_x=0, \end{aligned}$$

(14)

$$\begin{aligned} \begin{aligned} \Gamma _t&+\Gamma (\frac{H_{\text {xxxx}} \mathcal {R}_6(H)}{\text {Ca}}+\text {Ma} H_x \mathcal {R}_4(H) \Gamma _x+\text {Ma} \mathcal {R}_5(H) \Gamma _{\text {xx}}\\&+H_x H_{\text {xxx}} \mathcal {R}_7(H)+\mathcal {S} H_x^2 \mathcal {R}_2(H)+H_x \mathcal {R}_1(H)+\mathcal {S} H_{\text {xx}} \mathcal {R}_3(H))\\&+\text {Ma} \mathcal {Q}_3(H) \Gamma _x^2+\Gamma _x (\mathcal {Q}_1(H)+\mathcal {S} \mathcal {Q}_2(H) H_x+\mathcal {Q}_4(H) H_{\text {xxx}})=\frac{\Gamma _{\text {xx}}}{\text {Pe}}, \end{aligned} \end{aligned}$$

(15)

where

$$\begin{aligned} q=\frac{\mathcal {T}_3(H) H_{\text {xxx}}}{\text {Ca}}+f(H)+\text {Ma} \mathcal {T}_2(H) \Gamma _x+\mathcal {S} \mathcal {T}_1(H) H_x. \end{aligned}$$

(16)

The system of evolution Eqs. (14), (15) and (16), where the tildes are dropped, are derived under the assumptions of lubrication approximation, and retain a number of salient physical properties: Gravitational forces are incorporated in the diffusion term $\mathcal {S} \mathcal {T}_1(H) H_x$ and are responsible for making the flow susceptible to the classical Couette-Poiseuille instability that appears when a heavy fluid lies above a lighter fluid beside the difference between basic velocities. This scenario emerges only when $\rho > 1$, in which case the diffusion term destabilizes the waves motion. For $\rho < 1$, diffusion term causes stabilization of the flow. The Marangoni forces come into model flow through the $\text {Ma} \mathcal {T}_2(H) \Gamma _x,~\text {Ma} \mathcal {Q}_3(H) \Gamma _x^2,~\text {Ma} H_x \mathcal {R}_4(H) \Gamma _x$ and $\text {Ma} \mathcal {R}_5(H) \Gamma _{\text {xx}}$ terms. The terms of capillary number coefficients cause a damping in a range of the interfacial waves. The term f(H) is the flux function of the flow evolution.

Linear Instability Analysis

Growth Rate

In this section we proceed to investigate the stability properties of the flow as a result to small disturbances of small amplitudes superimposed on the basic state solution as $H=1+H_{p}(x,t),\; \Gamma =1+\Gamma _{p}(x,t)\;$ where $H_{p}(x,t)$ is a small deflection from the flat interface solution $H=1,\;$ and $\Gamma _{p}(x,+t)$ is a small deviation from the initial case of uniform surfactant. Substituting $H, \Gamma$ into evolution Eqs. (14), (15), and then linearizing with respect to $H_{p}, \Gamma _{p}$ to have

$$\begin{aligned} \frac{\partial H_p}{\partial t}+\mathcal {C}_1\frac{\partial H_p}{\partial x}+\mathcal {C}_2\frac{\partial ^2H_p}{\partial x^2}+\mathcal {C}_3\frac{\partial ^2\Gamma _p}{\partial x^2} +\mathcal {C}_4\frac{\partial ^4H_p}{\partial x^4}=0, \end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial \Gamma _p}{\partial t}+\mathcal {C}_5\frac{\partial H_p}{\partial x}+\mathcal {C}_6\frac{\partial \Gamma _p}{\partial x}+\mathcal {C}_7\frac{\partial ^2H_p}{\partial x^2}+\mathcal {C}_8\frac{\partial ^2\Gamma _p}{\partial x^2} +\mathcal {C}_9\frac{\partial ^4H_p}{\partial x^4}=0, \end{aligned}$$

(18)

where the coefficients $\mathcal {C}_i$ are given in the Appendix.

We seek traveling wave solutions for Eqs. (17) and (18) in the form

$$\begin{aligned} H_p(x,t)=\tilde{H} e^{i k x+ \omega t}+\bar{\tilde{H}} e^{-i k x+ \omega t},\; \Gamma _p(x,t)=\tilde{\Gamma } e^{i k x+ \omega t}+\bar{\tilde{\Gamma }} e^{-i k x+\omega t}, \end{aligned}$$

(19)

where over bar denotes the complex conjugate, k is the positive real wave number, $\omega =\omega _r+i \omega _i$ is the complex angular frequency while $\tilde{H},\ \tilde{\Gamma }$ stand for the initial constant disturbances. The symbols $i=\sqrt{-1}.$ Here $\omega _r$ is the growth wave while $\omega _i/k$ represents the phase speed. Insertion these solutions into Eqs. (17) and (18) yields the dispersion relation

$$\begin{aligned} \omega ^2+\mathcal {F}_1\omega +\mathcal {F}_0=0, \end{aligned}$$

(20)

where

$$\mathcal {F}_1=\alpha _1+i\alpha _2,\;\mathcal {F}_0=\alpha _3+i\alpha _4,$$

$$\begin{aligned}\alpha _1&=k^2\big (-\mathcal {C}_2 +\mathcal {C}_4 k^2-\mathcal {C}_8 \big ),\;\alpha _2=k(\mathcal {C}_1+\mathcal {C}_6),\;\alpha _3\\&=k^2 \Big (-\mathcal {C}_1 \mathcal {C}_6+k^2 \big (\mathcal {C}_2 \mathcal {C}_8+k^2 (\mathcal {C}_3 \mathcal {C}_9-\mathcal {C}_4 \mathcal {C}_8)-\mathcal {C}_3 \mathcal {C}_7\big )\Big ),\end{aligned}$$

$$\alpha _4=k^3\big (-\mathcal {C}_1 \mathcal {C}_8-\mathcal {C}_2 \mathcal {C}_6+\mathcal {C}_3 \mathcal {C}_5+\mathcal {C}_4 \mathcal {C}_6 k^2\big ).$$

In view of the dispersion relation (20), what we’re interested in here with the real part $\omega _r$ of the angular frequency that governing the stability criteria of the linearized surface waves. It is clear that when the growth rate $\omega _r$ is negative, the disturbance of wave elevation will oscillates periodically or decay with time, while the positive values of $\omega _r$ admit s growing or a nonuniform disturbance for such waves. Each curve grows monotonically as the wave number increases until it reaches its maximum value (peak value). After reaching that value, the curve gradually begins to decrease, which is attributed to the stabilization effect that played by the surface tension. In Fig. 2, we have plotted the growth rate as a function of the wave number at various the velocity of the upper plate $\mathcal {V}.\;$ In our model calculations, we have considered the fixed values of the parameters $\text {Ca}=1000, {\mathcal {Z}}=1.3,\beta =.1,\mu =0.8,\rho =0.5,q=-.005,S=1,\text {Pe}=600,\text {Ma}=100.$ We observe that the growth rate as well as the cut- off wave number separating the stable region about the unstable one is monotonically increases with the increase in the values of $\mathcal {V}$ as pointed by Frenkel and Halpern (2017) and Frenkel et al. (2019). This enhances the destabilizing impact of the parameter $\mathcal {V}.$ Numerical simulations are plotted in Fig. 3 to study the variation of $\omega _r$ with respect to the wave number for $\beta = 0.1,1,3,\;$ while the values of the remaining physical parameters are held constant, as given in caption of Fig. 3. It is to be noted that both the growth rate and the instability window are extending due to the increase in $\beta ,\;$ which means that this parameter also tends to grow the disturbance of the interfacial waves profile. As for Fig. 4, we have displayed the evolution of the growth rate with the wave number as a result of the increase in the values of q. It is evident that the parameter q has acquired a tenuous destabilizing effect on stability behavior of the liquid films where the vales of the maximum growth rate and the cut-off wave number posses a slight increase owing to the increase in values of q. Unlike to the effects of $\mathcal {V},q,\;$ the numerical computations displayed in Fig. 5 indicate that the Marangoni number Ma has a considerable stabilizing effect, where the cut-off wave number, growth rate and the stability window have a significant contract with respect to larger values of $\text {Ma}.$ This clarifies that the stability property is very sensitive to the variation in the values of Ma. Such a result is in a well agreement with several of previous studies such as (Frenkel et al. 2019; Sirwah and Alkharashi 2021). In Fig. 6, we proceed to investigate the influence of the location of the upper plate, specified by the parameter $\mathcal {Z},$ on the temporal growth rate versus the waves number. We distinctly note that the cut-off wave number kc, the maximum growth rate $\omega _m$ and the corresponding wave number km will diminish with increasing $\mathcal {Z}.\;$ This confirms that the more the upper plate is repositioned, the more stable the system becomes where the growth rate as well as well as the instability window is constantly decreasing. Figure 7 illustrates the effect of the density ratio on stability picture of the linearized system where the temporal growth rate of the interfacial waves is plotted as a function of the Marangoni number at several values of for the sake of comparison. Demonstration of the graphs displayed in Fig. 7 show that as $\rho =0.1\;$ there are two modes of the flow pattern, one is unstable region specified by $\;\text {Ma}< 70\;$ where the growth rate has negative values and the other is the stable for $\text {Ma} > 70.\;$ It is also noticed that when $\rho$ is increasing to the value to.5, there is a noticeable contraction in the stability region to become limited in range $\text {Ma} > 150.\;$ With a further increase in the value of the density ratio $\rho =0.7,$ the shrinkage continues further in the wave surface motion stability region separating the two liquid films to be characterized by $\text {Ma} > 267.\;$ Accordingly, that is, the more dense the upper fluid is than the lower liquid, the less stable the movement of the interfacial surface separating them, and it also weakens the stabilizing role of the Marangoni number and these results, also, is similar to resluts of Frenkel and Halpern (2017), taking into account the difference in the hypotheses of the two problems.

Fig. 2

Effect of the velocity of the upper plate $\mathcal {V}\;$ on the wave growth rate $\omega _r$ against the wave number for a system having $\text {Ca} = 1000, \, \mathcal {Z} = 1.3, \, \beta =.1, \, \mu =0.8, \, \rho = 0.5, \, q = -.005 \, S = 1 \, \text {Pe} = 600 \, \text {Ma} = 100$

Fig. 3

Influence of the inverse sliplength parameter $\beta$ on the wave growth rate against the wave number for the same system considered in Fig. 2 as $\mathcal {V}=2$

Fig. 4

Variation of the wave growth rate with the wave number as a result to changing in the parameter $\;q$, for the same selected parameters as in Fig. 1 with $\mathcal {V} = 2$

Fig. 5

Impact of the Marangoni number $\text {Ma}$ on the evolution of the wave growth rate with wave number for the same system of parameters of Fig. 4 as $q=--0.005$

Fig. 6

Represents the influence of the location of the upper plate, quantified by the parameter $\mathcal {Z},$ on behavior of the wave growth as $\text {Ma}=100,\;$ while the other parameters are held constants as considered in Fig. 5

Fig. 7

Displays the evolution of $\omega _r$ versus $\text {Ma}$ at different values of the density ratio $\rho$ for the same system of parameters selected in Fig. 2 with $\mathcal {V}=2,\;k=0.4$

Neutral Stability Curves

We now proceed to obtain the equations of the transition curves that separate the regions of linearizes stable flow from those of destabilizing flow. To do so, we substitute for $\omega$ by $\omega _r+i \omega _i$ into Eq. (20) and then split the real and imaginary parts to have

$$\begin{aligned} \alpha _3-\alpha _2 \omega _i-\omega _i^2+\alpha _1\omega _r+\omega _r^2=0,\;\alpha _4+\alpha _1 \omega _i+2 \omega _i \omega _r+\alpha _2\omega _r=0. \end{aligned}$$

(21)

As we eliminate $\omega _i$ from these two equations, a fourth- order polynomial equation of $\omega _r$ will be yielded

$$\begin{aligned} -\alpha _4^2&+\alpha _1^2 \alpha _3+\alpha _1 \alpha _2 \alpha _4+8 \alpha _1 \omega _r^3+\left( 5 \alpha _1^2+\alpha _2^2+4 \alpha _3\right) \omega _r^2\\&+\alpha _1 \left( \alpha _1^2+\alpha _2^2+4 \alpha _3\right) \omega _r+4 \omega _r^4=0. \end{aligned}$$

(22)

The required marginal curves that separate the stable from unstable regions will be specified as we set $\omega _r=0,\;$ which in turn gives

$$\begin{aligned} \alpha _1^2 \alpha _3+\alpha _1 \alpha _2 \alpha _4-\alpha _4^2=0. \end{aligned}$$

(23)

which can be rewritten in the form

$$\begin{aligned} Ma^3+\mathcal {G}_1 Ma^2+\mathcal {G}_2 Ma+\mathcal {G}_3=0, \end{aligned}$$

(24)

where

$$\begin{aligned} \mathcal {G}_1=&\frac{1}{\text {Pe} \mathcal {G}}k^6 \tilde{\mathcal{C}}^2 (\text {Pe} (16 k^2 (\mathcal {C}_2-\mathcal {C}_4 k^2) (8 \mathcal {C}_2+k^2 (3 \mathcal {C}_9-8 \mathcal {C}_4)-3 \mathcal {C}_7)\\&-3 \mathcal {C}_5 (-8 \mathcal {C}_1+3 \mathcal {C}_5+8 \mathcal {C}_6)) +48 k^2\,s (-4 \mathcal {C}_2+k^2 (4 \mathcal {C}_4-\mathcal {C}_9)+\mathcal {C}_7)),\end{aligned}$$

$$\begin{aligned} \mathcal {G}_2=&\frac{1}{\text {Pe}^2 \mathcal {G}}k^6 \tilde{\mathcal{C}} (8 \mathcal {C}_1^2 \text {Pe}^2 (\mathcal {C}_2-\mathcal {C}_4 k^2)+\mathcal {C}_1 \text {Pe} (\text {Pe} (-(3 \mathcal {C}_5+16 \mathcal {C}_6))\\& (\mathcal {C}_2-\mathcal {C}_4 k^2)-3 \mathcal {C}_5 s) +\text {Pe}^2 (\mathcal {C}_2-\mathcal {C}_4 k^2) (k^2(\mathcal {C}_2-\mathcal {C}_4 k^2) \\&(8 \mathcal {C}_2 +k^2 (3 \mathcal {C}_9-8 \mathcal {C}_4)-3 \mathcal {C}_7)+3 \mathcal {C}_5 \mathcal {C}_6+8 \mathcal {C}_6^2)\\&+\text {Pe} s (3 \mathcal {C}_5 \mathcal {C}_6 -2 k^2 (\mathcal {C}_2-\mathcal {C}_4 k^2) (16 \mathcal {C}_2+k^2 (3 \mathcal {C}_9-16 \mathcal {C}_4)-3 \mathcal {C}_7))\\& -3 k^2\,s^2 (-8 \mathcal {C}_2+k^2 (8 \mathcal {C}_4-\mathcal {C}_9)+\mathcal {C}_7)),\end{aligned}$$

$$\mathcal {G}_3=\frac{k^6\,s (\mathcal {C}_4 k^2-\mathcal {C}_2) (\mathcal {C}_1^2 \text {Pe}^2-2 \mathcal {C}_1 \mathcal {C}_6 \text {Pe}^2+k^2 (-\mathcal {C}_2 \text {Pe}+\mathcal {C}_4 k^2 \text {Pe}+s)^2+\mathcal {C}_6^2 \text {Pe}^2)}{\text {Pe}^3 \mathcal {G}},$$

$$\mathcal {G}=-64 k^8 \tilde{\mathcal{C}}^3 (-8 \mathcal {C}_2+k^2 (8 \mathcal {C}_4-3 \mathcal {C}_9)+3 \mathcal {C}_7).$$

Equation (24) has in general two complex conjugate roots and a third real root which utilized to control stability criterion of the linearized flow. This real root is expressed as

$$\begin{aligned} Ma=\frac{\root 3 \of {2}\root 3 \of {\mathcal {G}_0^2}+2\mathcal {G}_1^2-6\mathcal {G}_2}{3\root 3 \of {4}\root 3 \of {\mathcal {G}_0}}-\frac{\mathcal {G}_1}{3}, \end{aligned}$$

(25)

$$\begin{aligned}\mathcal {G}_0=&\sqrt{4(3\mathcal {G}_2-\mathcal {G}_1^2)^3+(9\mathcal {G}_1\mathcal {G}_2-2\mathcal {G}_1^3-27\mathcal {G}_3)^2}\\&+9\mathcal {G}_1\mathcal {G}_2-2\mathcal {G}_1^3-27\mathcal {G}_3.\end{aligned}$$

The wave number $k_{max}$ corresponding to the maximum growth rate $\omega _{r max}$ will be determined by simultaneously solving (22) and the equation designated by differentiating (22) with respect to k, taking into consideration that $\frac{\partial \omega _r}{\partial k} = 0$ at the maximum growth rate. The last equation is expressed as

$$\begin{aligned} \frac{\partial }{\partial k}&\left( -\alpha _4^2+\alpha _1^2 \alpha _3+\alpha _1 \alpha _2 \alpha _4\right) +8\omega _r^3\frac{\partial \alpha _1}{\partial k}+\omega _r^2\frac{\partial }{\partial k}\left( 5 \alpha _1^2+\alpha _2^2+4 \alpha _3\right)\\& + \omega _r\frac{\partial }{\partial k}\left( \alpha _1\left( \alpha _1^2+\alpha _2^2+4 \alpha _3\right) \right) =0. \end{aligned}$$

(26)

The numerical results displayed in Figs. 8, 9, 10 and 11 represent the transition curves that separate regions of stability, specified by S, from regions of instability, specified by U, in the plane $k-\text {Ma}\;$ In Fig. 8, the critical curves are plotted at three different values of the travel velocity of the upper plate. It is to be observed that there is a noticeable increase in the regions of instability, and in turn a large contraction in the regions of stability as a result of increasing the velocity values $\mathcal {V},$ particularly at small values of the wavelength. Hence, these results reinforce the unstable role of the upper plate velocity, especially for long waves. As for Fig. 9, the neutral curves are computed for various values of parameter $\beta .\;$. We also note that the variable $\beta$ tends to generate growing waves at the interface separating the two liquids, but this effect appears to be moderate and very weak for short waves when compared to the effect of the traveling velocity of the upper plate, as was observed in Fig. 8 and as it appeared in the results of Bhat and Samanta (2018) and Samanta (2020). The curves presented in Fig. 10 clearly show that there is a monotonic increasing in the long wave stabilization regions with increasing the values of $\mathcal {Z}$, while this increase grows at a smaller rate for short waves. This means that the stability of the wave motion can be controlled by increasing the thickness of the fluid layers. Figure 9 clarifies that the parameter q has a similar destabilizing effect as well as that of the parameters $\mathcal {Z}, \beta \;$ and the unstable role of q is much more than of that of $\beta$ and less than the instability influence of $\mathcal {V}.$

Fig. 8

Shows effect of the $\mathcal {V}$ on the behavior of the neutral curves in the plane $k-\text {Ma}\;$ as $\text {Ca}= 1000,\mathcal {Z}= 1.3,\beta = 0.1,\mu = 0.8, k_2= 0,\rho = 0.5, q= -0.005,\mathcal {S}= 1,\text {Pe}= 600$

Fig. 9

Represents the neutral curves in the plane $k-\text {Ma}$ as $\beta =0.1, 3, 10$ and $\mathcal {V}=1$ for the same values for the remaining parameters as taken in Fig. 8

Fig. 10

Inspects the effect of $\mathcal {Z}$ on the variation of the neutral curves with k when $\text {Ca}= 1000,\beta = 0.1,\mu = 0.8,\rho = 0.5,\mathcal {V}= 1,q= -0.005,\mathcal {S}= 1,\text {Pe}=600$

Fig. 11

Effects of $q=(-0.2,-0.005,0.1)$ on the neutral stability curves in $k-\text {Ma}\;$ plane for the same system as in Fig. 10, but with $\mathcal {Z}=1.3$

To gain a deeper understanding of flow behavior,

In order to better understand the flow behavior, Fig. 12 clarifies the structures of the dimensionless growth rate in the plane $k-\rho$ by changing the values of q corresponding to the sections of this graph. In Fig. 12a, where the value $-0.2$ is assigned for q,  the zero-value contour corresponds to the neutral case that separate the stable regions specified by counters of negative values from the unstable regions represented by counters of positive values. When increasing the value of q to $-0.005,$ represented in Fig. 12b, we notice the zero-value contour will be shifted up results in an increase in the $k-\rho$ region corresponding to the contours with positive values and a contraction of the domain associated with the counters with positive values. Further increase in values of q to 0.01 as performed in Fig. 12c causes more enlargement in the $k-\rho$ domain of unstable flow pattern and more shrinking of negative- values contours admitting stable flow. In order to examine the influence of variation of the parameter $\mathcal {Z}$ on the stability criteria of the linearized model, we have plotted the critical wave number against the viscosity ratio $\mu$ for several values of $\mathcal {Z}$ in Fig. 13. In Fig. 13a, where $\mathcal {Z}=1.1,$ we have some contours with positive values and others of negative values and then according to the specified parameters two modes of an unstable and one stable system are observed. In Fig. 13b and c, we display graphically the numerical results of the same system investigated in Fig. 13a with increasing $\mathcal {Z}$ values to 1.2 and 1.4,  respectively. An investigation of contours of the growth rate curves of Fig. 13 shows that the greater the thickness of the fluid layer represented by the increase in $\mathcal {Z},$ the more significant shrinkage occurs in the regions of instability. It is expected that at large enough values for $\mathcal {Z}\;$ we will only have a stable flow behavior pattern. The effect of increasing the velocity of the upper plate in the $k-\text {Ma}\;$ plane on the stability picture can easily be observed through the comparison Fig. 14a-c. It is worth noting by investigating these graphs that as $\mathcal {V}\;$ increases there will be an expansion in the unstable region along the $\text {Ma}$-axis and it will also increase the critical Marangoni number $\text {Ma}_\text {c}$.

Fig. 12

Illustrates the dimensionless growth rate features in the plane $k-\rho$ for a system has $\text {Ca}= 1000, \, \mathcal {Z}= 1.1, \, \beta = 0.1, \, \text {Ma}= 200, \, k_2= 0, \, \mu = 0.8, \, \mathcal {V}= -2, \, \mathcal {S}= 1, \, \text {Pe}= 600, \; \text {Ma}=200$ as a result of changing the values of q: a $q=-0.2,$ b $q=-0.005,$ c $q=0.25$

Fig. 13

Investigates the dimensionless growth rate features in the plane $k-\nu$ for the same system of parameter’ values used in Fig. 12 and $q = -.005$ when: a $\mathcal {Z} = 1.1,$ b $\mathcal {Z}=1.2 \; \mathcal {Z} = 1.4$

Fig. 14

Clarifies the effect of $\mathcal {V}$ on the linear stability picture in the plane $k-\text {Ma}$ as $\text {Ca}= 1000, \, \mathcal {Z}= 1.3, \, \beta = 0.1, \, \mu = 0.8, \, k_2= 0, \, \rho = 0.5, \, -7, \, q= -0.005, \, \mathcal {S}= 1, \, \text {Pe}= 600$ where: a $\mathcal {V}=2,$ b $\mathcal {V}=5 \; \mathcal {V}=7$

Limit of Long Waves

The study of special case of long waves can yield some analytical asymptotic formulas to calculate the wave growth rate as well as its maximum value. The solutions of Eq. (20) are then given by

$$\begin{aligned} \omega =\frac{1}{2}\left( -\mathcal {F}_1\pm \left( \mathcal {F}_1^2-4\mathcal {F}_0\right) ^{1/2}\right) , \end{aligned}$$

(27)

or

$$\begin{aligned} \omega =-\frac{\mathcal {F}_1}{2}\pm \frac{\mathcal {F}_1}{2}\left( 1-\left( \frac{4\mathcal {F}_0}{\mathcal {F}_1^2}\right) \right) ^{1/2}, \end{aligned}$$

(28)

It is clear that $\mid \mathcal {F}_1\mid$ is of $\mathcal {O}(k^4)$ and $\mid \mathcal {F}_0\mid$ is of $\mathcal {O}(k^6)$ and then $\mid \frac{\mathcal {F}_0}{\mathcal {F}_1^2 }\mid$ is of $\mathcal {O}(k^{-2}).$ Therefore, keeping the four leading terms in the series to have

$$\begin{aligned} \omega \sim \frac{1}{2}{}\left( -\mathcal {F}_1\pm \mathcal {F}_1 \left( 1-\frac{1}{2}\left( \frac{4 \mathcal {F}_0}{\mathcal {F}_1^2}\right) -\frac{1}{8} \left( \frac{4 \mathcal {F}_0}{\mathcal {F}_1^2}\right) ^2-\frac{1}{16} \left( \frac{4 \mathcal {F}_0}{\mathcal {F}_1^2}\right) ^3\right) \right) . \end{aligned}$$

(29)

Therefore

$$\begin{aligned} \begin{aligned} \omega&=-\frac{2 \mathcal {F}_0^3}{\mathcal {F}_1^5}-\frac{\mathcal {F}_0^2}{\mathcal {F}_1^3}-\frac{\mathcal {F}_0}{\mathcal {F}_1},\\&\text {or}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \omega&=\frac{2 \mathcal {F}_0^3}{\mathcal {F}_1^5}+\frac{\mathcal {F}_0^2}{\mathcal {F}_1^3}+\frac{\mathcal {F}_0}{\mathcal {F}_1}-\mathcal {F}_1. \end{aligned} \end{aligned}$$

(30)

Then the approximated wave growth rate is given by

$$\begin{aligned} \omega _r=\mathcal {H}_1 k^2 + \mathcal {H}_2 k^4, \end{aligned}$$

(31)

where the expressions of $\mathcal {H}_1$ and $\mathcal {H}_2$ are defined in the Appendix.

To determine the wave number corresponding to the maximum growth rate $k_{max},$ we must solve the equation $\frac{\partial \omega _r}{\partial k}=0$. Then we have

$$\begin{aligned} k_{\max }=\frac{\sqrt{\mathcal {H}_1}}{\sqrt{2} \sqrt{\mathcal {H}_2}}, \end{aligned}$$

(32)

and thereby the maximum growth rate is given by

$$\begin{aligned} \omega _{r max }=\frac{3 \mathcal {H}_1^2}{4 \mathcal {H}_2}, \end{aligned}$$

(33)

or

$$\begin{aligned} \omega _r= \mathcal {H}_3 k^2-\mathcal {H}_4 k^4 , \end{aligned}$$

(34)

with

$$\begin{aligned} k_{\max }=\frac{\sqrt{\mathcal {H}_3}}{\sqrt{2} \sqrt{\mathcal {H}_4}}, \end{aligned}$$

(35)

and

$$\begin{aligned} \omega _{r max }=\frac{\mathcal {H}_3^2}{4 \mathcal {H}_4}, \end{aligned}$$

(36)

where the formula of $\mathcal {H}_3$ and $\mathcal {H}_4$ are given in the Appendix.

In Figs. 15, 16 and 17, we investigate the variation of maximum growth $\omega _{r max}$ and its corresponding wave number $k_{max}$ with respect to the Marangoni number $\text {Ma}, \mathcal {Z}$ and $\beta .\;$ The solid curves display such variations as calculated from the general growth rate carried by the dispersion relation (20), while the dashed curves are corresponding to these evaluated from the long- wave approximation model represented by Eq. (32) and (33). We observe that there is a good agreement between the two models. The other parameter values are held constant, such as given in the caption of these figures. It is evident from Fig. 15 that there is an increase in both $\omega _{r max}$ and $k_{r max}$ with an increase in Ma up to the value of $\text {Ma}=24.7.$ The opposite occurs as $\text {Ma} > 24.7$ where increasing Ma leads to a monotonic decrease in values of $\omega _{r max},\; k_{max}$. Figure 16 clarifies the evolution in both $\omega _{r max}$ and $k_{r max}$ with $\beta .$ We notice that the values of $\omega _{r max}$ and $k_m$ grow gradually with increasing $\beta$ which confirms the initializing role of $\beta$. Figure 17 indicates that increasing the velocity of the upper plate in either direction will increase the values of $\omega _{r max},\; k_{max}$ and thus the growing waves are dominated.

Fig. 15

The variation of maximum growth $\omega _{r max}$ and its corresponding wave number $k_{max}$ with the Marangoni number. The solid curves are calculated from the general growth rate (20), while the dashed curves are computed based on the long- wave approximation model given by Eq. (30) and (31), where $\text {Ca}= 1000, \, \mathcal {Z}= 1.3, \, \beta = 0.1, \, \mu = 0.8, \, \rho = 0.5, \, \mathcal {V}= -7, \, q= -0.005, \, \mathcal {S}= 1, \, \text {Pe}=600$

Fig. 16

The variation of $\omega _{r max}$ and $k_{max}$ with $\mathcal {Z}$ according to the general growth rate (20), and the long- wave approximation model given by Eqs. (30) and (31), for the same parameter’ values utilized in the computations of Fig. 15, but with $\text {Ma} = 100$

Fig. 17

Represents the evolution of both $\omega _{r max}$ and $k_{max}$ with $\beta$ when the parameters have acquired the same values used in computations of Fig. 15 and for $\mathcal {Z}=-7$

Weakly Nonlinear Analysis of Surface Resonated Waves

In this section, we will focus our efforts to study the weakly nonlinear dynamical behavior of interacting surface waves. To accomplish this, we will resort to using Taylor’s expansion about the unperturbed flat interface $h=1$ and initial uniform concentration $\Gamma =1$ to obtain the evolution equations while keeping the terms in h and $\Gamma$ to the second degree, and then solve the resulting system of equations using the multiple scales method, as will be explained later. Such weakly nonlinear equations read

$$\begin{aligned} \begin{aligned} \frac{\partial H_p}{\partial t}&+\zeta _1 \frac{\partial H_p}{\partial x}+\zeta _2 \frac{\partial ^2H_p}{\partial x^2}+\zeta _3 \frac{\partial ^4H_p}{\partial x^4}+\zeta _4 \frac{\partial ^2\Gamma _p}{\partial x^2}+\zeta _5 \left( \frac{\partial H_p}{\partial x}\right) ^2\\&+\zeta _6 H_p \frac{\partial H_p}{\partial x}+\zeta _7 \frac{\partial H_p}{\partial x} \frac{\partial \Gamma _p}{\partial x}+\zeta _8 H_p \frac{\partial ^2H_p}{\partial x^2}\\&+\zeta _9 H_p \frac{\partial ^2\Gamma _p}{\partial x^2}+\zeta _{10} H_p \frac{\partial ^4H_p}{\partial x^4}=0, \end{aligned} \end{aligned}$$

(37)

$$\begin{aligned} \begin{aligned} \frac{\partial \Gamma _p}{\partial t}&+\xi _1 \frac{\partial H_p}{\partial x}+\xi _2 \frac{\partial \Gamma _p}{\partial x}+\xi _3 \frac{\partial ^2H_p}{\partial x^2}+\xi _4 \frac{\partial ^4H_p}{\partial x^4}+\xi _5 \frac{\partial ^2 \Gamma _p}{\partial x^2}+\xi _6 \left( \frac{\partial \Gamma _p}{\partial x}\right) ^2\\&+\xi _7 \frac{\partial H_p}{\partial x} \frac{\partial \Gamma _p}{\partial x}+\xi _8 \Gamma _p \frac{\partial ^2\Gamma _p}{\partial x^2}+\xi _9 H_p \frac{\partial ^2\Gamma _p}{\partial x^2}+\xi _{10} \left( \frac{\partial H_p}{\partial x}\right) ^2+\xi _{11} \Gamma _p \frac{\partial ^2H_p}{\partial x^2}\\&+\xi _{12} H_p \frac{\partial ^2H_p}{\partial x^2}+\xi _{13} \frac{\partial \Gamma _p}{\partial x} \frac{\partial ^3H_p}{\partial x^3}+\xi _{14} \frac{\partial H_p}{\partial x} \frac{\partial ^3H_p}{\partial x^3}+\xi _{15} \Gamma _p \frac{\partial ^4H_p}{\partial x^4}\\&+\xi _{16} H_p \frac{\partial ^4H_p}{\partial x^4}+\xi _{17} \Gamma _p \frac{\partial H_p}{\partial x}+\xi _{18} H_p \frac{\partial \Gamma _p}{\partial x}+\xi _{19} H_p \frac{\partial H_p}{\partial x}=0, \end{aligned} \end{aligned}$$

(38)

No, we proceed to utilize the method of multiple scales to obtain second-order convergent solutions of Eqs. (37) and (38) describing the wave motion of small but finite amplitude. To do so we introduce the new slow variables $t_1$ and $x_1$ as well the two variables $t_0$ and $x_0$ that correspond to rapid variations in such away that Nayfeh and Balachandran (2004)

$$\begin{aligned} \frac{\partial }{\partial t}\rightarrow \frac{\partial }{\partial t_0}+\epsilon \frac{\partial }{\partial t_1}\;\; \text {and}\;\; \frac{\partial }{\partial x}\rightarrow \frac{\partial }{\partial x_0}+\epsilon \frac{\partial }{\partial x_1}, \end{aligned}$$

(39)

where $\epsilon$ is a small dimensionless parameters expressing the wave steepness ratio. In this analysis the unknown functions of wave interfacial elevation and surfactant concentration are expressed in powers of $\epsilon$ in the form

$$\begin{aligned} H_p(x,t;\epsilon )&= \epsilon H_1(x_0,t_0;x_1,t_1)+\epsilon ^2 H_2(x_0,t_0;x_1,t_1)+...,\;\Gamma _p(x,t;\epsilon )\\&= \epsilon \Gamma _1(x_0,t_0;x_1,t_1)+\epsilon ^2 \Gamma _2(x_0,t_0;x_1,t_1)+....\;\; \end{aligned}$$

(40)

As the expression of Eqs. (39) and (40) are inserted in Eqs. (37) and (38) and then equating the coefficients of the same powers of $\epsilon ,$ we have two system of equations corresponding to the first and second order of $\epsilon$.

The Problem of First-Order ($\mathcal {O}(\epsilon )$)

$$\begin{aligned} \frac{\partial H_1}{\partial t_0}+\zeta _1 \frac{\partial H_1}{\partial x_0}+\zeta _2 \frac{\partial ^2H_1}{\partial x_0^2}+ \zeta _3 \frac{\partial ^4H_1}{\partial x_0^4}+\zeta _4 \frac{\partial ^2\Gamma _1}{\partial x_0^2}=0, \end{aligned}$$

(41)

$$\begin{aligned} \frac{\partial \Gamma _1}{\partial t_0}+\xi _1 \frac{\partial H_1}{\partial x_0}+\xi _2 \frac{\partial \Gamma _1}{\partial x_0}+\xi _3 \frac{\partial ^2H_1}{\partial x_0^2}+\xi _4 \frac{\partial ^4H_1}{\partial x_0^4}+\xi _5 \frac{\partial ^2\Gamma _1}{\partial x_0^2}=0. \end{aligned}$$

(42)

The Problem of Second-Order ($\mathcal {O}(\epsilon ^2)$)

$$\begin{aligned} \begin{aligned} \frac{\partial H_2}{\partial t_0}&+\zeta _1 \frac{\partial H_2}{\partial x_0}+\zeta _2 \frac{\partial ^2H_2}{\partial x_0^2}+\zeta _3 \frac{\partial ^4H_2}{\partial x_0^4}+\zeta _4 \frac{\partial ^2\Gamma _2}{\partial x_0^2}\\&+\frac{\partial H_1}{\partial t_1}+\zeta _1 \frac{\partial H_1}{\partial x_1}+2 \zeta _2 \frac{\partial ^2H_1}{\partial x_0 \partial x_1}+4 \zeta _3 \frac{\partial ^4H_1}{\partial x_0^3 \partial x_1}\\&+2 \zeta _4 \frac{\partial ^2\Gamma _1}{\partial x_0\ \partial x_1}+\zeta _5 \left( \frac{\partial H_1}{\partial x_0}\right) ^2+\zeta _6 H_1 \frac{\partial H_1}{\partial x_0}\\&+\zeta _7 \frac{\partial H_1}{\partial x_0} \frac{\partial \Gamma _1}{\partial x_0}+\zeta _8 H_1 \frac{\partial ^2H_1}{\partial x_0^2}+\zeta _9 H_1 \frac{\partial ^2\Gamma _1}{\partial x_0^2}\\&+\zeta _{10} H_1 \frac{\partial ^4H_1}{\partial x_0^4}=0, \end{aligned} \end{aligned}$$

(43)

$$\begin{aligned} \begin{aligned} \frac{\partial \Gamma _2}{\partial t_0}&+\xi _1 \frac{\partial H_2}{\partial x_0}+\xi _2 \frac{\partial \Gamma _2}{\partial x_0}+\xi _3 \frac{\partial ^2H_2}{\partial x_0^2}+\xi _4 \frac{\partial ^4H_2}{\partial x_0^4}+\xi _5 \frac{\partial ^2\Gamma _2}{\partial x_0^2}\\&+\frac{\partial \Gamma _1}{\partial x_1}+\xi _1 \frac{\partial H_1}{\partial x_1}+\xi _2 \frac{\partial \Gamma _1}{\partial x_1}+2 \xi _3 \frac{\partial ^2H_1}{\partial x_0\, \partial x_1}+4 \xi _4 \frac{\partial ^4H_1}{\partial x_0^3 \partial x_1}\\&+2 \xi _5 \frac{\partial ^2\Gamma _1}{\partial x_0\ \partial x_1}+\xi _6 \left( \frac{\partial \Gamma _1}{\partial x_0}\right) ^2+\xi _7 \frac{\partial H_1}{\partial x_0} \frac{\partial \Gamma _1}{\partial t_0} +\xi _8 \Gamma _1 \frac{\partial ^2\Gamma _1}{\partial x_0^2} \\&+ \xi _9 H_1\frac{\partial ^2\Gamma _1}{\partial x_0^2}+\xi _{10} \left( \frac{\partial H_1}{\partial x_0}\right) ^2 +\xi _{11}\Gamma _1\frac{\partial ^2H_1}{\partial x_0^2} +\xi _{12} H_1\frac{\partial ^2H_1}{\partial x_0^2}\\&+\xi _{13} \frac{\partial \Gamma _1}{\partial x_0} \frac{\partial ^3H_1}{\partial x_0^3}+\xi _{14} \frac{\partial H_1}{\partial x_0} \frac{\partial ^3H_1}{\partial x_0^3}+\xi _{15}\Gamma _1 \frac{\partial ^4H_1}{\partial x_0^4}+ \xi _{16}H_1 \frac{\partial ^4H_1}{\partial x_0^4}\\&+\xi _{17} \Gamma _1\frac{\partial H_1}{\partial x_0}+\xi _{18}H_1\frac{\partial \Gamma _1}{\partial t_0}+\xi _{19} H_1\frac{\partial H_1}{\partial x_0}=0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned} \end{aligned}$$

(44)

The coefficients $\zeta _i,\;\xi _i$ are very lengthy and not included here and are ready on request from the authors.

In what follows, we proceed to discuss the dynamical behavior of the weak;y nonlinear surface waves owing to the interacting between two-to- one internal waves. Such case of resonance has been demonstrated in several works, for example, Henderson and Miles (1991), Zakaria (2008) and Sirwah (2014). Henderson & Miles studied both theoretically and experimentally the behavior of surface waves arising from resonance between internal waves that are preserved against the effect of the weakly damped viscosity inside a closed basin subjected to periodic vertical vibrational motion. Zakaria (2008) studied Faraday waves with three modes, on the interface between superposed liquids in an infinite boxed basin subjected to vertical excitation. Sirwah (2014) considered the chaotic behavior of the three-dimensional resonated standing surface waves propagated at the interface of a weakly viscous, incompressible magnetic liquid within a rectangular basin as the system is subjected to a normal time-periodic magnetic field as well as external vertical excitation. The solutions of the first order problem are sought in the form

$$\begin{aligned} H_1=A_1\left( x_1,t_1\right) e^{i \left( k_1 x_0-t_0 \omega _1\right) }+A_2\left( x_1,t_1\right) e^{i \left( k_2 x_0-t_0 \omega _2\right) }, \end{aligned}$$

(45)

$$\begin{aligned} \Gamma _1=f A_1\left( x_1,t_1\right) e^ {i \left( k_1 x_0-t_0 \omega _1\right) }+g A_2\left( x_1,t_1\right) e^ {i \left( k_2 x_0-t_0 \omega _2\right) }, \end{aligned}$$

(46)

with

$$f=\frac{\zeta _3 k_1^4-\zeta _2 k_1^2+i \zeta _1 k_1-i \omega _1}{\zeta _4 k_1^2},\;g=\frac{\zeta _3 k_2^4-\zeta _2 k_2^2+i \zeta _1 k_2-i \omega _2}{\zeta _4 k_2^2}.$$

Here, $A_1\left( x_1,t_1\right) ,\; A_2\left( x_1,t_1\right)$ are two complex unknown functions to be governed by the solvability conditions of the second order problem and $\omega _1,\; \omega _2$ are the roots of the dispersion relation (20).

The next step is to insert the first order solutions in the second order equation. Then, the resulting equations will posses uniform convergent solutions are obtained when the probable secular terms are omitted. Such process will result the so called the solvability conditions. We must distinguish between two basic cases: the first one is nonresonance case in which there is no nearness between the two frequencies of the internal waves, while the second one occurs when the frequency $\omega _2$ approaches the frequency $\omega _1$.

In the nonresonance case, the solvability condition read

$$\begin{aligned} \begin{aligned} \left( \mathcal {J}_{11}+i \mathcal {J}_{12}\right) \frac{\partial A_1}{\partial t_1}+\left( \mathcal {J}_{13}+i \mathcal {J}_{14}\right) \frac{\partial A_1}{\partial x_1}=0, \end{aligned} \end{aligned}$$

(47)

$$\begin{aligned} \left( \mathcal {K}_{11}+i \mathcal {K}_{12}\right) \frac{\partial A_2}{\partial t_1}+\left( \mathcal {K}_{13}+i \mathcal {K}_{14}\right) \frac{\partial A_2}{\partial x_1}=0. \end{aligned}$$

(48)

We are interested in the resonance case specified by $\omega _2 \sim 2\omega _1.$ To express this nearness, we introduce the detuning parameter $\sigma$ according to

$$\begin{aligned} \omega _2=2\omega _1+\epsilon \sigma . \end{aligned}$$

(49)

Such case of resonance will admit the following solvability conditions

$$\begin{aligned} \begin{aligned} \left( \mathcal {J}_{11}+i \mathcal {J}_{12}\right) \frac{\partial A_1}{\partial t_1}+\left( \mathcal {J}_{13}+i \mathcal {J}_{14}\right) \frac{\partial A_1}{\partial x_1}+\left( \mathcal {J}_{15}+i \mathcal {J}_{16}\right) e^{-i \sigma t_1 } A_2 \bar{A}_1=0, \end{aligned} \end{aligned}$$

(50)

$$\begin{aligned} \left( \mathcal {K}_{11}+i \mathcal {K}_{12}\right) \frac{\partial A_2}{\partial t_1}+\left( \mathcal {K}_{13}+i \mathcal {K}_{14}\right) \frac{\partial A_2}{\partial x_1}+ \left( \mathcal {K}_{15}+i \mathcal {K}_{16}\right) e^{i \sigma t_1} A_1^2=0, \end{aligned}$$

(51)

where the coefficients $\mathcal {J}_{ij},\mathcal {K}_{ij}\;$are given in the Appendix.

It is convenient to use the transformation

$$\begin{aligned} A_1=\mathcal {A}_1e^{\frac{1}{2} i \sigma t_1},\;A_2=\mathcal {A}_2e^{2 i \sigma t_1}, \end{aligned}$$

(52)

to remove the step mismatch of the non-linear terms. Consequently, the solvability conditions (50) and (51) take the form

$$\begin{aligned} &\left( \mathcal {J}_{11}+i \mathcal {J}_{12}\right) \frac{\partial \mathcal {A}_1}{\partial t_1}+\left( \mathcal {J}_{13}+i \mathcal {J}_{14}\right) \frac{\partial \mathcal {A}_1}{\partial x_1}+ \left( \mathcal {J}_{15}+i \mathcal {J}_{16}\right) \mathcal {A}_2 \bar{\mathcal {A}}_1\\&\qquad\, +\frac{1}{2} i \sigma \left( \mathcal {J}_{11}+i \mathcal {J}_{12}\right) \mathcal {A}_1=0, \end{aligned}$$

(53)

$$\begin{aligned} &\left( \mathcal {K}_{11}+i \mathcal {K}_{12}\right) \frac{\partial \mathcal {A}_2}{\partial t_1}+\left( \mathcal {K}_{13}+i \mathcal {K}_{14}\right) \frac{\partial \mathcal {A}_2}{\partial x_1}+\left( \mathcal {K}_{15}+i \mathcal {K}_{16}\right) \mathcal {A}_1^2\\&\qquad\,+2 i \sigma \left( \mathcal {K}_{11}+i \mathcal {K}_{12}\right) \mathcal {A}_2=0. \end{aligned}$$

(54)

The solution to the modal dynamical system of these equations can be assumed to be in the form

$$\begin{aligned} \mathcal {A}_1=\eta _1\left( t_1\right) e^{i \kappa x_1},\;\mathcal {A}_2=\eta _2\left( t_1\right) e^{2 i \kappa x_1}. \end{aligned}$$

(55)

The two amplitudes $\eta _1,\; \eta _2$ are, therefore, related via the equations

$$\begin{aligned} &\left( \mathcal {J}_{11}+i \mathcal {J}_{12}\right) \frac{\partial \eta _1}{\partial t _1}+\left( \mathcal {J}_{15}+i \mathcal {J}_{16}\right) \eta _1 \eta _2+\frac{1}{2} i \big (2 \kappa \left( \mathcal {J}_{13}+i \mathcal {J}_{14}\right) \\&\qquad\,+\sigma (\mathcal {J}_{11}+i \mathcal {J}_{12})\big )\eta _1 =0, \end{aligned}$$

(56)

$$\begin{aligned}\\& \left( \mathcal {K}_{11}+i \mathcal {K}_{12}\right) \frac{\partial \eta _2}{\partial t _1}+\left( \mathcal {K}_{15}+i \mathcal {K}_{16}\right) \eta _1^2+2 i\big (\kappa \left( \mathcal {K}_{13}+i \mathcal {K}_{14}\right)\\& \qquad\,+\sigma \left( \mathcal {K}_{11}+i \mathcal {K}_{12}\right) \big ) \eta _2=0. \end{aligned}$$

(57)

In order to determine the possible steady-state solutions of the dynamic system represented by the Eqs. (56) and (57), it is very appropriate to make use of the polar form

$$\begin{aligned} \eta _1=\mathfrak {a}_1\left( \tau \right) e^{i \theta _1\left( \tau \right) },\;\eta _2=\mathfrak {a}_2\left( \tau \right) e^{i \theta _2\left( \tau \right) }, \end{aligned}$$

(58)

where $\tau =t_1$; and $\mathfrak {a}_i,\; \theta _i$ stand for the amplitudes and phases of the two modes, which are presumed to be real. Substituting (58) into Eqs. (56) and (57) and then separating the real and imaginary parts, we get

$$\begin{aligned} \frac{\partial \mathfrak {a}_1}{\partial \tau }=\mathcal {B}_{11}\mathfrak {a}_1+\left( \mathcal {B}_{12} \sin \delta +\mathcal {B}_{13}\cos \delta \right) \mathfrak {a}_1\mathfrak {a}_2, \end{aligned}$$

(59)

$$\begin{aligned} \frac{\partial \mathfrak {a}_2}{\partial \tau }=\mathcal {B}_{21} \mathfrak {a}_2+\left( \mathcal {B}_{22} \sin \delta +\mathcal {B}_{23}\cos \delta \right) \mathfrak {a}_1^2, \end{aligned}$$

(60)

$$\begin{aligned} \mathfrak {a}_2\frac{\partial \delta }{\partial \tau }=& \mathcal {B}_{31}\mathfrak {a}_2+2\left( \mathcal {B}_{21} \cos \delta -\mathcal {B}_{13} \sin \delta \right) \mathfrak {a}_2^2\\&+\left( \mathcal {B}_{22} \cos \delta -\mathcal {B}_{23} \sin \delta \right) \mathfrak {a}_1^2, \end{aligned}$$

(61)

where

$$\begin{aligned} \begin{aligned}&\mathcal {B}_{11}=\frac{\kappa (\mathcal {J}_{11} \mathcal {J}_{14}- \mathcal {J}_{12} \mathcal {J}_{13})}{\mathcal {J}_{11}^2+\mathcal {L}_{12}^2},\; \mathcal {B}_{12}=\frac{\mathcal {J}_{12} \mathcal {J}_{15}-\mathcal {J}_{11} \mathcal {J}_{16}}{\mathcal {J}_{11}^2+\mathcal {J}_{12}^2},\;\\&\mathcal {B}_{13}=-\frac{\mathcal {J}_{11} \mathcal {J}_{15}+\mathcal {J}_{12} \mathcal {J}_{16}}{\mathcal {J}_{11}^2+\mathcal {J}_{12}^2},\;\mathcal {B}_{21}=\frac{2 \kappa \left( \mathcal {K}_{11} \mathcal {K}_{14}-\mathcal {K}_{12} \mathcal {K}_{13}\right) }{\mathcal {K}_{11}^2+\mathcal {K}_{12}^2},\end{aligned} \end{aligned}$$

$$\mathcal {B}_{22}=\frac{\mathcal {K}_{11} \mathcal {K}_{16}-\mathcal {K}_{12} \mathcal {K}_{15}}{\mathcal {K}_{11}^2+\mathcal {K}_{12}^2},\;\mathcal {B}_{23}=-\frac{\mathcal {K}_{11} \mathcal {K}_{15}+\mathcal {K}_{12} \mathcal {K}_{16}}{\mathcal {K}_{11}^2+\mathcal {K}_{12}^2},\;$$

$$\begin{aligned} \begin{aligned}\mathcal {B}_{31}=&\frac{1}{\left( \mathcal {K}_{11}^2+\mathcal {K}_{12}^2\right) \left( \mathcal {J}_{11}^2+\mathcal {J}_{12}^2\right) }\big (\mathcal {K}_{11}^2 (\mathcal {J}_{12} \left( \sigma \mathcal {J}_{12}-2 \kappa \mathcal {J}_{14}\right)\\& -2 \kappa \mathcal {J}_{13} \mathcal {J}_{11}+\sigma \mathcal {J}_{11}^2)+\end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned}\mathcal {K}_{12}& \left( \mathcal {K}_{12} \left( -2 \kappa \mathcal {J}_{13} \mathcal {J}_{11}-2 \kappa \mathcal {J}_{12} \mathcal {J}_{14}+\sigma \mathcal {J}_{11}^2+\sigma \mathcal {J}_{12}^2\right) +2 \kappa \mathcal {K}_{14} \left( \mathcal {J}_{11}^2+\mathcal {J}_{12}^2\right) \right) \\&+2 \kappa \mathcal {K}_{13} \mathcal {K}_{11} \left( \mathcal {J}_{11}^2+\mathcal {J}_{12}^2\right) \big ),\delta =2\theta _1-\theta _2.\end{aligned} \end{aligned}$$

The steady-state solution of the dynamical system (59)-(61) are the values of $a_1, a_2, \delta _0$ that correspond to the conditions $\;\frac{\partial \mathfrak {a}_i}{\partial \tau }= \frac{\partial \delta }{\partial \tau }=0.$ Therefore, such solution can be calculated by solving the following equations

$$\begin{aligned} \mathcal {B}_{11}a_1+\left( \mathcal {B}_{12} \sin \delta _0+\mathcal {B}_{13}\cos \delta _0\right) a_1a_2=0, \end{aligned}$$

(62)

$$\begin{aligned} \mathcal {B}_{21} a_2+\left( \mathcal {B}_{22} \sin \delta _0 +\mathcal {B}_{23}\cos \delta _0\right) a_1^2=0, \end{aligned}$$

(63)

$$\begin{aligned} \mathcal {B}_{31}a_2&+2\left( \mathcal {B}_{21} \cos \delta _0 -\mathcal {B}_{13} \sin \delta _0 \right) a_2^2\\&+\left( \mathcal {B}_{22} \cos \delta _0-\mathcal {B}_{23} \sin \delta _0 \right) a_1^2 =0. \end{aligned}$$

(64)

Thus, we have the possible solutions

$$\begin{aligned} a_1=a_2=0, \end{aligned}$$

(65)

or

$$\begin{aligned} \begin{aligned} a_1^2&=\frac{\left( \mathcal {D}_{14} \mathcal {D}_{15}+\mathcal {D}_{11} \mathcal {D}_{16}\right) \mathcal {D}_{17}-2 \mathcal {D}_{12} \mathcal {D}_{15} \mathcal {D}_{16}}{2 \mathcal {D}_{13} \mathcal {D}_{15} \mathcal {D}_{16}}\\&~~~\pm \frac{\sqrt{-\mathcal {D}_{13}^2 \left( \mathcal {D}_{14} \mathcal {D}_{15}-\mathcal {D}_{11} \mathcal {D}_{16}\right) ^2 \left( 4 \mathcal {D}_{15} \mathcal {D}_{16}-\mathcal {D}_{17}^2\right) }}{2 \mathcal {D}_{13}^2 \mathcal {D}_{15} \mathcal {D}_{16}},\\ a_2^2&=\frac{\left( \mathcal {D}_{12} \mathcal {D}_{15}-\mathcal {D}_{11} \mathcal {D}_{17}\right) \sqrt{-\mathcal {D}_{13}^2 \left( \mathcal {D}_{14}\mathcal {D}_{15}-\mathcal {D}_{11} \mathcal {D}_{16}\right) ^2 \left( 4 \mathcal {D}_{15} \mathcal {D}_{16}-\mathcal {D}_{17}^2\right) }}{2 \mathcal {D}_{13}^2 \mathcal {D}_{15}^2 \left( \mathcal {D}_{14} \mathcal {D}_{15}-\mathcal {D}_{11} \mathcal {D}_{16}\right) }\\ {}&~~~\pm \frac{-\mathcal {D}_{11} \mathcal {D}_{17}^2+\mathcal {D}_{12} \mathcal {D}_{15}\mathcal {D}_{17}+2 \left( \mathcal {D}_{11} \mathcal {D}_{16} \mathcal {D}_{15}-\mathcal {D}_{14}\mathcal {D}_{15}^2\right) }{2 \mathcal {D}_{13} \mathcal {D}_{15}^2},\\\;\delta _0 &=\tan ^{-1}\left( \frac{a_1^2 \mathcal {B}_{11} \mathcal {B}_{23}-a_2^2 \mathcal {B}_{13} \mathcal {B}_{21}}{a_2^2 \mathcal {B}_{12} \mathcal {B}_{21}-a_1^2 \mathcal {B}_{11} \mathcal {B}_{22}}\right) , \end{aligned} \end{aligned}$$

(66)

with

$$\begin{aligned}&\;\mathcal {D}_{11}=\mathcal {B}_{21}^2 \left( \mathcal {B}_{12}^2+\mathcal {B}_{13}^2\right) ,\\&\;\mathcal {D}_{12}=-2 \mathcal {B}_{11} \mathcal {B}_{21} \left( \mathcal {B}_{13} \mathcal {B}_{23}+\mathcal {B}_{12} \mathcal {B}_{22}\right) ,\\&\;\mathcal {D}_{13}=-\left( \mathcal {B}_{12} \mathcal {B}_{23}-\mathcal {B}_{13} \mathcal {B}_{22}\right) ^2,\end{aligned}$$

$$\begin{aligned}&\;\mathcal {D}_{14}=\mathcal {B}_{11}^2 \left( \mathcal {B}_{23}^2+\mathcal {B}_{22}^2\right) ,\\&\;\mathcal {D}_{15}=-2 \mathcal {B}_{21} \left( \mathcal {B}_{13}^2+\mathcal {B}_{12}^2\right) ,\\&\;\mathcal {D}_{16}=\mathcal {B}_{11} \left( \mathcal {B}_{23}^2+\mathcal {B}_{22}^2\right) ^2,\end{aligned}$$

$$\mathcal {D}_{17}=\left( 2 \mathcal {B}_{11}-\mathcal {B}_{21}\right) \left( \mathcal {B}_{13} \mathcal {B}_{23}+\mathcal {B}_{12} \mathcal {B}_{22}\right) +\left( \mathcal {B}_{12} \mathcal {B}_{23}-\mathcal {B}_{13} \mathcal {B}_{22}\right) \mathcal {B}_{31}.$$

Stability Analysis

To illustrate the steady-state solutions’ stability, we presume that they have some small deviations $\;\hat{a}_1(\tau ),\;\hat{a}_2(\tau ),\;$ and $\hat{\delta }(\tau )\;$ from their equilibrium values $a_1, a_2,\delta _0$ in such away

$$\begin{aligned} \mathfrak {a}_1(\tau )=a_1 +\hat{a}_1(\tau ),\; \mathfrak {a}_2(\tau )=a_2 +\hat{a}_2(\tau ),\ \delta (\tau )=\delta _0 +\hat{\delta }(\tau ). \end{aligned}$$

(67)

As a result, depending on whether the functions $\hat{a}_1, \hat{a}_2,\;\text {and}\;\hat{\delta }\;$ decay or evolve with time, the solutions of Eqs. (61)-(63) are stable or unstable. Substituting (67) into Eqs. (59)-(61), exploiting the assigned fixed point solutions and retaining only the linear terms of the disturbed quantities, give

$$\begin{aligned} \frac{\partial \hat{a}_1}{\partial \tau }=\vartheta _{11}\hat{a}_1+\vartheta _{12}\hat{a}_2+\vartheta _{13} \hat{\delta }, \end{aligned}$$

(68)

$$\begin{aligned} \frac{\partial \hat{a}_2}{\partial \tau }=\vartheta _{21}\hat{a}_1+\vartheta _{22}\hat{a}_2+\vartheta _{23} \hat{\delta }, \end{aligned}$$

(69)

$$\begin{aligned} \frac{\partial \hat{\delta }}{\partial \tau }=\vartheta _{31}\hat{a}_1+\vartheta _{32}\hat{a}_2+\vartheta _{33} \hat{\delta }, \end{aligned}$$

(70)

where

$$\begin{aligned} \begin{aligned}\vartheta _{11}&=a_{2} \left( \mathcal {B}_{12} \sin \delta _0+\mathcal {B}_{13} \cos \delta _0\right) +\mathcal {B}_{11},\vartheta _{12}\\&=\;a_{1}\left( \mathcal {B}_{12} \sin \delta _0+\mathcal {B}_{13} \cos \delta _0\right) ,\vartheta _{13}\\&=a_{1} a_{2}\left( -\mathcal {B}_{13} \sin \delta _0+\mathcal {B}_{12} \cos \delta _0\right) ,\end{aligned} \end{aligned}$$

$$\begin{aligned}\vartheta _{21}&=2 a_{1}\left( \mathcal {B}_{22} \sin \delta _0+\mathcal {B}_{23} \cos \delta _0\right) ,\;\vartheta _{22}=\mathcal {B}_{21},\;\vartheta _{23}\\&=a_{1}^2 \left( -\mathcal {B}_{23} \sin \delta _0+\mathcal {B}_{22} \cos \delta _0\right) ,\end{aligned}$$

$$\begin{aligned}&\;\vartheta _{31}=\frac{2 a_{1}\left( -\mathcal {B}_{23} \sin \delta _0+\mathcal {B}_{22} \cos \delta _0\right) }{a_{2}},\\&\;\vartheta _{32}=\frac{\left( a_{1}^2 \left( \mathcal {B}_{23} \sin \delta _0-\mathcal {B}_{22} \cos \delta _0\right) +2 a_{2}^2 \left( -\mathcal {B}_{13} \sin \delta _0+\mathcal {B}_{12} \cos \delta _0\right) \right) }{a_2^2},\;\end{aligned}$$

$$\vartheta _{33}=-\frac{ \left( a_{1}^2 \left( \mathcal {B}_{22} \sin \delta _0+\mathcal {B}_{23} \cos \delta _0\right) +2 a_{2}^2 \left( \mathcal {B}_{12} \sin \delta _0+\mathcal {B}_{13} \cos \delta _0\right) \right) }{a_{2}}.$$

Equations (68)-(70) is clearly a third-order linear system of ordinary differential equations that controlled the perturbed quantities and so their solutions are sought in the form $\hat{a}_1,\;\hat{a}_2,\;\hat{\delta }\;\propto e^{\Omega \tau }.\;$ For a non-trivial solution, the coefficients’ matrix of the obtained algebraic system must vanish. As a consequence, the following dispersion relation for the non-trivial fixed points emerges:

$$\begin{aligned} \Omega ^3+\varrho _1\Omega ^2+\varrho _2\Omega +\varrho _3=0, \end{aligned}$$

(71)

where

$$\begin{aligned}\varrho _1=&-(\vartheta _{11}+\vartheta _{22}+\vartheta _{33}),\;\varrho _2=\vartheta _{22}\vartheta _{33}+\vartheta _{11} \left( \vartheta _{22}+\vartheta _{33}\right)\\& -\vartheta _{12} \vartheta _{21}-\vartheta _{13} \vartheta _{31}-\vartheta _{23}\vartheta _{32},\end{aligned}$$

$$\begin{aligned} \begin{aligned}\;\varrho _3=&\vartheta _{11} \left( \vartheta _{23} \vartheta _{32-\vartheta _{22}\vartheta _{33}}\right) +\vartheta _{12} \left( \vartheta _{21}\vartheta _{33}-\vartheta _{23} \vartheta _{31}\right)\\& +\vartheta _{13} \left( \vartheta _{22} \vartheta _{31}-\vartheta _{21} \vartheta _{32}\right) .\end{aligned} \end{aligned}$$

The non-trivial fixed point solutions will be stable when the real parts of all the roots of Eq. (71) are negative. However, we can examine the signs of those roots without specifying them by using Routh-Hurwitz criterion, which states that the necessary and sufficient conditions for all roots of the equation to have negative real parts are

$$\begin{aligned} \varrho _1> 0,\;\varrho _3> 0,\;\varrho _1\varrho _2-\varrho _3 > 0.\; \end{aligned}$$

(72)

Similarly, the eigenvalue equation for trivial steady-state solutions is given by

$$\begin{aligned} \Omega ^2-\left( \mathcal {B}_{11}+\mathcal {B}_{21}\right) \Omega +\mathcal {B}_{11} \mathcal {B}_{21}=0, \end{aligned}$$

(73)

associated with the stability conditions

$$\begin{aligned} \mathcal {B}_{11} \mathcal {B}_{21} > 0,\;\mathcal {B}_{11}+\mathcal {B}_{21} < 0. \end{aligned}$$

(74)

In order to have a deep insight on the properties of stability criteria of the complex amplitudes of the interacting two modes of surface waves through the patterns of phase portraits and time history, we introduce the transformation

$$\begin{aligned} &\;A_1(x_1, \tau )=\big (p_1(x_1, \tau )+i q_1(x_1, \tau )\big )e^{i \left( \frac{\sigma \tau }{2}+\kappa x_1\right) },\\&\; A_2(x_1, \tau )=\big (p_2(x_1, \tau )+i q_2(x_1, \tau )\big )e^{i \left( \frac{\sigma \tau }{2}+\kappa x_1\right) } \end{aligned}$$

(75)

Then separation of Eqs. (50) and (51) into real and imaginary parts gives

$$\begin{aligned} \begin{aligned} \frac{\partial p_1}{\partial \tau }=&\frac{1}{2 \left( \mathcal {J}_{11}^2+\mathcal {J}_{12}^2\right) }\big ( 2\left( \mathcal {J}_{11} \mathcal {J}_{16}- \mathcal {J}_{12} \mathcal {J}_{15}\right) p_1q_2\\&+2\left( \mathcal {J}_{12} \mathcal {J}_{15}-\mathcal {J}_{11} \mathcal {J}_{16}\right) p_2q_1+2\kappa (\mathcal {J}_{11} \mathcal {J}_{14}-\mathcal {J}_{12} \mathcal {J}_{13})p_1\\&-2 \left( \mathcal {J}_{11} \mathcal {J}_{15}+\mathcal {J}_{12} \mathcal {J}_{16}\right) p_2 p_1+\left( \mathcal {J}_{12} \left( 2 \kappa \mathcal {J}_{14}+\sigma \mathcal {J}_{12}\right) \right. \\ & \left.+2 \kappa \mathcal {J}_{13} \mathcal {J}_{11}+\sigma \mathcal {J}_{11}^2\right) q_1-2 \left( \mathcal {J}_{11} \mathcal {J}_{15}+\mathcal {J}_{12} \mathcal {J}_{16}\right) q_1q_2\big ), \end{aligned} \end{aligned}$$

(76)

$$\begin{aligned} \begin{aligned} \frac{\partial q_1}{\partial \tau }=&-\frac{1}{2 \left( \mathcal {J}_{11}^2+\mathcal {J}_{12}^2\right) }\big ( (\mathcal {J}_{12} \left( -2 \mathcal {J}_{15} p_2+2 \mathcal {J}_{16} q_2\right. \\ & \left.+2 \kappa \mathcal {J}_{14}+\sigma \mathcal {J}_{12}\right) +2 \mathcal {J}_{11} (\mathcal {J}_{16} p_2+\mathcal {J}_{15} q_2+\kappa \mathcal {L}_{13})\\&+\sigma \mathcal {L}_{11}^2)p_1-2 \left( \mathcal {L}_{12} \left( \mathcal {J}_{16} p_2+\mathcal {J}_{15} q_2-\kappa \mathcal {J}_{13}\right)\right. \\ & \left.+\mathcal {J}_{11} \left( \mathcal {J}_{15} p_2-\mathcal {J}_{16} q_2+\kappa \mathcal {J}_{14}\right) \right) q_1\big ), \end{aligned} \end{aligned}$$

(77)

$$\begin{aligned} \begin{aligned} \frac{\partial p_2}{\partial \tau }=&\frac{1}{\mathcal {K}_{11}^2+\mathcal {K}_{12}^2}\big (2\left( \mathcal {K}_{11} \mathcal {K}_{16}-\mathcal {K}_{12} \mathcal {K}_{15}\right) p_1 q_1\\&+2 \kappa \left( \mathcal {K}_{11} \mathcal {K}_{14}-\mathcal {K}_{12} \mathcal {K}_{13}\right) p_2\\&+\left( -\mathcal {K}_{11} \mathcal {K}_{15}-\mathcal {K}_{12} \mathcal {K}_{16}\right) p_1^2\\&+2\left( \mathcal {K}_{12} \left( \kappa \mathcal {K}_{14}+\sigma \mathcal {K}_{12}\right) +\kappa \mathcal {K}_{13} \mathcal {K}_{11}+\sigma \mathcal {K}_{11}^2\right) q_2 \\&+\left( \mathcal {K}_{11} \mathcal {K}_{15}+\mathcal {K}_{12} \mathcal {K}_{16}\right) q_1^2\big ), \end{aligned} \end{aligned}$$

(78)

$$\begin{aligned} \begin{aligned} \frac{\partial q_2}{\partial \tau }&=\frac{1}{\mathcal {K}_{11}^2+\mathcal {K}_{12}^2}\left( \left( \mathcal {K}_{12} \mathcal {K}_{15}-\mathcal {K}_{11} \mathcal {K}_{16}\right) p_1^2 \right. \\ &\quad-2 \left( \mathcal {K}_{12} \left( \kappa \mathcal {K}_{14}+\sigma \mathcal {K}_{12}\right) +\kappa \mathcal {K}_{13} \mathcal {K}_{11}+\sigma \mathcal {K}_{11}^2\right) p_2 \\ &\quad\left. -2 \left( \mathcal {K}_{11} \mathcal {K}_{15}+\mathcal {K}_{12} \mathcal {K}_{16}\right) p_1 q_1+\left( \mathcal {K}_{11} \mathcal {K}_{16}-\mathcal {K}_{12} \mathcal {K}_{15}\right) q_1^2\right. \\ &\quad \left.+2 \kappa \left( \mathcal {K}_{11} \mathcal {K}_{14}-\mathcal {K}_{12} \mathcal {K}_{13}\right) q_2\right) . \end{aligned} \end{aligned}$$

(79)

The first part of this section’s computations aims to portray graphical representation for the evolutions of the assigned fixed points or the equilibria of the autonomous dynamical system controlling the modified amplitudes of the interacting resonance waves of the weakly nonlinear system in the presence of insoluble interfacial surfactant. Secondly, we proceed to discuss several two-dimensional projections of the phase portraits of the modulation dynamical system onto some planes as well as the time histories of the involved parameters. The linear stability of the assigned equilibria will be demonstrated via the eigenvalues of the Jacobian of the dynamical system governing the perturbed quantities superimposed on the fixed points. Figure 18 shows the effect of the change in the variable $\mathcal {Z}$ on the behavior of the specified fixed points. These points are drawn as functions of the variable sigma corresponding to the values $\mathcal {Z} = 1.2, 1.4, 1.5\;$ in the parts Fig. 18a-c, respectively. In our model calculations, the values of other parameters are given in the caption of figure. Having noted the curves displayed in Fig. 18a, it is to be noted that the dynamical system has always three pairs of fixed points whatever the value of sigma, the zero fixed point which is stable in the region specified by the relation $\sigma > -0.39$ and is unstable as $\sigma < -0.39.$ The other two nontrivial fixed points $(a_1,a_2)$ are found to be stable as $\sigma < -0.39\;$ and $\sigma > 0.61,$ while these equilibria become unstable as $-0.39< \sigma < 0.61.\;$ Note that the stable equilibrium is presented by solid line whereas unstable one presented by dashed line. We observe that at the point $\sigma =-0.39,\;$ the three equilibria exchange stability which in turn suggests that $\sigma =-0.39\;$ represents a transcritical bifurcation point. Nevertheless, there are several scientific positions in which this type of bifurcation may occur, for example, in the case of logistic equation and models for the growth of a single species where there exists a fixed point at zero population despite the value of the growth rate.

At the point $\sigma =-0.61,$ the characteristic equation admits two pairs of imaginary conjugate eigenvalues. Also, it is found that as $\sigma$ decreases below the value 0.61,  the equilibria lose their stabilities with pairs of complex conjugate eigen values of positive real parts. Hence, the system is subject to Hopf bifurcation at $\sigma =0.61$ and thereby results in creating a limit-cycle solution near the point $\sigma =0.61\;$ of amplitude proportional to $\sigma = -0.61$ as it will be enhanced by the numerical results illustrated later in the rest of figures. Limit cycle solutions appear in such systems that fluctuate even if there are no periodic forces exerted on the system or equivalently the self-sustained oscillating systems. These solutions are of increasing scientific importance because of their many applications in various fields. Among them, we mention the systems of heart beat, spontaneous oscillating chemical reactions, dangerous self-vibrations in bridges and wings of aircraft. The conditions for Hopf bifurcation, are given in Lee and Mei (1996) and Usha and Uma (2000) by $\varrho _1> 0,\;\varrho _2 > 0$ and $\varrho _1 \varrho _2 = \varrho _3.$

An investigation of Fig. 18b clearly shows that the qualitative behavior of equilibria to variation of the detuning parameter $\sigma$ are similar to those of Fig. 18a. However, the increase in $\mathcal {Z}$ leads to the displacement of the Hopf bifurcation point to the left to occur at $\sigma =0.05,$ while the transcritical bifurcation point shifts to the right to become at $\sigma =-0.3,$ which indicates that there is a contraction of the sigma range corresponding to the unstable solutions of the system. Consequently, such behavior enhances the stabilizing role of $\mathcal {Z},$ which is consistent with the results of the linear case studied above. As expected, another increase in $\mathcal {Z}$ will lead to a further contraction of the unstable fixed solution regions without a qualitative change in the system behavior as shown in Fig. 18c. The hopf bifurcation point has occurred at $\sigma =-0.004,$ and the transcritical bifurcation point came at $\sigma =-0.17.$ Fig. 19 shows the points of both transcritical (TC) and Hopf bifurcations (HF) in the $(\mathcal {Z}-\sigma )$ plane.

The influence of variation of the parameter $\beta$ on the evolution of the steady-state solutions of system (61)-(63) with the detuning parameter is shown in Fig. 20. Figure 20a is drawn as $\beta =0.1,$ while Fig. 20b and c are plotted at $\beta =.3\;$ and $0.7,\;$ respectively. The frequency response curves of Fig. 20a show that there are three possible fixed point solution. The trivial steady-state solution is found to be stable (sink) as $\;\sigma > -0.07\;$ and unstable (saddle) when $\sigma < -0.07.\;$ As for the nontrivial stationary solutions, they are unstable in the region specified by $-0.07< \sigma < 0.06$ while otherwise are stable solutions. Moving to Fig. 20b-c, the numerical calculations show that there are no essential differences regarding the qualitative behavior of these solutions, except that there is an expansion in the region of stability of trivial solutions, and on the contrary, there is a contraction in the domain of stability of non-trivial steady state solutions. These results reinforce the dual role of stability that the $\beta$ variable plays within the nonlinear system, in contrast to the unstable role of the Beta, which was previously observed in the framework of linear theory. It is shown that the system exhibits transcritical bifurcation at $\sigma = -0.07$ and Hopf bifurcation at $\sigma = 0.06$ corresponding to the case of $\beta =0.3$; while these types of bifurcations are occurred at the points $\sigma = -0.2\;$ and $\sigma = 0.22\;$ when $\beta =0.7.\;$ Then an increase in the $\beta$ values will cause the points of the two types of bifurcations to move away from each other, as shown in Fig. 21.

The numerical results presented through Fig. 22 were accomplished by solving the modified equations for the dynamical system using the fourth-order Runge Kutta fourth - order method. In these figures, the phase portraits have been drawn in the planes $p_1-q_1, p_2-q_2,$ as well as time history of the modified amplitudes $p_1, p_2, q_1, q_2$ are demonstrated. The graphics of Fig. 22 are achieved for selected parametric values $\text {Ca}= 1000,\mathcal {Z}= 1.3,\beta = 0.1,\mu = 0.15,\rho = 0.5,\mathcal {V}= -2,q= -0.005,\mathcal {S}= 1,\text {Pe}= 600,\text {Ma}= 100,k= 0.1,= 0.01,\epsilon = 0.1,\sigma = -2.98\;$ which are satisfying the stability conditions (72). The parts (a), (b) of Fig. 22 show that the trajectories are presented by stable spiral and the period of oscillation will decrease as the time increases. Such a spiral or helical trajectory may occur as the harmonic oscillator were slightly damped. In this case, the path fails to close, because the oscillator loses very little energy per cycle. The path of the helical tip is an important characteristic distinctive of a spiral wave. It can be round in shape, among other things. The spiral is rigid as the path is circular. Otherwise it slaloms. In exciting systems, the helical meander caused by a bifurcation that resembles a Hopf bifurcation. The spiral paths can be modified by external influence fashions (Zykov and Mtiller 1996; Hu et al. 2010).

In Fig. 23, we have selected the parametric values, which are not satisfying the stability conditions (72). The graphs of Fig. 23a, b show unstable spiral trajectories where trajectories are outgoing spirals. Moreover, the time histories shown in Figs. 23c, d indicate there are growing irregular oscillations.

The aim of the graphics shown in Figs. 24 and 25 is to study the qualitative behavior of the dynamic system (76)-(79) in the vicinity of the Hopf bifurcation point, which was observed in Fig. 18a at $\sigma =-0.61,\;$ by drawing the projections of the trajectories as well as the change of the modified amplitudes with the development of time. Figures 24a and 25a, where $\sigma =-0.59,\;$ shows that a typical non-circular limit-cycle solution is born accompanied by periodic solutions with constant amplitudes similar to sinusoidal solutions as shown in the figures. The numerical results show that the system admits a doubling limit-cycle solution when $\sigma = -0.53.\;$ As the detuning parameter is increased to $-$0.44, the system undergoes a quadrable bifurcation period demonstrated. Additional increases in $\sigma$ are likely to lead to a series of a more doubling period solutions with some noise. Such results are in a well agreements of those of Arafat et al. (1998), Sirwah (2014). When $\sigma$ has the value $-0.4,$ the system behavior is no longer periodic and it exhibits some noise. The phase portraits evaluated at $\sigma =-0.33\;$ show that the system behaves in a chaotic manner where chaotic attractor will merge. Moreover, the time histories expresses an attractor that is expected to grow and deform as $\sigma$ is increased further. Consequently, the system behavior is no longer periodic or quasi-periodic as a result of increasing the values of the variable $\sigma$ to $-0.33$ and then an irregular movement of the surface waves at the surface separating the two fluid layers.

Fig. 18

Displayers the variations of the fixed point solutions of the dynamical system (58)-(60) with the deuning parameter $\sigma$ as $\text {Ca}=1000,\beta = 0.1,\mu =0.3,\rho =0.5,\mathcal {V}= -2,q= -0.005,\mathcal {S}= 1,\text {Pe}=600,\text {Ma}=100,k= 0.1,\kappa = 0.01,\epsilon =0.1,\;$ a $\mathcal {Z}= 1.2,\;$ b $\mathcal {Z}= 1.5\;$ c $\mathcal {Z}=1.7$

Fig. 19

Bifurcation diagram in the plane $\sigma -\mathcal {Z}$ for the same system investigated in Fig. 18

Fig. 20

Examines the frequency response curves for the steady- state solutions for the dynamical system (58)-(60) when the parameters take the same values employed in Fig. 19 and $\mathcal {Z}=1.3\;$ at a $\;\beta =0.1\;$ b$\;\beta =2\;$ c $\;\beta =5$

Fig. 21

Variations of the transcritical and Hopf bifurcations in the plane $\sigma -\mathcal {Z}$ for the same system investigated in Fig. 20

Fig. 22

Phase portraits in the planes $p_1-q_1, p_2-q_2,$ and time evolutions of the modified amplitudes $p_1, p_2, q_1, q_2$ for particular parametric values $\text {Ca}= 1000, \, \mathcal {Z}= 1.3, \, \beta = 0.1, \, \mu = 0.15, \, \rho = 0.5, \, \mathcal {V}= -2, \, q= -0.005, \, \mathcal {S}= 1, \, \text {Pe}= 600, \, \text {Ma}= 100, \, k= 0.1, \, = 0.01, \, \epsilon = 0.1, \, \sigma = -2.98$

Fig. 23

Two-dimensional projections onto the planes $p_1-q_1, p_2-q_2,$ and time histories of the modified amplitudes $p_1, p_2, q_1, q_2$ for a system having $\text {Ca}= 1000, \, \mathcal {Z}= 1.2, \, \beta = 0.1, \, \mu = 0.3, \, \rho = 0.5, \, \mathcal {V}= -2, \, q= -0.005, \, \mathcal {S}= 1, \, \text {Pe}= 600, \, \text {Ma}= 100, \, k= 0.1, \, \kappa = 0.01, \, \epsilon = 0.1, \, \sigma = - 0.2$

Fig. 24

Two-dimensional projections of the phase portraits onto the $p_1-q_1,$ plane as well as the long-time histories of $p_1, q_1,$ in the vicinity of the Hopf bifurcation occurred at $\sigma =-0.61.$ for a system of parameters $\text {Ca}=1000, \, \beta = 0.1, \, \mu =0.3, \, \rho = 0.5, \, \mathcal {V}= -2, \, q= -0.005, \, \mathcal {S}= 1, \, \text {Pe}=600, \, \text {Ma}=100, \, k= 0.1, \, \kappa = 0.01, \, \epsilon =0.1, \, \mathcal {Z}= 1.2$

Fig. 25

Two-dimensional projections of the phase portraits onto the $p_2-q_2,$ plane and the long-time histories of $p_2, q_2,$ for the same system studied in Fig. 24

Conclusion

In this study, the behavior of surface waves propagating at the separating interface between two layers of viscous Newtonian fluids has been studied taking into account the influence of insoluble surface surfactant. The mathematical equations describing the problem under study are communicated with the Navier–Stokes equations, continuity equation for incompressible fluids as well as the evolution equation for surface surfactant. We have reformulated the equations of motion and the associated boundary conditions in the dimensional form. We have applied long-wave technique for obtaining analytical solutions of the mathematical system describing for the physical model.

The two fluid layers are confined between a non-permeable top plate and a permeable one located at the bottom. The analysis is performed under the slippery state experiments that designate the condition necessary to determine the tangential component of the velocity at the interface between the lower fluid layer and the permeable plate. Consequently, we have derived two nonlinear coupled evolution equations governing the wave elevation at the free surface between the two films and the concentration of the surface surfactant. The multiple scales method is exploited to specify the solvability conditions necessary for obtaining asymptotic analytical solutions. In the frame work of the linear analysis, the technique of the normal mode is exploited to obtain the dispersion relation that relates the wave growth rate to the wave number and other parameters. Thereby the stability criteria of the linear system via numerical simulations are developed to demonstrate the effect of some parameters on the stability picture. Moreover, we have given a focusing to study the special case of small wave number limit which allows to obtain an analytical formula for the wave growth rate. The results of numerical simulation of the linear problem show that the dimensionless growth rate and the peak of wave number increase small with increasing the parameter q, indicating that q has a weak destabilizing influence on the linear stability of the flow. It is also found that the growth rate as well as the peak wave number increases significantly, revealing that theses parameters further enhance the surface instability. In contrast, it has been shown that the instability region, maximum growth rate and the corresponding wave number decreases pointedly, manifesting that such parameters suppress the flow instability significantly. In the nonlinear stage, we have devoted our attention to discuss the instability analysis of weakly nonlinear interfacial resonant waves. Such waves are structured by the interaction between the first and second modes or the case of two-to-one internal resonance. We have applied the modulation concept to the non-secular conditions of the resonate nonlinear waves and then derived a third-order autonomous dynamic system that governs the modified amplitudes and phases of the interacting waves. The steady- state solutions of this system are thereby obtained and their stability analysis is discussed. Numerical calculations are achieved by means of Runge–Kutta fourth-order method and their results are graphically illustrated to reveal the response of the system behavior to variation in some selected parameters. These influences are investigated through some diagrams include the frequency-response curves, phase portraits on some planes and time histories of the modulated amplitudes. Numerical results have also shown that the system undergoes two types of bifurcations with the detuning parameter as a control parameter: the transcritical and Hopf bifurcations. It worth noting that increasing the parameter $\mathcal {Z}$ leads to contracting the instability region of nontrivial stationary solutions while increase the instability region of the trivial fixed point solutions. In other words, the stabilizing or destabilizing role of $\mathcal {Z}$ on the fluid flow depends on the type of the assigned steady-state solution. Whereas, we have concluded that the increase in $\beta$ values causes an enlargement in instability region of the nontrivial fixed points and shrinks this of instability of the zero fixed point solutions. Moreover, it is remarked that system response does not qualitatively depend on the variation in $\mathcal {Z}$ or $\beta$. The projections of the modulation equations as well as the time histories of modulated amplitudes in the vicinity of the transcritical bifurcation points are illustrated which explained that the behavior of the system varies between the centered stable and unstable spiral depending on the type of the stationary solution, whether it is stable or unstable. In the vicinity of the Hopf bifurcation points, the numerical computations admit periodic solutions and thereby a limit cycle is born. the limit cycle develops, distorts, and experiences reduplicated period-doubling bifurcations and in turn transmitted to a chaotic behavior.

Appendix

$$\begin{aligned} f(H)&=\frac{H \left( -A_5 H^5 (\rho -1)+3 A_4 H^4+A_3 H^3+A_2 H^2+3 A_1 H \mathcal {Z}^2+A_0+\beta H^6 (\mu -1) (\rho -1)\right) }{3 \mathcal {L}_1(H)}, \\ \mathcal {T}_1(H) &= -\frac{H^2 (\rho -1) (H-\mathcal {Z})^3 (H \mu (\beta H+4)+(\beta H+3) (\mathcal {Z}-H))}{3 \mathcal {L}_1(H)}, \\ \mathcal {T}_2(H)& =\frac{H^3 \mu (\beta H+4) (H-\mathcal {Z})^2-H (\beta H+2) (H-\mathcal {Z})^4}{2 \mathcal {L}_1(H)}, \\ \mathcal {T}_3(H)&=-\frac{H^2 (H-\mathcal {Z})^3 (H\mu (\beta H+4)+(\beta H+3) (\mathcal {Z}-H))}{3 \mathcal {L}_1(H)},\end{aligned}$$

$$\begin{aligned} \mathcal {L}_1(H)=&\beta H^4 (\mu -1)^2+4 H^3 (\mu -1) (\mu +\beta \mathcal {Z})\\&-6 \beta H^2 (\mu -1) \mathcal {Z}^2+4 \beta H (\mu -1) \mathcal {Z}^3+\mathcal {Z}^3 (4 \mu +\beta \mathcal {Z}), \end{aligned}$$

$$\begin{aligned} A_0&= -6 \mu \mathcal {Z}^2 (\mathcal {V} \mathcal {Z}-3 Q), \\ A_1&= 3 \beta \mu Q+\mathcal {Z} (-\beta \mu \mathcal {V}-\rho \mathcal {Z}+\mathcal {Z}), \\ A_2&= 6 \mu (2 \mu -3) Q-6 \mu \mathcal {Z} (\beta q+2 \mu \mathcal {V}-3 \mathcal {V})+3 \beta \mu \mathcal {V} \mathcal {Z}^2\\&\quad+\mathcal {Z}^4 (\beta -\beta \rho )-4 (\mu -3) (\rho -1) \mathcal {Z}^3, \\ A_3&=3 (\mu -1) \mu (\beta Q+4 \mathcal {V})-3 \beta (\mu -1) \mu \mathcal {V} \mathcal {Z}-\beta (\mu -4)\\&\quad(\rho -1) \mathcal {Z}^3+6 (2 \mu -3) (\rho -1) \mathcal {Z}^2, \\ A_4&=\beta (\mu -1) \mu \mathcal {V}+\beta (\mu -2) (\rho -1) \mathcal {Z}^2\\&\quad+4 \mathcal {Z} (\mu (-\rho )+\mu +\rho -1), \\ A_5&=-4 \mu +\beta (3 \mu -4) \mathcal {Z}+3,\end{aligned}$$

$$\begin{aligned} \mathcal {C}_1=& ((-4 \mathcal {C} (\mu -1) (3 \mu +\beta (\mu +(\mathcal {Z}-1)^3))) (+(\mathcal {C} (4 \mu (\mu +\mathcal {Z}^3-1) \\&+\beta (\mu ^2+2 \mu (\mathcal {Z} (2 \mathcal {Z}-1)+1) (\mathcal {Z}-1)+(\mathcal {Z}-1)^4))))\\&+(4 \mu (\mu +\mathcal {Z}^3-1) +\beta (\mu ^2+2 \mu (\mathcal {Z} (2 \mathcal {Z}-1)+1) (\mathcal {Z}-1)\\&+(\mathcal {Z}-1)^4)) (3 \beta (\mu -1) (3 \mu q+2 \rho +4 \mu \mathcal {V}-2) \\ &+4 \mu (6 \mu q-9 q+5 \rho +9 \mu \mathcal {V}-9 \mathcal {V}-5)+3 \mathcal {Z}^2 (6 (2 \mu -3) (\rho -1) \\ &+\beta (\mu (3 q+4 \rho +2 \mathcal {V}-4)-8 \rho +8))+\mathcal {Z} (\beta (20 (\rho -1)\\&-3 \mu (4 q+5 \rho +3 \mu \mathcal {V}-3 \mathcal {V}-5))-12 (-4 \rho +\mu (4 \rho +2 \mu \mathcal {V}-3 \mathcal {V}-4)+4))\\&-15 (\rho -1)+\mathcal {Z}^3 (-8 (\mu -3) (\rho -1) -3 \beta (-4 \rho +\mu (\rho +\mathcal {V}-1)+4))\\&-(2 \beta +3) (\rho -1) \mathcal {Z}^4))/3 (4 \mu (\mu +\mathcal {Z}^3-1)\\&+\beta (\mu ^2+2 \mu (\mathcal {Z} (2 \mathcal {Z}-1)+1) (\mathcal {Z}-1)+(\mathcal {Z}-1)^4))^2\end{aligned}$$

$$\mathcal {C}_2=\frac{(\rho -1) \mathcal {S} (\mathcal {Z}-1)^3 (\beta \mu -\beta +4 \mu +\beta \mathcal {Z}+3 \mathcal {Z}-3)}{3 \left( \mathcal {Z}^3 (4 \mu +\beta \mathcal {Z})+(\mu -1) \left( \beta \mu -\beta +4 \mu +4 \beta \mathcal {Z}^3-6 \beta \mathcal {Z}^2+4 \beta \mathcal {Z}\right) \right) },$$

$$\mathcal { C}_3=\tilde{\mathcal{C}}_3 \text {Ma},\; \tilde{\mathcal{C}}_3=-\frac{ (\mathcal {Z}-1)^2 \left( -\beta \mu +\beta -4 \mu +\beta \mathcal {Z}^2+2 \mathcal {Z}^2-2 \beta \mathcal {Z}-4 \mathcal {Z}+2\right) }{2 \left( \mathcal {Z}^3 (4 \mu +\beta \mathcal {Z})+(\mu -1) \left( \beta \mu -\beta +4 \mu +4 \beta \mathcal {Z}^3-6 \beta \mathcal {Z}^2+4 \beta \mathcal {Z}\right) \right) },$$

$$\mathcal {C}_4=\frac{(\mathcal {Z}-1)^3 (\beta \mu -\beta +4 \mu +\beta \mathcal {Z}+3 \mathcal {Z}-3)}{3 \text {Ca} \left( \mathcal {Z}^3 (4 \mu +\beta \mathcal {Z})+(\mu -1) \left( \beta \mu -\beta +4 \mu +4 \beta \mathcal {Z}^3-6 \beta \mathcal {Z}^2+4 \beta \mathcal {Z}\right) \right) },$$

$$\mathcal {C}_4=\frac{(\mathcal {Z}-1)^3 (\beta \mu -\beta +4 \mu +\beta \mathcal {Z}+3 \mathcal {Z}-3)}{3 \text {Ca} \left( \mathcal {Z}^3 (4 \mu +\beta \mathcal {Z})+(\mu -1) \left( \beta \mu -\beta +4 \mu +4 \beta \mathcal {Z}^3-6 \beta \mathcal {Z}^2+4 \beta \mathcal {Z}\right) \right) },$$

$$\begin{aligned} \mathcal {C}_5=&(-\beta ^2 (-(\mu -1)^3 (6 \mu q+\rho +2 \mu \mathcal {V}-1)\\&+\mathcal {Z}^5 (\mu (-(34 \mu -87) (\rho -1)+24 (\mu -1) q\\&+ 42 (\mu -1) \mathcal {V})-56 (\rho -1))+(\mu -1) \mathcal {Z}^4\\&(\mu (-102 q+61 (\rho -1)+6 (4 \mu -15) \mathcal {V})\\&-70 (\rho -1)) -2 (\mu -1) \mathcal {Z}^3 (\mu (-(\mu -29) \\&(\rho -1)+12 (\mu -7) q+(32 \mu -50) \mathcal {V})-28 (\rho -1))\\&+4 (\mu -1) \mathcal {Z}^2 ((\rho -1) +\mathcal {Z}^8)(\mu (-(\mu -8) (\rho -1)\\&+3 (5 \mu -11) q+15 (\mu -1) \mathcal {V})-7 \rho +7)\\&+(\mu -1)^2 \mathcal {Z} (3 \mu (-16 q+\rho +2 (\mu -3) \mathcal {V}-1)\\&-8 \rho +8)+\mathcal {Z}^6 (28 (\rho -1) +2 \mu ((4 \mu -15) (\rho -1)\\&-4 (\mu -1) \mathcal {V}))+4 (\mu -2) (\rho -1) \mathcal {Z}^7)\\&+4 \mu (2 (\mu -1) (\mu ((6 \mu +3) q+\rho -1)-\rho +1)\\&+\mathcal {Z}^3 (2 \mu (-2 (\mu -2) (\rho -1) \end{aligned}$$

$$\mathcal {C}_7=\frac{\mathcal {S} \left( (\rho -1) (\mathcal {Z}-1)^2 \left( -\beta \mu +\beta -4 \mu +\beta \mathcal {Z}^2+2 \mathcal {Z}^2-2 \beta \mathcal {Z}-4 \mathcal {Z}+2\right) \right) }{2 \left( 4 \mu \left( \mu +\mathcal {Z}^3-1\right) +\beta \left( (\mu -1)^2+\mathcal {Z}^4+4 (\mu -1) \mathcal {Z}^3-6 (\mu -1) \mathcal {Z}^2+4 (\mu -1) \mathcal {Z}\right) \right) },$$

$$\mathcal {C}_8=\tilde{\mathcal{C}}_8 \text {Ma} -\frac{1}{\text {Pe}}s,\; \tilde{\mathcal{C}}_8=\frac{ -(\mathcal {Z}-1) \left( \beta \mu -\beta +4 \mu +\beta \mathcal {Z}^3+\mathcal {Z}^3-3 \beta \mathcal {Z}^2-3 \mathcal {Z}^2+3 \beta \mathcal {Z}+3 \mathcal {Z}-1\right) }{4 \mu \left( \mu +\mathcal {Z}^3-1\right) +\beta \left( (\mu -1)^2+\mathcal {Z}^4+4 (\mu -1) \mathcal {Z}^3-6 (\mu -1) \mathcal {Z}^2+4 (\mu -1) \mathcal {Z}\right) },$$

$$\mathcal {C}_9=\frac{(\mathcal {Z}-1)^2 \left( -\beta \mu +\beta -4 \mu +\beta \mathcal {Z}^2+2 \mathcal {Z}^2-2 \beta \mathcal {Z}-4 \mathcal {Z}+2\right) }{2\text {Ca} \left( 4 \mu \left( \mu +\mathcal {Z}^3-1\right) +\beta \left( (\mu -1)^2+\mathcal {Z}^4+4 (\mu -1) \mathcal {Z}^3-6 (\mu -1) \mathcal {Z}^2+4 (\mu -1) \mathcal {Z}\right) \right) },$$

$$\begin{aligned} \mathcal {C}=&\beta (\mu -1) (3 \mu (q+\mathcal {V})+\rho -1)+2 \mu (6 \mu (q+\mathcal {V})\\&-9 q+2 \rho -6 \mathcal {V}-2)+3 \mathcal {Z}^2 (\mu (6 q+4 \rho -4)\\& +\beta (\mu (3 q+\rho +\mathcal {V}-1)-2 \rho +2)-6 \rho +6)\\&+\mathcal {Z} (\beta (4 (\rho -1)-3 \mu (2 q+\rho +(\mu -1) \mathcal {V}-1))\\&-6 (-2 \rho +\mu (2 \rho +2 \mu \mathcal {V}-3 \mathcal {V}-2)+2))-3 \rho \\&-\mathcal {Z}^3 (\beta (-4 \rho +\mu (\rho +3 \mathcal {V}-1)+4)+2 (-6 \rho \\&+\mu (2 \rho +3 \mathcal {V}-2)+6)) -(\beta +3) (\rho -1) \mathcal {Z}^4+3. \end{aligned}$$

$$\begin{aligned} \mathcal {H}_1=&\frac{1}{(\mathcal {C}_1+\mathcal {C}_6)^6}(\mathcal {C}_8 C_1^6+(6 \mathcal {C}_6 \mathcal {C}_8-\mathcal {C}_3 \mathcal {C}_5) \mathcal {C}_1^5 +\mathcal {C}_6 (15 \mathcal {C}_6 \mathcal {C}_8\\&-7 \mathcal {C}_3 \mathcal {C}_5) \mathcal {C}_1^4 -22 \mathcal {C}_3 \mathcal {C}_5 \mathcal {C}_6^2 \mathcal {C}_1^3+\mathcal {C}_6^3 (15 \mathcal {C}_2 \mathcal {C}_6-22 \mathcal {C}_3 \mathcal {C}_5) \mathcal {C}_1^2\\&+\mathcal {C}_6^4 (6 \mathcal {C}_2 \mathcal {C}_6-7 \mathcal {C}_3 \mathcal {C}_5) \mathcal {C}_1+\mathcal {C}_6^5 (\mathcal {C}_2 \mathcal {C}_6-\mathcal {C}_3 \mathcal {C}_5)), \end{aligned}$$

$$\begin{aligned} \mathcal {H}_2=&\frac{1}{( \mathcal {C}_1+ \mathcal {C}_6)^8} ( \mathcal {C}_3 \mathcal {C}_7 ( \mathcal {C}_8-C_2) \mathcal {C}_1^6+(20 \mathcal {C}_6 C_8^3+ \mathcal {C}_3 (10 \mathcal {C}_6 \mathcal {C}_7\\&+ \mathcal {C}_5 \mathcal {C}_8) \mathcal {C}_8+ \mathcal {C}_2^2 \mathcal {C}_3 \mathcal {C}_5 -2 \mathcal {C}_3^2 \mathcal {C}_5 \mathcal {C}_7 -2 \mathcal {C}_2 \mathcal {C}_3 (5 \mathcal {C}_6 \mathcal {C}_7+ \mathcal {C}_5 \mathcal {C}_8)) \mathcal {C}_1^5\\&+(-15 \mathcal {C}_4 \mathcal {C}_6^4-50 \mathcal {C}_8^3 \mathcal {C}_6^2-13 \mathcal {C}_3 \mathcal {C}_7 \mathcal {C}_8 \mathcal {C}_6^2-49 \mathcal {C}_3 \mathcal {C}_5 \mathcal {C}_8^2 \mathcal {C}_6 \\&+11 \mathcal {C}_2^2 \mathcal {C}_3 \mathcal {C}_5 \mathcal {C}_6-22 \mathcal {C}_3^2 \mathcal {C}_5 \mathcal {C}_7 \mathcal {C}_6-3 \mathcal {C}_3^2 \mathcal {C}_5^2 \mathcal {C}_8+ \mathcal {C}_2 (3 \mathcal {C}_3^2 \mathcal {C}_5^2\\&-90 \mathcal {C}_6^2 \mathcal {C}_8^2- \mathcal {C}_3 \mathcal {C}_6 (47 \mathcal {C}_6 \mathcal {C}_7 +22 \mathcal {C}_5 \mathcal {C}_8))) \mathcal {C}_1^4+2 ( \mathcal {C}_3^3 \mathcal {C}_5^3\\ {}& +2 \mathcal {C}_3^2 \mathcal {C}_6 (9 \mathcal {C}_2 \mathcal {C}_5+6 \mathcal {C}_8 \mathcal {C}_5-14 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_5+6 \mathcal {C}_6^3 (10 \mathcal {C}_2 \mathcal {C}_8 ( \mathcal {C}_2+ \mathcal {C}_8)\\& -3 \mathcal {C}_4 \mathcal {C}_6^2)- \mathcal {C}_3 \mathcal {C}_6^2 (-29 \mathcal {C}_5 \mathcal {C}_2^2+(30 \mathcal {C}_6 \mathcal {C}_7-62 \mathcal {C}_5 \mathcal {C}_8) \mathcal {C}_2\\&+ \mathcal {C}_8 (30 \mathcal {C}_6 \mathcal {C}_7+ \mathcal {C}_5 \mathcal {C}_8))) \mathcal {C}_1^3- \mathcal {C}_6 (-6 \mathcal {C}_3^3 \mathcal {C}_5^3 -4 \mathcal {C}_3^2 \mathcal {C}_6 (15 \mathcal {C}_2 \mathcal {C}_5\\&+15 \mathcal {C}_8 \mathcal {C}_5 -14 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_5 +2 \mathcal {C}_6^3 (25 \mathcal {C}_2^3+45 \mathcal {C}_8 \mathcal {C}_2^2+14 \mathcal {C}_4 \mathcal {C}_6^2)\\&+ \mathcal {C}_3 \mathcal {C}_6^2 (2 \mathcal {C}_5 \mathcal {C}_2^2+(13 \mathcal {C}_6 \mathcal {C}_7-124 \mathcal {C}_5 \mathcal {C}_8) \mathcal {C}_2+ \mathcal {C}_8 (47 \mathcal {C}_6 \mathcal {C}_7 \\&-58 \mathcal {C}_5 \mathcal {C}_8))) \mathcal {C}_1^2+ \mathcal {C}_6^2 (-8 \mathcal {C}_4 \mathcal {C}_6^5+20 \mathcal {C}_2^3 \mathcal {C}_6^3+ \mathcal {C}_3 (-49 \mathcal {C}_5 \mathcal {C}_2^2\\&+2 (5 \mathcal {C}_6 \mathcal {C}_7-11 \mathcal {C}_5 \mathcal {C}_8) \mathcal {C}_2 + \mathcal {C}_8 (11 \mathcal {C}_5 \mathcal {C}_8 -10 \mathcal {C}_6 \mathcal {C}_7)) \mathcal {C}_6^2\\&+2 \mathcal {C}_3^2 \mathcal {C}_5 (12 \mathcal {C}_2 \mathcal {C}_5+18 \mathcal {C}_8 \mathcal {C}_5 -11 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_6+6 \mathcal {C}_3^3 \mathcal {C}_5^3) \mathcal {C}_1\\ {}& + \mathcal {C}_6^3 (- \mathcal {C}_4 \mathcal {C}_6^5+ \mathcal {C}_3 ( \mathcal {C}_2- \mathcal {C}_8) ( \mathcal {C}_2 \mathcal {C}_5- \mathcal {C}_8 \mathcal {C}_5+ \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_6^2 \\&+ \mathcal {C}_3^2 \mathcal {C}_5 (-3 \mathcal {C}_2 \mathcal {C}_5+3 \mathcal {C}_8 \mathcal {C}_5-2 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_6+2 \mathcal {C}_3^3 \mathcal {C}_5^3)), \end{aligned}$$

$$\begin{aligned} \mathcal {H}_3=&\frac{1}{( \mathcal {C}_1+ \mathcal {C}_6)^6} \mathcal {C}_2 \mathcal {C}_1^6+( \mathcal {C}_3 \mathcal {C}_5+6 \mathcal {C}_2 \mathcal {C}_6) \mathcal {C}_1^5+ \mathcal {C}_6 (7 \mathcal {C}_3 \mathcal {C}_5+15 \mathcal {C}_2 \mathcal {C}_6) \mathcal {C}_1^4\\&+2 \mathcal {C}_6^2 (11 \mathcal {C}_3 \mathcal {C}_5+10 \mathcal {C}_6 ( \mathcal {C}_2+ \mathcal {C}_8)) \mathcal {C}_1^3+ \mathcal {C}_6^3 (22 \mathcal {C}_3 \mathcal {C}_5+15 \mathcal {C}_6 \mathcal {C}_8) \mathcal {C}_1^2\\&+ \mathcal {C}_6^4 (7 \mathcal {C}_3 \mathcal {C}_5+6 \mathcal {C}_6 \mathcal {C}_8) \mathcal {C}_1+ \mathcal {C}_6^5 ( \mathcal {C}_3 \mathcal {C}_5+ \mathcal {C}_6 \mathcal {C}_8), \end{aligned}$$

$$\begin{aligned} \mathcal {H}_4=&\frac{1}{(\mathcal {C}_1+\mathcal {C}_6)^8}\mathcal {C}_4 \mathcal {C}_1^8+8 \mathcal {C}_4 \mathcal {C}_6 \mathcal {C}_1^7+(28 \mathcal {C}_4 \mathcal {C}_6^2+\mathcal {C}_3 \mathcal {C}_7 (\mathcal {C}_8-\mathcal {C}_2)) \mathcal {C}_1^6\\&+(56 \mathcal {C}_4 \mathcal {C}_6^3+20 \mathcal {C}_8^3 \mathcal {C}_6+10 \mathcal {C}_3 \mathcal {C}_7 \mathcal {C}_8 \mathcal {C}_6+\mathcal {C}_3 \mathcal {C}_5 \mathcal {C}_8^2+\mathcal {C}_2^2 \mathcal {C}_3 \mathcal {C}_5\\&-2 \mathcal {C}_3^2 \mathcal {C}_5 \mathcal {C}_7-2 \mathcal {C}_2 \mathcal {C}_3 (5 \mathcal {C}_6 \mathcal {C}_7+\mathcal {C}_5 \mathcal {C}_8)) \mathcal {C}_1^5+(55 \mathcal {C}_4 \mathcal {C}_6^4-50 \mathcal {C}_8^3 \mathcal {C}_6^2\\&-13 \mathcal {C}_3 \mathcal {C}_7 \mathcal {C}_8 \mathcal {C}_6^2-49 \mathcal {C}_3 \mathcal {C}_5 \mathcal {C}_8^2 \mathcal {C}_6+11 \mathcal {C}_2^2 \mathcal {C}_3 \mathcal {C}_5 \mathcal {C}_6 -22 \mathcal {C}_3^2 \mathcal {C}_5 \mathcal {C}_7 \mathcal {C}_6\\&-3 \mathcal {C}_3^2 \mathcal {C}_5^2 \mathcal {C}_8+\mathcal {C}_2 (3 \mathcal {C}_3^2 \mathcal {C}_5^2-90 \mathcal {C}_6^2 \mathcal {C}_8^2-\mathcal {C}_3 \mathcal {C}_6 (47 \mathcal {C}_6 \mathcal {C}_7+22 \mathcal {C}_5 \mathcal {C}_8))) \mathcal {C}_1^4\\&+2 (\mathcal {C}_3^3 \mathcal {C}_5^3+2 \mathcal {C}_3^2 \mathcal {C}_6 (9 \mathcal {C}_2 \mathcal {C}_5+6 \mathcal {C}_8 \mathcal {C}_5 -14 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_5 \\&+10 \mathcal {C}_6^3 (\mathcal {C}_4 \mathcal {C}_6^2+6 \mathcal {C}_2 C_8 (\mathcal {C}_2+\mathcal {C}_8))-\mathcal {C}_3 \mathcal {C}_6^2 (-29 \mathcal {C}_5 \mathcal {C}_2^2 +(30 \mathcal {C}_6 \mathcal {C}_7\\&-62 \mathcal {C}_5 \mathcal {C}_8) \mathcal {C}_2+\mathcal {C}_8 (30 \mathcal {C}_6 \mathcal {C}_7+\mathcal {C}_5 \mathcal {C}_8))) \mathcal {C}_1^3+\mathcal {C}_6 (6 \mathcal {C}_3^3 \mathcal {C}_5^3 +4 \mathcal {C}_3^2 \mathcal {C}_6 \\&(15 \mathcal {C}_2 \mathcal {C}_5+15 \mathcal {C}_8 \mathcal {C}_5 -14 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_5-10 \mathcal {C}_2^2 \mathcal {C}_6^3 (5 \mathcal {C}_2+9 \mathcal {C}_8)\\&+\mathcal {C}_3 \mathcal {C}_6^2 (-2 \mathcal {C}_5 \mathcal {C}_2^2+(124 \mathcal {C}_5 \mathcal {C}_8-13 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_2+\mathcal {C}_8 (58 \mathcal {C}_5 \mathcal {C}_8\\&-47 \mathcal {C}_6 \mathcal {C}_7))) \mathcal {C}_1^2 +\mathcal {C}_6^2 (6 \mathcal {C}_3^3 \mathcal {C}_5^3+2 \mathcal {C}_3^2 \mathcal {C}_6 (12 \mathcal {C}_2 \mathcal {C}_5+18 \mathcal {C}_8 \mathcal {C}_5-11 \mathcal {C}_6 \mathcal {C}_7) \mathcal {C}_5\\&+20 \mathcal {C}_2^3 \mathcal {C}_6^3+\mathcal {C}_3 \mathcal {C}_6^2 (-49 \mathcal {C}_5 \mathcal {C}_2^2(5+2 \mathcal {C}_6 \mathcal {C}_7-11 \mathcal {C}_5 \mathcal {C}_8) \mathcal {C}_2 \\&+\mathcal {C}_8 (11 \mathcal {C}_5 \mathcal {C}_8-10 \mathcal {C}_6 \mathcal {C}_7))) \mathcal {C}_1+\mathcal {C}_3 \mathcal {C}_6^3 (2 \mathcal {C}_3 \mathcal {C}_5\\ &+\mathcal {C}_6 (\mathcal {C}_8-\mathcal {C}_2)) (\mathcal {C}_3 \mathcal {C}_5^2-\mathcal {C}_6 (\mathcal {C}_2 \mathcal {C}_5-\mathcal {C}_8 \mathcal {C}_5+\mathcal {C}_6 \mathcal {C}_7)), \end{aligned}$$

$$\begin{aligned} \begin{aligned}&\;\mathcal {J}_{11}=k_1^2 \left( \zeta _2-\zeta _3 k_1^2+\xi _5\right) ,\\&\;\mathcal {J}_{12}= -k_1\zeta _1-k_1 \xi _2+2 \omega _1,\\&\;\mathcal {J}_{13}= k_1^2 \left( -\zeta _4 \xi _1+\zeta _2 \xi _2+\zeta _1 \xi _5-3 \zeta _3 k_1^2 \xi _2+2 \zeta _3 k_1 \omega _1\right) ,\end{aligned} \end{aligned}$$

$$\mathcal {J}_{14}=\frac{-k_1 \omega _1 \left( \zeta _1+\xi _2\right) +4 k_1^6 \left( \zeta _4 \xi _4-\zeta _3 \xi _5\right) +k_1^4 \left( 2 \zeta _2 \xi _5-2 \zeta _4 \xi _3\right) +2 \omega _1^2}{k_1},$$

$$\begin{aligned} \mathcal{J}_{15}=&\frac{1}{\zeta _4 k_2^2}\Big (2 \zeta _3 \zeta _4 k_2^2 k_1^5 \xi _7 \omega _1-k_2^2 k_1 \omega _1 \left( \zeta _4 \left( \zeta _1 \xi _{18}+\zeta _6-2 \xi _{17}\right) \right. \\ & \left.-\left( 2 \zeta _7-\zeta _9\right) \left( \zeta _1+\xi _2\right) \right) +k_2^2 \omega _1^2 \left( \zeta _4 \xi _{18}-2 \zeta _7+\zeta _9\right) \\ & +8 \zeta _3 \zeta _4 k_2^2 k_1^8 \left( \xi _{13}-2 \xi _{15}\right) +k_2^2 k_1^6 (\zeta _4 \left( 17 \zeta _{10} \xi _5\right. \\ & \left.+\zeta _2 \left( 17 \xi _{15}-10 \xi _{13}\right) +\zeta _4 \left( 10 \xi _{14}-17 \xi _{16}\right) \right) \\&+\zeta _3^2 k_2^2 \left( 5 \xi _8-4 \xi _6\right) +\zeta _3 \left( 2 \zeta _7 \xi _5-\zeta _9 \xi _5+4 \zeta _2 \xi _6\right. \\ & \left.-5 \zeta _2 \xi _8+\zeta _4 \xi _9+4 \zeta _4 \xi _{11}+2 \zeta _4 k_2^2 \xi _{13}-\zeta _4 k_2^2 \xi _{15}\right) )\\&+k_2^2 k_1^4 (\zeta _2^2 \left( 5 \xi _8-4 \xi _6\right) +\zeta _4^2 \left( 5 \xi _{12}-4 \xi _{10}\right) \\ & +2 \zeta _3 \left( \zeta _7-2 \zeta _9\right) k_2^2 \xi _5+\zeta _2 \left( -4 \zeta _7 \xi _5+5 \zeta _9 \xi _5+\zeta _3 k_2^2 \left( 4 \xi _6-5 \xi _8\right) \right) \\&+\zeta _4 (4 \zeta _5 \xi _5-5 \zeta _8 \xi _5-5 \zeta _2 \xi _9-5 \zeta _2 \xi _{11} +4 \zeta _3 k_2^2 \xi _9+\zeta _3 k_2^2 \xi _{11}))\\&+k_1^3 (\omega _2 \left( -2 \zeta _7 \xi _2+4 \zeta _9 \xi _2+4 \zeta _1 \xi _6-5 \zeta _1 \xi _8+\zeta _4 \xi _{17}\right) \\&-\zeta _1 k_2 (-2 \zeta _7 \xi _2+4 \zeta _9 \xi _2+4 \zeta _1 \xi _6-5 \zeta _1 \xi _8 +\zeta _4 \xi _{17})\\&+\zeta _3 \zeta _4 k_2^4 \xi _7 \left( \sigma \epsilon +2 \varpi _1\right) -\zeta _2 \zeta _4 k_2^2 \xi _7 \left( \sigma \epsilon +4 \omega _1\right) )\\&+k_1^2 (k_2^2 \left( \zeta _1 \left( \zeta _9-2 \zeta _7\right) \xi _2+\zeta _4 \left( \zeta _6 \xi _2-2 \zeta _1 \xi _{17}\right) \right) \\ & -\zeta _1 k_2 \left( \omega _1 \left( 2 \zeta _7-4 \zeta _9-4 \xi _6+5 \xi _8\right) +\zeta _4 \xi _{18} \left( \sigma \epsilon +2 \omega _1\right) \right) \\&+\omega _2 \left( \omega _1 \left( 2 \zeta _7-4 \zeta _9-4 \xi _6+5 \xi _8\right) +\zeta _4 \xi _{18} \left( \sigma \epsilon +2 \omega _1\right) \right) )\Big ), \end{aligned}$$

$$\begin{aligned} \mathcal {J}_{16}&=\frac{k_1}{\zeta _4 k_2^2}\Big (k_1^5 \left( -\left( \zeta _3 \left( 4 \xi _6-5 \xi _8\right) +\zeta _4 \left( \xi _{15}-2 \xi _{13}\right) \right) \right) \left( \zeta _1 k_2-\omega _2\right) \\&\quad+k_1^3 (-\omega _2 (2 \zeta _7 \xi _5-4 \zeta _9 \xi _5+4 \zeta _2 \xi _6-5 \zeta _2 \xi _8+4 \zeta _4 \xi _9+\zeta _4 \xi _{11}) \\ &\quad +k_2^2\omega _1 \left( \zeta _4 \left( 17 \zeta _{10}+8 \xi _{13}-16 \xi _{15}\right) +\zeta _3 \left( -\zeta _4 \xi _{18}+2 \zeta _7-\zeta _9\right) \right) \\&\quad+\zeta _1 k_2 \left( 2 \zeta _7 \xi _5-4 \zeta _9 \xi _5+4 \zeta _2 \xi _6-5 \zeta _2 \xi _8+4 \zeta _4 \xi _9+\zeta _4 \xi _{11}\right) ) \\ &\quad +2 \zeta _4 k_2^2 \xi _7\omega _1^2+k_2^2 k_1^4 \left( \zeta _4 \left( -17 \zeta _{10} \xi _2-8 \zeta _1 \left( \xi _{13}-2 \xi _{15}\right) \right) \right.\\& \quad\left.+\zeta _3 \left( -2 \zeta _7 \xi _2+\zeta _9 \xi _2-2 \zeta _4 \xi _{17}\right) \right) +k_1^2 (\zeta _3 k_2^4 (-2 \zeta _7 \xi _2 +4 \zeta _9 \xi _2\\ & \quad+4 \zeta _1 \xi _6-5 \zeta _1 \xi _8+\zeta _4 \xi _{17})+k_2^2 (\zeta _4^2 \left( -\xi _{19}\right) +\zeta _4 \left( -4 \zeta _5 \xi _2\right.\\&\quad\left.+5 \zeta _8 \xi _2+\zeta _6 \xi _5-\zeta _1 \xi _9-4 \zeta _1 \xi _{11}+\zeta _2 \xi _{17}\right) +\zeta _1 \left( \zeta _9-2 \zeta _7\right) \xi _5 \\ & \quad +\zeta _2 \left( 4 \zeta _7 \xi _2-5 \zeta _9 \xi _2+\zeta _1 \left( 5 \xi _8-4 \xi _6\right) \right) )+\zeta _1 \zeta _4 k_2 \xi _7 \left( \sigma \epsilon +2\omega _1\right) \\&\quad-\zeta _4 \xi _7\omega _2 \left( \sigma \epsilon +2\omega _1\right) )+k_2^2 k_1 (\omega _1 (\left( 2 \zeta _7-\zeta _9\right) \xi _5+\zeta _4 (-2 \zeta _1 \xi _7 \\ & \quad +4 \zeta _5-5 \zeta _8+\xi _9+4 \xi _{11}))+\zeta _3 k_2^2 \left( \omega _1 \left( 2 \zeta _7-4 \zeta _9-4 \xi _6+5 \xi _8\right) \right.\\&\quad\left.+\zeta _4 \xi _{18} \left( \sigma \epsilon +2\omega _1\right) \right) -\zeta _2 (\omega _1 \left( 4 \zeta _7-5 \zeta _9-4 \xi _6+5 \xi _8\right) \\ &\quad +\zeta _4 \xi _{18} \left( \sigma \epsilon +\omega _1\right) ))\Big ), \end{aligned}$$

$$\mathcal {K}_{11}=4 k_1^2 \left( \zeta _2-\zeta _3 k_2^2+\xi _5\right) ,\;\mathcal {K}_{12}=\frac{4 \zeta _1 k_1^2}{k_2}-2 k_1 \xi _2+\frac{4 k_1^2 \omega _2}{k_2^2}+\omega _2,$$

$$\begin{aligned} \begin{aligned}\mathcal {K}_{13}=& 4 k_1 \left( -16 \zeta _3 k_1^3 \xi _2+k_1 \left( -\zeta _4 \xi _1+\zeta _2 \xi _2\right.\right.\\&\left.\left.+\zeta _1 \xi _5+\zeta _3 k_2^2 \xi _2\right) +8 \zeta _3 k_1^2 \omega _2-\zeta _3 k_2^2 \omega _2\right) ,\end{aligned} \end{aligned}$$

$$\mathcal {K}_{14}=\frac{4 k_1^2 \xi _2 \left( \zeta _1 k_2-\omega _2\right) -2 k_1 \left( \zeta _1 k_2^2 \xi _2+2 \zeta _1 k_2\omega _2-2\omega _2^2\right) +128 k_2^2 k_1^5 \left( \zeta _4 \xi _4-\zeta _3 \xi _5\right) -16 k_2^2 k_1^3 \left( \zeta _4 \xi _3-\zeta _2 \xi _5\right) +\zeta _1 k_2^2 \omega _2}{k_2^2},$$

$$\begin{aligned} \begin{aligned}\mathcal {K}_{15}=&\frac{1}{\zeta _4}\Big (4 \zeta _3 k_1^8 \left( \zeta _3 \left( \xi _6+\xi _8\right) -\zeta _4 \left( \xi _{13}+\xi _{15}\right) \right)\\& -4 k_1^6(\zeta _3 \left( \zeta _7 \xi _5+\zeta _9 \xi _5+2 \zeta _2 \xi _6+2 \zeta _2 \xi _8-\zeta _4 \xi _9-\zeta _4 \xi _{11}\right)\end{aligned} \end{aligned}$$

$$\begin{aligned} \mathcal {K}_{15}&=\frac{1}{\zeta _4}\Big (4 \zeta _3 k_1^8 \left( \zeta _3 \left( \xi _6+\xi _8\right) -\zeta _4 \left( \xi _{13}+\xi _{15}\right) \right) \\&\quad-4 k_1^6(\zeta _3 \left( \zeta _7 \xi _5+\zeta _9 \xi _5+2 \zeta _2 \xi _6+2 \zeta _2 \xi _8-\zeta _4 \xi _9-\zeta _4 \xi _{11}\right) \\ &\quad +\zeta _4 \left( -\zeta _{10} \xi _5-\zeta _2 \left( \xi _{13}+\xi _{15}\right) +\zeta _4 \left( \xi _{14}+\xi _{16}\right) \right) )\\&\quad+4 k_1^4 (\zeta _4^2 \left( \xi _{10}+\xi _{12}\right) -\zeta _4 \left( \zeta _5 \xi _5+\zeta _8 \xi _5+\zeta _2 \left( \xi _9+\xi _{11}\right) \right) \\ &\quad +\zeta _2 \left( \zeta _7 \xi _5+\zeta _9 \xi _5+\zeta _2 \left( \xi _6+\xi _8\right) \right) )+2 k_1^2 \left( \zeta _4 \left( \zeta _6 \xi _2+2 \zeta _1 \xi _{17}\right) \right.\\&\quad \left.-\zeta _1 \left( \zeta _7 \xi _2+\zeta _9 \xi _2+2 \zeta _1 \left( \xi _6+\xi _8\right) \right) \right) +2 \zeta _3 \zeta _4 k_1^5 \xi _7 \left( \sigma \epsilon -\omega _2\right) \\ &\quad +2 \zeta _2 \zeta _4 k_1^3 \xi _7 \left( \omega _2-\sigma \epsilon \right) +k_1 (2 \zeta _7 \xi _2 \omega _1+2 \zeta _9 \xi _2 \omega _1-4 \zeta _4 \xi _{17}\omega _1\\&\quad-\zeta _4 \zeta _6 \omega _2+\zeta _1 (\zeta _7\omega _2+\zeta _9\omega _2+8 \xi _6\omega _1 +8 \xi _8\omega _1\\&\quad+2 \zeta _4 \xi _{18} \left( \sigma \epsilon -\omega _2\right) ))-\omega _1 \left( \zeta _7\omega _2+\zeta _9 \omega _2+4 \xi _6 \omega _1\right.\\&\quad\left.+4 \xi _8\omega _1+2 \zeta _4 \xi _{18} \left( \sigma \epsilon -\omega _2\right) \right) \Big ), \end{aligned}$$

$$\begin{aligned} \mathcal {K}_{16}&=\frac{k_1}{\zeta _4}\Big (2 k_1^4 \left( \zeta _3 \left( \zeta _7 \xi _2+\zeta _9 \xi _2+4 \zeta _1 \xi _6+4 \zeta _1 \xi _8-2 \zeta _4 \xi _{17}\right)\right. \\ &\quad \left. -\zeta _4 \left( \zeta _{10} \xi _2+2 \zeta _1 \left( \xi _{13}+\xi _{15}\right) \right) \right) -2 k_1^2 (2 \zeta _4^2 \xi _{19} \\ &\quad -\zeta _4 \left( \zeta _5 \xi _2+\zeta _8 \xi _2+2 \left( \zeta _6 \xi _5+\zeta _1 \left( \xi _9+\xi _{11}\right) +\zeta _2 \xi _{17}\right) \right) \\&\quad+2 \zeta _1 \left( \zeta _7+\zeta _9\right) \xi _5+\zeta _2 \left( \zeta _7 \xi _2+\zeta _9 \xi _2+4 \zeta _1 \left( \xi _6+\xi _8\right) \right) ) \\& \quad -k_1^3 \left( \zeta _3 \left( \zeta _7\omega _2+\zeta _9\omega _2+8 \xi _6\omega _1+8 \xi _8\omega _1+2 \zeta _4 \xi _{18} \left( \sigma \epsilon -\omega _2\right) \right) \right.\\&\quad\left.-\zeta _4 \left( \zeta _{10}\omega _2+4 \xi _{13}\omega _1+4 \xi _{15}\omega _1\right) \right) +k_1 (4 \zeta _7 \xi _5\omega _1+4 \zeta _9 \xi _5\omega _1\\&\quad-4 \zeta _4 \xi _9\omega _1-4 \zeta _4 \xi _{11}\omega _1-\zeta _4 \zeta _5\omega _2-\zeta _4 \zeta _8\omega _2+2 \zeta _1 \zeta _4 \xi _7 \left( \sigma \epsilon -\omega _2\right) \\ & \quad +\zeta _2 \left( \zeta _7\omega _2+\zeta _9\omega _2+8 \xi _6\omega _1+8 \xi _8\omega _1+2 \zeta _4 \xi _{18} \left( \sigma \epsilon -\omega _2\right) \right) )\\&\quad+2 \zeta _4 \xi _7\omega _1 \left( \omega _2-\sigma \epsilon \right) \Big ). \end{aligned}$$