Introduction

Gravitational acceleration affects important colloids by changing sedimentation (DeLucas et al. 1989), convection (Sen et al. 1999; Lösch et al. 2011), and the resulting mechanical stresses (Cheng et al. 2001; Maier et al. 2015; Unsworth and Lelkes 1998). The gravitational level can affect the crystallization of macromolecules (McPherson 1997; Lorber 2002), proteins (DeLucas et al. 1989; Erdmann et al. 1989; McPherson et al. 1999; McPherson and DeLucas 2015), viruses (Lorber 2008), semiconductors (Ahari et al. 1997) and the formation of ionic crystals from solution, for example calcium phosphate (Madsen et al. 1995). In biology, microgravity offers potentials for tissue engineering by enabling the aggregation of cells and therefore the formation of larger cell constructs. Simulated microgravity conditions were found to enhance nutrient supply and oxygen diffusion, resulting in reduced necrosis centers during the assembly of tissue aggregates (Unsworth and Lelkes 1998; Freed and Vunjak-Novakovic 1997; Barzegari and Saei 2012).

Gravity also changes the distribution of particles in composites that are prepared from colloidal precursors, thus affecting bulk properties. Nanocomposites contain nanoparticles in polymer or other matrices (Hanemann and Szabó 2010), where they tune mechanical, dielectric or optical properties. The resulting properties depend on the composition, shape and size of the nanofillers, their volume fraction and their spatial distribution inside the matrix (Liu and Webster 2010; Nan et al. 2010; Parola et al. 2016). The particle distribution is commonly tuned in order to change key material properties (Meth et al. 2011). A homogeneous distribution of nanoparticles can be used to enhance mechanical strength without decreasing flexibility (Ribeiro et al. 2014). Percolating superstructures of conductive or porous particles such as silver or carbon black increase electrical or ion transport (Huang 2002). The structure of nanocomposites has been tuned beyond random particle distribution by external manipulation or through particle self-assembly. For example, carbon black networks were aligned by applying an electrical field on the composite (Huynh et al. 2018). Self-assembly has been used to obtain nanowires networks for nanoelectronics (Hassenkam et al. 2004; Bayrak et al. 2018), to arrange semiconductor nanorods in solar cells (Huynh et al. 2002; Ryan et al. 2006), and to combine gold nanorods guided by DNA into drug carriers (Raeesi et al. 2016), for example.

The sedimentation of nanoparticles or their superstructures and their convective transport during material preparation can establish concentration gradients inside the composite that change material properties (Leeuwenburgh et al. 2010; Zhao et al. 2015). It is difficult to assess the relevance of gravity in composite preparation because the density of the matrix changes during processing, filler particle densities cannot be easily changed, and growing superstructures increase their sedimentation and friction coefficients. Microgravity experiments are one of very few practical approaches to study nanoparticle dynamics during materials formation. Microgravity conditions can be realized in drop tower facilities (van Zoest et al. 2010), during parabolic flights, with sounding rockets, or on the international space station (Maier et al. 2015).

Particle dynamics are often analyzed using Dynamic Light Scattering (DLS). DLS resolves average particle dynamics on a microsecond time - and micrometer length scale (Pecora 1985; Berne and Pecora 2000; Pecora 2000), allowing for a detailed investigation of nanoparticle dynamics such as the growth of particles (Tobler et al. 2009) or the formation of superstructures (Carl et al. 2017; Lorber et al. 2012). The measurements yield hydrodynamic sizes, particle polydispersity, and can indicate the colloidal stability of nanoparticles (Parola et al. 2016; Pecora 1985), polymers (Berne and Pecora 2000; Pecora 2000) and proteins (Tobler et al. 2009; Lorber et al. 2012). Light scattering set-ups can be built compact and sufficiently robust for the conditions during a rocket or drop tower lift-off and landing phase (Mazzoni et al. 2013; Okubo et al. 1999).

Okuba et. al investigated the formation of colloidal silica particles during parabolic flights using a commercial ALV-5000 DLS set-up (Okubo et al. 1999). Rogers et. al cooperated with NASA and built a compact DLS instrument to measure dynamic and static light scattering during a space shuttle mission. They studied the phase transition of dispersed poly(methyl methacrylate) particles as a model system for hard spheres (Rogers et al. 1997). Potenza et al. studied the temperature dependent agglomeration of polytetrafluoroethylene particles on the international space station (ISS) by measuring static and dynamic near field scattering using the Selectable Optical Diagnostic Instrument (SODI-Colloid) of the European Space agency (ESA) (Mazzoni et al. 2013).

Interactions in colloids are often temperature dependent, and there are systems where the agglomeration of particles can be manipulated through temperature (Potenza et al. 2018; Veen et al. 2012; Monego et al. 2018). This enables experiments where the effect of gravity on agglomeration is directly studied. Previous to this study, the only reported experiments on temperature-dependent colloid behavior in microgravity that we are aware of were performed using the SODI-Colloid instrument on the ISS. Here, we report on a more accessible approach where a temperature controlled DLS set-up, developed in cooperation with the company LS Instruments (Fribourg, Switzerland), was introduced to a drop tower and a system for fluid temperature control was established. The overall set-up enabled DLS measurements on colloidal dispersions of nanoparticles in a temperature range between 5 \({}^{\circ }\text {C}\) and 85 \({}^{\circ }\text {C}\), enabling experiments with rapid temperature changes and temperature gradients.

We used the set-up to study the influence of sedimentation and convection on nanoparticles under different accelerations. Gold nanoparticles stabilized with non-polar ligands are used as well-defined filler particles. Gold nanoparticles have found a number of applications in materials, for example in thermochromic composites (Doblas et al. 2018), sensing (Korotcenkov et al. 2016; Priyadarshini and Pradhan 2017), imaging (Falahati et al. 2020; Boisselier and Astruc 2009) and catalysis (Priecel et al. 2016). We use gold particles here because they possess a high density and they can be prepared in a size range between 1 and 10 nm and covered with highly defined organic shells.

We performed DLS measurements at the ZARM (center of applied space technology and microgravity) drop tower located in Bremen, Germany, which provides microgravity intervals up to 9.1 s and exerts accelerations around 40 g on the set-up during lift-off and landing phase (Von Kampen et al. 2006). A commercial DLS instrument from LS Instruments was adapted to be used in the drop tower. We used it to study the dynamics of non-agglomerating non-polar gold nanoparticles (average core diameter 7.8 nm) in microgravity and compared the results to ground experiments. The samples were heated to 70 \({}^{\circ }\text {C}\) and then rapidly cooled to 10 \({}^{\circ }\text {C}\). This enables future studies where the temperature change induces agglomeration, for example of hexadecanethiol capped gold nanoparticles that start agglomerating at temperatures below 60 \({}^{\circ }\text {C}\) (Kister et al. 2018).

This manuscript is structured as follows: We first discuss the dedicated set-up in detail. Dynamic light scattering experiments at constant temperature and with a rapid temperature drop on ground are introduced, their results are analyzed, and the changes of particle mobility are investigated. In the final set of experiments, light scattering experiments at a constant temperature and with a rapidly cooled nanoparticle dispersion in microgravity are introduced and compared to the ground experiments.

Results and Discussions

Instrumental Set-Up

Fig. 1
figure 1

Drop tower capsule with integrated heating block and liquid handling system on the topmost platform and the dynamic light scattering set-up on the platform underneath

Full size image
Fig. 2
figure 2

Liquid handling system with the heating block used to heat the dispersion before injecting into the cooled measurement cell

Full size image
Fig. 3
figure 3

Schematic view of the dynamic light scattering set-up, with the optical path marked in red

Full size image

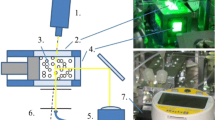
Experiments in microgravity were performed at the drop tower of ZARM in Bremen using a catapult launch. The drop tower tube had a height of 122 m and provided a microgravity interval of 9.1 s (Von Kampen et al. 2006). This set the boundaries for integration times of the measurements and the rates of change in temperature-dependent experiments. An experimental set-up was integrated into the catapult capsule (Fig. 1) with limited space. The capsule held four platforms, with the heating stage and liquid handling system on the first platform. The second platform held the DLS instrument with laser, Peltier temperature-controlled measurement cell, two photo detectors, and the correlator. The two lower platforms carried the capsule computer and the power supplies. The capsule computer provided access to the liquid handling and the instrument via remote control. The complete capsule was used to perform microgravity experiments in the drop tower. All parts were designed to withstand the acceleration forces of the catapult (\(\approx\) 30 g), the deceleration impact of \(\approx\) 50 g and the vibrations during the drop. Schematics of the dynamic light scattering set-up and the optical path are shown in Fig. 3.

The DLS set-up was built in cooperation with the company LS Instruments. A quartz glass cuvette was used as measurement cell. The cuvette was 46 mm tall and had a square cross-section with 12.5 mm outer side length. The inner diameter was 10 mm and the base had a thickness of 1.25 mm. A laser with a wavelength of 638 nm was chosen to avoid absorption by the gold particles’ surface plasmon resonance at 526 nm. Scattering was recorded at an angle of \(2\theta = {90\,\mathrm{{}^{\circ }}}\) in intervals of 1 s that were successively analyzed for sufficient time resolution. The accelerations during catapult launch and impact at the end of the drop required mechanical damping to prevent misalignment of the optics so that a second drop could immediately follow. Deceleration upon impact affected the autocorrelation functions recorded during the landing phase and rendered them unusable. The microgravity interval of 9.1 s allowed for the measurement of 8 consecutive autocorrelation functions with integration times of 1 s with qualities that were sufficient for the analysis of particle dynamics. The autocorrelation function at 9 s was affected by the landing of the capsule. Dynamic light scattering can measure hydrodynamic particle diameters ranging from nanometers to micrometers (Karow et al. 2015). An integration time of 1 s is adequate to resolve the corresponding specific mean residence times \(\tau\)Diff between nanoseconds and microseconds. Longer integration times are often used to increase the signal-to-noise-ratio (Goldburg 1999).

A temperature control set-up was designed where the sample was pumped through a tube and heated externally to 70 \({}^{\circ }\text {C}\) using a heating block of aluminum with a silicon heating mat (Fig. 2). The hot sample was injected into a cooled measurement cell (10 \({}^{\circ }\text {C}\)) just before the measurement using a syringe pump. This ensured rapid cooling at the beginning of the microgravity phase.

Ground Experiments

A dispersion of spherical gold nanoparticles with core diameters of 7.8 nm (± 0.4 nm) (determined by SAXS measurements) stabilized with oleylamine (ligand length of \({2\,\mathrm{\text {n}\text {m}}}\) (Mourdikoudis and Liz-Marzán 2013)) and an optical absorption maximum at \(\lambda ={526\,\mathrm{\text {n}\text {m}}}\) in tetradecane was analyzed during reference DLS experiments on ground. A gold concentration of 0.72 mg mL\(^{-1}\) (± 0.03 mg mL\(^{-1}\)), corresponding to a particle concentration of 1.5 1014 mL\(^{-1}\), was used.

Eight consecutive autocorrelation functions (shown in the SI) were obtained from scattering experiments with integration times of 1 s at a constant temperature of 20 \({}^{\circ }\text {C}\). The experiment was repeated three times on the same sample consecutively. The autocorrelations showed a single exponential decay as expected for the Brownian Motion of uniform particles. An exponential fit (see SI) (Gabriel et al. 2015) yielded mean residence times \(\tau_\mathrm {_{Diff}}\) of 0.29 ms (± 0.01 ms), corresponding to a mean hydrodynamic diameter \(d_\mathrm {H}\) of 21 nm (± 1 nm).

The large hydrodynamic diameter indicates the formation of a soft shell, a well-known phenomenon for oleylamine-coated gold nanoparticles. Bilayers or multilayers of oleylamine form on the first, moderately strongly bound shell. We compared the hydrodynamic diameters at different stages of preparation and found that the soft shell grew when preparing the samples for DLS experiments from the stored particles, a few weeks after the synthesis, where excess oleylamine was added in order to replace desorbed molecules. Additional measurements (see SI) showed that the hydrodynamic diameter stayed constant after the sample preparation. In the following, we use the final diameter of 21 nm as starting diameter.

Fig. 4
figure 4

Temperatures (T) over time (t) after injecting different samples at 70 \({}^{\circ }\text {C}\) into the pre-cooled measurement cell (10 \({}^{\circ }\text {C}\)). Three measurements were performed with pure tetradecane and three measurements were performed with a nanoparticle dispersion in tetradecane on ground. The mean temperatures and their standard deviation are shown. One measurement was performed with a nanoparticle dispersion in tetradecane in microgravity

Full size image
Table 1 Time-dependent mean residence time (\(\tau\)Diff) of the nanoparticles according to DLS measurements after a temperature drop on ground (1 g). The apparent hydrodynamic diameters (\(d_\mathrm {H}\)) were calculated assuming the given evolution of temperature (\(T\)), viscosity (\(\eta\)), and refractive index (\(n\)) of the solvent
Full size table

The changes of particle dynamics during a rapid temperature drop (70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\)) were observed on ground. We performed preliminary experiments to estimate the temperature change inside the measurement cell during the temperature drop using a thermocouple (type K). Three measurements were performed in pure tetradecane, with the thermocouple placed close to the scattering volume at the bottom of the cuvette. Three measurements were performed using a gold nanoparticle dispersion, with the thermocouple placed sufficiently far above to enable concurrent temperature measurements during DLS experiments. The measured temperatures varied between experiments by an average of \(\approx\) 10 K, probably due to variations of the thermocouple position in the cuvette. A direct measurement of the temperatures inside the measurement is cell is difficult, because the precise position of the temperature sensor inside the cuvette and the liquid flow around it during the sample injection are hard to control. This leads to an uncertainty of the temperature measurements. An analysis of the scattering results (see below) indicates that the repeatability of the scattering experiment is better than that of the temperature measurement. The starting temperature of the liquid, the sample volume, the length of the tubing, and the temperature of the cuvette were carefully kept constant and led to a reproducible temperature profile inside the measurement cell.

One additional temperature measurement with a thermocouple was performed in microgravity. The resulting temperature profile was in good agreement with the experiments on ground, see Fig. 4. The good agreement between the temperature measurements on ground and in microgravity suggests (within the accuracy limits of the temperature measurements with thermocouples explained above) that the effect of natural convection due to density differences in the liquid during the temperature drop is limited, even on the ground. We calculated an average temperature profile from all measurements given, in Table 1, that we used to calculate the apparent hydrodynamic diameters reported below.

Fig. 5
figure 5

Selected autocorrelation functions and fits (dashed line) of gold nanoparticles in tetradecane while cooling from 70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\) on ground. 8 consecutive autocorrelation functions with an integration time of 1 s were recorded and analyzed by using a simple exponential decay

Full size image
Fig. 6
figure 6

Mean residence times (\(\tau\)Diff) over time (t) of oleylamine capped gold nanoparticles in tetradecane under normal (1 g) and microgravity conditions (\(\mu\)g) at a constant temperature of 20 \({}^{\circ }\text {C}\) and after a temperature drop (70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\)). The DLS measurements at 1 g at 20 \({}^{\circ }\text {C}\) and with a temperature drop were repeated three times. One experiment at 20 \({}^{\circ }\text {C}\) and two experiments with a temperature drop (70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\)) were performed in \(\mu\)g

Full size image

The results of the DLS experiments during a temperature drop on ground (1 g) are shown in Fig. 5. The first autocorrelation function was recorded at \(t={1\,\mathrm{\text {s}}}\) after injection. It was possible to record reliable autocorrelation functions with an integration time of 1 s, enabling high time resolution measurements. A comparison of the exponential decay of the autocorrelations after injection indicated an increase of the residence time, as expected for a cooling dispersion (Fig. 6). We used the temperatures measured with the thermocouple as explained above and the measured mean residence times in order to calculate apparent hydrodynamic diameters, correcting for the temperature-dependent change of the solvent’s viscosities and refractive indices.

Table 2 Temperature change in the scattering volume during a temperature drop from 70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\) as calculated from mean residence times (\(\tau_\mathrm{_{Diff}}\)) on ground (1 g) assuming a constant hydrodynamic particle diameter of 22 nm. The corresponding viscosities (\(\eta\)) and refractive indices (\(n\)) of the solvent are given for the specific temperatures
Full size table

The calculated hydrodynamic particle diameters were consistently smaller than expected. Gold nanoparticles of the type used here are not expected to agglomerate or change their hydrodynamic diameter in this temperature range. We performed ground experiments and measured the change of diffusivity with temperature in the same DLS set-up. The results (see SI, Fig. 7) indicate that the particles behave as expected from the Einstein-Smoluchovski relation and the changes in solvent viscosity and refractive index with a constant hydrodynamic diameter of \(d_H={22\,\mathrm{\text {n}\text {m}}}\). We performed additional experiments and confirmed that the liquid injection does not change the particle size either (see SI, Fig. 10). We conclude that the smaller apparent particles size in Table 1 are due to an unreliable temperature measurement and reflect temperature differences inside the cuvette. Our aim was to increase the accuracy of the temperature using DLS data. To this end, we assumed a constant hydrodynamic particle diameter of \(d_{H} = 22\) nm and calculated the temperature in the scattering volume from the scattering data. We repeated the experiment and compared the resulting profile in order to assess the repeatability. The DLS experiments yielded mean residence times \({\mathrm{\tau}}_{\mathrm{_{Diff}}}\). Solving the Stokes-Einstein equation (equation 4 in the SI) assuming a constant hydrodynamic particle diameter leads to a temperature of the scattering volume. The calculations are complicated by the temperature dependence of viscosity and (to a smaller degree) refractive index, so that there exists no simple relation \(T(\tau_{\mathrm{_{Diff}}}, d_{_{H}})\). We used standard expressions for the temperature-dependent liquid properties (see SI) and solved the equation system numerically using Mathematica 11. Mean temperatures and their standard deviations for three subsequent experiments are given in Table 2. The values measured in the first second strongly deviated across experiments; they are probably affected by forced convection and possibly by the rapidly changing temperatures. We used the mean temperatures in Table 2 for all further calculations. Note that the remaining uncertainties are considerable but small enough to assess e.g., agglomeration of the particles, which will typically change their diameters by one or more orders of magnitude.

Microgravity Experiments

Dynamic light scattering experiments were repeated under microgravity conditions at ZARM using catapult launches that provided microgravity intervals of 9.1 s. Selected autocorrelation functions obtained at 20 \({}^{\circ }\text {C}\) and after the temperatures drop are shown in Figs. 7 and 8. All parameters were identical with those of the respective ground experiments.

Fig. 7
figure 7

Selected autocorrelation functions and fits (dashed line) of gold nanoparticles in tetradecane at a constant temperature of 20 \({}^{\circ }\text {C}\) in microgravity. 8 consecutive autocorrelation functions with an integration time of 1 s were recorded and analyzed by using a simple exponential decay

Full size image
Fig. 8
figure 8

Selected autocorrelation functions and fit (dashed line) of gold nanoparticles in tetradecane while cooling from 70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\) in microgravity. 8 consecutive autocorrelation functions with an integration time of 1 s were recorded and analyzed by using a simple exponential decay

Full size image

The autocorrelation functions show a reduced intercept, i.e., a reduced plateau value at short correlation times, under microgravity conditions, probably due to slight misalignment of the optics during the catapult launch. The single exponential decay was preserved and fitting led to a good agreement between data and model. The resulting mean residence times and apparent hydrodynamic diameters of the particles under normal and microgravity conditions are summarized in Figs. 6 and 9. They were calculated using the temperature profile in Table 2.

Fig. 9
figure 9

Apparent hydrodynamic diameters (\(d_\mathrm {H}\)) over time (t) of oleylamine capped gold nanoparticles in tetradecane on ground (1 g) and in microgravity (\(\mu\)g) at a constant temperature of 20 \({}^{\circ }\text {C}\) and while cooling from 70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\) in microgravity (\(\mu\)g). The DLS measurements at 1 g at 20 \({}^{\circ }\text {C}\) were repeated three times. One experiment at 20 \({}^{\circ }\text {C}\) and two experiments with a temperature drop (70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\)) were performed in \(\mu\)g

Full size image

One measurement was performed under microgravity conditions at a constant temperature of 20 \({}^{\circ }\text {C}\), and 8 sequential autocorrelation functions were recorded. An average mean residence time of 0.32 ms (\(\pm\, {0.07\,\mathrm{\text {m}\text {s}}}\)) and a corresponding apparent hydrodynamic diameter of 23 nm (\(\pm\, {5\,\mathrm{\text {n}\text {m}}}\)) were measured. The results are consistent with the expected particle diameter and the measurements on ground.

Table 3 Time-dependent mean residence times (\(\tau_\mathrm{_{Diff}}\)) of the nanoparticles according to DLS measurements after a temperature drop in microgravity. The apparent hydrodynamic diameters (\(d_\mathrm {H}\)) were calculated using the calculated evolution of temperature (\(T\)) and the corresponding viscosity (\(\eta\)), and refractive index (\(n\)) of the solvent. The uncertainties of the diameters were estimated by error propagation of the calculated temperature uncertainties (see text for details)
Full size table

Two experiments with temperature drops from 70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\) were performed in microgravity. Analysis of the autocorrelation functions indicated mean residence times ranging from 0.10 ms to 0.13 ms, corresponding to apparent hydrodynamic diameters from 27 nm to 15 nm, see Table 3. The uncertainty of the hydrodynamic diameters was estimated using error propagation by calculating the partial derivative of equation 4 in the SI with respect to the temperature. Excluding the value at 1 s, for which no valid temperature could be calculated in the previous section, uncertainties were well below 10 \({}^{\circ }\text {C}\). A mean average hydrodynamic diameter of 19 nm (\(\pm {3\,\mathrm{\text {n}\text {m}}}\)) was obtained. The apparent hydrodynamic diameters are in good agreement with the hydrodynamic diameter obtained at a constant temperature (20 \({}^{\circ }\text {C}\)). The results indicate that it will be possible to assess the growth of agglomerates to diameters of several hundred nanometers, with relative experimental uncertainties below 10 %.

In summary, hydrodynamic diameters calculated from measurements on ground and under microgravity conditions at constant temperatures of 20 \({}^{\circ }\text {C}\) were in good agreement, with a common mean value of \(\tau_\mathrm{_{Diff}}\) = 0.29 ms (± 0.01 ms) (on ground) and 0.32 ms (± 0.07 ms) (in microgravity) (see Fig. 9). The catapult launch (with approximately 30 g) did not significantly deteriorate the DLS measurements. The results of DLS measurements after rapid cooling were consistent both on ground and in microgravity, too (\(\tau_\mathrm{_{Diff}}\) = 0.08 ms to 0.19 ms on ground versus \(\tau_\mathrm{_{Diff}}\) = 0.10 ms to 0.17 ms in microgravity). Temperature measurement with thermocouples proved too imprecise, and we calculated the temperatures in the scattering volume directly from particle mobility in reference experiments.

Conclusion

The set-up introduced here is suitable for dynamic light scattering experiments in microgravity in a drop tower capsule after a catapult launch. The obtained results are in good accordance with the corresponding ground experiments. No influence of microgravity on nanoparticle diffusion was observed, but the accelerations affected the intercept of the autocorrelation functions.

We quantified the dynamics of nanoparticles with a gold core and an oleylamine shell in tetradecane at constant temperature and after rapid cooling. The diffusivities measured on ground (1 g) and in microgravity (\(\mu\)g) were in good agreement. Separate measurements of the liquid temperature during the experiments proved unreliable, but the temperature-dependent changes in particle dynamics during rapid cooling were similar both on ground and under microgravity conditions. The overall relative uncertainty in particle diameters as estimated from the variations of independent microgravity experiments and uncertainties in temperature measurements was on the order of 10%.

The set-up will be used in experiments on temperature-responsive nanoparticles that agglomerate below a known temperature. Our aim is an analysis of structure formation processes during the preparation of materials, in particular, particle-matrix nanocomposites. Comparisons between normal and microgravity conditions will indicate the role of gravity in the formation of such materials.

Experimental

Materials and Methods

Synthesis Gold Nanoparticles

All materials were used without any further purification. Gold nanoparticles with a core diameter of 7.8 nm and a hydrodynamic diameter of 21 nm were synthesized according to the established synthesis route of Wu et al. (2013) 1g chloroauric acid was dissolved in a mixture of 90 mL benzene (Sigma Aldrich, Darmstadt, Germany) and 90 mL oleylamine (Acros Organics, c18 content 80-90%, Geel, Belgium). The reaction mixture was stirred for 2.5 min and a solution of 400 mg borane tert-butylamine (Aldrich, 97 %, Darmstadt, Germany) in 10 mL benzene and 10 mL oleylamine was added. The gold-colored reaction mixture turned dark red immediately and was stirred for additional three hours. The particles were washed by precipitation with a mixture of methanol and ethanol and centrifuged. The supernatant was discarded and the particles were redispersed in 100 mL toluene. The washing step was repeated three times and finally the particles were redispersed in 100 mL tetradecane (abcr, 99 %, Karlsruhe, Germany).

Particle Characterization

The size of the core diameter was determined using small angle X-Ray measurements. The measurements were performed using a Xeuss 2.0 from Xenocs (Grenoble, France) working on K\(\alpha\) of a copper anode (\(\lambda = {0.154\,\mathrm{\text {n}\text {m}}}\)) equipped with a PILATUS Hybrid Photon Counting Detector from Dectris (Baden-Daettwil, Switzerland). A sample to detector distance of 1200 mm was chosen. The recorded 2D diffraction patterns were fully isotropic and thus radially averaged into 1D scattering curves with the FOXTROT v3.4.9 software. The data were analyzed using sasfit_0.94.11 (PSI, Villingen, Switzerland).

The gold concentration was determined using ICP-OES (inductive coupled plasma optical emission spectroscopy) with a Horiba Jobin Yvon Ultima 2 spectrometer (Oberursel, Germany) at an emission wavelength of 242.795 nm.

DLS Measurements

Dynamic light scattering measurements were performed with the set-up built in collaboration with LS Instruments (Fribourg, Switzerland) described above. A quartz glass cuvette was used as measurement cell. The cuvette was 46 mm and had a square cross-section with 12.5 mm outer side length. The inner diameter was 10 mm and the bottom had a thickness of 1.25 mm. All measurements were performed at a gold concentration of 0.72 mg mL\(^{-1}\) (± 0.03 mg mL\(^{-1}\)). The experiments were either performed at normal gravity conditions (1 g) or microgravity conditions (\(\mu\)g = 10–6 g). The autocorrelation functions were recorded using the 2D pseudo cross mode. The scattering volume is illuminated with a single laser beam but the intensity of the scattered light is detected with two detectors, resulting in a cross-correlation function. The autocorrelation functions were calculated and fitted with a simple exponential decay to obtain the mean residence time, which is used to calculate the hydrodynamic diameter by using the Stokes-Einstein relation, see SI. Mathematica 11.2 from Wolfram Research (Campaign, Illinois, USA) was used to calculate the temperatures of the scattering volume from the autocorrelation in reference experiments assuming constant hydrodynamic particle diameters.

The measurements were performed at a constant temperature of 20 \({}^{\circ }\text {C}\) or after rapid temperature drop from 70 \({}^{\circ }\text {C}\) to 10 \({}^{\circ }\text {C}\). A sample volume of 3 mL was injected at a rate of 1 mL s\(^{-1}\) at the start of the temperature drop. A dead volume of approximately 1 mL remained in the tubing, so that the final sample volume was 2 mL, with a standard deviation across multiple injections of approximately 50 \(\upmu\)L. The injection of the hot sample was effected using a Cetoni syringe pump (Korbussen, Germany). The temperature inside the measurement cell was measured using the type K GFT 300 UV thermocouple from Greisinger (Regenstauf, Germany). The data were analyzed by using Origin 2017 (Northampton, United States).

Microgravity Experiments

The microgravity experiments were performed in the drop tower at the ZARM Institute in Bremen, Germany. DLS instrument, liquid handling system, capsule computer and power supplies were integrated in a drop tower capsule and sealed inside a steel shell (Fig. 10). The capsule was filled with argon to prevent condensation during the cooling of the measurement cell. The sealed capsule was placed inside the catapult at the bottom of the drop tower. The tower was sealed and evacuated (\(\approx {2\,\mathrm{\text {h}}}\)), the sample was heated to 70 \({}^{\circ }\text {C}\). Injection of the sample into the measurement cell was initiated just before the catapult launch. The DLS measurements were triggered as soon as the capsule had entered microgravity.

Fig. 10
figure 10

Photograph of the dynamic light scattering instrument and the liquid handling set-up inside the open drop tower capsule (left) and of the sealed capsule (right)

Full size image