Hopf bifurcations in plasma layers between rigid planes in thermal magnetohydrodynamics, via a simple formula

Abstract

The phenomenon produced by the Hopf bifurcations is of notable importance. In fact, a Hopf bifurcation—guaranteeing the existence of an unsteady periodic solution of the linearized problem at stake—is also an optimum limit cycle candidate of the nonlinear associated problem and, if non linearly globally attractive, is an absorbing set and an effective limit cycle. The present paper deals with the onset of Hopf bifurcations in thermal magnetohydrodynamics (MHD). Precisely, it is devoted to characterization—via a simple formula—of the Hopf bifurcations threshold in horizontal plasma layers between rigid planes, heated from below and embedded in a constant transverse magnetic field. This problem, remarked clearly and notably by the Nobel Laureate Chandrasekhar (Nature 175:417–419, 1955), constitutes a difficulty met by him and—for plasma layers between rigid planes electricity perfectly conducting—is, as far as we know, still not removed. Let $m_0$ be the thermal conduction rest state and let $P_r, P_m, R, Q$, be the Prandtl, the Prandtl magnetic, the Rayleigh and the Chandrasekhar number, respectively. Recognized (according to Chandrasekhar) that the instability of $m_0$ via Hopf bifurcation can occur only in a plasma with $P_m>P_r$, in this paper it is shown that the Hopf bifurcations occur if and only if

$$\begin{aligned} Q>Q_c=\displaystyle \frac{4\pi ^2[1+P_r(\mu /2\pi )^4]}{P_m-P_r}, \end{aligned}$$

with $\mu =7.8532$. Moreover, the critical value of R at which the Hopf bifurcation occurs is characterized via the smallest zero of the second invariant of the spectrum equation governing the most destabilizing perturbation. The critical value of Q, in the free-rigid and rigid-free cases is shown to be $\displaystyle \frac{1}{4}$ of the previous value.

1 Introduction

Let L be a horizontal layer heated from below, filled by a plasma and embedded in a transverse uniform magnetic field and let $m_0$ denote the thermal conduction in L: the temperature field arising when the fluid is in rest and L is heated from below by a constant transverse gradient of temperature. The linear stability of $m_0$—in the scheme of the nonrelativistic thermal MHD—has been analyzed by Chandrasekhar in the early of 1950 (Chandrasekhar 1952, 1954) and it appeared in 1961 in the celebrated monograph (Chandrasekhar 1981). The Chandrasekhar results—for any type of boundaries (rigid–rigid, rigid–free, free–rigid, free–free)—have been since then a basic paradigm for all the subsequent researchers. In particular, he obtained a relevant inhibition of convection (stabilizing effect) by a magnetic field, verified successively experimentally (Nakagawa 1955). As concerns the occurring of the Hopf bifurcations at the onset of $m_0$ instability, he restricted himself mostly to the case when the fluid is confined between two free planes, showing that bifurcations can occur only if $P_m>P_r$ and envisaging the existence of a bound $Q_c(P_r,P_m)>0$ such that if and only if

$$\begin{aligned} P_m>P_r, \quad Q>Q_c \end{aligned}$$

Hopf bifurcations occur. He wrote: “there is no simple formula which gives $Q_c$ as function of $P_r$ and $P_m$” (see Chandrasekhar 1981, p. 184). Recently, Rionero (2019a) has shown that in the free–free case, this difficulty can be removed and that the Hopf bifurcations occur if and only if

$$\begin{aligned} P_m>P_r,\quad Q>Q_c=\displaystyle \frac{1+P_r}{P_m-P_r}\pi ^2. \end{aligned}$$

(1)

Let

$$\begin{aligned} {{\mathcal {P}}}(\lambda )=\lambda ^n+A_1\lambda ^{n-1}+\cdots +A_{n-1}\lambda +A_n=0 \end{aligned}$$

be the spectrum equation governing the linear stability of a steady state of a dynamical system and let the coefficients depend on a positive bifurcation parameter R and on the wave number $a^2$ of the perturbations in such a way that

$$\begin{aligned} A_k=0\,\,\Leftrightarrow \,\, R={{\mathcal {F}}}_k(a^2),\quad k\in \{1,2,3,\ldots , n\} \end{aligned}$$

(2)

with ${{\mathcal {F}}}_k(a^2)$ differentiable function of $a^2\in {{\mathbb {R}}}^+$. Taking into account that the instability can occur only via a zero eigenvalue ($\lambda =0\Leftrightarrow A_n=0$), or via a couple of pure imaginary eigenvalues ($\lambda _{1,2}=\pm i\omega$)—with i imaginary unit and $\omega =$const.$\in {{\mathbb {R}}}^+$ such that ${{\mathcal {P}}}(i\omega )=0$—the ideas that lead Rionero to the solution of the problem can be summarized as follows:

• 1. the application of the critical numbers

  $$\begin{aligned} R_{c_k}={{\mathcal {F}}}_k(a^2_{c_k})=\displaystyle \min _{a^2\in {{\mathbb {R}}}^+}{{\mathcal {F}}}_k(a^2) \end{aligned}$$

  (3)

  introduced by him, for $k<n$, about 10 years ago (Rionero 2012, 2013, 2019a, b, 2020; Flavin and Rionero 1996);

• 2. at the growing of R, from a stable state, the Hopf bifurcations occur if and only if exists at least a $k<n$ such that $R_{c_k}<R_{c_n}$, i.e. $A_k$ becomes zero before $A_n$: this is because—as it is well known—$A_k>0,\,\forall k\in \{1,2,\ldots , n\}$, is necessary for the linear stability, i.e. for letting all the eigenvalues have negative real part;

• 3. if the coefficients depend also on other parameters $Q, P_m,P_r$, then one has $R_{c_k}=R_{c_k}(Q,P_m,P_r)$ and the Hopf bifurcations can occur if and only if the inequality

  $$\begin{aligned} R_{c_k}(Q,P_m,P_r)<R_{c_n}(Q,P_m,P_r), \end{aligned}$$

  for at least a $k<n$, holds.

The free–free layers—of relevant interest in astrophysics applications—do not have the same interest in terrestrial—geophysics and industrial—applications when rigid boundary planes occur. In the present paper, aimed to remove the difficulty remarked by Chandrasekhar, in the presence of rigid boundary, we return to look for the Hopf bifurcations threshold in plasma layers between rigid planes, electricity perfectly conducting, via the guidelines (1)–(3).

In the case, at stake, the spectrum equation is

$$\begin{aligned} {{\mathcal {P}}}(\lambda )=\lambda ^3-{\texttt {I}}_1\lambda ^2+{\texttt {I}}_2\lambda -{\texttt {I}}_3=0, \end{aligned}$$

(4)

with the coefficients such that

$$\begin{aligned} {\texttt {I}}_k={\texttt {I}}_k(a^2, P_m,P_r, R, Q)\Leftrightarrow R={{\mathcal {F}}}_k(a^2,P_m,P_r,Q),\,\,\, k=1,2,3 \end{aligned}$$

(5)

with ${{\mathcal {F}}}_k$ differentiable function of $a^2,P_m,P_r,Q$. Choosing—as it is standard in the convection problems—R as bifurcation parameter, via (1)–(3) the properties (1)–(3) will be proven in the in the rest of the paper, with $A_2$ and $A_3$ given in (51) and (52).

Property 1

Let $m_0$ be linearly stable, for any wave number, at $R=0$. Then, if and only if

$$\begin{aligned} R_{c_2}(Q,P_m,P_r)<R_{c_3}(Q,P_m,P_r), \end{aligned}$$

(6)

an Hopf bifurcation occurs and occurs at $R_*\in ]0,R_{c_2}[$ lowest root of

$$\begin{aligned} {\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3=0, \end{aligned}$$

(7)

with $a^2=a^2_{c_2}$ and has the frequency

$$\begin{aligned} \omega (Q,P_m,P_r)=(\sqrt{{\texttt {I}}_2})_{(R=R_*)}^{(a^2=a^2_{c_2})}. \end{aligned}$$

(8)

It remains to satisfy (6). In other words, since $P_m$ and $P_r$ are structural parameters characterizing the fluid, the question is: in which fluids the Hopf bifurcations occur and for which values of Q? The answer is given by the following property.

Property 2

(Main result) If and only if

$$\begin{aligned} P_m>P_r,\quad Q\ge Q_c=\displaystyle \frac{4\pi ^2\left[ 1+P_r(\mu /2\pi )^4\right] }{P_m-P_r},\quad \mu =7.8532 \end{aligned}$$

(9)

$R_{c_2}<R_{c_3}$ holds.

Property 2 reduces the linear stability of $m_0$ to a standard type of stability in convection problem. In fact, setting

$$\begin{aligned} \xi =a^2+4\pi ^2,\quad \gamma =a^2+8a^2\pi ^2+\mu ^4, \end{aligned}$$

(10)

one has

Property 3

The steady state $m_0$ is linearly stable if and only if $P_m<P_r$ and

$$\begin{aligned} R<R_{c_2}=\displaystyle \min _{a^2\in \mathbb R^+}\displaystyle \frac{\xi ^4+\left[ 4\pi ^2QP_r+\gamma (P_m+P_r)\right] }{a^2},\quad Q\ge Q_c, \end{aligned}$$

(11)

or

$$\begin{aligned} R<R_{c_3}=\displaystyle \min _{a^2\in {{\mathbb {R}}}^+}\displaystyle \frac{(\gamma +4\pi ^2Q)\xi }{a^2},\,\, P_m<P_r,\,\,\forall Q \end{aligned}$$

(12)

or

$$\begin{aligned} R<R_{c_3},\,\,\,P_m>P_r,\,\,\, Q<Q_c. \end{aligned}$$

(13)

The plan of the paper is the following. Section 2 is devoted to preliminaries. After having recalled the $m_0$ thermal conduction rest state, the nonlinear MHD equations governing the perturbations to $m_0$ are introduced. In Sect. 3, the linear stability of $m_0$ is introduced and it is shown that it depends on the behaviour of the essential variables $w, h, \theta$ with w, h vertical perturbations to velocity and magnetic fields, respectively, and $\theta$ perturbation to the thermal field. The boundary conditions for $w,h,\theta$, in the presence of rigid perfect conductor boundary planes, are considered in Sect. 4. In Sect. 5, the functional spaces of $w,h,\theta$—admissible by the boundary conditions—are introduced and the Sturm–Liouville type problem associated with w is taken into account: w can be expanded either in a Fourier series of even or odd functions. In Sect. 6, it is shown that $m_0$ is linearly stable with respect to the perturbations $(w,h,\theta )$ with w even function. Successively, in Sect. 7, w odd is taken into account and the spectrum equation for the nth ($n\in {{\mathbb {N}}}$), Fourier components of the perturbations, is obtained. Property 1 is obtained in Sect. 8, while the other two are obtained in the subsequent section. The onset of Hopf bifurcations in the free-rigid and rigid-free cases is studied in Sect. 10. Final remarks are given in Sect. 11. The paper ends with an Appendix (Sect. 12) with three subsections concerning the invariants of $3\times 3$ matrices, the Hurwitz criterion and the linear and nonlinear energy decay.

2 Preliminaries

Misregarding the displacement currents, the equations governing the thermal MHD under the validity of the state equation for the density $\rho$,

$$\begin{aligned} \rho =\rho _0\left[ 1-\alpha \left( T-T_0\right) \right] , \end{aligned}$$

are (see Chandrasekhar 1981, chapter 5)

$$\begin{aligned} {\left\{ \begin{array}{ll} {\displaystyle \frac{\partial {{\mathbf{v }}}}{\partial t}+\mathbf{v }\cdot \nabla {\mathbf{v }}= -\nabla \frac{p}{\rho _0}+\left[ 1-\alpha \left( T-T_0\right) \right] {\mathbf{g }}+\frac{\mu }{\rho _0}\nabla {\mathbf{H }}\times {\mathbf{H }}+\nu \varDelta {\mathbf{v }}},\\ \\ {\displaystyle \frac{\partial {{\mathbf{H }}}}{\partial t}+\nabla \times \left( {\mathbf{H }}\times {\mathbf{v }} \right) =\eta \varDelta {\mathbf{H }}},\\ \\ {\displaystyle \frac{\partial T}{\partial t}+{\mathbf{v }}\cdot \nabla T=k\varDelta T},\\ \\ \nabla \cdot {\mathbf{H }}=\nabla \cdot {\mathbf{v }}=0, \end{array}\right. } \end{aligned}$$

with

$$\begin{aligned} \begin{array}{ll} {\mathbf{v }}&{} \text{ velocity } \text{ field }\\ {\mathbf{H }}&{}\text{ magnetic } \text{ field }\\ T &{} \text{ temperature } \text{ field }\\ T_0 &{} \text{ assigned } \text{ reference } \text{ temperature }\\ \nu &{} \text{ kinematic } \text{ viscosity }\\ k &{} \text{ thermal } \text{ diffusivity } \text{ coefficient }\\ \eta &{} \text{ resistivity }\\ \mu &{} \text{ magnetic } \text{ permeability }\\ g&{} \text{ gravitational } \text{ acceleration }\\ \alpha &{} \text{ coefficient } \text{ of } \text{ volume } \text{ expansion }\\ p &{} \text{ pressure } \text{ field }. \end{array} \end{aligned}$$

Let L be an infinite horizontal plasma layer, permeated by an imposed uniform magnetic field ${\mathbf{H }}_0$ normal to the layer, under the action of a vertical gravity field ${\mathbf{g }}=-g\mathbf{k}$, and in which a constant adverse temperature gradient $\beta$ is maintained. Let $d>0$, $\varOmega _d={{\mathbb {R}}}^2\times (0,d)$ and Oxyz be a Cartesian frame of reference with unit vectors ${\mathbf{i }}, {\mathbf{j }}, {\mathbf{k }}$, respectively. We assume that the plasma is confined between the planes $z=0$ and $z=d$, with assigned temperatures ${{{\tilde{T}}}}(x,y,0)={{{\tilde{T}}}}_0,$ ${{{\tilde{T}}}}(x,y,d)=-\beta d+{{{\tilde{T}}}}_0$. Here we consider the rest state $m_0=(\tilde{\mathbf{v }},\tilde{{\mathbf{H }}}, {{{\tilde{T}}}}, {{{\tilde{p}}}})= (0,H_0{\mathbf{k }}, -\beta z+{{{\tilde{T}}}}_0, {{{\tilde{p}}}})$ (thermal conduction), which is a solution to the stationary previous equations. In the sequel, ${\mathbf{x }}=(x,y,z)$ will denote the coordinates in the unity of length d and, in view of the symmetry with respect to the two bounding planes, the origin of z is fixed at the midway between the two planes and one has then $z\in \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right]$. The following symbols are also used:

$$\begin{aligned} \begin{array}{ll} {\mathbf{u }}=(u,v,w)&{} \text{ perturbation } \text{ in } \text{ the } \text{ velocity } \text{ field }\\ {\mathbf{h }}=(h_1,h_2,h)&{}\text{ perturbation } \text{ in } \text{ the } \text{ magnetic } \text{ field }\\ \theta &{} \text{ perturbation } \text{ in } \text{ the } \text{ temperature } \text{ field }\\ f_t=\displaystyle \frac{\partial f}{\partial t}, f_z=\displaystyle \frac{\partial f}{\partial z}&{} \varDelta _1=\displaystyle \frac{\partial ^2}{\partial x^2}+\displaystyle \frac{\partial ^2}{\partial y^2}, \, \varDelta =\varDelta _1+\displaystyle \frac{\partial ^2}{\partial z^2}\\ P_r=\displaystyle \frac{\nu }{k}, \; \text{ Prandtl } \text{ number }&{} P_m=\displaystyle \frac{\nu }{\eta }, \text{ magnetic } \text{ Prandtl } \text{ number }\\ R=\displaystyle \frac{g\alpha \beta d^4}{k\nu }, \text{ Rayleigh } \text{ number },&{}Q=\displaystyle \frac{\mu H_0^2 d^2}{4\pi \rho \nu \eta } \text{ Chandrasekhar } \text{ number }\\ \langle \cdot ,\cdot \rangle L^2\text{-scalar } \text{ product}, &{} \left\| \cdot \right\| L^2\text{-norm}. \end{array} \end{aligned}$$

The (non-dimensional) equations for a perturbation $(\mathbf{u} ,{\mathbf{h }},\theta , p_1)$ to $m_0$ are

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbf{u }}_t+{\mathbf{u }}\cdot \nabla {\mathbf{u }}-P_m{\mathbf{h }}\cdot \nabla {\mathbf{h }}=-\nabla p_1+\sqrt{R}\theta {\mathbf{k }}+\varDelta \mathbf{u} +\sqrt{Q} {\mathbf{h }}_z,\\ \\ \nabla \cdot {\mathbf{u }}=0,\\ \\ P_m({\mathbf{h }}_t+{\mathbf{u }}\cdot \nabla {\mathbf{h }}-{\mathbf{h }}\cdot \nabla {\mathbf{u }})=\sqrt{Q}{\mathbf{u }}_z+\varDelta {\mathbf{h }},\\ \\ \nabla \cdot {\mathbf{h }}=0,\\ \\ P_r(\theta _t+{\mathbf{u }}\cdot \nabla \theta )=\sqrt{R}w+\varDelta \theta . \end{array}\right. } \end{aligned}$$

(14)

To system (14), we add the kinematically admissible initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbf{u }}({\mathbf{x }},0)={\mathbf{u }}_0({\mathbf{x }}),\,\, {\mathbf{h }}({\mathbf{x }},0)={\mathbf{h }}_0({\mathbf{x }}),\,\theta ({\mathbf{x }},0)=\theta _0({\mathbf{x }}),\\ \nabla \cdot {\mathbf{u }}_0=\nabla \cdot {\mathbf{h }}_0=0, \end{array}\right. } \end{aligned}$$

(15)

where $\theta _0,{\mathbf{u }}_0,{\mathbf{h }}_0$ are assigned initial fields. As concerns the boundary conditions, we assume that the two planes bounding L are rigid and electricity perfectly conducting $\{$case B of Chandrasekhar (1981)$\}$ and at assigned temperatures. Then in view of the fluid viscosity and its complete adherence to the rigid boundaries, there will be no motions on the boundaries:

$$\begin{aligned} u=v=w=0,\quad \forall t\ge 0, z\in \left\{ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right\} . \end{aligned}$$

(16)

On the other hand, in view of the perfect electric conductibility, no magnetic field can cross the boundary

$$\begin{aligned} h_1=h_2=h=0,\quad \forall t\ge 0,\,z\in \left\{ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right\} . \end{aligned}$$

(17)

Finally, since the boundaries are at assigned temperatures, one has

$$\begin{aligned} \theta =0,\quad \forall t\ge 0,z\in \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right] . \end{aligned}$$

(18)

We assume that

• (i) the perturbations $(\nabla \pi ,u,v,w,\theta ,h_1,h_2,h)$ are periodic in the x and y directions of periods $2\pi /a_x,\, 2\pi /a_y$, respectively;

• (ii) $\varOmega =[0, 2\pi /a_x]\times [0,2\pi /a_y]\times \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right]$ is the periodicity cell;

• (iii) $u,v,w,\theta , h_1,h_2,h$ are such that together with all their first derivatives and second spatial derivatives are square integrable in $\varOmega ,\forall t\in {{\mathbb {R}}}^+$ and can be expanded in a Fourier series uniformly convergent in $\varOmega$.

We end by recalling that, along the time, many theorems of existence of weak and strong solution for MHD equations, under various circumstances, have been given. We confine ourselves to mentioning the recent papers concerning the existence of smooth solutions for large data $\{$see Lin et al. (2016), Ren et al. (2014), Zhou and Zhu (2018), Zhang (2019) and reference therein$\}$.

3 Essential fields

Neglecting the non-linear terms of (14), one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{{\mathbf{u }}}_t=-\nabla {{\hat{\pi }}}+\sqrt{R}{{{\hat{\theta }}}}{} \mathbf{k} +\varDelta \hat{{\mathbf{u }}}+\sqrt{Q} \hat{{\mathbf{h }}}_z,\\ \\ \nabla \cdot \hat{{\mathbf{u }}}=0,\,\,\,\nabla \cdot \hat{{\mathbf{h }}}=0,\\ \\ P_m\hat{{\mathbf{h }}}_t=\sqrt{Q}\hat{{\mathbf{u }}}_z+\varDelta \hat{{\mathbf{h }}},\\ \\ P_r{{{\hat{\theta }}}}_t=\sqrt{R}{{{\hat{w}}}}+\varDelta {{{\hat{\theta }}}} \end{array}\right. } \end{aligned}$$

(19)

under the initial-boundary conditions analogous to (15) and (16). Since the vertical component of the double curl of (19)$_1$ is

$$\begin{aligned} \displaystyle \frac{\partial }{\partial t}\varDelta \hat{w}=\sqrt{R}\varDelta _1{{{\hat{\theta }}}}+\varDelta \varDelta \hat{w}+\sqrt{Q}\varDelta \displaystyle \frac{\partial {{{\hat{h}}}}}{\partial z}, \end{aligned}$$

(20)

one has the linear system in the essential fields $({{{\hat{w}}}}, {{{\hat{h}}}}, {{{\hat{\theta }}}})$ in $\varOmega \times [0,\infty ]$

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial }{\partial t}\varDelta {{{\hat{w}}}}=\sqrt{R}\varDelta _1{{{\hat{\theta }}}}+\varDelta \varDelta {{{\hat{w}}}}+\sqrt{Q}\varDelta \displaystyle \frac{\partial {{{\hat{h}}}}}{\partial z},\\ \\ P_m\displaystyle \frac{\partial {{{\hat{h}}}}}{\partial t}=\sqrt{Q}\displaystyle \frac{\partial {{{\hat{w}}}}}{\partial z}+\varDelta {{{\hat{h}}}}, \qquad z\in \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right] \\ \\ P_r\displaystyle \frac{\partial {{{\hat{\theta }}}}}{\partial t}=\sqrt{R}\hat{w}+\varDelta {{{\hat{\theta }}}}, \end{array}\right. } \end{aligned}$$

(21)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} {{{\hat{w}}}}=\displaystyle \sum _{n=1}^\infty {{{\hat{w}}}}_n,\,\,{{{\hat{w}}}}_n={{{\tilde{w}}}}_n(t)F(x,y)F_{1n}(z),\\ \\ {{{\hat{h}}}}=\displaystyle \sum _{n=1}^\infty {{{\hat{h}}}}_n,\,\,{{{\hat{h}}}}_n={{{\tilde{h}}}}_n(t)F(x,y)F_{2n}(z),\\ \\ {{{\hat{\theta }}}}=\displaystyle \sum _{n=1}^\infty {{{\hat{\theta }}}}_n,\,\,{{{\hat{\theta }}}}_n={{{\tilde{\theta }}}}_n(t)F(x,y)F_{3n}(z),\\ \\ F(x,y)=\exp [i(a_xx+a_yy)], \end{array}\right. } \end{aligned}$$

(22)

which is the same class of perturbations considered in Chandrasekhar (1981) (normal modes). Therefore, setting

$$\begin{aligned} {{\hat{Z}}}=\displaystyle \frac{\partial {{{\hat{h}}}}}{\partial z}, \end{aligned}$$

(23)

in view of the linearity of (21) one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial }{\partial t}\varDelta {{{\hat{w}}}}_n=\sqrt{R}\varDelta _1{\hat{\theta _n}}+\varDelta \varDelta {{{\hat{w}}}}_n+\sqrt{Q}\varDelta {{{\hat{Z}}}}_n,\\ \\ P_m\displaystyle \frac{\partial }{\partial t} {{{\hat{Z}}}}_n=\sqrt{Q}\displaystyle \frac{\partial ^2{{{\hat{w}}}}_n}{\partial z^2}+\varDelta {{{\hat{Z}}}}_n,\,\,\,\,\,z\in \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right] \\ \\ P_r\displaystyle \frac{\partial {\hat{\theta _n}}}{\partial t}=\sqrt{R}\hat{w}_n+\varDelta {\hat{\theta _N}}, \end{array}\right. } \end{aligned}$$

(24)

with

$$\begin{aligned} {{{\hat{Z}}}}_n=\tilde{Z}_n(t)F\displaystyle \frac{\partial }{\partial z}F_{2n},\,\,\tilde{Z}_n(t)={{{\tilde{h}}}}_n(t). \end{aligned}$$

(25)

4 Additional boundary conditions

Requiring that (19)$_2$ continues to hold also for $z=\pm \displaystyle \frac{1}{2}$, the following supplementary boundary condition holds: $\displaystyle \frac{\partial w}{\partial z}=0,$ at $z=\pm \displaystyle \frac{1}{2}$.

In fact, (19)$_2$ implies

$$\begin{aligned} \displaystyle \frac{\partial {{{\hat{u}}}}}{\partial x}=\displaystyle \frac{\partial \hat{v}}{\partial y}=0,\qquad \forall t\ge 0, z=\pm \displaystyle \frac{1}{2}. \end{aligned}$$

Then

$$\begin{aligned} \nabla \cdot \hat{{\mathbf{u }}}=0,\,\,\left( \forall t\ge 0, z=\pm \displaystyle \frac{1}{2}\right) \Rightarrow \displaystyle \frac{\partial {{{\hat{w}}}}}{\partial z}=0,\,\,\left( \forall t\ge 0, z=\pm \displaystyle \frac{1}{2}\right) . \end{aligned}$$

(26)

Moreover, in view of (16) and (18), (21)$_2$ and (21)$_3$ imply, respectively,

$$\begin{aligned}&\varDelta {{{\hat{h}}}}=0, \qquad \forall t\ge 0, \quad z=\pm \displaystyle \frac{1}{2}, \end{aligned}$$

(27)

$$\begin{aligned}&\varDelta {{{\hat{\theta }}}}=0,\qquad \forall t\ge 0, \quad z=\pm \displaystyle \frac{1}{2}. \end{aligned}$$

(28)

Collecting all the boundary conditions, one has

$$\begin{aligned} {{{\hat{h}}}}_1={{{\hat{h}}}}_2=\hat{w}=\displaystyle \frac{\partial {{{\hat{w}}}}}{\partial z}={{{\hat{h}}}}=\varDelta \hat{h}={{{\hat{\theta }}}}=\varDelta {{{\hat{\theta }}}}=0,\qquad \forall t\ge 0, z=\pm \displaystyle \frac{1}{2}. \end{aligned}$$

(29)

5 Admissible perturbations

One easily verifies that (29) is verified by (22), on choosing $\forall z\in \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right]$

$$\begin{aligned} {\left\{ \begin{array}{ll} F_{2n}=\displaystyle \frac{1}{2n\pi }\left( \cos n\pi -\cos 2 n\pi z\right) ,\\ \\ F_{3n}=\sin 2 n\pi z=Z_{2n}, \end{array}\right. } \end{aligned}$$

(30)

and $F_{1n}$ solution of the Sturm–Liouville type problem

$$\begin{aligned} {\left\{ \begin{array}{ll} f^{(iv)}=\mu ^4 f,\quad z\in \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right] ,\\ \\ f=f^\prime =0,\quad z=\pm \displaystyle \frac{1}{2} \end{array}\right. } \end{aligned}$$

(31)

whose solutions are given by the set of the even orthogonal functions $\{$Chandrasekhar (1981), p. 635$\}$

$$\begin{aligned} {\left\{ \begin{array}{ll} f_n=\displaystyle \frac{\cosh \mu _nz}{\cosh \mu _n}-\displaystyle \frac{\cos \mu _nz}{\cos \mu _n},\quad z\in \left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right] ,\\ \\ \mu _n: \tanh \displaystyle \frac{\mu _n}{2}+\tan \displaystyle \frac{\mu _n}{2}=0 \end{array}\right. } \end{aligned}$$

(32)

and the set of the odd orthogonal functions

$$\begin{aligned} {\left\{ \begin{array}{ll} f_n^*=\displaystyle \frac{\sinh \mu _nz}{\sinh \mu _n}-\displaystyle \frac{\sin \mu _nz}{\sin \mu _n},\\ \\ \mu _n: \coth \displaystyle \frac{\mu _n}{2}-\cot \displaystyle \frac{\mu _2}{2}=0. \end{array}\right. } \end{aligned}$$

(33)

It is found that Chandrasekhar (1981)

$$\begin{aligned} \left\{ \begin{array}{l} \mu _1=4.73004074,\,\,\mu _2=10.99560784,\,\,\mu _3=17.27875066,\\ \\ \mu _4=23.5619449,n>4\Rightarrow \mu _n\Rightarrow \left( 2n-\displaystyle \frac{1}{2}\right) \pi , n\rightarrow \infty \end{array}\right. \end{aligned}$$

(34)

in the case (32) and by

$$\begin{aligned} \left\{ \begin{array}{l} \mu _1=7.85320462,\,\,\mu _2=14.13716549,\,\,\mu _3=26.70353726,\\ \\ \mu _4=20.42035225,n>4\Rightarrow \mu _n\Rightarrow \left( 2n+\displaystyle \frac{1}{2}\right) \pi , n\rightarrow \infty \end{array}\right. \end{aligned}$$

(35)

in the case (33).

6 Stability with ${{{\hat{w}}}}$ even

In view of

$$\begin{aligned} {\left\{ \begin{array}{ll} \varDelta _1=-a^2,\,\,a^2=a^2_x+a^2_y,\,\,\varDelta =a^2+\displaystyle \frac{\partial ^2}{\partial z^2},\,\,\displaystyle \frac{\partial ^2}{\partial z^2}\varDelta =-a^2\displaystyle \frac{\partial ^2}{\partial z^2}+\displaystyle \frac{\partial ^4}{\partial z^4},\\ \\ \varDelta \varDelta =\left( -a^2+\displaystyle \frac{\partial ^2}{\partial z^2}\right) =\left( a^2-2a^2\displaystyle \frac{\partial ^2}{\partial z^2}+\displaystyle \frac{\partial ^4}{\partial z^4}\right) , \end{array}\right. } \end{aligned}$$

(36)

one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \varDelta \varDelta {{{\hat{w}}}}_n={{{\tilde{w}}}}_n\varDelta \varDelta (FF_{1n})={{{\tilde{w}}}}_n F\left( a^4-2a^2\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}+\displaystyle \frac{\mathrm{{d}}^4}{\mathrm{{d}}z^4}\right) F_{1n},\\ \\ \varDelta {{{\hat{Z}}}}_n=-\xi _n \hat{Z}_n,\,\,\varDelta {\hat{\theta _n}}=-\xi _n{\hat{\theta _n}},\,\,\xi _n=a^2+4n^2\pi ^2 \end{array}\right. } \end{aligned}$$

(37)

and (24) implies

$$\begin{aligned} {\left\{ \begin{array}{ll} \left[ \left( -a^2+\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}\right) \displaystyle \frac{\mathrm{{d}}}{\mathrm{{d}}t}-\left( a^4-2a^2\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}+\displaystyle \frac{\mathrm{{d}}^4}{\mathrm{{d}}z^4}\right) \right] F_{1n}{{{\tilde{w}}}}_n=-\sin 2n\pi z\left( a^2\sqrt{R}{{{\tilde{\theta }}}}_n+\xi _n \sqrt{Q}{{{\tilde{Z}}}}_n\right) , \\ \\ \sin 2n\pi z\left[ \displaystyle \frac{\mathrm{{d}}{{{\tilde{Z}}}}_n}{\mathrm{{d}}t}+\displaystyle \frac{\xi _n}{P_m}{{{\tilde{Z}}}}_n\right] =\displaystyle \frac{\sqrt{Q}}{P_m}{{{\tilde{w}}}}_n F^{\prime \prime }_{1n},\\ \\ \sin 2n\pi z\left( \displaystyle \frac{\mathrm{{d}}{{{\tilde{\theta }}}}_n}{\mathrm{{d}}t}+\displaystyle \frac{\xi _n{{{\tilde{\theta }}}}_n}{P_r}\right) =\displaystyle \frac{\sqrt{R}}{P_r}F_{1n}\tilde{w}_n. \end{array}\right. } \end{aligned}$$

(38)

In the case $F_{1n}=f_n$, the functions

$$\begin{aligned}&F_{1n},\quad \left( -a^2+\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}\right) F_{1n},\,\,\left( a^4-2a^2\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}\right. \nonumber \\&\quad \left. +\displaystyle \frac{\mathrm{{d}}^4}{\mathrm{{d}}z^4}\right) F_{1n}=\left( a^4+\mu ^4_n+\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}\right) F_{1n} \end{aligned}$$

(39)

are even in $\left[ -\displaystyle \frac{1}{2},\displaystyle \frac{1}{2}\right]$ and one has

$$\begin{aligned} \langle F_{1n},\sin 2m\pi z\rangle =\langle F^{\prime \prime }_{1n}, \sin 2m\pi z\rangle =0,\quad \forall m\in {{\mathbb {N}}}. \end{aligned}$$

(40)

Then (38) implies

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}{{{\tilde{Z}}}}_n}{\mathrm{{d}}t}=-\displaystyle \frac{\xi _n}{P_m}{{{\tilde{Z}}}}_n,\quad \displaystyle \frac{\mathrm{{d}}{{{\tilde{\theta }}}}_n}{\mathrm{{d}}t}=-\displaystyle \frac{\xi _n}{P_r}{{{\tilde{\theta }}}}_n, \end{aligned}$$

i.e.

$$\begin{aligned} {{{\tilde{Z}}}}_n=Z_n^{(0)} e^{-\xi _n/P_m \, t},\quad \tilde{\theta }_n={{{\tilde{\theta }}}}_n^{(0)}e^{-\xi _n/P_r\, t}, \end{aligned}$$

for any initial data and $P_m, P_r, \sqrt{R}$ and $\sqrt{Q}$. In view of (38)$_2$ the exponential decay of ${{{\tilde{w}}}}$—for any initial data—immediately follows. In Appendix, the linear and nonlinear $L^2(\varOmega )$-energy decay is investigated.

7 Stability with ${{{\hat{w}}}}$ odd

Setting

$$\begin{aligned} A_n=\langle \sin 2 n\pi z, f^*_n\rangle ,\quad B_n=\left\| \sin 2n\pi z\right\| ^2, \end{aligned}$$

(41)

one has

$$\begin{aligned} \bigg \langle \sin 2n \pi z, \displaystyle \frac{\mathrm{{d}}^2 f^*_n}{\mathrm{{d}}z^2}\bigg \rangle= & {} -2n\pi \bigg \langle \cos 2n\pi z, \displaystyle \frac{\mathrm{{d}}}{\mathrm{{d}}z}f^*_n\bigg \rangle \\= & {} -4n^2\pi ^2A_n,\\ \bigg \langle \left( a^4-2a^2\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}+\mu ^4_n\right) f^*_m, \sin 2 n\pi z\bigg \rangle= & {} (a^4+8a^2n^2\pi ^2+\mu ^4_n)A_n,\\ \bigg \langle \left( -a^2+\displaystyle \frac{\mathrm{{d}}^2}{\mathrm{{d}}z^2}\right) f^*_n,\sin 2 n\pi z\bigg \rangle= & {} -\xi _nA_n. \end{aligned}$$

Then (38) gives

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}}{\mathrm{{d}}t}\left( \begin{array}{l} {{{\tilde{w}}}}_n\\ {{{\tilde{Z}}}}_n\\ {{{\tilde{\theta }}}}_n \end{array} \right) =L_n\left( \begin{array}{l} {{{\tilde{w}}}}_n\\ {{{\tilde{Z}}}}_n\\ {{{\tilde{\theta }}}}_n \end{array} \right) , \end{aligned}$$

(42)

with $L_n$ given by

$$\begin{aligned} L_n=\left\| \begin{array}{ccc} -\displaystyle \frac{\alpha _n}{\xi _n}&{}\displaystyle \frac{\sqrt{Q}B_n}{A_n}&{}\displaystyle \frac{a^2\sqrt{R}B_n}{A_n\xi _n}\\ -\displaystyle \frac{4n^2\pi ^2 \sqrt{Q}A_n}{P_m B_n}&{}-\displaystyle \frac{\xi _n}{P_m}&{}0\\ \displaystyle \frac{\sqrt{R}A_n}{P_rB_n}&{}0&{}-\displaystyle \frac{\xi _n}{P_r} \end{array} \right\| \end{aligned}$$

(43)

and

$$\begin{aligned} \alpha _n=a^4+8a^2n^2\pi ^2+\mu ^4_n. \end{aligned}$$

(44)

The spectrum equation of (42) is

$$\begin{aligned} \lambda ^3-{\texttt {I}}_{1n}\lambda ^2+{\texttt {I}}_{2n}\lambda -{\texttt {I}}_{3n}=0, \end{aligned}$$

(45)

with the characteristic values ${\texttt {I}}_{rn}, (r=1,2,3)$, given by $\{$see Appendix $\}$

$$\begin{aligned} {\left\{ \begin{array}{ll} {\texttt {I}}_{1n}=-\left( \displaystyle \frac{\alpha _n}{\xi _n}+\displaystyle \frac{P_m+P_r}{P_mP_r}\xi _n\right) ,\\ \\ {\texttt {I}}_{2n}=\displaystyle \frac{1}{P_r\xi _n}\left[ (4n^2\pi ^2Q\xi _n)\displaystyle \frac{P_r}{P_m}+\displaystyle \frac{1}{P_m}\xi ^3_n+\alpha _n\xi _n\left( 1+\displaystyle \frac{P_r}{P_m}\right) -a^2R\right] ,\\ \\ {\texttt {I}}_{3n}=\displaystyle \frac{1}{P_rP_m}\left[ a^2R-(\alpha _n+4n^2\pi ^2Q)\xi _n\right] . \end{array}\right. } \end{aligned}$$

(46)

8 Proof of property 1

The following properties hold.

• (i) Only if

  $$\begin{aligned} {\texttt {I}}_{1n}<0,\,\,\,{\texttt {I}}_{2n}>0,\,\,\,{\texttt {I}}_{3n}<0,\,\,\,\forall (a^2,n)\in {{\mathbb {R}}}^+\times {{\mathbb {N}}}, \end{aligned}$$

  (47)

  the roots of (44) (eigenvalues of L) have all negative real parts (Appendix);

• (ii) if and only if the Liénard–Chipart conditions

  $$\begin{aligned} {\texttt {I}}_{1n}<0,\,\,\,{\texttt {I}}_{2n}>0,\,\,\,{\texttt {I}}_{3n}<0,\,\,\, {\texttt {I}}_{1n}{\texttt {I}}_{2n}-{\texttt {I}}_{3n}<0,\,\, \forall n\in {{\mathbb {N}}} \end{aligned}$$

  (48)

  hold, all the eigenvalues have negative real part (Appendix 79).

Since $\xi _n=a^2+4n^2\pi ^2$, ${\texttt {I}}_{1n}, {\texttt {I}}_{3n}$ are decreasing functions of n while ${\texttt {I}}_{2n}$ is an increasing function of n. Therefore, to satisfy i), it is necessary and sufficient to consider $n=1$ (most destabilizing perturbation). Setting

$$\begin{aligned} {\texttt {I}}_{k1}={\texttt {I}}_k,\quad \xi =\xi _1=a^2+4\pi ^2,\quad \alpha _1=\gamma \end{aligned}$$

(49)

(45) reduces to (4) with

• 1. ${\texttt {I}}_1$ independent of Q and R given by

  $$\begin{aligned} {\left\{ \begin{array}{ll} {\texttt {I}}_1=-\left( \displaystyle \frac{\gamma }{\xi }+\displaystyle \frac{P_m+P_r}{P_mP_r}\right) <0,\\ \\ \gamma =a^4+8a^2\pi ^2+\mu ^4; \end{array}\right. }\end{aligned}$$

  (50)

• 2. ${\texttt {I}}_2$ is a decreasing function of $R, \forall (a^2, P_m, P_r, Q)\in ({{\mathbb {R}}}^+)^4$ and

  $$\begin{aligned} {\texttt {I}}_2=0\Leftrightarrow {\left\{ \begin{array}{ll} R=R_2=\displaystyle \frac{F_2}{a^2},\\ F_2=\xi ^3+\left[ 4\pi ^2QP_r+\gamma (P_m+P_r)\right] \xi ; \end{array}\right. }\end{aligned}$$

  (51)

• 3. ${\texttt {I}}_3$ is an increasing function of $R,\,\forall (a^2, P_m, P_r, Q)\in ({{\mathbb {R}}}^+)^4$ and

  $$\begin{aligned} {\texttt {I}}_3=0\Leftrightarrow {\left\{ \begin{array}{ll} R=R_3=\displaystyle \frac{F_3}{a^2},\\ \\ F_3=(\gamma +4\pi ^2Q)\xi . \end{array}\right. } \end{aligned}$$

  (52)

Property 4

Let

$$\begin{aligned} \exists (a^2, P_m, P_r, Q, R)\in ({{\mathbb {R}}}^+)^5 \Rightarrow {\texttt {I}}_2>0, {\texttt {I}}_3<0. \end{aligned}$$

(53)

Then at $(a^2, P_m, P_r, Q, R)$ an Hopf bifurcation occurs if and only if one has that

$$\begin{aligned} {\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3=0 \end{aligned}$$

(54)

and has the frequency $\omega ^2={\texttt {I}}_2=\displaystyle \frac{{\texttt {I}}_3}{{\texttt {I}}_1}$.

Proof

Let (4) admit the couple of pure imaginary roots $\lambda =\pm i \omega$. Then one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega (\omega ^2-{\texttt {I}}_2)=0,\\ \\ {\texttt {I}}_1\omega ^2-{\texttt {I}}_3=0. \end{array}\right. } \end{aligned}$$

(55)

Vice versa, let (54) holds. Then (4) becomes

$$\begin{aligned} \lambda ^3-{\texttt {I}}_1\lambda ^2+{\texttt {I}}_2\lambda -{\texttt {I}}_1{\texttt {I}}_3=0, \end{aligned}$$

i.e.

$$\begin{aligned} (\lambda -{\texttt {I}}_1)(\lambda ^2+{\texttt {I}}_2)=0 \end{aligned}$$

(56)

having the roots $\lambda _1={\texttt {I}}_1,\,\lambda _2=i\sqrt{{\texttt {I}}_2},\,\lambda _3=-i\sqrt{{\texttt {I}}_2}$. $\square$

Property 5

At $R=0$, $m_0$ is stable for any $a^2$.

Proof

In fact, (42) reduces to

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}}{\mathrm{{d}}t}\left( \begin{array}{l} {{{\tilde{w}}}}_1\\ {{{\tilde{Z}}}}_1 \end{array} \right) =\left\| \begin{array}{cc} -\gamma &{}\sqrt{Q}\displaystyle \frac{B_1}{A_1}\\ -\displaystyle \frac{4\pi ^2\sqrt{Q}A_1}{P_mB_1}&{}-\displaystyle \frac{\xi _n}{P_m} \end{array}\right\| \left( \begin{array}{l} {{{\tilde{w}}}}_1\\ {{{\tilde{Z}}}}_1 \end{array} \right) ,\,\, \displaystyle \frac{\mathrm{{d}}{{{\tilde{\theta }}}}_1}{\mathrm{{d}}t}=-\displaystyle \frac{\xi }{P_r}{{{\tilde{\theta }}}}_1. \end{aligned}$$

(57)

Being $\gamma +4\pi ^2Q>0,\,\forall a^2$, the linear stability of $m_0$ $\forall a^2$, immediately follows. $\square$

Property 6

The critical numbers $R_{c_2}, R_{c_3}$ are given by

$$\begin{aligned} R_{c_2}= & {} \displaystyle \min _{a^2\in {{\mathbb {R}}}^+} \displaystyle \frac{\xi ^3+\left[ 4\pi ^2QP_r+\gamma (P_r+P_m)\right] \xi }{a^2},\,\,\nonumber \\ R_{c_3}= & {} \displaystyle \min _{a^2\in \mathbb {R}^+}\displaystyle \frac{(\gamma +4\pi ^2Q)\xi }{a^2}. \end{aligned}$$

(58)

Proof

In view of

$$\begin{aligned} F_2>0,\,\,\forall a^2\in {{\mathbb {R}}}^+,\,\,\displaystyle \lim _{a^2\rightarrow 0} \displaystyle \frac{F_2}{a^2}=\displaystyle \lim _{a^2\rightarrow \infty }\displaystyle \frac{F_2}{a^2}=\infty , \end{aligned}$$

(59)

it follows that exists a finite wave number $a^2_{c_2}$, root of $a^2\displaystyle \frac{\mathrm{{d}}F_2}{\mathrm{{d}}a^2}=F_2$, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} R_{c_2}=\left\{ (a^2_{c_2}+4\pi ^2)^3+\left[ 4\pi ^2QP_r+\gamma _{c_2}(P_r+P_m)\right] (a^2_{c_2}+4\pi ^2)\right\} (a^2_{c_2})^{-1},\\ \\ \gamma _{c_2}=(\gamma )_{(a^2=a^2_{c_2})}. \end{array}\right. } \end{aligned}$$

(60)

Analogously one has that exists a finite wave number $a^2_{c_3}$—root of the equation $a^2\displaystyle \frac{\mathrm{{d}}F_3}{\mathrm{{d}}a^2}=F_3$—such that

$$\begin{aligned} R_{c_3}=\displaystyle \frac{(\gamma _{c_3}+4\pi ^2\sqrt{Q})\xi }{a^2_{c_3}},\,\,\,\gamma _{c_3}=(\gamma )_{(a^2=a^2_{c_3})}. \end{aligned}$$

(61)

$\square$

Property 7

Property 1 holds.

Proof

In view of properties 4 and 5, it remains only to show its sufficiency. Let then (6) holds. On the other hand, the stability of $m_0$ at $R=0$ for any wave number, implies—in view of the Liénard–Chipart conditions

$$\begin{aligned} {\texttt {I}}_1<0,\,\,{\texttt {I}}_2>0,\,\,{\texttt {I}}_3<0,\,\,{\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3<0,\,\,\text{ at } R=0. \end{aligned}$$

(62)

But, at $\{R=R_{c_2}, a^2=a^2_{c_2}\}$, one has

$$\begin{aligned} {\texttt {I}}_1<0,\,\,{\texttt {I}}_2=0,\,\,{\texttt {I}}_3<0,\,\,{\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3=-{\texttt {I}}_3>0; \end{aligned}$$

(63)

therefore,

$$\begin{aligned} ({\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3)_{(R=0)}^{(a^2=a^2_{c_2})}<0,\,\,\, ({\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3)_{(R=R_{c_2})}^{(a^2=a^2_{c_2})}>0 \end{aligned}$$

(64)

implies the existence in $]0, R_{c_2}[$ of an $R_*$ such that

$$\begin{aligned} ({\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3)_{(R=R_*)}^{(a^2=a^2_{c_2})}=0. \end{aligned}$$

(65)

$\square$

9 Proof of Properties 2 and 3

Property 8

In plasma layers between two electricity perfectly conducting rigid planes, the MHD-Hopf bifurcations occur only in the plasma with $P_m>P_r$ and only for Q sufficiently high. Precisely if and only if

$$\begin{aligned} P_r<P_m,\quad Q>Q_c=\displaystyle \frac{4\pi ^2}{P_m-P_r}\left[ 1+P_r\left( \displaystyle \frac{\mu }{2\pi }\right) ^4\right] ,\,\mu =7.8532.\end{aligned}$$

(66)

Proof

(66) are necessary. In fact,

$$\begin{aligned} P_r\ge P_m\Rightarrow R_{c_2}>R_{c_3},\quad \forall Q>0. \end{aligned}$$

(67)

Let then $P_r<P_m$ and set

$$\begin{aligned} \varPsi =\displaystyle \frac{P_m}{\xi _1}(F_2-F_3)=(P_r-P_m)4\pi ^2Q+\xi ^2_1+P_r \gamma . \end{aligned}$$

(68)

In view of

$$\begin{aligned} \displaystyle \frac{\partial \varPsi }{\partial a^2}=2\xi _1>0, \end{aligned}$$

(69)

one has

$$\begin{aligned} (\varPsi )_{(a^2=0)}\ge 0\Rightarrow \displaystyle \frac{F_2}{a^2}>\displaystyle \frac{F_3}{a^2},\quad \forall a^2>0, \end{aligned}$$

(70)

which implies $R_{c_2}>R_{c_3}$. Therefore, $(\varPsi )_{(a^2=0)}<0$, i.e. (66)$_2$ is necessary too. Vice versa, let (66) hold. Then

$$\begin{aligned} {\left\{ \begin{array}{ll} (\varPsi )_{(a^2=0)}<0,\quad \displaystyle \frac{\partial \varPsi }{\partial a^2}>0,\quad \forall a^2,\\ \\ \displaystyle \lim _{a^2\rightarrow \infty }\varPsi =\infty \end{array}\right. } \end{aligned}$$

(71)

implies the existence of a positive number $a^2_*$ such that

$$\begin{aligned} \displaystyle \frac{F_2}{a^2}\le (\ge ) \displaystyle \frac{F_3}{a^2}, \end{aligned}$$

(72)

according to $a^2\le (\ge ) a^2_*$, respectively, and one has

$$\begin{aligned} R_{c_2}=\displaystyle \min _{a^2\in {{\mathbb {R}}}^+} \displaystyle \frac{F_2}{a^2}<\displaystyle \min _{a^2<a^2_*} \displaystyle \frac{F_3}{a^2}=R_{c_3}. \end{aligned}$$

(73)

$\square$

Property 9

Property 3holds.

Proof

Property defines precisely the frontier between the onset of Hopf bifurcation (and hence the instability for $R\ge R_{c_2}$) and the onset of steady bifurcation (and hence the instability for $R\ge R_{c_3}$). Property 3 immediately follows. $\square$

Remark 1

We remark that $a^2_*$ is obtained requiring $(\varPsi )_{(a^2=a^2_*)}=0\Leftrightarrow (F_2-F_3)_{(a^2=a^2_*)}=0$. One has

$$\begin{aligned} (a^2_*+4\pi ^2)^2+(a^4_*+8a^2_*\pi ^2+\mu ^4_1)P_r=(P_m-P_r)4\pi ^2Q, \end{aligned}$$

i.e.

$$\begin{aligned} (1+P_r)(a^2_*+4\pi ^2)^2=(P_m-P_r)4\pi ^2Q-P_r[\mu ^4_1-(4\pi ^2)^2]. \end{aligned}$$

Therefore,

$$\begin{aligned} (a^2_*+4\pi ^2)^2= & {} \displaystyle \frac{(P_m-P_r)4\pi ^2Q-P_r[\mu ^4_1-(4\pi ^2)^2]}{1+P_r}\\> & {} (P_m-P_r)4\pi ^2Q_c-P_r[\mu ^4_1-(4\pi ^2)2] \end{aligned}$$

and—in view of (66)$_2$—is guaranteed

$$\begin{aligned} (a^2_*+4\pi ^2)^2>(4\pi ^2)^2+P_r\mu ^4_1-P_r\mu ^4_1+(4\pi ^2)^2=2(4\pi ^2)^2 \end{aligned}$$

and hence

$$\begin{aligned} a^2_*>4\sqrt{2}\pi ^2-4\pi ^2=(\sqrt{2}-1)4\pi ^2. \end{aligned}$$

Remark 2

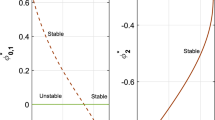
In Fig. 1, the behaviour of $Q_c$ at the increasing of $P_m(>P_r)$ for $P_r\in \{1,2,4\}$ is evaluated.

In Fig. 2, the behaviour of the ratio ${{{{\mathcal {R}}}}}$,

$$\begin{aligned} {{{{\mathcal {R}}}}}=\frac{4\left[ 1 + Pr(\mu /2\pi )^4 \right] }{1+Pr}, \;\;\;\mu =7.8532, \end{aligned}$$

between the critical values of Q in the rigid–rigid case (given by (66)) and free–free case (given by (1)) at the growing of $P_r$ is considered.

Fig. 1

Asymptotic behaviour of $Q_c$ for $P_r=1$ (continuous line); $P_r=2$ (dashed line); $P_r=4$ (dotted line)

Fig. 2

Asymptotic behaviour of ${{\mathcal {R}}}$ versus $P_r$

10 Hopf bifurcation threshold in the rigid–free and free–rigid cases in MHD

In view of

$$\begin{aligned} f^*_n(0)=(\sin 2n\pi z)_{(z=0)}=0, \end{aligned}$$

it follows that $w_n,\theta _n,Z_n$ verify the conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n=w^\prime _n=\theta _n=Z_n=0,\quad z=\displaystyle \frac{1}{2},\\ \\ w_n=\theta _n=Z_n=0,\quad z=0, \end{array}\right. } \end{aligned}$$

(74)

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n=\theta _n=Z_n=0,\quad z=0,\\ \\ w_n=w^\prime _n=\theta _n=Z_n=0,\quad z=-\displaystyle \frac{1}{2}. \end{array}\right. } \end{aligned}$$

(75)

One easily realizes that (74) and (75) are, respectively, the boundary MHD conditions for a layer of depth $\displaystyle \frac{1}{2}$ in the free–rigid and rigid–free cases respectively, when the rigid plane bounding the layer is electricity perfectly conducting. Therefore, the results of the previous sections can be used but taking into account of the different depth. The Rayleigh and Chandrasekhar numbers of the free–rigid and rigid–free cases, ${{{\bar{R}}}}, {{{\bar{Q}}}}$ are defined by

$$\begin{aligned} {{\bar{R}}}=\displaystyle \frac{g\alpha \beta \left( \displaystyle \frac{d}{2}\right) ^4}{k\nu }=\displaystyle \frac{1}{16}R,\qquad \bar{Q}=\displaystyle \frac{\mu H^2\left( \displaystyle \frac{d}{2}\right) ^2}{4\pi \rho \nu }=\displaystyle \frac{1}{4}Q_*, \end{aligned}$$

(76)

which implies

$$\begin{aligned} {\left\{ \begin{array}{ll} \sqrt{{{{\bar{R}}}}_{c_i}}=\displaystyle \frac{1}{16}\sqrt{R_{c_i}},\quad (i=1,2,3,4),\\ \\ {{{\bar{Q}}}}=\displaystyle \frac{1}{4}Q,\,\,{{{\bar{Q}}}}_c=\displaystyle \frac{1}{4}Q_c. \end{array}\right. } \end{aligned}$$

(77)

11 Discussion, final remarks and perspectives

• 1. The onset of Hopf bifurcations in plasma horizontal layers between two perfect conductor rigid planes and embedded in a constant transverse magnetic field, in non-relativistic thermal MHD, is investigated.

• 2. The threshold of Hopf bifurcation characterization—via a simple formula—problem introduced by Chandrasekhar Chandrasekhar (1981)—is solved by introducing a critical value $R_{c_2}$ for the Rayleigh number and requiring $R_{c_2}<R_{c_3}$ with $R_{c_3}$ steady convection critical value.

• 3. The property of each coefficient of the spectrum equation to drive the instability and the type of bifurcation, is shown and applied.

• 4. The threshold $Q_c$ that, in the structural assumption $P_r<P_m$, the Chandrasekhar number Q has to cross for the onset of Hopf bifurcations, is given by (66) in the rigid–rigid case and by (10.4) in the rigid–free and free–rigid cases.

• 5. The onset of Hopf bifurcations in rotating layers between perfect conductor rigid planes, in MHD and in presence of Hall currents, is under investigation.

Appendix

1.1 Characteristic values of a $3\times 3$ matrix

Let ${{\mathcal {L}}}=\left\| a_{ij}\right\|$ be a quadratic matrix of order 3, with real entries. The algebraic cubic equation

$$\begin{aligned} P(\lambda )=0, \end{aligned}$$

(78)

with

$$\begin{aligned} P(\lambda )=\left| \begin{array}{ccc} a_{11}-\lambda &{}a_{12}&{}a_{13}\\ a_{21}&{}a_{22}-\lambda &{} a_{23}\\ a_{31}&{}a_{32}&{}a_{33}-\lambda \end{array} \right| , \end{aligned}$$

(79)

is the spectral equation of ${{\mathcal {L}}}$ and its roots are the eigenvalues of ${{\mathcal {L}}}$. $P(\lambda )$, being a polynomial of 3 degree, can be written (McLaurin)

$$\begin{aligned} P(\lambda )=\displaystyle \sum _{n=1}^3 \displaystyle \frac{P(0)^{(n)}}{n!}\lambda ^n. \end{aligned}$$

(80)

In view of

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{{d}}P}{\mathrm{{d}}\lambda }=-\left[ \left| \begin{array}{cc} a_{22}-\lambda &{}a_{23}\\ a_{32}&{}a_{33}-\lambda \end{array} \right| +\left| \begin{array}{cc} a_{11}-\lambda &{}a_{13}\\ a_{31}&{}a_{33}-\lambda \end{array} \right| +\left| \begin{array}{cc} a_{11}-\lambda &{}a_{12}\\ a_{21}&{}a_{22}-\lambda \end{array} \right| \right] ,\\ \\ \displaystyle \frac{\mathrm{{d}}^2P(\lambda )}{\mathrm{{d}}\lambda ^2}=2[a_{11}+a_{22}+a_{33}-3\lambda )],\quad \displaystyle \frac{\mathrm{{d}}^3 P}{\mathrm{{d}}\lambda ^3}=-6 \end{array}\right. } \end{aligned}$$

(81)

setting

$$\begin{aligned} P(0)={\texttt {I}}_3,\,\,P^\prime (0)=-{\texttt {I}}_2,\,\, P^{\prime \prime }(0)=2{\texttt {I}}_1,\,\,P^{\prime \prime \prime }(0)=-6\end{aligned}$$

(82)

one has

$$\begin{aligned} {\left\{ \begin{array}{ll} {\texttt {I}}_1=a_{11}+a_{22}+a_{33},\,\,{\texttt {I}}_3=\det L,\\ \\ {\texttt {I}}_2=\left| \begin{array}{cc} a_{22}&{}a_{23}\\ a_{32}&{}a_{33} \end{array} \right| +\left| \begin{array}{cc} a_{11}&{}a_{13}\\ a_{31}&{}a_{33} \end{array} \right| +\left| \begin{array}{cc} a_{11}&{}a_{12}\\ a_{21}&{}a_{22} \end{array} \right| \end{array}\right. } \end{aligned}$$

(83)

and the spectral equation becomes

$$\begin{aligned} \lambda ^3-{\texttt {I}}_1\lambda ^2+{\texttt {I}}_2\lambda -{\texttt {I}}_3=0. \end{aligned}$$

(84)

The quantities ${\texttt {I}}_1,{\texttt {I}}_2,{\texttt {I}}_3$ are called characteristic values or invariants of ${{\mathcal {L}}}$ since are invariant with respect to nonsingular linear transformations.

1.2 Liénard–Chipart criterion

Let $a_{ij}$ be real numbers and let

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}}{\mathrm{{d}}t}\left( \begin{array}{l} u_1\\ u_2\\ u_3 \end{array} \right) ={{\mathcal {L}}}\left( \begin{array}{l} u_1\\ u_2\\ u_3 \end{array} \right) , \end{aligned}$$

(85)

with

$$\begin{aligned} {{\mathcal {L}}}=\left\| a_{ij}\right\| . \end{aligned}$$

(86)

Then (84) is the spectral equation of (85) i.e. the roots of (84) are the eigenvalues of (85). Therefore, the zero solution is stable if and only if all the eigenvalues have all negative real parts. The algebraic Liénard–Chipart’s criterion Merkin (1997); Gantmacher (2000), applied to (84), allows to determine the stability of the zero solution of (85) without solving the spectral equation. In fact, introducing the Hurwitz matrix of (84)

$$\begin{aligned} \text{ Hurwitz } \text{ matrix }=\left\| \begin{array}{ccc} -{\texttt {I}}_1&{}-{\texttt {I}}_3&{}0\\ 1&{}{\texttt {I}}_2&{}0\\ 0&{}-{\texttt {I}}_1&{}-{\texttt {I}}_3 \end{array} \right\| , \end{aligned}$$

(87)

the criterion is the roots of (84) have negative real part if and only if

$$\begin{aligned} {\texttt {I}}_1<0,\,\,{\texttt {I}}_2>0,\,\,{\texttt {I}}_3<0,\, -\left| \begin{array}{cc} -{\texttt {I}}_1&{}{\texttt {I}}_3\\ 1&{}{\texttt {I}}_2 \end{array}\right| = {\texttt {I}}_1{\texttt {I}}_2-{\texttt {I}}_3<0. \end{aligned}$$

(88)

In particular, it follows that each one of the conditions

$$\begin{aligned} {\texttt {I}}_1<0,\,\,{\texttt {I}}_2>0,\,\,{\texttt {I}}_3<0 \end{aligned}$$

(89)

is necessary for all the roots have negative real parts (otherwise some roots will have positive real parts) (Merkin 1997; Gantmacher 2000).

1.3 $L^2(\varOmega )$-linear and nonlinear energy decay

Let $R_L$ be the R critical value of linear stability of $m_0$ and let $\lambda _i,\, (i=1,2,3)$, be the eigenvalues associated to $R<R_L$. Denoting by $R_e(\lambda )$ the real part of an eigenvalue $\lambda$ and setting

$$\begin{aligned} -{{\overline{\alpha }}}=\displaystyle \sup _{i\in \{1,2,3\}} R_e(\lambda _i), \end{aligned}$$

(90)

one has not only ${{\overline{\alpha }}}>0$ but also

$$\begin{aligned} \left( \displaystyle \frac{\mathrm{{d}}\hat{{{\mathcal {E}}}}}{\mathrm{{d}}t}\right) _{(t=0)}<0,\quad \forall ({{{\hat{w}}}}_0,{{{\hat{h}}}}_0,{\hat{\theta }_0}), \end{aligned}$$

(91)

with $\hat{{{\mathcal {E}}}}$ partial $L^2(\varOmega )$ linear energy given by

$$\begin{aligned} \hat{{{\mathcal {E}}}}=\displaystyle \frac{1}{2} \left( \left\| \hat{w}\right\| ^2+\displaystyle \frac{1}{P_m}\left\| \hat{h}\right\| ^2+\displaystyle \frac{1}{P_r}\left\| {{{\hat{\theta }}}}\right\| ^2\right) . \end{aligned}$$

(92)

In fact, setting

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbf{X }}=(X_1,X_2,X_3)^\mathrm{{T}}=({{{\tilde{w}}}}_1,{{{\tilde{h}}}}_1, {{{\tilde{\theta }}}}_1)^\mathrm{{T}},\\ |{\mathbf{X }}|=\left( \displaystyle \sum _{i=1}^3 X^2_i\right) ^\frac{1}{2}, \end{array}\right. } \end{aligned}$$

(93)

(42) and (43), for $n=1$, give

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}{\mathbf{X }}}{\mathrm{{d}}t}=L{\mathbf{X }},\quad L=L_1. \end{aligned}$$

(94)

Since there exists a nonsingular transformation

$$\begin{aligned} {\mathbf{X }}=U\mathbf{Y },\quad \det U\ne 0, \end{aligned}$$

(95)

such that

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}}{\mathrm{{d}}t}|{\mathbf{Y }}|\le -\displaystyle \frac{{{\overline{\alpha }}}}{2}|{\mathbf{Y }}|, \end{aligned}$$

(96)

$\{$see Gantmacher (1975), p. 196, formula (10) with $\delta =\displaystyle \frac{\alpha }{2},\eta =0\}$, then (95) and (96) imply

$$\begin{aligned} {\left\{ \begin{array}{ll} {\displaystyle |{\mathbf{Y }}|\le |{\mathbf{Y }}_0|e^{-\frac{{{\overline{\alpha }}}}{2}t}},\quad \forall |{\mathbf{Y }}_0|\\ {\displaystyle |{\mathbf{X }}|\le |\mathbf{X} _0|e^{-\frac{{{\overline{\alpha }}}}{2}t}},\quad \forall |{\mathbf{X }}_0| \end{array}\right. } \end{aligned}$$

(97)

with $|{\mathbf{X }}_0|\ge |U||{\mathbf{Y }}_0|$ and hence $\forall |{\mathbf{X }}_0|$, since $|{\mathbf{Y }}_0|$ is arbitrary. Setting

$$\begin{aligned} |{\varvec{\varPsi }}|=|{\mathbf{X }}_0|e^{-\frac{{{\overline{\alpha }}}}{2}t}, \end{aligned}$$

(98)

one has

$$\begin{aligned} \left( \displaystyle \frac{\mathrm{{d}}|{\mathbf{X }}|}{\mathrm{{d}}t}\right) _{(t=0)}\le \displaystyle \lim _{t\rightarrow 0^+}\displaystyle \frac{|{\varvec{\varPsi }}|-|{\varvec{\varPsi }}_0|}{t}=-\displaystyle \frac{\alpha }{2}|\mathbf{X }_0|<0,\quad \forall |{\mathbf{X }}_0|\ne 0, \end{aligned}$$

(99)

and (91) immediately follows together with

$$\begin{aligned} \hat{{\mathcal {E}}}\le \hat{{{\mathcal {E}}}}_0 e^{-{{\overline{\alpha }}} t}. \end{aligned}$$

(100)

Finally, introducing the total $L^2(\varOmega )-$linear energy

$$\begin{aligned} {{{\hat{E}}}}=\displaystyle \frac{1}{2}\left( \left\| \hat{\mathbf{u }}\right\| ^2+\displaystyle \frac{1}{P_m}\left\| \hat{\mathbf{h }}\right\| ^2+\displaystyle \frac{1}{P_r}\left\| {{{\hat{\theta }}}}\right\| ^2\right) , \end{aligned}$$

(101)

one easily obtains

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}{{{\hat{E}}}}}{\mathrm{{d}}t}=2\sqrt{R}\langle {{{\hat{w}}}}, {\hat{\theta \rangle }}+\langle \hat{{\mathbf{u }}},\varDelta \hat{\mathbf{u }}\rangle +\displaystyle \frac{1}{P_m}\langle {\mathbf{h }},\varDelta \mathbf{h} \rangle +\displaystyle \frac{1}{P_r} \langle {{{\hat{\theta }}}},\varDelta {{{\hat{\theta }}}} \rangle , \end{aligned}$$

(102)

and taking into account that the boundary conditions and the Poincaré inequality Flavin and Rionero (1996) imply

$$\begin{aligned} \langle {{\varphi }},\varDelta \varphi \rangle =-\left\| \nabla \varphi \right\| ^2\le -\pi ^2\left\| \varphi \right\| ^2,\quad \forall \varphi \in \{\hat{{\mathbf{u }}}, \hat{{\mathbf{h }}}, {\hat{\theta \}}} \end{aligned}$$

one easily obtains

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}\hat{E}}{\mathrm{{d}}t}<2\sqrt{R}\hat{{{\mathcal {E}}}}-\gamma {{{\hat{E}}}}, \end{aligned}$$

(103)

and hence

$$\begin{aligned} {{{\hat{E}}}}\le {{{\hat{E}}}}_0 e^{-\gamma t}+2\sqrt{R}e^{-\gamma t}\displaystyle \int _0^t e^{\gamma t} \mathcal E(\tau )\,\mathrm{{d}}\tau . \end{aligned}$$

(104)

In view of (100), one has

$$\begin{aligned} {{{\hat{E}}}}\le \hat{E}_0\left( 1+\displaystyle \frac{2\sqrt{R_L}}{\gamma -\alpha }\right) e^{-{{\bar{\alpha }}} t},\quad {{\bar{\alpha }}}<\min (\alpha ,\gamma ). \end{aligned}$$

(105)

Passing to the nonlinear $L^2(\varOmega )$-energy decay and setting

$$\begin{aligned} E=\displaystyle \frac{1}{2}\left( \left\| \mathbf{u} \right\| ^2+\displaystyle \frac{1}{P_m}\left\| \mathbf{h} \right\| ^2+\displaystyle \frac{1}{P_r}\left\| \theta \right\| ^2\right) , \end{aligned}$$

(106)

in view of

$$\begin{aligned} {\left\{ \begin{array}{ll} \langle {\mathbf{u }}, {\mathbf{u }}\cdot \nabla {\mathbf{u }}\rangle =\langle {\mathbf{u }},{\mathbf{h }}\cdot \nabla {\mathbf{h }}\rangle =\langle \theta , {\mathbf{u }}\cdot \nabla \theta \rangle =0,\\ \\ \langle {\mathbf{h }}, {\mathbf{u }}\cdot \nabla {\mathbf{h }}\rangle =\langle {\mathbf{h }}, {\mathbf{h }}\cdot \nabla {\mathbf{u }}\rangle =0,\\ \\ \langle {\mathbf{h }}_z, {\mathbf{u }}\rangle +\langle {\mathbf{h }}, {\mathbf{u }}_z\rangle =0, \end{array}\right. } \end{aligned}$$

(107)

one has

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}E}{\mathrm{{d}}t}=2\sqrt{R}\langle w, \theta \rangle +\langle {\mathbf{u }},\varDelta {\mathbf{u }}\rangle +\displaystyle \frac{1}{P_m}\langle {\mathbf{h }},\varDelta {\mathbf{h }}\rangle +\displaystyle \frac{1}{P_r}\langle \theta ,\varDelta \theta \rangle . \end{aligned}$$

(108)

On the other hand, (103) and (106) imply

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}{{\hat{E}}}}{\mathrm{{d}}t}<2\sqrt{R}\hat{{{\mathcal {E}}}}\le 2\sqrt{R_L} \hat{{{\mathcal {E}}}}_0 e^{-\frac{{{\overline{\alpha }}}}{2}t},\qquad \forall \hat{{{\mathcal {E}}}}_0 \end{aligned}$$

(109)

and hence

$$\begin{aligned} \displaystyle \frac{\mathrm{{d}}{{{\hat{E}}}}}{\mathrm{{d}}t}\le {{{\hat{E}}}}_0 e^{-\frac{{{\overline{\alpha }}}}{2}t}, \end{aligned}$$

(110)

with ${{{\hat{E}}}}_0>2\sqrt{R_L} \hat{{{\mathcal {E}}}}_0$ and hence $\forall {{{\hat{E}}}}_0$ since $\hat{{{\mathcal {E}}}}_0$ is arbitrary. Setting

$$\begin{aligned} {{{\hat{\varPsi }}}}=E_0e^{-\frac{{{\overline{\alpha }}}}{2}t}, \end{aligned}$$

(111)

one has

$$\begin{aligned} \left( \displaystyle \frac{\mathrm{{d}}{{{\hat{E}}}}}{\mathrm{{d}}t}\right) _{(t=0)}\le \displaystyle \lim _{t\rightarrow 0^+} \displaystyle \frac{{{{\hat{\varPsi }}}}(t)-{{{\hat{\varPsi }}}}(0)}{t}=-\displaystyle \frac{{{\overline{\alpha }}}}{2}\hat{E}_0<0,\,\forall {{{\hat{E}}}}_0. \end{aligned}$$

(112)

On choosing

$$\begin{aligned} {\hat{\mathbf{u }}}_0={\mathbf{u }}(\tau ),\,\hat{{\mathbf{h }}}_0=\mathbf{h} (\tau ),\,\,{\hat{\theta }_0}=\theta (\tau ), \end{aligned}$$

(113)

one has

$$\begin{aligned} \left( \displaystyle \frac{\mathrm{{d}}E}{\mathrm{{d}}t}\right) _{(t=\tau )}=\left( \displaystyle \frac{\mathrm{{d}}\hat{E}}{\mathrm{{d}}t}\right) _{(t=0)}<0,\,\,\forall \tau \ge 0, \end{aligned}$$

(114)

i.e. $R<R_L$ implies the global nonlinear asymptotic $L^2(\varOmega )$-stability.