Abstract
The paper addresses the preparatory studies of future ESA mission concepts devoted to improve our understanding of the Earth’s mass change phenomena causing temporal variations in the gravity field, at different temporal and spatial scales, due to ice mass changes of ice sheets and glaciers, continental water cycles, ocean masses dynamics and solid Earth deformations. The ESA initiatives started in 2003 with a study on observation techniques for solid Earth missions and continued through several studies focusing on the satellite system, technology development for propulsion and distance metrology, preferred mission concepts, the attitude and orbit control system, as well as the optimization of the satellite constellation. These activities received precious inputs from the GOCE, GRACE and GRACE-FO missions. More recently, several studies related to new sensor concepts based on cold atom interferometry (CAI) were conducted, mainly focusing on technology development for different instrument configurations (GOCE-like and GRACE-like) and including validation activities, e.g. a first successful airborne survey with a CAI gravimeter. The latest results concerning the preferred satellite architectures and constellations, payload design and estimated science performance will be presented as well as remaining open issues for future concepts.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Mass change can be caused by numerous geophysical processes in the Earth system, including the water cycle, changes in the mass of the ice sheets and the oceans, and the solid Earth. The temporal and spatial scales range from instantaneous (earthquakes) to centuries/millennia (glacial isostatic adjustment) and a few kilometres (lake/river levels) to thousands of kilometres (global sea level), respectively. Thus, mass change may be regarded as a crosscutting variable that is related to essential climate variables in all domains. The most direct way to observe mass change is measuring the tiny changes over time in Earth’s gravity field, as demonstrated by the GRACE and GRACE-FO missions. The time-variable gravity field reflects the total mass change by definition and, therefore, provides the context that many other measurement types cannot provide. In addition, measurements of the time-variable gravity field are sensitive to mass change deep beneath the Earth’s surface, e.g. to ground water changes, which is not the case for any other type of observation from space.
The ESA initiatives on future gravity mission concepts started in 2003 with a study on observation techniques for solid Earth missions, continued recently through several system studies and technology developments, either for propulsion, e.g., tests on miniaturized ion thruster, or distance metrology, e.g. laser interferometry. Preferred mission concepts fitting the defined programmatic boundary conditions were identified in the “Assessment of a Next Generation Gravity Mission to Monitor the Variations of the Earth’s Gravity Field” (concisely: NGGM) and studied with prioritized science requirements and detailed system designs. These activities received precious inputs from the in-flight lesson learnt from the GOCE and GRACE missions. The technology studies were complemented with scientific studies, consolidating the science requirements and focusing on the optimization of the satellite constellation and advancing the gravity field retrieval algorithms. The scientific objectives for NGGM are the measurement of the geoid with an accuracy of 1 mm at a spatial resolution of 500 km every 3 days and 150 km every 10 days. The NGGM concept is thus expected to improve both spatial and temporal resolution of the time-variable gravity field with respect to previous and present missions.
More recently, ESA launched studies on utilizing cold atom interferometry in the context of Earth observation, focusing on the development of a gravity gradiometer and a hybrid quantum/electrostatic accelerometer. While the first requires substantial technological developments, the principle of the latter is already demonstrated in lab experiments. In addition, first airborne and shipborne campaigns over Iceland using a quantum gravimeter provided very promising results.
The remainder of the paper is split into two parts. The first focuses on the NGGM concept, which is technologically more mature and could theoretically be implemented within the next decade. The second part describes developments of the quantum sensors, which could be used for a gravity field mission in the long term.
1.1 The NGGM concept
In the same way as the GRACE and GRACE-FO missions, NGGM observes mass change through measuring tiny changes in the time-variable gravity field. For that purpose, two satellites are flying in the same orbit in an in-line formation, separated by a distance of approximately 100 km. Due to the spatial separation, the satellites are subject to slightly different gravitational accelerations, which causes changes in the distance between the two satellites that are measured extremely precisely by laser interferometry. The effect of non-gravitational accelerations on the satellites is measured by accelerometers, noting that both the laser ranging and accelerometer measurements must reference to the satellite’s center of mass. GNSS receivers for positioning, star sensors for attitude determination, and an angle-lateral metrology for ensuring the inter-satellite pointing, required by the laser interferometer, complement the measurement system illustrated in Fig. 1. To compensate non-gravitational forces and torques, the satellites are equipped with an attitude and orbit control system (AOCS) that uses ion thrusters for both attitude and orbit control.

Figure reproduced from Silvestrin et al. (2015)
Measurement principle of NGGM.
1.2 Bender constellation
One of the limitations of present-day time-variable gravity field models is related to fast mass change in the atmosphere and oceans, which is typically reduced from the ranging observations using atmosphere and ocean models. Though these models were significantly improved in the past decade, they are still regarded as one of the largest error sources for time-variable gravity models (Flechtner et al. 2016). In addition, the measurement system is inherently sensitive in the direction of the laser axis, which for a single pair of satellites flying in an in-line formation in a polar orbit, as illustrated in Fig. 1, results in sensitivity in the North–South direction for a large part of the globe, whereas the sensitivity in the East–West direction is significantly lower.
To overcome these limitations, Bender et al. (2008) proposed the constellation shown in Fig. 2 that consists of two satellite pairs flying in an in-line formation, one in a polar orbit and the other in an orbit with an inclination of approximately 67°. This has the advantages of doubling the space–time sampling and adding a significantly improved East–West sensitivity of the measurements in the latitude range covered by the satellite pair flying in the inclined orbit. As a result, the time-variable gravity field model errors are much more isotropic than those based on a single polar satellite pair, which reduces the need for sophisticated post-processing. More importantly, it is possible to use the approach described by Wiese et al. (2011) for retrieving the effect of non-tidal mass change in the atmosphere and oceans directly from the measurements instead of relying on models for reducing the effect. For tidal mass change in the oceans, Hauk and Pail (2018) demonstrated that imperfections in the ocean tide models could be compensated by co-estimating their effect in the time-variable gravity field, provided that the observation period is sufficiently long (multiple years).
1.3 Technology studies
Past and present gravity missions provide valuable experience and lessons learned. The GOCE mission provides experience on the drag-free system and control, the satellite structure that is stable under varying thermal loads, ultra-sensitive accelerometers, and thermal control (Floberghagen et al. 2011). The GRACE mission proved the measurement concept of ranging between two low-flying satellites and initiated the time series of monthly snapshots of the time-variable gravity field (Tapley et al. 2004). The GRACE-FO mission not only extends this time series, but also demonstrated laser ranging between two low-flying satellites (Abich et al. 2019; Kornfeld et al. 2019). To prepare the technology required for the NGGM concept, several complementary and basic Technology Research Programme (TRP) studies were initiated and are currently running, notably:
1.3.1 Next-generation gravity mission
AOCS Solutions and Technologies: The objectives are to define and evaluate the mission-critical Attitude and Orbit Control System (AOCS) solutions and technologies to identify the critical technologies and to assess their feasibility and the design drivers.
1.3.2 Miniaturized gridded ion engine (GIE) breadboarding and testing
The latest results from the NGGM studies show that a miniaturised GIE with increased thrust level ranging from 50 μN to 2 mN is needed for coping with the large variation of the drag forces encountered in a long-duration mission.
1.3.3 Consolidation of the micro-PIM field emission thruster design for NGGM
A sharp, porous tungsten crown FEEP multi-emitter is capable of producing thrust from the μN-range to the mN-range. The study aims to demonstrate that the mN-FEEP thruster is an excellent candidate for the lateral thrusting on NGGM.
1.3.4 High-stability laser with fibre amplifier and laser stabilisation unit for interferometric Earth gravity measurements
The objective of this development is the manufacturing of an elegant breadboard of a high-stability laser.
1.3.5 Assessment of satellite constellations for monitoring the variations in Earth's gravity field
The study aims at the optimization of Bender-type constellations of two pairs of satellites for the retrieval of the time-variable gravity field for inferring mass change with special attention to the reduction of temporal and spatial aliasing.
1.4 Satellite system studies
The Assessment of Satellite Constellations for Monitoring the Variations in Earth's Gravity Field study investigated the satellite system together with potential satellite formations and constellations. The study clearly revealed that more advanced formations such as the pendulum formation and the cartwheel formation required much more complex, technically challenging satellite systems than the in-line formation. For that reason, the Bender constellation consisting of two pairs of satellites flying in in-line formation was recommended.
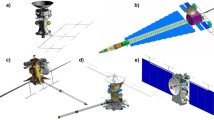
The combination of the orbit and the mission lifetime objectives is a design driver for the satellite system (Dionisio et al. 2018a). As for all gravity missions, the orbit shall be as low as possible, while the mission lifetime was intended to cover a full solar cycle, i.e. 11 years. Furthermore, the ultra-sensitive accelerometers require a “quiet” environment for ultimate performance and the laser interferometer requires accurate pointing of the satellites, which is equivalent to the pointing of the laser beam, for establishing and maintaining the ranging between the satellites. Further constraints result from the launch vehicle, where the Vega-C rocket served as the reference. For the orbits considered for NGGM, Vega-C supports a maximum launch mass of 2250 kg. Assuming a mass of 250 kg for the satellite dispenser and that the two satellites forming a pair are launched together, the upper limit for each satellite is 1000 kg.
The technical solution to this set of requirements was to develop a sophisticated attitude and orbit control system that is based on electric propulsion, where eight smaller ion thrusters, supported by three magnetic torquers, control the attitude of the satellites and one larger ion thruster compensates the effect of drag in the along-track direction (Dionisio et al. 2018a). Since the mean thermosphere neutral density could vary by a factor of ten throughout a full solar cycle, the ion thrusters need to support a wide thrust range. The power demand of the satellite system, driven by the electric propulsion, is approximately 1 kW, which requires solar arrays with a surface of 15 m2 to raise enough power also in unfavorable solar illumination conditions. Such large solar arrays can only be accommodated in the launch vehicle, when they are deployable. At this stage of the development, we believe that the deployable solar arrays can be designed with sufficient structural stability to ensure the “quiet” environment required by the accelerometers. The NGGM satellite and launch configuration are illustrated in Fig. 3. Table 1 provides a list of the satellites’ payload, AOCS sensors and actuators.

Figure reproduced from Dionisio et al. (2018a)
The NGGM satellite and the launch configuration.
The distance between the satellites forming a pair is 100 km, which was identified in simulations to be optimal, also noting that the laser ranging noise increases with the distance. To maintain the distance between the satellites, a loose formation control algorithm is implemented in the AOCS. In short, the formation control bandwidth is below the payload’s measurement bandwidth, so that only variations of the distance that are longer than one orbit are controlled. Variations of the distance shorter than the orbital period are not affected by the formation control algorithm, which results in variations of the distance caused by the varying gravitational acceleration of the flattened Earth (C20 coefficient of gravity field models). Furthermore, such formation control enables a full compensation of the effect of non-gravitational accelerations within the payload’s measurement bandwidth.
Two options for the laser ranging system were investigated by Nicklaus et al. (2018): an optical transponder and a retroreflector scheme. The transponder scheme is very similar to the laser ranging scheme of the GRACE-FO mission (Sheard et al. 2012; Abich et al. 2019), where a laser beam, generated on one satellite, is received by the other satellite, which regenerates the laser with its own laser source and retransmits the laser beam back to the first satellite. In contrast, in the retroreflector scheme, a heterodyne laser interferometer transmits a laser beam from one satellite, which is passively reflected by the other satellite. The ranging noise is estimated to be lower than the goal of 10 nm/√Hz × NSF(f) for both schemes, where the noise shape function (NSF) is defined by NSF(f) = (1 + (10 mHz/f)2)1/2 (Nicklaus et al. 2018). It is possible to implement both schemes such that the laser beam is either on the line connecting the centers of mass of the two satellites (“on-axis configuration”) or parallel to that line (“racetrack configuration”). In the latter, the laser beams are reflected by a triple mirror assembly, which offers the advantage that the center of mass is not occupied by the ranging system, while the measured range refers directly to the distance between the centers of mass of the satellites (Kornfeld et al. 2019). Moreover, the racetrack configuration offers advantages in view of polarization, stray light, complexity of operation and verification during instrument development and is, therefore, the preferred configuration for NGGM.
The configuration of the two accelerometers depends on the configuration of the laser ranging system. For the on-axis configuration of the laser ranging system, we favor a design where the ranging is performed directly from one satellite center of mass to the other, which implies that satellite center of mass is occupied by the laser ranging system. In this case, the two accelerometers are placed symmetrically around the satellite center of mass, either “vertically” as indicated in Fig. 1 or “horizontally”. The non-gravitational acceleration of the satellite is then obtained as mean of the measurements of the two accelerometers. In case one of the two accelerometers fails, the measurements of the other accelerometer need to be corrected for centrifugal acceleration, gravity gradient and Euler acceleration effects. For the racetrack configuration of the laser ranging system, it is possible to place the two accelerometers either symmetrically around the satellite center of mass or place the main unit at the satellite center of mass and the redundant unit at a small distance to the satellite center of mass. In case of the latter configuration, the measurements of the redundant accelerometer need to be corrected for centrifugal acceleration, gravity gradient and Euler acceleration effects to obtain the non-gravitational acceleration of the satellite. In past studies, we also assumed that the two accelerometers are place symmetrically around the satellite center of mass.
1.5 Science studies
The Assessment of Satellite Constellations for Monitoring the Variations in Earth's Gravity Field study also included the implementation of a method for the reduction of aliasing due to the undersampling of fast atmospheric and oceanic mass change. Since the Bender constellation doubles the sampling in space and time, Wiese et al. (2011) proposed to estimate daily low spatial resolution gravity field models together with monthly higher spatial resolution gravity field models. This approach proved to be effective in absorbing fast non-tidal atmosphere and ocean mass change signals in the daily gravity field models, so that the non-tidal atmosphere and ocean models were not needed anymore for reducing their effect from the measurements. Instead, it was demonstrated that the daily gravity field models contain significant non-tidal atmosphere mass change signals and represent thus a potential new data product.
The Additional Constellation Analysis study aimed at further optimizing the Bender constellation. In general, there are three essential needs for gravity field measurements: flying as low as possible to maximize the signal strength, keeping the retrieval period as short as possible to maximize the time resolution of the time-variable gravity field models, and to ensure that the ground track coverage is dense enough within the retrieval period for maximizing spatial resolution. For specific retrieval periods, there are only limited options for altitudes available. It is, however, not required to fly exactly at the altitude of the repeat cycle. Instead, flying close to the altitude of the desired repeat cycle still provides acceptable ground track coverage. With these needs in mind, the scenario of drifting ground tracks with fixed interleaving of the ground tracks of the polar and inclined satellite pair was investigated in detail.
Initially, seven simulations were defined where the altitudes were chosen such that the orbits of both satellites had the same (sub-) cycle, ranging from 3 to 23 days to find the optimal cycle. In addition, the ground track pattern of the inclined and polar pair drifted in longitude at the same rate, i.e., the combined ground track pattern of the inclined and polar pair is allowed to drift westwards or eastwards, which makes the choice of the altitude more flexible. Though not within the scope of this study that flexibility would allow to tune the altitudes with respect to e.g., the co-estimation of parameters for modeling ocean tides. An eighth simulation was defined, learning from the experience gained from analyzing the initial seven simulations and taking into account refined knowledge of the capabilities of the satellites to fly at a low altitude. The constellation of the eighth simulation is the same as for the third simulation, except that the altitude of the polar satellite pair was reduced from 385 to 340 km. A full list of the simulation is provided in Table 2, noting that simulations 11−15 are similar to the eighth simulation.
A peculiarity of the simulations was that the gravity field retrieval was tailored to the orbits for each simulation individually. In particular, the retrieval period was selected to be identical to the cycle of the orbit and the maximum spherical harmonic degree was chosen in dependence of the signal-to-noise ratio. Obviously, simulations with lower orbits and longer retrieval periods resulted in more accurate time-variable gravity field models. However, after normalizing the performance using a rule of thumb for the impact from the different altitudes and the √n law, the gravity field retrieval performance across all simulations was highly consistent. In other words, using the constellation design guidelines used for selecting the simulations of this study guarantees accurate time-variable gravity field models. This is an important aspect when advancing from a science-driven satellite mission to a service-driven satellite mission.
Another objective of the Additional Constellation Analysis study was to investigate a real-time processing scheme in view of hydrological services such as drought monitoring. The processing scheme essentially implements a sliding window on the input data for the gravity field retrieval, thereby minimizing the latency of the gravity field models. For the purpose of drought monitoring, a climatology was established based on ESA’s Earth system model and additional data, which was then used for producing drought indices that indicate how severe the gravimetric drought is. In this context, it is important to realize that different definitions of drought exist, e.g. an agricultural drought or a meteorological drought, which are all different from the definition of gravimetric drought, which is a deficit in water mass.
From all simulations, scenario 13 was investigated in greater detail, because it offers the lowest orbits considered feasible from the satellite system engineering point of view and, therefore, the best gravity field performance. Since scenario 13 offers a 7-day sub-cycle, the study team estimated weekly gravity field solutions. The performance of these solutions is illustrated in Fig. 4, which shows the average degree standard deviation of the time-variable gravity signal (blue curve) and the average retrieval error (red curve). The signal and error curves cross each other at degree 50, which indicates that the weekly solutions have a spatial resolution of approximately 400 km half-wavelength. The yellow curve is an approximation of the retrieval error, which we use for extrapolating the retrieval performance from weekly to monthly (or multi-annual) solutions. Assuming that the retrieval errors obey the law of √n, we obtain the retrieval error for monthly solutions (purple curve) through scaling the yellow curve by a factor of 7/30. For the monthly solutions, the signal and error curves cross at degree 70, corresponding to a spatial resolution of 286 km.
Performance of NGGM scenario 13 as defined in Table 2
Figure 5 compares the performance of monthly gravity field solutions with the threshold requirements defined by the international user, where the term “threshold requirements” is defined to represent “a significant improvement with respect to the current situation” community (Pail et al. 2015). For that purpose, we calculated the cumulative error of a monthly gravity field solution (blue curve in the left panel of Fig. 5) from the extrapolation of the retrieval error of weekly solutions (purple curve in Fig. 4). Considering that a monthly solution has a spatial resolution of approximately 286 km as discussed above, it appears reasonable to consider only the requirement for the spatial resolution of 400 km. At this spatial resolution, the cumulative error of a weekly solution is estimated to be 8 mm equivalent water height (EWH), which is marginally worse than the threshold requirement of 5 mm EWH. In this context, it is worth noting that we made conservative assumptions on the ocean tide model performance in the simulations. Considering that ocean tide model errors are one of the major limitations for present-day time-variable gravity field model performance (Flechtner et al. 2016), we anticipate that recent as well as future advances in modelling and/or co-estimating the effect of ocean tides will improve the performance of gravity field solution and hence reduce or even close the gap to the threshold requirement.
Square-root of cumulative degree variance of NGGM scenario 13 as defined in Table 2. The left panel shows the extrapolation from weekly to monthly gravity field solutions (blue curve) and the threshold requirements for the monthly gravity field solutions (red crosses). The right panel shows the extrapolation from weekly solutions to a 5-year trend (blue curve) and the threshold requirements for the trend. The threshold requirements are defined by the international user community as reported by Pail et al. (2015) (colour figure online)
In the same way that we extrapolated the retrieval error from weekly to monthly gravity field solutions, we also extrapolated to the retrieval error of a linear trend determined on the basis of an observation period of 5 years. The cumulative error of the trend is illustrated in the right panel of Fig. 5 (blue curve) and again compared with the threshold requirements defined by the international user community as defined by Pail et al. (2015). The cumulative retrieval error at 400 km spatial resolution is estimated to be 1.4 mm/year EWH, which exceeds the requirement of 0.5 mm/year EWH. However, the requirements at 200 km, 150 km and 100 km spatial resolution are all fulfilled.
1.6 Cold atom interferometry for Earth observation
Cold Atom Interferometry (CAI) inertial sensor is based on measuring the motion of a cold atom cloud with high precision using a stabilized laser. The laser frequency stabilization is ensured using an atomic transition as a reference. The measurement principle is illustrated in Fig. 6, where the initial cloud of cold atoms, indicated by the green dot in the left of the figure, is prepared through capturing atoms in a magneto-optical trap and reducing their temperature through a laser cooling technique. The temperature controls the velocity dispersion of the atoms, where lower velocities enable longer interrogation times and, consequently, more precise measurements. The first step in the procedure is a π/2 Raman laser pulse of duration τs = π/(2Ωeff), where Ωeff is the Rabi effective frequency. This laser pulse transfers half of the atoms from one state to another and delivers an impulse to the transferred atoms that changes their trajectory. As a result, the cloud of atoms splits in two possible trajectories, which are allowed to move in free fall during time T. Then, another π Raman laser pulse of duration τs = π/Ωeff reverses the state of both atom clouds and changes their trajectory, so that the two clouds join again after time T’. A final π/2 Raman laser pulse transfers half of the atoms in both clouds from one state to another. In the end, the proportion of atoms in the two stable states depends sinusoidally on the phase of the interferometer, which is proportional to the acceleration of the atoms along the direction of the laser axis. During the whole procedure, a mirror that reflects the laser serves as the reference frame.
Depending on the particular implementation of the CAI, it is sensitive to the acceleration of the mirror and the gravity gradient along the laser axis. The measurement principle is used for developing the CAI gravity gradiometer concept and a hybrid quantum/electrostatic accelerometer. The same technology was also used in an airborne gravimetric campaign over Iceland.
1.7 Study of a CAI gravity gradiometer sensor and mission concepts
The concept of a CAI gravity gradiometer was proposed by Carraz et al. (2014) and further investigated in several ESA studies focusing on the instrument and mission concept as well as studies supporting technological developments needed for the instrument such as the vacuum chamber, laser system, etc. (Trimeche et al. 2019). Since the instrument relies on atom transitions, the instrument noise is expected to yield a flat amplitude spectral density of a few mE, where E is the symbol for the Eötvös unit (1 E = 10–9 s−2). This offers a large advantage over the electrostatic gravity gradiometer of the GOCE mission, which has a flat noise amplitude spectral density of 10 − 20 mE in the frequency range 2 −100 mHz and a large increase of the noise amplitude spectral density below 2 mHz. Mission simulations suggest that a mission with a CAI gravity gradiometer would provide gravity field models with an accuracy that is comparable to the GOCE mission or up to ten times more accurate, noting that not only the instrument performance, but also the duration of the mission and the altitude of the orbit are performance drivers (Douch et al. 2018). This does, however, not mean that a mission with a CAI gravity gradiometer is suited for measuring the time-variable gravity field. Even in a best-case scenario, such a mission would perform worse than the GRACE and GRACE-FO missions for this purpose.
1.8 Hybrid atom electrostatic system for satellite geodesy follow-on
Electrostatic accelerometers provide a good performance in their measurement band, which typically range from a few mHz to approximately 100 mHz. In the frequency range below the measurement band, the noise level typically increases reciprocally to the frequency.
All dedicated gravity field missions, i.e. the CHAMP, GRACE, GOCE and GRACE-FO missions, relied on electrostatic accelerometers for measuring the non-gravitational acceleration acting on the satellite. In the case of the GRACE and GRACE-FO missions, the measurement comprises of the ranging metrology and the accelerometers. The combined measurement system noise is at low frequencies dominated by the accelerometer noise, while the ranging noise dominates at higher frequencies. Since CAI accelerometers offer a flat noise amplitude spectral density, they have a great potential to reduce the measurement system noise for future gravity mission concepts such as NGGM. For this reason, a hybrid quantum/electrostatic accelerometer was developed by ONERA under ESA contract. The concept joins the measurements of the electrostatic accelerometer and the CAI accelerometer measurements using the proof mass of the electrostatic accelerometer as the mirror of the CAI accelerometer (Christophe et al. 2019). The amplitude spectral density resulting from first lab tests is shown in Fig. 7, which shows that the CAI accelerometer indeed yields a flat amplitude noise spectrum (blue line), whereas the one of the electrostatic accelerometer (black line) increases, as expected, proportional to the reciprocal of the frequency. The noise amplitude spectral density of the joined measurements (red line) is indeed combining the strengths of both instruments.
The impact of a hybrid accelerometer on the time-variable gravity field retrieval is analysed in detail by Abrykosov et al. (2019), who find that the low degree coefficients of the time-variable gravity field could be improved. However, it should be noted that the low degree coefficients are also affected by inaccurately modelled atmosphere and ocean mass change, partly masking the improvements in the measurement system noise.
Another, yet unexplored benefit of a hybrid accelerometer is the possibility of an improved calibration of the electrostatic accelerometer. Since the CAI accelerometer relies on atom transitions, it provides absolute measurements that may be used as a reference for the measurements of the electrostatic accelerometer.
1.9 First successful airborne and marine surveys with a CAI gravimeter
A CAI gravimeter was tested during the CryoVex/KAREN airborne campaign over Iceland in 2017. The flight paths illustrated in Fig. 8 included a first return flight from Akureyri to Snaefellsjoekull in the Northwest of Iceland and a grid pattern near Vatnajökull in the Southeast part of Iceland. Despite strong turbulences during the first return flight, the gravimeter’s measurements of the outbound agreed very well with those of the return flight, where the differences indicate a measurement precision of 4 −5 mGal. For the grid pattern, the airborne measurements showed a good agreement with existing on-ground measurements. The analysis of crossovers of the airborne measurements indicated that a precision of 2 mGal was reached. It was, therefore, concluded that the first airborne survey using a matter wave gravimeter was successful.
In addition to the airborne campaign, a shipborne campaign in the North Atlantic Ocean to the west of French Brittany collected gravity measurements October 2015 and January 2016. Despite rough sea conditions with wave heights of 2− 5 m, Bidel et al. (2018) conclude from the analysis of crossing points that measurement precision of 0.9 mGal was achieved.
2 Summary
In this paper, we discussed ESA’s NGGM concepts for the near and far future. In the near future, concepts based on laser ranging between low-flying pairs of satellites offer the most mature solution for measuring the time-variable gravity field. The required technological and scientific developments are on-going and it seems theoretically to be feasible to implement such a mission within the next decade. We expect that the performance of the retrieved time-variable gravity field models is compatible with the threshold requirements of the international user community as stated by Pail et al. (2015).
For the far future, CAI offers an interesting perspective for measuring the time-variable gravity field as well as the mean gravity field with improved measurement system performance. First lab experiments and airborne as well as marine campaigns indicate the large potential of this new technology for Earth observation.
References
Abich K et al (2019) In-Orbit Performance of the GRACE Follow-On Laser Ranging Interferometer. Phys Rev Lett 123:031101. https://doi.org/10.1103/PhysRevLett.123.031101
Abrykosov P, Pail R, Gruber T, Zahzam N, Bresson A, Hardy E, Christophe B, Bidel Y, Carraz O, Siemes C (2019) Impact of a novel hybrid accelerometer on satellite gravimetry performance. Adv Space Res 63:3235–3248. https://doi.org/10.1016/j.asr.2019.01.034
Bender P, Wiese D, Nerem R (2008) A possible dual-grace mission with 90 degree and 63 degree inclination orbits. In: Proceedings of the 3rd International Symposium on Formation Flying, Missions and Technologies. ESA/ESTEC, Noordwijk, pp 1–6
Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette MF (2018) Absolute marine gravimetry with matter-wave interferometry. Nat Comm 9:627. https://doi.org/10.1038/s41467-018-03040-2
Carraz O, Siemes C, Massotti L, Haagmans R, Silvestrin P (2014) A Spaceborne gravity gradiometer concept based on cold atom interferometers for measuring earth’s gravity field. Micrograv Sci Tech 26:139–145
Christophe B, Foulon B, Liorzou F, Lebat V, Boulanger D, Huynh P-A, Zahzam N, Bidel Y, Bresson A (2019) Status of development of the future accelerometers for next generation gravity missions. In: Freymueller J, Sánchez L (eds) International Symposium on Advancing Geodesy in a Changing World, International Association of Geodesy Symposia, Springer, Cham. https://doi.org/10.1007/1345_2018_42
Dionisio S, Anselmi A, Bonino L, Cesare S, Massotti L, Silvestrin P (2018a) The “Next Generation Gravity Mission” challenges, consolidation of the system concepts and technological innovations. https://doi.org/10.2514/6.2018-2495
Dionisio S, Anselmi A, Cesare S, Novara C, Colangelo L, Massotti L, Silvestrin P (2018b) System and AOCS challenges for the design consolidation of the next generation gravity mission. In: Proceedings of the 2018 AIAA Guidance, Navigation, and Control Conference, Kissimmee. https://doi.org/10.2514/6.2018-0869
Douch K, Wu H, Schubert C, Müller J, Pereira dos Santos F (2018) Simulation-based evaluation of a cold atom interferometry gradiometer concept for gravity field recovery. Adv Space Res 61:1307–1323. https://doi.org/10.1016/j.asr.2017.12.005
Flechtner F, Neumayer K-H, Dahle C, Dobslaw H, Fagiolini E, Raimondo J-C, Güntner A (2016) What can be expected from the GRACE-FO laser ranging interferometer for earth science applications? Surv Geophys 37:453–470. https://doi.org/10.1007/s10712-015-9338-y
Floberghagen R, Fehringer M, Lamarre D, Muzi D, Frommknecht B, Steiger C, Piñeiro J, da Costa A (2011) Mission design, operation and exploitation of the gravity field and steady-state ocean circulation explorer mission. J Geod 85:749–758. https://doi.org/10.1007/s00190-011-0498-3
Hauk M, Pail R (2018) Treatment of ocean tide aliasing in the context of a next generation gravity field mission. Geophys J Int 214:345–365. https://doi.org/10.1093/gji/ggy145
Kornfeld RP, Arnold BW, Gross MA, Dahya NT, Klipstein WM, Gath PF, Bettadpur S (2019) GRACE-FO: the gravity recovery and climate experiment follow-on mission. J Spacecraft Rockets 56:931–951. https://doi.org/10.2514/1.A34326
Nicklaus K, Cesare S, Massotti L, Bonino L, Mottini S, Pisani M, Silvestrin P (2018) Laser metrology concept consolidation for NGGM. In: Proceedings of the International Conference on Space Optics 2018, Chania. https://doi.org/10.1117/12.2536071
Pail R, Bingham R, Braitenberg C, Dobslaw H, Eicker A, Güntner A, Horwath M, Ivins E, Longuevergne L, Panet I, Wouters B (2015) Science and user needs for observing global mass transport to understand global change and to benefit society. Surv Geophys 36:743–772. https://doi.org/10.1007/s10712-015-9348-9
Sheard BS, Heinzel G, Danzmann K, Shaddock DA, Klipstein WM, Folkner WM (2012) Intersatellite laser ranging instrument for the GRACE follow-on mission. J Geod 86:1083–1095. https://doi.org/10.1007/s00190-012-0566-3
Silvestrin P, Carnicero Dominguez B, Haagmans R, Massotti L, Regan A, Siemes C (2015) Satellite formations and constellations for synergetic missions: a paradigm for international cooperation in earth observation. In: Proceedings of the 66th International Astronautical Congress, Jerusalem
Tapley BD, Bettadpur S, Watkins M, Reigber C (2004) The gravity recovery and climate experiment: mission overview and early results. Geophys Res Lett 31:L09607. https://doi.org/10.1029/2004GL019920
Trimeche A, Battelier B, Becker D, Bertoldi A, Bouyer P, Braxmaier C, Charron E, Corgier R, Cornelius M, Douch K, Gaaloul N, Herrmann S, Müller J, Rasel E, Schubert C, Wu H, Pereira dos Santos F (2019) Concept study and preliminary design of a cold atom interferometer for space gravity gradiometry. Class Quant Grav 36:215004. https://doi.org/10.1088/1361-6382/ab4548
Wiese D, Visser P, Nerem R (2011) Estimating low resolution gravity fields at short time intervals to reduce temporal aliasing errors. Adv Space Res 48:1094–1107. https://doi.org/10.1016/j.asr.2011.05.027
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Research involving human participants and/or animals
No human participants and/or animals have been involved in this research.
Informed consent
No human participants have been involved in this research.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haagmans, R., Siemes, C., Massotti, L. et al. ESA’s next-generation gravity mission concepts. Rend. Fis. Acc. Lincei 31 (Suppl 1), 15–25 (2020). https://doi.org/10.1007/s12210-020-00875-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12210-020-00875-0