Investigation of the Vibration Behavior of Fluidelastic Instability in Closely Packed Square Tube Arrays

Abstract

Flow-induced vibrations in heat exchanger tubes have led to numerous accidents and economic losses in the past. Fluidelastic instability is the most critical flow-induced vibration mechanism in heat exchangers. Both experimental and computational studies conducted to determine fluidelastic instability were presented in this paper. In the experiment, a water channel was built, and a closely packed normal square tube array with a pitch-to-diameter ratio of 1.28 was tested, and significant fluidelastic instability was observed. A numerical model adopting large-eddy simulation and moving mesh was established using ANSYS CFX, and results showed good agreement with the experimental findings. The vibration behaviors of fluidelastic instability were discussed, and results showed that the dominant vibration direction of the tubes changed from streamwise to transverse beyond a critical velocity. A 180° phase lag between adjacent tubes was observed in both the experiment and simulations. Normal and rotated square array cases with pitch-to-diameter ratios of 1.28 and 1.5 were also simulated. The results of this study provide better insights into the vibration characteristics of a square tube array and will help improve the fundamental research and safety design of heat exchangers.

Introduction

Fluidelastic instability is considered the most critical flow-induced vibration mechanism in tube and shell heat exchangers that can cause short-term failure of tubes. Such failures are often expensive and potentially dangerous. Fluidelastic instability results from coupling between fluid-induced dynamic forces and the motion of structures. Instability occurs when the flow velocity is sufficiently high so that the energy absorbed from the fluid forces exceeds the energy dissipated by damping. Fluidelastic instability usually leads to excessive vibration amplitudes. The minimum velocity at which instability occurs is called the critical velocity. To ensure the safety of facilities, the operating flow velocity should be strictly controlled below the critical velocity.

Fluidelastic instability in heat exchangers has been intensively researched over the past 60 years. Several theoretical models have been developed [1], and a number of important reviews on this topic have been published [2,3,4]. Fluidelastic instability is mainly attributed to two fluid–structure interaction mechanisms [5, 6]. The first mechanism, which is called the stiffness mechanism, is associated with the fluid coupling of neighboring tube vibrations and related to relative tube displacement. Here, the fluid forces are proportional to the displacements of the cylinders, and with the increasing velocity, the fluid-stiffness forces can reduce the modal damping. When the modal damping becomes negative, the cylinders become unstable. The second fluidelastic instability mechanism is associated with fluid force components in phase with the tube velocity and is called the damping mechanism. Here, the dominant fluid force is proportional to the velocity of the cylinders and may reduce the system damping when it acts as an excitation mechanism. Once the modal damping of a mode becomes negative, the cylinders lose stability [7]. A fully flexible array can become fluidelastically unstable due to either one or a combination of both mechanisms.

Numerous experiments [8] have been conducted in research on fluidelastic instability in tube arrays, and findings have helped develop a better understanding of the phenomenon. One of the earlier experiments conducted on square tube arrays was reported by Tanaka and Takahara [9], who tested a normal square array with a pitch ratio of 1.33 and concluded that unsteady fluid dynamic forces on a cylinder are mainly induced by the vibrations of the cylinder itself and its four neighboring cylinders. Tanaka et al. [10] measured tube arrays of P/d = 2.0 and P/d = 1.33, and clarified the characteristics of the critical velocity with respect to the pitch-to-diameter ratio. Weaver and Yeung [11] conducted experiments on a normal square array with a pitch ratio of 1.5 in water flow and showed that a single flexible tube in an array of rigid tubes becomes unstable at or near the same flow velocity as that found in a fully flexible array. Price and Paidoussis [12] conducted experiments on five-row and six-column normal square tube arrays of P/d = 1.5 in both air and water flows and concluded that the position of the flexible cylinder in the array has little effect on its stability in water flow but does influence its stability in air flow. Chen et al. [13] used water channels to perform a series of experiments measuring motion-dependent fluid force coefficients for normal square arrays with a pitch ratio of 1.35. Fluid damping and stiffness coefficients based on the unsteady flow theory were obtained as a function of reduced flow velocity, excitation amplitude, and Reynolds number. Al-Kaabi et al. [14] used a test rig to test square array of P/d = 1.45. Measurements were conducted to identify the flow-induced dynamic coefficients, the developed scheme was utilized to predict the onset of flow-induced vibrations in two configurations of tube bundles, and results were examined in light of Tubular Exchange Manufacturers Association (TEMA) predictions. Scott [15] conducted experiments on a normal square array with a pitch ratio of 1.33. In the case of fully flexible array, fluidelastic instability occurred at a point very close to the local peak in tube response, and the stability threshold was difficult to determine precisely. The response of a third-row tube, which was a single flexible tube in a rigid array, showed no fluidelastic instability behavior. Austermann and Popp [16] did not observe fluidelastic instability in their wind tunnel study of square arrays with a pitch ratio of 1.25.

In summary, most of the present research on normal square tube arrays is devoted to tube arrays with a relatively large pitch ratio, and little work has been done on tube arrays with small tube ratios. Available results show that a single flexible tube in a rigid array does not become unstable in both air and water for pitch ratios less than 1.33; thus, the stiffness mechanism appears to be the dominant mechanism for the fluidelastic instability of tubes with small pitch ratios. The vibration characteristics of tubes with small pitch ratios are also slightly different from those of tubes with large pitch ratios.

The development of computer technology has enabled the use of computation fluid dynamics in the engineering industry. This branch of fluid mechanics provides a new way for solving problems of fluid dynamics in tube arrays. Due to the complexity of actual tube array problems, most presented numerical simulations of the flow around tube array were limited to two dimensions based on the solution of Reynolds averaged Navier–stokes (RANS) equations. However, as RANS models cannot accurately predict the problems of fluid dynamics in tube arrays, they have not yet been widely employed in this regard. Pioneering direct numerical simulations (DNS) in tube array flows were reported by Moulinec et al. [17, 18]; in this work, the disappearance of wakes was presented and compared with theoretical asymptotic limits for laminar and turbulent strained flows. Although DNS is considered the most accurate solution for fluid analysis, it is not feasible for practical engineering problems involving high Reynolds number flows. Few computers can afford the high computational expense required by even a simple model.

In large-eddy simulations (LES), large eddies are resolved directly, while small eddies are modeled. Therefore, LES falls between DNS and RANS in terms of the fraction of the resolved scales. As momentum, mass, energy, and other passive scalars are mostly transported by large eddies in tube arrays, the LES technique is a promising approach for solving many complicated problems. Early simulations of LES were two-dimensional [19,20,21,22], but some important mechanisms, such as vortex stretching, could not be reproduced by this technique. Rollet-Miet et al. [23] and Benhamadouche and Laurence [24] pioneered the use of 3D LES calculations in staggered tube arrays. In their papers, period elemental cells of tube arrays in a flow were simulated in both the streamwise and transverse directions, and improved predictions were compared with the RANS approach for mean and turbulence quantities. Liang and Papadakis [25] used LES to analyze a 3D staggered tube array at subcritical Reynolds number; in their computations, two distinct and independent shedding frequencies were detected behind the first two rows, but the high-frequency component vanished in downstream rows. The corresponding Strouhal numbers obtained agreed well with measurements available in the literature. Unsteady RANS calculations can provide consistent data for a tube undergoing forced displacement within a fixed bundle [26,27,28]. Attempts to fully capture the free motions of a single moving tube within a fixed array were proposed by Shinde et al. [29] using URANS and delayed detached eddy simulations (DDES). Similarly, a single tube in a fixed array at a moderate Reynolds number of 60000 using LES was achieved by Berland et al. [30]; here, good agreement with the experimental reference data was obtained.

Despite decades of intensive research, many important vibration characteristics of normal square tube arrays have not yet been fully understood, especially for tube arrays with a small pitch ratio. This paper intensively investigates the vibration behaviors of normal square tube arrays with a pitch-to-diameter ratio of 1.28 at different velocities using both experimental and numerical methods. The basic characteristics of fluidelastic instability are discussed, and the change in dominant vibration direction, phase lag between adjacent tubes, and tube vibration patterns related to the instability of tube arrays are analyzed in detail. The influence of tube arrangement and pitch ratio on the critical velocity and resulting vibration patterns is also discussed using simulation data. The results afford a better understanding of the vibration behavior of square tube arrays.

Experimental Setup

The experimental setup is shown schematically in Fig. 1. The setup is a closed water loop system comprising a water channel, a water tank, a pump, and the related pipelines. A tube bundle is placed in the middle of water channel, and a dynamic data acquisition and analysis system is connected to the test section.

Fig. 1

Schematic of the experimental setup

Water Channel

The water channel (Fig. 2a) is 3 m long with a square cross-section of 0.16 m × 0.17 m. Water is pumped from the water tank to the channel and flows through a series of screens to generate uniform water flow before reaching the test section. A weir is installed near the outlet of the water channel to maintain the water level, and the flow rate is controlled by two valves in the pipeline and measured by a flow meter. A maximum flow of 45 m³/h can be achieved by the system.

Fig. 2

Experimental facility: a water channel, b test section

Test Section and Tube Array

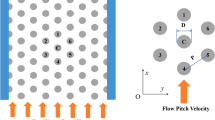
The test section (Fig. 2b) is located in the middle of the water channel, and a test boss is designed to support and fix the tube array. Sight glasses are set on both sides of the test section for observation. Figure 3 shows the tube array used for the tests; this array is originally designed as a cluster of cantilever tubes with a pitch-to-diameter ratio of 1.28. The tube array is arranged as a normal square, and the diameter of the tubes is 25 mm. Each tube is supported by a flexible thin steel rod to effectively reduce the natural frequency, and the tube array is vertically mounted on the test box, as shown in Fig. 3a, to ensure that the active part of the tubes is submerged in the flow.

Fig. 3

a Tube array (unit: mm) and b measuring configuration

Strain gauges are mounted on the rod end of the test tubes (Fig. 3a), which is free from water. Two sets of strain gauges are used on each tube to enable measurement in two perpendicular directions. The accuracy of the strain gauge is less than 1%, and a dynamic data acquisition system (DH5922, Dong Hua Testing Technology Co., Ltd., China) is used to obtain the data. As the dominant frequency is smaller than 20 Hz, the sample frequency is set to 200 Hz in the system. Tubes denoted by 1, 2, and 3 in Fig. 3b are measured in each test.

Velocity

The velocity in the water channel is controlled by the flow meter, and the incoming velocity can be calculated by the following equation.

$$ V = G/A $$

(1)

where V is the incoming velocity, G is the flow rate, and A is effective cross-section of the water channel.

In analyses of tube array systems, the mean gap velocity (or pitch velocity), which reflects the velocity between the gaps of adjacent tubes, is usually used as a reference. The gap velocity of normal and rotated square tube arrays can be expressed by Eqs. (2) and (3), respectively.

Normal square tube array:

$$ V_{\text{p}} = \frac{P}{P - d}V $$

(2)

Rotated square tube array:

$$ V_{\text{p}} = \frac{P}{\sqrt 2 (P - d)}V $$

(3)

Note that V_p is the gap velocity, P is the pitch length, and d is the outer tube diameter.

Natural Frequency

The natural frequency of a tube is a basic parameter in vibration analysis. Experimental and numerical computations are used to obtain this parameter. Two types of natural frequencies are observed in tubes.

• (a) Tube frequency in air

The free vibration method can be used to measure the natural frequency of a single tube. As the density of air is very small, the effect of the inertial forces of a fluid on the tube can be neglected. The frequency obtained is practically identical to the natural frequency in a vacuum. A frequency f_a of 19.531 Hz and logarithmic decrement δ_a of 0.046 can be obtained from experiments. The test result is shown in Fig. 4.

Fig. 4

Free vibration of a single tube in air: a time history, b spectrum

• (b) Tube frequency in water

The frequency of tubes is reduced if they are immerged in water due to the mass of water that weighs on them. Considering the coupling effect of tube arrays, testing the free vibration of a single tube directly in a fully flexible tube array enveloped by closed water channel may be difficult; thus, a numerical method is used to estimate the natural frequency of a tube in a tube array in water. Calculations are carried out in ANSYS CFX 14.0, and the f_a of the experimental structure and δ_a in air are input as initial conditions. A natural frequency f_w of 16.480 Hz and a logarithmic decrement δ_w of 0.074 can be obtained from the computation. The result is shown in Fig. 5.

Fig. 5

Free vibration of a tube in still water: a time history, b spectrum

Vibration Behaviors at Different Velocities

According to the vibration characteristics of tube arrays at different velocities, the velocities can be divided into four regions:

• (a) V_p = 0.65–0.89 m/s, irregular turbulent buffeting region (Fig. 6): Tube vibrations in this velocity range are mainly affected by random turbulent buffeting, in which tubes vibrate slightly under a range of coupled frequencies f_c of tube array.

  Fig. 6

  

  Vibration response at 0.65 m/s: a time history, b spectrum

• (b) V_p = 0.89–1.02 m/s, vortex shedding resonance region (Fig. 7): The vortex shedding frequency f_v corresponds to the f_w of the tubes in this region, and this relationship causes tube resonance. Significant vibrations occur in the front two rows of the tube array, and the dominant frequency is close to f_w.

  Fig. 7

  

  Vibration response at 0.89 m/s: a time history, b spectrum

• (c) V_p= 1.02–1.17 m/s, turbulence buffeting phase before fluidelastic instability (Fig. 8): With the increasing velocity, f_v deviates from f_w. A significant decrease in vibration amplitude occurs, and the vibration frequencies shift to a broader spectrum.

  Fig. 8

  

  Vibration response at 1.02 m/s: a time history, b spectrum

• (d) V_p = 1.17–1.41 m/s, fluidelastic instability region (Fig. 9): In this region, the vibration amplitude increases abruptly, and obvious tube instability occurs.

  Fig. 9

  

  Vibration response at 1.41 m/s: a time history, b spectrum

Numerical Model

Assumption

The computations are carried out using the commercial software ANSYS CFX 14.0. To simplify the fluid–structure model, several assumptions are made before establishment.

• (a) Period boundary condition

A 3D model is needed to capture the vortex stretch along the tube length [17]. Large computational resources are needed to construct a full model of the tube array due to the large length-to-diameter ratio applied. A period boundary condition along the tube length can be used to reduce the calculation cost by considering periodic characteristics along the tube length statistically [23,24,25]. In previous research on a numerical model [31], model size is reduced in the tube direction for both time savings and numerical accuracy.

• (b) Rigid body movement

As a period boundary is adopted, tube deformation in a period can be neglected in comparison to tube displacement. Tubes can be considered rigid, and springs can be mounted on the rigid body to substitute elastic forces (Fig. 10). The spring coefficient can be calculated as:

$$ k = \omega^{2} m $$

(4)

where k is the spring coefficient used to set the elastic boundary of the tube, $\omega$ is the circular frequency of the tube, and m is the mass per length of the tube.

Fig. 10

Rigid body-spring system

Modeling

A 3D tube model, shown in Fig. 11, can be established based on the experimental parameters (Table 1) and assumptions above. A cubic fluid field with a uniform flow inlet and pressure outlet is adopted to simulate the test section in a water channel. A total of 25 tubes are arranged 5 × 5 to achieve a normal square in the fluid domain. Moving mesh boundaries and rigid body movements are established to ensure that the tubes can vibrate under the fluid forces. All tubes feature their own local coordinates and are free to oscillate in the streamwise and transverse directions.

Fig. 11

Model of the tube array

Table 1 Parameters of the model

In previous work [31], a numerical model for fluidelastic instability, including the choice of turbulence model, model size, and reliability of the coarse grid, was elaborated in detail. Here, only the results are utilized. LES WALE is used as the turbulence model, and transient analysis is carried out with a time step of 0.0002 s. The mesh of the model is shown in Fig. 12.

Fig. 12

Meshing: a plane mesh, b local mesh, c 3D structure

Computations are performed in an HP Z800 workstation (8 cores with 96 GB RAM) in the High-performance Computing Center of Tianjin University (12 CPUs allocated).

Results and Discussion

Comparison Between the Experiment and Numerical Simulations

Comparisons between the experiment and numerical simulation are shown in Fig. 13, which illustrates the ratio of RMS tube displacement to tube diameter versus velocity for tubes 2 and 3. Due to the linear correlation of strain and displacement in the range of measurement, the strain data obtained from experiment are converted to displacements by directly calibrating strains with displacement values to enable convenient comparison. The results show good agreement between the experiment and simulations.

Fig. 13

Comparison of RMS tube response versus velocity diagrams obtained by numerical calculations and the experiment. a streamwise direction of tube 2, b transverse direction of tube 2, c streamwise direction of tube 3, d transverse direction of tube 3

A comparison of the spectra of tube 2 obtained at different velocities from the experiment and simulations is shown in Fig. 14. Simulations show good agreement in the spectra. The dominant frequency determined by the simulation agrees well with that obtained from the experiment, which verifies the reliability of the proposed simulation method in investigating the characteristics of fluidelastic instability.

Fig. 14

Comparison between the experimental and computational spectra at different velocities: a streamwise direction spectrum of the experiment at 0.94 m/s, b streamwise direction spectrum of the simulation at 0.94 m/s, c transverse direction spectrum of the experiment at 0.94 m/s, d transverse direction spectrum of the simulation at 0.94 m/s, e streamwise direction spectrum of the experiment at 1.06 m/s, f streamwise direction spectrum of the simulation at 1.06 m/s, g transverse direction spectrum of the experiment at 1.06 m/s, h transverse direction spectrum of the simulation at 1.06 m/s, i streamwise direction spectrum of the experiment at 1.2 m/s, j streamwise direction spectrum of simulation at 1.2 m/s, k transverse direction spectrum of the experiment at 1.2 m/s, l transverse direction spectrum of the simulation at 1.2 m/s

According to the changes in the tube vibration spectra in Fig. 14, the tubes mainly respond in two regions of the spectra. The first region occurs around f_w. Significant vibrations at this frequency occur when f_v corresponds to f_w (Fig. 14a–d). As f_v varies with velocity, vibrations at this frequency decrease sharply when f_v deviates from f_w, and only a small influence of shedding frequency can be seen in the spectra (Fig. 14g–l). The second region involves a series of frequencies around 14 Hz. These frequencies are related to several values of f_c in the whole tube system and mainly affect turbulent buffeting and fluidelastic instability. Turbulent buffeting is a random vibration phenomenon in which the spectrum disperses over a broad range of f_c with relatively small amplitudes. Turbulent buffeting is affected by fluctuations in turbulent flow. The dominant frequency of fluidelastic instability also occurs within f_c. In contrast to the behavior of turbulent buffeting, the vibration of fluidelastic instability occurs in a narrow band of the spectrum with very large vibration amplitudes, corresponding to a single peak frequency. Typical spectra of fluidelastic instability are shown in Fig. 14e–j. According to the analysis above, a critical velocity of 1.06 m/s can be estimated from the transformations of the spectra.

Changes in the Dominant Vibration Direction

Another interesting phenomenon that can be observed in the experiment is that the dominant vibration direction of each tube changes significantly as the velocity increases beyond the critical velocity. This observation is seldom reported in previous research. Responses in the streamwise and transverse directions are added to each plot for comparison in Fig. 15. Vibrations in the streamwise direction are larger than those in the transverse direction for tubes 2 and 3 at 1.17 m/s. As the velocity increases to 1.45 m/s, however, this trend changes. The vibration amplitudes of tube 2 in the streamwise and transverse direction becomes nearly identical, while the amplitude of the transverse vibration of tube 3 becomes much larger than that of the streamwise vibration.

Fig. 15

Transformation of the dominant vibration direction: a response of tube 2 at 1.17 m/s, b response of tube 3 at 1.17 m/s, c response of tube 2 at 1.45 m/s, d response of tube 3 at 1.45 m/s

This same trend can be seen in Fig. 13. According to the response curves obtained, the increases in vibration amplitudes in the streamwise and transverse directions with respect to velocity do not occur at the same pace. The vibration amplitudes in the streamwise direction of tubes 2 and 3 increase at about 1.06 m/s, which is estimated as the critical velocity of the tube array. The vibration amplitudes in the transverse direction increase later but faster than those in the streamwise direction at about 1.2 m/s. As such, following this trend, we can predict that the dominant vibration direction for most tubes will change to the transverse direction.

The change in dominant vibration direction is mainly related to the change in vibration patterns of the tube array. Figure 16 shows the orbits of tube movement at 1.2 and 1.41 m/s plotted by simulation. While all the tubes vibrate streamwise at 1.2 m/s (Fig. 16a), most of the principle axes of the orbits of movement change significantly at 1.4 m/s (Fig. 16b). Transverse vibrations dramatically increase with the increasing velocity. The dominant vibration direction of the first row of tubes completely changes during transverse vibration, but the tube motions of the 2nd and 4th rows are more likely to point toward the center after instability occurs. This pattern is slightly different from the vibration pattern of tube arrays with a large pitch ratio [9], where all of the tubes show mainly transverse vibrations. The observed change in dominant vibration direction may be related to some vibration patterns of the tube array that enable easier conveyance of energy from the fluid to the tube system, which reflects more “unstable” movement.

Fig. 16

Orbits of tube movement (scale: 4): aV_p = 1.2 m/s, bV_p = 1.41 m/s

Phase Lag Relationship Between Adjacent Tubes

As tube arrays in water flow always have a small mass damping parameter δ_s (the δ_s calculated in the experiment is about 0.283), fluidelastic instability is generally controlled by the damping mechanism. However, no fluidelastic instability is observed [14] when only a flexible tube in a rigid tube array with a P/d = 1.33 is present. In this case, instability is only affected by the damping mechanism. Thus, a fully flexible tube array becomes unstable only when the pitch ratio is relatively small, which means that the stiffness mechanism may be used to explain unstable behaviors despite a small δ_s. Fluidelastic instability in a tube array with a small pitch may be significantly affected by the interaction of neighboring tubes. As such, the relationship between vibrating tubes must be clarified to obtain a better understanding of the instability of tube arrays.

A specific phase lag between adjacent tubes can be observed in both the experiment and simulations. Figure 17 shows the phase relationship of adjacent tubes at different velocities. The time-history curves of tubes 2 and 3 are given in each plot. In Fig. 17a, b, the vibrations of tubes 2 and 3 do not show a fixed phase lag relationship before 1.06 m/s, which is the critical velocity V_c of the tube array. When the velocity increases to V_c, a phase lag of 180° begins to emerge (Fig. 17c), and this phenomenon is maintained as long as the velocity is larger than V_c (Fig. 17d). This change coincides with the occurrence of fluidelastic instability, so it may also be used as a method to predict the threshold of fluidelastic instability. We emphasize here that this phase relationship is not continuously sustained at 1.06 m/s. Over the whole response history of the tubes, sudden increases and decreases in amplitude are observed, and only in the period where a large-amplitude vibration exists is the 180° phase relationship assured. This finding further indicates that the tube array at this velocity is in a subcritical state of fluidelastic instability. The same relationship can be seen in the simulations (Fig. 18), but notable phenomena occur at about 1.2 m/s, which is slightly later compared with that in the experiment.

Fig. 17

Phase relationship between adjacent tubes (experiment): aV_p = 0.84 m/s, bV_p = 1.02 m/s, cV_p = 1.06 m/s, dV_p=1.35 m/s

Fig. 18

Phase relationship between adjacent tubes (simulation): aV_p= 0.94 m/s, bV_p=1.02 m/s, cV_p=1.12 m/s, dV_p=1.2 m/s

Influence of Pitch-to-Diameter Ratio and Array Pattern

Simulations for other pitch-to-diameter ratios and array patterns (Fig. 19) are presented here for further discussion. The normal and rotated square configurations are simulated, and different behaviors under fluidelastic instability are observed.

Fig. 19

Square array configuration: a normal square array, b rotated square array

In contrast to the simulation above, damping of the material and structure is not counted. Figures 20a, b and 21a, b show the velocity field and tube movement orbits of a normal square array of P/d = 1.28 and P/d = 1.5 under fluidelastic instability, respectively. The most obvious difference between these two cases is that significant vortices are formed behind tubes of P/d = 1.5, whereas only several flow lanes can be seen between columns of P/d = 1.28. With increasing tube amplitude, the vortices become irregular because they are disturbed by the movement of the tubes. The movement orbits observed at P/d = 1.5 (Fig. 21b) are more regular than those at P/d = 1.28 (Fig. 21a) because the tubes mainly vibrate in the transverse direction. Figure 22a and b infers that the critical velocities of the two tube arrays are 0.81 and 0.88 m/s, respectively.

Fig. 20

Velocity fields of different tube arrays: a normal square array, P/d =1.28, b normal square array, P/d =1.5, c rotated square array, P/d =1.28, d rotated square array, P/d =1.5

Fig. 21

Orbits of tube movement of different tube arrays. a normal square array, P/d =1.28, V_p= 0.964 m/s, b normal square array, P/d =1.5, V_p = 1.15 m/s, c rotated square array, P/d = 1.28, V_p = 0.97 m/s, d rotated square array, P/d =1.5, V_p = 0.96 m/s

Fig. 22

RMS tube response versus velocity diagrams of different tube arrays: a normal square array, P/d =1.28, b normal square array, P/d =1.5, c rotated square array, P/d =1.28, d rotated square array, P/d =1.5

On account of the staggered arrangement of the tubes, the flow paths of the rotated square array are quite complicated, which makes the vibration of the tubes much more chaotic. Figures 20c–d and 21c–d show some cases of the rotated square array. In a tube array, tubes feature their own special orientations, and most tubes show an angle of approximately 45° relative to the flow direction. Many small vortices are formed behind tubes even in a tube array with a pitch ratio of 1.28, but these vortices immediately collide with other tubes, causing large turbulences in the flow field. The critical velocities of P/d = 1.28 and P/d = 1.5 are 0.71 and 0.77 m/s, respectively (Fig. 22c–d).

Connors’ formula with an empirical value of K is often used to determine the critical velocity in practice. The Connors’ formula can be expressed as:

$$ \frac{{V_{\text{c}} }}{{f_{\text{w}} D}} = K\left( {\frac{{m\delta_{\text{w}} }}{{\rho D^{2} }}} \right)^{0.5} = K\delta_{\text{s}}^{0.5} $$

(5)

The K values obtained from the experiment and simulations in this paper are compared with those in different references in Table 2.

Table 2 Comparison of fluidelastic coefficients

Table 2 reveals that the K values obtained from formulas besides the Connors’ formula are smaller than the present results. The K in references is obtained by the mean value or low boundary of all published experimental data. Neither theory nor the data are sufficient to establish values of K for δ_s < 0.7, and a much more conservative value of K is usually chosen in this range to ensure design safety. This limitation explains why the results of this paper are generally larger than the reference values provided.

Conclusions

This paper investigated some characteristics of fluidelastic instability in square tube arrays using both experimental and numerical methods. A closely packed normal square array with a pitch ratio of 1.28 was tested under a range of flow velocities, and different ranges of tube responses were presented. A fluid–structure coupling model for fluidelastic instability was established, and calculation results were compared with experimental results. Predictions of the critical velocity and spectrum were in good agreement with the experimental findings, although poor predictions of the amplitude of tube vibrations were observed. Changes in dominant vibration direction under fluidelastic instability were observed in both the experiment and simulations. This transformation was related to changes in the vibration patterns of the whole tube system. The vibration direction of tubes in rows 2–4 pointed toward the central tube in a fully unstable tube array, which was different from the vibration pattern observed in tube arrays with a large pitch ratio. A phase lag of 180° between adjacent tubes was observed, which was consistent with the instability of the tube array; this phase lag can be used to estimate the critical velocity and only appeared when large-amplitude vibrations occur in time history. The influence of tube configuration and pitch ratio was also discussed in this paper, and the basic vibration patterns of normal and rotated square array were compared. In a normal square array, movement orbits of P/d =1.5 were more regular than those of P/d =1.28 and tubes in row vibrate in the same orientation. Tubes in a rotated square array feature special orientations, most of which showed an angle of approximately 45° relative to the flow direction. The coefficient K obtained from the Connors’ formula presented in this paper was compared with those obtained from other formulas, and the results enrich the data at δ_s < 0.7, especially for tube arrays with a small pitch ratio.