Skip to main content
SpringerLink
Log in

Study on the prediction method of onset and propagation of damage of unit composite lattice structure

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

The progressive failure behavior of a unit composite lattice structure under compressive load was predicted using cohesive zone model (CZM). Mode I, II and mixed mode I/II interlaminar fracture toughness tests were conducted to obtain a set of cohesive zone parameters. To predict failure behavior through numerical analysis, a FEM was generated by considering the three problems of composite lattice structure: differences in the fiber volume fraction, discontinuity in mechanical properties, and generation of wedge-shaped resin rich parts. To select the position of cohesive elements, first numerical analysis was performed, and cohesive elements were applied to the layer with the highest failure index of quadratic nominal stress criterion. The results of numerical analysis with cohesive element were well matched with the test result. These results showed that CZM based numerical analysis method is an effective way to predict and evaluate the onset and growth of progressive failure of unit composite lattice structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

Crack length

a c :

Distance between hoop ribs

a h :

Distance between helical ribs

b :

Width of the specimen

c :

Lever length

E f :

Fiber modulus

E L :

Longitudinal direction modulus

E m :

Matrix modulus

E T :

Transverse direction modulus

G I :

Mode I energy release rate

G II :

Mode II energy release rate

G Ic :

Critical energy release rate for mode I

G IIC :

Critical energy release rate for mode II

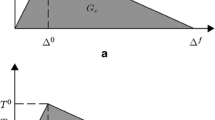
G C :

Sum of GIC and GIIC

G T :

Total energy release rate

H :

Thickness of lattice structure

h :

Half-thickness of specimen

K :

Cohesive stiffness

L :

Half-span of specimen

L’ :

Length of lattice structure

M :

Mass of lattice structure

N max :

Maximum interlaminar normal tensile strength

P :

Load

R :

Radius of lattice structure

S max :

Maximum interlaminar sliding shear strength

T max :

Maximum interlaminar scissoring shear strength

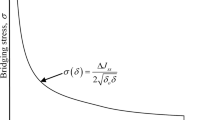
δ :

Displacement

δ c :

Thickness of hoop rib

δ f :

Cohesive ductility

δ h :

Thickness of helical rib

λ :

Crack length correction parameter

ν f :

Fiber Poisson ratio

ν m :

Matrix Poisson ratio

ρ c :

Density of hoop rib

ρ h :

Density of helical rib

σ n :

Nominal stress in the pure normal direction

ρ s :

Nominal stress in the first shear direction

ρ t :

Nominal stress in the second shear direction

τ i (I = 1, 2, 3):

Interfacial normal or shear tractions for pure mode i

ρ ulf :

Ultimate stress

References

  1. V. V. Vasiliev and A. F. Rasin, Anisogrid composite lattice structures for spacecraft and aircraft applications, Composite Structures, 76 (2006) 182–189.

    Article  Google Scholar 

  2. V. V. Vasiliev, V. A. Barynin and A. F. Rasin, Anisogrid lattice structures-survey of development and applications, Composite Structures, 54 (2011) 361–370.

    Article  Google Scholar 

  3. V. V. Vasiliev, V. A. Barynin and A. F. Razin, Anisogrid composite lattice structures-development and aerospace applications, Composite Structures, 94 (2012) 1117–1127.

    Article  Google Scholar 

  4. V. A. Barynin, V. A. Bunakov, A. F. Rasin and V. V. Vasiliev, Aerospace composite lattice structure, Proc. of ICCM, Paris, France (2009).

  5. M. Belardo, N. Paletta and U. Mercurio, Conceptual design of the composite sandwich fuselage of a re-entry vehicle, Materialwissenschaft und Werkstofftechnik, 46(4–5) (2015) 420–430.

    Article  Google Scholar 

  6. P. K. Krishan and P. Muruganantham, Design and analysis of a typical inter-tank structure of a launch vehicle using integrally stiffened construction, International J. of Research in Engineering and Technology, 1(1) (2013) 21–34.

    Google Scholar 

  7. O. M. Querin et al., Topology and Parametric Optimization of a Lattice Composite Fuselage Structure, Altair University, Retrieved April 13 (2021) https://altairuniversity.com/wp-content/uploads/2014/04/Topology_and_Parametric_Optimization-of-a-Latice_Composite_Fuselage_Structure_as_published.pdf (2014).

  8. H. Kanou, S. M. Nabavi and J. E. Jam, Numerical modeling of stresses and buckling loads of isogrid lattice composite structure cylinders, International of Engineering, Science and Technology, 5(1) (2013) 42–54.

    Article  Google Scholar 

  9. ASTM D5528, Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-reinforced Polymer Matrix Composites, ASTM International (2001).

  10. ASTM D6671, Standard Test Method for Mixed Mode I-Mode II Interlaminar Fracture Toughness of Unidirectional Fiber Reinforced Polymer Matrix Composites, ASTM International (2006).

  11. ASTM D6641, Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials Using a Combined Loading Compression (CLC) Test Fixture, ASTM International (2009).

  12. R. F. Gibson, Principles of Composite Material Mechanics, CRC Press, Florida, USA (2011).

    Book  Google Scholar 

  13. W. D. Callister, Jr. and D. G. Rethwisch, Fundamentals of Materials Science and Engineering: An Integrated Approach, 2nd ed., Wiley, Hoboken, USA (2004) 592.

    Google Scholar 

  14. D. Hull and T. W. Clyne, An Introduction to Composite Materials, 2nd ed, Cambridge University Press, New York, USA (1996) 177–179.

    Book  Google Scholar 

  15. W. Cui, M. Wisnom and M. Jones, A comparison of failure criteria to predict delamination of unidirectional glass/epoxy specimens waisted through the thickness, Composites, 23(3) (1992) 158–166.

    Article  Google Scholar 

  16. P. P. Camanho, C. G. Davila and M. F. de Moura, Numerical simulation of mixed-mode progressive delamination in composite materials, J. of Composite Materials, 37(16) (2003) 1415–1438.

    Article  Google Scholar 

  17. M. Kenane and M. L. Benzeggagh, Mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites under fatigue loading, Composites Science and Technology, 57(5) (1997) 597–605.

    Article  Google Scholar 

  18. T. Diehl, On using a penalty-based cohesive-zone finite element approach, part I: elastic solution benchmarks, International J. of Adhesion and Adhesives, 28(4) (2008) 237–255.

    Article  Google Scholar 

  19. J. M. Im, S. G. Kang, K. B. Shin and T. K. Hwang, Prediction of onset and propagation of damage of in the adhesive joining of a dome-separated composite pressure vessel including temperature effects, International J. of Precision Engineering and Manufacture, 18(12) (2017) 1795–1804.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Mechanical Engineering, Hanbat National University, Daejeon, 34158, Korea

    Jae-Moon Im

  2. Department of Mechanical Engineering, Hanbat National University, Daejeon, 34158, Korea

    Kwang-Bok Shin

Authors
  1. Jae-Moon Im
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kwang-Bok Shin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kwang-Bok Shin.

Additional information

Jae-Moon Im is a Ph.D. candidate in Mechanical Engineering, Hanbat National University, Daejeon, Rep. of Korea. His research interest is in composite materials and structures.

Kwang-Bok Shin is a Professor of Mechanical Engineering, Hanbat National University, Daejeon, Rep. of Korea. His research interest is in composite material, composite structures and CAE.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Im, JM., Shin, KB. Study on the prediction method of onset and propagation of damage of unit composite lattice structure. J Mech Sci Technol 36, 3081–3088 (2022). https://doi.org/10.1007/s12206-022-0538-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-022-0538-3

Keywords

Search

Navigation