Skip to main content
SpringerLink
Log in

Implicit CP FEM scheme for twinning materials

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

Many computational papers have dealt with twinning in a crystal plasticity framework. Considerable former works have proposed constitutive theories based on continuum mechanics and crystal plasticity to consider the complex response of materials deformed by twinning. However, many of the former computational twinning papers did not provide the detailed implementation procedures that were used to produce their simulation results. Given that the mechanical response of materials deformed by twinning is highly nonlinear and complex, a sophisticated numerical scheme is needed. The complex interaction among various slip and twin modes causes different kinds of interaction hardening in their slip/twin systems and therefore makes the mechanical response of twinning materials change abruptly. Such a change causes difficulty in convergence and typically requires the use of small time steps, making the simulation time lengthy. To deal with this highly nonlinear and rapidly changing mechanical response of twinning materials effectively, an implicit time integration scheme that considers the constitutive theories of twinning materials is proposed in this study. The proposed implicit computational scheme for twinning materials is derived in a way that the scheme is effectively implemented in a large deformation finite element (FE) code. This study uses the experimental data of single and poly crystal magnesium shown in Refs. [1, 2] and successfully reproduces the strain-strain responses. The simulation results indicate that twinning causes more numerical difficulties than the slip process. The proposed implicit time integration crystal plasticity FE method (CP FEM) scheme provides better efficiency, accuracy, stability, and robustness than previously used explicit CP FEM schemes, especially in dealing with the numerical difficulties associated with twinning.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

Length of a side in the basal plane hexagon

C e :

Elasticity modulus tensor

c :

C-axis length of the HCP atomic structure

D :

Symmetric part of the velocity gradient

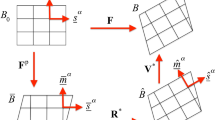
F:

Deformation gradient

f β :

Twin volume fraction of the β -th twin system

h :

Self-hardening modulus

K :

Bulk modulus

L :

Velocity gradient

\({\underline {\hat m} ^\alpha }\) :

Slip direction of the α -th slip system

\({\underline {\hat m} ^\beta }\) :

Twin direction of the β -th twin system

N s :

Number of slip systems

N tw :

Number of twin systems

n :

Rate-dependent law power constant

q αβ :

Latent hardening modulus between two modes of α and β

R*:

Deformation gradient related to elastic lattice rotation

\({{\bar r}^\alpha }\) :

Relative activity of the α -th (twin or slip) mode

\({\underline {\hat s} ^\alpha }\) :

Slip plane normal of the α -th slip system

\({\underline {\hat s} ^\beta }\) :

Twin plane normal of the β -th twin system

\({{\bf{\hat T}}^ \ast }\) :

Second Piola-Kirchhoff stress at \({\hat B}\) configuration

\(\underline T \) :

Traction vector

\(\underline U \) :

Displacement vector

V*:

Deformation gradient related to elastic stretching

W :

Antisymmetric part of velocity gradient

Ẏ α :

Plastic strain rate in the α -th slip or twin system

Ẏ 0 sl :

Referential strain rate for slip

Ẏ 0 tw :

Referential strain rate for twinning

Y tw :

Constant related to shear strain

ε*:

Small strain elasticity tensor

λ :

Lamé constant

μ :

Shear modulus

σ :

Cauchy stress

σ m :

Hydrostatic part of the Cauchy stress

σ′:

Deviatoric part of the Cauchy stress

τ :

Kirchhoff stress

τ 0 :

Initial CRSS

τ α :

Stress magnitude in the α -th slip/twin system

τ α0 :

CRSS in the α -th slip/twin system

τ (i)0 :

CRSS in the i-th slip/twin mode

References

  1. E. W. Kelley and W. F. Hosford, The Plastic Deformation of Magnesium, Technical Report, U.S. Army Research Office-Durham, Durham, NC (1967).

    Google Scholar 

  2. E. W. Kelley and W. F. Hosford, Plane-strain compression of magnesium and magnesium alloy crystals, Transactions of the Metallurgical Society of AIME, 242 (1968) 5–13.

    Google Scholar 

  3. C. N. Tomé, R. A. Lebensohn and U. F. Kocks, A model for texture development dominated by deformation twinning: application to zirconium alloys, Acta Metall. Mater., 39 (1991) 2667–2680.

    Article  Google Scholar 

  4. S. R. Kalidindi, Incorporation of deformation twinning in crystal plasticity models, J. Mech. Phys. Solids, 46(2) (1998) 267–290.

    Article  Google Scholar 

  5. A. Izadbakhsh, K. Inal, R. K. Mishra and M. Niewczas, New crystal plasticity constitutive model for large strain deformation in single crystals of magnesium, Computational Materials Science, 50 (2011) 2185–2202.

    Article  Google Scholar 

  6. J. Zhang and S. P. Joshi, Phenomenological crystal plasticity modeling and detailed micromechanical investigations of pure magnesium, J. Mech. Phys. Solids, 60 (2012) 945–972.

    Article  Google Scholar 

  7. J. Selvarajou, B. Kondori, A. A. Benzerga and S. P. Joshi, On plastic flow in notched hexagonal close packed single crystals, J. Mech. Phys. Solids, 94 (2016) 273–297.

    Article  Google Scholar 

  8. A. Staroselsky and L. Anand, Inelastic deformation of polycrystalline face centered cubic materials by slip and twinning, J. Mech. Phys. Solids, 46(4) (1998) 671–696.

    Article  Google Scholar 

  9. A. Staroselsky and L. Anand, A constitutive model for HCP materials deforming by slip and twinning: application to magnesium alloy AZ31B, Int. J. Plasticity, 19 (2003) 1843–1864.

    Article  Google Scholar 

  10. S. Graff, W. Brocks and D. Steglich, Yielding of magnesium: from single crystal to polycrystalline aggregates, Int. J. Plasticity, 23 (2007) 1957–1978.

    Article  Google Scholar 

  11. E. Popova, Y. Staraselski, A. Brahme, R. K. Mishra and K. Inal, Coupled crystal plasticity — probabilistic cellular automata approach to model dynamic recrystallization in magnesium alloys, Int. J. Plasticity, 66 (2015) 85–102.

    Article  Google Scholar 

  12. E. Popova, A. P. Brahme, Y. Staraselski, S. R. Agnew, R. K. Mishra and K. Inal, Effect of extension {1012} twins on texture evolution at elevated temperature deformation accompanied by dynamic recrystallization, Materials and Design, 96 (2016) 446–457.

    Article  Google Scholar 

  13. H. Qiao, M. R. Barnett and P. D. Wu, Modeling of twin formation, propagation and growth in a Mg single crystal based on crystal plasticity finite element method, Int. J. Plasticity, 86 (2016) 70–92.

    Article  Google Scholar 

  14. R. Lebensohn and C. N. Tomé, A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: application to zirconium alloys, Acta Metallurgica et Materialia, 41(9) (1993) 2611–2644.

    Article  Google Scholar 

  15. S. R. Agnew, C. N. Tomé, D. W. Brown, T. M. Holden and S. C. Vogel, Study of slip mechanisms in a magnesium alloy by neutron diffraction and modeling, Scripta Materialia, 48 (2003) 1003–1008.

    Article  Google Scholar 

  16. A. Jain and S. R. Agnew, Modeling the temperature dependent effect of twinning on the behavior of magnesium alloy AZ31b sheet, Materials Science and Engineering A, 462 (2007) 29–36.

    Article  Google Scholar 

  17. S.-H. Choi, E. J. Shin and B. S. Seong, Simulation of deformation twins and deformation texture in an AZ31 Mg alloy under uniaxial compression, Acta Materialia, 55 (2007) 4181–4192.

    Article  Google Scholar 

  18. H. Wang, B. Raeisinia, P. D. Wu, S. R. Agnew and C. N. Tomé, Evaluation of self-consistent polycrystal plasticity models for magnesium alloy AZ31b sheet, International Journal of Solids and Structure, 47 (2010) 2905–2917.

    Article  Google Scholar 

  19. X. Q. Guo, A. Chapuis, P. D. Wu and S. R. Agnew, On twinning and anisotropy in rolled Mg alloy AZ31 under uniaxial compression, International Journal of Solids and Structure, 64–65 (2015) 42–50.

    Article  Google Scholar 

  20. H. Qiao, S. R. Agnew and P. D. Wu, Modeling twinning and detwinning behavior of Mg alloy ZK60a during monotonic and cyclic loading, Int. J. Plasticity, 65 (2015) 61–84.

    Article  Google Scholar 

  21. P. D. Wu, X. Q. Guo, H. Qiao, S. R. Agnew, D. J. Lloyd and J. D. Embury, On the rapid hardening and exhaustion of twinning in magnesium alloy, Acta Materialia, 122 (2017) 369–377.

    Article  Google Scholar 

  22. S. Kweon and D. S. Raja, Investigation of the mechanical response of single crystal magnesium considering slip and twin, International Journal of Plasticity, 112 (2019) 1–17.

    Article  Google Scholar 

  23. S. Kweon, Edge cracking in rolling of an aluminum alloy AA2024-O, PhD Thesis, University of Illinois Urbana-Champaign, USA (2009).

    Google Scholar 

  24. S. Kweon, Damage at negative triaxiality, Eur. J. Mech., 31 (2012) 203–212.

    Article  Google Scholar 

  25. E. B. Marin and P. R. Dawson, On modelling the elastoviscoplastic response of metals using polycrystal plasticity, Comput. Methods Appl. Mech. Engrg., 165 (1998) 1–21.

    Article  Google Scholar 

  26. S. Kweon, Investigation of shear damage considering the evolution of anisotropy, J. Mech. Phys. Solids, 61 (2013) 2605–2624.

    Article  MathSciNet  Google Scholar 

  27. W. F. Hosford, The Mechanics of Crystals and Textured Polycrystals, Oxford University Press, New York (1993).

    Google Scholar 

  28. S. Kweon and A. A. Benzerga, Finite element implementation of a macromolecular viscoplastic polymer model, Int. J. Numer. Meths. Engrg., 94 (2013) 895–919.

    Article  MathSciNet  Google Scholar 

  29. D. Tromans, Elastic anisotropy and HCP metal crystals and polycrystals, International Journal of Recent Research and Applied Studies (IJRRAS), 6(4) (2011) 462–483.

    MathSciNet  Google Scholar 

  30. T. R. Long and C. S. Smith, Single-crystal elastic constants of magnesium and magnesium alloys, Acta Metallurgica et Materialia, 5(4) (1957) 200–207.

    Article  Google Scholar 

  31. L. Slutsky and C. Garland, Single-crystal elastic constants of magnesium and magnesium alloys, Physical Review, 107(4) (1957) 972–976.

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by a grant from Seed grants for Transitional and Exploratory Projects at Southern Illinois University Edwardsville, whose title is “investigation on the effect of anisotropy on the ductile fracture process of metals.”

Author information

Authors and Affiliations

  1. Mechanical Engineering, Southern Illinois University Edwardsville, Edwardsville, Illinois, 62026, USA

    Soondo Kweon & Daniel S. Raja

Authors
  1. Soondo Kweon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Daniel S. Raja
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Soondo Kweon.

Additional information

Soondo Kweon is an Associate Professor in the Mechanical Engineering Department at Southern Illinois University Edwardsville, USA. He received his Ph.D. in Mechanical Engineering from the University of Illinois at Urbana-Champaign. His research interests include crystal plasticity, finite element methods, solid mechanics, ductile fracture, and J2 plasticity.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kweon, S., Raja, D.S. Implicit CP FEM scheme for twinning materials. J Mech Sci Technol 35, 4585–4603 (2021). https://doi.org/10.1007/s12206-021-0928-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-021-0928-y

Keywords

Search

Navigation