Investigation of the effects of twinning on the mechanical response of polycrystal magnesium

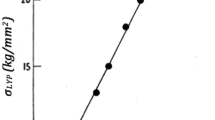
Abstract

Hexagonal close-packed (HCP) metals show highly anisotropic mechanical responses due to twinning, slip and the interaction among various slip and twin systems. Each HCP metal shows different sets of activated slip and twin systems. The interaction among slip and twin systems causes highly nonlinear and rapidly changing hardening behaviors in the critical resolved shear stress (CRSS) of each slip/twin system. To accurately understand the anisotropic mechanical response of HCP metals, both single-crystal and polycrystal tests must be performed. The interaction among different slip and twin systems shows different behaviors in the single-crystal and polycrystal settings since the interacting environments are different. The fitting process of the single crystal and polycrystal stress–strain data involves a series of trials and errors to find the correct interaction patterns among various slip and twin systems. The fitting procedures used in previous researches take a lot of times of trials and errors and are not guided by any physical property. Therefore, this study employs a recently proposed new fitting procedure, which is based on a physical property, the saturation strength of the material, to fit magnesium experimental data more efficiently with a less number of trials and errors. Compared to the slip process, twinning is computationally more difficult to take into account due to the directionality of the twin process, i.e., twinning occurs only in one direction, not in the opposite direction unlike the slip process. The rapidly changing highly nonlinear interaction hardening behaviors among various slip and twin systems are computationally challenging. Both of the above computational difficulties require a more robust and accurate numerical scheme than previously used ones to obtain accurate representations of experimental data. Therefore, this study proposes a more accurate and robust numerical scheme for the hardening strengths (CRSS) of twin/slip systems and interaction hardening. The newly proposed scheme is based upon implicit time integration, which enhances accuracy and stability. Using the proposed fitting procedure and the implicit integration scheme for hardening strength (CRSS) and interaction hardening, the experimental stress–strain data of polycrystal magnesium shown in Kelley and Hosford (The plastic deformation of magnesium. Technical report, 1967, Trans Metall Soc AIME 242:5–13, 1968) are successfully reproduced.

Appendices

Appendix A: Implementation of the constitutive theory

The constitutive equations are written into residual vector forms with a vector set of variables as follows:

$$\begin{aligned}{}[{\varvec{R}}]^T= & {} \bigg [{\varvec{R}}_{{{{\varvec{\sigma }}}}'}, \; R_{{{\sigma }}_{\mathrm{m}}}, \; {\varvec{R}}_{f^{\alpha }},\; {\varvec{R}}_{\tau _0^{(i)}} \bigg ]. \end{aligned}$$

(A.1)

$$\begin{aligned} ^T= & {} \bigg [{{{\varvec{\sigma }}}}', \;{ {\sigma }}_{\mathrm{m}}, \; f^{\alpha }, \; \tau _0^{(i)} \bigg ] \end{aligned}$$

(A.2)

where ${{{\varvec{\sigma }}}}'$ and ${ {\sigma }}_{\mathrm{m}}$ are the deviatoric part and hydrostatic part of the Cauchy stress ${{{\varvec{\sigma }}}}$, respectively. $\tau _0^{(i)}$ is the CRSS of the i-th mode. $\alpha$ varies from 1 to $N_{tw}$, which is the number of the twin systems; twelve systems (six for tensile twin and six for compressive twin) are used, i.e., $N_{tw}=12$ in this study. (i) varies from 1 to $N_{\mathrm{modes}}$, which is the number of the slip/twin modes; seven modes are employed, i.e., $N_{\mathrm{modes}}=7$ in this study. The hardening of the CRSS of a slip/twin mode is traced at the mode level, not at the system level, in order to better take into account the physics of hardening, i.e., accumulations of dislocations and to facilitate the data fitting process. The residual equations for the stress tensors ${{{\varvec{\sigma }}}}'$ and ${ {\sigma }}_{\mathrm{m}}$ are derived from Eqs. (7), (8), (9) and (10). The residual equation for the state variable $f^{\alpha }$ is derived from Eq. (16) or (18) depending on the level of the twin volume fraction and their evolution rate. The residual equation for the state variable $\tau _0^{(i)}$ is derived from Eq. (20). The residual equations are derived using an implicit time integration scheme (backward Euler) as follows:

$$\begin{aligned} {\varvec{R}}_{{ {{\varvec{\sigma }}}}'} = \frac{1}{2 \mu } \bigg ( \frac{{{\varvec{\sigma }}}'- {{\varvec{\sigma }}}_0'}{\Delta t} \bigg ) + \hat{{\varvec{D}}}^\mathrm{p} + \frac{1}{2 \mu } ( {\varvec{\sigma }}' \hat{{\varvec{W}}}^{\mathrm{p}} - \hat{{\varvec{W}}}^{\mathrm{p}} {\varvec{\sigma }}' ) -\frac{\Delta {{\varvec{D}}}'}{\Delta t} \end{aligned}$$

(A.3)

where

$$\begin{aligned} \hat{{\varvec{W}}}^{\mathrm{p}}= & {} {\varvec{W}} - \frac{1}{2\mu } ( {\varvec{\sigma }}' \hat{{\varvec{D}}}^{\mathrm{p}} - \hat{{\varvec{D}}}^{\mathrm{p}} {\varvec{\sigma }}') + \frac{1}{(2\Delta t)}\frac{1}{(4\mu ^2)} ( {\varvec{\sigma }}' {\varvec{\sigma }}'_0 - {\varvec{\sigma }}'_0 {\varvec{\sigma }}' ) \end{aligned}$$

(A.4)

$$\begin{aligned} \hat{{\varvec{D}}}^{\mathrm{p}}= & {} \sum ^{N_s}_{\alpha =1}{\dot{\gamma }}^{\alpha }\hat{{\varvec{P}}}^{\alpha } + \sum ^{N_{tw}}_{\beta =1}{\dot{\gamma }}^{\beta }\hat{{\varvec{P}}}^{\beta }, {\hat{P}}^{\alpha }_{ij}=\frac{1}{2}( {\hat{s}}^{\alpha }_{i} {\hat{m}}^{\alpha }_{j} + {\hat{s}}^{\alpha }_{j} {\hat{m}}^{\alpha }_{i}) \end{aligned}$$

(A.5)

$$\begin{aligned} R_{\sigma _{\mathrm{m}}}= & {} \sigma _{\mathrm{m}} - (\sigma _{\mathrm{m}})_0 - K \Delta D_{{kk}} \end{aligned}$$

(A.6)

$$\begin{aligned} {\varvec{R}}_{f^{\alpha }}= & {} \frac{(f^{\alpha }-(f^{\alpha })_0)}{\Delta t} - \frac{{\dot{\gamma }}^0_{tw}}{\gamma ^{tw}} \bigg< \frac{{\varvec{\sigma }}':{\varvec{P}}^{\alpha }}{\tau _0^{(i)}} \bigg >^{n}, \;\mathrm{for} \; f^{\alpha }< f_{\mathrm{crit}}(=0.6) \; \mathrm{and} \;{\bar{r}}^{(i)} < {\bar{r}}_{\mathrm{crit}}(=0.5) \end{aligned}$$

(A.7)

$$\begin{aligned} {\varvec{R}}_{f^{\alpha }}= & {} \frac{(f^{\alpha }-(f^{\alpha })_0)}{\Delta t} - \frac{{\dot{\gamma }}^0_{tw}}{\gamma ^{tw}} \bigg < \frac{{\varvec{\sigma }}':{\varvec{P}}^{\alpha }}{\tau _0^{(i)}} \bigg >^{n} {\bar{r}}^{(i)}, \;\mathrm{for} \; f^{\alpha } \ge f_{\mathrm{crit}}(=0.6) \; \mathrm{or} \;{\bar{r}}^{(i)} \ge {\bar{r}}_{\mathrm{crit}}(=0.5) \end{aligned}$$

(A.8)

$$\begin{aligned} {\varvec{R}}_{\tau _0^{(i)}}= & {} \tau _0^{(i)}-(\tau _0^{(i)})_0 - h^{(i)}\Delta {\bar{\gamma }}^{(i)} -\sum _{(j)=1, (j)\ne (i)}^{(j)=N_{\mathrm{modes}}} q_{(i)(j)}\Delta {\bar{\gamma }}^{(j)} \end{aligned}$$

(A.9)

where ${{\varvec{V}}}_0$ and ${\varvec{V}}$ denote the variables at the beginning and at the end of the increment $\Delta t$, respectively. K and $\mu$ are the bulk and shear moduli, respectively. Note that Eq. (A.7) is derived from Eqs. (16) and  (A.8) is derived from Eq. (18); critical values of the twin volume fraction and the relative activity of a twinning mode, i.e., $f_{\mathrm{crit}}$ and ${\bar{r}}_{\mathrm{crit}}$, are used to slow down the rate of twin formation due to interaction hardening among different twin and slip modes.

The above residual equations ($[{\varvec{R}}]^T={\varvec{0}}$) are solved using the Newton–Raphson procedure as follows:

$$\begin{aligned}{}[{\varvec{V}}]_{i+1} = [{{\varvec{V}}}]_i - \bigg [ \frac{\partial [{\varvec{R}}]}{\partial [{{\varvec{V}}}]_{i}} \bigg ]^{-1} [{\varvec{R}}]_{i} \end{aligned}$$

(A.10)

where the subscript i represents the iteration number, $[{\varvec{V}}]_{i}$ represents the value of the variable $[{\varvec{V}}]$ at the beginning of the iteration and $[{\varvec{V}}]_{i+1}$ represents the value of the variable $[{\varvec{V}}]$ at the end of the iteration. The consistent tangent matrices $( \frac{\partial {\varvec{\sigma }}}{\partial {\varvec{L}}}, \frac{\partial {\varvec{\sigma }}}{\partial {\varvec{D}}}, \frac{\partial {\varvec{\sigma }}}{\partial {\varvec{W}}} )$ need to be provided in a crystal plasticity finite element code to find the converged displacement vector at each node. The detailed expressions for the components of the Jacobian matrix $\bigg [ \frac{\partial [{\varvec{R}}]}{\partial [{\varvec{V}}]} \bigg ]$ are provided in “Appendix B.”

The evolution of the grain orientation is expressed by Eq. (10). Equation (10) is integrated employing an explicit scheme with the exponential map function as follows:

$$\begin{aligned} {\varvec{R}}^*=\mathrm{expm}\bigg [ \bigg \{\hat{{\varvec{W}}}^{\mathrm{p}} -\bigg ( \sum ^{N_s}_{\alpha =1}{\dot{\gamma }}^{\alpha }\hat{{\varvec{Q}}}^{\alpha } + \sum ^{N_{tw}}_{\beta =1}{\dot{\gamma }}^{\beta }\hat{{\varvec{Q}}}^{\beta } \bigg ) \bigg \} \Delta t \bigg ] {\varvec{R}}_0^*,\;\;\;{\hat{Q}}^{\alpha }_{ij}=\frac{1}{2}( {\hat{s}}^{\alpha }_{i} {\hat{m}}^{\alpha }_{j} - {\hat{s}}^{\alpha }_{j} {\hat{m}}^{\alpha }_{i}) \end{aligned}$$

(A.11)

Note that ${\varvec{R}}^*$ is the only variable that is explicitly updated in this study, which allows the use of a larger time step than codes that employ mainly explicit updates for the stress tensor and its state variables.

Appendix B: Jacobian Matrix

The expressions for each component of the Jacobian matrix $\bigg [ \frac{\partial [{\varvec{R}}]}{\partial [{\varvec{V}}]} \bigg ]$ are provided as follows:

$$\begin{aligned} \frac{\partial {\varvec{R}}_{{\varvec{\sigma }}'}}{\partial {\varvec{\sigma }}'} = \frac{1}{2 \mu \Delta t }\mathbb {J} + {\mathcal {B}} +{\mathcal {N}} \end{aligned}$$

(B.1)

where $\mathbb {J}$ denotes the deviatoric projection operator, i.e., $\mathbb {J}_{ijkl} = \frac{1}{2}(\delta _{ik} \delta _{jl} + \delta _{il} \delta _{jk} ) - \frac{1}{3} \delta _{ij} \delta _{kl}$,¹ and the fourth-order tensor ${\mathcal {B}}$ is defined as

$$\begin{aligned} {\mathcal {B}}= & {} \frac{\partial \hat{{\varvec{D}}}^{\mathrm{p}}}{\partial {\varvec{\sigma }}'}, \;\; {\mathcal {B}}_{ijkl}= \sum _{\alpha =1}^{N_s}\frac{\partial {\dot{\gamma }}^{\alpha }}{\partial \tau ^{\alpha }} {\hat{P}}^{\alpha }_{ij} {\hat{P}}^{\alpha }_{kl} + \sum _{\beta =1}^{N_{tw}}\frac{\partial {\dot{\gamma }}^{\beta }}{\partial \tau ^{\beta }} {\hat{P}}^{\beta }_{ij} {\hat{P}}^{\beta }_{kl} \end{aligned}$$

(B.3)

$$\begin{aligned} \frac{\partial {\dot{\gamma }}^{\alpha }}{\partial \tau ^{\alpha }}= & {} n {\dot{\gamma }}^0_{sl} \bigg | \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{\tau ^{(i)}_0} \bigg |^{n-1} \frac{1}{\tau ^{(i)}_0}, \;\;\;\ \frac{\partial {\dot{\gamma }}^{\beta }}{\partial \tau ^{\beta }} = n {\dot{\gamma }}^0_{tw} \bigg <\frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\beta }}{\tau ^{(i)}_0} \bigg >^{n-1} \frac{1}{\tau ^{(i)}_0} \end{aligned}$$

(B.4)

and the fourth-order tensor ${\mathcal {N}}$ is defined as

$$\begin{aligned} {\mathcal {N}} = \frac{\partial }{\partial {\varvec{\sigma }}'} \bigg [ \frac{1}{2\mu } ({\varvec{\sigma }}'\hat{{\varvec{W}}}^{\mathrm{p}} - \hat{{\varvec{W}}}^{\mathrm{p}} {\varvec{\sigma }}') \bigg ] \end{aligned}$$

(B.5)

The expression of ${{\mathcal {N}}}_{ijkl}$ is referred to [30, 32].

$$\begin{aligned} \frac{\partial {\varvec{R}}_{{\varvec{\sigma }}'}}{\partial {\sigma }_{\mathrm{m}}} = {\varvec{0}}_{(\mathrm 9x1)} \end{aligned}$$

(B.6)

where ${\varvec{0}}_{(\mathrm 9x1)}$ denotes a zero tensor of which dimension is 9 by 1 and components are all zero.

$$\begin{aligned} \frac{\partial {\varvec{R}}_{{\varvec{\sigma }}'}}{\partial f^{\alpha }}= & {} {\varvec{0}}_{( 9 \mathrm{x} N_{tw})} \end{aligned}$$

(B.7)

$$\begin{aligned} \frac{\partial {\varvec{R}}_{{\varvec{\sigma }}'}}{\partial \tau _0^{(i)}}= & {} \frac{\partial \hat{{\varvec{D}}}^{\mathrm{p}}}{\partial \tau _0^{(i)}} + \bigg ({\varvec{\varepsilon }}^{*'}\frac{\partial \hat{{\varvec{W}}}^{\mathrm{p}}}{\partial \tau _0^{(i)}} - \frac{\partial \hat{{\varvec{W}}}^{\mathrm{p}}}{\partial \tau _0^{(i)}} {\varvec{\varepsilon }}^{*'} \bigg ) \end{aligned}$$

(B.8)

$$\begin{aligned} \frac{\partial \hat{{\varvec{D}}}^{\mathrm{p}}}{\partial \tau _0^{(i)}}= & {} \sum _{\alpha =1}^{N_s} \frac{\partial {\dot{\gamma }}^{\alpha }}{\partial \tau _0^{(i)}} \hat{{\varvec{P}}}^{\alpha } + \sum _{\beta =1}^{N_{tw}} \frac{\partial {\dot{\gamma }}^{\beta }}{\partial \tau _0^{(i)}} \hat{{\varvec{P}}}^{\beta } \end{aligned}$$

(B.9)

$$\begin{aligned} \frac{\partial {\dot{\gamma }}^{\alpha }}{\partial \tau _0^{(i)}}= & {} n {\dot{\gamma }}^0_{sl} \bigg | \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{\tau _0^{(i)}} \bigg |^{(n-1)} ({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }) (-1) (\tau _0^{(i)})^{-2} \end{aligned}$$

(B.10)

$$\begin{aligned} \frac{\partial {\dot{\gamma }}^{\beta }}{\partial \tau _0^{(i)}}= & {} n {\dot{\gamma }}^0_{tw} \bigg < \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\beta }}{\tau _0^{(i)}} \bigg >^{(n-1)} ({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\beta }) (-1) (\tau _0^{(i)})^{-2} \end{aligned}$$

(B.11)

$$\begin{aligned} \frac{\partial \hat{{\varvec{W}}}^{\mathrm{p}}}{\partial \tau _0^{(i)}}= & {} - \bigg ({\varvec{\varepsilon }}^{*'}\frac{\partial \hat{{\varvec{D}}}^{\mathrm{p}}}{\partial \tau _0^{(i)}} - \frac{\partial \hat{{\varvec{D}}}^{\mathrm{p}}}{\partial \tau _0^{(i)}} {\varvec{\varepsilon }}^{*'} \bigg ) \end{aligned}$$

(B.12)

$$\begin{aligned} \frac{\partial {R}_{\sigma _{\mathrm{m}}}}{\partial {\varvec{\sigma }}'}= & {} {\varvec{0}}_{(1\mathrm{x}9)} \end{aligned}$$

(B.13)

$$\begin{aligned} \frac{\partial {R}_{\sigma _{\mathrm{m}}}}{\partial \sigma _{\mathrm{m}}}= & {} 1 \end{aligned}$$

(B.14)

$$\begin{aligned} \frac{\partial {R}_{\sigma _{\mathrm{m}}}}{\partial f^{\alpha }}= & {} {\varvec{0}}_{(1\mathrm{x}N_{tw})} \end{aligned}$$

(B.15)

$$\begin{aligned} \frac{\partial {R}_{\sigma _{\mathrm{m}}}}{\partial \tau _0^{(i)}}= & {} {\varvec{0}}_{(1\mathrm{x}N_{\mathrm{modes}})} \end{aligned}$$

(B.16)

$$\begin{aligned} \frac{\partial {R}_{f^{\alpha }}}{\partial {\varvec{\sigma }}'}= & {} \left\{ \begin{array}{l l l} \displaystyle { - n\frac{{\dot{\gamma }}^0_{tw}}{\gamma ^{tw}} \bigg< \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{{\tau _0^{(i)}}} \bigg>^{n-1} \frac{1}{\tau _0^{(i)}} \hat{{\varvec{P}}}^{\alpha } , \;\; \mathrm{for} \;\; f^{\alpha }< f_{\mathrm{crit}} \;\mathrm{and} \;\;{\bar{r}}^{(i)}< {\bar{r}}_{\mathrm{crit}}} \\ \displaystyle { - n\frac{{\dot{\gamma }}^0_{tw}}{\gamma ^{tw}} \bigg < \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{{\tau _0^{(i)}}} \bigg >^{n-1} \frac{1}{\tau _0^{(i)}} \hat{{\varvec{P}}}^{\alpha }{\bar{r}}^{(i)} , \;\; \mathrm{for} \;\; f^{\alpha } \ge f_{\mathrm{crit}} \;\mathrm{or} \;\;{\bar{r}}^{(i)} \ge {\bar{r}}_{\mathrm{crit}}} \end{array} \right. \end{aligned}$$

(B.17)

$$\begin{aligned} \frac{\partial {R}_{f^{\alpha }}}{\partial \sigma _{\mathrm{m}}}= & {} {\varvec{0}}_{(N_{tw}\mathrm{x}1)} \end{aligned}$$

(B.18)

$$\begin{aligned} \frac{\partial {R}_{f^{\alpha }}}{\partial f^{\beta }}= & {} \frac{1}{\Delta t} \delta _{\alpha \beta } \end{aligned}$$

(B.19)

$$\begin{aligned}&\frac{\partial {R}_{f^{\alpha }}}{\partial \tau _0^{(i)}} \nonumber \\&\quad = \left\{ \begin{array}{l l l l l} \displaystyle { 0, \;\; \mathrm{for \; i=1\;to\;5} }\\ \\ \displaystyle { - n\frac{{\dot{\gamma }}^0_{tw}}{\gamma ^{tw}} \bigg< \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{{\tau _0^{(i)}}} \bigg>^{n-1} ({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }) (-1)(\tau _0^{(i)})^{-2}, \; \mathrm{for} \;\; f^{\alpha }< f_{\mathrm{crit}} \;\mathrm{and} \;\;{\bar{r}}^{(i)}< {\bar{r}}_{\mathrm{crit}}} \\ \\ \displaystyle { - n\frac{{\dot{\gamma }}^0_{tw}}{\gamma ^{tw}} \bigg < \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{{\tau _0^{(i)}}} \bigg >^{n-1} ({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }) (-1)(\tau _0^{(i)})^{-2} {\bar{r}}^{(i)}, \; \mathrm{for} \;\; f^{\alpha } \ge f_{\mathrm{crit}} \;\mathrm{or} \;\;{\bar{r}}^{(i)} \ge {\bar{r}}_{\mathrm{crit}}} \end{array} \right. \end{aligned}$$

(B.20)

$$\begin{aligned}&h^{(i)}({\bar{\gamma }}) \nonumber \\&\quad =\left\{ \begin{array}{l l l l l} \displaystyle { h_0 \bigg ( 1- \frac{\tau _0}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) \exp {\bigg ( - \frac{h_0({\bar{\gamma }}_0+\sum _{i=1}^{N_{\mathrm{modes}}}\Delta {\bar{\gamma }}^{(i)})}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg )}, \;\; \mathrm{for \; i=1\;to\;5} } \\ \\ \left\{ \begin{array}{l l l} h_0, \;\;\;\mathrm{for}\; {\bar{\gamma }}^{(6)}\le \gamma _{\mathrm{ref}} \\ \\ \displaystyle { h_0 \left( \frac{{\bar{\gamma }}^{(6)}}{\gamma _{\mathrm{ref}}} \right) ^{m-1} }, \;\;\;\mathrm{for}\; {\bar{\gamma }}^{(6)} > \gamma _{\mathrm{ref}} \end{array} \right\} \; \mathrm{for \; i=6 } \\ \\ \displaystyle { h_0}, \; \;\;\mathrm{for\; i=7\;} \end{array} \right. \end{aligned}$$

(B.21)

$$\begin{aligned} \zeta ^{(i)}= & {} [ 1, \zeta , 1, 1, 1]^T \end{aligned}$$

(B.22)

$$\begin{aligned} \kappa ^{(i)}= & {} [ 1, 1, 1, \kappa , \kappa ]^T \end{aligned}$$

(B.23)

$$\begin{aligned} (\tau _{\infty })_0^{(i)}= & {} [ 3, 73.44, 86.4, 198, 165]^T \end{aligned}$$

(B.24)

$$\begin{aligned} \Delta {\bar{\gamma }}^{(i)}= & {} \left\{ \begin{array}{l l l} \displaystyle { \sum _{\alpha =1}^{N^{(i)}}{\dot{\gamma }}^0_{sl} \bigg | \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{{\tau _0^{(i)}}} \bigg |^{n} \Delta t , \;\; \mathrm{for \; i=1\;to\;5} }\\ \\ \displaystyle { \sum _{\beta =1}^{N^{(i)}}{\dot{\gamma }}^0_{tw} \bigg < \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\beta }}{{\tau _0^{(i)}}} \bigg >^{n} \Delta t , \;\; \mathrm{for \; i=6\;and\;7}} \end{array} \right. \end{aligned}$$

(B.25)

Note that $N^{(i)}$ is the number of systems in a slip or twin mode.

$$\begin{aligned} \frac{\partial {\varvec{R}}_{\tau _0^{(i)}}}{\partial {\varvec{\sigma }}'}= & {} -\sum _{j=1}^{N_{\mathrm{modes}}}\frac{\partial h^{(i)}}{\partial \Delta {\bar{\gamma }}^{(j)}} \frac{\partial \Delta {\bar{\gamma }}^{(j)}}{\partial {\varvec{\sigma }}'} \Delta {\bar{\gamma }}^{(i)} -h^{(i)}\frac{\partial \Delta {\bar{\gamma }}^{(i)}}{\partial {\varvec{\sigma }}'} -\sum _{j=1}^{N_{\mathrm{modes}}} q_{(i)(j)} \frac{\partial \Delta {\bar{\gamma }}^{(j)}}{\partial {\varvec{\sigma }}'}, \;\; \mathrm{no \;summation\; on\; (i)}\nonumber \\ \end{aligned}$$

(B.26)

$$\begin{aligned} \frac{\partial \Delta {\bar{\gamma }}^{(i)}}{\partial {\varvec{\sigma }}'}= & {} \left\{ \begin{array}{l l l} \displaystyle { \sum _{\alpha =1}^{N^{(i)}} n {\dot{\gamma }}^0_{sl} \bigg | \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{{\tau _0^{(i)}}} \bigg |^{n-1} \mathrm{sgn}({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }) \frac{1}{\tau _0^{(i)}} \hat{{\varvec{P}}}^{\alpha } \Delta t , \;\; \mathrm{for \; i=1\;to\;5} }\\ \\ \displaystyle { \sum _{\beta =1}^{N^{(i)}} n {\dot{\gamma }}^0_{tw} \bigg < \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\beta }}{{\tau _0^{(i)}}} \bigg >^{n-1} \frac{1}{\tau _0^{(i)}} \hat{{\varvec{P}}}^{\beta } \Delta t, \;\; \mathrm{for \; i=6\;and\;7}} \end{array} \right. \end{aligned}$$

(B.27)

$$\begin{aligned} \begin{aligned}&\frac{\partial h^{(i)}}{\partial \Delta {\bar{\gamma }}^{(j)}} \\&\quad =\left\{ \begin{array}{l l l | |} \left. \begin{aligned} &{}\displaystyle { h_0 \bigg ( 1- \frac{\tau _0}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) \exp {\bigg ( - \frac{h_0 {\bar{\gamma }}}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) } \bigg ( -\frac{h_0}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg )} \\ \\ &{}\displaystyle { + h_0 \bigg ( - \frac{\tau _0}{\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) (-1)(\zeta ^{(i)})^{-2} \frac{\partial \zeta ^{(i)}}{\partial \Delta {{\bar{\gamma }}}^{(j)}} \exp {\bigg ( - \frac{h_0 {\bar{\gamma }}}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) } \delta _{i2} } \\ \\ &{}\displaystyle { + h_0 \bigg ( 1- \frac{\tau _0}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) \exp {\bigg ( - \frac{h_0 {\bar{\gamma }}}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) } \bigg ( -\frac{h_0 {{\bar{\gamma }}}}{\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg )*} \\ \\ &{}\displaystyle {(-1)(\zeta ^{(i)})^{-2} \frac{\partial \zeta ^{(i)}}{\partial \Delta {{\bar{\gamma }}}^{(j)}}\delta _{i2} } \end{aligned} \;\; \right\} \mathrm{for \; i=1\;to\;5}\\ \\ \left\{ \begin{aligned} &{}\displaystyle { 0, \;\; \mathrm{for}\;\; {{\bar{\gamma }}}^{(6)} \le \gamma _{\mathrm{ref}} } \\ \\ &{}\displaystyle { \delta _{6j}h_0(m-1)\bigg (\frac{{{\bar{\gamma }}}^{(6)}}{\gamma _{\mathrm{ref}}}\bigg )^{m-2}\frac{1}{\gamma _{\mathrm{ref}}}, \;\; \mathrm{for}\;\; {{\bar{\gamma }}}^{(6)} > \gamma _{\mathrm{ref}}} \end{aligned} \;\; \right\} \mathrm{for \; i=6} \\ \\ \left. \displaystyle { 0 } \;\; \right\} \mathrm{for \; i=7} \end{array} \right. \end{aligned} \end{aligned}$$

(B.28)

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} &{}\frac{\partial \zeta ^{(i)}}{\partial \Delta {{\bar{\gamma }}}^{(j)}} = 0, \;\; \mathrm{except} \\ \\ &{} \frac{\partial \zeta ^{(2)}}{\partial \Delta {{\bar{\gamma }}}^{(1)}} = \left\{ \begin{array}{l l l} 0, \;\; \mathrm{for} \; {{\bar{\gamma }}}^{(1)} \le {{\bar{\gamma }}}^{(1)}_{\mathrm{crit}} \\ \\ 2.7563*0.2160*({{\bar{\gamma }}}^{(1)})^{(0.2160-1)}, \;\; \mathrm{for} \; {{\bar{\gamma }}}^{(1)}> {{\bar{\gamma }}}^{(1)}_{\mathrm{crit}} \end{array} \right. \\ \\ &{} \frac{\partial \zeta ^{(2)}}{\partial \Delta {{\bar{\gamma }}}^{(5)}} = \left\{ \begin{array}{l l l} 0, \;\; \mathrm{for} \; {{\bar{\gamma }}}^{(5)} \le {{\bar{\gamma }}}^{(5)}_{\mathrm{crit}} \\ \\ 1.559*0.0558*({{\bar{\gamma }}}^{(5)})^{(0.0558-1)}, \;\; \mathrm{for} \; {{\bar{\gamma }}}^{(5)} > {{\bar{\gamma }}}^{(5)}_{\mathrm{crit}} \end{array} \right. \end{aligned} \end{array} \right\} \qquad \qquad \qquad \qquad \qquad \quad \ \end{aligned}$$

(B.29)

$$\begin{aligned} \frac{\partial {\varvec{R}}_{\tau _0^{(i)}}}{\partial \sigma _{\mathrm{m}}} =&{\varvec{0}}_{(N_{\mathrm{modes}}\mathrm{x}1)} \end{aligned}$$

(B.30)

$$\begin{aligned} \frac{\partial {\varvec{R}}_{\tau _0^{(i)}}}{\partial f^{\alpha }} =&-\frac{\partial h^{(i)}}{\partial f^{\alpha }} \Delta {\bar{\gamma }}^{(i)},\; \mathrm{no\;summation\;on\;(i)} \end{aligned}$$

(B.31)

$$\begin{aligned}&\frac{\partial h^{(i)}}{\partial f^{\alpha }} \nonumber \\&\quad =\left\{ \begin{array}{l l l} \left. \begin{array}{l l l | |} \displaystyle { h_0 \bigg ( - \frac{\tau _0}{\zeta ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) (-1)(\kappa ^{(i)})^{-2} \frac{\partial \kappa ^{(i)}}{\partial f^{\alpha }} \exp {\bigg ( - \frac{h_0 {\bar{\gamma }}}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) } } \\ \\ \displaystyle { + h_0 \bigg ( 1 - \frac{\tau _0}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) \exp {\bigg ( - \frac{h_0 {\bar{\gamma }}}{\zeta ^{(i)}\kappa ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg ) } * }\\ \\ \displaystyle { \bigg \{ - \frac{h_0 {\bar{\gamma }}}{\zeta ^{(i)}(\tau _{\infty })_0^{(i)}} \bigg \} (-1)(\kappa ^{(i)})^{-2} \frac{\partial \kappa ^{(i)}}{\partial f^{\alpha }} } \end{array} \right\} \;\;\mathrm{for \; i=1\;to\;5} \\ \\ \displaystyle {0, \;\; \mathrm{for \; i=6\;and\;7}} \end{array} \right. \end{aligned}$$

(B.32)

$$\begin{aligned}&\quad \frac{\partial \kappa ^{(i)}}{\partial f^{\alpha }} \nonumber \\&\quad = \left\{ \begin{array}{l l l} \displaystyle {0, \;\; \mathrm{for \; i=1\;to\;3}} \\ \\ \left\{ \begin{array}{l l l} \displaystyle { 3.3892*0.5956*f_{TT}^{(0.5956-1)}*\delta _{1-6,\alpha }+7.5*\delta _{7-12,\alpha }, \;\mathrm{for}\;f_{TT} \le f_{\mathrm{crit}}} \\ \\ \left\{ \begin{array}{l l l} \displaystyle { 4.2128*10^{-11}*\exp {(41.9051*f_{TT})} } \\ \\ \displaystyle { *41.9051*\delta _{1-6,\alpha }+7.5*\delta _{7-12,\alpha }} \end{array} \right\} , \;\;\mathrm{for}\;f_{TT} > f_{\mathrm{crit}} \end{array} \right\} \;\;\mathrm{for \; i=4\;and\;5} \end{array} \right. \end{aligned}$$

(B.33)

where $\delta _{1-6,\alpha }$ and $\delta _{7-12,\alpha }$ are defined as follows.

$$\begin{aligned} \delta _{1-6,\alpha }= & {} \left\{ \begin{array}{l l l} 1, \;\; if\;\alpha =1 \;to\; 6 \\ \\ 0, \;\; if\;\alpha =7 \;to\; 12 \end{array} \right. \end{aligned}$$

(B.34)

$$\begin{aligned} \delta _{7-12,\alpha }= & {} \left\{ \begin{array}{l l l} 0, \;\; if\;\alpha =1 \;to\; 6 \\ \\ 1, \;\; if\;\alpha =7 \;to\; 12 \end{array} \right. \end{aligned}$$

(B.35)

$$\begin{aligned}&\frac{\partial {\varvec{R}}_{\tau _0^{(i)}}}{\partial \tau _0^{(j)}}=\delta _{ij} -\bigg ( \frac{\partial h^{(i)}}{\partial \Delta {{\bar{\gamma }}}^{(j)}} \frac{\partial \Delta {{\bar{\gamma }}}^{(j)}}{\partial \tau _0^{(j)}} \Delta {{\bar{\gamma }}}^{(i)} + h^{(i)} \delta _{ij} \frac{\partial \Delta {{\bar{\gamma }}}^{(i)}}{\partial \tau _0^{(j)}} \bigg ) \nonumber \\&-q_{(i)(j)}\frac{\partial \Delta {{\bar{\gamma }}}^{(j)}}{\partial \tau _0^{(j)}},\;\;\mathrm{no\;summation\;on\;}(i)\;\mathrm{and}\; (j) \end{aligned}$$

(B.36)

$$\begin{aligned} \begin{aligned}&\frac{\partial \Delta {{\bar{\gamma }}}^{(j)}}{\partial \tau _0^{(j)}} \\ \\&\quad = \left\{ \begin{array}{l l l} \displaystyle { \delta _{ij}\sum _{\alpha =1}^{N^{(i)}} n {\dot{\gamma }}^0_{sl} \bigg | \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }}{{\tau _0^{(i)}}} \bigg |^{n-1} \mathrm{sgn}({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }) ({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\alpha }) (-1)( \tau _0^{(i)})^{-2} \Delta t , \;\; \mathrm{for \; i=1\;to\;5} }\\ \\ \displaystyle { \delta _{ij}\sum _{\beta =1}^{N^{(i)}} n {\dot{\gamma }}^0_{tw} \bigg < \frac{{\varvec{\sigma }}':\hat{{\varvec{P}}}^{\beta }}{{\tau _0^{(i)}}} \bigg >^{n-1} ({\varvec{\sigma }}':\hat{{\varvec{P}}}^{\beta }) (-1)( \tau _0^{(i)})^{-2} \Delta t, \;\; \mathrm{for \; i=6\;and\;7}} \end{array} \right. \end{aligned} \end{aligned}$$

(B.37)

Appendix C: How to integrate the proposed CP theory and numerical scheme into a finite element code

The PDEs of the boundary value problem are the static force equilibrium equation, the strain compatibility equations (strain–displacement relationship) and the constitutive equation (stress–strain relationship). The PDEs of static force equilibrium are written as follows:

$$\begin{aligned} \sigma _{ij,j}+f_i=0 \end{aligned}$$

(C.1)

Fig. 9

Flowchart that describes the solving procedure for a boundary value problem with the CP constitutive theory and numerical scheme proposed in this study using FEM

where $f_i$ denotes the body force in the i-th direction. The PDEs of strain compatibility (strain–displacement relationship) in the rate form are expressed as follows:

$$\begin{aligned} D_{ij}={\dot{\varepsilon }}_{ij}=\frac{1}{2}({\dot{U}}_{i,j}+{\dot{U}}_{j,i})=\frac{1}{2}(v_{i,j}+v_{j,i}) \end{aligned}$$

(C.2)

where ${\varvec{D}}$ is the symmetric part of velocity gradient, ${\underline{U}}$ is the displacement vector and ${\underline{v}}$ is the velocity vector ($v_i=\frac{\Delta U_i}{\Delta t}$). The constitutive equation (stress–strain relationship) part is explained in detail in Sect. 2. Section 2 describes an isotropic elasticity crystal plasticity constitutive theory. The key constitutive equations are Eqs. (4), (5), (13) (or (15)) and (17). These key equations are converted into residual forms using an implicit time integration scheme, which are Eqs. (A.3) to (A.9). The PDEs of static force equilibrium have 3 equations since they are written in the vector form. The PDEs of strain compatibility (strain-displacement relationship) in the rate form have 6 equations since they are written in the second-order tensor form. The constitutive equation (stress–strain relationship) part has 6 equations since they are written in the second-order tensor form. To solve a boundary value problem, the above 15 equations (3 equilibrium PDEs + 6 compatibility PDEs + 6 constitutive equations) need to be solved simultaneously together with boundary conditions to obtain the displacement (or velocity) field. The numerical techniques needed to solve the entire PDEs above mentioned are not presented since describing all the numerical techniques to solve the entire PDEs is beyond the scope of one single paper; the main numerical scheme to solve the entire PDEs is finite element method; since finite element method is well explained by many books and papers in the past, detailed explanations are skipped in this paper; this paper includes only part of the solving procedures for the entire PDEs; this paper as done in typical constitutive theory papers proposes and presents numerical schemes needed to solve only the constitutive equation (stress–strain relationship) part leaving the solving procedure for the rest PDEs handled by finite element method; the proposed numerical schemes for the constitutive equation part are explained in detail in Appendices A and B. Although detailed explanation of the solving procedure for the rest PDEs is impossible in this single paper, a rough flowchart that explains the solving steps and how the solving procedure for the constitutive equation is connected to the solving procedure for the entire PDEs is presented in Fig. 9.