Skip to main content
SpringerLink
Log in

Development of the large increment method in analysis for thin and moderately thick plates

  • Published:
Journal of Shanghai Jiaotong University (Science) Aims and scope Submit manuscript

Abstract

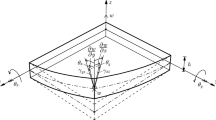
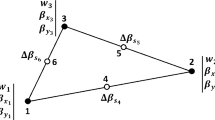
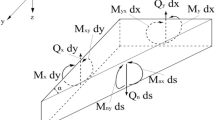
Many displacement-based quadrilateral plate elements based on Mindlin-Reissner plate theory have been proposed to analyze the thin and moderately thick plate problems. However, numerical inaccuracies of some elements appear since the presence of shear locking and spurious zero energy modes for thin plate problems. To overcome these shortcomings, we employ the large increment method (LIM) for the analyses of the plate bending problems, and propose a force-based 8-node quadrilateral plate (8NQP) element which is based on Mindlin-Reissner plate theory and has no extra spurious zero energy mode. Several benchmark plate bending problems are presented to illustrate the accuracy and convergence of the plate element by comparing with the analytical solutions and displacement-based plate elements. The results show that the 8-node plate element produces fast convergence and accurate stress distributions in both the moderately thick and thin plate bending problems. The plate element is insensitive to mesh distortion and it can avoid the shear locking for thin plate analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zienkiewicz O C, Taylor R L, Too J M. Reduced integration technique in general analysis of plates and shells [J]. International Journal Numerical Methods in Engineering, 1971, 3(2): 275–290.

    Article  Google Scholar 

  2. Hughes T J R, Cohen M, Haron M. Reduced and selective integration techniques in the finite element analysis of plates [J]. Nuclear Engineering and Design, 1978, 46(1): 203–222.

    Article  Google Scholar 

  3. Hinton E, Huang H C. A family of quadrilateral Mindlin plate elements with substitute shear strain fields [J]. Computers and Structures, 1986, 23(3): 409–431.

    Article  Google Scholar 

  4. Darilmaz K. An assumed-stress finite element for static and free vibration analysis of Reissner-Mindlin plates [J]. Structural Engineering and Mechanics, 2005, 19(2): 199–215.

    Article  Google Scholar 

  5. Cheung Y K, Chen W J. Hybrid quadrilateral element based onMindlin/Reissner plate theory [J]. Computers and Structures, 1989, 32(2): 327–339.

    Article  MATH  Google Scholar 

  6. Zhang H X, Kuang J S. Eight-node Reissner-Mindlin plate element based on boundary interpolation using Timoshenko beam function [J]. International Journal for Numerical Methods in Engineering, 2007, 69(7): 1345–1373.

    Article  MATH  Google Scholar 

  7. Zhang C J, Liu X L. A large increment method for material nonlinearity problems [J]. Advances in Structural Engineering, 1997, 1(2): 99–109.

    Google Scholar 

  8. Long D B, Liu X L. Development of 2D hybrid equilibrium elements in large increment method [J]. Journal of Shanghai Jiaotong University (Science), 2013, 18(2): 205–215.

    Article  Google Scholar 

  9. Jia Hong-xue, Long Dan-bing, Liu Xi-la. Application of large increment method in plate analysis [J]. Journal of Shanghai Jiaotong University, 2013, 47(2): 187–206 (in Chinese).

    MathSciNet  Google Scholar 

  10. Barham W, Aref A J, Dargush G. Development of the large increment method for elastic perfectly plastic analysis of plane frame structures under monotonic loading [J]. International Journal of Solids and Structures, 2005, 42: 6586–6609.

    Article  MATH  Google Scholar 

  11. Barham W, Aref A J, Dargush G F. On the elastoplastic cyclic analysis of plane beam structures using a flexibility-based finite element approach [J]. International Journal of Solids and Structures, 2008, 45: 5688–5704.

    Article  MATH  Google Scholar 

  12. Wang Kai-jian. Network parallel computation based on the large increment method [D]. Beijing: Department of Civil Engineering, Tsinghua University, 2004 (in Chinese).

    Google Scholar 

  13. Ben-Israel A, Greville T N E. Generalized inverse: Theory and application [M]. New York: Wiley, 1974.

    Google Scholar 

  14. Dhananjaya H R, Pandey P C, Nagabhushanam J. New eight node serendipity quadrilateral plate bending element for thin and moderately thick plates using integrated force method [J]. Structural Engineering and Mechanics, 2009, 33(4): 485–502.

    Article  Google Scholar 

  15. Timoshenko S, Woinowsk-Krieger S. Theory of plates and shells [M]. New York: McGraw-Hill, 1959.

    Google Scholar 

  16. Liu J, Riggs H R, Tessler A. A four node sheardeformable shell element developed via explicit Kirchhoff constraints [J]. International Journal Numerical Methods in Engineering, 2000, 49: 1065–1086.

    Article  MATH  Google Scholar 

  17. Morley L S D. Skew plates and structures, series of monographs in aeronautics and astronautics [M]. New York: MacMillan, 1963.

    Google Scholar 

  18. Ayad R, Rigolot A. An improved four-node hybridmixed element based upon Mindlin’s plate theory [J]. International Journal for Numerical Methods in Engineering, 2002, 55: 705–731.

    Article  MATH  Google Scholar 

  19. Wang Shou-mei, Liu Zhi-yong. The essence and elimination of shear locking [J]. Acta Aeronautica et Astronautica Sinica, 1989, 10(1): 74–78 (in Chinese).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Shanghai Jiaotong University, Shanghai, 200240, China

    Hong-xue Jia  (贾红学)

  2. Department of Architectural Engineering, Southwest Jiaotong University, Chengdu, 610031, China

    Dan-bing Long  (龙丹冰)

  3. Department of Civil Engineering, Shanghai Jiaotong University, Shanghai, 200240, China

    Xi-la Liu  (刘西拉)

Authors
  1. Hong-xue Jia  (贾红学)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dan-bing Long  (龙丹冰)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xi-la Liu  (刘西拉)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hong-xue Jia  (贾红学).

Additional information

Foundation item: the National Natural Science Foundation of China (No. 10872128)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jia, Hx., Long, Db. & Liu, Xl. Development of the large increment method in analysis for thin and moderately thick plates. J. Shanghai Jiaotong Univ. (Sci.) 19, 265–273 (2014). https://doi.org/10.1007/s12204-014-1498-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12204-014-1498-2

Key words

CLC number

Search

Navigation