1 Introduction

Outbreaks of infectious diseases pose a significant threat to human health. One of the most dangerous epidemic diseases that causes a large number of deaths worldwide is hepatitis B. Hepatitis B infection is a viral disease caused by the hepatitis B virus (HBV), which primarily affects the liver. It is a significant global health issue. If left undetected and untreated, this disease can lead to cirrhosis, liver cancer, or liver failure, resulting in substantial morbidity and mortality worldwide. Notably, it is associated with approximately 800,000 deaths annually, primarily from liver cancer and cirrhosis, making it a significant global threat. Additionally, it is estimated that there are over 350 million chronic HBV carriers worldwide. In chronic carriers, HBV persists within the host’s body for an extended period, posing a significant risk to overall health. While many individuals with carrier hepatitis never experience an acute infection, hepatic fibrosis can develop, eventually leading to liver failure. Medical research has revealed that HBV infection is responsible for approximately \(80\%\) of all primary liver cancer cases, highlighting the urgent need for effective techniques to predict and eradicate HBV. Advanced preventive treatments are available to prevent the spread of HBV. Among these measures, routine vaccination programs have been highly effective in controlling the spread of HBV. The virus spreads through contact with an infected person’s blood, semen, or other bodily fluids (see [1,2,3]).

In response to this urgent need, an effective technique is highly necessary to predict and eradicate HBV. Mathematical modeling, like many other epidemiological diseases, is one of the most effective tools used for hepatitis B. Extensive research has been conducted to develop deterministic and stochastic mathematical models for the spread dynamics of infectious diseases (see [2,3,4,5,6,7,8,9,10,11,12,13,14,15] and references therein). The classical SIR model, introduced as early as 1927 by Kermack and McKendrick, remains one of the oldest and most extensively used models in the field of mathematical epidemiology (see [16]). In this study, we will formulate a deterministic model for the transmission of HBV using the classical SIR model concept.

1.1 Mathematical tools and literature survey

In mathematical epidemiology, models depend on an incidence rate which represents the number of individuals who become infected per unit of time, and plays a crucial role in ensuring that the models accurately capture the qualitative dynamics of disease transmission. In the classical SIR model proposed by Kermack and McKendrick, the incidence rate is given by \(\beta SI\), where \(\beta \) represents the infection rate and S and I represent susceptible and infected individuals, respectively. This type of incidence rate is commonly known as mass action incidence or bilinear incidence (see [13, 14, 16, 17]). A widely used alternative to the bilinear incidence rate in epidemic models is the standard incidence rate \(\frac{\beta SI}{N}\), where N represents the total population size. While the bilinear and standard incidence rates coincide when the total population size remains constant, they diverge in cases where the total population size varies. Bilinear incidence is employed in diseases where disease-related contact rises as the population size increases. Standard incidence is utilized in diseases where the contact rate cannot continually increase and is constrained, even with an increase in the population size (see [18]). It is important to note that, bilinear incidence rate might yield unrealistic outcomes for large populations since it implies that the number of individuals getting infected per unit of time increases as the number of susceptible individuals increases, which may not be a realistic assumption. To address this concern, various alternative incidence rates have been proposed in the literature. For instance, in 1978, Anderson and May [19] introduced a saturated incidence rate in the form of \(\frac{\beta SI}{1+\alpha _1S}\), where the saturation factor \(\alpha _1\) represents the effect of epidemic control. Another approach suggested by Capasso and Serio in [20] involves a saturated incidence rate of \(\frac{\beta SI}{1+\alpha _2 I}\), where \(\frac{1}{1+\alpha _2 I}\) accounts for the inhibitory effect resulting from behavioral changes among susceptible individuals or the crowding effect caused by infectives. These alternative approaches aim to overcome the limitations of the bilinear incidence rate and offer a more realistic representation of the infection dynamics. These saturated incidence rates have been utilized by several authors in epidemiological models (see [2, 15]). In 1975, Beddington in [21] and DeAngelis in [22] independently introduced the non-linear incidence rate known as the Beddington–DeAngelis type, expressed as \(\frac{\beta SI}{1+\alpha _1S+\alpha _2I}\). Many researchers have employed this non-linear incidence rate in subsequent studies to describe their epidemiological models (see [23,24,25]). Beddington–DeAngelis type incidence rate can be expressed in three different forms:

  1. (i)

    \(\beta SI\) when both \(\alpha _1\) and \(\alpha _2\) are equal to zero,

  2. (ii)

    \(\frac{\beta SI}{1+\alpha _1S}\) when \(\alpha _2\) is equal to zero,

  3. (iii)

    \(\frac{\beta SI}{1+\alpha _2I}\) when \(\alpha _1\) is equal to zero.

Therefore the Beddington–DeAngelis type incidence rate is a generalization of the bilinear and saturated incidence rates. This is because the Beddington–DeAngelis type incidence rate takes into account inhibition effects such as susceptible individuals taking preventive measures and infected individuals undergoing treatment (\(\alpha _1\) and \(\alpha _2\) parameters). Also, vaccination plays a pivotal role in the prevention of infectious diseases from spreading. Including the vaccination parameter in the model may be necessary to develop models suitable for the disease. Numerous researchers in the literature have extensively investigated mathematical models with vaccination (see [2, 3, 17, 18, 26, 27]).

Epidemiological models are often formulated as systems of non-linear differential or difference equations. When a model represented by a nonlinear system of differential equations is given, this model can be discretized using certain methods. It is important to ensure that the discretized model retains as many dynamical properties of the continuous model as possible. For the purpose of discretization, Euler and Runge–Kutta methods, along with numerous other finite-difference techniques, are commonly used. However, these methods can give rise to certain undesirable dynamical behaviors. These include convergence to incorrect equilibrium points or periodic cycles, as well as numerical instabilities (see [15, 28, 29]). Mickens introduced an innovative approach known as the non-standard finite difference (NSFD) method to address these issues (see [30, 31]). If a property P is observed in both a differential equation and/or its solutions, as well as in the corresponding discrete equation and/or its solutions, it is stated that these two equations are dynamically consistent in terms of property P. For a mathematical model and its finite difference discretization to be considered valid, it is crucial that they are dynamically consistent with each other. The NSFD method has found applications in a wide range of problems, where it has been observed that the resulting discrete models successfully retain the dynamical properties of the corresponding continuous models (see [13, 15, 29, 32,33,34]).

In [23, 24], Kaddar proposed a delayed SIR model with the Beddington–DeAngelis incidence rate given by the system

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}&=\Lambda -\frac{\beta SI}{1+\alpha _1S+\alpha _2I}-\mu S, \\ \frac{dI}{dt}&=\frac{\beta SI}{1+\alpha _1S+\alpha _2I} -(\mu +\nu +\sigma )I, \\ \frac{dR}{dt}&=\nu I-\mu R, \end{aligned} \end{aligned}$$
(1.1)

where \(\Lambda \) denotes the recruitment rate, \(\beta \) is the disease transmission rate, \(\mu \) is the natural death rate. \(\nu \) is the proportion of the infectives that are treated per unit of time, \(\sigma \) is the death rate induced by the disease. Kaddar analyzed some dynamics of the model (1.1). In [15], the model (1.1) was discretized by using a non-standard finite difference scheme using Mickens’s idea, and the authors showed that the discretized model is dynamically consistent with continuous model in terms of some dynamical properties.

In [2], the authors proposed and analyzed an SIR model for the control of HBV spreading by the system

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}&=\Lambda -\frac{\beta SI}{1+\alpha _2I}-(p+\mu ) S, \\ \frac{dI}{dt}&=\frac{\beta SI}{1+\alpha _2I} -(\mu +\nu +\sigma )I, \\ \frac{dR}{dt}&=pS+\nu I-\mu R, \end{aligned} \end{aligned}$$
(1.2)

where p is the proportion of the susceptibles that are vaccinated per unit of time. In [3], the authors constructed a non-standard difference scheme for the model (1.2):

$$\begin{aligned} \frac{S_{n+1}-S_n}{\varphi }= & {} \Lambda -\frac{\beta S_{n}I_n}{1+\alpha _2I_n}-(p+\mu ) S_{1}, \\ \frac{I_{n+1}-I_n}{\varphi }= & {} \frac{\beta S_{n}I_n}{1+\alpha _2I_{n}} -(\mu +\nu +\sigma )I_{n}, \\ \frac{R_{n+1}-R_n}{\varphi }= & {} pS_{n}+\nu I_{n}-\mu R_{n}. \end{aligned}$$

They reached dynamically consistent results with the continuous model under some assumptions on the time step size value h. In [33], the authors discretized the model (1.2) by a different approach:

$$\begin{aligned} \frac{S_{n+1}-S_n}{\varphi }= & {} \Lambda -\frac{\beta S_{n+1}I_n}{1+\alpha _2I_n}-(p+\mu ) S_{n+1}, \\ \frac{I_{n+1}-I_n}{\varphi }= & {} \frac{\beta S_{n+1}I_n}{1+\alpha _2I_{n}} -(\mu +\nu +\sigma )I_{n+1}, \\ \frac{R_{n+1}-R_n}{\varphi }= & {} pS_{n+1}+\nu I_{n+1}-\mu R_{n+1}. \end{aligned}$$

Here \(\varphi \) is a function of h and called the denominator function. The authors have dynamically consistent results with the continuous model without any constraint on the value of h.

In this study, motivated by the papers discussed above, an HBV model incorporating the Beddington–DeAngelis type incidence rate, constant vaccination, and treatment rates has been presented. Firstly, a dynamical analysis has been conducted to determine the existence of positive solutions for the proposed deterministic model, and disease-free and endemic states have been identified. The threshold quantity known as the basic reproduction number \(\mathcal {R}_0\) has been determined using the next-generation matrix method. Subsequently, the local asymptotically stability (LAS) of the model has been analyzed using the linear stability theorem. Poincare-Bendixson theorem has been employed in the global asymptotically stability (GAS) analysis. The presence of a transcritical bifurcation has been established. Then, an NSFD scheme has been developed using Mickens’ approach. By examining the stability properties of the discretized model and comparing them with the corresponding continuous model, their dynamical consistency has been analyzed. Finally, some numerical simulations have been provided to illustrate our theoretical results.

1.2 The formulation of hepatitis B epidemic model

Let N(t) represent the entire population at time t, divided into three classes: susceptible individuals, infected individuals, and recovered individuals denoted respectively by S(t), I(t), and R(t). So, we have \(N(t)=S(t)+I(t)+R(t)\). Here we take into account a constant recruitment rate for the susceptible class, an incidence rate following the Beddington–DeAngelis type, vaccination of the susceptible class, and both natural and disease-induced death rates. Furthermore, we assume that certain infected individuals with sufficient physical strength can recover on their own without requiring medical treatment. Moreover, we make several assumptions for the model that are listed below:

\(a_1.\):

The initial population sizes must be non-negative and denoted as S(0), I(0) and R(0).

\(a_2.\):

All newborn individuals are initially assigned to the susceptible class.

\(a_3.\):

The incidence rate is assumed to follow the Beddington–DeAngelis type.

\(a_4.\):

Successfully vaccinated individuals will be moved to the recovered class.

\(a_5.\):

The recovered population acquires permanent immunity.

By including all of the assumptions, the differential equation system of the HBV model can be formulated as follows:

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}&=\Lambda -\frac{\beta SI}{1+\alpha _1S+\alpha _2I}-(p+\mu )S, \\ \frac{dI}{dt}&=\frac{\beta SI}{1+\alpha _1S+\alpha _2I} -(\mu +\nu +\sigma )I, \\ \frac{dR}{dt}&=pS+\nu I-\mu R, \end{aligned} \end{aligned}$$
(1.3)

with

$$\begin{aligned} S(0)>0, \, I(0)>0, \, R(0)>0. \end{aligned}$$

Parameters used in HBV model (1.3) are non-negative.

1.3 The novelty of the paper

Most of the models examined in the literature are continuous epidemic models. However, as an important part of epidemiology, great importance is given to studies on epidemic models defined in a discrete structure. However, studies on discrete epidemic models are currently very few in the literature. Defining the model discretely or examining the continuous model by discretizing it has many advantages in epidemiology. The fact that epidemic data is generally collected in separate time units (such as daily, monthly or annual) is just one of them. Thus, using discrete models in the mathematical modeling of epidemic diseases may be more useful. These models are more advantageous than continuous ones. On the other hand, difference equations are discrete analogues of ordinary differential equations and are used to study their numerical solutions. In cases where analytical solutions of the system of differential equations cannot be obtained, its discrete structure can be used. Therefore, there is a need to discretize the system to calculate good analytical approximations of the solutions. Meanwhile, the resulting discrete model should preserve the dynamic properties of the original continuous model as much as possible. Recently, the nonstandard finite difference scheme was proposed by Mickens [30, 31] and has received much attention. An important advantage of the Mickens method is that it provides more effective protection of global asymptotic stability (compared to Euler and Runga Kutta methods). To our knowledge, there is no study in the literature that includes both vaccination and general incidence rates that examines both continuous and discrete models. Therefore, we consider a deterministic model that is more general than the models given in the literature and examine both its continuous structure and discrete structure.

1.4 Paper layout

The organization of this paper is as follows. In Sect. 2, we have investigated the dynamical properties of the HBV model (1.3), including the non-negativity and boundedness of solutions, the existence of equilibria, and the computation of the basic reproduction number. The local asymptotic stability of disease-free and endemic equilibria has been conducted. Lastly, the transcritical bifurcation behavior has been investigated. In Sect. 3, the NSFD scheme of the HBV model (1.3) has been constructed. Section 4 is dedicated to studying the dynamical properties of the discretized model that corresponds to the HBV model (1.3). The analysis of non-negativity, boundedness, and stability for the discretized model has been presented in this section. The obtained results indicate that there is dynamical consistency in terms of these properties between the discrete and continuous models. Finally, in the last section, we supplement our results with several numerical simulations for further clarification.

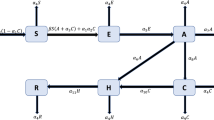
The schematic diagram of the HBV model (1.3) is shown in Fig. 1.

Fig. 1
figure 1

Flow diagram of the HBV model (1.3)

Full size image

2 Dynamical analysis of the continuous model

In this section, we will analyze the qualitative behavior of the solutions of the HBV epidemic model (1.3) at the equilibrium points. First, we will examine the invariance interval and boundedness of solutions.

The requirement of non-negativity for S(t), I(t), and R(t), along with non-negative initial values for all \(t\ge 0\), is a fundamental condition in the HBV model (1.3) due to its biological nature. It is easy to see that the non-negative region \({\mathbb {R}}^3_+\) is a positively invariant set for the HBV model (1.3). Furthermore, it is essential to establish the boundedness of solutions in the HBV model as it reflects the constraints on available resources and prevents uncontrolled population growth. As such, ensuring the non-negativity and boundedness of solutions in the HBV model (1.3) is a biologically relevant consideration, which will be demonstrated in the following analysis. By summing the three equations in the HBV model (1.3) side by side, we reach the following population conservation law

$$\begin{aligned} \frac{dN}{dt}=\Lambda -\mu N-\sigma I\le \Lambda -\mu N. \end{aligned}$$
(2.1)

By solving this ODE, we have

$$\begin{aligned} N(t)\le \frac{\Lambda }{\mu }+\left( N(0) -\frac{\Lambda }{\mu } \right) e^{-\mu t}, \end{aligned}$$
(2.2)

which implies that

$$\begin{aligned} \limsup _{t\rightarrow \infty }N(t)\le \frac{\Lambda }{\mu }, \end{aligned}$$

where \(N(t)=S(t)+I(t)+R(t)\) denotes the total population size. Based on these results, it is enough to examine the HBV model (1.3) within the feasible region

$$\begin{aligned} \Omega _1=\left\{ (S,I,R)\in {\mathbb {R}}^3_+\mid S+I+R \le \frac{\Lambda }{\mu } \right\} . \end{aligned}$$

Remark 1

As the first two equations in the HBV model (1.3) are independent of the third equation, it can be excluded without loss of generality. This leads to the reduction of the HBV model (1.3) as follows:

$$\begin{aligned} \frac{dS}{dt}= & {} \Lambda -\frac{\beta SI}{1+\alpha _1S+\alpha _2I}-(p+\mu )S \nonumber \\ \frac{dI}{dt}= & {} \frac{\beta SI}{1+\alpha _1S+\alpha _2I}-(\mu +\nu +\sigma )I, \end{aligned}$$
(2.3)

with

$$\begin{aligned} S(0)>0, \quad I(0)>0. \end{aligned}$$

We will perform our analysis on the following feasible set:

$$\begin{aligned} \Omega =\left\{ (S,I)\in {\mathbb {R}}^2_+\mid S+I\le \frac{\Lambda }{\mu } \right\} . \end{aligned}$$

2.1 Stability nature of the DFE

If we set the equations’ side on the right in the reduced HBV model (2.3) to zero and assume \(I=0\), it becomes immediately clear that the system always possesses a DFE point

$$\begin{aligned} E_0=(S_0,I_0)=\left( \frac{\Lambda }{p+\mu },0 \right) . \end{aligned}$$

Now, by determining the basic reproduction number denoted as \(\mathcal {R}_0\), locally asymptotically stability at the DFE point will be examined. We can find \(\mathcal {R}_0\) using the next-generation matrix method (see [35]). In the HBV model (2.3), there exists just one infected compartment, identified as I. The basic reproduction number is defined as the spectral radius of the next-generation matrix \(FV^{-1}\), where

$$\begin{aligned} F= & {} \left( \frac{\beta S(1+\alpha _1S)}{(1+\alpha _1S+\alpha _2I)^2} \right) \Bigg |_{E_0} =\frac{\beta \Lambda }{p+\mu +\alpha _1\Lambda } \\ V= & {} \left( \mu +\nu +\sigma \right) \Big |_{E_0}=\mu +\nu +\sigma . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \mathcal {R}_0=\rho (FV^{-1}) =\frac{\beta \Lambda }{(p+\mu +\alpha _1\Lambda )(\mu +\nu +\sigma )}. \end{aligned}$$

Let us note that \(\mathcal {R}_0\) is the average number of secondary infections caused by a single infected individual in a population fully susceptible to the disease.

Theorem 1

The DFE point \(E_0\) of the HBV model (2.3) is LAS if \(\mathcal {R}_0<1\), and \(E_0\) is an unstable saddle point if \(\mathcal {R}_0>1\).

Proof

The Jacobian matrix of the HBV model (2.3) at the DFE point is

$$\begin{aligned} J_0=\left( \begin{array}{cc} -(p+\mu ) &{} \displaystyle -\mathcal {R}_0(\mu +\nu +\sigma ) \\ 0 &{} (\mathcal {R}_0-1)(\mu +\nu +\sigma ) \end{array}\right) . \end{aligned}$$

It is easy to obtain the eigenvalues of \(J_0\):

$$\begin{aligned} \lambda _1=-(p+\mu ), \quad \lambda _2 =(\mu +\nu +\sigma )(\mathcal {R}_0-1). \end{aligned}$$

Clearly if \(\mathcal {R}_0<1\), then \(\lambda _{1,2}<0\). Hence the HBV model (2.3) is LAS at \(E_0\). Conversely, if \(\mathcal {R}_0>1\), then Jacobian matrix \(J_0\) has eigenvalues of both positive and negative signs. That is, \(\lambda _1\) is negative, while \(\lambda _2\) is positive. This indicates that the HBV model (2.3) is unstable, and \(E_0\) is also an unstable saddle point. Then, the proof is completed, as desired. \(\square \)

The result mentioned above indicates that when the basic reproduction number \(\mathcal {R}_0\) is less than 1, a small population of infected individuals will not be able to spread the infection. The spread of infection in this case depends on the initial size of the sub-populations.

Theorem 2

The DFE point \(E_0\) of the HBV model (2.3) is GAS if \(\mathcal {R}_0<1\).

Proof

If \(\mathcal {R}_0<1\), then there is no other equilibrium point than the disease-free equilibrium point (see (2.4)). Also, from Remark 1, positive solutions of the HBV model (2.3) are ultimately bounded and the S-axis is positively invariant, the I-axis repels the positive solutions. Since \(E_0\) is a locally asymptotically stable point, it follows from the Bendixson Theorem that every positive solution of the HBV model (2.3) approaches \(E_0\) as t approaches infinity. So, DFE point \(E_0\) of the HBV model (2.3) is globally asymptotically stable. The proof is completed, as desired. \(\square \)

2.2 Stability nature of the EE

To find the endemic equilibrium points, we have to set the differential equations of the HBV model (2.3) equal to zero. Then, we can obtain the endemic equilibrium \(E^*=(S^*,I^*)\), where

$$\begin{aligned} \begin{aligned} S^*&= \frac{\mu +\nu +\sigma +\alpha _2\Lambda }{\beta -\alpha _1(\mu +\nu +\sigma )+\alpha _2(p+\mu )} \\&=\frac{\Lambda (\mu +\nu +\sigma +\alpha _2\Lambda )}{(\mu +\nu +\sigma )[\mathcal {R}_0(p+\mu )+\alpha _1 \Lambda (\mathcal {R}_0-1)]+\alpha _2\Lambda (p+\mu )} \\ I^*&=\frac{(p+\mu +\alpha _1\Lambda )(\mathcal {R}_0-1)}{\beta -\alpha _1(\mu +\nu +\sigma )+\alpha _2(p+\mu )}\\&=\frac{\Lambda (p+\mu +\alpha _1\Lambda )(\mathcal {R}_0-1)}{(\mu +\nu +\sigma )[\mathcal {R}_0(p+\mu )+\alpha _1\Lambda (\mathcal {R}_0-1)]+\alpha _2\Lambda (p+\mu )}. \end{aligned} \end{aligned}$$
(2.4)

From the above equations, one can easily see that if \(\mathcal {R}_0>1\), then the EE point exists.

Theorem 3

The EE point \(E^*\) of the HBV model (2.3) is LAS if \(\mathcal {R}_0>1\).

Proof

Let’s assume \(\mathcal {R}_0>1\). After performing some algebraic calculations, one can easily find the Jacobian matrix evaluated at \(E^*\) as follows:

$$\begin{aligned} J^*=\left( \begin{array}{cc} -\frac{[\beta \Lambda -a(b+\alpha _1\Lambda )](\beta -\alpha _1a)}{\beta (a+\alpha _2\Lambda )}-b &{} -\frac{a^2[\beta +\alpha _2 (b+\alpha _1\Lambda )]}{\beta (a+\alpha _2\Lambda )} \\ \frac{[\beta \Lambda -a(b+\alpha _1\Lambda )](\beta -\alpha _1a)}{\beta (a+\alpha _2\Lambda )} &{} \frac{a^2[\beta +\alpha _2 (b+\alpha _1\Lambda )]}{\beta (a+\alpha _2\Lambda )}-a \end{array}\right) , \end{aligned}$$
(2.5)

where

$$\begin{aligned} a= & {} \mu +\nu +\sigma \\ b= & {} p+\mu . \end{aligned}$$

To have negative eigenvalues for the matrix mentioned above, both conditions must be satisfied: \(\text{ Tr }(J^*)<0\), and \(\det (J^*)>~0\) (see [26]). The trace of \(J^*\) can be easily obtained by

$$\begin{aligned} \text{ Tr }(J^*)=-\frac{(\mathcal {R}_0-1)a^2 (b+\alpha _1\Lambda )[\mathcal {R}_0b+(\mathcal {R}_0-1) \alpha _1\Lambda +\alpha _2\Lambda ]}{\beta \Lambda (a+\alpha _2\Lambda )}-b. \end{aligned}$$

Also, the determinant of the matrix (2.5), after some algebraic calculations can be determined as follows:

$$\begin{aligned} \det (J^*)=\frac{(\mathcal {R}_0-1)a^2(b+\alpha _1\Lambda ) \left[ \mathcal {R}_0ab+(\mathcal {R}_0-1)a\alpha _1\Lambda +\alpha _2b\right] }{\beta \Lambda (a+\alpha _2\Lambda )}. \end{aligned}$$

Obviously if \(\mathcal {R}_0>1\), then the trace is negative while the determinant is positive for \(J^*\), which means that the EE point of the HBV model (2.3) is LAS. Thus, the proof is completed, as desired. \(\square \)

In the following theorem, we provide a necessary condition for the globally asymptotically stability of the endemic equilibrium point \(E^*\).

Theorem 4

If \(\mathcal {R}_0>1\), then the EE point \(E^*\) of the HBV model (2.3) is GAS in the interior of the positive quadrant \(\Omega \).

Proof

Let’s assume \(\mathcal {R}_0>1\). Consider the functions f(S, I) and g(S, I) as the functions right-hand side of the HBV model (2.3). Consider the Dulac function defined by

$$\begin{aligned} B(S,I)=I^{-1}. \end{aligned}$$

Then, we have

$$\begin{aligned} \frac{\partial (Bf)}{\partial S}+\frac{\partial (Bg)}{\partial I} =-\frac{\beta (1+\alpha _2I)}{(1+\alpha _1S+\alpha _2I)^2} -\frac{p+\mu }{I}-\frac{\alpha _2\beta S}{(1+\alpha _1S+\alpha _2I)^2}<0 \end{aligned}$$

for all \((S,I)\in \Omega \). Hence the HBV model (2.3) has no periodic orbits in the \(\Omega \). Since all solutions of (2.3) are bounded and \(E_0\) is an unstable saddle point for \(\mathcal {R}_0>1\), from the Poincare-Bendixson theorem, we obtain the globally asymptotically stability of the endemic equilibrium \(E^*\). Thus, the proof is completed, as desired. \(\square \)

2.3 Transcritical bifurcation

The occurrence of a change in the stability behavior or dynamics of equilibrium points is commonly referred to as bifurcation (see [2, 36, 37]). An equilibrium point at which this change occurs is known as the bifurcation point. In this subsection, we will examine the behavior of the HBV model (2.3) when \(\mathcal {R}_0=1\).

Let \(S=\gamma _1\) and \(I=\gamma _2\) and denote by \(f_1(\gamma _1,\gamma _2)\) and \(f_2(\gamma _1,\gamma _2)\) the right-hand side functions of the HBV model (2.3). Then, the HBV model (2.3) can be rewritten as

$$\begin{aligned} \frac{d\gamma _1}{dt}= & {} \Lambda -\frac{\beta \gamma _1\gamma _2}{1+\alpha _1\gamma _1+\alpha _2\gamma _2}-(p+\mu )\gamma _1=f_1 (\gamma _1,\gamma _2) \nonumber \\ \frac{d\gamma _2}{dt}= & {} \frac{\beta \gamma _1\gamma _2}{1+\alpha _1\gamma _1+\alpha _2\gamma _2}-(\mu +\nu +\sigma ) \gamma _2=f_2(\gamma _1,\gamma _2). \end{aligned}$$
(2.6)

The Jacobian matrix at DFE of the HBV model (2.3) evaluated at \(\mathcal {R}_0=1\) and \(\beta =\beta ^*\) where \(\beta ^*=\frac{(p+\mu +\alpha _1\Lambda )(\mu +\nu +\sigma )}{\Lambda }\) is given by

$$\begin{aligned} J=\left( \begin{array}{cc} -(p+\mu ) &{} -\frac{\beta ^*\Lambda }{p+\mu +\alpha _1\Lambda } \\ 0 &{} \frac{\beta ^*\Lambda }{p+\mu +\alpha _1\Lambda }-(\mu +\nu +\sigma ) \end{array} \right) . \end{aligned}$$

Indeed, the existence of a zero eigenvalue in matrix J indicates the existence of a bifurcation. Let the left and right eigenvectors corresponding to the zero eigenvalue of J be denoted as \(u=[u_1,u_2]^T\) and \(w=[w_1,w_2]\), respectively. One can easily calculate the components of u and w as follows:

$$\begin{aligned} u_1=0, \quad u_2=1, \quad \text{ and } \quad w_1 =-\frac{\beta ^*\Lambda }{(p+\mu )(p+\mu +\alpha _1\Lambda )}, \quad w_2=1. \end{aligned}$$

From Theorem 4.1 in [37], the bifurcation constants can be computed as

$$\begin{aligned} \xi _1= & {} \sum _{i,j,k=1}^2u_kw_iw_j\frac{\partial ^2f_k(E_0)}{\partial \gamma _i\partial \gamma _j}=-\frac{2\beta S_0}{(1+\alpha _1S_0)^2}\left( \alpha _2+\frac{\beta ^*\Lambda }{(p{+}\mu )(p{+}\mu {+}\alpha _1\Lambda )}\right) <0 \\ \xi _2= & {} \sum _{i,k=1}^2v_kw_i\frac{\partial ^2f_k(E_0)}{\partial \gamma _i\partial \beta ^*}=\frac{S_0}{1+\alpha _1S_0}>0. \end{aligned}$$

Therefore, the HBV model (2.3) undergoes transcritical bifurcation at \(\mathcal {R}_0=1\). In other words, the stability of the DFE point transitions from stable to unstable when \(\mathcal {R}_0\) reaches a value of 1, indicating the existence of a positive equilibrium as \(\mathcal {R}_0\) crosses this threshold.

3 Constructing of the NSFD scheme

In this section, we will develop an NSFD scheme for the HBV model (1.3). Our aim is to formulate numerical approaches that preserve the essential features of the HBV model (1.3). These features include non-negativity of populations, population conservation law, and stability properties of DFE and EE points.

In the subsequent sections of this section, the variables \(S_n\), \(I_n\), and \(R_n\) will be used to denote the numerical approximations of S(t), I(t), and R(t), respectively, at discrete time points \(t=nh\), where \(n=0,1,2,\ldots \). Here, h represents the time-step size. To discretize the HBV model (1.3), we follow the approach proposed by Mickens (see [30]) in the following manner:

$$\begin{aligned} \begin{aligned} \frac{S_{n+1}-S_n}{\varphi (h)}&=\Lambda -\frac{\beta S_{n+1}I_n}{1+\alpha _1S_n+\alpha _2I_n}-(p+\mu )S_{n+1}, \\ \frac{I_{n+1}-I_n}{\varphi (h)}&=\frac{\beta S_{n+1}I_n}{1+\alpha _1S_n+\alpha _2I_n}-(\mu +\nu +\sigma )I_{n+1}, \\ \frac{R_{n+1}-R_n}{\varphi (h)}&=pS_{n+1}+\nu I_{n+1}-\mu R_{n+1}, \end{aligned} \end{aligned}$$
(3.1)

with

$$\begin{aligned} S_0>0, \quad I_0>0, \quad R_0>0, \end{aligned}$$

where \(\varphi (h)\) is the denominator function to be determined later. By adding all terms on both sides of the equations in the HBV model (3.1), we can obtain the expression:

$$\begin{aligned} \frac{N_{n+1}-N_n}{\varphi (h)}=\Lambda -\mu N_{n+1}-\sigma I_{n+1}, \end{aligned}$$
(3.2)

which leads to the inequality:

$$\begin{aligned} \frac{N_{n+1}-N_n}{\varphi (h)}\le \Lambda -\mu N_{n+1}, \end{aligned}$$
(3.3)

where \(N_n=N(t_n)=S_n+I_n+R_n\). Notably, (3.3) serves as an approximation of the continuous population conservation law (2.1). To ensure the conservation of the population, we decide on the following formulation for the denominator function:

$$\begin{aligned} \varphi (h)=\frac{e^{\mu h}-1}{\mu }. \end{aligned}$$
(3.4)

It is easy to see that substituting the denominator function (3.4) into the inequality (3.3) gives

$$\begin{aligned} N_{n+1}\le \frac{\Lambda }{\mu }+\left( N_n-\frac{\Lambda }{\mu } \right) e^{-\mu h}. \end{aligned}$$
(3.5)

Thus, by using mathematical induction, it is easy to see that for any \(h>0\), the solution of (3.3) satisfies the exact population conservation law (2.2):

$$\begin{aligned} N_n\le \frac{\Lambda }{\mu }+\left( N_0-\frac{\Lambda }{\mu } \right) e^{-\mu nh}. \end{aligned}$$
(3.6)

Let us rewrite the HBV model (3.1) in the explicit form:

$$\begin{aligned} \begin{aligned} S_{n+1}&=\frac{\Lambda \varphi (h)+S_n}{1+\varphi (h)[\Phi (S_n,I_n)+p+\mu ]} \\ I_{n+1}&=\frac{I_n+\varphi (h)\Phi (S_n,I_n)S_{n+1}}{1+\varphi (h)(\mu +\nu +\sigma )}\\ R_{n+1}&=\frac{R_n+\varphi (h)(pS_{n+1}+\nu I_{n+1})}{1+\mu \varphi (h)},\\&S_0>0, \quad I_0>0, \quad R_0>0, \end{aligned} \end{aligned}$$
(3.7)

where

$$\begin{aligned} \varphi (h)=\frac{e^{\mu h}-1}{\mu } \, \text{ and } \, \Phi (S,I)=\frac{\beta I}{1+\alpha _1S+\alpha _2I}. \end{aligned}$$

4 Dynamical analysis of the discrete HBV model

Here, we will explore the dynamical properties of the discrete HBV model (3.7). The results to be obtained here will demonstrate that the discrete HBV model (3.7) and the continuous HBV model (1.3) are dynamically consistent with the following properties:

  • Non-negativity of solutions,

  • Boundedness of solutions,

  • The existence of steady states,

  • Stability nature of equilibrium points.

Because of the non-negativity of all parameters in (3.7), and that \(\varphi (h)>0\) for all values of h, clearly \(S_{n+1},I_{n+1},R_{n+1}\ge 0\) if \(S_n,I_n,R_n\ge 0\). Therefore, the non-negative region \({\mathbb {R}}^3_+\) is a positively invariant set for the discrete HBV model (3.7). From (3.6), we have

$$\begin{aligned} \limsup _{n\rightarrow \infty }N_n\le \frac{\Lambda }{\mu }. \end{aligned}$$

These results imply that the discrete model is dynamically consistent with the continuous model concerning non-negativity and boundedness. Based on these result, we can conclude that a feasible region \(\Omega _2\) can be defined for analyzing the solutions of the HBV model (3.7) as follows;

$$\begin{aligned} \Omega _2=\left\{ (S_n,I_n,R_n)\in {\mathbb {R}}^3_+\mid S_n+I_n+R_n \le \frac{\Lambda }{\mu } \right\} . \end{aligned}$$

Remark 2

By observing that the first two equations of the HBV model (3.7) are independent of \(R_n\), it is enough to only consider the first two equations without loss of generality. Thus, we can rewrite the HBV model (3.7) as

$$\begin{aligned} S_{n+1}= & {} \frac{\Lambda \varphi +S_n}{1+\varphi (\phi +p+\mu )},\nonumber \\ I_{n+1}= & {} \frac{I_n+\varphi \phi S_{n+1}}{1+\varphi (\mu +\nu +\sigma )}, \end{aligned}$$
(4.1)

where \(S_n\ge 0\), \(I_n\ge 0\), \(\phi =\phi (S,I)=\frac{\beta I}{1+\alpha _1S+\alpha _2 I}\), \(\varphi =\varphi (h)\), and analyze it on the feasible set:

$$\begin{aligned} \Omega _d=\left\{ (S_n,I_n)\in {\mathbb {R}}^2_+\mid S_n+I_n \le \frac{\Lambda }{\mu } \right\} . \end{aligned}$$

4.1 Stability nature of the DFE

We can verify that the discrete HBV model (4.1) and the continuous HBV model (2.3) share the same equilibrium points, namely, the DFE point \(E_0=(S_0,I_0)\) and the EE point \(E^*=(S^*,I^*)\). It should be noted that the EE point exists when the basic reproduction number \(\mathcal {R}_0\) is greater than 1.

Let us define the following functions for simplicity:

$$\begin{aligned} F(S,I)= & {} \frac{\Lambda \varphi +S_n}{1+\varphi (\phi +p+\mu )},\nonumber \\ G(S,I)= & {} \frac{I_n+\varphi \phi S_{n+1}}{1+\varphi (\mu +\nu +\sigma )}. \end{aligned}$$
(4.2)

So, the Jacobian matrix of the discrete HBV model (4.1) at an equilibrium point \(E=(S,I)\) can be represented as:

$$\begin{aligned} J(E)=\left( \begin{array}{cc} \frac{\partial F}{\partial S}(S,I) &{} \frac{\partial F}{\partial I}(S,I) \\ \frac{\partial G}{\partial S}(S,I) &{} \frac{\partial G}{\partial I}(S,I) \end{array}\right) . \end{aligned}$$

To analyze the locally asymptotically stability of equilibrium points, we examine the magnitudes of eigenvalues of the Jacobian matrix evaluated at these points.

Theorem 5

If \(\mathcal {R}_0<1\), then the DFE point \(E_0\) of the discrete HBV model (4.1) is locally asymptotically stable regardless of the magnitude of h. Conversely, if \(\mathcal {R}_0>1\), then \(E_0\) is unstable regardless of the magnitude of h.

Proof

The Jacobian matrix of the HBV model (4.1) at \(E_0\) is

$$\begin{aligned} J(E_0)=\left( \begin{array}{cc} \frac{1}{1+\varphi (p+\mu )} &{} -\frac{\mathcal {R}_0 \varphi (h)(\mu +\nu +\sigma )}{1+\varphi (h)(p+\mu )} \\ 0 &{} \frac{1+\mathcal {R}_0\varphi (h)(\mu +\nu +\sigma )}{1+\varphi (h) (\mu +\nu +\sigma )} \end{array}\right) . \end{aligned}$$

The eigenvalues of the matrix are

$$\begin{aligned} \lambda _1=\frac{1}{1+\varphi (p+\mu )}, \quad \lambda _2=\frac{1+\mathcal {R}_0\varphi (h) (\mu +\nu +\sigma )}{1+\varphi (h)(\mu +\nu +\sigma )}. \end{aligned}$$

Obviously if \(\mathcal {R}_0<1\), then \(|\lambda _{1,2}|<1\) for all h. Therefore the discrete HBV model (4.1) is locally asymptotically stable at \(E_0\). Conversely, it is evident that if \(\mathcal {R}_0>1\), then \(\lambda _2>1\). This indicates that \(E_0\) is unstable. Thus, the proof is completed. \(\square \)

4.2 Stability nature of the EE

By conducting algebraic computations, we can establish that the discrete HBV model (4.1) shares the same positive equilibrium point as the continuous HBV model (2.3), that is the endemic equilibrium point as given in (2.4). This equilibrium point exists only if \(\mathcal {R}_0>1\).

Theorem 6

The EE point \(E^*\) of the discrete HBV model (4.1) is LAS if \(\mathcal {R}_0>1\), for all time-step sizes h.

Proof

Suppose that \(\mathcal {R}_0>1\). The Jacobian matrix of the HBV model (4.1) at EE is

$$\begin{aligned} J(E^*)=\left( \begin{array}{cc} \frac{1}{x}+\frac{\alpha _1tI^*}{x^2} &{} -\frac{(1+\alpha _1S^*)t}{x^2} \\ \frac{1}{xy}\left[ z+\frac{\alpha _1tI^*}{x}(z-x) \right] &{} \frac{1}{y}\left[ 1+\frac{t(1+\alpha _1S^*)(x-z)}{x^2} \right] \end{array}\right) . \end{aligned}$$

where

$$\begin{aligned} x= & {} 1+\varphi (\phi ^*+p+\mu )>1, \\ y= & {} 1+\varphi (\mu +\nu +\sigma )>1, \\ z= & {} \varphi \phi ^*>0, \\ t= & {} \frac{\beta \varphi (\varphi \Lambda +S^*)}{(1+\alpha _1S^*+\alpha _2I^*)}>0, \end{aligned}$$

and \(\phi ^*=\frac{\beta I^*}{1+\alpha _1S^*+\alpha _2I^*}\). From \(J(E^*)\), we have

$$\begin{aligned} Tr(J(E^*))=\frac{1}{x}+\frac{\alpha _1tI^*}{x^2}+\frac{1}{y} \left[ 1+\frac{1(1+\alpha _1S^*)(x-z)}{x^2} \right] \end{aligned}$$

and

$$\begin{aligned} \det (J(E^*))=\frac{1}{x^2y}(x+t(1+\alpha _1S^*+\alpha _1I^*)). \end{aligned}$$

Therefore, the EE point \(E^*\) is LAS if the condition \(|Tr(J)|<1+\det (J)<2\) is satisfied (see [26]). Hence, the proof is completed. \(\square \)

Table 1 Parameter values used in examples
Full size table

5 Numerical simulations and discussion

Simulations are used as important tools to assess the suitability of the proposed mathematical model for real-world scenarios. Here, some numerical simulations are provided to validate the theoretical results obtained in the paper. We will provide two examples for cases where \(\mathcal {R}_0\) is less and greater than 1. Through these examples, we will compare the Euler and RK4 schemes with the proposed NSFD scheme of the HBV model (1.3) and highlight the advantages of the NSFD approach. The simulations we will provide have been conducted using the MATLAB software.

Fig. 2
figure 2

Comparison of numerical solutions obtained by Euler and RK4 schemes with by NSFD scheme for \(S(0)=100\), \(I(0)=40\) and \(h=4\)

Full size image
Fig. 3
figure 3

Numerical solutions obtained by NSFD scheme for \(h=4\), \(h=2.5\), \(h=1\) and \(h=0.5\)

Full size image

Example 1

(\(\mathcal {R}_0<1\) Case) The parameters chosen for this example are provided in the Table 1. According to the parameters given in Table 1, it can be observed that

$$\begin{aligned} \mathcal {R}_0=0.31353151869<1 \, \text{ and } \, E_0=(8.33055648117,0). \end{aligned}$$

In Fig. 2, we simulate a comparison of numerical solutions of the HBV model (1.3) obtained by the Euler, RK4 and proposed NSFD scheme. We choose the initial values as \(S(0)=100\) and \(I(0)=40\) and time-step size \(h=4\). While Euler and RK4 schemes exhibit numerical inconsistencies such as unrealistic negative populations and failure to converge to the equilibrium point, the NSFD scheme does not suffer from these issues. In Fig. 3, it is demonstrated that the NSFD scheme provides consistent results for different time-step size values.

Example 2

(\(\mathcal {R}_0>1\) Case) Apart from the previous example, here \(\beta =2\), while all other parameters remain the same. In this case,

$$\begin{aligned} \mathcal {R}_0=2.09021012464>1 \, \text{ and } \, E^*=(1.11294571815,0.41653942114). \end{aligned}$$

In Fig. 4, the global asymptotically stability of \(E^*\) can be observed from the \(S-I\) phase plane. There, the NSFD scheme is used for \(h=0.08\). Also, Fig. 5 illustrates the effect of vaccination rate p on susceptible and infected populations. Moreover, Figs. 6 and 7 show the effect of the parameters \(\alpha _1\) and \(\alpha _2\) on susceptible and infected populations, respectively.

Fig. 4
figure 4

Global stability of \(E^*\) in the NSFD scheme for \(h=0.08\)

Full size image
Fig. 5
figure 5

Effect of vaccination rate p on the susceptible and infected populations

Full size image
Fig. 6
figure 6

Effect of \(\alpha _1\) on the susceptible and infected populations

Full size image
Fig. 7
figure 7

Effect of \(\alpha _2\) on the susceptible and infected populations

Full size image

6 Conclusions and remarks

In this study, we have investigated the dynamical properties of an HBV model with Beddington–DeAngelis type incidence and constant vaccination rate. We used the Beddington–DeAngelis type incidence rate, which includes both a measure of inhibition effect, such as preventive measures taken by susceptible individuals, and a measure of inhibition effect, such as treatment concerning infectives. This approach enabled us to study the HBV model (1.3), which yields results that are more meaningful and realistic when compared to the bilinear and saturated incidence rates. The non-negativity, boundedness, basic reproduction number, stability properties, and bifurcation of the HBV model (1.3) have been examined in detail. While locally asymptotically stability properties are demonstrated using the linear stability theorem, globally asymptotically stability of \(E^*\) has been shown using the Poincaré-Bendixson theorem. Stability conditions have been derived based on the threshold quantity \(\mathcal {R}_0\). The transcritical bifurcation has been proven using the center manifold theory.

Mathematical epidemic models are often expressed through systems of nonlinear differential or difference equations. It’s also worth noting that the model can be directly constructed using a system of difference equations. Given a model expressed in a system of differential equations, it is usually necessary to discretize it for practical purposes. In the literature, various standard numerical methods such as Euler or Runge–Kutta methods have been used to solve nonlinear differential equation systems. It has been demonstrated that these methods can potentially fail to preserve the dynamical properties of the corresponding continuous model. To avoid this dynamical inconsistency, discretized HBV model (3.1) has been derived by applying a non-locally approach to the non-linear terms for the continuous HBV model (1.3) and choosing a denominator function to satisfy the population conservation law. The discrete HBV model has been analyzed in terms of its non-negativity, boundedness, and stability properties. It has been concluded that both the discrete and continuous models maintain dynamical consistency for any finite step size. Finally, by presenting some numerical simulations, the theoretical results have been validated. Moreover, the provided simulations demonstrate that the parameters \(\alpha _1\), \(\alpha _2\) and p are significant factors in preventing the spread of the disease within the population.

In the near future, with the HBV model given by the system (1.3), further studies can be conducted on control strategies, rate of convergence, bifurcation analysis, local sensitivity analysis, and other related topics. Also, dynamically consistent NSFD schemes will be developed for several other epidemiological models to study their dynamical behavior.

Finally, let’s conclude the article by presenting a conjecture.

Conjecture

The DFE point \(E^0\) of the discrete HBV model (4.1) is GAS if \(\mathcal {R}_0<1\), and the EE point \(E^*\) is GAS if \(\mathcal {R}_0>1\), for all time-step sizes h.