Stochastic behavior of within-host progression in primary dengue infection

Abstract

Dengue is a mosquito-borne viral infection that triggers a series of intracellular events in the host immune system, which may result in an invasion of the virus into the host and cause illness with a spectrum of severity. Depending on the degree of the infection, mild to severe clinical symptoms appear when the T-cell and B-cell-initiated immune responses fail to eradicate the virus particles and subsequently become compromised. Here, we propose a mathematically tractable simple model that exhibits important biological features of dengue infection. Dynamical analysis of our model explores the factors influencing viral persistence in the body over an extended period. To investigate plausible variability in viral dynamics in different hosts, we perform stochastic simulations of our model using Gillespie’s algorithm. Our simulation results recapitulate the distribution of the intrinsic incubation period, daily viral load, and the day of peak viremia. In addition, we observe that the invasion probability of the virus into the host is correlated with the initial virus population injected by the mosquito. However, considering the biting behavior of Aedes mosquitoes, a lower initial virus injection could end up increasing the epidemic potential of the virus.

1 Introduction

Dengue is one of the most prevalent vector-borne viral infections in tropical and subtropical regions. The risk of dengue outbreaks has recently increased worldwide [1] owing to climate change caused by global warming [2, 3]. The virus has four serotypes: from dengue virus 1 (DENV1) to dengue virus 4 (DENV4). Generally, infection by any of the four strains appears first as a febrile illness with headache, muscle pain, and joint pain, which is characterized as a primary infection. During the initiation of the primary infection, the viral particles invade the bloodstream and start infecting monocytes, in addition to proliferating. When a human is infected with DENV, the body’s innate and adaptive immune responses function together [4]. When the immune system detects an increase in the number of infected cells, it activates T-cells, which then activate B-cells. T-cells and B-cells combat the infected cells and viral particles.

Both types of immune cells control the infection; however, their mechanisms of action are different. T-cells produce a group of cytokines that suppress infection and recognize and eliminate infected cells [5, 6]. By contrast, B-cells produce antibodies that target and neutralize dengue virus particles [4]. In addition, B-cells produce antibodies that remain preserved as memory and can be activated in an extremely short period of time if exposed to the same virus a second time. Therefore, immune memory reacts to a second exposure to the same virus more quickly and extensively. However, if a heterologous strain of dengue virus infects, it causes more severe symptoms, including life-threatening shock, compared with the primary infection. This is known as a secondary infection. Whether the two serotypes result in lifelong immunity or whether subsequent infections may occur remains unclear [4, 7], the entire immune mechanism is complex and remains poorly understood. Owing to the coexistence of several strains and the cross-immunity among them, developing a vaccine and implementing it effectively is challenging. Furthermore, no medication is available for treating dengue fever; only medications to relieve the symptoms are available. To overcome these limitations, the gaps in dengue pathophysiology must be elucidated. Mathematical models can be used to better understand immune mechanisms and may have significant utility in the development of therapeutic hypotheses.

Numerous mathematical modeling studies have been performed to investigate the transmission dynamics of dengue from mosquitoes to humans and subsequently back to humans via mosquitoes [3, 8,9,10,11]. Several mathematical studies have investigated the in-host progression of DENV [12,13,14,15]. However, these studies modeled infections with multiple serotypes and primarily investigated the role of antibodies, acquired during the primary infection, in enhancing disease severity during the secondary infection. In [4], the authors presented a mathematical model describing the adaptive immunity initiated by T-cells in primary dengue infections. These results demonstrate that cytokine-mediated viral clearance plays a critical role in viral dynamics. A couple of recent studies developed stochastic models for both primary and secondary dengue infections [16, 17]. In particular, Nguyen et al. [17] proposed a sophisticated stochastic model for secondary dengue infections. The model captures detailed biology of the immune mechanisms, and the results summarize the key characteristics of the immune response that differ from primary to secondary dengue infection. Although the study offers helpful details about the latter phases of infection, the early dynamics before the beginning of viremia are not sufficiently covered. For instance, the incubation period before the beginning of viremia is not taken into account by the model. Additionally, the invasion probability was not calculated in the study. This is crucial because not every infected mosquito bite causes viremia, making it feasible that the virus may not always be able to successfully invade a host. The study also lacks a thorough dynamical characterization of the interaction between the viral particle and immune cells.

The proposed model in this study is relatively simple and easy to conduct rigorous mathematical analysis; further, it can capture all the essential features observed in primary dengue infections. This study aimed to explore the following key questions. What are the daily viral loads in the body during the primary infection? How soon does the viral load start to increase; that is, and what is the incubation period of the virus? What is the time of peak viremia? Does the establishment of viremia depend on the initial viral load injected by mosquitoes? The answers to these questions should be very useful in taking personal and clinical measures for dengue patients. This information should also be useful in developing more sophisticated mathematical models of the in-host transmission of dengue infection. However, the answers to these questions are random as they may vary significantly from person to person. Viral dynamics is expected to be highly dependent on the immune system and initial viral load. The temperature may also have a significant influence on dynamics [18].

We first introduce a deterministic nonlinear ordinary differential equation (ODE) model describing the in-host progression of primary DENV infection. Primarily, the ODE model was analyzed to explore the factors influencing viral persistence in the body for an extended period. Subsequently, stochastic simulations of the model were performed using Gillespie’s direct simulation algorithm [19] and the results were compared with those of the deterministic model. The stochastic model allows for incorporating uncertainties in the conditions that vary from person to person. The remainder of this paper is organized as follows. Section 2 introduces the proposed mathematical model and presents the mathematical analyses of the model. Section 3 presents the results of the deterministic model, and Sect. 4 presents the stochastic model and its results. Finally, Sect. 5 summarizes and discusses the results in the context of biology.

Fig. 1

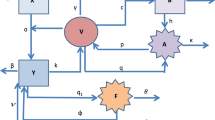
Model schematic diagram. Schematic depiction of the flow of cells between the compartments. The dashed red arrow indicates the contact of healthy cells with virus particles, the solid red arrows demonstrate the infection of healthy cells and production of virus particles from dead infected cells, the dashed blue lines demonstrate natural decay as well as activation of effector cells, and the solid blue lines demonstrate the suppression of infection because of the anti-inflammatory effects of activated effector cells. (Color figure online)

2 Mathematical model

2.1 Model formulation

The host cells were classified into susceptible (S) and infected (I) classes. The susceptible cells become infected because of contact with the free virus (V), which is modeled as $\beta SV$. Susceptible cells are assumed to be produced by the body at a constant rate $\Pi$ and die at a natural death rate $\mu _S$. The infected cells die at a rate $\mu _I$ and release mature virus particles, which are modeled as $p\mu _I I$. The virus particles naturally decay at a rate $\mu _V$. To neutralize infection, the immune system produces infection-specific immune cells, comprising T-cells and B-cells. In this model, the two types of immune cells were not distinguished, although the operating mechanisms of the two cell types are different. These cells were grouped as effector cells (E). Because this study is concerned with primary dengue infection, the antibodies that remain preserved as immune memory was not modeled. Rather, the activation of effector cells was modeled (E) at a rate of $\lambda I$, which controls the infection either by killing the infected cells at a rate $\delta IE$ or neutralizing the virus particles at a rate $\gamma VE$. Figure 1 summarizes the cellular dynamics described above. Applying the law of mass of action, the aforementioned cellular dynamics can be described by the following system of ordinary differential equations

$$\begin{aligned} \frac{dS}{dt}= & {} \Pi -\beta S V-\mu _S S,\nonumber \\ \frac{dI}{dt}= & {} \beta S V-\mu _I I-\delta I E,\nonumber \\ \frac{dV}{dt}= & {} p\mu _I I-\mu _V V-\gamma V E,\nonumber \\ \frac{dE}{dt}= & {} \lambda I-\mu _E E, \end{aligned}$$

(1)

with the initial conditions $S(0)\ge 0$, $E(0)\ge 0$, $V(0)\ge 0$, and $I(0)\ge 0$.

2.2 Mathematical analysis

The system was studied in the following biologically feasible regions.

$$\begin{aligned} \Omega =\left\{ (S, I, V, E)\in \mathcal {R}_+^4| 0\le S\le \bar{S}; 0\le I\le \bar{I}; 0\le V\le \bar{V}; \text { and }\, 0\le E\le \bar{E}\right\} \end{aligned}$$

because the concentration and number of cells were not negative. The parameters over the bars represent their upper bounds. In addition, all parameters involved in the model were assumed positive. The infection-free equilibrium of the system  (1), $E^0$ is given by $E^0=(\frac{\Pi }{\mu _S}, 0, 0, 0)$. Herein, this equilibrium was characterized as infection-free because it contains neither viruses nor infected cells.

2.2.1 Virus reproductive number

Following the method and notations developed in [20], we obtain $\mathcal {F}=\begin{pmatrix} \beta S V\\ 0 \end{pmatrix}$ and $\mathcal {V}=\begin{pmatrix} \mu _I I+\delta I E\\ -p\mu _I I+\mu _V V+\gamma V E \end{pmatrix}$.

At $E^0=(\frac{\Pi }{\mu _S}, 0, 0, 0)$, the Jacobian of $\mathcal {F}$ and $\mathcal {V}$ is reduced to $F_0=\begin{pmatrix} 0 &{} \frac{\beta \Pi }{\mu _S}\\ 0 &{} 0 \end{pmatrix}$ and $V_0=\begin{pmatrix} \mu _I &{} 0\\ -p\mu _I &{} \mu _V \end{pmatrix}$, respectively.

The next-generation matrix K can be obtained using $F_0 V_0^{-1}$, which is expressed by $K=\begin{pmatrix} \frac{\beta \Pi p}{\mu _S \mu _V} &{} \frac{\beta \Pi }{\mu _S \mu _V}\\ 0 &{} 0 \end{pmatrix}$.

The spectral radius of K provides the virus reproductive number $\chi _v=\frac{p \beta \Pi }{\mu _S \mu _V}$. Notably, the viral reproductive number represents the average number of newly produced viral particles through infecting a susceptible cell in the lifetime of a single virus particle right after invading the host blood.

$$\begin{aligned} \begin{aligned} \chi _v&=\frac{1}{\mu _V}\times \frac{\Pi }{\mu _S}\beta \times p\\&=\text { average lifetime of a virus particle }\times \text { per-capita rate of infecting susceptible cells } \times \\&\text { number of viral offspring released per dead infected cell }. \end{aligned} \end{aligned}$$

Therefore, the expression for $\chi _v$ is well-defined.

2.2.2 Equilibrium points and their stability criterion

Theorem 1

The infection-free equilibrium $E^0$ is locally asymptotically stable for $\chi _v<1$.

Theorem 2

System (1) possesses a unique diseased equilibrium $E^1$, which exists only when $\chi _v>1$. Also, it is locally asymptotically stable when exists.

The proofs theorems 1 and 2 are shown in details in Appendix A and B respectively. The local stability of the infection-free equilibrium was analyzed using Jacobian analysis. However, due to complexity in nature, the local stability of the diseased equilibrium was analyzed using the Monte Carlo method [21, 22] (see Appendix B).

The global stability of the equilibrium points was also confirmed. Theorems and proofs related to the global stability of the infection-free and diseased equilibrium points can be found in Appendix C.

Table 1 Parameter values used in the deterministic and stochastic simulations

3 Deterministic simulations

Thus far, the model was analyzed to prove the positivity of the solution. Additionally, $\chi _v$ and the equilibrium points were derived and their stability was tested. To further understand the propagation of the viral load in the host, the system was numerically solved with a known set of model parameters. The MATLAB routine ODE45 [24] was used to solve the system (1) numerically. The parameter and initial values of the variables used in the simulations are listed in Table 1. Figure 9 in Appendix D shows that the virus cannot invade the host immune system and establish infection a favorable outcome is obtained when the value of $\chi _v$ is less than one. By contrast, viremia is established after 4–6 days of infection if the value of $\chi _v$ is greater than one, which demonstrates the dynamics we discussed in the previous section. The figure shows that the amount of virus increased slowly at the beginning for approximately 3 days. This period was defined as the incubation period because the symptoms are not expected to appear with a low viral load. Following the incubation period, the viral load suddenly increased to a maximum value with a peak viral load around day 7.5 since infection. Subsequently, the load decreases to zero around day 11 as the immune system clears the infection.

Fig. 2

Weak anti-inflammatory effects. Maximum viral load (left) and the amount of time required for the maximum viral load in the body (right) as functions of $\beta$ and $\delta$, respectively. Notably, $\beta$ represents the transmission rate, and $\delta$ represents the clearance rate of infected cells by the anti-inflammatory effect of effector cells (T and B-cells)

3.1 Inefficient effector cells suppression

In the proposed model, the anti-inflammatory roles of both T and B-cells, as characterized by the parameters $\delta$ and $\gamma$, respectively, are expected to play a significant role in disease dynamics. However, the sensitivity analysis, shown in Fig.  10, demonstrates that the PRCC indices of the parameters associated with these biological processes are extremely low. Essentially, the PRCC indices of these parameters indicate that they have an extremely low impact on model outcomes. To investigate the reasons for this, the maximum viral loads were calculated as a function of $\beta$ and $\delta$, as shown in the left panel of Fig.  2. This figure shows that the maximum viral load is mainly dominated by the value of $\beta$. However, a large value of $\delta$ seems to have a negligible impact on the maximum viral load. To investigate this further, the time required to reach the maximum viral load (peak viremia time) was calculated as a function of $\beta$ and $\delta$, as shown in the right panel of Fig.  2. This figure shows that the peak viremia time is nearly independent of the value of $\delta$ when $\beta$ is large. By contrast, when the value of $\beta$ is relatively small, a large value of $\delta$ appears to have a low impact on the peak viremia time. These combinations of $\beta$ and $\delta$ tend to produce unrealistic peak viremia times when considering that the typical incubation period of DENV infection is approximately 4–7 d, and then approximately 7 d of viral load with a maximum load around the middle days [18]. Similar phenomena were observed corresponding to combinations of $\beta$ and $\gamma$ as well as $\beta$ and $\lambda$ (figures omitted). These analyses suggest that the anti-inflammatory properties of B and T cells are not highly effective at suppressing infection when $\beta$ is large, indicating that viral infectivity is the dominating factor influencing the dynamics of infection.

4 Stochastic simulations

As mentioned in Sect. 1, the incubation period, size of viral loads, and peak time are host-specific and may vary from person to person. Although the deterministic model can produce the basic characteristics of the disease, it is unable to produce consequences of host-to-host variability and another inherent biological stochasticity. In addition, the ODE model assumes that the time evolution of the reacting cells and virus particles is both deterministic and continuous. However, their time evolution cannot be a continuous process, as their population levels can only vary by discrete integer amounts. This drawback can be overcome by employing a stochastic formulation, in which the reaction constants are seen as reaction probabilities per unit of time rather than reaction rates. According to this method, the system’s temporal behavior is represented by a Markovian random walk in the four-dimensional space of the four species population $x=[S, I, V, E]$. It is worth mentioning that, similar to the deterministic method, the stochastic formulation regards the distribution of the cells and virus particles as spatially homogeneous. The stochastic formulation of the deterministic system (1) is briefly discussed below:

Following the work presented in [19], we begin by sub-diving the deterministic model into the following reactions:

$$\begin{aligned} \begin{array}{ll} R_1: \rightarrow S; &{}R_2: S\rightarrow I;\\ R_3: S \rightarrow \emptyset ;&{} R_4: I\rightarrow \emptyset ;\\ R_5: I\rightarrow ;&{} R_6: \rightarrow V;\\ R_7: V\rightarrow \emptyset ; &{} R_8: V\rightarrow ;\\ R_9: \rightarrow E; &{}R_{10}: E\rightarrow \emptyset . \end{array} \end{aligned}$$

Therefore, we have four reacting species $x=[S, I, V, E]$ which participate in 10 unidirectional reactions $R_\mu \,(\mu =1, 2, \dots , 10)$. Here, the reaction $R_\mu$ is characterized by stochastic reaction constant $c_\mu$ as follows:

$$\begin{aligned} \begin{array}{ll} c_\mu \,\delta t\equiv &{}\text { average probability (first order in } \delta t) \text { that molecules relevant to } \\ &{} \hbox { reaction} R_\mu \hbox {will react in the next time interval} \delta t\\ \end{array} \end{aligned}$$

(2)

where $c_\mu$ is specified by the corresponding reaction rate constants in the deterministic system (1). In order to fully characterize the reaction channels $R_\mu$, besides $c_\mu$, we require two more entities: the reaction functions for all channels $(a_\mu )$, and the state change vectors $v_{\mu i} (\mu =1, 2,\dots ,10; i=1, 2, 3, 4)$. The reaction functions corresponding to 10 reaction channels are:

$$\begin{aligned} \begin{array}{ll} a_1=1; &{} a_2=x_1 x_3;\\ a_3=x_1; &{} a_4=x_2;\\ a_5=x_2 x_4; &{} a_6= x_2;\\ a_7=x_3; &{} a_8=x_3 x_4;\\ a_9=x_2; &{} a_{10}=x_4. \end{array} \end{aligned}$$

where each $x_i$ indicates the exact number of populations of the reacting species S, I, V and E present at time t. The state change vectors $v_{\mu i}$ corresponding to these channels constitute the following stoichiometry matrix $F = [v_{\mu i}],$

$$\begin{aligned} F=\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -1 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ -1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad -1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad -1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -1\\ \end{pmatrix}. \end{aligned}$$

The functional form of $a_\mu$ uniquely characterizes the corresponding reaction channel $R_\mu$ and the state change vector $v_{\mu i}$ uniquely characterizes the production through this reaction channel. Our aim is to calculate the species population vector x(t) taking the influence of the reaction channels $R_\mu$ which are specified by its stochastic reaction rate $c_\mu$, its reaction functions $a_\mu$ and state change vector $v_{\mu i}$ into consideration (where $\mu =1, 2, \ldots , 10$). One possible way to handle this task is to derive the time-evolution of the probability function $P(x, t|x_0, 0)$, which serves as the key element of a differential-difference equation called chemical master equation (CME). Here $x_0$ indicates the species population vector at time $t=0$. In this single equation, time and the population of four species will appear as independent variables, contrary to the deterministic system, where four differential equations represent the time evolution of the population of four species. The probability function $P(x, t|x_0, 0)$ represents the following:

$$\begin{aligned} \begin{array}{ll} P(x, t|x_0, 0)\equiv ~&{}\text {probability that there will be} x_1 \text { population of } S,\\ &{} \hbox {} x_2 \hbox {population of} I, \dots , ~\text { and } x_4 \text { population of }E \text { at time }t,\\ &{} \hbox { given that}\ x(0)=x_0. \end{array} \end{aligned}$$

The time-evolution of the probability function $P(x, t|x_0, 0)$ is dependent on how the species population vector is updated from x(0) to x(t). Population vector can be updated through two mutually exclusive events: there will be exactly one reaction $R_\mu$ in time dt with probability $c_\mu a_\mu (x) dt+ o(dt)$, and no reaction will occur in time dt with probability $1-\sum _{\mu =1}^{10}c_\mu a_\mu (x) dt+ o(dt)$. The probability of having more than one reaction at a time is o(dt) [19]. Therefore, the probability function $P(x, t+dt|x_0, 0)$ can be written as

$$\begin{aligned} P(x, t+dt|x_0, 0)&=P(x, t|x_0, 0)\times \left( 1-\sum _{\mu =1}^{10}c_\mu a_\mu (x) dt+ o(dt)\right) \\&\quad {+}\sum _{\mu =1}^{10}\left( P(x{-}v_\mu , t|x_0, 0){\times }[c_\mu a_\mu (x{-}v_\mu ) dt{+} o(dt)]\right) {+}o(dt), \end{aligned}$$

which on limit $dt\rightarrow 0$ gives the following

$$\begin{aligned} \begin{aligned} \dfrac{\partial }{\partial t} P(x, t|x_0, 0)=&\sum _{\mu =1}^{10}[c_\mu a_\mu (x-v_\mu )P(x-v_\mu , t|x_0, 0)\\&-c_\mu a_\mu (x)P(x, t|x_0, 0)]. \end{aligned} \end{aligned}$$

This is the master equation. The solution to this equation provides a comprehensive understanding of the stochastic state of the system at any given moment t. For example, it allows us to calculate the average number of the species population at t obtained from many repeated realizations. However, solving the CME is not possible except for some fairly simple systems. An alternative approach for stochastic simulation is the next reaction density function (NRDF) $p(\tau , \mu |x, t)$ [19], which gives the conditional probability that only an $R_\mu$ will occur in the infinitesimal time interval $[t+\tau , t+\tau +d\tau ]$ for given species population x at time t. Here $\tau \, (0\le 0 \le \infty )$ represents the time taken for the next reaction to occur and $\mu \,(1, 2, \dots , 10)$ represents the index of the next reaction. Let

$$\begin{aligned} h(x)=\sum _{\mu =1}^{10}c_\mu a_\mu (x) \end{aligned}$$

(3)

and assume that the time interval $[t, t+\tau +d\tau ]$ be subdivided into $N+1$ intervals, provided $N>1$. The first N subdivisions over the interval $[t, t+\tau ]$ have equal length $\epsilon =\tau /N$, where no reaction occurs, and the last subdivision has length $d\tau$, where exactly one $R_\mu$ reaction occurs. Therefore, we have

$$\begin{aligned} p(\tau , \mu |x, t)=[1-h(x)\epsilon +o(\epsilon )]^N[c_\mu a_\mu (x) d\tau + o(d\tau )], \end{aligned}$$

which on limit $d\tau \rightarrow 0$ yields

$$\begin{aligned} p(\tau , \mu |x, t)=[1-h(x)\epsilon +o(\epsilon )]^Nc_\mu a_\mu (x), \end{aligned}$$

which on limit $N\rightarrow \infty$ leads to

$$\begin{aligned} p(\tau , \mu |x, t)=h(x)e^{-h(x)\tau }\dfrac{c_\mu a_\mu (x)}{h(x)} \end{aligned}$$

The above expression shows that the NRDF $p(\tau , \mu |x, t)$ is a function of two independent random variables $\tau$ and $\mu$, where $\tau$ has an exponential density function with decay constant h(x), and $\mu$ has the integer density function $\dfrac{c_\mu a_\mu (x)}{h(x)}$. With the assist of two random numbers $r_1$ and $r_2$, generated using a unit-interval uniform random number generator, $\tau$ can be defined as

$$\begin{aligned} \tau =\frac{1}{h_0}\ln \left( \frac{1}{r_1}\right) , \end{aligned}$$

(4)

and $\mu$ as the smallest integer for which

$$\begin{aligned} \sum _{\mu =1}^\mu c_\mu a_\mu (x)>r_2 h_0, \end{aligned}$$

(5)

where $h_0\equiv \sum _{\mu =1}^{10}c_\mu a_\mu (x)$. Having chosen the value of $\tau$ and $\mu$, the population vector from time t to $t+\tau$ can be update using $x(t)+v_\mu$. Repeated application of this advancement procedure allows us to stochastically determine the population of S, I, V, E at any time $t>0$, starting from S(0), I(0), V(0), E(0) at time $t=0$. The simulation algorithm of the DSSA described above is outlined below:

Step 1: Initialize the four classes of population and their initial numbers

S(0), I(0), V(0), E(0);

Step 2: Initialize the 10 reaction functions and their associated stochastic

reaction rate constants $c_\mu$;

Step 3: Initialize the current time t=0;

Step 4: Calculate the propensities $c_\mu a_\mu (x)$ for all 10 reactions;

Step 5: For each reaction, generate the reaction waiting time $\tau$ using

equation  4 and reaction index $\mu$ using equation  5;

Step 6: Update the population vector using $x_0+v_\mu$ and set $t\leftarrow t+\tau ;$

Step 7: Go to Step 4 and repeat the process until the final time is reached.

The initial populations S(0), I(0), V(0), E(0) and the parameter values used in the simulation are summarized in Table 1.

4.1 Invasion probability and epidemic potential

According to the results of the deterministic model the virus invades and establishes infection if $\chi _v>1$. However, due to heterogeneity in host response, virus invasion may not be successful in establishing infection. In the case of a successful invasion, that the virus enters the host and does not die out. We approximated the invasion probability by the ratio of successful invasions to the total number of stochastic realizations. Further, the invasion probability of the virus was calculated as a function of the initial virus population (Fig. 3) as well as a function of the virus reproductive number, $\chi _v$. The initial values of the variables and parameters used in the stochastic simulations are listed in Table 1. The invasion probability increased with an increase in the initial virus population. However, the increase in invasion probability slowed as the number of initial viral particles increased, thus suggesting that the virus may not successfully invade, even with an exceedingly large number of initial viral particles. It is most sensitive when the viral load is low, and an increase in the viral load does not ensure a proportionate increase in the establishment of the infection in an individual.

Considering the feeding behavior of infected Aedes mosquitoes, this may have crucial implications for the epidemic spread of the disease [25]. As Aedes is a domestic mosquito and does not fly a considerably long distance to feed, it is more likely to feed on members of the same family or individuals living in neighboring houses. As infected mosquitoes are more eager to feed on [26] and have higher locomotor activity than noninfected mosquitoes [27], an infected mosquito is likely to feed on several hosts and injects a smaller initial viral load in each of them instead of having a complete meal from one host and injecting a high amount of viral load. Although it reduces the individual’s probability of developing the infection, it increases the probability of transmission from a mosquito to an individual. For instance, we consider two scenarios of five people living nearby, scenario I: one infected mosquito feeds on one individual, and 50 RNA per ml virus particles are injected, vs. scenario II: the infected mosquito is disturbed during feeding and ends up biting all the people injecting 10 RNA per ml to each of them. In scenario I, 16% ($=100\times 0.8/5$) of the people will be infected, and in Scenario II, 40% ($=0.4\times 5\times 100/5$) of the people will be infected.

Fig. 3

Invasion probability. Figures showing invasion probability as a function of the initial virus population (left) and the invasion probability as a function of the virus reproductive number $\chi _v$ (right)

The invasion probability of the virus was also calculated as a function of the virus reproductive number (Fig. 3). It shows that a successful mosquito bite may not result in an infection even if $\chi _v>1$. It resembles prompt clearance of the virus by the host immune response. Also, it could be representative of asymptomatic infections. This figure shows that the invasion probability of the virus increases as the successful number of viral offspring increases. However, it tends to saturate at some point due to the inherent uncertainty introduced by the stochasticity of the dynamics.

4.2 Intrinsic incubation period

In the case of a successful invasion of the virus, dengue fever is likely to occur after an intrinsic period of 4–10 days after the bite by a dengue-carrying mosquito [1]. During this incubation period, the injected virus particles infect the healthy immune cells with the motive of hacking the immune system. The virus particles start to multiply quickly, and as a result, viremia is established due to the presence of a high level of the virus in the bloodstream. The number of initially injected virus particles evolves slowly during the incubation period. Then the body temperature starts to rise when their numbers exceed a threshold, as their increased numbers come to the attention of the immune system. However, mathematically, there is no specific measure to obtain this inherent triggering time of the virus. In this section, we intend to quantify the intrinsic incubation period using stochastic simulations of the dynamics. We monitored the intrinsic incubation period from every stochastic realization as follows:

• (i) In the case of a successful invasion, the time required for the initial viral load to increase by 10% was recorded as the incubation period.

• (ii) In the case of an unsuccessful invasion, no such time was recorded, as the initial viral load was never increased by 10%.

The intrinsic incubation period estimated from all 20,000 independent stochastic realizations was then fitted to an exponential distribution using the maximum likelihood method, which produces an estimate of 5.9 days with a 95% confidence interval [5.8, 6.0]. The estimate from our model is in good agreement with the existing literature as shown in Fig. 4 [18].

Fig. 4

Incubation period and peak viremia time. Incubation time of the virus (left) and peak viremia time (right) since the day of infection. The solid curve in the left figure shows an approximate probability density function (pdf) of an exponential distribution fitting the incubation periods obtained from 20,000 independent realizations, whereas the solid curve in the right figure shows an approximation pdf of a normal distribution fitting the peak viremia times obtained from the same number of realizations. The dashed curve in the left figure is the pdf of the exponential distribution of the incubation period calculated in [18]

4.3 Daily viral load and peak viremia time

Further, we calculate the daily viral load and peak viremia time using stochastic simulations. Figure  5 shows the daily viral loads from days 1–15 after infection. The results shown in this figure align, to some extent, with the predictions of the deterministic model. However, this graph provides better insights into the daily viral load patterns compared with the graph shown in Fig. 9. Evidently, the medians shown in every box of this figure are biased toward the lower quartile, thus suggesting lower daily viral loads in primary dengue infection. Further observations can be made from the bar plot showing the daily median of the viral load in this figure. It shows that the daily viral loads stay close to those of the initially injected virus. Then suddenly, from around day 6, the viral load starts rising sharply, reaching its maximum on day 8. The overall course of the viral load lasts around 7 days. The incubation and febrile phages of a typical dengue infection [1] are replicated in our results fairly closely.

Fig. 5

Daily viral load. Boxplot shows daily viral load since mosquito bites based on 20,000 independent stochastic realizations. The central red mark in each rectangular box represents the median, with the bottom and top boundaries of the boxes representing the 25th and 75th percentiles, respectively. (Color figure online)

5 Discussion and conclusion

This study presents mathematical models to investigate the in-host progression of primary DENV infections. Herein, we present a deterministic ODE model that describes the dynamics of the disease. First, the ODE model was analyzed to explore the factors influencing viral persistence in the body for an extended period. The deterministic model revealed that viremia occurs when $R_0>1$. In addition, the deterministic model showed that the virus cleared within 11 or 12 days from the day of infection, which is an important feature observed in primary dengue infection. Parameter sensitivity analysis revealed that the anti-inflammatory effects of B and T-cells are inefficient in suppressing infection when the transmission rate $\beta$ is high. Further analysis revealed that viral infectivity plays a dominant role in the dynamics of infection when $\beta$ is high.

Next, to incorporate uncertainties in conditions that may vary from person to person, a stochastic model was derived from the ODE model. The stochastic model is proven to provide better insights into viral dynamics. The stochastic model provides a wide range of results, including different sizes of viral loads and different times of maximum infection occurring in the body. Using this model, the daily viral load patterns during infection were calculated and found to be consistent with the pathophysiology of primary dengue infection. The incubation of the virus was calculated to be 5.9 days with a 95% confidence interval [5.8, 6]. This result is more in line with the existing study and clinical data [18, 28] compared to the incubation period of four days conjectured, but not directly calculated, in the study conducted by Nguyen et al. [17]. Additionally, the peak viremia time, that is, the time of the maximum viral load in the body from the day of infection was calculated. The mean peak viremia was found to occur around day 10.1 since the day of infection, with a 95% confidence interval [10, 10.2], as reported in [28].

The most significant feature of the stochastic model is that it exhibited a non-zero probability of viral extinction in terms of different initial virus loads, even when the virus reproductive number $\chi _v>1$, as opposed to the deterministic model. The viral invasion probability was calculated as a function of the initial viral load, and the invasion probability was found to increase with an increasing initial value of the viral load, thus suggesting that the size of the initial viral load may have a significant impact on disease dynamics. A successful invasion is likely, corresponding to a high initial viral load. This result accords well with the experimental study conducted by Novelo et al. [29], wherein the authors found that a threshold level of initial viral dose is required to establish body-wide infections in mosquitoes.

Feeding behavior in infected mosquitoes changes significantly [25]. Infected mosquitoes are more attracted to blood than uninfected mosquitoes and bite more often to obtain sufficient blood [26]. The increased biting tendency of infected mosquitoes influences the transmission of DENV to the host. The increased biting tendency is because the locomotor activity of infected mosquitoes increases by up to 50% compared to the uninfected ones [27], which allows them to stay alert while biting and fly away even when the slightest threat is observed. Therefore, they require numerous bites to obtain sufficient blood, and these unsuccessful or partially successful bites often lead to a low initial viral load in the host, which decreases the probability of establishing the disease in one individual, albeit increasing the epidemic potential of the disease. In addition, invasion probability of the virus was also calculated as a function of the virus reproductive number. The invasion probability of the virus was found to increase as the successful number of viral offspring increased, which, however, was found to saturate at some point due to the inherent uncertainty introduced by the stochasticity of the dynamics.

In summary, this study investigated several key questions associated with the progression of primary DENV infection, taking the stochasticity of the dynamics into consideration. The results are expected to be useful in understanding the clinical diagnosis and conditions of dengue patients during infection and treatment. However, the dynamics of secondary infections are relatively complex because of the enhanced inflammatory responses triggered by the antibody acquired through the primary infection. The results and analysis provided herein are expected to lay the foundation for understanding the improved model presenting in-host dynamics of secondary DENV infections. Moreover, the estimated parameters can be used to simulate such a model. Future studies in this direction could consider re-investigating the facts explored in this study to better understand the reasons that secondary infection often leads to the development of a critical dengue infection. In addition, stochastic simulations of such models could be used to single out the role of enhanced inflammatory responses in the development of critical dengue infection.

Appendices

Proof of Theorem 1

Proof

The model possesses an infection-free equilibrium, $E^0=(\frac{\Pi }{\mu _S}, 0, 0, 0)$. Herein, this equilibrium was characterized as infection-free because the virus cannot spread in the host. The local stability of the equilibrium points can be determined by calculating the eigenvalues of the Jacobian in a steady state. At the infection-free equilibrium $E^0$, the Jacobian of system 1 adopts the following form.

$$\begin{aligned} J_{E^0}=\begin{pmatrix} -\mu _S &{}\quad 0 &{}\quad -\frac{\beta \Pi }{\mu _S} &{}\quad 0\\ 0 &{}\quad -\mu _I &{}\quad \frac{\beta \Pi }{\mu _S} &{}\quad 0\\ 0 &{}\quad p\mu _I &{}\quad \mu _V &{}\quad 0\\ 0 &{}\quad \lambda &{}\quad 0 &{}\quad -\mu _E \end{pmatrix} \end{aligned}$$

Two of the eigenvalues are $-\mu _S$ and $-\mu _E$. The remaining two terms can be obtained by solving the characteristic polynomial

$$\begin{aligned} \lambda ^2+\lambda (\mu _I+\mu _V)+\mu _I\mu _V(1-\chi _v)=0. \end{aligned}$$

One of the roots of this polynomial is positive or has a positive real part when $\chi _v>1$. By contrast, both roots will be negative or will have a negative real part when $\chi _v<1$. Therefore, the infection-free equilibrium is locally asymptotically stable when $\chi _v<1$. $\square$

Proof of Theorem 2

Proof

The diseased equilibrium of the model is given by,

$$\begin{aligned} E^1=\left( \frac{\Pi \lambda (\gamma E^*+\mu _V)}{p\beta \mu _I\mu _E E^*+\lambda \mu _S(\gamma E^*+\mu _V)}, \frac{\mu _E E^*}{\lambda }, \frac{p\mu _I\mu _E E^*}{\lambda (\mu _V+\gamma E^*)}, E^*\right) , \end{aligned}$$

where $E^*$ is a positive solution to the quadratic equation of

$$\begin{aligned} AE^{*^2}+BE^*+C=0, \end{aligned}$$

(6)

where $A=\frac{p\beta \delta \mu _I}{\lambda \mu _V\mu _S}+\frac{\delta \gamma }{\mu _E\mu _V}$, $B=\frac{p\beta \mu _I\mu _E}{\lambda \mu _V\mu _S}+\frac{\delta }{\mu _E}+\frac{\gamma }{\mu _V}$ and $C=1-\chi _v$. As mentioned previously, the equilibrium in the first orthant is of interest. Equation 6 shows that system (1) has a unique diseased equilibrium that exists only when $\chi _v>1$. This is demonstrated by plotting the quadratic function $\mathcal {F}(E)=AE^{*^2}+BE^*+C$ against E for different values of $\chi _v$, as shown in Fig. 6. This figure shows that as the value of $\chi _v$ approaches one, a unique diseased equilibrium emerges in the positive orthant.

Fig. 6

Existence of diseased equilibrium. Graphical representation for the existence of the unique diseased equilibrium corresponding to different values of $\chi _v$ in the range [0, 2]. The blue dashed lines correspond to $\chi _v<1$, whereas the blue solid lines correspond to $\chi _v>1$. (Color figure online)

Fig. 7

Local stability of $E^0$. Local stability of $E^0$ corresponding to the cases $\chi _v<1$ (upper row) and $\chi _v>1$ (lower row). The left panel shows the choices of $\chi _v$ values, whereas the right panel shows the eigenvalues of the Jacobean corresponding to these $\chi _v$ values

Jacobian analysis is not feasible for the diseased equilibrium $E^1$ because it is extremely complicated to obtain an explicit expression for it. Therefore, we preferred the Monte Carlo method [21, 22] to analyze the stability of equilibrium points by repeatedly verifying the condition on $\chi _v$ and calculating the eigenvalues at the steady states $E^0$ and $E^1$. The sampling was done by means of the Latin hypercubic sampling (LHS) [30] method under the uniform distribution of 10 parameters with $20\%$ deviation around their baseline values (as shown in Table 1). We repeated this sampling technique 10,000 times to form a sampling pool $\mathcal {S}\in \mathcal {R}_+^{10}$ of 10,000 random choices of parameter values within their given range, and with no correlation among them. The dynamical system (1) was then solved to calculate the eigenvalues at the steady states corresponding to every single sample that satisfied the condition on $\chi _v$. The simulation results are shown in Figs. 7 and 8. The upper row in Fig. 7 shows that the condition $\chi _v<1$ always holds, and all eigenvalues of the Jacobian at $E^0$ have a negative real part, suggesting that $E^0$ is locally asymptotically stable when $\chi _v<1$. The lower row in this figure shows that $E^0$ is unstable when $\chi _v>1$. Furthermore, Fig. 8 shows that $E^1$ is locally asymptotically stable when $\chi _v>1$. $\square$

Fig. 8

Local stability of $E^1$. Local stability of $E^1$ corresponding to the case $\chi _v>1$. The left panel shows the choices of $\chi _v$ values, whereas the right panel shows the eigenvalues of the Jacobean corresponding to these $\chi _v$ values

Global stability of the equilibrium points

Theorem 3

The infection-free equilibrium $E^0$ is globally asymptotically stable when $\chi _v\le 1$; otherwise, it becomes unstable.

Proof

Using the Lyapunov candidate function

$$\begin{aligned} L(t)=(S-S_0\ln S)+I+\frac{\Pi \beta }{\mu _S\mu _V}V, \end{aligned}$$

we obtain $\frac{dL}{dt}\le \mu _I (\chi _v-1)I$. Therefore, the proof is complete. $\square$

Lemma 1

System (1) exhibits forward bifurcation at $\chi _v=1$.

Proof

The center manifold theorem was used to prove this theorem. Using $\mu _V$ as a bifurcation parameter and following the method developed in [31], we obtain

$$\begin{aligned} a=-\frac{\mu _I\mu _E p}{\mu _V^*}(\Pi \mu _E \mu _I \mu _V^*+\lambda ^2\gamma )-p\lambda \delta \mu _E<0, \end{aligned}$$

and

$$\begin{aligned} b=\lambda p \mu _E \mu _I \mu _V^*>0, \end{aligned}$$

where $\mu _V^*=\frac{\Pi p\beta }{\mu _S}$. Therefore, the proof is complete. $\square$

Theorem 4

Diseased equilibrium $E^1$ is globally asymptotically stable when $\chi _v>1.$

Proof

System 1 possesses only two equilibrium points, where the infection-free equilibrium $E^0$ has already been proven globally unstable when $\chi _v>1$ (see Theorem 4). Hence, Lemma 1 indicates that $E^1$ is the only stable equilibrium when $\chi _v>1$, suggesting that $E^1$ is globally asymptotically stable when it exists. $\square$

Fig. 9

Viral load dynamics predicted by the deterministic model. Temporal evolution of viral load counts for $\chi _v<1$ (left) and $\chi _v>1$ (right)

Fig. 10

Global sensitivity indices. The figure on the left shows PRCC indices of $I+V$ corresponding to respective parameters labeled in the horizontal axis, whereas the figure on the right shows PRCC indices of $\chi _v$ corresponding to respective parameters labeled in the horizontal axis. The highest PRCC index implies the greatest influence on the model outcomes

Deterministic results and sensitivity analysis

The simplest way to analyze the sensitivity of the model to its parameters is to use the expression of the virus reproductive number $\chi _v$ and use the following relation to calculate the local sensitivity indices (Fig. 9)

$$\begin{aligned} \gamma _\rho ^{\chi _v}= \frac{\partial \chi _v}{\partial \rho } \times \frac{\rho }{\chi _v}. \end{aligned}$$

For example, $\gamma _\rho ^{\chi _v}=\pm 1$ implies that $\rho$ is a highly sensitive parameter. However, not all parameters that have a significant influence on the model outcomes always appear in the expression of $\chi _v$. Therefore, global sensitivity is recommended to explore the influence of model parameters on the model outcome. Herein, the partial rank correlation coefficient (PRCC) method was used to conduct a global sensitivity analysis [32]. A PRCC graph is shown in Fig. 10. The transmission rate ($\beta$) and death rate of infected cells ($\mu _I$) have the greatest impact on the sum of the number of infected cells and the number of virus particles ($I+V$). The transmission rate ($\beta$), death rate of susceptible cells ($\mu _S$), and death rate of virus particles ($\mu _V$) are important for determining the reproductive number $\chi _v$. The sensitivity indices of the parameters can also be used to design the prevention and selection of control strategies [33].