On the qualitative and quantitative analysis for two fourth–order difference equations

Abstract

Our aim in the present paper is to derive the closed-form solutions for the two fourth-order difference equations

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{ax_{n}+bx_{n-3}}, \ n\ge 0, \end{aligned}$$

and

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{-ax_{n}+bx_{n-3}}, \ n\ge 0, \end{aligned}$$

with positive arbitrary real parameters a, b and arbitrary real initial conditions, as well as study the qualitative behaviors for each. For the first equation, we show that every admissible solution converges to a period-3 solution when $a+b=1$. For the second equation, we show that every admissible solution converges to zero if $b>2$ when $b^2\ge 4a$. When $b^2<4a$, we show the existence of periodic solutions under certain conditions. We introduce the forbidden sets as well as provide some illustrative examples for the above-mentioned equations.

1 Introduction

The interest in the theory of difference equations is progressing rapidly. Research in this theory is carried out with three different approaches: quantitative, qualitative and numerical. Quantitative study is carried out by determining the analytical solutions of the equation, qualitative study is carried out by examining the behavior of the solutions of the equation, and numerical study is carried out by determining the approximate values of the solution of the equation by various methods. Therefore, the study discussed in this article can be seen as both a qualitative and a quantitative investigations of the difference equation theory. Therefore, it can be seen as a detailed study in this respect. Now let’s give a detailed background and motivation for the difference equation we discuss in this article;

Elabbasy et al. [17] solved some difference equations. One of these equations is

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-1}}{x_{n}+x_{n-2}},\ n\ge 0, \end{aligned}$$

with positive real initial values.

In [25], Stević derived a representation of the general solution to the difference equation

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-1}}{\check{a}x_{n}+\check{b}x_{n-2}},\ n\ge 0, \end{aligned}$$

with real-valued parameters and real initial values.

For more on difference equations, see [1]–[16, 18]–[24] and the references cited therein.

Motivated by the above-mentioned equations, we shall study the long-term behavior of all admissible solutions for the two fourth-order difference equations

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{ax_{n}+bx_{n-3}},\ n\ge 0, \end{aligned}$$

(1.1)

and

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{-ax_{n}+bx_{n-3}},\ n\ge 0, \end{aligned}$$

(1.2)

with positive real parameters a, b and real initial values, in terms of the closed-form solution to both.

Consider the difference equation

$$\begin{aligned} x_{n+1}=g(x_n,x_{n-1},...,x_{n-k}), n\ge 0, \end{aligned}$$

(1.3)

The good set of Eq. (1.3) is the set of all initial points for which the corresponding solution $\{x_n\}_{n=-k}^\infty$ is well-defined or admissible.

2 The difference Eq. (1.1)

Equation (1.1) can be written as

$$\begin{aligned} \frac{x_{n-2}}{x_{n+1}}= a\frac{x_n}{x_{n-3}}+b,\ n\ge 0. \end{aligned}$$

(2.1)

If we set

$$\begin{aligned} \frac{x_{n-3}}{x_{n}}=\frac{w_{n}}{w_{n-1}},\ \text {with}\ w_{-1}=1,\ n\ge 0, \end{aligned}$$

(2.2)

we get

$$\begin{aligned} w_{n+1}-bw_n-aw_{n-1}=0 \end{aligned}$$

During this section, suppose that

$$\begin{aligned} L_n=\frac{\lambda _{+}^{n+1}-\lambda _{-}^{n+1}}{\sqrt{b^2+4a}},\ n\ge -1, \end{aligned}$$

where

$$\begin{aligned} \lambda _{\pm }=\frac{b}{2}\pm \frac{\sqrt{b^2+4a}}{2}. \end{aligned}$$

By solving Equation (2.2), we get the solution form for Equation (1.1).

Theorem 2.1

Every admissible solution for Equation (1.1) is of the form

$$\begin{aligned} x_{n}=\left\{ \begin{array}{rcc} x_{-2}\prod _{j=0}^{\frac{n-1}{3}}\frac{x_{-3}L_{3j}+ax_0L_{3j-1}}{x_{-3}L_{3j+1}+ax_0L_{3j}},&{}n=1,4,...,\\ x_{-1}\prod _{j=0}^{\frac{n-2}{3}}\frac{x_{-3}L_{3j+1}+ax_0L_{3j}}{x_{-3}L_{3j+2}+ax_0L_{3j+1}},&{}n=2,5,...,\\ x_{0}\prod _{j=0}^{\frac{n}{3}-1}\frac{x_{-3}L_{3j+2}+ax_0L_{3j+1}}{x_{-3}L_{3j+3}+ax_0L_{3j+2}},&{}n=3,6,.... \end{array}\right. \end{aligned}$$

(2.3)

Proof

We can write the solution formula (2.3) as

$$\begin{aligned} x_{3m+i}=x_{-3+i}\prod _{j=0}^{m}M_{j,i},i=1,2,3 \ \text {and}\ m\ge 0, \end{aligned}$$

where

$$\begin{aligned} M_{j,i}=\frac{x_{-3}L_{3j+i-1}+ax_0L_{3j+i-2}}{x_{-3}L_{3j+i}+ax_0L_{3j+i-1}},\ i=1,2,3 \ \text {and}\ j\ge 0. \end{aligned}$$

The proof is by induction on m. For $m=0$,

$$\begin{aligned} x_{1}&=x_{-2}M_{0,1} =x_{-2}\frac{x_{-3}L_{0}+ax_{0}L_{-1}}{x_{-3}L_{1}+ax_{0}L_{0}} =\frac{x_{-2}x_{-3}}{ax_{0}+bx_{-3}},\\ x_{2}&=x_{-1}M_{0,2} =x_{-1}\frac{x_{-3}b+ax_{0}}{x_{-3}(b^2+a)+ax_{0}b}\\&=\frac{x_{-1}}{b+a\frac{x_{1}}{x_{-2}}}= \frac{x_{-1}x_{-2}}{ax_{1}+bx_{-2}},\\ x_{3}&=x_{0}M_{0,3} =x_{0}\frac{x_{-3}(b^2+a)+ax_{0}b}{x_{-3}(b(b^2+2a))+ax_{0}(b^2+a)}\\&=x_{0}\frac{b(ax_{0}+bx_{-3})+ax_{-3}}{b^2(ax_{0}+bx_{-3})+a(ax_{0}+bx_{-3})+abx_{-3}}\\&=x_{0} \frac{b+a\frac{x_{-3}}{ax_{0}+bx_{-3}}}{b^2+ab\frac{x_{-3}}{ax_{0}+bx_{-3}}+a}\\&=x_{0}\frac{b+a\frac{x_1}{x_{-2}}}{b^2+a+ab\frac{x_1}{x_{-2}}}\\&=x_{0}\frac{ax_1+bx_{-2}}{ax_{-2}+b(ax_1+bx_{-2})}\\&=\frac{x_{0}x_{-1}}{ax_{2}+bx_{-1}}. \end{aligned}$$

Suppose that for $m\ge 1$, the solution form (2.3) is satisfied.

Then

$$\begin{aligned} x_{3m+1}&=\frac{x_{3m-2}x_{3m-3}}{ax_{3m}+bx_{3m-3}}= \frac{x_{-2}\prod _{j=0}^{m-1}M_{j,1}x_{0}\prod _{j=0}^{m-2}M_{j,3}}{ax_{0}\prod _{j=0}^{m-1}M_{j,3}+bx_{0}\prod _{j=0}^{m-2}M_{j,3}}\\&= \frac{x_{-2}\prod _{j=0}^{m-1}M_{j,1}}{aM_{m-1,3}+b} . \end{aligned}$$

But we have

$$\begin{aligned} aM_{m-1,3}+b&=a\frac{x_{-3}L_{3m-1}+ax_0L_{3m-2}}{x_{-3}L_{3m}+ax_0L_{3m-1}}+b\\&=\frac{x_{-3}(aL_{3m-1}+bL_{3m})+ax_0(aL_{3m-2}+bL_{3m-1})}{x_{-3}L_{3m}+ax_0L_{3m-1}}\\&=\frac{x_{-3}L_{3m+1}+ax_0L_{3m}}{x_{-3}L_{3m}+ax_0L_{3m-1}}=\frac{1}{M_{m,1}}. \end{aligned}$$

Then

$$\begin{aligned} x_{3m+1}&=\frac{x_{-2}\prod _{j=0}^{m-1}M_{j,1}}{aM_{m-1,3}+b}=x_{-2}\prod _{j=0}^{m}M_{j,1}. \end{aligned}$$

The proof for $x_{3m+2}$ and $x_{3m+3}$ is similar and is omitted.

The proof is completed. $\square$

The forbidden set for Equation (1.1) is

$$\begin{aligned} \Gamma&=\bigcup _{n=0}^\infty \{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-3}=-ax_{0}\frac{L_{n-1}}{L_n}\}\\&\cup \bigcup _{t=0}^3\{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-t}=0\}. \end{aligned}$$

Theorem 2.2

Assume that $\{x_n\}_{n=-3}^\infty$ is an admissible solution to Equation (1.1). Then we have the following:

• (1) If $a+b>1$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to zero.

• (2) If $a+b=1$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to a period-3 solution.

• (3) If $a+b<1$, then the solution $\{x_n\}_{n=-3}^\infty$ is unbounded.

Proof

We have that

$$\begin{aligned} M_{j,i}=\frac{x_{-3}L_{3j}+ax_0L_{3j-1}}{x_{-3}L_{3j+1}+ax_0L_{3j}} \rightarrow \frac{1}{\lambda _{+}} \ \text {as}\ j\rightarrow \infty , \ i\in \{1,2,3\}. \end{aligned}$$

• (1) If $a+b>1$, then for each $i\in \{1,2,3\}$

  $$\begin{aligned} M_{j,i} \rightarrow \frac{1}{\lambda _{+}}<1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

  Now suppose that $1-\frac{1}{\lambda _{+}}>\epsilon >0$. Then for each $i\in \{1,2,3\}$ there exists $j_i\in \mathbb {N}$, $M_{j,i}<\frac{1}{\lambda _{+}}+\epsilon$ for all $j\ge j_i$. If we take $j_0=\max \{j_1,j_2,j_3\}$, then

  $$\begin{aligned} \begin{aligned} |x_{3m+i}|<|x_{-3+i}||\prod _{j=0}^{j_0-1}M_{j,i}| (\frac{1}{\lambda _{+}}+\epsilon )^{m-j_0+1} \end{aligned} \end{aligned}$$

  Therefore, $|x_{3m+i}|\rightarrow 0$ as $m\rightarrow \infty$, $i\in \{1,2,3\}$.

• (2) Suppose that $a+b=1$, then for each $i\in \{1,2,3\}$

  $$\begin{aligned} M_{j,i} \rightarrow 1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

  Suppose that $1>\epsilon >0$. Then for each $i\in \{1,2,3\}$ there exists $j''_i\in \mathbb {N}$, $M_{j,i}>0$ for all $j\ge j''_i$. If we take $j''_0=\max \{j''_1,j''_2,j''_3\}$, then

  $$\begin{aligned} \begin{aligned} x_{3m+i}=x_{-3+i}\prod _{j=0}^{j''_0-1}M_{j,i} \left( e^{\sum _{j=j''_0}^m\ln M_{j,i}}\right) . \end{aligned} \end{aligned}$$

  Now, consider the series

  $$\begin{aligned} \ln \frac{1}{M_{j,i}}=\ln \frac{x_{-3}L_{3j+i}+ax_0L_{3j+i-1}}{x_{-3}L_{3j+i-1}+ax_0L_{3j+i-2}}. \end{aligned}$$

  But for each $i\in \{1,2,3\}$, we have

  $$\begin{aligned} |\frac{\ln M_{j+1,i}}{\ln M_{j,i}}|\rightarrow -\lambda _{-}^3\ \text {as}\ j\rightarrow \infty . \end{aligned}$$

  This implies that, the solution $\{x_n\}_{n=-3}^\infty$ converges to the period-3 solution

  $$\begin{aligned} \{...,\mu _1,\mu _2,\mu _3,\mu _1,\mu _2,\mu _3,...\}, \end{aligned}$$

  where

  $$\begin{aligned} \mu _i=x_{-3+i}\prod _{j=0}^{j''_0-1}M_{j,i} \left( e^{\sum _{j=j''_0}^m\ln M_{j,i}}\right) ,\ i\in \{1,2,3\}. \end{aligned}$$

• (3) If $a+b<1$, then for each $i\in \{1,2,3\}$

  $$\begin{aligned} M_{j,i} \rightarrow \frac{1}{\lambda _{+}}>1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

  Now suppose that $\frac{1}{\lambda _{+}}-1>\epsilon >0$. Then for each $i\in \{1,2,3\}$ there exists $j'_i\in \mathbb {N}$, $M_{j,i}>\frac{1}{\lambda _{+}}-\epsilon$ for all $j\ge j'_i$. If we take $j'_0=\max \{j'_1,j'_2,j'_3\}$, then

  $$\begin{aligned} \begin{aligned} |x_{3m+i}|>|x_{-3+i}||\prod _{j=0}^{j'_0-1}M_{j,i}| (\frac{1}{\lambda _{+}}-\epsilon )^{m-j'_0+1}. \end{aligned} \end{aligned}$$

  Therefore, for each $i\in \{1,2,3\}$, we have unbounded subsequences $\{x_{3m+i}\}_{m=-1}^\infty$.

This completes the proof. $\square$

We end this section with two illustrative examples.

Example 1

Figure 1. shows that, if $a=0.4,b=1$ ($a+b=1.4>1$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.1) with $x_{-3}=0.2$, $x_{-2}=-1$, $x_{-1}=1.5$ and $x_{0}=0.3$ converges to zero.

Example 2

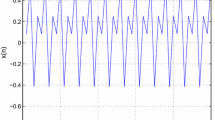
Fig. 2. shows that, if $a=0.26,b=0.74$ ($a+b=1$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.1) with $x_{-3}=-1.2$, $x_{-2}=3$, $x_{-1}=2.5$ and $x_{0}=2.3$ converges to the period-3 solution

$$\begin{aligned} \{...,12.0080,1.3885,2.5984,12.0080,1.3885,2.5984,...\}. \end{aligned}$$

Example 3

Fig. 3. shows that, if $a=0.4,b=1$ ($a+b=0.5<1$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.1) with $x_{-3}=1.2$, $x_{-2}=1.6$, $x_{-1}=-1.5$ and $x_{0}=1.1$ is unbounded.

Fig. 1

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{0.4x_{n}+x_{n-3}}$

Fig. 2

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{0.26x_{n}+0.74x_{n-3}}$

Fig. 3

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{0.3x_{n}+0.2x_{n-3}}$

3 The difference equation (1.2)

The difference equation (1.2) can be written as

$$\begin{aligned} \frac{x_{n-2}}{x_{n+1}}= -a\frac{x_n}{x_{n-3}}+b,\ n\ge 0. \end{aligned}$$

(3.1)

As in Section (2), we can get

$$\begin{aligned} w_{n+1}-bw_n+aw_{n-1}=0,\ n\ge 0, \end{aligned}$$

(3.2)

where

$$\begin{aligned} \frac{x_{n-3}}{x_{n}}=\frac{w_{n}}{w_{n-1}},\ \text {with}\ w_{-1}=1. \end{aligned}$$

If we set

$$\begin{aligned} \frac{x_{n-3}}{x_{n}}=\frac{w_{n}}{w_{n-1}},\ \text {with}\ w_{-1}=1,\ n\ge 0, \end{aligned}$$

(3.3)

Case $b^2>4a$

When $b^2>4a$, Equation (3.2) provides us with eigenvalues

$$\begin{aligned} \lambda _{1,2}=\frac{b\pm \sqrt{b^2-4a}}{2}.\end{aligned}$$

(3.4)

Solving for $w_n$, we can find the solution for Equation (1.2).

We give the following result without proof; its proof is similar to that of Theorem (2.1).

Theorem 3.1

Every admissible solution for Equation (1.2) is of the form

$$\begin{aligned} x_{n}=\left\{ \begin{array}{rcc} x_{-2}\prod _{j=0}^{\frac{n-1}{3}}\frac{x_{-3}L'_{3j}+ax_0L'_{3j-1}}{x_{-3}L'_{3j+1}+ax_0L'_{3j}},&{}n=1,4,...,\\ x_{-1}\prod _{j=0}^{\frac{n-2}{3}}\frac{x_{-3}L'_{3j+1}+ax_0L'_{3j}}{x_{-3}L'_{3j+2}+ax_0L'_{3j+1}},&{}n=2,5,...,\\ x_{0}\prod _{j=0}^{\frac{n}{3}-1}\frac{x_{-3}L'_{3j+2}+ax_0L'_{3j+1}}{x_{-3}L'_{3j+3}+ax_0L'_{3j+2}},&{}n=3,6,..., \end{array}\right. \end{aligned}$$

(3.5)

where

$$\begin{aligned} L'_n=\frac{\lambda _{1}^{n+1}-\lambda _{2}^{n+1}}{\sqrt{b^2+4a}},\ n\ge -1. \end{aligned}$$

When $b^2>4a$, the forbidden set for Equation (1.2) is

$$\begin{aligned} \Gamma _1&=\bigcup _{n=0}^\infty \{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-3}=ax_{0}\frac{L'_{n-1}}{L'_n}\}\\&\cup \bigcup _{i=0}^3\{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-i}=0\}. \end{aligned}$$

The following result is the main result when $b^2>4a$.

Theorem 3.2

Assume that $\{x_n\}_{n=-3}^\infty$ is an admissible solution to Equation (1.2). Then we have the following:

• (1) If $b>a+1$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to zero.

• (2) If $b=a+1$, then we have the following:

  • (a) If $b>2$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to zero.

  • (b) If $b<2$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to a period-3 solution.

• (3) If $b<a+1$, then we have the following:

  • (a) If $b>2$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to zero.

  • (b) If $b<2$, then the solution $\{x_n\}_{n=-3}^\infty$ is unbounded.

Proof

The solution formula (3.5) can be written as

$$\begin{aligned} x_{3m+t}=x_{-3+t}\prod _{j=0}^{m}M'_{j,t},t=1,2,3 \ \text {and}\ m\ge 0, \end{aligned}$$

where

$$\begin{aligned} M'_{j,t}=\frac{x_{-3}L'_{3j+t-1}+ax_0L'_{3j+t-2}}{x_{-3}L'_{3j+t}+ax_0L'_{3j+t-1}},\ t=1,2,3 \ \text {and}\ j\ge 0. \end{aligned}$$

The eigenvalues in (3.4) satisfy

$$\begin{aligned} \lambda _2<\frac{b}{2}<\lambda _1<b. \end{aligned}$$

• (1) Suppose that $b>a+1$. Then for each $t=1,2,3$ we get

  $$\begin{aligned} M'_{j,t}=\frac{x_{-3}L'_{3j+t-1}+ax_0L'_{3j+t-2}}{x_{-3}L'_{3j+t}+ax_0L'_{3j+t-1}} \rightarrow \frac{1}{\lambda _{1}}<1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

  The remainder is similar to that in Theorem 2.2(1).

• (2) Suppose that $b=a+1$.

  • (a) When $b>2$, we get $\lambda _2=1<\lambda _1$. This implies that for each $t=1,2,3$

    $$\begin{aligned} M'_{j,t}=\frac{x_{-3}L'_{3j+t-1}+ax_0L'_{3j+t-2}}{x_{-3}L'_{3j+t}+ax_0L'_{3j+t-1}} \rightarrow \frac{1}{\lambda _{1}}<1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

    The remainder is similar to that in Theorem 2.2(1).

  • (b) When $b<2$, we get $\lambda _1=1$. This implies that for each $t=1,2,3$

    $$\begin{aligned} M'_{j,t}=\frac{x_{-3}L'_{3j+t-1}+ax_0L'_{3j+t-2}}{x_{-3}L'_{3j+t}+ax_0L'_{3j+t-1}} \rightarrow \frac{1}{\lambda _{1}}=1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

    The remainder is similar to that in Theorem 2.2(2).

• (3) Suppose that $b<a+1$.

  • (a) When $b>2$, we get $\lambda _2>1$. This implies that for each $t=1,2,3$

    $$\begin{aligned} M'_{j,t}=\frac{x_{-3}L'_{3j+t-1}+ax_0L'_{3j+t-2}}{x_{-3}L'_{3j+t}+ax_0L'_{3j+t-1}} \rightarrow \frac{1}{\lambda _{1}}<\frac{1}{\lambda _{2}}<1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

    The remainder is similar to that in Theorem 2.2(1).

  • (b) When $b>2$, we get $\lambda _1<1$. This implies that for each $t=1,2,3$

    $$\begin{aligned} M'_{j,t}=\frac{x_{-3}L'_{3j+t-1}+ax_0L'_{3j+t-2}}{x_{-3}L'_{3j+t}+ax_0L'_{3j+t-1}} \rightarrow \frac{1}{\lambda _{1}}>1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

    The remainder is similar to that in Theorem 2.2(3).

$\square$

Example 4

Fig. 4. shows that, if $a=0.6,b=1.56$ ($b^2>4a$, $b<a+1$ and $b<2$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=-0.7$, $x_{-2}=-3.5$, $x_{-1}=-1.5$ and $x_{0}=2$ is unbounded.

Example 5

Fig. 5. shows that, if $a=0.9,b=1.9$ ($b^2>4a$, $b=a+1$ and $b<2$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=-1.5$, $x_{-2}=1.1$, $x_{-1}=-2$ and $x_{0}=-0.8$ converges to the period-3 solution

$$\begin{aligned} \{...,-0.5471, -1.1794, -0.5246,-0.5471, -1.1794, -0.5246,...\}. \end{aligned}$$

Fig. 4

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-0.6x_{n}+1.56x_{n-3}}$

Fig. 5

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-0.9x_{n}+1.9x_{n-3}}$

Example 6

Fig. 6. shows that, if $a=1,b=2.1$ ($b^2>4a$, $b>a+1$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=-1.2$, $x_{-2}=2$, $x_{-1}=-3.3$ and $x_{0}=0.7$ converges to zero.

Example 7

Fig. 7. shows that, if $a=1.2,b=2.2$ ($b^2>4a$, $b=a+1$ and $b>2$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=4$, $x_{-2}=-2$, $x_{-1}=3.3$ and $x_{0}=-1.7$ converges to zero.

Example 8

Fig. 8. shows that, if $a=1.4,b=2.38$ ($b^2>4a$, $b<a+1$ and $b>2$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=3$, $x_{-2}=1.5$, $x_{-1}=-4$ and $x_{0}=-5$ converges to zero.

Example 9

Fig. 9. shows that, if $a=0.08,b=1.08$ ($b^2>4a$, $b=a+1$ and $b<2$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=1$, $x_{-2}=-3$, $x_{-1}=4$ and $x_{0}=-2$ converges to the period-3 solution

$$\begin{aligned} \{...,-2.4191, 3.9390, -1.9976, -2.4191, 3.9390, -1.9976,...\}. \end{aligned}$$

Fig. 6

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-x_{n}+2.1x_{n-3}}$

Fig. 7

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{1.2x_{n}+2.2x_{n-3}}$

Fig. 8

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-1.4x_{n}+2.38x_{n-3}}$

Fig. 9

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-0.08x_{n}+1.08x_{n-3}}$

Case $b^2=4a$

The characteristic equation associated with Equation (3.2) in this case is

$$\begin{aligned} \lambda _1=\frac{b}{2}=\lambda _2. \end{aligned}$$

(3.6)

Solving for $w_n$, we get the form of the solution for Equation (1.2).

Theorem 3.3

Every admissible solution for Equation (1.2) is of the form

$$\begin{aligned} x_{n}=\left\{ \begin{array}{rcc} x_{-2}(\frac{2}{b})^{\frac{n+2}{3}} \prod _{j=0}^{\frac{n-1}{3}}\frac{2x_{-3}(3j+1)-bx_0(3j)}{2x_{-3}(3j+2)-bx_0(3j+1)},&{}n=1,4,...,\\ x_{-1}(\frac{2}{b})^{\frac{n+1}{3}} \prod _{j=0}^{\frac{n-2}{3}}\frac{2x_{-3}(3j+2)-bx_0(3j+1)}{2x_{-3}(3j+3)-bx_0(3j+2)},&{}n=2,5,...,\\ x_{0}(\frac{2}{b})^{\frac{n}{3}} \prod _{j=0}^{\frac{n}{3}-1}\frac{2x_{-3}(3j+3)-bx_0(3j+2)}{2x_{-3}(3j+4)-bx_0(3j+3)},&{}n=3,6,.... \end{array}\right. \end{aligned}$$

(3.7)

We can write the solution form (3.7) as

$$\begin{aligned} x_{3m+t}=x_{-3+t}(\frac{2}{b})^{m+1}\prod _{j=0}^{m}N_{j,t},t=1,2,3 \ \text {and}\ m\ge 0, \end{aligned}$$

where

$$\begin{aligned} N_{j,t}=\frac{2x_{-3}(3j+t)-bx_0(3j+t-1)}{2x_{-3}(3j+t+1)-bx_0(3j+t)},\ t=1,2,3 \ \text {and}\ j\ge 0. \end{aligned}$$

When $b^2=4a$, the forbidden set for Equation (1.2) is

$$\begin{aligned} \Gamma _2&=\bigcup _{n=0}^\infty \{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-3}=b\frac{x_{0}}{2}\frac{n}{n+1}\}\\&\cup \bigcup _{i=0}^3\{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-i}=0\}. \end{aligned}$$

When $b^2=4a$, the main result is the following:

Theorem 3.4

Assume that $\{x_n\}_{n=-3}^\infty$ is an admissible solution to Equation (1.2). The following statements are true:

• (1) If $b>2$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to zero.

• (2) If $b<2$, then the solution $\{x_n\}_{n=-3}^\infty$ is unbounded.

• (3) If $b=2$, then the solution $\{x_n\}_{n=-3}^\infty$ converges to zero.

Proof

The proof of (1) and (2) is a direct consequence.

For (3), suppose that $b=2$, then for each $t\in \{1,2,3\}$

$$\begin{aligned} N_{j,t} \rightarrow 1 \ \text {as}\ j\rightarrow \infty . \end{aligned}$$

Suppose that $1>\epsilon >0$. Then for each $t\in \{1,2,3\}$ there exists $j_t\in \mathbb {N}$, such that $M_{j,t}>0$ for all $j\ge j_t$.

If we take $j_0=\max \{j_1,j_2,j_3\}$, then

$$\begin{aligned} \begin{aligned} x_{3m+t}=x_{-3+t}\prod _{j=0}^{j_0-1}N_{j,t} \left( e^{\sum _{j=j_0}^m\ln N_{j,t}}\right) . \end{aligned} \end{aligned}$$

Now, consider the series

$$\begin{aligned} \ln \frac{1}{N_{j,t}}=\ln \frac{x_{-3}(3j+t+1)-x_0(3j+t)}{x_{-3}(3j+t)-x_0(3j+t-1)}. \end{aligned}$$

The divergence of the series $\sum _{j=j_0}^\infty \ln \frac{1}{N_{j,t}}$ (for each $t\in \{1,2,3\}$) is obtained by comparing it with the series $\sum _{j=j_0}^\infty \frac{1}{(3j+t)(x_{-3}-x_0)+x_0}$.

Therefore, for each $t\in \{1,2,3\}$ we get

$$\begin{aligned} x_{3m+t}\rightarrow 0\ \text {as}\ j\rightarrow \infty , \end{aligned}$$

and the result follows. $\square$

Example 10

Fig. 10. shows that, if $a=0.25,b=1$ ($b^2-=a$ and $b<2$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=1.2$, $x_{-2}=1.4$, $x_{-1}=-0.9$ and $x_{0}=-2.4$ is unbounded.

Example 11

Fig. 11. shows that, if $a=1,b=2$ ($b^2=4a$ and $b=2$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=4.2$, $x_{-2}=-1.4$, $x_{-1}=1.9$ and $x_{0}=-2.4$ converges to zero.

Fig. 10

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-0.25x_{n}+x_{n-3}}$

Fig. 11

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-x_{n}+2x_{n-3}}$

Case $b^2<4a$

When $b^2<4a$, Equation (3.2) provides us with eigenvalues

$$\begin{aligned} \lambda _1=\frac{b}{2}+ i\frac{\sqrt{4a-b^2}}{2}\ \text {and}\ \lambda _2=\frac{b}{2}-i\frac{\sqrt{4a-b^2}}{2}. \end{aligned}$$

(3.8)

Solving for $w_n$, the solution of Equation (3.2) is

$$\begin{aligned} w_n=\frac{a^{\frac{n}{2}}}{\sin \beta }(\frac{x_{-3}}{x_0} \sin (n+1)\beta -\sqrt{a}\sin n\beta ),\ n\ge -1. \end{aligned}$$

Using $w_n$, we get the solution form for Equation (1.2).

Theorem 3.5

Every admissible solution for Equation (1.2) is of the form

$$\begin{aligned} x_{n}=\left\{ \begin{array}{rcc} x_{-2} \prod _{j=0}^{\frac{n-1}{3}}\frac{1}{\sqrt{a}}\frac{x_{-3}\sin (3j+1)\beta -\sqrt{a}x_0\sin 3j\beta }{x_{-3}\sin (3j+2)\beta -\sqrt{a}x_0\sin (3j+1)\beta },&{}n=1,4,...,\\ x_{-1}\prod _{j=0}^{\frac{n-2}{3}}\frac{1}{\sqrt{a}}\frac{x_{-3}\sin (3j+2)\beta -\sqrt{a}x_0\sin (3j+1)\beta }{x_{-3}\sin (3j+3)\beta -\sqrt{a}x_0\sin (3j+2)\beta },&{}n=2,5,...,\\ x_{0}\prod _{j=0}^{\frac{n}{3}-1}\frac{1}{\sqrt{a}}\frac{x_{-3}\sin (3j+3)\beta -\sqrt{a}x_0\sin (3j+2)\beta }{x_{-3}\sin (3j+4)\beta -\sqrt{a}x_0\sin (3j+3)\beta },&{}n=3,6,.... \end{array}\right. \end{aligned}$$

(3.9)

where $\beta =tan^{-1}\frac{\sqrt{4a-b^2}}{b}\in ]0,\frac{\Pi }{2}[$.

When $b^2<4a$, the forbidden set for Equation (1.2) is

$$\begin{aligned} \Gamma _3&=\bigcup _{n=0}^\infty \{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-3}=\sqrt{a}x_{0}\frac{\sin n\beta }{\sin (n+1)\beta }\}\\&\cup \bigcup _{i=0}^3\{(x_0,x_{-1},x_{-2},x_{-3})\in \mathbb {R}^4:x_{-i}=0\}. \end{aligned}$$

The solution form for Equation (1.2) tells us the following:

When $a<1$, any admissible solution is unbounded.

When $a>1$, any admissible solution to Equation (1.2) is converging to zero.

When $a=1$, under certain conditions we have periodic solutions; that we shall show in the following result:

Theorem 3.6

Assume that $a=1$ and let $\beta =\frac{p}{q}\pi$ (p and q are relatively positive prime integers) such that $0<p<\frac{q}{2}$. Then every admissible solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with

$$\begin{aligned} \prod _{j=0}^{q-1}\frac{x_{-3}\sin (3j+t)\beta -\sqrt{a}x_0\sin (3j+t-1)\beta }{x_{-3}\sin (3j+t+1)\beta -\sqrt{a}x_0\sin (3j+t)\beta }=-1,\ t=1,2,3, \end{aligned}$$

is a 6q-periodic.

Proof

When $a=1$, we can write solution form (3.5) as

$$\begin{aligned} x_{3m+t}=x_{t-3}\prod _{j=0}^{m}S_{j,t},\ t=1,2,3, \end{aligned}$$

where

$$\begin{aligned} S_{j,t}=\frac{x_{-3}\sin (3j+t)\beta -x_0\sin (3j+t-1)\beta }{x_{-3}\sin (3j+t+1)\beta -x_0\sin (3j+t)\beta }. \end{aligned}$$

For each $t=1,2,3$, we can see that

$$\begin{aligned} S_{j+q,t}=S_{j,t},\ j\ge 0. \end{aligned}$$

Then

$$\begin{aligned} x_{3(m+2q)+t}&=x_{t-3}\prod _{j=0}^{m+2q}S_{j,t}= x_{t-3}(-1)(\prod _{j=q}^{2q-1}S_{j,t}) (\prod _{j=2q}^{m+2q}S_{j,t})\\&=-x_{t-3}(\prod _{j=0}^{q-1}S_{j+q,t})(\prod _{j=0}^{m}S_{j+2q,t})=x_{3m+t},\ t=1,2,3. \end{aligned}$$

$\square$

Example 12

Fig. 12. shows that, if $a=0.5,b=1.2$ ($b^2<4a$ and $a<1$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=2$, $x_{-2}=-2.5$, $x_{-1}=-1.5$ and $x_{0}=4.3$ is unbounded.

Example 13

Fig. 13. shows that, if $a=1,b=\sqrt{2}$ ($b^2<4a$ and $a=1$), then a solution $\{x_n\}_{n=-3}^\infty$ of Equation (1.2) with $x_{-3}=1.8$, $x_{-2}=-2.5$, $x_{-1}=-1.2$ and $x_{0}=0.6$ is periodic with prime period 24.

In this example, we have $\beta =\frac{\pi }{4}$, $p=1$, $q=4$ and $\prod _{j=0}^{3}S_{j,t}=-1$ for each $t=1,2,3$.

(This is an illustrative example for Theorem (3.6)).

Fig. 12

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-0.5x_{n}+1.2x_{n-3}}$

Fig. 13

$x_{n+1}=\frac{x_{n-2}x_{n-3}}{-x_{n}+\sqrt{2}x_{n-3}}$

4 Conclusions

In this work, the solution forms for the two difference equations

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{ \pm ax_{n}+bx_{n-3}}, \ n\ge 0, \end{aligned}$$

where the parameters are positive real numbers and the initial values $x_{-3}$, $x_{-2}$, $x_{-1}$, $x_{0}$ are arbitrary real numbers are obtained.

We also studied the long-term behavior of the solutions for each equation.

For the equation

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{ ax_{n}+bx_{n-3}}, \ n\ge 0, \end{aligned}$$

we showed that every admissible solution tends to a period-3 solution when $a+b=1$.

For the equation

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{ -ax_{n}+bx_{n-3}}, \ n\ge 0, \end{aligned}$$

we obtained a result for the periodicity of its solutions when $b^2<4a$ and provide an illustrative example for this case.

We conjecture that the obtained results can be satisfied for the more extended equation

$$\begin{aligned} x_{n+1}=\frac{x_{n-k+1}x_{n-k}}{ ax_{n}+bx_{n-k}}, \ n\ge 0, \end{aligned}$$

with a positive integer k, real-valued parameters and initial values.

Future work: Deriving the solution and studying the global behavior of the solutions of the difference equation

$$\begin{aligned} x_{n+1}=\frac{x_{n-2}x_{n-3}}{ a_nx_{n}+b_nx_{n-3}}, \ n\ge 0, \end{aligned}$$

where $\{a_n\}_{n=0}^\infty$ and $\{b_n\}_{n=0}^\infty$ are p-periodic sequences with $p\ge 2$, and real initial conditions will be considered in future work.