An application of a novel geometric criterion to global-stability problems of a nonlinear SEIVS epidemic model

Abstract

This work applies a novel geometric criterion for nonlinear autonomous differential equations developed by Lu and Lu (NARWA 36:20–43, 2017) to a nonlinear SEIVS epidemic model with temporary immunity and achieves its threshold dynamics. Specifically, global-stability problems for the SEIVS model of Cai and Li (AMM 33:2919–2926, 2009) are effectively solved. The corresponding optimal control system with vaccination, awareness campaigns and treatment is further established and four different control strategies are compared by numerical simulations to contain hepatitis B. It is concluded that joint implementation of these measures can minimize the numbers of exposed and infectious individuals in the shortest time, so it is the most efficient strategy to curb the hepatitis B epidemic. Moreover, vaccination for newborns plays the core role and maintains the high level of population immunity.

1 Introduction

In the persistent but nonexplosive warfare between mankind and infectious diseases, the population without immunity had once felt panic and powerless in the face of each epidemic outbreak. It is estimated that there were 4–5 million deaths worldwide during the 1918–1920 H1N1 influenza pandemic, well above 8.5 million deaths in the First World War that lasted 52 months [1]. Some emerging infectious diseases frequently have raged across the planet in almost two decades, such as SARS, H1N1, EVD, MERS, COVID-19. Fortunately the invention of vaccines led mankind to a landmark victory against the diseases and 2–3 million deaths are prevented annually [2], however the vaccine protection only lasts for months to years since the vaccine-induced immunity wanes [3, 4].

Epidemiological dynamical models with temporary immunity [5,6,7,8,9] were developed to capture the vital factors underlying the disease transmission mechanisms. In particular, much attention (e.g., [6,7,8,9]) has been paid to the susceptible-infectious-recovered-susceptible (SIRS) epidemic models with non-permanent acquired immunity and nonlinear incidence rates, Sf(I), which can model the inhibition effects from the change of S class in behaviours as their number grows or the crowding effect of I class (e.g., saturated case $f(I)=\lambda I/(1+\sigma I)$, $\sigma >0$ [10]), as well as psychological effects as their number of I class increases (e.g., nonmonotone case $f(I)=\beta I/(1+\sigma I^2)$ [11], nonmonotone and saturated case $f(I)=\beta I^2/(1+\varrho I+\sigma I^2)$, $\varrho >-2\sqrt{\sigma }$ [9]). These models may present out simple threshold stability or undergo complex dynamics, including saddle-node bifurcation, Bogdanov-Takens bifurcation, Hopf bifurcation [8, 9]. Indeed, nonlinear incidence rates keep more consistent with the reality than standard bilinear case when incidence increases/decreases more gradually [9, 10, 12].

The fact that, as Anderson and May pointed out in [13], a host may be infected but not yet infectious, suggests that it is desirable to make a distinction between infection and infectiousness in epidemic models by introducing an exposed compartment E, such as SEIRS/SEIVS models [3, 4, 14, 15], in which infected individuals in E class will transfer to I class with infectiousness after a latent period. However, their global-stability analysis becomes more of a challenge since Lyapunov–LaSalle methods may be not a viable option. For instance, with the second additive compound matrix theory, Cai and Li [3], Sahu and Dhar [4] applied the classical geometric approach of [16,17,18] to the SEIVS models with vaccination to establish global stability of positive equilibria under some restrict conditions besides the control reproduction number $\mathcal {R}_c>1$. More recently, Lu and Lu [14, 15] generalized the global-stability geometric criterion and successfully removed some additional restrictions on global stability of several SEIRS models with the incidence rate $\beta S^\alpha f(I)$ ($\alpha >0$) and standard incidence rate $\beta SI/N$. A recent work of Doungmo Goufo et al. [19] revealed that an HIV-COVID-19 model with standard incidence rate and variable total population size N due to host’s disease-induced mortality, exhibits backward bifurcation, which indicates that reducing $\mathcal {R}_c$ below 1 is no longer sufficient for disease elimination [19,20,21,22]. What’s more, backward bifurcation has also been observed in the epidemic models with standard incidence rate and imperfect vaccination [23, 24].

In general, for some infectious diseases with long latent period, such as HIV, tuberculosis, hepatitis B, it is quite difficult to find and treat the infected individuals timely, thereby greatly impeding the control and elimination of diseases [25]. Several public health measures besides vaccination are preached and used to prevent and contain the epidemics [1], thereinto awareness campaigns by media alert and education among the public are implemented to enhance the limited knowledge about disease control, change their behaviour ways and reduce the infection likelihood [26, 27]. It is also suggested that patients with chronic infectious diseases (e.g., HBV, HCV) receive timely treatment, which can shorten the disease course and further reduce the incidence of infection [28]. Another significant research topic for epidemic models is to investigate the effectiveness of control strategies. Optimal control theory [29, 30] admits use of control measures with time-varying intensities to avoid wasting resources and high costs. Recently, Khan et al. [22] introduced four control measures to a vector-host epidemic model with saturated treatment and found that combination of these controls is the most desired strategy to reduce the infection in humans. One refers the reader to recent works for more details concerning optimal control strategies, including vaccination [26, 31,32,33,34,35], awareness campaigns [26] and treatment [20, 26, 35].

In the present paper, by application of the new geometric criterion developed by [14], we are concerned with global threshold dynamics of an SEIVS model with perfect vaccination and nonlinear incidence rate $\beta I^\rho S^\alpha /(1+\sigma I^\kappa )$ ($0<\rho \le 1$, $0\le \kappa \le 2$), which can reflect the saturated effects ($\kappa =1$) or the psychological effects ($1<\kappa \le 2$) in diseases transmission when $\rho =1$. Compared with the existing works in global dynamics analysis for the SEIVS epidemic models, our main contributions of this study lie in the following several aspects. Firstly, we formulate a new nonlinear SEIVS epidemic model incorporating vaccine-induced, disease-acquired and natural immunities, in which the nonlinear incidence rate may be more general than the ones used in [3, 4]. Secondly, different from the method used in [3, 4], this work employs a more general geometric criterion based on the third additive compound matrix theory developed by [14] and carefully analyzes global threshold stability of the model proposed. Meanwhile, the additional condition for global stability of the positive equilibrium in Theorem 2.1 [3] is removed. Lastly, based on the SEIVS model proposed we further develop its optimal control system with vaccination, awareness campaigns and treatment to investigate the effective measures to prevent hepatitis B transmission. And the existence and uniqueness of the optimal control solution are verified. Numerical results for several different control strategies show that joint implementation of these three measures is the most cost-effective in mitigating the hepatitis B epidemic.

The outline of this paper is laid out as follows. In Sect. 2, a nonlinear SEIVS epidemic model with temporary immunity is formulated. And global threshold stability of the equilibria is investigated in Sect. 3. Section 4 proposes an optimal control problem with three measures of the SEIVS model and demonstrates its existence and uniqueness of the optimal control solution. We further perform numerical simulations to seek for the most effective strategy to contain hepatitis B transmission in Section 5. A concluding section ends this paper with several remarks.

2 Model formulation

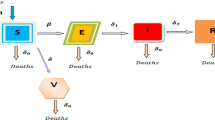
In this section, a nonlinear epidemic model with latency and temporary immunity is formulated. The total population with homogeneity N is classed into susceptible (S), exposed (E), infectious (I) and vaccinated/recovered (V) compartments. Based on the nonlinear SEIVS epidemic model in [3], which takes the form of

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{lll} \displaystyle \frac{dS}{dt}=(1-p)A-d S-\frac{\beta IS}{h(I)}+\delta V, \\ \displaystyle \frac{dE}{dt}=\frac{\beta IS}{h(I)}-(d+\varepsilon )E,\\ \displaystyle \frac{dI}{dt}=\varepsilon E-(d+\tau )I,\\ \displaystyle \frac{dV}{dt}=pA+\tau I-(d+\delta )V, \end{array}\right. \end{array} \end{aligned}$$

(2.1)

we make several basic assumptions motivated by the biological significances as follows:

• Vaccine-induced, disease-acquired and natural immunities [4] for the certain disease are temporary, and it may be realistic for most vaccine-preventable infectious diseases;

• The durations of these immunities are almost same, so V class consists of vaccinated and recovered individuals [3, 4]. For example, the recovered individuals from A/H1N1 influenza infection still have the risk of infection once their resistance fall;

• The death rate induced by the disease is low so it can be ignored, therefore the total population N can maintain constant, seeing [3, 4];

• Since susceptible individuals may change their behavior ways to avoid infection after awareness campaigns are conducted, we adopt the nonlinear incidence rate $\beta I^\rho S^\alpha /(1+\sigma I^\kappa )$ ($0<\rho \le 1$, $0\le \kappa \le 2$, $\alpha >0$), which can model the saturated effects ($\kappa =1$) or psychological effects ($1<\kappa \le 2$) when $\rho =1$, seeing the Refs. [10, 11].

Out of the above considerations, an SEIVS epidemic model with temporary immunity and general nonlinear incidence rate is constructed as follows:

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{lll} \displaystyle \frac{dS}{dt}=(1-p)A-d S-\frac{\beta I^\rho S^\alpha }{1 + \sigma I^\kappa }+\delta V,\\ \displaystyle \frac{dE}{dt}=\frac{\beta I^\rho S^\alpha }{1 + \sigma I^\kappa }-(d+\varepsilon +\eta )E,\\ \displaystyle \frac{dI}{dt}=\varepsilon E-(d+\tau )I,\\ \displaystyle \frac{dV}{dt}=pA+\tau I+\eta E-(d+\delta )V. \end{array}\right. \end{array} \end{aligned}$$

(2.2)

All parameters in model (2.2) maintain nonnegative, and their biological meanings are interpreted as follows. Individuals are born at a rate A into S class, and a fraction of newborns are effectively vaccinated at a rate p. Susceptible individuals become infected at a rate $\beta$. And $1/(1+\sigma I^\kappa )$ measures the inhibition effects or psychological effects owing to awareness campaigns. The temporary immunities induced by the perfect vaccine, the disease and inapparent infections, wane at a rate $\delta$. Meanwhile, all individuals in each class have the same natural death rate d. The individuals in E class may transfer to I class at a rate $\varepsilon$, also to V class at a rate $\eta$ because of acquiring natural immunity. The infectious individuals are effectively cured at a rate $\tau$.

For the convenience of presentation, we denote the infectious force

$$\begin{aligned} \begin{array}{lll} \displaystyle \varphi (I):=\frac{\beta I^\rho }{1+\sigma I^\kappa },\ \ 0<\rho \le 1, \ \ 0<\kappa \le 2. \end{array} \end{aligned}$$

(2.3)

The function is characterized by differentiability and $\varphi (0)=0$, $\varphi '(0)=+\infty$ (as $0<\rho <1$) or $\varphi '(0)=\beta$ (as $\rho =1$). What’s more,

$$\begin{aligned} \begin{array}{lll} \displaystyle I|\varphi '(I)|\le \varphi (I),\ \ \text{ for } \ I>0 \end{array} \end{aligned}$$

(2.4)

holds true. It is obvious that the nonlinear incidence rate $S^\alpha \varphi (I)$ in model (2.2) extends the monotone saturated one [10] and nonmonotone one with psychological effects [11]. In particular, when $\rho =\alpha =\kappa =1$ and $\eta =0$, model (2.2) becomes model (2.1) with saturated incidence rate, and global stability of its endemic equilibrium $Q_*$ was established by Cai and Li in [16] as follows:

Theorem 2.1

(seeing Theorem 4 in [3]) The endemic equilibrium $Q_*$ is global stable if the control reproduction number $\mathcal {R}_c:=\varepsilon \beta A[d(1-p)+\delta ]/[d(d+\varepsilon )(d+\tau )(d+\delta )]>1$ and

$$\begin{aligned} \begin{array}{lll} \displaystyle \delta \le \min \bigg \{\frac{\varepsilon }{2}, \frac{A\{\beta [\delta +d(1-p)]+\delta \}}{d(d+\delta )}\bigg \}. \end{array} \end{aligned}$$

A natural question will be raised: Is the endemic equilibrium for model (2.2) with the saturated incidence rate or even more general nonlinear incidence rate globally asymptotically stable only if $\mathcal {R}_c>1$ ? In what follows, we shall employ a more general geometric criterion for nonlinear autonomous differential equations developed by [14] to study global dynamics of model (2.2), and give an affirmative answer to the question above, improving Theorem 2.1.

3 Model analysis

This section focuses on analyzing global dynamics of model (2.2), including the positivity and boundedness of the solution, the existence, local and global stability of its equilibria.

3.1 Positivity and boundedness of the solution

Lemma 3.1

Each solution (S(t), E(t), I(t), V(t)) of model (2.2) with the positive initial data (S(0), E(0), I(0), V(0)) remains nonnegative for all $t>0$. Further, the biologically meaningful region

$$\begin{aligned} \begin{array}{lll} \displaystyle \Xi =\bigg \{(S(t),E(t),I(t),V(t))\in \mathbb {R}^4_+: N(t)=S(t)+E(t)+I(t)+V(t)\le \frac{A}{d}\bigg \}, \end{array} \end{aligned}$$

is a positively invariant set with respect to (2.2).

Proof

Following the idea of [20, 36, 37], let us denote $\phi :=\beta I^\rho S^{\alpha -1}/(1+\sigma I^\kappa )$ and $t_1:=\sup \{t>0: S>0, E>0, I>0, V>0, [0,t]\}$, so $t_1>0$. By the first equation of model (2.2), it can be seen that $dS(t)/dt=(1-p)A-(d+\phi (t))S(t)+\delta V(t)\ge (1-p)A-(d+\phi (t))S(t)$, which can be recast as

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{d}{dt}\bigg [S(t)\exp \bigg \{dt+\int ^t_0\phi (r)dr\bigg \}\bigg ]\ge (1-p)A\exp \bigg \{dt+\int ^t_0\phi (r)dr\bigg \}. \end{array} \end{aligned}$$

Integrating the equality above from 0 to $t_1$ yields

$$\begin{aligned} \begin{array}{lll} \displaystyle S(t_1)\exp \bigg \{dt_1+\int ^{t_1}_0\phi (r)dr\bigg \}-S(0) \ge (1-p)A\int ^{t_1}_0\exp \bigg \{dx+\int ^x_0\phi (r)dr\bigg \}dx, \end{array} \end{aligned}$$

and then one obtains

$$\begin{aligned} \begin{aligned} \displaystyle S(t_1)&\ge \displaystyle (1 - p)A\exp \bigg \{ - dt_1 - \int ^{t_1}_0 \phi (r)dr\!\bigg \}\!\!\int ^{t_1}_0\!\!\!\exp \bigg \{\!dx + \!\!\int ^x_0\!\!\!\phi (r)dr\!\bigg \}dx \\&\quad + S(0)\exp \bigg \{ - dt_1 - \!\!\int ^{t_1}_0\!\!\!\phi (r)dr\!\bigg \}\!>\!0. \end{aligned} \end{aligned}$$

Therefore, $S(t)>0$ for all $t>0$. By similar augments above it can be verified that $E(t)>0$, $I(t)>0$, $V(t)>0$ for all $t>0$.

Next, we shall show the boundedness of the solution for (2.2). It follows from $dN(t)/dt=A-dN(t)$ that $N(t)= N(0)e^{-dt}+A(1-e^{-dt})/d$, so $N(t)\le A/d$ provided that $N(0)\le A/d$. This suggests that the feasible region $\Xi$ can ensure that each solution (S(t), E(t), I(t), V(t)) of model (2.2) with the positive initial data in $\Xi$ remains unique, positive and bounded for all $t>0$ and is attracted in $\Xi$. Namely, $\Xi$ is a positively invariant set. $\square$

3.2 Stability of disease-free equilibrium

It is direct to show that there is always a disease-free equilibrium $Q_0=(S_0,0,0,V_0)$, where $S_0=A[(1-p)d+\delta ]/[d(d+\delta )]$, $V_0=pA/(d+\delta )$. It could be observed that model (2.2) admits another biologically feasible region $\widetilde{\Xi }=\{(S,E,I,V)\in \mathbb {R}^4_+: S\le S_0,\ V\le V_0,\ N\le A/d\}$, which is also positive-invariant and attracting such that model (2.2) is well-posed in $\widetilde{\Xi }$. The above result can be checked by the similar arguments in [38], only with minor modification.

Furthermore, the local stability of $Q_0$ will be achieved by virtue of the method of next generation operator developed in [39]. By means of the notation in [39], the matrices F and V for model (2.2) acquire the forms of

$$\begin{aligned} F=\left[ \begin{array}{ccc} \displaystyle 0\ \ &{}\displaystyle S^\alpha _0\varphi '(0)\\ \displaystyle 0\ \ &{} 0\\ \end{array} \right] ,\ \ \ V=\left[ \begin{array}{ccc} \displaystyle d+\varepsilon +\eta \ \ &{}\displaystyle 0\\ \displaystyle -\varepsilon \ \ &{} d+\tau \\ \end{array} \right] , \end{aligned}$$

(3.1)

so the control reproduction number for model (2.2)

$$\begin{aligned} \begin{array}{lll} \displaystyle \mathcal {R}_c=\rho (FV^{-1})=\frac{\varepsilon S^\alpha _0\varphi '(0)}{(d+\tau )(d+\varepsilon +\eta )}. \end{array} \end{aligned}$$

Following Theorem 2 in [39], we immediately obtain the following conclusion.

Theorem 3.1

The disease-free equilibrium $Q_0$ is locally asymptotically stable if $\mathcal {R}_c<1$ but unstable provided that $\mathcal {R}_c>1$.

Theorem 3.2

If ${\mathcal {R}}_c\le 1$, $Q_0$ is globally asymptotically stable in $\widetilde{\Xi }$.

Proof

Take the candidate Lyapunov function $\mathbf {V}(t)=E+(d+\varepsilon +\eta )I/\varepsilon$. A direct deduction from (2.4) gives $\varphi '(I)\le \varphi (I)/I$, which indicates $\varphi (I)/I$ is monotonously nonincreasing for $I>0$, so

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{\varphi (I)}{I}\le \lim _{I\rightarrow 0^+}\frac{\varphi (I)}{I}=\varphi '(0). \end{array} \end{aligned}$$

Along the solutions of model (2.2), the time derivative of $\mathbf {V}(t)$ can be calculated as

$$\begin{aligned} \begin{aligned} \displaystyle \frac{d\mathbf {V}(t)}{dt}&= \displaystyle I\bigg [S^\alpha \frac{\varphi (I)}{I}-\frac{(d+\tau )(d+\varepsilon +\eta )}{\varepsilon }\bigg ]\le \displaystyle I\bigg [S^\alpha _0\varphi '(0)-\frac{(d+\tau )(d+\varepsilon +\eta )}{\varepsilon }\bigg ]\\&=\displaystyle (\mathcal {R}_c-1)\frac{(d+\tau )(d+\varepsilon +\eta )}{\varepsilon }I\le 0. \end{aligned} \end{aligned}$$

Consequently, it can be deduced from the LaSalle’s Invariance Principle [40] and local stability of $Q_0$ that it is globally asymptotical stability in $\widetilde{\Xi }$ when ${\mathcal {R}}_c\le 1$. $\square$

3.3 Existence of endemic equilibrium

Theorem 3.3

Model (2.2) has a unique endemic equilibrium $Q_*$ iff $\mathcal {R}_c>1$.

Proof

For model (2.2), the coordinates of positive equilibrium are determined by

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{lll} \displaystyle 0=(1-p)A-d S-S^\alpha \varphi (I)+\delta V, \\ \displaystyle 0=S^\alpha \varphi (I)-(d+\varepsilon +\eta )E,\\ \displaystyle 0=\varepsilon E-(d+\tau )I,\\ \displaystyle 0=pA+\tau I+\eta E-(d+\delta )V. \end{array}\right. \end{array} \end{aligned}$$

(3.2)

For ease of notation, let us denote $\ell _1:=(d+\tau )(d+\varepsilon +\eta )/\varepsilon$, $\ell _2:=[(d+\tau )(d+\varepsilon +\eta +\delta )+\varepsilon \delta ]/[\varepsilon (d+\delta )]$. Utilizing the third equation of (3.2) gives $E=(d+\tau )I/\varepsilon$. Adding its first two equations and utilizing its last equation, one further respectively arrives at

$$\begin{aligned} \begin{array}{lll} \displaystyle (1-p)A-d S-\ell _1I+\delta V=0,\\ \displaystyle pA+\frac{\tau \varepsilon +(d+\tau )\eta }{\varepsilon }I-(d+\delta )V=0. \end{array} \end{aligned}$$

(3.3)

Eliminating V in (3.3) results in $S=S_0-\ell _2I$. Note that $S\ge 0$, then $I\le S_0/\ell _2$. By the second equation of (3.2), we further derive that

$$\begin{aligned} \begin{array}{lll} \Phi (I):=\displaystyle (S_0-\ell _2I)^\alpha \varphi (I)-\ell _1I=0,\ \ 0<I\le S_0/\ell _2. \end{array} \end{aligned}$$

(3.4)

Inspired by the idea in [41], the existence and the uniqueness of positive solution to equation (3.4) are discussed in the following three steps.

• Step 1 Now we are ready to demonstrate the existence of the positive solution for $\mathcal {R}_c>1$. In fact, from $\Phi '(I)=-\alpha \ell _2(S_0-\ell _2I)^{\alpha -1}\varphi (I)+(S_0-\ell _2I)^\alpha \varphi '(I)-\ell _1$, thanks to $\varphi (0)=0$, then $\Phi '(0)=\lim _{I\rightarrow 0^+}S^\alpha _0\varphi '(I)-\ell _1=\ell _1(\mathcal {R}_c-1)$ can be attained. Provided that $\mathcal {R}_c>1$, it can be easily deduced that $\Phi (I)>0$ holds true when I is sufficiently small since $\Phi '(0)>0$, $\Phi (0)=0$ and $\Phi (S_0/\ell _2)<0$. This amounts to the existence of at least one positive solution to equation (3.4), denoted by $I_*$.

• Step 2 It can be verified that the positive solution $I_*$ is unique when $\mathcal {R}_c>1$. Without loss of generality, assume that there exists another positive root which is nearest to $I_*$, denoted by $I^\dagger$, then $\Phi '(I^\dagger )\ge 0$ follows from the continuity of $\Phi (I)$. Using (2.4) further leads to

  $$\begin{aligned} \begin{array}{lll} \displaystyle \Phi '(I^\dagger )=(S^\dagger )^\alpha \varphi '(I^\dagger )-\alpha \ell _2(S^\dagger )^{\alpha -1}\varphi (I^\dagger )-(S^\dagger )^\alpha \varphi (I^\dagger )/I^\dagger <0. \end{array} \end{aligned}$$

  (3.5)

  A contradiction is attained and the uniqueness of $I_*$ is validated.

• Step 3 In the end, we shall the nonexistence of positive root to (3.4) in the case of $\mathcal {R}_c\le 1$ with reductio ad absurdum. Let us take its smallest positive root $I_+$, then it certainly satisfies $\Phi '(I_+)<0$ according to (3.5). Recall that $\Phi (0)=0$ and $\Phi '(0)\le 0$, thus $\Phi (I)\le 0$ is true when I is small enough. Namely, the continuous function $\Phi (I)$ increases from the non-positive value to 0, which implies $\Phi '(I_+)\ge 0$, resulting in a contradiction. Hence, we draw a conclusion from Steps 1-3 that model (2.2) admits a unique endemic equilibrium $Q_*\!=\!(S_{*},E_{*},I_{*},V_{*})$ if and only if $\mathcal {R}_c>1$, where $S_{*}$, $E_{*}$, $V_{*}$ can be determined uniquely according the results obtained above. $\square$

3.4 Local stability of endemic equilibrium

Theorem 3.4

The endemic equilibrium $Q_*$ is locally asymptotically stable iff $\mathcal {R}_c>1$.

Proof

The Jacobian matrix of model (2.2) reads

$$\begin{aligned} \mathbb {J}=\left[ \begin{array}{ccccc} -(d+\alpha S^{\alpha -1}\varphi (I))\ \ &{} 0\ \ &{} -\displaystyle S^\alpha \varphi '(I)\ \ &{} \delta \\ \alpha S^{\alpha -1}\varphi (I)\ \ &{} -(d+\varepsilon +\eta )\ \ &{} S^\alpha \varphi '(I)\ \ &{}0\\ 0\ \ &{} \varepsilon \ \ &{} -(d+\tau )\ \ &{} 0\\ 0\ \ &{} \eta \ \ &{} \tau \ \ &{} -(d+\delta ) \end{array} \right] , \end{aligned}$$

(3.6)

so the characteristic equation at $Q_*$ is evaluated as

$$\begin{aligned} \begin{array}{lll} &{}\displaystyle (\chi +d)[(\chi +d+\tau )(\chi +d+\varepsilon +\eta )(\chi +d+\delta +\alpha S^{\alpha -1}_*\varphi (I_*))\\ &{}\quad +\,\displaystyle \delta \alpha S^{\alpha -1}_*\varphi (I_*)(\chi +d+\tau +\varepsilon )-\varepsilon S^\alpha _*\varphi '(I_*)(\chi +d+\delta )]=0.\!\! \end{array} \end{aligned}$$

(3.7)

Apparently, $\chi _1=-d<0$. With regard to the remaining eigenvalues of the equation

$$\begin{aligned} \begin{array}{lll} &{}\displaystyle (\chi +d+\tau )(\chi +d+\varepsilon +\eta )(\chi +d+\delta +\alpha S^{\alpha -1}_*\varphi (I_*))\\ &{}\quad \ +\,\displaystyle \delta \alpha S^{\alpha -1}_*\varphi (I_*)(\chi +d+\tau +\varepsilon )=\displaystyle \varepsilon S^\alpha _*\varphi '(I_*)(\chi +d+\delta ), \end{array} \end{aligned}$$

(3.8)

the following 2 cases need discussing.

Case I$\varphi '(I_*)>0$. One asserts that all eigenvalues of Eq. (3.8) possess negative real parts. Otherwise, there at least is one eigenvalue $\tilde{\chi }$ satisfying $Re \tilde{\chi }\ge 0$. One derives from (3.8) and $\varphi '(I_*)\le \varphi (I_*)/I_*$ that

$$\begin{aligned} \begin{array}{lll} \displaystyle (d + \tau )(d + \varepsilon + \eta )\!\!\!&{}\!<\!\displaystyle \bigg |(\tilde{\chi } + d + \tau )(\tilde{\chi } + d + \varepsilon + \eta )\bigg (\!1 + \frac{\alpha S^{\alpha -1}_*\varphi (I_*)}{\tilde{\chi } + d + \delta }\!\bigg ) + \delta \alpha S^{\alpha -1}_*\varphi (I_*)\frac{\tilde{\chi } + d + \tau + \varepsilon }{\tilde{\chi } + d + \delta }\bigg |\!\!\!\!\!\!\!\\ \quad &{} = \displaystyle \varepsilon S^\alpha _*\varphi '(I_*)\le \frac{\varepsilon S^\alpha _*\varphi (I_*)}{I_*}=(d+\tau )(d+\varepsilon +\eta ), \end{array} \end{aligned}$$

(3.9)

generating a contradiction. So each eigenvalue $\chi$ of (3.7) meets $Re \chi <0$.

Case II$\varphi '(I_*)\le 0$. Equation (3.8) can be recast as $\chi ^3+H_1\chi ^2+H_2\chi +H_3=0$, where

$$\begin{aligned} \begin{array}{lll} \displaystyle H_1=h_1+h_2+h_3,\ \ \ \ H_2=h_1h_2+h_1h_3+h_2h_3+\delta \alpha S^{\alpha -1}_*\varphi (I_*)-\varepsilon S^\alpha _*\varphi '(I_*),\\ \displaystyle H_3=h_1h_2h_3+\delta \alpha S^{\alpha -1}_*\varphi (I_*)h_4-\varepsilon S^\alpha _*\varphi '(I_*)h_5, \end{array} \end{aligned}$$

and $h_1=d+\tau$, $h_2=d+\varepsilon +\eta$, $h_3=d+\delta +\alpha S^{\alpha -1}_*\varphi (I_*)$, $h_4=d+\tau +\varepsilon$, $h_5=d+\delta$. According to the Routh-Hurwitz stability criterion, the necessary and sufficient conditions for the stability of the $Q_*$ are (i): $H_i>0$, $i=1,2,3$; (ii): $H_1H_2-H_3>0$. Obviously, (i) holds since $h_i>0$. And (ii) can be guaranteed by virtue of

$$\begin{aligned} \begin{array}{lll} &{}\displaystyle H_1H_2-H_3=[(h_1+h_2+h_3)(h_1h_2+h_1h_3+h_2h_3)-h_1h_2h_3]\\ &{}\quad \quad \quad \quad \quad \quad +\displaystyle \delta \alpha S^{\alpha -1}_*\varphi (I_*)(h_1+h_2+h_3-h_4)-\varepsilon S^\alpha _*\varphi '(I_*)(h_1+h_2+h_3-h_5)>0. \end{array} \end{aligned}$$

Synthesizing Cases I and II yields that $Q_*$ is locally asymptotically stable iff $\mathcal {R}_c> 1$.

$\square$

3.5 Global stability of endemic equilibrium

Ultimately, a new geometric criterion for autonomous differential equations generalized by Lu and Lu [14] is utilized to study the endemic equilibrium for model (2.2) in the interior $\mathring{\widetilde{\Xi }}$ of the feasible region $\widetilde{\Xi }$. To this end, we consider a differential function $f(x): \Omega \rightarrow \mathbb {R}^n$, where $\Omega \subset \mathbb {R}^n$ is a simply connected open set. For the dynamical system

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{dx}{dt}=f(x),\ \ x\in \Omega , \end{array} \end{aligned}$$

(3.10)

let us denote its solution by $x(t,x_0)$, satisfying $x(0,x_0)=x_0$, and its equilibrium by $x_\star$. Consider that system (3.10) has a $n-k$ dimensional invariant manifold $\Theta =\{x\in \mathbb {R}^n|\mathcal {N}(x)=0\}$, where $\mathcal {N}(x)\in C^2: \Omega \rightarrow \mathbb {R}^n$, with $\dim (\partial \mathcal {N}/\partial x)=k$ if $\mathcal {N}(x)=0$. Following [16], one defines a real function $\nu (x)=tr(\mathcal {M}(x))$ on $\Theta$, where $\mathcal {M}(x)$ stands for a continuous $k\times k$ dimensional matrix-valued function determined by $\mathcal {N}_f(x)=(\partial \mathcal {N}/\partial x)\cdot f(x)=\mathcal {N}(x)\cdot \mathcal {M}(x)$.

Meanwhile, one assumes that

(H1) $\Theta$ is simply connected, and a compact absorbing set U is such that $U\subset \Omega \subset \Theta$.

(H2) The equilibrium $x_\star$ is unique in $\Theta$.

Lemma 3.2

(seeing Theorem 2.6 in [14]) The equilibrium $x_\star$ of (3.10) is globally asymptotically stable in $\Theta$ when (H1)-(H2) and the following condition (D) are satisfied.

(D) For the coefficient matrix $C(x(0,x_0))$ of system (3.10), there exists a matrix M(t), a large enough positive constant $\ell$ and positive ones $l_1, l_2,\ldots , l_n>0$ such that

$$\begin{aligned} \begin{array}{lll} \displaystyle c_{ii}(t)+\sum _{i\ne j}\frac{l_j}{l_i}|c_{ij}(t)|\le m_{ii}(t)+\frac{l_j}{l_i}|m_{ij}(t)|,\ \text{ for } \ \ t\ge \ell ,\ \ \forall x_0\in U, \end{array} \end{aligned}$$

(3.11)

and

$$\begin{aligned} \begin{array}{lll} \displaystyle \lim _{t\rightarrow \infty }\frac{1}{t}\int ^t_0\bigg (m_{ii}(s)+\frac{l_j}{l_i}|m_{ij}(s)|\bigg )ds=\bar{m}_i<0, \end{array} \end{aligned}$$

(3.12)

where $c_{ij}(t)$ and $m_{ij}$ stand for entries of matrices $C(x(0,x_0))$ and M(t), respectively.

Before giving the proof of global stability of endemic equilibrium, we first recall that $Q_0$ is unstable and $Q_0\in \partial \widetilde{\Xi }$ when $\mathcal {R}_c>1$, where $\partial \widetilde{\Xi }$ stands for the boundary of $\widetilde{\Xi }$, therefore the permanence of model (2.2) can be established.

Theorem 3.5

When $\mathcal {R}_c>1$, model (2.2) is permanent in $\mathring{\widetilde{\Xi }}$.

Now the main result on global stability of $Q_*$ is stated and proved as follows.

Theorem 3.6

The endemic equilibrium is globally asymptotically stable in $\mathring{\widetilde{\Xi }}$ iff $\mathcal {R}_c>1$.

Proof

Taking advantages of the definition of the third additive compound matrix of the Jacobian matrix $\mathbb {J}$ in [18], it is easy to obtain that

$$\begin{aligned} \mathbb {J}^{[3]}(x)\!=\!\left[ \begin{array}{ccccc} -(\Delta + \varepsilon + \tau + \eta )\ \ &{}0\ \ &{}0\ \ &{}\delta \\ \tau \ \ &{}-(\Delta + \varepsilon + \delta + \eta )\ \ &{}S^\alpha \varphi '(I)\ \ &{}S^\alpha \varphi '(I)\\ -\eta \ \ &{}\varepsilon \ \ &{}-(\Delta + \tau + \delta )\ \ &{}0\\ 0\ \ &{}0\ \ &{}\alpha S^{\alpha -1}\varphi (I)\ \ &{}-(3d + \varepsilon + \tau + \delta + \eta ) \end{array} \right] , \end{aligned}$$

where $\Delta =3d+\alpha S^{\alpha -1}\varphi (I)$.

Let us assign $\mathcal {N}(x)=S+E+I+V-A/d$ with $x=(S,E,I,V)\in \mathbb {R}^4_+$. The invariant manifold for model (2.2) is governed by $\Theta =\{x\in \mathbb {R}^4_+|\mathcal {N}(x)=0\}$. Following [18], we can show that $\nu (x)=tr(\mathcal {M}(x))=-d$ and $k=\text{ dim }(\partial \mathcal {N}/\partial x)=1$.

In the sequel, let $P(x)=\text{ diag }\{\pi V,\alpha I,\alpha E,S\}$ and $\mathbb {E}_{4\times 4}$ be the $4\times 4$ identity matrix, where the constant $\pi >0$ will be determined later. A little algebraic calculation leads to

$$\begin{aligned} \begin{array}{lll} C(t) &{}=\displaystyle P_fP^{-1}+P\mathbb {J}^{[3]}(x)P^{-1}-\nu \mathbb {E}_{4\times 4}\\ &{}=\left[ \begin{array}{ccccc}-(\varepsilon +\tau +\eta )\ \ &{}0\ \ &{}0\ \ &{}\displaystyle \frac{\pi \delta V}{S}\\ \displaystyle \frac{\alpha \tau I}{\pi V}\ \ &{}-(\varepsilon +\delta +\eta )\ \ &{}\displaystyle \frac{S^\alpha I\varphi '(I)}{E}\ \ &{}\displaystyle \alpha S^{\alpha -1}I\varphi '(I)\\ -\displaystyle \frac{\alpha \eta E}{\pi V}\ \ &{}\displaystyle \frac{\varepsilon E}{I}\ \ &{}-(\tau +\delta )\ \ &{}0\\ \displaystyle 0\ \ &{}0\ \ &{}\displaystyle \frac{S^\alpha \varphi (I)}{E}\ \ &{}-(\varepsilon +\tau +\delta +\eta ) \end{array} \right] +\mathcal {C}, \end{array} \end{aligned}$$

where $\mathcal {C}=\text{ diag }\{-(2d+\alpha S^{\alpha -1}\varphi (I))+V'/V,-(2d+\alpha S^{\alpha -1}\varphi (I))+I'/I,-(2d+\alpha S^{\alpha -1}\varphi (I))+E'/E,-2d+S'/S\}$.

Observe that model (2.2) can be rewritten as

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{lll} \displaystyle \frac{\delta V}{S}=\frac{S'}{S}-\frac{(1-p)A}{S}+S^{\alpha -1}\varphi (I)+d, \\ \displaystyle \frac{S^\alpha \varphi (I)}{E}=\frac{E'}{E}+d+\varepsilon +\eta ,\\ \displaystyle \frac{\varepsilon E}{I}=\frac{I'}{I}+d+\tau ,\\ \displaystyle \frac{\tau I}{V}=\frac{V'}{V}-\frac{pA}{V}+d+\delta -\frac{\eta E}{V}. \end{array}\right. \end{array} \end{aligned}$$

(3.13)

We shall proceed by considering the following two cases.

• Case I In the case of $\alpha \ge 1$, one chooses $\pi =1$. By (3.11) it can be revealed that

  $$\begin{aligned} \begin{array}{lll} C_1(t) = \displaystyle c_{11}(t) + \!\sum ^4_{i=2}|c_{ij}(t)| &{} = -\displaystyle (2d + \varepsilon +\tau +\eta +\alpha S^{\alpha -1}\varphi (I))+\frac{V'}{V}+\frac{\delta V}{S}\\ \ \ \ \ \ \ \ \ \ &{} = -\displaystyle (2d + \varepsilon + \tau + \eta + \alpha S^{\alpha -1}\varphi (I)) + \frac{V'}{V} \\ &{}\quad + \bigg (\!\frac{S'}{S} - \frac{(1 - p)A}{S} + S^{\alpha -1}\varphi (I) + d\bigg )\\ \ \ \ \ \ \ \ \ \ &{}\!\le \!\displaystyle \frac{S'}{S}+\frac{V'}{V} - \bigg (\!d+\varepsilon +\tau +\eta +\frac{(1-p)A}{S_0}\!\bigg )\triangleq m_1(t). \end{array} \end{aligned}$$

  Recall that $V\le V_0$ can ensure that $d+\delta -pA/V\le 0$ is true. Also, the permanence of (2.2) implies that there is a positive constant $\mu _0$ such that $\mu _0\le S,E,I,V\le A/d$. By virtue of (2.4), (3.11) and (3.13) one thus arrives at

  $$\begin{aligned} \begin{array}{lll} C_2(t) &{} = \displaystyle c_{22}(t)+\sum _{i\ne 2}|c_{ij}(t)|\\ &{}=-\displaystyle (2d+\varepsilon +\delta +\eta +\alpha S^{\alpha -1}\varphi (I))+\frac{I'}{I}+\frac{\alpha \tau I}{V}+\frac{S^\alpha I|\varphi '(I)|}{E}+\alpha S^{\alpha -1}I|\varphi '(I)|\\ &{}\le -\displaystyle (2d + \varepsilon + \delta + \eta + \alpha S^{\alpha -1}\varphi (I)) + \frac{I'}{I} + \alpha \bigg (\!\frac{V'}{V} - \frac{pA}{V} + d \\ &{}\quad + \delta - \dfrac{\eta E}{V}\!\bigg ) + \dfrac{S^\alpha \varphi (I)}{E} + \alpha S^{\alpha -1}\varphi (I)\\ &{}\le -\displaystyle (2d+\varepsilon +\delta +\eta +\alpha S^{\alpha -1}\varphi (I))+\frac{I'}{I}\\ &{}\quad +\displaystyle \alpha \bigg (\!\frac{V'}{V} - \frac{pA}{V}+d+\delta - \frac{\eta E}{V}\!\bigg )+\bigg (\!\frac{E'}{E}+d+\varepsilon +\eta \!\bigg )+\alpha S^{\alpha -1}\varphi (I)\\ &{}\le \displaystyle \frac{E'}{E}+\frac{I'}{I}+\alpha \frac{V'}{V}-\bigg (\!d+\delta +\frac{\alpha \eta \mu _0}{V_0}\!\bigg )\triangleq m_2(t). \end{array} \end{aligned}$$

  Similarly, it can be inferred that

  $$\begin{aligned}&\begin{array}{lll} C_3(t) &{}= - \displaystyle (2d + \tau + \delta + \alpha S^{\alpha - 1}\varphi (I)) + \frac{E'}{E} + \frac{\alpha \eta E}{V} + \frac{\varepsilon E}{I}\le \displaystyle \frac{E'}{E} + \frac{I'}{I} + \alpha \frac{V'}{V} \\ {} &{}\quad - \bigg (\!d + \delta + \dfrac{\alpha \tau \mu _0}{V_0}\!\bigg )\!\triangleq \!m_3(t), \end{array} \\&\begin{array}{lll} C_4(t)=-\displaystyle (2d+\varepsilon +\tau +\delta +\eta )+\frac{S'}{S}+\frac{S^\alpha \varphi (I)}{E}\le \displaystyle \frac{S'}{S}+\frac{E'}{E} - (d+\tau +\delta )\triangleq m_4(t). \end{array} \end{aligned}$$

  Taking the matrix $M(t)=\text{ diag }\{m_1(t),m_2(t),m_3(t),m_4(t)\}$ in Lemma 4.3 results in

  $$\begin{aligned} \begin{array}{lll} \displaystyle \lim _{t\rightarrow \infty }\frac{1}{t}\int ^t_0m_i(s)ds=m_i<0,\ \ i=1,2,3,4, \end{array} \end{aligned}$$

  where $m_1=-(d+\varepsilon +\tau +\eta +(1-p)A/S_0)$, $m_2=-(d+\delta +\alpha \eta \mu _0/V_0)$, $m_3=-(d+\delta +\alpha \tau \mu _0/V_0)$, $m_4=-(d+\tau +\delta )$.

• Case II In the case of $0<\alpha <1$, one requires $\pi =\alpha$. Using similar arguments with Case I yields

  $$\begin{aligned} \begin{array}{lll} C_1(t) &{}=-\displaystyle (2d+\varepsilon +\tau +\eta +\alpha S^{\alpha -1}\varphi (I))+\frac{V'}{V}+\frac{\alpha \delta V}{S}\\ &{}\le \displaystyle \alpha \frac{S'}{S}+\frac{V'}{V} - \bigg [(2-\alpha )d+\varepsilon +\tau +\eta +\frac{(1-p)A}{S_0}\bigg ]\triangleq \tilde{m}_1(t),\\ C_2(t) &{}=-\displaystyle (2d+\varepsilon +\delta +\eta +\alpha S^{\alpha -1}\varphi (I))+\frac{I'}{I}+\frac{\tau I}{V}+\frac{S^\alpha I|\varphi '(I)|}{E}+\alpha S^{\alpha -1}I|\varphi '(I)|\\ &{}\le -\displaystyle (2d + \varepsilon + \delta + \eta + \alpha S^{\alpha -1}\varphi (I)) + \frac{I'}{I}\\ {} &{}\quad +\bigg (\!\frac{V'}{V} - \frac{pA}{V} + d + \delta - \frac{\eta E}{V}\!\bigg ) + \frac{S^\alpha \varphi (I)}{E} + \alpha S^{\alpha -1}\varphi (I)\\ &{}\le \displaystyle \frac{E'}{E}+\frac{I'}{I}+\frac{V'}{V}-\bigg (\!d+\delta +\frac{\eta \mu _0}{V_0}\!\bigg )\triangleq \tilde{m}_2(t),\\ C_3(t) &{}=-\displaystyle (2d+\tau +\delta +\alpha S^{\alpha -1}\varphi (I))+\frac{E'}{E}+\frac{\eta E}{V}+\frac{\varepsilon E}{I}\\ &{}\le \displaystyle \frac{E'}{E}+\frac{I'}{I}+\frac{V'}{V}-\bigg (\!d+\delta +\frac{\tau \mu _0}{V_0}\!\bigg )\triangleq \tilde{m}_3(t),\\ C_4(t) &{}=-\displaystyle (2d+\varepsilon +\tau +\delta +\eta )+\frac{S'}{S}+\frac{S^\alpha \varphi (I)}{E}\\ &{}\le \displaystyle \frac{S'}{S}+\frac{E'}{E} - (d+\tau +\delta )\triangleq \tilde{m}_4(t). \end{array} \end{aligned}$$

  Thus, the matrix M(t) in Lemma 3.2 is governed by $M(t)=\text{ diag }\{\tilde{m}_1(t),\tilde{m}_2(t),\tilde{m}_3(t),\tilde{m}_4(t)\}$. It is straightforward to check that when $0<\alpha <1$,

  $$\begin{aligned} \begin{array}{lll} \displaystyle \lim _{t\rightarrow \infty }\frac{1}{t}\int ^t_0\tilde{c}_i(s)ds=\tilde{m}_i<0,\ \ i=1,2,3,4, \end{array} \end{aligned}$$

  where $\tilde{m}_1=-[(2-\alpha )d+\varepsilon +\tau +\eta +(1-p)A/S_0]$, $\tilde{m}_2=-(d+\delta +\eta \mu _0/V_0)$, $\tilde{m}_3=-(d+\delta +\tau \mu _0/V_0)$, $\tilde{m}_4=-(d+\tau +\delta )$. Accordingly, putting Cases I and II together and employing Lemma 3.2 can lead to the globally asymptotical stability of $Q_*$ in $\mathring{\widetilde{\Xi }}$ for any $\alpha >0$. $\square$

4 Optimal control problem

For the purpose of fighting against the epidemic of infectious diseases, it is necessary to adopt some control measures, including timely vaccination for newborns or susceptible population [26, 31,32,33,34,35], reduction in the disease transmission coefficient [21, 22, 26, 42] and treatment [20, 22, 26, 35]. By application of optimal control theory [29, 30], it is more practical to utilize the time-varying control intensities instead of constant intensity from the economical perspective, e.g., [20,21,22, 26, 31,32,33,34,35, 42]. Moreover, direct calculations reveal that the fraction of vaccinated newborns p, the treatment rate $\tau$ have negative impacts on the control reproduction number $\mathcal {R}_c$ and the disease transmission coefficient $\beta$ has positive impact on it. In what follows, we thus apply model (2.2) incorporating three time-dependent control measures to study effective strategies for diseases control: vaccination for newborns $u_1(t)$, awareness campaigns aiming at reducing the disease transmission coefficient $u_2(t)$ and antiviral treatment $u_3(t)$, such that $p\rightarrow p(1+u_1(t))$, $\beta \rightarrow \beta (1-u_2(t))$ and $\tau \rightarrow \tau (1+u_3(t))$, and the state equations of the state variables S, E, I and V with associated control variables $u_i(t)$ (denoted by $u_i$, $i=1,2,3$) are described by

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{lll} \displaystyle \frac{dS}{dt}=[1-p(1+u_1)]A-d S-\frac{\beta (1-u_2)IS}{1 + \sigma I^2}+\delta V:=\mathcal {G}_1,\\ \displaystyle \frac{dE}{dt}=\frac{\beta (1-u_2)IS}{1 + \sigma I^2}-(d+\varepsilon +\eta )E:=\mathcal {G}_2,\\ \displaystyle \frac{dI}{dt}=\varepsilon E-[d+\tau (1+u_3)]I:=\mathcal {G}_3,\\ \displaystyle \frac{dV}{dt}=p(1+u_1)A+\tau (1+u_3)I+\eta E-(d+\delta )V:=\mathcal {G}_4, \end{array}\right. \end{array} \end{aligned}$$

(4.1)

with non-negative initial conditions, where we choose $\rho =\alpha =1$ and $\kappa =2$ for simplification.

It is reasonable to assume that the control variable triple $u=(u_1, u_2, u_3)\!\in \mathcal {U}$ is bounded and measurable, namely, the control set $\mathcal {U}$ reads

$$\begin{aligned} \begin{array}{lll} \displaystyle \mathcal {U}&{}\!=\!\big \{(u_1, u_2, u_3)\mid u_i\ \text{ is } \text{ Lebsegue } \text{ measurable } \text{ on }\ [0,u_{i\max }],\ 0\!\le \!u_i\!\\ {} &{}\le u_{i\max }, t\!\in \![0, T], i\!=\!1,2,3\big \}, \end{array} \end{aligned}$$

where T is the terminal control time and $u_{i\max }\le 1$.

For the control system (4.1), the objective functional to minimize the numbers of exposed class E and infectious class I and the required control costs, is defined as

$$\begin{aligned} \begin{array}{lll} \displaystyle J(u(t))=\int ^T_0\Big [\Psi _1E+\Psi _2I+\frac{1}{2}\!\sum ^3_{i=1}\phi _iu^2_i\Big ]dt. \end{array} \end{aligned}$$

(4.2)

Here, $\Psi _1$, $\Psi _2$ and $\phi _i$ ($i=1,2,3$) are weighted constants for exposed and infectious individuals and the relative costs of these three interventions $u_1$, $u_2$ and $u_3$ over the interval [0, T], respectively. Hereinafter, we denote the integrand $\mathcal {J}:=\Psi _1E+\Psi _2I+\!\sum ^3_{i=1}\phi _iu^2_i/2$. Therefore, our optimal control problem can be formulated as

$$\begin{aligned} \begin{array}{lll} \displaystyle J(u^*)=\min J(u),\ \ s.t.\ \ u\in \mathcal {U},\\ \displaystyle E, I \ \text{ are } \text{ the } \text{ solution } \text{ of } \text{ system } \text{(4.1) } \text{ with } \text{ non-negative } \text{ initial } \text{ conditions }. \end{array} \end{aligned}$$

(4.3)

Now, it is imperative to demonstrate the existence of solution for system (4.1). To this end, system (4.1) is recast into

$$\begin{aligned} \xi _t=\left[ \begin{array}{cc} \dot{S}\\ \dot{E}\\ \dot{I}\\ \dot{V} \end{array} \right] =\mathcal {G}(t,\xi ,u)=\left[ \begin{array}{cc} [1-p(1+u_1)]A-d S-\frac{\beta (1-u_2)IS}{1 + \sigma I^2}+\delta V\\ \frac{\beta (1-u_2)IS}{1 + \sigma I^2}-(d+\varepsilon +\eta )E\\ \varepsilon E-[d+\tau (1+u_3)]I\\ p(1+u_1)A+\tau (1+u_3)I+\eta E-(d+\delta )V \end{array} \right] . \end{aligned}$$

(4.4)

Next, we shall show the existence of an optimal control to system (4.1).

Theorem 4.1

For the objective functional J(u) associated with system (4.1), there is an optimal control triple $u^*=(u^*_1, u^*_2, u^*_3)$ such that $J(u^*)=\min _{u\in \mathcal {U}} J(u)$.

Proof

According to Theorem 4.1 in Chapter III of [30], in order to examine the existence of the optimal control solution of system (4.1), it is sufficient to verify the following five assumptions:

• (A1) The state variables S, E, I and V and the control set $\mathcal {U}$ are non-empty;

• (A2) $\mathcal {U}$ is convex and closed;

• (A3) $\mathcal {G}_i$ ($i=1,2,3,4$) in system (4.1) are continuous, bounded above by a sum of the bounded control and the state, and can be expressed as a linear function on u with time-dependent and state-dependent coefficients;

• (A4) The integrand $\mathcal {J}$ is concave;

• (A5) There are constants $\kappa _1, \kappa _2>0$ and constant $\ell >1$, s.t., $\mathcal {J}(t,\xi ,u)\ge \kappa _1|u|^\ell -\kappa _2$.

From the definition of $\mathcal {U}$ and the boundary of u, it follows that $\mathbf{(A1)}$ and $\mathbf{(A2)}$ hold true. We proceed with checking $\mathbf{(A3)}$. It can be derived that

$$\begin{aligned}&\begin{aligned} \displaystyle |\mathcal {G}(\xi _1)-\mathcal {G}(\xi _2)| =&\displaystyle \left| \left[ \begin{array}{cccc} d(S_2-S_1)+\frac{\beta (1-u_2)I_2S_2}{1 + \sigma I_2^2}-\frac{\beta (1-u_2)I_1S_1}{1 + \sigma I_1^2}+\delta (V_1-V_2)\\ \frac{\beta (1-u_2)I_1S_1}{1 + \sigma I_1^2}-\frac{\beta (1-u_2)I_2S_2}{1 + \sigma I_2^2}+(d+\varepsilon +\eta )(E_2-E_1)\\ \varepsilon (E_1-E_2)+[d+\tau (1+u_3)](I_2-I_1)\\ \tau (1+u_3)](I_1-I_2)+\eta (E_1-E_2)+(d+\delta )(V_2-V_1) \end{array} \right] \right| \end{aligned} \\&\begin{aligned} \displaystyle \quad \quad \quad \quad \quad \quad \le&d|S_2-S_1|+2\beta (1-u_2)\left| \frac{I_2S_2}{1 + \sigma I_2^2}-\frac{I_1S_1}{1 + \sigma I_1^2}\right| +(d+2\delta )|V_2-V_1|\\&+(d+2\varepsilon +2\eta )|E_2-E_1|+[d+2\tau (1+u_3)]|I_2-I_1|. \end{aligned} \end{aligned}$$

Recalling that $0<S\le S_0$, $0<I\le A/d$ from Lemma 3.1, we can estimate that

$$\begin{aligned} \begin{aligned} \displaystyle \left| \frac{I_2S_2}{1 + \sigma I_2^2}-\frac{I_1S_1}{1 + \sigma I_1^2}\right|&=\left| \frac{I_2S_2}{1 + \sigma I_2^2}-\frac{I_2S_1}{1 + \sigma I_2^2}+\frac{I_2S_1}{1 + \sigma I_2^2}-\frac{I_1S_1}{1 + \sigma I_1^2}\right| \\&\le \frac{I_2}{1+\sigma I_2^2}|S_2-S_1|+\frac{(1+\sigma I_1I_2)S_1}{(1+\sigma I_2^2)(1+\sigma I_1^2)}|I_2-I_1|\\&\le \max \bigg \{\frac{1}{2\sqrt{\sigma }},\frac{A}{d}\bigg \}|S_2-S_1|+\max \bigg \{\frac{5}{4},1+\frac{\sigma A^2}{d^2}\bigg \}S_0|I_2-I_1|, \end{aligned} \end{aligned}$$

where we also make use of

$$\begin{aligned} \begin{aligned}&\displaystyle \frac{I_2}{1+\sigma I_2^2}\le \frac{1}{2\sqrt{\sigma }},\ \ \frac{1+\sigma I_1I_2}{(1+\sigma I_2^2)(1+\sigma I_1^2)}\le 1+\sigma \cdot \frac{1}{2\sqrt{\sigma }}\cdot \frac{1}{2\sqrt{\sigma }}=\frac{5}{4}, \ \ \\&\quad \text{ if }\ \ I\le \frac{1}{\sqrt{\sigma }}\le \frac{A}{d}. \end{aligned} \end{aligned}$$

Let us denote $\omega _1=d+2\beta (1-u_2)\max \{1/(2\sqrt{\sigma }),A/d\}$, $\omega _2=d+2\varepsilon +2\eta$, $\omega _3=d+2\tau (1+u_3)+2\beta (1-u_2)S_0\max \{5/4,1+\sigma A^2/d^2\}$, $\omega _4=d+2\delta$, and $\omega =\max (\omega _1, \omega _2, \omega _3, \omega _4)$. As a consequence,

$$\begin{aligned} \begin{aligned} \displaystyle |\mathcal {G}(\xi _1)-\mathcal {G}(\xi _2)|&\le \omega _1|S_2-S_1|+\omega _2|E_2-E_1| +\omega _3|I_2-I_1|+\omega _4|V_2-V_1|\\&\le \omega (|S_2-S_1|+|E_2-E_1|+|I_2-I_1|+|V_2-V_1|)=\omega |\xi _1-\xi _2|, \end{aligned} \end{aligned}$$

which suggests that (A3) is also true.

Let $l\in (0,1)$ and u, $v\in \mathcal {U}$, we have

$$\begin{aligned} \begin{aligned}&\displaystyle \mathcal {J}(t,\xi (t),(1-l)u+lv)-(1-l)\mathcal {J}(t,\xi (t),u)-l\mathcal {J}(t,\xi (t),v)\\&\quad =\frac{\phi _i}{2}[(1-l)^2u^2+l^2v^2+2l(1-l)uv]-\frac{\phi _i}{2}(1-l)u^2 -\frac{\phi _i}{2}lv^2\\&\quad =\frac{\phi _i}{2}\big (l^2-l)(u-v\big )^2<0, \end{aligned} \end{aligned}$$

so the integrand $\mathcal {J}$ is concave, further (A4) is satisfied.

Lastly, it is easy to check that (A5) is valid since

$$\begin{aligned} \displaystyle \xi (t)+\frac{\phi _i}{2}u^2(t)\ge \frac{\phi _i}{2}u^2(t)\ge \kappa _1|u|^\ell -\kappa _2,\ \ \text{ with }\ \ \kappa _1=\frac{\phi _i}{2}, \ \ \ell =2,\ \ \kappa _2>0. \end{aligned}$$

In conclusion, there exists an optimal control $u^*$ that can minimize J(u). $\square$

In what follows, we require the adjoint vector $\lambda :=(\lambda _1, \lambda _2, \lambda _3, \lambda _4)$, then the Hamiltonian function for the optimal control problem (4.1)–(4.3) reads

$$\begin{aligned} \begin{array}{lll} \mathcal {H}\!=\!\displaystyle \mathcal {H}(t,\xi ,\lambda ,u)\!=\!\displaystyle \Psi _1E+\Psi _2I+\frac{1}{2}\!\sum ^3_{i=1}\phi _iu^2_i + \sum ^4_{j=1}\lambda _j\mathcal {G}_j. \end{array} \end{aligned}$$

(4.5)

From Pontryagin’s Maximum Principle [29], suppose that $(\xi ^*,u^*)$ is an optimal solution for the control problem (4.1)–(4.3), then there exists a non-trivial vector function $\lambda$ such that

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{d\xi }{dt}=\frac{\partial \mathcal {H}(t,\xi ^*,\lambda ,u^*)}{\partial \lambda },\ \ 0=\displaystyle \frac{\partial \mathcal {H}(t,\xi ,\lambda ,u^*)}{\partial u},\ \ \displaystyle \frac{d\lambda }{dt}=-\frac{\partial \mathcal {H}(t,\xi ,\lambda ,u^*)}{\partial \xi }. \end{array} \end{aligned}$$

(4.6)

Applying the necessary conditions (4.6) to the Hamiltonian function $\mathcal {H}$ in (4.5), by similar arguments in [20,21,22, 31, 33, 34] we can come to the conclusion as follows.

Theorem 4.2

For optimal control problem (4.1)-(4.3), if $\xi ^*$ is the optimal control with associated optimal control variable $u^*$, then there exist adjoint variables $\lambda _i$, satisfying

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{lll} \displaystyle \frac{d\lambda _1}{dt}=\lambda _1\bigg (\!d+(1-u_2)\frac{\beta I}{1 + \sigma I^2}\!\bigg )-\lambda _2(1-u_2)\frac{\beta I}{1 + \sigma I^2},\\ \displaystyle \frac{d\lambda _2}{dt}=-\Psi _1+\lambda _2(d+\varepsilon +\eta )-\lambda _3\varepsilon -\lambda _4\eta ,\\ \displaystyle \frac{d\lambda _3}{dt}=-\Psi _2+(\lambda _1-\lambda _2)(1-u_2)\frac{\beta S(1-\sigma I^2)}{(1 + \sigma I^2)^2}+\lambda _3[d+\tau (1+u_3)]-\lambda _4\tau (1+u_3),\\ \displaystyle \frac{d\lambda _4}{dt}=-\lambda _1\delta +\lambda _4(d+\delta ), \end{array}\right. \end{array} \end{aligned}$$

(4.7)

with the transversality conditions $\lambda _i(T)=0$ ($i=1,2,3,4$). Meanwhile, the optimal control $u^*=(u^*_1,u^*_2,u^*_3)$ is governed by

$$\begin{aligned} \begin{array}{lll} \begin{array}{lll} \displaystyle u^*_1(t)=\max \bigg \{0,\min \bigg \{\frac{pA(\lambda _1-\lambda _4)}{\phi _1},u_{1\max }\bigg \}\bigg \},\\ \displaystyle u^*_2(t)=\max \bigg \{0,\min \bigg \{\frac{(\lambda _2-\lambda _1)}{\phi _2}\frac{\beta I^*S^*}{1 + \sigma (I^*)^2},u_{2\max }\bigg \}\bigg \},\\ \displaystyle u^*_3(t)=\max \bigg \{0,\min \bigg \{\frac{(\lambda _3-\lambda _4)\tau I^*}{\phi _3},u_{3\max }\bigg \}\bigg \}. \end{array} \end{array} \end{aligned}$$

(4.8)

5 Numerical simulations

This section is devoted to exploring the numerical solution of the control problem (4.1)–(4.3) by forward and backward iteration algorithm (e.g., [26, 42]). Since model (2.2) incorporates vaccination for newborns, latency and temporary immunity, it may be applicable to utilize the parameter values of (2.2) related to hepatitis B to explore the effective control strategies for the disease, as shown in Table 1.

Table 1 The parameter values in numerical simulation of the control problem (4.1)–(4.3)

To demonstrate the approach of numerical simulations, we fix the terminal time of the control as $T=40$ years and the initial condition $(S(0), E(0), I(0), V(0))=(290800,200,300,20)$, and take $\Psi _1=500$, $\Psi _2=1000$, $\phi _1=0.001$, $\tau _0=0.002$ and $\tau _3=10$ according to the actual situation, where the costs of vaccination $u_1$ and awareness campaigns by media alert and education $u_2$ are far below that of antiviral treatment $u_3$ for the chronic disease. In addition, currently it is difficult to vaccinate all newborns, reduce the transmission rate among population to zero, or significantly improve the cure rate for hepatitis B, so these three control measures are considered to possess the limited intensities $u_{1\max }=0.1$, $u_{2\max }=0.3$, $u_{3\max }=0.4$. It should be mentioned that the maximal intensity $u_{1\max }=0.1$ of vaccination for newborns is utilized in light of $1-p(1+u_1)>0$.

The following four different control strategies are proposed to compare the effects of the three measures $u_1$, $u_2$, $u_3$ on the control of hepatitis B (seeing Figs. 1 and 2 for details):

• Strategy I$u_1\ne 0, u_2\ne 0, u_3\ne 0$. The control intensities of $u_1$, $u_2$, $u_3$ are kept non-zero until the terminal time T, please see Fig. 2(a) and the red dashed lines in Fig. 1;

• Strategy II$u_1=0, u_2\ne 0, u_3\ne 0$. The measure $u_1$ is not implemented, and the control intensities of $u_2$, $u_3$ remain non-zero during the control period T, see Fig. 2(b) and the blue lines in Fig. 1;

• Strategy III$u_2=0, u_1\ne 0, u_3\ne 0$. The control $u_2$ is set to zero, and the control intensities of $u_1$, $u_3$ remain non-zero until the time T, seeing Fig. 2(c) and the red solid lines in Fig. 1;

• Strategy IV$u_3=0, u_1\ne 0, u_2\ne 0$. The control $u_3$ is not conducted, and the control intensities of $u_1$, $u_2$ are kept non-zero during the period T, see Fig. 2(d) and the blacked dashed lines in Fig. 1.

Fig. 1

The numbers of S, E, I and V with optimal controls and no controls

At the same time, the simulation results of the case where none of the measures $u_1$, $u_2$, $u_3$ is implemented (i.e., $u_1=u_2=u_3=0$) are also presented in Fig. 1 (seeing green solid lines). It can be seen from Fig. 1(a)–(d) that the epidemic will outbreak in this case. What’s more, Strategy I minimizes the numbers of both exposed and infectious individuals in the shortest time among all the four strategies. It follows from Fig. 2(a) that the measures $u_1$, $u_2$ are carried out at maximal intensities for much longer time than the measure $u_3$, which may be attributed to the highest costs of the latter, and then they are gradually relaxed owing to the application of the optimal control.

Fig. 2

The control intensities of $u_1$, $u_2$, $u_3$ in Strategies I–IV

On the other hand, it can be observed from Fig. 1(a)–(d) that there is a small difference in the effects on the numbers of the individuals in S, E, I and V classes between Strategies III and IV, which reveals the core role in mitigating the hepatitis B transmission since the vaccination is carried out almost over the whole control process for the both strategies (as shown in Fig. 2(c) and (d)).

Finally, compared Strategy I with Strategy II, corresponding to red dashed lines and blue lines in Fig. 1, we find that the vaccination $u_1$ brings out fewer susceptible individuals and more individuals with immunity than $u_2$ and $u_3$. Meanwhile, it follows from Fig. 1(b)–(c) that Strategies I and II achieve almost the same levels of exposed and infectious individuals under nearly identical intensities of $u_2$ and $u_3$ during the control period, seeing Fig. 2(a) and (b). However, if awareness campaigns $u_2$ are not carried out, antiviral treatment $u_3$ will persist for the longer time by comparing Strategy II with Strategy III in Fig. 2(b) and (c), which would incur greater costs of treatment. It should be noticed that none of the control intensities for $u_1$ and $u_2$ can not be relaxed until the terminal time if $u_3$ is not implemented by comparing Strategy I with Strategy IV, such that the optimal control strategy fails.

To sum up, it is of great necessity and importance to adopt these three measures at the same time to curb the hepatitis B epidemic. In details, vaccination for newborns $u_1$ can maintain high level of population immunity, awareness campaigns by media alert and education $u_2$ can sharply reduce the control costs, and antiviral treatment $u_3$ is a requisite for the optimal control of hepatitis B transmission.

6 Concluding remarks

In this work, we proposed a novel nonlinear SEIVS epidemic model with latency, temporary immunity. By application of the new geometric criterion in [14], the model still maintains its global threshold dynamics characterized by the control reproduction number $\mathcal {R}_c$ in spite of the introduction of vaccine-induced, disease-acquired and natural immunities and general incidence rate $\beta I^\rho S^\alpha /(1+\sigma I^\kappa )$, $0<\rho \le 1$, $0\le \kappa \le 2$.

It should be emphasized that the property $I|\varphi '(I)|\le \varphi (I)$ in (2.4) of the infectious force function plays an indispensable role in achieving the global threshold dynamics of model (2.2), seeing the proof of Theorems 3.2-3.4 and 3.6. In model (2.1) of Cai and Li, the incidence rate $\beta IS/h(I)$ (where h satisfies $h(0)=1$, $h'(I)\ge 0$) was utilized to generalize the incidence rate $\beta I^\rho S/(1+\sigma I^\kappa )$ [3]. However, global stability of the endemic equilibrium for model (2.1) is still an open question. In fact, let us assign $\varphi (I)=\beta I/h(I)$. Making use of (2.4), we can derive that

$$\begin{aligned} \begin{array}{lll} \displaystyle h(I)\ge \frac{Ih'(I)}{2}\ge 0. \end{array} \end{aligned}$$

(6.1)

Particularly, when $\beta I/h(I)=\beta I^\rho /(1+\sigma I^\kappa )$, together with (6.1), the following condition ensuring the global threshold dynamics is obtained

$$\begin{aligned} \begin{array}{lll} \left\{ \begin{array}{lll} \displaystyle \sigma I^\kappa (\rho -\kappa -1)\le 1-\rho , \\ \displaystyle \sigma I^\kappa (\rho -\kappa +1)\ge -1-\rho . \end{array}\right. \end{array} \end{aligned}$$

(6.2)

Obviously, when $0<\rho \le 1$, it can be found that $0<\kappa \le 2$ can guarantee (6.1), corresponding to the infectious force function (2.3) considered in this work, so our study may effectively solve global stability of model (2.1). More particularly, suppose that $\rho =\alpha =1$ and $\eta =0$, model (2.2) reduces to model (2.1) with $h(I)=1+\sigma I^\kappa$. From Theorem 3.6, an immediate consequence of global threshold stability of $Q_*$ follows only if $0<\kappa \le 2$. So we improve Theorem 2.1 and give a complete affirmative answer to the question in Section 2 ($\kappa =1$), what’s more, our global-stability results can be extended to model (2.1) with nonmonotone incidence rate measuring psychological effects (i.e., $1<\kappa \le 2$).

Additionally, it may be an alternative adopting a constant vaccination rate $\upsilon$ in model (2.2) instead of vaccination for newborns pA for many vaccine-preventable infectious diseases, as pointed by Sahu and Dhar in [4]. With the classical geometric approach, [4] also concluded that the endemic equilibrium for an SVEIS model with partial temporary immunity and saturation incidence rate is global stable if the control reproduction number is greater than unit and two conditions are attached. Based on our analysis process in this work, the global threshold dynamics for model (2.2) with constant vaccination rate and the model in [4] can also be established via the new geometric criterion of [14].

Retrospectively, one of innovations in this contribution is to successfully resolve global-stability issues of the novel SEIVS epidemic model proposed and completely remove the unnecessary condition in Theorem 2.1 for global stability of the endemic equilibrium for model (2.1) with saturated incidence rate. We also obtained the sufficient conditions of the endemic equilibrium for the model with general nonlinear incidence rate $\beta I/h(I)$. Another innovation lies in exploring the corresponding optimal control system with vaccination, awareness campaigns and antiviral treatment, four different control strategies were numerically simulated and compared. It was concluded that joint implementation of these three measures, minimizing the numbers of both exposed and infectious individuals in the shortest time, is the most cost-effective in mitigating the hepatitis B epidemic, and vaccination for newborns plays the core role and maintains the high level of population immunity. Moreover, awareness campaigns sharply reduce the control costs and antiviral treatment is a requisite for optimal control of hepatitis B transmission.

There are still several limitations in our study. First of all, owing to the complexity the nonlinear incidence rate $\beta I^\rho S^\alpha /(1+\sigma I^\kappa )$, this work only established global dynamics of model (2.2) when $0<\rho \le 1$, $0\le \kappa \le 2$. In case of $\rho >1$ and $\kappa =0$, according to [47], we can guess that our SEIVS model with the incidence $\beta I^\rho S$ admits two, one or no endemic equilibria, so the model may exhibit backward bifurcation and Hopf bifurcation, however, more advanced research methods and more careful analysis are needed. For the more general case where $\rho >1$ and $\kappa \ge 0$, the SEIVS model may present more complex dynamics. Another limitation of this work is that we only formulated the SEIVS model of ordinary differential equations (ODEs). However, in order to capture the memory effects of immunity, learning mechanism of awareness campaigns, heredity of life process, etc., some recent works have already developed the epidemic models governed by fractional order differential equations (FODEs), which can be modelled by the classical Caputo’s fractional derivative [19] and the modified Riemann-Liouville derivative [48,49,50]. We will construct the fractional order epidemic model with temporary immunity and nonlinear incidence rate and investigate its numerical solution by application of some efficient algorithms, such as the fractional homotopy perturbation method [48, 50,51,52,53,54,55], the fractional variational iteration method [49] and Auxiliary Laplace Parameter Method [56]. These are interesting and valuable study topics in our future efforts.