The influence of vaccination on the control of JE with a standard incidence rate of mosquitoes, pigs and humans

Abstract

In this article, a nonlinear mathematical model used for the impact of vaccination on the control of infectious disease, Japanese encephalitis with a standard incidence rate of mosquitoes, pigs and humans has been planned and analyzed. During the modeling process, it is expected that the disease spreads only due to get in touch with the susceptible and infected class only. It is also assumed that due to the effect of vaccination, the total human population forms a separate class and avoids contact with the infection. The dynamical behaviors of the system have been explored by using the stability theory of differential equations and numerical simulations. The local and global stability of the system for both equilibrium states under certain conditions has been studied. We have set up a threshold condition in the language of the vaccine-induced reproduction number $R(\alpha _{1})$, which is fewer than unity, the disease dies in the absence of the infected population, otherwise, the infection remains in the population. Furthermore, it is found that vaccine coverage has a substantial effect on the basic reproduction number. Also, by continuous efforts and effectiveness of vaccine coverage, the disease can be eradicated. It is also found a more sensitive parameter for the transmission of Japanese encephalitis virus by using sensitivity analysis. In addition, numerical results are used to investigate the effect of some parameters happening the control of JE infection, for justification of analytical results.

1 Introduction

Japanese encephalitis (JE) is an illness of the brain caused through the Japanese encephalitis virus (JEV) and is transmitted from the pig population to the human population through bloodsucking insects Culex mosquitoes, Centers for Disease Control, (CDC). The JEV is maintained in a natural enzootic cycle between reservoir population (especially pigs), mosquitoes and humans. The transmission of JEV, for the most part, happens in the country in horticultural zones, where floodwater system and rice development are related [1,2,3,4]. In the areas where JEV is endemic the annual incident range from 1 to 10 cases per 10,000 person per year affected children are under 16 years of age [5]. The time duration of infection to illness in infected humans is about 5–15 days and initial symptoms are fever, headache and vomiting [3, 6,7,8]. Most humans who are infected with only a few symptoms or have no symptoms and JE can be more deadly in advanced stages, National Vector Borne Disease Control Program, (NVBDCP).

The first human case of JEV was registered in Japan in 1935 and in India in 1955 [3, 9]. Unfortunately, there is no specific treatment available that can cure Japanese encephalitis, including the management of some basic supportive medical care and complications in medicine. Those who experience a more severe form of the disease will have to undergo treatment at the hospital. The finding of JE disease ought to be performed by utilizing a JEV-explicit immunoglobulin M (IgM) counteracting agent catch ELISA for serum and cerebrospinal liquid (CSF). JEV-explicit IgM can be estimated in the CSF of most patients by four days after the commencement of side effects and in serum by seven days after inception. The prevention of JE is mainly based on the control of mosquitoes and the vaccination of the human population. To control the mosquito population, some methods like using insecticides, reducing the number of breeding sites on your property, by killing the mosquito larvae where the insect’s breed and bed nets are used in endemic regions. Mathematical modeling of infectious disease has a long history for understanding the effects of vaccination. Through the speedy rate of vaccine development, medical science has saved millions of lives. Smallpox, influenza, polio and lots of supplementary diseases are conquering examples in this regard [10]. In the present life, it is bizarre and uncommon for a youngster not to get an antibody. An individual can get accessible immunizations for a malady common in his general vicinity. Some sickness immunizations are as of now created and anybody can take the antibody if the specific malady is in danger for it. Currently, several groups of vaccines available in the world like inactivated Vero cell culture-derived JE vaccine, SA 14-14-2 live attenuated JE vaccine, Ixiaro JE vaccine, etc. But Ixiaro is the only licensed JE vaccine available in the United States [11]. It was avowed in march 2009 for the use of the human population aged more than 17 years. Later on, May 2013, avowed for the use of children whose aged lies between 2 months to 16 years [1, 6, 12]. The essential inoculation plans for Ixiaro is two portions intramuscularly administrated on 0–28 days. For youngsters from 2 months to 2 years, each dose is 0.25 ml, for grownups and kids for more than 3 years, each dose is 0.5 ml. Prior, In India, the mouse brain-derived JE antibody was utilized, yet the productivity was insufficient to meet the national prerequisite [13, 14]. The SA 14-14-2 live attenuated JE vaccine has been utilized in China for over 20 years with an effectiveness of 80% for single-dose and 97.5% for a two-doses routine with 1 year interim among youngsters under 15 years old [11, 14]. Thus, the effectiveness of the JE vaccine is more than 90%, but the time duration of protection with the JE vaccine is not clear, but its effectiveness appears to decrease over time [1, 6].

Japanese encephalitis spreading fast in all states of India except Meghalaya, Himachal Pradesh, Jammu and Kashmir, Dadra, Daman, Punjab, Diu, Nagar Haveli, Gujarat, Lakshadweep and Sikkim [1]. This disease is seasonal, most human cases reported in north India in May–October. The highest rate of this disease reported from the states of Uttar Pradesh, Bihar, Andhra Pradesh, Assam, Kerala, Goa, Haryana, Karnataka, Tamil Nadu and West Bengal [5, 9]. In modeling of such infectious disease, many authors have already worked on epidemic models to minimize the infection of JE and maximize the rate of recovered population [15]. In recent years, mathematical models have been used to understand the interplay between various traditional measures such as the mobility of epidemic outbreaks [16, 17] and vaccination [5, 18,19,20] quarantine, behavior change [21].

When the immunization is accessible, a general inquiry emerges; How to allocate and implement this immunization. Unquestionably, we can’t inoculate all people to control the sickness from the human population on account of social and moral issues, significant expenses, and so forth. In this manner, the legitimate conveyance and usage systems are critical to controlling JEV using vaccines. The adequacy of such a vaccination assignment procedure can be resolved through the investigation of a mathematical model. Right now, we need to illuminate this significant issue and would like to give a valuable rule to the arrangement producer.

To appropriately actualize vaccination battles in the human population, the recognized and insightful idea may be to inoculate individuals having a spot with explicit social affairs or territories vulnerable to contamination. On account of mosquito dependent infectious diseases, the vaccination can be an important tool to help control the spread of infection in such infectious disease and encephalitis is one of them. It is pointed out that in the above model, vaccination has been studied without considering the effective role of the mosquito population which depends on the human population-related factor. In this work, we construct and analyze a modified mathematical model of De et al. [9], by incorporating the effect of vaccination on the spread of JE, which is the most effective control strategy against JE. In addition, we use a realistic standard incidence rate for direct contact between susceptible and infectious. We might want to express that we don’t consider any structure in the model analyzed down right now, these references can be utilized to improve the present work.

Kar et al. [19] have been studied the SIR epidemic mathematical model to minimize the infection rate and to maximize the recovered rate of the human population by using vaccination program and optimal control strategy to SIR model. Singh et al. [22] have found that the development rate of the mosquito population relies upon the increasing density of ecological discharge by the human population. Also, the growth rate of the mosquito populations can be controlled by controlling the increasing density of ecological discharge. Iannelli et al. [23] build an SIS mathematical model to contemplate the effect of inoculation by expecting the immunization age, super-infection, immaculate immunization and furthermore talked about the asymptotic behavior of the equilibriums state. Raul Prealta et al. [24], developed an SVIR mathematical model to study the effect of the vaccine by considering the immune loss rate, which depends on the vaccine-age under the condition that during vaccination individuals have the same immunity.

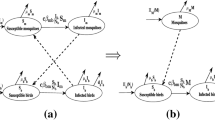
In the present investigation, modifications to the SVIR model for JEV-affected humans and SI model for JEV-affected pigs [9] are considered by reducing the vaccinated compartment of a pig. The main objective is to analyze the effect of vaccination on the human population for the prevention of Japanese encephalitis with a standard incidence rate of mosquitoes and pigs. In the case of mosquitoes there is nothing to explain because it is obvious that vaccination, medicine is not possible for that compartment. Hence we consider susceptible, vaccinated, infected and recovered (SVIR) compartment for humans and susceptible, infected (SI) compartment of mosquitoes and pigs (cf. the Fig. 1). Disease transmission of the susceptible human population depends on the standard incidence rate of infected mosquitoes. Similarly, JEV spreads among the susceptible mosquito population when it comes in contact with infected human and pig populations. In this way, JE transmission for the susceptible mosquito population should be dependent on the rate of standard incidence on infected pig and human populations.

The organization of the manuscript is as follows: In the next Sect. 2, notations and assumptions along with full explanation are provided. In Sect. 3, the mathematical formulation of the JE endemic model with a schematic diagram of the transmission of JEV puts in place and derive the model equations. We provide the region of biologically feasible solutions in Sect. 4, together with their positivity and boundedness. Dynamical behavior (existence of equilibrium states, basic reproduction number and stability) of the framework has been discussed in Sect. 5. In Sect. 6, vaccine-induced reproduction number and model parameters sensitivity investigation has been discussed to study the effects of controllable parameters of the JE model on the basic reproduction number and infected human population in Sect. 7 while the simulations and discussions are presented in Sect. 8 and conclusions in Sect. 9.

2 Notations and assumptions

In our proposed model, it is assumed that the JEV starts its life cycle from the pig population and then spreads into the human population through Culex mosquitoes. It is also assumed that all the newborn’s pigs and mosquitoes are susceptible, but newborn humans are not susceptible. In addition, JEV transmitted only in susceptible individuals. Many variables and constants(parameters) symbols have utilized in our proposed mathematical epidemiological model, including four compartments for humans, two compartments for pigs and mosquitoes, which are given in Tables 1 and 2.

Table 1 Model variables and their descriptions

Table 2 Model parameters, its description and their values used for numerical calculation

3 Model formulation

In our present investigation, we consider susceptible, vaccinated, infected and recovered (SVIR) model for human population, susceptible, infected (SI) models for mosquito and pig population. The model sub-divides the total human population $N_{h}$ into sub-population of susceptible humans $(S_{h}(t))$, vaccinated humans $(V_{h}(t))$, infected humans $(I_{h}(t))$ and recovered humans $(R_{h}(t))$, so that $N_{h} = S_{h}(t)+V_{h}(t)+I_{h}(t)+R_{h}(t)$. The total mosquito population $N_{m}$ is divided into sub-population of susceptible mosquitoes $(S_{m}(t))$ and infected mosquitoes $(I_{m}(t))$, so that $N_{m}= S_{m}(t)+I_{m}(t)$. Also, the total pig population $N_{p}$ is sub-divided into susceptible pigs $S_{p}(t)$ and infected pigs $(I_{p}(t))$ such that $N_{p}= S_{p}(t)+I_{p}(t)$. In SVIR model, humans are recruited at vaccinated birth rate $\alpha _{1}\lambda _{h}$ and unvaccinated birth rate $(1-\alpha _{1})\lambda _{h}$. It is assumed that the JE spreads among the $S_{h}(t)$ due to contribution of the $I_{m}(t)$ [5]. Hence, the transmission of JE disease to susceptible humans should be a standard incidence rate of an infected mosquito population and it is in the form of $B\beta _{mh}\frac{I_{m}}{N_{h}}S_{h}$. Similarly, the JE transmitted among susceptible mosquitoes ($S_{m}(t)$) due to contact with infected pigs and human populations. Hence, the transmission of JE disease to susceptible mosquitoes should be standardized incidence rate of infected pig and human population and it is in the form of $\left( C\beta _{pm}\frac{I_{p}}{N_{p}}+B\beta _{hm}\frac{I_{h}}{N_{p}}\right) S_{m}$. The interaction between $I_{m}(t)$ and $S_{h}(t)$, $I_{p}(t)$ and $S_{m}(t)$ are assumed to be rated B, C respectively. Ultimately, the JE spreads among $S_{p}(t)$ due to contact with $I_{m}(t)$. Hence, the JE transmission to susceptible pigs should be a standard incidence rate of infected mosquitoes and it is in the form of $C\beta _{mp}\frac{I_{m}}{N_{p}}S_{p}$. Also, we consider the proportion of the infected human population become recovered naturally and with medicine control at a rate of $\tau _{1}$ and $\tau _{2}$ respectively. After that, some of the recovered individuals go to susceptible class at rate $f_{1}$. Humans in each compartment are assumed to die with a natural mortality $\mu _{h}$ and die with the disease at a rate of $\lambda$. In the SI model, the recruitment rate of mosquitoes and pigs is $\lambda _{m}$ and $\lambda _{p}$ respectively. The natural mortality of the mosquito population in each compartment is $\mu _{m}$. Also, the pig populations in each compartment are assumed to die with natural mortality of $\mu _{p}$. Further, we consider that in the whole modeling process the disease transmission is possible only in susceptible individual class, for other classes JE spreads among them after they become susceptible class only. So, we do not consider direct JE transmission from vaccinated humans class to infected human class. The schematic diagram for the dynamics of transmission of JE has appeared in Fig. 1.

Fig. 1

Schematic diagram representing dynamics for the transmission of JE disease in humans, pigs and mosquitoes

The mathematical model is described by following system of ODEs:

$$\begin{aligned} \frac{dS_{h}}{dt}= & {} (1-\alpha _{1})\lambda _{h}+f_{1}R_{h}+ \beta _{1}V_{h}-\left( B\beta _{mh}\frac{I_{m}}{N_{h}}+\mu _{h}\right) S_{h} \end{aligned}$$

(1)

$$\begin{aligned} \frac{dV_{h}}{dt}= & {} \alpha _{1}\lambda _{h}-(\beta _{1}+\mu _{h})V_{h} \end{aligned}$$

(2)

$$\begin{aligned} \frac{dI_{h}}{dt}= & {} B\beta _{mh}\frac{I_{m}}{N_{h}}S_{h}-(\tau _{1}\eta _{h}+\tau _{2}\delta +\mu _{h}+\lambda )I_{h} \end{aligned}$$

(3)

$$\begin{aligned} \frac{dR_{h}}{dt}= & {} (\tau _{1}\eta _{h}+\tau _{2}\delta )I_{h}-(f_{1}+\mu _{h})R_{h} \end{aligned}$$

(4)

$$\begin{aligned} \frac{dS_{m}}{dt}= & {} \lambda _{m}-\left( C\beta _{pm}\frac{I_{p}}{N_{p}} +B\beta _{hm}\frac{I_{h}}{N_{h}}+\mu _{m}\right) S_{m} \end{aligned}$$

(5)

$$\begin{aligned} \frac{dI_{m}}{dt}= & {} \left( C\beta _{pm}\frac{I_{p}}{N_{p}}+B\beta _{hm} \frac{I_{h}}{N_{h}}\right) S_{m}-\mu _{m}I_{m} \end{aligned}$$

(6)

$$\begin{aligned} \frac{dS_{p}}{dt}= & {} \lambda _{p}+\alpha _{2}u_{1}I_{p}-C\beta _{mp} \frac{I_{m}}{N_{p}}S_{p}-\mu _{p}S_{p} \end{aligned}$$

(7)

$$\begin{aligned} \frac{dI_{p}}{dt}= & {} C\beta _{mp}\frac{I_{m}}{N_{p}}S_{p}-\alpha _{2}u_{1} I_{p}-\mu _{p}I_{p} \end{aligned}$$

(8)

For our simplicity we can re-write Eqs. (1)–(8) in notations form as-

$$\begin{aligned} \frac{dS_{h}}{dt}= & {} a_{11}+f_{1}R_{h}+\beta _{1} V_{h}-(a_{13}I_{m}+\mu _{h})S_{h} \end{aligned}$$

(9)

$$\begin{aligned} \frac{dV_{h}}{dt}= & {} a_{21}-a_{22}V_{h} \end{aligned}$$

(10)

$$\begin{aligned} \frac{dI_{h}}{dt}= & {} a_{13}I_{m}S_{h}-AI_{h} \end{aligned}$$

(11)

$$\begin{aligned} \frac{dR_{h}}{dt}= & {} a_{12}I_{h}-(f_{1}+\mu _{h})R_{h} \end{aligned}$$

(12)

$$\begin{aligned} \frac{dS_{m}}{dt}= & {} \lambda _{m}-(a_{31}I_{p}+a_{32}I_{h} +\mu _{m})S_{m} \end{aligned}$$

(13)

$$\begin{aligned} \frac{dI_{m}}{dt}= & {} (a_{31}I_{p}+a_{32}I_{h})S_{m} -\mu _{m}I_{m} \end{aligned}$$

(14)

$$\begin{aligned} \frac{dS_{p}}{dt}= & {} \lambda _{p}+a_{41}I_{p}-a_{42}I_{m}S_{p}-\mu _{p}S_{p} \end{aligned}$$

(15)

$$\begin{aligned} \frac{dI_{p}}{dt}= & {} a_{42}I_{m}S_{p}-dI_{p} \end{aligned}$$

(16)

with initial conditions  $S_{h}(0)=S_{h0}> 0,~ V_{h}(0)=V_{h0} \ge 0, ~I_{h}(0)=I_{h0}\ge 0, R_{h}(0)=R_{h0}> 0, S_{m}(0)=S_{m0}>0, I_{m}(0)=I_{m0}\ge 0, S_{p}(0)=S_{p0}>0, I_{p}(0)=I_{p0}\ge 0$.

where,

$$\begin{aligned} a_{11}= & {} (1-\alpha _{1})\lambda _{h},~~a_{12}=\tau _{1} \eta _{h}+\tau _{2}\delta ,~~a_{13}=\frac{B\beta _{mh}}{N_{h}},~~a_{22} =\beta _{1}+\mu _{h},~~ a_{31}=\frac{C\beta _{pm}}{N_{p}}\\ a_{21}= & {} \alpha _{1}\lambda _{h}, ~~a_{32}=\frac{B\beta _{hm}}{N_{h}}, ~~a_{41}=\alpha _{2}u_{1}, ~~a_{42}=\frac{C\beta _{mp}}{N_{p}}, ~~d=a_{41}+\mu _{p},\\ A= & {} a_{12}+\mu _{h}+\lambda . \end{aligned}$$

4 Positivity and boundedness of solutions

Now, we present the positivity and boundedness of solutions of the system of Eqs. (1)–(8). For the system of Eqs. (1)–(8) to be biologically significant and well-proposed, essentially we have to show that all the solutions with non-negative initial conditions will remain positive for all time $\mathrm{t}>0$. In the theoretical study of disease transmission, the boundedness of the system measures that the system is biologically legitimate and well-behaved [16]. Biologically, validation of the model will be appeared by the accompanying theorem.

Theorem 4.1

If $S_{h}(0),~ V_{h}(0),~ I_{h}(0),~R_{h}(0),~ S_{m}(0),~ I_{m}(0), ~ S_{p}(0) ~\text{ and }~ I_{p}(0)$ are non negative, then $S_{h}(t),~ V_{h}(t),~ I_{h}(t), ~R_{h}(t),~ S_{m}(t),~ I_{m}(t), ~ S_{p}(t) ~\text{ and }~ I_{p}(t)$ are also non-negative for all time $\mathrm{t}>0$. Moreover

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } \sup N_{h}(t)\le \frac{\lambda _{h}}{\mu _{c}},~\lim \limits _{t\rightarrow \infty } \sup N_{m}(t)\le \frac{\lambda _{m}}{\mu _{m}}~\text{ and }~\lim \limits _{t\rightarrow \infty } \sup N_{p}(t)\le \frac{\lambda _{p}}{\mu _{p}} \end{aligned}$$

where $\mu _{c}=\min \{\mu _{h},\lambda \}$,  $N_{h}(t) = S_{h}(t)+V_{h}(t)+I_{h}(t)+R_{h}(t)$,  $N_{m}(t) = S_{m}(t)+I_{m}(t)$,  $N_{p}(t) = S_{p}(t)+I_{p}(t)$

Furthermore,

$$\begin{aligned} \text{ If }~ N_{h}(0)\le \frac{\lambda _{h}}{\mu _{c}}~\text{ then }~N_{h}(t)\le \frac{\lambda _{h}}{\mu _{c}}.~\text{ Similarly }~ N_{m}(0)\le \frac{\lambda _{m}}{\mu _{m}}~\text{ then }~N_{m}(t)\le \frac{\lambda _{m}}{\mu _{m}} \end{aligned}$$

and $N_{p}(0)\le \frac{\lambda _{p}}{\mu _{p}}~\text{ then }~N_{p}(t)\le \frac{\lambda _{p}}{\mu _{p}}.$

The proof is excluded. The feasible region for the system of Eqs. (1)–(8) is given by

$$\begin{aligned} D = D_{h} \times D_{m}\times D_{p}\subset \mathrm IR_{+}^4\times \mathrm IR_{+}^2\times \mathrm{IR}_{+}^2 \end{aligned}$$

where,

$$\begin{aligned} D_{h}= & {} \left\{ (S_{h}, V_{h}, I_{h}, R_{h})\in \mathrm{IR}_{+}^4: S_{h}+V_{h}+I_{h}+R_{h}\le \frac{\lambda _{h}}{\mu _{c}}\right\} \\ D_{m}= & {} \left\{ (S_{m}, I_{m})\in \mathrm{IR}_{+}^2: S_{m}+I_{m}\le \frac{\lambda _{m}}{\mu _{m}}\right\} \end{aligned}$$

and

$$\begin{aligned} D_{p}=\left\{ (S_{p}, I_{p})\in \mathrm{IR}_{+}^2: S_{p} + I_{p}\le \frac{\lambda _{p}}{\mu _{p}}\right\} \end{aligned}$$

is positive invariant.

5 Dynamical behavior of the system

5.1 Equilibrium states and basic reproductive number

Clearly, the system (9)–(16) has following two equilibrium states, namely

(1) Disease or infection-free steady state $E_{0} = (\bar{S_{h}}, \bar{V_{h}}, \bar{I_{h}}, \bar{R_{h}}, \bar{S_{m}},\bar{I_{m}}, \bar{S_{p}}, \bar{I_{p}})$.

where,

$$\begin{aligned} \bar{S_{h}}= & {} \frac{a_{11}a_{22}+a_{21}\beta _{1}}{a_{22}\mu _{h}}, \bar{V_{h}}=\frac{a_{21}}{a_{22}}, \bar{I_{h}}=0, \bar{R_{h}}=0, \bar{S_{m}}=\frac{\lambda _{m}}{\mu _{m}}, \bar{I_{m}}=0,\\ \bar{S_{p}}= & {} \frac{\lambda _{p}}{\mu _{p}}, \bar{I_{p}}=0. \end{aligned}$$

The existence of equilibrium $E_{0}$ is obvious. It demonstrates that if the model has an infected population, then the equilibrium magnitude of susceptible human, mosquito and pig population will reach the value  $\bar{S_{h}}=\frac{a_{11}a_{22}+a_{21}\beta _{1}}{a_{22}\mu _{h}},~~\bar{S_{m}} =\frac{\lambda _{m}}{\mu _{m}},~~\bar{S_{p}}=\frac{\lambda _{p}}{\mu _{p}}$  respectively and vaccinated human population will remain at its equilibrium $\bar{V_{h}}=\frac{a_{21}}{a_{22}}$.

Let us define threshold parameter $R_{01}$, as

$$\begin{aligned} R_{01} =\frac{C^2\beta _{pm}\beta _{mp}\lambda _{m}\lambda _{p}}{N_{p}^2\mu _{m}^2\mu _{p} (\alpha _{2}u_{1}+\mu _{p})} \end{aligned}$$

Biologically, $R_{01}$ is the average number of secondary Culex mosquitoes produced by single Culex mosquitoes [25]. To maintain the Culex mosquitoes in the environment, $R_{01}$ must be greater than one. To measure the disease transmission potential in such a population, the basic reproduction number $R_{0}$ can be established by using the concept of the next-generation matrix approach method. Since the system of Eqs. (9)–(16) are consistent, therefore the conditions for new infection and transition terms are given by the matrices

$$\begin{aligned} F= & {} \left( \begin{array}{ccc} \frac{\partial F_{1}}{\partial I_{h}}&{}\frac{\partial F_{1}}{\partial I_{m}}&{}\frac{\partial F_{1}}{\partial I_{p}}\\ \frac{\partial F_{2}}{\partial I_{h}}&{}\frac{\partial F_{2}}{\partial I_{m}}&{}\frac{\partial F_{2}}{\partial I_{p}}\\ \frac{\partial F_{3}}{\partial I_{h}}&{}\frac{\partial F_{3}}{\partial I_{m}}&{}\frac{\partial F_{3}}{\partial I_{p}}\\ \end{array} \right) ;~~~~ V = \left( \begin{array}{ccc} \frac{\partial V_{1}}{\partial I_{h}}&{}\frac{\partial V_{1}}{\partial I_{m}}&{} \frac{\partial V_{1}}{\partial I_{p}}\\ \frac{\partial V_{2}}{\partial I_{h}}&{} \frac{\partial V_{2}}{\partial I_{m}}&{}\frac{\partial F_{2}}{\partial I_{p}}\\ \frac{\partial V_{3}}{\partial I_{h}}&{}\frac{\partial V_{3}}{\partial I_{m}}&{} \frac{\partial V_{3}}{\partial I_{p}}\\ \end{array} \right) \end{aligned}$$

where,

$$\begin{aligned} F_{1}= & {} a_{13}I_{m}S_{h},~~F_{2}=(a_{31}I_{p}+a_{32} I_{h})S_{m},~~F_{3}=a_{42}I_{m}S_{p},~~V_{1}=AI_{h},~~ V_{2}=\mu _{m}I_{m}\\ V_{3}= & {} dI_{p} \end{aligned}$$

then,

$$\begin{aligned} F = \left( \begin{array}{ccc} 0&{}a_{13}\bar{S_{h}}&{}0\\ a_{32}\bar{S_{m}}&{}0&{}a_{31}\bar{S_{m}}\\ 0&{}a_{42}\bar{S_{p}}&{}0\\ \end{array} \right) ;~~~~ V = \left( \begin{array}{ccc} A&{}0&{}0\\ 0&{}\mu _{m}&{}0\\ 0&{}0&{}d\\ \end{array} \right) \end{aligned}$$

For infection-free equilibrium state, the next generation matrix ($FV^{-1}$) is calculated as:

$$\begin{aligned} FV^{-1} = \left( \begin{array}{ccc} 0&{}\frac{a_{13}\bar{S_{h}}}{\mu _{m}}&{}0\\ \frac{a_{32}\bar{S_{m}}}{A}&{}0&{}\frac{a_{31}\bar{S_{m}}}{d}\\ 0&{}\frac{a_{42}\bar{S_{p}}}{\mu _{m}}&{}0\\ \end{array} \right) \end{aligned}$$

The potent characteristic root of matrix $FV^{-1}$ is the basic reproduction number $R_{0}$ [26]. It is calculated as

$$\begin{aligned} R_{0}^{2}= & {} \frac{a_{31}a_{42}\bar{S_{p}}\bar{S_{m}}}{\mu _{m}d} +\frac{a_{13}a_{32}\bar{S_{h}}\bar{S_{m}}}{\mu _{m}A} \nonumber \\= & {} \frac{B^2\beta _{mh}\beta _{hm}\lambda _{m}\lambda _{h}}{N_{p}N_{h}\mu _{m}^2 A\mu _{h}}\left[ 1-\frac{\alpha _{1}\mu _{h}}{\lambda _{h}(\beta _{1}+\mu _{h})}\right] +\frac{C^2\beta _{pm}\beta _{mp}\lambda _{m}\lambda _{p}}{N_{p}^2\mu _{m}^2\mu _{p} (\alpha _{2}u_{1}+\mu _{p})} \end{aligned}$$

(17)

Biologically, $R_{0}$ is the average number of secondary cases generated by one primary JEV infected person, which has been introduced in the susceptible population, in which some individuals have been vaccinated. From Eq. (17), it is found that as the increase with the parameters $\beta _{1}, \mu _{h}, \mu _{m}, \mu _{p}$  and $\alpha _{2}$, the value of $R_{0}$ decreases. Also the parameters B, C, $\beta _{mh}~ \text{ and }~ \beta _{pm}$ affects the value of $R_{0}$ significantly. From the expression of $R_{0}$, it is also found that vaccination rate $\alpha _{1}$ affects the value of $R_{0}$. It is imperative to take note that, the above parameters assume a significant job in the investigation of global threshold dynamics with regards to $R_{0}$. Pronouncedly, if $R_{0} <1$, the disease will stop after some time and $R_{0} >1$ disease will stay endemic and irresistible population will arrive at positive continued levels [2, 4, 27, 28]. Clearly, from the perspective of controlling the JE infection, one would normally need to decrease the $R_{0}$. In this way, it is advantageous to research how we can successfully diminish $R_{0}$ by sensible usage of vaccines and different parameters. The variation of $R_{0}$ w.r.t. some $\mu _{m}, B, \mu _{h}, \mu _{p}$ are shown in the Figs. 2, 3, 4 and 5 (Table 3).

Fig. 2

This figure shows the variation of $R_{0}$ with respect to $\mu _{m}$

Fig. 3

The figure shows the changes in $R_{0}$ with respect to B

Fig. 4

This figure shows the variation in $R_{0}$ with respect to $\mu _{h}$

Fig. 5

This figure shows the variation in $R_{0}$ with respect to $\mu _{p}$

Table 3 The impact of the basic reproduction number ($R_{0}$) as for parameters $\mu _{m}, B, \mu _{h}$ and $\mu _{p}$ where all the parameter esteem continue as before as in Table 2

5.2 Local stability around $E_{0}$

The local stability of infection-free equilibrium state ($E_{0}$) is determined after the characteristic roots of the Jacobian matrix $J(E_{0})$ of system (9)–(16) by following theorem:

Theorem 5.1

The infection-free equilibrium state ($E_{0}$) is locally asymptotically stable (LAS) if $R_{0}< R_{01}<1$ and unstable if  $R> R_{01}>1$.

See “Appendix A” for proof of this theorem.

Remark 5.1

The local stability of $E_{0}$ will depend as the sign of $\phi _{6}(=-\mu _{m}(1-R_{01}))$ and $\phi _{8}\left( =\frac{-d(1-R_{0}^2)}{1-R_{01}}\right)$. The infection-free equilibrium is locally asymptotically stable if $R_{0}<1$ and $R_{01}<1$. Biologically, $R_{01}<1$ implies the absence of Culex mosquito population. In this manner, the infection-free equilibrium must be steady without the Culex mosquito population, in any case, disease despite everything perseveres, regardless of whether the susceptible have no immediate contact with the infected population.

5.3 Global stability around $E_{0}$

In this section, we have studied the global behavior of infection-free equilibrium point for the system of Eqs. (9)–(16).

Theorem 5.2

Assumed that

$$\begin{aligned} \mu _{p} = a_{31}\bar{S_{m}} \end{aligned}$$

(18)

If $R_{0}\le 1,$ the the infection-free equilibrium state $E_{0}$ is globally asymptotically stable (GAS) on D.

See “Appendix B” for proof of this theorem.

(2) Endemic or positive equilibrium $E_{1}=( S_{h}^*, V_{h}^*, I_{h}^*, R_{h}^*, S_{m}^*, I_{m}^*, S_{p}^*, I_{p}^*)$.

where,

$$\begin{aligned} S_{h}^*= & {} \frac{a_{11}+f_{1}R_{h}^{*}+\beta _{1}V_{h}^{*}}{a_{13} I_{m}^{*}+\mu _{h}},~V_{h}^*=\bar{V_{h}},~I_{h}^*=\frac{a_{13}I_{m}^*S_{h}^*}{A},~ R_{h}^*=\frac{a_{12}I_{h}^{*}}{f_{1}+\mu _{h}} \end{aligned}$$

(19)

$$\begin{aligned} S_{m}^*= & {} \frac{\lambda _{m}}{a_{31}I_{p}^*+a_{32}I_{h}^*+\mu _{m}},~~ I_{m}^*=\frac{(a_{31}I_{p}^*+a_{32}I_{h}^*)S_{m}}{\mu _{m}} \end{aligned}$$

(20)

$$\begin{aligned} S_{p}^*= & {} \frac{\lambda _{p}+a_{41}I_{p}^*}{a_{42}I_{m}^*+\mu _{p}},~~ I_{p}^*=\frac{a_{42}I_{m}^*S_{p}^*}{d} \end{aligned}$$

(21)

Using the value of Eqs. (19) and (21) in the expression for $I_{m}^*$ in the Eq. (20). This shows that the endemic equilibrium of this model satisfy the Eq.

$$\begin{aligned} I_{m}^*(K_{1}I_{m}^{*2}+K_{2}I_{m}^{*}+K_{3})=0 \end{aligned}$$

(22)

where,

$$\begin{aligned} K_{1}= & {} a_{13}a_{42}[a_{31}\lambda _{m}\lambda _{p}\{f_{1}(\lambda +\mu _{h}) +\mu _{h}A\}+\mu _{m}\mu _{p}\{a_{11}a_{32}(f_{1}+\mu _{h})+f_{1}(\lambda \mu _{m}\\&+\, \mu _{h}\mu _{m}+a_{32}\beta _{1}V_{h}^*)+\mu _{h}(A\mu _{m}+a_{32}\beta _{1}V_{h}^*)\}]\\ K_{2}= & {} A\mu _{h}(f_{1}+\mu _{h})(T_{0}d+a_{42})\mu _{m}^2\mu _{p} +a_{13}[\mu _{m}\mu _{p}d\{(f_{1}+\mu _{h})(a_{11}a_{13}+a_{32}\beta _{1}V_{h}^*)\\&+\,f_{1}\mu _{m}(\lambda +\mu _{h})+A\mu _{m}\mu _{h}\}-a_{31}a_{42} \lambda _{m}\{(a_{11}\mu _{p}+\beta _{1}\mu _{p}V_{h}^*)(1+f_{1}) +\lambda _{p}(A\mu _{h}\\&+\, f_{1}(\lambda +\mu _{h}))\}]\\ K_{3}= & {} -(f_{1}+\mu _{h})\mu _{m}\mu _{h}d[A\mu _{h}\mu _{m}\mu _{p}(R_{01}-1) +a_{22}a_{31}\lambda _{p}(R_{0}^2-R_{01})] \end{aligned}$$

The root $I_{m}^*=0$ of Eq. (22) correspond to the infection-free equilibrium $(E_{0})$ and the positive roots of the equation

$$\begin{aligned} K_{1}I_{m}^{*2}+K_{2}I_{m}^{*}+K_{3} = 0 \end{aligned}$$

(23)

correspond to endemic equilibria point. From Eq. (23) we have

$$\begin{aligned} I_{m}^* = \frac{-K_{2}\pm \sqrt{K_{2}^2-4K_{1}K_{3}}}{2K_{1}} \end{aligned}$$

If $R_{0}> R_{01}>1$,  $K_{3}<0$ and hence $(K_{2}^2-4K_{1}K_{3})>0$. Thus, the positive equilibrium point is as

$$\begin{aligned} I_{m}^* = \frac{-K_{2}+\sqrt{K_{2}^2-4K_{1}K_{3}}}{2K_{1}} \end{aligned}$$

(24)

But if $R_{0}< R_{01}<1$,  $K_{3}>0$ and hence $(K_{2}^2-4K_{1}K_{3})<0$, this gives imaginary value of $I_{m}^*$. To verify above numerically, we use the set of parametric values from Table 2. Thus, the components of the endemic equilibrium point ($E_{1}$) are found as

$$\begin{aligned} S_{h}^*= & {} 300.251,~~ V_{h}^* = 206.667,~~ I_{h}^* = 0.329196,~~ R_{h}^* = 2.5561,~~ S_{m}^* = 40.9769\\ I_{m}^*= & {} 3.9106, ~~S_{p}^* = 16.3444, I_{p}^* = 1.2642 \end{aligned}$$

5.4 Local stability around $E_{1}$

Theorem 5.3

The endemic equilibrium state ($E_{1}$) is LAS if and only if $b_{1}>0,$  $b_{3}>0,$  $b_{4}>0$  and   $b_{1}b_{2}b_{3}> b_{3}^2+b_{1}^2b_{4}$ where,

$$\begin{aligned} b_{1}= & {} A+f_{1}+a_{13}I_{m}^*+a_{22}+\mu _{h}+\mu _{m}\\ b_{2}= & {} \frac{1}{a_{13}I_{m}^*+\mu _{m}}[-a_{12}a_{13}f_{1}I_{m}^*+A(a_{13} I_{m}^*+\mu _{m})(f_{1}+a_{22}+a_{13}I_{m}^*+\mu _{h}+\mu _{m})\\&+\, (a_{13}I_{m}^*+\mu _{m})\{(f_{1}+\mu _{h})(a_{13}I_{m}^*+\mu _{m}) +a_{22}(f_{1}+a_{13}I_{m}^*+\mu _{h}+\mu _{m})\}]\\ b_{3}= & {} \frac{1}{a_{13}I_{m}^*+\mu _{m}}[\{a_{22}(f_{1}+\mu _{h})(a_{13} I_{m}^*+\mu _{m})+b_{4}+a_{22}\}(a_{13}I_{m}^*+\mu _{m})+a_{22}(f_{1}\\&+\, \mu _{h}-a_{12}a_{22}a_{13}f_{1}I_{m}^*)]\\ b_{4}= & {} a_{22}\{A(f_{1}+\mu _{h})(a_{13}I_{m}^*+\mu _{m})-2a_{12}a_{13}f_{1}I_{m}^*\} \end{aligned}$$

See “Appendix C” for proof of this theorem.

Remark 5.2

To verify Theorem 5.3 numerically, we use the set of parametric values from Table 2. Thus, the conditions are as

$$\begin{aligned} b_{1}= & {} 0.285495,~ b_{2}= 1.87217 \times 10^{-2},~b_{3} = 3.23177\times 10^{-4},~\\ b_{4}= & {} 8.08664\times 10^{-7} ~\text{ and }~\\ b_{1}b_{2}b_{3}= & {} 1.7273\times 10^{-6},~b_{3}^2+b_{1}^2b_{4} = 1.70355\times 10^{-7}. \end{aligned}$$

5.5 Global stability around $E_{1}$

Theorem 5.4

The endemic steady state ($E_{1}$) is GAS in the region D, if the following inequalities are satisfied:

$$\begin{aligned} \text{ max }\left\{ \frac{2f_{1}^2}{f_{1}+\mu _{h}}, \frac{\beta _{1}^2}{a_{22}}, \frac{5a_{13}^2I_{m}^{*2}}{A}\right\}< & {} (\mu _{h}+a_{13}I_{m}^*)\\ a_{13}^2S_{h}^{*2}< & {} \min \left\{ \frac{\mu _{m}(a_{13}I_{m}^*+\mu _{h})}{6}, \frac{2\mu _{m}A}{15}\right\} \\a_{12}^2< & {} \frac{2A(f_{1}+\mu _{h})}{5}\\ \frac{1}{2}\text{ max }\left\{ \frac{9a_{31}^2S_{m}^{*2}}{d},~ \frac{9(a_{31}^2I_{p}^{*2}+a_{32}I_{h}^*)^2}{\mu _{m}+a_{31}I_{p}^*+a_{32}I_{h}^*},~ \frac{15a_{32}^2S_{m}^{*2}}{2A}\right\}< & {} \mu _{m}\\ 3 \text{ max }\left\{ \frac{a_{41}^2}{2d}, \frac{a_{42}^2S_{p}^{*2}}{\mu _{m}}\right\}< & {} (\mu _{p}+a_{42}I_{m}^*) \end{aligned}$$

See “Appendix D” for proof of this theorem.

Remark 5.3

To verify Theorem 5.4 numerically, we use the set of parametric values from Table 2. The simulations are done in the following seven cases for different initial starts and graphically displayed in Figs. 6 and 7. In this figure, the variation of susceptible humans with susceptible mosquitoes and vaccinated humans with infected humans have been shown respectively. The trajectories start with different initial points reach at the equilibrium point ($S_{h}^*, S_{m}^*$) and ($V_{h}^*, I_{h}^*$). Therefore, we infer that the system of Eqs. (1)–(8) may be non-linear global asymptotically stable about equilibrium points ($S_{h}^*, S_{m}^*$) and ($V_{h}^*, I_{h}^*$) for the following set of parameters (Table 4).

Table 4 The components of endemic equilibrium points for non-linear global asymptotically stable

Also for following set of parameter values, the conditions for the global asymptotical stability of the endemic equilibrium $E_{1}$ are satisfied.

Fig. 6

The plot represents the non-linear stability of ($S_{h}^*, S_{m}^*$)

Fig. 7

The plot represents the non-linear stability of ($V_{h}^*, I_{h}^*$)

6 Vaccine-induced reproduction number

From Eq. (17), we define the vaccine-induced reproduction number ($R(\alpha _{1})$) as

$$\begin{aligned} R(\alpha _{1})= & {} \sqrt{R_{01}+\frac{B^2\beta _{mh}\beta _{hm}\lambda _{m}\lambda _{h}}{A\mu _{m}^2 N_{h}\mu _{h}N_{p}}\left[ 1-\frac{\alpha _{1}\mu _{h}}{\lambda _{h}(\beta _{1}+\mu _{h})}\right] } \end{aligned}$$

(25)

Now,

$$\begin{aligned} R^{'}(\alpha _{1})= -\frac{B^2\beta _{mh}\beta _{hm}\lambda _{m}}{ 2R(\alpha _{1})AN_{p}N_{h}\mu _{m}^2(\beta _{1}+\mu _{h})}<0 \end{aligned}$$

From above it is clear that $R(\alpha _{1})$ is a decreasing function of $\alpha _{1}$ if $\alpha _{1}\ge 0$. This signalize that the effect of vaccination in reducing vaccine-induced reproduction number. Also, when vaccination is zero i.e. $(\alpha _{1}=0)$ then Eq. (25) can be written as

$$\begin{aligned} \sqrt{R_{01}+\frac{B^2\beta _{mh}\beta _{hm}\lambda _{m}\lambda _{h}}{A\mu _{m}^2N_{h} \mu _{h}N_{p}}} = R^*_{c} \end{aligned}$$

(26)

From Eqs. (25) and (26), we can write the vaccination as

$$\begin{aligned} R(\alpha _{1})\le R^*_{c} ~~\text{ for }~~ 0\le \alpha _{1} \le 1 \end{aligned}$$

If $R^*_{c}<1$ then $R(\alpha _{1})<1$, therefore $E_{0}$ is locally asymptotically stable. Also if $R^*_{c}=1$, then $R(\alpha _{1})\le 1$ this is also the case in which $E_{0}$ locally asymptotically stable. From Eqs. (25) and (26) we can write,

$$\begin{aligned} \sigma R^*_{c} \le R(\alpha _{1}) \le R^*_{c} ~~\text{ where }~~ \sigma = 1-\frac{\alpha _{1}\mu _{h}}{\lambda _{h}(\beta _{1}+\mu _{h})}~~\text{ and }~~0\le \sigma \le 1 \end{aligned}$$

If $\sigma R^*_{c}>1$ then $\sigma > \sigma _{c} = \frac{1}{R^*_{c}}$. From this we find $R(\alpha _{1})>1$, therefore no amount of vaccination can bring $R(\alpha _{1})$ less then one.

Hence, $\sigma _{c}$ defines the stationary values for the vaccine related reduction rate of infection. Therefore, if the vaccination level $\alpha _{1}> \sigma _{c}$, then possibility of disease eradication from population can be maximized (Fig. 8).

Solving Eq. (17) for $\alpha _{1}$, we get a critical vaccination level $\alpha _{1c_{1}}$, is given by

$$\begin{aligned} \alpha _{1c_{1}} = \frac{(R^{*2}_{c}-R^2_{0})N_{p}A\lambda _{h}\mu _{m}^2}{a_{13}a_{32}V_{h}^*} \end{aligned}$$

Fig. 8

The graph represents the variation of vaccine-induced reproduction number $R(\alpha _{1})$ with vaccination rate $\alpha _{1}$

Here, $\alpha _{1c_{1}}$ is always positive, since $R^{*2}_{c}> R^2_{0}$. If $\alpha _{1}> \alpha _{1c_{1}}$, $R(\alpha _{1})< 1$ as $R(\alpha _{1})$ is a decreasing function for $\alpha _{1}\ge 0$. In this manner, in the event that the vaccination coverage $\alpha _{1}$ surpasses the condition $\alpha _{1c_{2}}$, at that point disease can be eradicated.

From Eq. (19), we also find that

$$\begin{aligned} \alpha _{1c_{2}} = \frac{V_{h}^*(\beta _{1}+\mu _{h})}{\lambda _{h}} \end{aligned}$$

This critical vaccination level $\alpha _{1c_{2}}$ guarantees that the disease annihilation when inoculated people stay at its harmony. Along these lines, if the vaccination rate $\alpha _{1}$ is with the end goal that $\alpha _{1}>\max \{\alpha _{1c_{1}}, \alpha _{1c_{2}}\}$, at that point disease annihilation is conceivable in the human population.

7 Model parameters sensitivity investigation

In this section, we want to examine the relationship between input parameters and the results of the proposed model using the reproduction number $R_{0}$. To assist us with discovering the parameters that highly affect $R_{0}$, we dissected the $R_{0}$ to decide if immunization, treatment of infectives and mortality of mosquitoes can prompt the successful disposal or control of the JE in the population. The parameters chosen to perform the sensitivity analysis were B, $\mu _{m}, \delta$ and  $\alpha _{1}$. We evaluate the sensitivity indices for  $B = 0.7,~ \mu _{m} = 0.06, \delta = 0.1, ~\alpha _{1} = 0.5$  and all other parameters are same as in Table 2. For sensitivity analysis of the model, we define

$$\begin{aligned} Z^{s}_{x} = \frac{\partial x}{\partial s}.\frac{s}{x} \end{aligned}$$

called normalized forward sensitivity index for a variable x and it depends on a parameter s [29]. The sensitivity indices of  $R_{0}$ w. r. t. the parameters B,  $\mu _{m},~ \delta$  and $\alpha _{1}$ are calculated as

$$\begin{aligned} Z^{B}_{R_{0}} = 0.01743,~~ Z^{\mu _{m}}_{R_{0}} =-0.01587 , ~~Z^{\delta }_{R_{0}} =-0.001987,~~Z^{\alpha _{1}}_{R_{0}} =-0.00495 \end{aligned}$$

The fact is that $Z^{B}_{R_{0}} = 0.01743$ signify that 1% increase in B, will produce 0.01743% increase in $R_{0}$, keeping all other parameters fixed. When the parameters $\mu _{m},~\delta$  and $\alpha _{1}$ increase by 1%, while keeping all others fixed then the values of $R_{0}$ decrease by 0.01587%, 0.001987% and 0.00495% respectively. Overall a lower value of $R_{0}$ is better because it increases the chance of disease eradication in the areas. Therefore, all the above prevention practices should be considered to reduce the parameter B, while increases the parameters $\mu _{m},~ u_{1}$  and $\alpha _{1}$, instead it should be favored. It is seen that the impact of vaccination on people assumes an overwhelming job in the control of the disease. On the off chance that the contact rate (B) between susceptible people and infected mosquitoes can be managed then Japanese encephalitis can be killed totally from the population. It is additionally seen that the infected human population consistently expanding as for B and it is progressively delicate for the spread of JE disease, (cf. Figs. 9, 10). That’s why we have chosen the parameter B only for the model sensitivity investigation.

Fig. 9

The surface plot shows the variation of $R_{0}$ with respect to $\beta _{1}$ and $\alpha _{1}$

Fig. 10

The surface plot shows the variation of $R_{0}$ with respect to B and $\alpha _{1}$

Figure 9 shows the sensitivity plot of the basic reproduction number $R_{0}$ for $\alpha _{1}$ and $\beta _{1}$. From this, we found that a higher vaccination rate $\alpha _{1}$ and a low contact rate $\beta _{1}$ will keep $R_{0}< 1$. Also, in Fig. 10, the sensitivity plot of the $R_{0}$ regarding B and $\alpha _{1}$ has appeared. This implies a higher estimation of $\alpha _{1}$ and a low contact pace of B will keep $R_{0} < 1$.

Fig. 11

The graph shows the variation of human population with vaccination at endemic equilibrium

Fig. 12

The graph shows the variation of human population without vaccination at endemic equilibrium

Fig. 13

The figure shows the variation of mosquito population at endemic equilibrium

Fig. 14

The figure shows the variation of pig population at endemic equilibrium

Fig. 15

The figure shows the effect of susceptible human with no control, all control, vaccine control and medicine control

Fig. 16

The figure shows the effect of vaccinated human with no control, all control, vaccine control and medicine control

Fig. 17

The plot shows the effect of infected  human  with  no control, all control, vaccine control and medicine control

Fig. 18

The plot shows the effect of recovered human with no control, all control, vaccine control and medicine control

8 Simulations and discussions

In this paragraph, we provide some simulations on the dynamics of the system (1)–(8). Moreover, to check how the human, mosquito and pig populations are affected by various parameters, we perform simulations by using the parameter values as shown in Table 2, and numerical results are manifested graphically in Figs. 11, 12, 13, 14, 15, 16, 17 and 18 by using MATLAB(R2014a) software. In Fig. 11, the variation of the human population with vaccination is shown and in Fig. 12, the variation of the human population without vaccination is shown. From these two figures, we can study the effect of vaccination on the human population. In the case of vaccination, the susceptible population is below 50 and the vaccinated population is above 50, whereas in case of without vaccination, the vaccinated level goes to zero and susceptible level increases. We also see that vaccination does not affect the infected and recovered human population. This signifies that vaccination only affects susceptible individuals if individuals infected, vaccination does not affect the infected population. Figures 13 and 14, show the variation of mosquito and pig population at an endemic equilibrium point. These two figures (Figs. 13, 14) show the stability of the endemic equilibrium when $R_{0}$ is larger than one and the threshold condition $T_{0}$ of the JE virus larger than one. This reflects that the virus can be dominant when the $T_{0}$ and $R_{0}$ are larger than one. We observed in Fig. 15, that due to the control strategy, the number of susceptible human decreases in society. This signifies that the spread of JE infection in society can also be controlled through the proper implementation of vaccines, medicine and some effective prevention. This strategy also shows that the effect of vaccine and medicine control on susceptible humans is almost the same. This reflects that some effective medical treatment and medicine can also control the spread of JE infection. Whereas in Fig. 16, the number of vaccinated human increases in the community. This shows that the community can make infection-free through the effective treatment and vaccination control of a human. From Fig. 17, we observed that due to the control strategy, initially decreases the infected human but after some time it stabilized. This shows that the vaccination strategy has no significant impact on the infected human. Finally, in Fig. 18 we observed that due to controlled strategy, the number of recovered human increases in the community but after some time it stabilized. This shows that infected humans can be immune (but not completely) through some basic supportive medical care and treatment.

9 Conclusions

In this article, perspective on human, mosquito and pig population, a nonlinear scientific model for JEV has been proposed and examined to contemplate the impact of vaccination on control of infectious disease, Japanese encephalitis. The model displays two equilibria, to be a specific disease-free and endemic equilibrium. The first equilibrium exists without any conditions but the second equilibrium exists if the threshold parameter $R_{01}>1$. We have discovered another threshold parameter in terms of vaccine, vaccine-induced reproduction number $R(\alpha _{1})$ which is, if not as much as unity, the disease ceases to exist, without infected population otherwise the infection is kept up in the population and disease turns out to be progressively endemic. The system of the differential equations has a unique infection-free steady state which is locally asymptotically stable if $R_{01}< 1$ and unstable if $R_{01}>1$. Furthermore if $R_{01}$ approaches to 1, $E_{0}$ becomes unstable but $E_{1}$ exist. If $R_{01}> 1$ then $E_{1}$ exists and it is locally asymptotically stable under certain condition. Also for both the equilibrium point global stability have to show by using Liapunov’s function in the region of attraction $\Omega$ under certain conditions. Model analysis shows, if the vaccination program has adequate capacity to mobilize a high degree of population, there is an abundance of mosquitoes in the environment, then the disease can be controlled. Moreover, it is found that vaccine coverage has a substantial effect on the basic reproduction number, $R_{0}$. Also, by continuous efforts and effectiveness of vaccine coverage, the disease can be eradicated. Also, found by sensitivity investigation, if 1% increase in the parameters $\mu _{m}, \delta ~\text{ and }~\alpha _{1}$ keeping all others parameters fixed, then the value of $R_{0}$ decreases by 0.01587%, 0.001987% and 0.00495% respectively. Also, if we increase 1% in B then $R_{0}$ increases by 0.01743%. This signifies that the parameter B is more sensitive to the transmission of JEV. Then again, in the event that the vaccination rate is over a critical level $\alpha _{1c_{1}}$, at that point the JE doesn’t take a type of pestilence gave the density of mosquito population stays at its equilibrium level. During the entire investigation of the JEV model, it is discovered that vaccination is the main long haul control measure against JE in the population. The mosquitoes reduction strategies may incorporate the end of mosquito breeding sites, keeping environmental factors perfect and clean. On the other hand, vaccinating the susceptible individuals in the human population with the end goal that vaccination level is kept up over the critical vaccination level $\alpha _{1c_{2}}$ and the vaccine efficacy is sufficiently high so that vaccinated individuals are not infected by infected mosquitoes. Along these lines, our present paper has been investigated various sorts of control procedures and their adequacy in controlling the JE disease by utilizing the steadiness hypothesis of differential conditions and the basic reproduction number. From the clinical perspective, we accept that our model examination is gainful for persons and control of the JE disease.

Appendices

Appendix A. Proof of Theorem. 5.1

Proof

The Jacobian matrix ($J(E_{0})$) of the system (9)–(16) corresponding to equilibrium state $E_{0}$ is given by

$$\begin{aligned} J(E_{0}) = \left( \begin{array}{cccccccc} -\mu _{h}&{}\beta _{1}&{}0&{}f_{1}&{}0&{}-a_{13}\bar{S_{h}}&{}0&{}0 \\ 0&{}-a_{22}&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}-A&{}0&{}a_{13}\bar{S_{h}}&{}0&{}0 \\ 0&{}0&{}0&{}-(f_{1}+\mu _{h})&{}0&{}0&{}0&{}0\\ 0&{}0&{}-a_{32}\bar{S_{m}}&{}0&{}-\mu _{m}&{}0&{}0&{}-a_{31}\bar{S_{m}}\\ 0&{}0&{}a_{32}\bar{S_{m}}&{}0&{}0&{}-\mu _{m}&{}0&{}a_{31}\bar{S_{m}}\\ 0&{}0&{}0&{}0&{}0&{}-a_{42}\bar{S_{p}}&{}-\mu _{p}&{}a_{42}\\ 0&{}0&{}0&{}0&{}0&{}a_{42}\bar{S_{p}}&{}0&{}-d\\ \end{array} \right) \end{aligned}$$

The characteristic roots of Jacobian matrix  ($J(E_{0})$) are

$$\begin{aligned} \phi _{1}= & {} -\mu _{h}, ~\phi _{2} = -a_{22},~\phi _{3} = -A,~\phi _{4} = -(f_{1}+\mu _{h}),~\phi _{5} = -\mu _{m},\\ \phi _{6}= & {} -\mu _{m}(1-R_{01})\\ \phi _{7}= & {} -\mu _{p},~\phi _{8} = \frac{-d(1-R_{0}^2)}{1-R_{01}} \end{aligned}$$

In this article, all parameters are considered positive, therefore all  $\phi _{i}(i=1,2,3,4,5,6,7)<0$. Then, Routh–Hurwitz criterion all the characteristic roots of Jacobian matrix ($J(E_{0})$) have negative real part if $\phi _{8}<0$ [27, 30]. Thus, the infection-free steady state ($E_{0}$) is LAS if $R_{0}< R_{01}< 1$, and unstable if $R_{0}> R_{01}> 1$. $\square$

Appendix B. Proof of Theorem 5.2

Proof

To establish the global stability of the infection-free steady state ($E_{0})$, consider the following Lyapunov function,

$$\begin{aligned} V(t)= & {} (S_{h}-\bar{S_{h}}ln S_{h})+V_{h}+I_{h}+R_{h}+(S_{m}-\bar{S_{m}}ln S_{m})+I_{m}\\&+(S_{p}-\bar{S_{p}}ln S_{p})+I_{p} \end{aligned}$$

Differentiating V(t) w.r.t. ‘t’ along the solutions of Eqs. (9)–(16), we get

$$\begin{aligned} \dot{V(t)}= & {} \dot{S_{h}}\left( 1-\frac{\bar{S_{h}}}{S_{h}}\right) +\dot{V_{h}} +\dot{I_{h}}+\dot{R_{h}}+\dot{S_{m}}\left( 1-\frac{\bar{S_{m}}}{S_{m}}\right) +\dot{I_{m}}+\dot{S_{p}}\left( 1-\frac{\bar{S_{p}}}{S_{p}}\right) +\dot{I_{p}} \nonumber \\= & {} (a_{11}+f_{1}R_{h}+\beta _{1}V_{h}-(a_{13}I_{m}+\mu _{h})S_{h}) \left( 1-\frac{\bar{S_{h}}}{S_{h}}\right) \nonumber \\&+\,a_{21}-a_{22}V_{h} +a_{13}I_{m}S_{h}-AI_{h}\nonumber \\&+\, a_{12}I_{h}-(f_{1}+\mu _{h})R_{h}+(\lambda _{m}-(a_{31}I_{p}+a_{32}I_{h} +\mu _{m})S_{m})\left( 1-\frac{\bar{S_{m}}}{S_{m}}\right) \nonumber \\&+\,(a_{31}I_{p}+a_{32}I_{h})S_{m}\nonumber \\&-\,\mu _{m}I_{m}+(\lambda _{p}+a_{41}I_{p}-a_{42}I_{m}S_{p}-\mu _{p} S_{p})\left( 1-\frac{\bar{S_{p}}}{S_{p}}\right) +a_{42}I_{m}S_{p}-dI_{p} \nonumber \\= & {} -V_{h}\left( \mu _{h}+\beta _{1}\frac{\bar{S_{h}}}{S_{h}}\right) -R_{h} \left( \mu _{h}+f_{1}\frac{\bar{S_{h}}}{S_{h}}\right) \nonumber \\&-\,I_{h} \left( \lambda +\mu _{h}+a_{32}\bar{S_{m}}+a_{12}\frac{\bar{S_{h}}}{S_{h}}\right) -a_{41}I_{p}\frac{\bar{S_{p}}}{S_{p}}\nonumber \\&+\, I_{m}(a_{13}\bar{S_{h}}+a_{42}\bar{S_{p}}-\mu _{m})+I_{p}(a_{31}\bar{S_{m}}-\mu _{p})\nonumber \\&+\,a_{11}\left( 1-\frac{\bar{S_{h}}}{S_{h}}\right) -\mu _{h}S_{h} \left( 1-\frac{\bar{S_{h}}}{S_{h}}\right) \nonumber \\&+\, \lambda _{m}\left( 1-\frac{\bar{S_{m}}}{S_{m}}\right) -\mu _{m}S_{m} \left( 1-\frac{\bar{S_{m}}}{S_{m}}\right) +\lambda _{p} \left( 1-\frac{\bar{S_{p}}}{S_{p}}\right) -\mu _{p}S_{p} \left( 1-\frac{\bar{S_{p}}}{S_{p}}\right) \nonumber \\ \end{aligned}$$

(27)

Using the condition (18) and feasible region D (as explain in Sect. 4), Eq. (27) can be rewritten as

$$\begin{aligned}\le & {} -V_{h}\left( \mu _{h}+\beta _{1}\frac{\bar{S_{h}}}{S_{h}}\right) -R_{h} \left( \mu _{h}+f_{1}\frac{\bar{S_{h}}}{S_{h}}\right) \\&-\,I_{h} \left( \lambda +\mu _{h}+a_{32}\bar{S_{m}}+a_{12}\frac{\bar{S_{h}}}{S_{h}}\right) -a_{41}I_{p}\frac{\bar{S_{p}}}{S_{p}}\\&+\, I_{m}\mu _{m}\left( \frac{a_{13} \bar{S_{h}}+a_{42}\bar{S_{p}}}{\mu _{m}}-1\right) +a_{11}\left( 2-\frac{\bar{S_{h}}}{S_{h}}-\frac{S_{h}}{\bar{S_{h}}}\right) +\lambda _{m}\left( 2-\frac{\bar{S_{m}}}{S_{m}}-\frac{S_{m}}{\bar{S_{m}}}\right) \\&+\,\lambda _{p}\left( 2-\frac{\bar{S_{p}}}{S_{p}}-\frac{S_{p}}{\bar{S_{p}}}\right) \\= & {} -\,V_{h}\left( \mu _{h}+\beta _{1}\frac{\bar{S_{h}}}{S_{h}}\right) -I_{h} \left( \lambda +\mu _{h}+a_{12}\frac{\bar{S_{h}}}{S_{h}}\right) \\&-\,a_{41}I_{p} \frac{\bar{S_{p}}}{S_{p}}+I_{m}\mu _{m}\left( \frac{a_{13}\bar{S_{h}} +a_{42}\bar{S_{p}}}{\mu _{m}}-1\right) \\&-\, \frac{a_{11}(S_{h}-\bar{S_{h}})^2}{S_{h}\bar{S_{h}}} -\frac{\lambda _{m}(S_{m}-\bar{S_{m}})^2}{S_{m}\bar{S_{m}}} -\frac{\lambda _{p}(S_{p}-\bar{S_{p}})^2}{S_{p}\bar{S_{p}}} \end{aligned}$$

Thus $\dot{V(t)}\le 0$ whenever $\left( \frac{a_{13}\bar{S_{h}}+a_{42}\bar{S_{p}}}{\mu _{m}}\right) \le 1$ i.e. $R_{0}\le 1$. Therefore, LaSalle’s invariance Principle, [18, 31] implies that $E_{0}$ is GAS in D. The proof is complete. $\square$

Appendix C. Proof of Theorem 5.3

Proof

The Jacobian matrix for the model system (9)–(16) corresponding to equilibrium $E_{1}$ is given by

$$\begin{aligned} J(E_{1}) = \left( \begin{array}{cccccccc} -(a_{13}I_{m}^*+\mu _{h})&{}\beta _{1}&{}0&{}a_{12}&{}0&{}-a_{13}S_{h}^*&{}0&{}0 \\ 0&{}-a_{22}&{}0&{}0&{}0&{}0&{}0&{}0\\ a_{13}I_{m}^*&{}0&{}-A&{}0&{}0&{}a_{13}S_{h}^*&{}0&{}0 \\ 0&{}0&{}a_{12}&{}-(f_{1}+\mu _{h})&{}0&{}0&{}0&{}0 \\ 0&{}0&{}-a_{32}S_{m}^*&{}0&{}0&{}0&{}0&{}-a_{31}S_{m}^*\\ 0&{}0&{}a_{32}S_{m}^*&{}0&{}0&{}-\mu _{m}&{}0&{}a_{31}S_{m}^*\\ 0&{}0&{}0&{}0&{}0&{}-a_{42}S_{p}^*&{}a_{42}I_{m}^*&{}a_{42}\\ 0&{}0&{}0&{}0&{}0&{}a_{42}S_{p}^*&{}a_{42}I_{m}^*&{}-d\\ \end{array} \right) \end{aligned}$$

Clearly, three characteristic roots of $J(E_{1})$ are $-\mu _{m}, ~-(a_{31}I_{p}^*+a_{32}I_{h}^*+\mu _{m}),~ -a_{42}I_{m}^* \text{ and } -d+a_{42}$. The other four characteristic roots of $J(E_{1})$ are given by the equation

$$\begin{aligned} x^4+b_{1}x^3+b_{2}x^2+b_{3}x+b_{4}=0 \end{aligned}$$

(28)

where,

$$\begin{aligned} b_{1}= & {} A+f_{1}+a_{13}I_{m}^*+a_{22}+\mu _{h}+\mu _{m}\\ b_{2}= & {} \frac{1}{a_{13}I_{m}^*+\mu _{m}}[-a_{12}a_{13}f_{1}I_{m}^*+A(a_{13} I_{m}^*+\mu _{m})(f_{1}+a_{22}+a_{13}I_{m}^*+\mu _{h}+\mu _{m})\\&+\, (a_{13}I_{m}^*+\mu _{m})\{(f_{1}+\mu _{h})(a_{13}I_{m}^*+\mu _{m}) +a_{22}(f_{1}+a_{13}I_{m}^*+\mu _{h}+\mu _{m})\}]\\ b_{3}= & {} \frac{1}{a_{13}I_{m}^*+\mu _{m}}[\{a_{22}(f_{1}+\mu _{h}) (a_{13}I_{m}^*+\mu _{m})+b_{4}+a_{22}\}(a_{13}I_{m}^*+\mu _{m})+a_{22}(f_{1}+\mu _{h}\\&-\, a_{12}a_{22}a_{13}f_{1}I_{m}^*)]\\ b_{4}= & {} a_{22}\{A(f_{1}+\mu _{h})(a_{13}I_{m}^*+\mu _{m})-2a_{12}a_{13}f_{1}I_{m}^*\} \end{aligned}$$

Eq.(28) has negative solutions if and only if $b_{1}>0,$  $b_{3}>0,$  $b_{4}>0$  and  

$b_{1}b_{2}b_{3}> b_{3}^2+b_{1}^2b_{4}$ i.e. satisfies Routh–Hurwitz criteria [9, 32]. Therefore, positive equilibrium ($E_{1}$) is LAS. $\square$

Appendix D. Proof of Theorem 5.4

Proof

To establish the global stability of the endemic equilibrium state ($E_{1})$, consider the following positive definite function [29].

$$\begin{aligned} V= & {} \frac{1}{2}(S_{h}-S_{h}^*)^2+\frac{1}{2}(V_{h}-V_{h}^*)^2 +\frac{1}{2}(I_{h}-I_{h}^*)^2+\frac{1}{2}(R_{h}-R_{h}^*)^2\\&+\,\frac{1}{2}(S_{m}-S_{m}^*)^2+\frac{1}{2}(I_{m}-I_{m}^*)^2\\&+\, \frac{1}{2}(S_{p}-S_{p}^*)^2+\frac{1}{2}(I_{p}-I_{p}^*)^2 \end{aligned}$$

Diff. V w.r.t. time t along the solution of system of Eqs. (9)–(16), we get

$$\begin{aligned} {\dot{V}}= & {} (S_{h}-S_{h}^*)\{f_{1}R_{h}+\beta _{1}V_{h}-(a_{13}I_{m} +\mu _{h})S_{h}-\beta _{1}V_{h}^*-f_{1}R_{h}^*+(a_{13}I_{m}^*+\mu _{h})S_{h}^*\}\\&+\, (V_{h}-V_{h}^*)\{-a_{22}(V_{h}-V_{h}^*)\}+(I_{h}-I_{h}^*)\{a_{13}I_{m}S_{h} -AI_{h}-a_{13}I_{m}^*S_{h}^*+AI_{h}^*\}\\&+\, (R_{h}-R_{h}^*)\{a_{12}I_{h} -(f_{1}+\mu _{h})R_{h}-a_{12}I_{h}^*+(f_{1}+\mu _{h})R_{h}^*\}+(S_{m}-S_{m}^*) \{(-a_{31}I_{p}\\&+\, a_{32}I_{p})S_{m}-\mu _{m}S_{m}+(a_{31}I_{p}^* +a_{32}I_{h}^*)S_{m}^*+\mu _{m}S_{m}^*\}+(I_{m}-I_{m}^*)\{(a_{31}I_{p}+a_{32}I_{h})S_{m}\\&-\, \mu _{m}I_{m}-(a_{31}I_{p}^*+a_{32}I_{h}^*)S_{m}^*+\mu _{m}I_{m}^*\} +(S_{p}-S_{p}^*)\{a_{41}I_{p}-a_{42}I_{m}S_{p}-\mu _{p}S_{p}-a_{41}I_{p}^*\\&+\, a_{42}I_{m}^*S_{p}^*+\mu _{p}S_{p}^*\}+(I_{p}-I_{p}^*) \{a_{42}I_{m}S_{p}-dI_{p}-a_{42}I_{m}^*S_{p}^*+dI_{p}^*\} \end{aligned}$$

On rearranging the terms, ${\dot{V}}$ reduced to,

$$\begin{aligned} {\dot{V}}= & {} -(\mu _{h}+a_{13}I_{m}^*)(S_{h}-S_{h}^*)^2+\beta _{1}(V_{h} -V_{h}^*)(S_{h}-S_{h}^*)-a_{22}(V_{h}-V_{h}^*)^2\\&+\, (a_{12}+a_{13}I_{m})(S_{h}-S_{h}^*)(I_{h}-I_{h}^*)-A(I_{h}-I_{h}^*)^2 -a_{31}S_{h}(S_{h}-S_{h}^*)(I_{m}-I_{m}^*)\\&-\, \mu _{m}(I_{m}-I_{m}^*)^2+a_{13}S_{h}^*(I_{m}-I_{m}^*)(I_{h}-I_{h}^*) +(a_{31}I_{p}^*-\mu _{m})(I_{m}-I_{m}^*)(S_{m}-S_{m}^*)\\&-\,a_{31}I_{p}^*(S_{m}-S_{m}^*)^2+(a_{31}S_{m}+a_{42}S_{p}) (I_{m}-I_{m}^*)(I_{p}-I_{p}^*)-d(I_{p}- I_{p}^*)^2\\&-\,a_{42}S_{p}(I_{m}-I_{m}^*)(S_{p}-S_{p}^*)-(\mu _{p}+a_{42}I_{m}^*) (S_{p}-S_{p}^*)^2-a_{31}S_{m}(I_{p}-I_{p}^*)(S_{m}-S_{m}^*)\\&+\, (a_{41}+a_{42}I_{m}^*)(I_{p}-I_{p}^*)(S_{p}-S_{p}^*) \end{aligned}$$

Using the region of attraction D (as explain in Sect. 4), we conclude that ${\dot{V}}$ will be negative definite if it satisfy the following inequalities:

$$\begin{aligned} f_{1}^2< & {} \frac{1}{2}(f_{1}+\mu _{h})(\mu _{h}+a_{13}I_{m}^*) \end{aligned}$$

(29)

$$\begin{aligned} \beta _{1}^2< & {} a_{22}(\mu _{h}+a_{13}I_{m}^*) \end{aligned}$$

(30)

$$\begin{aligned} a_{13}^2S_{h}^{*2}< & {} \min \left\{ \frac{\mu _{m}(a_{13}I_{m}^* +\mu _{h})}{6},\frac{2\mu _{m}A}{15}\right\} \end{aligned}$$

(31)

$$\begin{aligned} a_{13}^2I_{m}^{*2}< & {} \frac{A(\mu _{h}+a_{13}I_{m}^*)}{5} \end{aligned}$$

(32)

$$\begin{aligned} a_{12}^2< & {} \frac{2A(f_{1}+\mu _{h})}{5} \end{aligned}$$

(33)

$$\begin{aligned} \left( \frac{9a_{31}^2S_{m}^{*2}}{2d}\right)< & {} \min \{2(\mu _{m} +a_{31}I_{p}^*+a_{32}I_{h}^*),~\mu _{m}\} = \mu _{m} \end{aligned}$$

(34)

$$\begin{aligned} (a_{31}I_{p}^*+a_{32}I_{h}^*)^2< & {} \frac{2\mu _{m}(\mu _{m}+a_{31} I_{p}^*+a_{32}I_{h}^*)}{9} \end{aligned}$$

(35)

$$\begin{aligned} \frac{15a_{32}^2S_{m}^{*2}}{2A}< & {} \min \{\mu _{m},~ \mu _{m}+a_{31}I_{p}^*+a_{32}I_{h}^*\}=\mu _{m} \end{aligned}$$

(36)

$$\begin{aligned} a_{41}^2< & {} \frac{2d(\mu _{p}+a_{42}I_{m}^*)}{3} \end{aligned}$$

(37)

$$\begin{aligned} a_{42}^2S_{p}^{*2}< & {} \frac{\mu _{m}(\mu _{p}+a_{42}I_{m}^*)}{3} \end{aligned}$$

(38)

From Eqs. (29), (30), (31), (32) and (33) we get

$$\begin{aligned} \text{ max }\left\{ \frac{2f_{1}^2}{f_{1}+\mu _{h}}, \frac{\beta _{1}^2}{a_{22}},\frac{5a_{13}^2I_{m}^{*2}}{A}\right\}< & {} (\mu _{h}+a_{13}I_{m}^*) \end{aligned}$$

(39)

$$\begin{aligned} a_{13}^2S_{h}^{*2}< & {} \min \left\{ \frac{\mu _{m}(a_{13}I_{m}^*+\mu _{h})}{6},\frac{2\mu _{m}A}{15}\right\} \end{aligned}$$

(40)

$$\begin{aligned} a_{12}^2< & {} \frac{2A(f_{1}+\mu _{h})}{5} \end{aligned}$$

(41)

Similarly from Eqs. (34), (35) and (36), we get

$$\begin{aligned} \frac{1}{2}\text{ max }\left\{ \frac{9a_{31}^2S_{m}^{*2}}{d},~ \frac{9(a_{31}^2I_{p}^{*2}+a_{32}I_{h}^*)^2}{\mu _{m}+a_{31}I_{p}^*+a_{32}I_{h}^*},~ \frac{15a_{32}^2S_{m}^{*2}}{2A}\right\}< & {} \mu _{m} \end{aligned}$$

(42)

Also, from Eqs. (37) and (38), we get

$$\begin{aligned} 3\text{ max }\left\{ \frac{a_{41}^2}{2d}, \frac{a_{42}^2S_{p}^{*2}}{\mu _{m}}\right\} < (\mu _{p}+a_{42}I_{m}^*) \end{aligned}$$

(43)

Hence, we shows that V is a Liapunov’s function for the system of equations (9)–(16), provided the conditions (39)–(43) hold. $\square$