The Dynamics of Multidimensional Poverty in a Cohort of Irish Children

Abstract

This paper examines multidimensional poverty for three waves of a cohort of Irish children ranging from ages 9 to 17. Poverty is measured over the dimensions of health, education and family resources and both unidimensional and multidimensional poverty is examined. Both show a clear gradient with respect to maternal education. The dynamics of both unidimensional and multidimensional poverty are also analysed. The greatest degree of mobility is observed with respect to family resources. Mobility also is higher for children whose mothers have lower levels of education, with net movements into rather than out of poverty.

1 Introduction

This paper examines multidimensional deprivation for a cohort of Irish children using the landmark Growing Up in Ireland (GUI) survey which follows two cohorts of children from ages ranging from nine months to seventeen years: the Infant cohort born in the period December 2007–June 2008 and the Child cohort born in the period November 1997–October 1998 (see Thornton et al., 2013; Williams et al., 2009). Our analysis in this paper focuses on the Child cohort, for which there are three waves of data, with information on the cohort aged 9, 13 and 17 years respectively.

The motivation for studying child poverty is clear. Child poverty can have long term consequences lasting into adolescence and adulthood in areas such as health, education and the labour market (Brooks-Gunn & Duncan, 1997; Dickerson & Popli, 2018). Much analysis of poverty and deprivation focusses upon one dimension, usually income or expenditure or some other measure of family resources and in the case of children the analysis typically looks at children in poor families (e.g. Thévenon et al., 2018).¹

We refer to this as the “traditional” approach to analysing child poverty. However it does have a number of drawbacks. First, it has long been acknowledged that poverty can occur in dimensions other than monetary/material ones, for example in areas such as health and education and hence while a unidimensional approach to studying poverty will clearly detect poverty in the critical dimension of income/resources it may fail to detect poverty in other critical areas. As we will see below, correlations across different dimensions of poverty are far from perfect and so a focus on just one dimension runs the risk of under-reporting of poverty and failing to provide adequate policy responses. Acknowledgement of this issue has led in recent years to studies examining poverty across a number of dimensions, and we discuss some of these in greater detail below (for a survey see Alkire et al., 2015).

The second drawback with what we label the “traditional” approach is that by focussing on children in poor households the issue of within household distribution is not addressed. This is not meant as a criticism of this approach as data on within household distribution is typically very difficult to acquire. There are some exceptions such as Whelan and Maitre (2012) who explore the distinction between children who directly experience deprivation and children who live in households where basic deprivation is present. However, there is evidence particularly from research in developing countries that within households certain members (typically women and children) can experience systematic discrimination (Jayachandran, 2015; Jayachandran & Pande, 2017). It might also be the case that when a family transitions into poverty adults choose to protect children so that while overall household resources are less, they are reallocated towards children. Thus, data permitting, analysis should try to focus on outcomes specific to the child herself.

Finally, and again reflecting the availability of data, much analysis of child poverty has provided a static picture of poverty at a given point in time. This is clearly valuable information to have but it is also important to supplement this information with knowledge regarding the dynamics of poverty. Is poverty a transient or a persistent phenomenon for children? Is there much “churning” in the sense of children moving in and out of poverty? And, in the case of multidimensional poverty is there much transitioning between different dimensions of poverty or do transitions mainly happen within the same dimensions?

The contribution of this paper is to address these drawbacks of the traditional approach. Using the breadth of information available in GUI we examine poverty across a number of dimensions including outcomes which directly pertain to the children themselves. The longitudinal nature of the data also permits analysis of mobility and dynamics. We choose to focus upon three dimensions of child welfare and to examine deprivation in these measures. The three dimensions are education, health and family income/resources.² The first two of these are direct measures of outcomes for the children, which is consistent with the UNICEF Multidimensional Overlapping Deprivation Analysis (MODA) framework as outlined in Hjelm et al. (2016), whereby the child is the unit of analysis, where possible.

In the case of education we employ an index based upon educational tests which the children undergo. The health index is based upon obesity as defined by body mass index with the threshold adjusted for age and gender. The final index which is based upon family resources is not a direct outcome measure of the children. Instead, it is the response to a question addressed to the principal carer (in almost all cases the biological mother of the child) concerning how difficult it is for the family to make ends meet. This is not a direct outcome measure for the child since, as outlined above, within household allocation of resources could in principle work in favour, or against, the child. Recent research has investigated the allocation of resources within households and the fraction going to children (e.g. Dunbar et al., 2013). However, this analysis requires detailed data on household spending patterns which is not available in GUI and indeed is rarely available in many measures of household income/resources. Nevertheless, we feel it is still vital that some measure of resources be included and that without it any picture of child poverty would be incomplete.

A further contribution of this paper is that apart from just analysing transitions into and out of multidimensional poverty, we also examine transitions across specific deprivations e.g. is there more churning in education poverty compared to health poverty? Are there many transitions across different dimensions of poverty? We are able to analyse these issues in some detail.

Finally, unlike much of the existing research in this area applying to Ireland, this paper covers not just the entry into the Great Recession (which started around 2008–2009) but also Ireland’s subsequent recovery, which can be dated from around 2013–14. The timing of field work for the three waves of GUI serendipitously coincide with a period just before the Great Recession, a period during the Great Recession and a final period when recovery from the Recession was under way.

As we outline in more detail in our data section, the breadth of information in GUI implies that other possible dimensions of poverty are available for inclusion. While it is possible to aggregate information across dimensions into overall measures of multidimensional poverty (and we carry out such analysis below), we are also anxious to examine correlations between dimensions and also movements into and across different dimensions. We wish to exploit the panel nature of the data and given that we have three dimensions and three waves of data the view taken was that the inclusion of extra dimensions would run the risk of falling foul of a version of the curse of dimensionality, whereby there is so much information that it becomes difficult to distil it into a coherent picture. For example, with n dimensions of poverty the transition matrix between successive waves is of dimension 2ⁿ × 2ⁿ. We take the view that n = 3 is the limit of manageability.

In the next section we briefly review some of the relevant studies on multidimensional deprivation, paying particular attention to work carried out for Ireland. We also cover work on the dynamics of poverty as opposed to snapshots at a moment in time. In Section 3 we review the measurement of multidimensional poverty while Section 4 covers our data and our choice of deprivation indicators in some detail. Section 5 presents our results while Section 6 provides discussion and concluding comments, and also discusses some limitations of the study.

2 A Review of Evidence Concerning Multidimensional Poverty Amongst Children

In this section we review some work on multidimensional poverty in children. Rather than adopt a paper-by-paper approach, we focus on a small number of key studies that are most relevant to our paper.

As outlined in the introduction, two of the principal innovations of this paper are to examine child poverty across multiple dimensions and also to specifically analyse the dynamics of transitions into and out of these dimensions. An important paper which examines the first of these issues is Williams et al. (2014) who examine multidimensional deprivation using wave 1 of the child cohort of GUI. Their scope is broader than ours using ten indicators of deprivation which cover seven domains: material well-being, housing and environment, education, health, risk behaviours, quality of school life and emotional well-being. They define poverty as someone who suffers deprivation in at least three of these dimensions and calculate a poverty rate of 29.4%. They also stratify their analysis along a number of dimensions including social class and find that for professional and managerial classes deprivations tend to be in the areas of behaviour, overweight and bullying (being a victim of) whereas for lower skilled and unskilled classes deprivations are more concentrated in education and material resources. They also observe a gradient for the total number of deprivations by social class and maternal education. As their study only examines one wave, they are able to cover a broad range of dimensions without running into the curse of dimensionality. Our paper can explicitly examine dynamics, but at the cost of employing a narrower range of dimensions.

The issue of poverty dynamics for children in a multidimensional setting was examined in an early paper by Nolan et al. (2001). They look not just at income poverty dynamics but also at dynamics for other indicators of material deprivation using data from the 1993 and 1994 waves of the Irish part of the European Community Household Panel Survey (ECHP). They identified a number of dimensions of deprivation (basic, secondary and housing) and examined households with both low incomes (below a typical poverty line of say a fixed fraction of average income) and enforced basic deprivation (i.e. the absence of items such as food, clothing, heating). The authors point out though, that similar to much other work in the area, they are lacking in measures of direct outcomes for children. Data is typically available at household level and little is known about within household sharing. The authors construct a summary deprivation measure which shows a correlation with income of around −0.43, with the correlation of individual deprivations with income ranging from about −0.5 for housing to around −0.3 for basic and secondary items. As we will see below, these correlations are similar to correlations which we find across our measures of deprivation.

In terms of dynamics, Nolan et al. find that about 10% of children stay in high deprivation households (as indicated by the summary indication score) over the two waves of ECHP. However, they do not examine deprivation specific transitions. They also show reasonably high levels of mobility for households who had very low incomes, suggesting that identifying very poor households solely from single snaps of cross-sectional data can be misleading.

Two other studies which are of relevance to our work in that they use GUI data and overlap with our analysis in terms of the period they cover are those by Whelan et al. (2015) and Watson et al. (2017). They examine the first two waves of GUI data specifically focussing upon the impact of the Great Recession which began just after the first wave of GUI was surveyed. Rather than examining a conventional multidimensional poverty index, they employ a measure which they term economic vulnerability which encompasses a low level of income, household joblessness and economic stress. They note that families with children were badly hit by the Great Recession, particularly compared to the elderly. They also examine a child specific outcome, in this case the emotional health and problem behaviours of children as measured by responses to the Strength and Difficulties Questionnaire (SDQ). A high value of the SDQ score, indicating the presence of emotional health problems, is associated with their vulnerability measure, in particular if the family experienced persistent vulnerability i.e. vulnerability in both waves 1 and 2 of GUI. Persistent economic vulnerability was the case for 10% of families, while 15% of families became vulnerable during the recession and 5% escaped out of vulnerability. They also note that the profile of families entering vulnerability in the second wave of GUI was different from those experiencing permanent vulnerability in terms of characteristics such as lone parenthood and maternal education. Our results below will cast further light on dynamics into and out of our measure of resource based poverty, bearing in mind that it is a narrower measure than employed in these two papers.

Finally, it is worth noting the work of Dickerson and Popli (2018), who examine multidimensional poverty in the UK, using the Millenium Cohort Study, a dataset similar to GUI, and who also examine poverty dynamics. They look at poverty over five dimensions: financial constraints, material deprivation, parental involvement, housing environment and neighbourhood. In line with most of the work in this area they find that multidimensional poverty overlaps to a significant degree, but far from perfectly, with traditional income poverty. They also find that similar demographic characteristics such as workless households and ethnicity are associated with both types of poverty and also that persistence across time for both types of poverty is comparable. One area however where their approach differs from ours is that they do not examine transitions between specific dimensions of poverty.

To summarise, we note that studies up to now have examined multidimensional poverty using GUI data in a static setting (Williams et al), while studies explicitly looking at dynamics used different data from an earlier period (Nolan et al., 2001). Studies using GUI and looking at dynamics have employed measures of economic vulnerability rather than standard measures of multidimensional poverty. The gap that we attempt to fill here is to look at multidimensional poverty in a dynamic setting. We can also examine transitions into and out of specific deprivations and, as far as the data permits, our measurers are child based outcomes, as opposed to outcomes for families with children.

We now proceed to briefly outline the construction of a multidimensional poverty index.

3 Measuring Multidimensional Poverty

As outlined in the introduction, historically research into poverty concentrated on monetary measures such as income or expenditure, despite the acknowledgement that poverty can occur in dimensions other than monetary ones, such as health, education, housing etc. Hence the attempts in recent years to set the measurement of multidimensional poverty on a more rigorous footing (for recent surveys see Alkire et al., 2015). The approach which has probably gained most support is the AF dual cut-off method (Alkire & Foster, 2011). This breaks down the identification of the poor into two parts: first of all, those who are deprived in each individual dimension are identified. Then there is a second round of identification whereby those who have a (weighted) number of deprivations above a certain threshold are deemed to be poor. As we will see below, once the poor have been identified this information can be aggregated into an overall index. This index takes account of not just the number of people who are deemed multidimensionally poor but also the number of dimensions in which they are deprived.

The AF methodology assumes there are N individuals and there are D ≥ 2 deprivation indicators (in dimensions such as income, health, education, housing etc.). Y is the DxN matrix whose i,jth entry y_ij denotes the level of indicator j for person i. For each indicator, j, there is a deprivation cut-off, z_j, whereby if a person’s level of that indicator is below this cut-off, they are deemed to be deprived in this dimension and hence we have a 1xD vector of cut-offs z = (z₁, z₂, …,z_D).

There is also a 1xD vector of the weights to be assigned to each deprivation, w = (w₁, w₂,,,.w_D) with 0 < w_j < 1 and $\sum_{j=1}^D{w}_j=1$. We follow the standard approach of assuming equal weights for each deprivation.

We can define a matrix g⁰ which summarises deprivations across all dimensions such that ${g}_{ij}^0=1$ whenever y_ij < z_j and ${g}_{ij}^0=0$ otherwise. The measure of deprivation in each dimension is then calculated to obtain an overall deprivation score for each individual ${c}_i=\sum_{j=1}^D{w}_j{g}_{ij}^0,0<{c}_i<D$.

Given the deprivation score for each individual we then identify the multidimensionally poor via the indicator ${MP}_i^{(k)}$ such that ${MP}_i^{(k)}=I\left({c}_i\ge k\right)$, 0 < k ≤ D, and k is the poverty cut-off i.e. to be multidimensionally poor you must have a number of deprivations equal to or in excess of the second cut-off, k. The poverty cut-off k is then applied to the matrix g⁰ to obtain the censored deprivation matrix g⁰(k) whose ijth element is ${g}_{ij}^0(k)={g}_{ij}^0\times {MP}_i^{(k)}.$ This then gives the censored deprivation score for each observation as ${c}_i^{(k)}=\sum_{j=1}^D{w}_j{g}_{ij}^0(k),0<{c}_i^{(k)}<D$, where ${c}_i^{(k)}={c}_i$when c_i ≥ k and zero otherwise.

Given individual deprivation scores we can calculate the population average deprivation score, $M=\frac{1}{N}\sum_{i=1}^N{c}_i^{(k)}$. This measure can be usefully expressed as M = H × A where $H=\frac{q}{N}$ where q is the number of people who are multidimensionally poor and $A=\frac{\sum_{i=1}^N{c}_i^{(k)}}{qD}$ is the intensity of multidimensional poverty amongst the poor. M is referred to as the “adjusted headcount ratio” and it has the desirable property that it is sensitive to both the number of people who are multidimensionally poor and also to the number of dimensions in which they are poor. Note that it is not sensitive to the intensity of poverty within a given dimension i.e. how far an individual is below any given poverty line.

The choice of k is clearly up to the discretion of the analyst but it is worth pointing out two limiting cases. If k = 1 then we have what is known as the union approach whereby being poor in just one dimension identifies you as multidimensionally poor. If k = D then we have the intersection approach whereby you must be poor in all dimensions to qualify as multidimensionally poor.

We now turn to discuss our data and the particular dimensions of poverty we choose to analyse.

4 Data

Our data comes from the first three waves of the Growing Up in Ireland (GUI) 9 year old cohort. This tracks the development of a cohort of children born in Ireland in the period November 1997–October 1998 (see Williams et al., 2009). The sampling frame of the data was the national primary school system, with 910 randomly selected schools participating in the study. The field work for wave 1 was carried out between August 2007 and May 2008, that for wave 2 between August 2011 and March 2012 and that for wave 3 between April 2015 and August 2016. As mentioned earlier, this conveniently includes a period before the Great Recession, a period during the depths of the Recession and finally a period of recovery from the Recession.

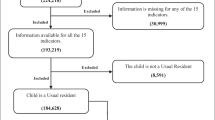
As we explain in more detail below, we analyse multidimensional poverty over three dimensions: health, education and a measure of family resources. We work with a complete case balanced panel, consisting of only those children who were sampled in each of the three waves and dropping observations where the underlying health, educational or family resource data are missing and also where the primary caregiver changes between waves. Thus given an original sample in wave 1 of 8568 children, this leaves us with an ultimate sample of 5117 (2614 female and 2503 male). Naturally in making these adjustments the issue of attrition arises. Attrition in surveys such as GUI is rarely random and this is confirmed in Murphy et al. (2018) who show that attrition tends to be higher for those with lower maternal education. Correspondingly the data are re-weighted so that the sampling weight in the balanced panel which we analyse is the product of the original sampling weight for wave 1 and the attrition weights which take account of non-random attrition in subsequent waves (details of sample design and weighting are available in Appendix 1). We now turn to discuss the measures we use in the dimensions of health, education and family resources.

4.1 Health Measure

In the area of health we were anxious to employ a measure which was clearly an outcome, as opposed to an input measure (e.g. usage of medical resources). Consequently, we use obesity as measured by body mass index (BMI, which is defined as weight in kilos divided by height in metres squared). Weight was measured to the nearest 0.5 kg using a medically approved flat mechanical scales and children were advised to wear light clothing. Height was measured to the nearest mm using a height measuring stick. We make an additional adjustment to the data which facilitates our analysis. As the obesity threshold for BMI differs by age and gender a simple comparison of BMI can be misleading. Consequently, we analyse normalized BMI figures, where BMI is divided by the appropriate obesity threshold which varies by age and gender (we take these thresholds from Cole et al., 2000). Thus a normalized BMI of 1.1 indicates that the child had a BMI which was 1.1 times the relevant threshold for their age and gender. This facilitates comparisons across age and gender where these thresholds differ. Naturally, as our threshold for this measure we use a normalized BMI figure of 1.0. Thus anyone with a normalized BMI greater than or equal to unity is deemed “health poor”. While the use of obesity as our measure of health poverty may appear narrow in focus, Lindberg et al. (2020) show that childhood obesity can be associated with higher risk of all cause mortality in early adulthood and so it is arguably a good proxy for overall health.

4.2 Education Measure

As our education measure we again use an outcome rather than an input, in this case a measure based upon child scores in cognitive tests. The first set of tests administered to the children were the curriculum based Drumcondra Reading and Maths Tests administered by teachers in the classroom in wave 1 when the vast majority of the children were aged 9 (very small numbers were aged 8 and 10). In wave 2 of the Child Cohort the tests administered were the Drumcondra Numerical and Verbal Ability tests and the children were aged 13. It should be noted that unlike the Drumcondra Reading and Maths tests, these are not curriculum based tests. In wave 3 of the cohort three tests were carried out: a Cognitive Naming Test, a Cognitive Maths Test and Cognitive Vocabulary Test (details in Williams et al. (2019)). More details are available in Appendix 2 and table 3 in that appendix also provides the rank correlations across the different subscales and components within each cohort. In most cases these correlations are at least 0.3 and in some cases as high as 0.7, correlations which are comparable to those obtained by Feinstein (2003) in his influential study of the socioeconomic gradient of tests scores in the UK. The children were all of similar ages and hence for the most part at the same educational grade. However, there was some differentiation and so it was necessary to standardise the results. Hence the data we use are the logit scores which were obtained from the original raw data using the principles of Item Response Theory (see Lord, 1980).

Given the wide range of cognitive test scores, we follow Feinstein (2003) in using all the information available for each wave to construct a general measure via principal components analysis (PCA). PCA is the eigenvalue decomposition of the correlation matrix R of the different individual test score measures available in each wave. If we have, say, n measures, x₁…x_n then the first principal component, y₁ is given by

$${y}_1={a}_{11}{x}_1+{a}_{12}{x}_2\dots +{a}_{1n}{x}_n$$

where a_1i are the weights which are chosen to maximise the variance of y₁ and must also satisfy the normalising constraint $\sum_{i=1}^n{a}_{1i}^2=1$ .

Using the first principal component has the advantage of combining information from the different cognitive tests. As noted above, the rank correlations across the different measures are sufficiently high to be confident that we are picking up a similar underlying process.

In appendix 2 we show the scree plots for the PCA. Using the rule of thumb that components where the eigen value exceeds unity should be selected, we see that in nearly all cases it is only the first principal component which satisfies this condition. Table 4 in appendix 2 also shows the fraction of variance explained by the first principal component. Where we have only two measures entering into the PCA then the first component explains about 75–80% of variance. When there are more measures then the fraction of variance explained falls to 40–50%. In all instances the value of Kaiser-Meyer-Olkin test statistic for sampling adequacy for PCA meets the rule of thumb threshold of 0.5, though in some cases only barely. Then, in terms of identifying who is “education poor” we use a z score of the first principal component of −1.5 or lower.³

4.3 Family Resource Measure

The final dimension we include in our measure of multidimensional poverty is one of family resources. We employ a subjective measure of family resources. In each wave of GUI the principal carer (almost always the biological mother of the child) is asked the question: Concerning your household’s total monthly or weekly income, with which degree of ease or difficulty is the household able to make ends meet? The available answers range from “very easily” to “with great difficulty”. We use as our threshold the following responses: “with great difficulty” or “with difficulty”. One advantage of such a measure is that as well as capturing a shortage of household resources it also reflects the stress which such shortages can cause within families with possible implications for child behavioural problems (Schenck-Fontaine & Panico, 2019).

Our choice of a subjective measure compared to a measure such as equivalised after-tax disposable family income is also motivated by the details of the GUI income data. Child income poverty is typically defined as being in a family whose income is below a threshold such as 50% (or sometimes 60%) of median equivalised disposable income. However, calculating such a poverty line for GUI is problematic as the sample from which median income is drawn will be a sample of those households where a child was born in the period September 1997–October 1998 and this sample will not be nationally representative. In addition, the use of a relative poverty line is problematic when there is a discrete fall in income (as happened between wave 1 and wave 2). If the poverty line itself falls, then even though many if not most families have experienced a decline in living standards, poverty (as measured by a purely relative poverty line) may remain unchanged or even fall. A final, additional problem with the GUI data in waves 2 and 3 is that the income data is rounded off to the nearest €1000, which creates measurement error when identifying people below a poverty threshold.

In the next section we present our results for the complete sample and stratified by maternal education as parental education has been found to play a role in subsequent adult health outcomes (Bjorkegren et al., 2020), and it is also in line with previous, similar, work using this dataset (Madden, 2020a, b).

5 Results

We now present results, concentrating first of all on uni-dimensional poverty and then moving on to multidimensional poverty. Initially, we also focus on what we could term a static view of the issue, merely looking at each cross-section and not examining dynamics which we postpone until later.

5.1 Unidimensional Poverty

We first look at the correlations between the different measures of unidimensional poverty (following the spirit of the dashboard approach outlined by Ferreira & Lugo, 2013). In Table 1 we show the tetrachoric correlations between each dimension of poverty for each wave. Concentrating first of all on correlations for a given dimension over time, we see that correlations for education are around 0.6–0.7, those for health around 0.75–0.85 and those for income around 0.5–0.55. This suggests quite a high level of persistence within unidimensional poverty, and persistence appears to be increasing since in general the wave 2-wave 3 correlations are higher than the wave 1-wave 2 correlations, and persistence also appears to be higher for health.

Table 1 Tetrachoric Correlations across Poverty in Individual Dimensions

Turning now to within wave correlations between the different dimensions, we see wave 1 correlations ranging from 0.16–0.24, correlations in wave 2 from 0.15–0.19 and correlations in wave 3 around 0.16–0.18. Thus, not surprisingly, correlations between dimensions in a given wave are considerably lower than correlations for the same dimension over time. There is also no clear trend in terms of inter-dimension correlation over time, nor in terms of higher correlations between any two particular dimensions. These results underline the importance of analysing poverty across a number of dimensions, since clearly there is far from perfect overlap between people who are poor in different dimensions.

Turning now to how each unidimensional index developed over time, Table 2 shows the incidence of uni-dimensional poverty across the three dimensions with the results stratified by maternal education. We employ four categories of education: (1) completion of lower secondary schooling (2) completion of secondary schooling (3) obtaining a post-secondary school diploma or cert and (4) completion of third level education. We choose to present these results by maternal education level in wave 1. While there is some change in maternal education levels between waves 1, 2 and 3, it is relatively minimal and by fixing on wave 1 maternal level we ensure that it is the same sample of observations in each category for each wave.

Table 2 Uni-Dimensional Poverty Rates

It perhaps is more instructive to look at the trends and socioeconomic gradients in unidimensional poverty rather than the actual levels, as the levels will be sensitive to precise cutoffs. Health poverty, as defined by obesity shows little change between wave 1 and wave 2 but then increases to nearly 7% in wave 3. The gradient by maternal education is clear. Obesity levels where the mother has lower secondary education are four to five times higher than where the mother has third level education. Where the mother has completed secondary education or has a post-school diploma/cert levels are intermediate and differ very little from each other. There are some signs that the gradient may be getting slightly steeper over time and this is explored in more depth in Madden (2017).

In terms of education poverty, while the absolute level is higher than in the case of obesity, it shows little sign of changing over time. Again a gradient by maternal education is visible and this gradient shows a clear sign of becoming steeper over time. In wave 1 children whose mother had lower secondary education show a prevalence of poverty four to five times higher compared to children whose mothers had third level education. By wave 3 relative prevalence for the lowest level of maternal education is around nine times that of the highest. This phenomenon is driven by an improvement in the situation of children whose mothers have third level education. Their relative performance in wave 3 is considerably better than in wave 1 and it is this which lies behind the steepening of the gradient.

The most dramatic change in unidimensional poverty is observed in resource poverty where the headcount rate increases from just under 6% in wave 1 to 20% in wave 2 and then falls back slightly to around 17% in wave 3. This is not unexpected as the Great Recession occurs in between waves 1 and 2 and this clearly has a major impact upon families perceived ability to make ends meet. It is interesting to note that the gradient by maternal education is not as steep here as in the case of health and education. This may reflect the fact that the measure we use for resource poverty is self-assessed and subjective rather than objectively measured.

5.2 Multidimensional Poverty

Figures 1 and 2 provide graphical evidence of the extent of multidimensional poverty across the three waves, though not taking account of correlations between different dimensions of poverty. Figure 1 shows the breakdown of the total number of uni-dimensional poverty spells (or deprivations) experienced by children. We see that in total about 53% of the children experience no deprivations over the three waves and just over 22% of them experience only one deprivation. Thus multiple deprivation, in terms of either experiencing different deprivations or the same deprivation more than once, is experienced by just under one quarter of the children. Figure 2 shows the gradient by maternal education. As is the case for most of our results, the pattern is for a clear difference between highest and lowest levels of maternal education, with the two intermediate levels showing little difference between each other. For example, only one third of children with the lowest level of maternal education experience no deprivations, while the corresponding ratio for children with the highest level of maternal education is around 70%. Correspondingly, multiple (i.e. two or more deprivations) is experienced by only about 10% of children with the highest maternal education but by over 40% of those with lowest maternal education.

Fig. 1

Total Number of Deprivations over 3 waves

Fig. 2

Total Number of Deprivations over 3 waves by Maternal Education

Table 3 presents results for multidimensional poverty for the whole sample, while Table 4 presents the results by maternal education. The first column presents the adjusted headcount ratio and the second column the raw headcount ratio. Column 3 provides the deprivation intensity while column 4 gives the average number of deprivations for each person identified as multidimensionally poor. The results are also presented for different levels of k, the dimension cut-off. As might be expected, trends in multidimensional poverty reflect trends in the individual dimensions, in particular the increase in resource poverty after wave 1. There is very little change in either the deprivation intensity or in the average number of deprivations per poor person.

Table 3 Multidimensional Poverty

Table 4 Multidimensional Poverty by Maternal Education

The gradient by maternal education is also very similar to those for the individual dimensions. Taking the union approach to multidimensional poverty (k = 1), poverty rates for the lowest level of maternal education are about three times that of the highest level. The two intermediate levels of maternal education lie in between and have very similar rates of multidimensional poverty.

The gradient does get steeper for values of k in excess of 1, but the cell sizes here are very small. Even if we look at the total sample and not by maternal education we see that the raw headcounts for when k = 3, the intersection approach, are all less than 1%, even in waves 2 and 3 following the increase in income poverty. Even for the lowest level of maternal education and in the “worst” wave (wave 2), the fraction of children experiencing all three deprivations is 0.013.

In summary, the “static” results for multidimensional poverty show that just under one quarter of the children experience more than one deprivation over the three waves and about 12% experience more than two. However, this includes children who experience the same deprivation in different waves. In terms of children experiencing multiple deprivations within a given wave, rates of multidimensional poverty appear low, not even exceeding 5% in wave 2, when the Great Recession was at its peak. Much of this reflects the fact that while resource poverty increases between waves 1 and 2, there is little change in health poverty and education poverty falls slightly. The rise in health poverty in wave 3 is offset by a fall in resource poverty and thus the fraction of children experiencing more than one deprivation within a given wave does not exceed 5%.

5.3 Multidimensional Poverty Dynamics

In this part of the paper we exploit the panel nature of the data to examine the dynamics of multidimensional poverty. We first of all examine the overall degree of persistence: how many children are poor in one or more than one dimension of poverty over time. We then examine transitions into and out of poverty, again for uni-dimensional and multi-dimensional poverty and calculate indices of mobility into and out of poverty between waves. As in previous sections we stratify the analysis by maternal education. We do not explicitly model the factors affecting transitions into and out of poverty, though that is an issue we hope to return to in future research.

We first analyse the total amount of “churning” over the three waves. Figure 3 shows the total number of “moves” made by children over the three waves. A move is defined as a change in the number of deprivations experienced by a child from wave to wave (this can include increases or decreases in the number). Thus if a child has no deprivations in wave 1 but has one deprivation in wave 2, that counts as one move. If they had no deprivations in wave 1 and two deprivations in wave 2 that counts as two moves. The histogram in Fig. 3 not surprisingly is similar to that in Fig. 1. If you have never had a deprivation then clearly you will not move, though those in Fig. 3 with zero moves also includes that small number of children (nearly 4%) who are deprived in at least one dimension and who remain in that situation over the three waves. Figure 4 shows these histograms by maternal education. Once again a clear social gradient can be observed. Children whose mothers have not completed second level education experience more transitions, while the lowest number of transitions are experienced by those who’s mothers have third level education.

Fig. 3

Total Number of Moves over 3 waves

Fig. 4

Total Number of Moves over 3 waves by Maternal Education

We now look more explicitly at transitions between waves and critically in which direction they go. In Fig. 5a-b we present what are effectively transition matrices, with each cell entry a form of histogram. In Fig. 5a, the column shows how many deprivations are experienced in the original wave (wave 1) and the row shows how many are experienced in the subsequent wave (wave 2). Thus for example, reading across the first row of Fig. 5a we see that 62.5% of children experienced no deprivations in waves 1 or 2, 16.6% went from zero deprivations in wave 1 to one deprivation in wave 2, 1.4% went from zero deprivations to two deprivations etc.

Fig. 5

a. Transition Matrix, Wave 1 to Wave 2. b. Transition Matrix, Wave 2 to Wave 3

In terms of rough rules of thumb of how to interpret these matrices, low mobility will be reflected in large entries along the main diagonal, as children experience no change in their number of deprivations. In terms of off-diagonal entries, then large fractions to the north-east of the main diagonal indicate a position where children are acquiring deprivations (moving into poverty), while large fractions to the south-west of the main diagonal indicate a situation where children are shedding deprivations.

In terms of a welfare perspective, then assuming we prefer less deprivations to more and that we prefer to see children moving out of rather than into deprivations, then what we ideally want to see is the greatest amount of mass in the top left hand corner i.e. no deprivations in either wave. After that we prefer mass to the left of the main diagonal and preferably higher up i.e. moving from a low number of deprivations towards zero.

In terms of comparing the degree of mobility by simple visual inspection of the transition matrix, it is typical to look at entries on the main diagonal. High values along the main diagonal imply that a greater fraction stayed with the same number of deprivations. Thus comparing Fig. 5a and b we see in general higher entries along the main diagonal in Fig. 5b. This would seem to indicate greater persistence (or less mobility) between waves 2 and 3 compared to between waves 1 and 2. However care must also be taken to look at movements off the main diagonal, in particular the size of transitions between different categories.

In terms of looking at total deprivations rather than distinguishing between specific deprivations, which we do later, we see in Fig. 5a for wave 1 to wave 2 transitions that most of the mobility (the off-diagonal cells) is to the right of the main diagonal i.e. children acquiring deprivations rather than shedding them. However, we do see 7.5% of children moving from one deprivation to zero, so there is movement in both directions. Another striking feature of Fig. 5a is that most of the mass is in cells towards the north west, reflecting the fact that very few children experience more than one deprivation.

Turning to Fig. 5b and transitions between waves 2 and 3, we see that overall mobility looks very similar, the fractions along the main diagonal being almost identical. Note however that now the off-diagonal elements effectively cancel each other out, with 11.5% going from zero to one deprivation but 12.1% moving in the opposite direction.

In appendix 3 we present these results by maternal education. We note the greatest mobility (in the sense of lower fractions along the main diagonal) for children with the lowest level of maternal education between waves 1 and 2. The relatively greater mass to the north-east of the main diagonal reflects the acquisition rather than the shedding of deprivations, with children moving into resource poverty following the Great Recession. Visual inspection of the data also suggest that what we might regard as “good” mobility i.e. that located in the south-west of the matrix is more observed at higher education levels. Turning now to mobility patterns between waves 2 and 3, again we see more mobility at lower levels of maternal education in the sense that there is less mass along the main diagonal, but for all levels of maternal education we see that the off-diagonal cells on either side of the main diagonal effectively cancel each other out.

However simple visual inspection may not always be reliable and it is helpful to have a statistic which summarises the degree of mobility. The measure which we use is the Bartholomew average jump index. Thus we have four categories, from zero up to three deprivations and if a child moves from say zero to one deprivation between waves 1 and 2 that counts as one jump or transition. If they move from zero to two deprivations that counts as two transitions etc. We then add together the total number of transitions in either direction and take the average over the population.⁴ We also calculate the number of transitions up (an increase in the number of deprivations) minus the number of transitions down, which we term “net transitions” and this captures the welfare dimension referred to earlier.

Table 5 provides data on the average number of absolute and net transitions per child, with standard errors in brackets. A positive value for average net transitions indicates a situation where on balance more children acquire rather than shed extra deprivations.

Table 5 Mobility Indices

Overall, we can see that these results confirm the results from the graphical transition matrices. Average mobility in terms of the absolute number of transitions is effectively unchanged between waves 1 to 2 and waves 2 to 3. However, looking at net transitions we see that from wave 1 to wave 2 children were on average acquiring deprivations whereas between waves 2 and 3, deprivations were essentially unchanged. We also observe cross sectional difference by maternal education. Children whose mothers have the lowest level of education show much greater absolute mobility between waves 1 and 2, with an average of almost half a transition per child. Bear in mind though that not all these transitions involve acquiring a deprivation, though the average net transition is positive and statistically significant. Looking at transitions between waves 2 and 3 we again see a higher absolute number of transitions for this category but the net effect is effectively zero.

For the other levels of maternal education, we see the lowest level of mobility for those cases with the highest level of education, and intermediate levels of mobility for maternal education levels 2 and 3. Net moves are positive for these categories between waves 1 and 2, indicating that on balance children in these categories acquired deprivations, with the lowest rate of acquisition for those whose mothers had third level education. Similar to children with maternal education level 1, on balance there is no net acquisition of deprivations between waves 2 and 3.

So far we have examined transitions only in an overall sense i.e. we have not concerned ourselves with which particular deprivations are acquired or shed. We address this issue in the next sub section.

5.4 Dimension Specific Dynamics

In Fig. 6a and b we reproduce the transition matrices in histogram form which we used above to analyse transitions in terms of total deprivations. Now we have a separate row and column for each possible combinations of deprivations. As before, if we observe heavily populated cells along the main diagonal then we have a situation of low mobility. Observe also that the top left hand cell (where a child has no deprivations in either wave) is the same regardless of whether we are looking at total or specific deprivations. Again in terms of the off-diagonal patterns we generally wish to see greater mass towards the west of the main diagonal, indicating that children are shedding deprivations, as opposed to the east, where children are acquiring them. Of course what is of greatest interest in these diagrams is precisely which cells off the diagonal have the greatest mass, since that indicates which deprivations show the most movement into and out of.

Fig. 6

a. Deprivation Specific Transition Matrix, Wave 1 to Wave 2. b. Deprivation Specific Transition Matrix, Wave 2 to Wave 3

Figure 6a shows deprivation specific transitions for the whole sample between waves 1 and 2. As in Fig. 5a, about 63% of the sample experience no deprivations in either wave. The off-diagonal cell with the highest percentage in it (12%) is for those who had no deprivations at all in wave 1 and who became resource deprived in wave 2. Most other off-diagonal cells have very low percentages except perhaps for those who had been education deprived in wave 1 but moved back to no deprivations in wave 2 (4%). Cells in the south east quadrant have very low percentages indicating that thankfully very few children have multiple deprivations.

Figure 6b presents the same data except this time between waves 2 and 3. The fraction who have no deprivations in either wave is slightly lower, at just over 58%. We also see nearly 6% of children who are resource poor for both waves 2 and 3. The two biggest off-diagonal cells are 6.4% for children who have no deprivations in wave 2 but are resource poor in wave 3 and 8.3% for children who were resource poor in wave 2 but transit back to no deprivations in wave 3. We also observe around 3% moving between no deprivations and education poverty only but it seems to fair to say that most of the mobility between deprivations involve resources.

Appendix 4 shows these transition matrix histograms by maternal education. Briefly, as already discussed we see more mobility at lower levels of maternal education. For the lowest level of maternal education, between wave 1 and 2 the biggest transition is again for children who had no deprivation in wave 1 becoming resource poor in wave 2 (14.3%). For this group again we see some mobility in and out of education poverty (4.7% in and 6.6% out) and relatively little mobility elsewhere. The same pattern can be observed as maternal education levels increase, except that absolute levels of mobility are lower. The one (minor) exception to this is for the highest level of maternal education where we see some mobility out of resource poverty deprivation in wave 1 to no deprivations at all in wave 2 (2.9%).

Looking at the wave 2 to wave 3 transitions and again focusing on the lowest level of maternal education, we again observe a magnified version of what is happening to the complete sample. Just under 55% show no mobility (though 7.5% of that 55% stay resource poor), most mobility is into and out of resource poverty (6.5% in and 10% out) and again there is some mobility into and out of education but relatively little with respect to health. Similar to the wave 1-wave 2 transitions we see less absolute mobility with higher levels of maternal education. It is interesting to note however that for the highest level of maternal education we see quite high levels of mobility into and out of resource poverty (6% into and 8% out of). These figures indicate that for this group mobility with respect to resource poverty is similar to other levels of maternal education. This is not true for mobility in education and health where mobility for children whose mothers have the highest level of maternal education is a scaled down version of mobility for the rest of the sample.

Overall though, what is probably most notable about the pattern of mobility by maternal education level is that qualitatively it does not differ greatly. Lower levels of maternal education generally observe higher levels of mobility but for the most part it is a scaled up version of what happens elsewhere. Or to put it another way, in terms of transitions children with lower maternal education are not poor in a different way, they are just more poor in the same way.

Again, it is useful to go beyond visual inspection of the transition matrices and to see if we can more formally examine the different transition patterns. Given two transition matrices T₁ and T₂ what we are essentially looking for is some measure of how similar or alike are these matrices. Note that measures such as the Bartholomew jump index or the Shorrocks trace based measures are not useful here since those measures are insensitive to where exactly in the transition matrix transitions are occurring, and that is precisely what is of interest here. The approach we choose is to calculate the matrix T₁-T₂ and then to calculate the infinity norm of this matrix. The infinity norm of an nxn matrix A can be defined as follows (assuming a_ij is the element in the ith row and jth column): ${\left\Vert A\right\Vert}_{\infty }={\mathit{\max}}_{i=1:n}\sum_{j=1}^n\left\lceil {a}_{ij}\right\rceil$ i.e. the maximal row sum of the matrix. Intuitively the norm of a matrix gives an idea of the magnitude of a matrix and hence the norm of the matrix T₁-T₂ gives a sense of the magnitude of the difference between the transition matrices i.e. how different they are.

In Tables 6 and 7 we present the values of the infinity norms for all possible T_i-T_j combinations where we include the transition matrix for the sample as a whole and for each level of education.⁵ The absolute values of the norms are of little interest, what matters most is the relative magnitude. Thus if we look at how each maternal education level differs from the total sample, we see that it is the lowest and the highest levels which show the most difference. These levels also show the biggest pairwise difference with maternal education levels 2 and 3 relatively close to the total sample and also close to each other. Transition patterns for maternal education levels 2 and 3 are also considerably closer to maternal education level 4 than to maternal education level 1.

Table 6 Infinity Norm of Difference between Transition Matrices – Wave 1 to Wave 2

Table 7 Infinity Norm of Difference between Transition Matrices – Wave 2 to Wave 3

Finally, in our comparison of these transitions matrices we return to the question of whether the difference between matrices (e.g. between maternal education levels 1 and 4) arises from the fact that there are simply more transitions for education level 1 or whether the patterns of transitions differ between the education levels. Are transition levels for maternal education level 1 simply a scaled up version of those for maternal education level 4, or do we also observe a qualitative difference in the transitions?

To investigate this we need to scale transition matrices so that in some sense the total degree of transitions have been controlled for and what we pick up is merely the difference in the pattern of transitions. We take overall transitions as our base and let the transition matrix for the whole sample be T. Then, suppose we wish to normalize the transition matrix for maternal education level 1, T₁, so that its overall rate of transition has been normalized to that of T, we multiply the elements along the main diagonal of T₁ by the ratio of the trace of matrix T and the trace of T₁. This reflects the fact that overall transitions in the transition matrix can be captured by the trace, which tells us the fraction of observations which do not change between waves. The off-diagonal elements are scaled by the reciprocal of this measure, reflecting the fact that a low trace indicates a high fraction of off-diagonal elements and hence greater mobility. Thus the re-scaled matrix for T₁, which we label ${T}_1^s$ has elements ${a}_{ii}^s={a}_{ii}\frac{Tr(T)}{Tr\left({T}_1\right)}\ i=1,\dots, n$ and elements ${a}_{ij}^s={a}_{ij}\frac{Tr\left({T}_i\right)}{Tr(T)},i\ne j.$ We then calculate the infinity norm for the matrices ${T}_1^s-{T}_2^s$ etc. This approach provides a measure of the differing pattern of transition while controlling for its overall level. Results for the infinity norms for the difference between these scaled transitions matrices is provided in Tables 8 and 9.

Comparing the results of Tables 6, 7, 8 and 9 we see that the distance between the transition matrices has fallen considerably, in many cases by a factor of well over 50%. This is consistent with the impression provided by visual inspection of the transition matrices that the pattern of poverty transitions by maternal education does not differ too much, rather it is the overall scale which is key.

Table 8 Infinity Norm of Difference between Scaled Transition Matrices – Wave 1 to Wave 2

Table 9 Infinity Norm of Difference between Scaled Transition Matrices – Wave 2 to Wave 3

6 Discussion and Conclusion

This paper has analysed unidimensional and multidimensional poverty for three waves of a cohort of Irish children aged between 9 and 17 years of age. The study has, as much as possible, concentrated on direct child outcomes and also examines mobility across the waves. The focus is less on the levels of poverty but more on their development over time, the degree to which there is a gradient with respect to maternal education and also the correlations across the different dimensions of poverty.

In this section we now discuss the results in detail and also any policy implications which may arise. Before doing so however, it is also useful to briefly discuss some limitations of the paper. First of all, while we look at poverty in a multidimensional context, we are still limited in the number of dimensions we cover. The three dimensions we include are arguably the three most important determinants of child welfare, but there are other factors which we have not included e.g. the quality of housing and the lived environment. This primarily reflects the curse of dimensionality referred to earlier. GUI is an unusually rich dataset and there is other child related material which could have been included but that would have been at the expense of the dynamic analysis and we feel the focus on dynamics is one of the strengths of the paper. The specific indicators we chose to capture health, education and resources were also in our opinion the best measures available but other indicators (e.g. child mental health) could have been used. As explained above, data limitations forced the use of a more subjective measure of family resources rather than the more “objective” measure of after tax equivalised income. The subjective measure also precluded the calculation of depth-based multidimensional poverty indices and also was unable to address within family distribution.

While we regard the dynamic analysis as one of the strengths of the paper, we still need to acknowledge that there are unavoidable limitations here as well. We observe children at three stages of their lives and examine their poverty status at those points. We do not observe dynamics before the age of nine, nor do we observe any transitions which may happen in between the period of observation. Thus it is possible that a child might enter resource poverty aged 10 and exit such poverty aged 12, but this would not be observed in our data and hence a form of censoring exists. However, this is an inevitable limitation of panel data which is collected at intervals of 3–4 years.

These issues notwithstanding, what are the key messages from this paper? It should be borne in mind that the paper is primarily concerned with measurement and of obtaining a broader picture of child poverty across a number of dimensions and over time. Our discussion of policy implications thus follow on from this and hence are necessarily quite broad-brushed and we do not investigate the effectiveness of specific policy interventions. As we will see, given that we are looking at three different dimensions of poverty, over three different time periods and also with a socioeconomic gradient by maternal education, there are a lot of “moving parts”. We will discuss results/conclusions first with respect to unidimensional and then multidimensional poverty. We then discuss mobility both in overall terms and also with respect to specific dimensions. At all times we will be cognisant of how results differ across the socioeconomic gradient, before trying to summarise our findings at the end.

Dealing first with unidimensional poverty, education and health poverty show relatively little change over time, with just a slight increase in health poverty as children move from age 13 to age 17. One conclusion which can be drawn from this is that poverty in these areas has become established at an early age, and this provides support for early interventions, or perhaps more particularly, for prevention rather than cure.

The increase in health poverty however is not observed for children with the highest level of maternal education and thus we see a steepening of the gradient here. It is also noticeable that while the overall level of educational poverty as we define it is virtually unchanged over time, again there is a steepening of the gradient with respect to maternal education, arising from a reduction in educational poverty for children with the highest level of maternal education. This suggests that these families are able to identify and have the resources to act upon educational deficiencies to a greater extent than families with low levels of maternal education (e.g. the provision of private tuition). Again, these results provide more support for early interventions to prevent children becoming left behind in education and also more support for children who are identified as “educationally poor” but who do not have the private resources to address this. Previous work for Ireland and elsewhere has stressed that the socioeconomic gradient for education (across the whole of the distribution and not just below the educational “poverty line”) can set in as early as three years of age (Dearden et al., 2011; Madden, 2020b). The results here certainly suggest that in terms of educational poverty, children with higher maternal education are better equipped to escape from such poverty. Note also that it is possible that children who are in educational poverty but come from a background of higher maternal education may be nearer the poverty threshold. Thus a given absolute improvement in education is more likely to bring them over the threshold compared to children with lower maternal education.⁶

The greatest change in unidimensional poverty over the three waves is with respect to resource poverty, specifically the difficulties families have in making ends meet, going from when children were aged 9 to when children were aged 13. Of course, this captures the start of the Great Recession and regardless of maternal education, there was on average a threefold increase in poverty rates for this measure. This measure of poverty however showed a decline then between waves 2 and 3 when the children aged from 13 to 17. Changes in the overall gradient with respect to maternal education are more complex here. The highest and lowest levels of maternal education showed smaller increases between waves 1 and 2 and bigger decreases between waves 2 and 3 than was the case for the intermediate levels of maternal education. It is possible that the interaction between subjective assessments of poverty and the protection provided by social security for the most disadvantaged lies behind this complexity but this is more in the line of speculation rather than explanation.⁷

At one level, the stability of educational and health poverty even in the face of the onset of the Great Recession is reassuring. Despite families moving into resource poverty, there was not a corresponding increase in educational poverty (nor in health poverty between waves 1 and 2). The corollary of this is that when families moved back out of resource poverty in wave 3, again we did not see any reduction in educational poverty. We might conclude that educational poverty is deep rooted and seems relatively unaffected by the business cycle. Note that this does not necessarily imply that specific policy initiatives would not have an impact upon educational or health poverty, merely that over the period for which we observe these children, despite considerable changes in resource poverty, overall educational (and to a lesser extent health) poverty are relatively stable.⁸

Turning now to poverty in a multidimensional setting we first of all note that correlations across the different dimensions of poverty show signs of a slight decrease and this arises owing to some decoupling of resource poverty from health and education poverty. Correlations between resource poverty and the other two dimensions both fall and the biggest decrease is for the education-resources correlation which goes from 0.245 to 0.169. This may arise from a combination of educational poverty becoming relatively more concentrated amongst those with lowest maternal education while resource poverty becomes (relatively) more concentrated amongst those with intermediate maternal education.

Turning now to the multidimensional poverty indices, regardless of the choice for the second AF cut-off, the AF index for the sample as a whole increases between waves 1 and 2 and then falls back slightly in wave 3. These changes are very much driven by changes in resource poverty. It is also interesting to note that changes in the index arise mainly from changes in the headcount ratios of those who are multidimensionally poor, rather than from an increase in the intensity of multidimensional poverty (which is not entirely unexpected when we have “only” three dimensions of poverty).

Analysis of the AF indices by maternal education reveal complex patterns depending upon where we set the second cut-off. If we take the ratio of the indices for lowest and highest level of maternal education as a rough proxy for the social gradient then Table 4 shows that when the cut-off is one i.e. being poor in any dimension of poverty qualifies you as multidimensionally poor, this ratio stays pretty much unchanged between waves 1 and 3, with a value of around 3. However, with a second cut-off of two, the ratio increases from around 7 in wave 1 to around 16 in wave 3. This dramatic change in the gradient partially reflects the reassuring fact that absolute numbers are small and so small changes can lead to exaggerated changes in the ratio. However, examining the part of the AF index accounted for by the headcount ratio, we see that the reduction in education poverty for the highest level of maternal education means that even though overall multidimensional poverty levels increase between waves 1 and 3, the number of children from the highest level of maternal education who experience poverty in more than one dimensions falls. Consistent with the results from unidimensional poverty, while overall rates of educational poverty are quite stable, children with the highest level of maternal education are more mobile out of educational poverty, and thus are less likely to suffer from multiple deprivation in waves 2 and 3.

Turning now to the results for mobility, we see that mobility changes little when comparing wave 1-wave 2 transitions with wave 2-wave 3 transitions. What is different is the direction of transition, with the majority of movements into poverty (by this we mean entering into poverty in a specific dimension) between waves 1 and 2 (very much associated with the increase in resource poverty following the Great Recession), whereas between waves 2 and 3 movements into and out of poverty effectively cancel each other out. Mobility is inversely related to the level of maternal education, with highest mobility observed for children with the lowest level of maternal education. This is true at all ages but it is reassuring to see that there is mobility out of resource poverty, even for the lowest level of maternal education.

The different mobility patterns by dimension are noteworthy. Family resource poverty shows the highest level of mobility suggesting that escape from this type of poverty is possible. The much lower levels of mobility for health and education indicate that while movement into these types of poverty is more rare than for resources, escape is also much more difficult (one exception to this seems to be escape from education poverty for the highest level of maternal education). These poverties (health and education) seem to be more deep-rooted and structural suggesting that care needs to be taken in formulating policies in this area. As mentioned in the discussion on unidimensional poverty, prevention may be a better policy than cure.

With the exception of the aforementioned higher rates of escape from education poverty by those with the highest level of maternal education, the pattern of dimension specific mobility by maternal education does not seem that varied (following adjustment for the overall level of poverty). What this suggests is that the pattern of poverty mobility (in terms of movements into and out of specific dimensions) does not differ too much by maternal education, conditional on the overall level of poverty. It is more the case that there is simply more net mobility into poverty for lower levels of maternal education, rather than that the pattern is different. A tentative policy conclusion which could be drawn from this is that broad based policies could be effective rather than interventions tailored to specific parts of the socioeconomic gradient.

An analysis of multidimensional poverty over a number of time periods and with much of the analysis stratified by maternal education runs the risk of delivering a mixed and maybe incoherent set of policy conclusions. Here we try to distil our results into some simple messages. First of all, child poverty in health and education is relatively stable and arguably deep rooted, certainly by the stage at which we observe children in this dataset. Mobility is relatively limited with some sign of mobility out of educational poverty for children with higher maternal education. This suggests that policies here need to start early with prevention better than cure.

Family resource poverty shows much more mobility although it is possible that this is period specific with the onset of the Great Recession seeing many families move into poverty. Movement out of poverty between wave 2 and 3 was also significant, thankfully suggesting that higher mobility in this dimension can work in both directions.

Multidimensional poverty is thankfully comparatively rare and only a very small fraction of children experience persistent poverty across all three dimensions. Mobility is overall greater for children with lower maternal education. However, for a given level of overall poverty, the pattern of mobility by dimension does not appear to differ too much across the socioeconomic gradient. A general policy recommendation which could be drawn from this is that policies to increase mobility out of poverty, while they may be targeted at specific dimensions, perhaps need not be targeted by socioeconomic group.

Appendices

Appendix 1: Sample Design and Construction of Sampling Weights

The choice of sampling frame for the Child cohort of GUI was the National School System. A comprehensive list of all primary schools in the country was obtained from the Department of Education and Science. This list provided information on enrolment by age and gender and in addition details on the characteristics of the school such as region, disadvantaged status, size, school type, denominational status and gender mix. This information was used for pre-stratification prior to sample selection.

The sampling for the Child cohort was two-stage with the school being the primary sampling unit (PSU) and the child the secondary unit. As explained in Murray et al. (2011) the primary schools had many of the features suited to being PSUs. A comparison of the number of children in the school system (as reported by the Department of Education and Science) and the number of children for the relevant age group as reported in the nearest census shows that the discrepancy is very small (e.g. some children are home-schooled).

Since non-response in a survey such as GUI is rarely random, the eventual sample obtained had to be re-weighted in order to ensure that it aligned with the population from which it is sampled. These weights were constructed by comparing the distribution of various dimensions in the sample with the distribution derived from tables provided by the Central Statistics Office (CSO) and drawn from the census of population. Given the two-stage sampling procedure (at school and then child level) two weights had to be constructed and this was carried out via the procedure described in Gomulka (1994). The school based weight was constructed on the basis of the number of nine-year olds in the school, the type and region of the school, whether the school was designated with disadvantaged status, the religious denomination of the school and finally its co-educational status. The second stage weight was then constructed on the basis of the study child’s sex, family structure, maternal age, maternal PES, paternal PES, maternal education, maternal and paternal social class, household social class and tenure and maternal ethnicity. The second stage weights were also based upon some school dimensions used in the construction of the first stage weights viz. the number of nine year olds in school, the type and region of the school and whether it had disadvantaged status.

Between wave to wave attrition is not random and so re-weighting of the data each wave is necessary. The original sample in wave 1 consisted of 8568 children. Allowing for attrition due to migration etc. the relevant target for wave 2 was 8465 children of whom 7525 responded, giving a response rate of around 89%. Attrition was associated with primary caregiver education, family structure, household social class and income. Re-weighting was then carried out on the basis of child’s sex, family structure, maternal age, maternal PES, paternal PES, maternal and paternal social class, household social class and tenure and maternal ethnicity. Following analysis of non-response patterns in wave 2 the following dimensions were also used as a basis for constructing the attrition weight: maternal smoking and alcohol consumption, size of location of household, whether primary caregiver had experienced depression, family income and finally, willingness to complete the “sensitive” questionnaire (seen as an indication of commitment to the survey).

In wave 3 of the study the response rate was 81% of those who took part in wave 2 and in total just over 70% of the original 8568 children participated in all three waves. It is also important to remember that a much higher fraction of the responses in wave 3 of the survey were provided by the study child themselves, as opposed to the primary caregiver. Attrition nevertheless was associated with the same dimensions as in wave 2. In addition, higher rates of attrition were observed amongst study children who performed poorly in the wave 2 reasoning test and this may reflect engagement with the survey. The wave 2-wave 3 re-weighting was then based upon maternal education, family structure, family income, family social class, gender of study child and performance of study child in reasoning test in wave 2.

Appendix 2 Measure and Construction of Educational Outcomes

1.1 Wave 1

In wave 1 of the child cohort the vast majority of the children were aged 9 and part of the survey consisted of tests in mathematics and reading which were administered by the GUI fieldworkers at school. These tests are known in Ireland as the Drumcondra tests and have been a feature of the Irish educational system for a number of years and are linked to the national curriculum. These are administered on an annual basis to all children in the primary school system. However, the particular tests for the GUI survey had not been seen by schools, teachers or pupils in advance of their use in GUI, thus it seems unlikely that students would have been intensively prepared for these tests, although they would have had some familiarity with tests of this kind from previous years.⁹ It should be noted that the Drumcondra tests have no implications for further progression in the school system. The particular cohort of nine year olds in the GUI survey were spread over three different school grades (2nd, 3rd and 4th class) and three different levels of the test were administered, with the majority of the children in 3rd class (roughly equivalent to grade 3 in the US).

The test scores used for this wave are the results from these tests in maths and reading. As the tests were administered at three different levels it was necessary to standardise the results, hence the data we use are the logit scores which were obtained from the original raw data using the principles of Item Response Theory (see Lord, 1980). Results from tests at this age (and earlier) have been shown to have predictive power for subsequent later-life outcomes in areas such as education and health (Feinstein, 2003). It is important to note that the tests administered in wave 1 are achievement tests, based on the existing Irish primary school curriculum and essentially measures the amount the child would have learned at school up to then.

1.2 Wave 2

In wave 2 the children were now mostly aged 13 and the vast majority had entered the secondary school system. The secondary school system (which lasts from the ages of about 12–13 to 18) is more diverse in terms of curriculum and students have choice regarding what subjects they take (though practically every student will take Mathematics and English). The tests administered in wave 2 of GUI were shortened versions of the Drumcondra Reasoning Test focussing on items related to numerical ability and verbal reasoning. Thus critically they are measures of cognitive ability or aptitude rather than performance in school or academic achievement and the content of the test was not related to the school curriculum. As with wave 1, the scores which formed the basis of the composite measure are the logit scores from the test again obtained via Item Response Theory.

It must be stressed that ability/aptitude and achievement tests differ (see Jacob & Rothstein, 2016 and Williams et al., 2018). Aptitude tests refer to scholastic ability not related to the school curriculum. Since they do reflect the acquisition of certain skills it is highly likely that they will be influenced by the environment (school and home) where these skills are acquired but they are not specifically linked to the school curriculum. Achievement tests however measure performance and will be strongly influenced by school and home factors. The two measures are generally agreed to be quite strongly correlated (see Deary et al., 2007) and Hannan et al. (1996) finds that verbal and numerical performance in the Differential Aptitude Test was highly predictive of subsequent achievement in the Junior Certificate. The Drumcondra Reasoning Tests were also chosen on the basis that they would provide some comparability across the waves of GUI (Thornton et al., 2016). However it is important to bear in mind the warning of Williams et al. (2018): “Although the 13 year old’s results on the Drumcondra Reasoning Tests may be correlated with their academic achievement or school performance, it is important to emphasise the conceptual difference between the cognitive measure of ability captured by the DRT and a measure of school achievement or performance.”

1.3 Wave 3

Wave 3 of GUI Child Cohort has outcomes from three cognitive tests. These are the Cognitive Naming Tasks, Cognitive Maths Score and Cognitive Vocabulary Test.

The Naming Task, also known as the Semantic Fluency Test involved the participant naming as many animals as they could think of in one minute and draws on general knowledge in long term memory. The Maths test involved three short questions aimed at testing the participant’s ability to perform simple mathematical calculations and they also test financial literacy. The Vocabulary test consists of 20 words sharply increasing in difficulty. Each word is accompanied by five other words and the participant has to choose the word closest in meaning to the target word. Further details of the tests are available in Williams et al. (2019).

Table 10 Tests administered in each wave

Table 11 Rank Correlations Across Different Subscales/Components

Table 12 Rank Correlation of Composite Measure Across Waves

Table 13 Rank Correlations between components of Education Measure

Table 14 Fraction of Variance of Composite Measure Explained by 1st Principal Component

1.4 Scree Plots for PCA

Fig. 7

Scree plot of eigenvalues after PCA - Child Cohort, Wave 1

Fig. 8

Scree plot of eigenvalues after PCA - Child Cohort, Wave 2

Fig. 9

Scree plot of eigenvalues after PCA, Child Cohort Wave 3

Appendix 3: Transition Matrices by Maternal Education Wave 1 to Wave 2

Fig. 10

Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 1 Percent

Fig. 11

Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 2 Percent

Fig. 12

Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 3 Percent

Fig. 13

Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 4 Percent

1.1 Transition Matrices by Maternal Education Wave 2 to Wave 3

Fig. 14

Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 1 Percent

Fig. 15

Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 2 Percent

Fig. 16

Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 3 Percent

Fig. 17

Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 4 Percent

Appendix 4: Deprivation Specific Transition Matrices by Maternal Education, Wave 1 to Wave 2

Fig. 18

Deprivation Specific Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 1 Percent

Fig. 19

Deprivation Specific Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 2 Percent

Fig. 20

Deprivation Specific Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 3 Percent

Fig. 21

Deprivation Specific Transition Matrix, Wave 1 to Wave 2, Maternal Education Level 4 Percent

1.1 Deprivation Specific Transition Matrices by Maternal Education, Wave 2 to Wave 3

Fig. 22

Deprivation Specific Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 1 Percent

Fig. 23

Deprivation Specific Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 2 Percent

Fig. 24

Deprivation Specific Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 3 Percent

Fig. 25

Deprivation Specific Transition Matrix, Wave 2 to Wave 3, Maternal Education Level 4 Percent